Невизначеним інтегралом від функції f x називається. Математика

Первісна функція та невизначений інтеграл

Факт 1. Інтегрування - дія, зворотне диференціювання, а саме, відновлення функції за відомою похідною цієї функції. Відновлена таким чином функція F(x) називається первісноїдля функції f(x).

Визначення 1. Функція F(x f(x) на деякому проміжку Xякщо для всіх значень xз цього проміжку виконується рівність F "(x)=f(x), тобто дана функція f(x) є похідною від первісної функції F(x). .

Наприклад, функція F(x) = sin x є первісною для функції f(x) = cos x на всій числовій прямій, тому що при будь-якому значенні ікса (sin x)" = (cos x) .

Визначення 2. Невизначеним інтегралом функції f(x) називається сукупність всіх її первісних. При цьому використовується запис

∫

f(x)dx

де знак ∫ називається знаком інтеграла, функція f(x) – підінтегральною функцією, а f(x)dx - Підінтегральний вираз.

Таким чином, якщо F(x) – якась первісна для f(x) , то

∫

f(x)dx = F(x) +C

де C - Довільна постійна (константа).

Для розуміння сенсу безлічі первісних функцій як невизначеного інтеграла доречна наступна аналогія. Нехай є двері (традиційні дерев'яні двері). Її функція – "бути дверима". А з чого зроблено двері? З дерева. Значить, безліччю первісних підінтегральних функцій "бути дверима", тобто її невизначеним інтегралом, є функція "бути деревом + С", де С - константа, яка в даному контексті може позначати, наприклад, породу дерева. Подібно до того, як двері зроблені з дерева за допомогою деяких інструментів, похідна функції "зроблена" з первісної функції за допомогою формули, яку ми дізналися, вивчаючи похідну .

Тоді таблиця функцій поширених предметів та відповідних їм первісних ("бути дверима" - "бути деревом", "бути ложкою" - "бути металом" та ін.) аналогічна до таблиці основних невизначених інтегралів, яка буде наведена трохи нижче. У таблиці невизначених інтегралів перераховуються поширені функції із зазначенням первісних, у тому числі " зроблені " ці функції. У частині завдань перебування невизначеного інтеграла дані такі подинтегральные функції, які без особливих умов може бути проінтегровані безпосередньо, тобто за таблицею невизначених інтегралів. У завданнях складніше підінтегральну функцію потрібно попередньо перетворити те щоб можна було використовувати табличні інтеграли.

Факт 2. Відновлюючи функцію як первісну, ми маємо враховувати довільну постійну (константу) C, а щоб не писати список первісної з різними константами від 1 до нескінченності, потрібно записувати безліч первісних з довільною константою Cнаприклад, так: 5 x³+С . Отже, довільна стала (константа) входить у вираз первісної, оскільки первісна може бути функцією, наприклад, 5 x³+4 або 5 x³+3 і при диференціюванні 4 або 3, або будь-яка інша константа перетворюються на нуль.

Поставимо завдання інтегрування: для цієї функції f(x) знайти таку функцію F(x), похідна якоїдорівнює f(x).

приклад 1.Знайти безліч первісних функцій

Рішення. Для цієї функції першорядною є функція

Функція F(x) називається первісною для функції f(x), якщо похідна F(x) дорівнює f(x), або, що те саме, диференціал F(x) дорівнює f(x) dx, тобто.

(2)

Отже, функція - первісна для функції . Однак вона не є єдиною первісною для . Ними служать також функції

де З- Довільна постійна. У цьому вся можна переконатися диференціюванням.

Таким чином, якщо для функції існує одна первісна, то для неї існує нескінченна безлічпервісних, що відрізняються на постійне доданок. Усі первісні функції записуються в наведеному вище вигляді. Це випливає із наступної теореми.

Теорема (формальний виклад факту 2).Якщо F(x) – первісна для функції f(x) на деякому проміжку Х, то будь-яка інша первісна для f(x) на тому ж проміжку може бути представлена у вигляді F(x) + C, де З- Довільна постійна.

У наступному прикладі вже звертаємося до таблиці інтегралів, яка буде дана в параграфі 3, після властивостей невизначеного інтегралу. Робимо це до ознайомлення з усією таблицею, щоб було зрозуміло суть вищевикладеного. А після таблиці та властивостей будемо користуватися ними при інтегруванні у всій повноті.

приклад 2.Знайти безліч первісних функцій:

Рішення. Знаходимо безліч первісних функцій, у тому числі " зроблені " дані функції. При згадці формул з таблиці інтегралів поки що просто прийміть, що є такі формули, а повністю саму таблицю невизначених інтегралів ми вивчимо трохи далі.

1) Застосовуючи формулу (7) з таблиці інтегралів при n= 3, отримаємо

2) Використовуючи формулу (10) з таблиці інтегралів при n= 1/3, маємо

3) Оскільки

то за формулою (7) при n= -1/4 знайдемо

Під знаком інтеграла пишуть не саму функцію f, а її твір на диференціал dx. Це робиться насамперед для того, щоб вказати, за якою змінною шукається первісна. Наприклад,

, ;

тут обох випадках подинтегральная функція дорівнює , та її невизначені інтеграли у розглянутих випадках виявляються різними. У першому випадку ця функція сприймається як функція від змінної x, а у другому - як функція від z .

Процес знаходження невизначеного інтеграла функції називається інтегрування цієї функції.

Геометричний зміст невизначеного інтегралу

Нехай потрібно знайти криву y=F(x)і ми вже знаємо, що тангенс кута нахилу дотичної в кожній її точці є задана функція f(x)абсциси цієї точки.

Згідно геометричному зміступохідної, тангенс кута нахилу дотичної в даній точці кривої y=F(x)дорівнює значенню похідної F"(x). Отже, потрібно знайти таку функцію F(x)для якої F"(x)=f(x). Необхідна в завданні функція F(x)є первісною від f(x). Умову задачі задовольняє не одна крива, а сімейство кривих. y=F(x)- одна з таких кривих, а будь-яка інша крива може бути отримана з неї паралельним перенесеннямвздовж осі Ой.

Назвемо графік первісної функції від f(x)інтегральної кривої. Якщо F"(x)=f(x), то графік функції y=F(x)є інтегральна крива.

Факт 3. Невизначений інтеграл геометрично представлений насінням усіх інтегральних кривих як на малюнку нижче. Відстань кожної кривої від початку координат визначається довільною постійною (константою) інтегрування C.

Властивості невизначеного інтегралу

Факт 4. Теорема 1. Похідна невизначеного інтеграла дорівнює підінтегральної функції, яке диференціал – підинтегральному вираженню.

Факт 5. Теорема 2. Невизначений інтеграл від диференціалу функції f(x) дорівнює функції f(x) з точністю до постійного доданку , тобто.

(3)

Теореми 1 і 2 показують, що диференціювання та інтегрування є взаємно-зворотними операціями.

Факт 6. Теорема 3. Постійний множнику підінтегральному вираженні можна виносити за знак невизначеного інтегралу , тобто.

1. Первісна. Невизначений інтеграл. Властивості невизначеного інтегралу. Таблиця інтегралів. Заміна змінної. Інтегрування частинами.

Визначення.Функція F(x) називається первісноївід функції f(x) на відрізку, якщо у всіх точках цього відрізка виконується рівність F`(x) = f(x).

(-cos x )` = sin x

(1 -cos x)` = sin x

Функція f(x) безперервна функціяна відрізку.

Теорема . Якщо функція F 1 (x) b F2 (x) -дві первісні від функції f(x) на відрізку , то різниця з-поміж них дорівнює постійному числу.

Доказ.

F 1 `(x)= f(x) (1)

F 2 `(x)= f(x) , то F 1 `(x)- F 2 `(x)= Const.

φ(x) = F 1 - F 2

φ `(x) = F 1 ` - F 2 ` = 0

Тобто. позначимо:

F 1 (x) - F 2 (x) = φ(x) (2)

Тоді на підставі рівностей (1) буде:

F 1 `(x)- F 2 ` (x) = f(x) - f(x) = 0 або φ` (x) = `= 0 при будь-якому значенні x на відрізку. Але з рівності φ`(x) = 0 випливає, що φ(x) є постійна.

Справді, застосуємо теорему Лагранжа до функції φ(x ), яка, очевидно, безперервна та диференційована на відрізку . Якою була точка x на відрізку , ми маємо силу теореми Лагранжа.

φ(x) - φ(a) = φ`(x) (x-a) , де a< x< x.

Так як φ `(x) = 0, то φ(x) - φ(a) = 0 або φ(x) = φ(a) (3)

Таким чином, функція φ(x) у будь-якій точці x відрізка зберігає значення φ(a), а це означає, що функція φ(x) є постійною на відрізку . Позначаючи постійну φ(a ) через З, з рівностей (2), (3) одержуємо:

F 1 (x) - F 2 (x) = С

Визначення.Якщо функція F(x) є первісною для f(x), то вираз F(x) + С називається невизначеним інтеграломвід функції f(x) і позначається символом f(x) dx. Таким чином, за визначенням,

∫ f(x) dx = F(x) + С, якщо F(x) = f(x) .

При цьому функцію f(x) називають підінтегральною функцією, f(x) dx - підінтегральним виразом, знак ∫ - знаком інтегралу.

З цього визначення випливають властивості:
1. Похідна від невизначеного інтеграла дорівнює підінтегральної функції, тобто. якщо F`(x) = f(x), то й

(∫f(x) dx)` = (F(x) + C)` = f(x) (4)

Остання рівність потрібно приймати в тому сенсі, що похідна від будь-якої первісної дорівнює підінтегральної функції.

2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу

d (∫ f (x) dx) = f (x) dx (5)

Це виходить на підставі формули (4)

3. Невизначений інтеграл від диференціалу деякої функції дорівнює цій функції плюс довільна постійна

∫ dF(x) = F(x) + C

Справедливість останньої рівності легко перевірити диференціюванням (диференціала від обох частин рівності дорівнюють dFx) )

Таблиця невизначених інтегралів.

10.

11.

12.

13.

14.

Лінійні властивості.

Інтегрування – є лінійна операція.

1. ∫ dx =∫ f 1 (x) dx +∫ f 2 (x) dx

∫ a f(x) dx = a ∫ f(x) dx

∫ f(x) dx = F(x) + C

2. ∫ f (x+c) dx = F (x+c) + C

3. Підстановка. Перший метод обчислення невизначених інтегралів.

x = φ (t), тоді ∫ f (φ (t)) φ` (t) dt = F (x) + C = ∫ f (x) dx

x = φ(t) dx dt = φ`

Інтегрування частинами.

Нехай uі v- Дві диференційовані функції від x. Тоді, як відомо, диференціал твору uvобчислюється за наступною формулою:

d(uv) = udv + vdu

Звідси, інтегруючи, отримуємо:

uv =∫udv +∫vdu

або∫udv = uv -∫vdu

Остання формула називається формулою інтегрування частинами.Ця формула найчастіше застосовується до інтегрування виразів, які можна представити як твори двох співмножників u і dv , щоб відшукання функції v з її диференціалу dv і обчислення інтеграла∫ v du становили в сукупності завдання простіше, ніж безпосереднє обчислення інтеграла∫ u dv.

приклад. ∫x sin x dx =∫ - x cos x + ∫cos x dx = -x cos x + sin x + C

Т.к. u = v, dv= sin x dx і du = dx, v= - cos x.

Знайти невизначений інтеграл (безліч первісних або "антипохідних") означає відновити функцію за відомою похідною цієї функції. Відновлена безліч первісних F(x) + З для функції f(x) враховує константу інтегрування C. За швидкістю переміщення матеріальної точки(похідною) може бути відновлено закон руху цієї точки (первоподібна); щодо прискорення руху точки - її швидкість та закон руху. Як бачимо, інтегрування - широке полі діяльності Шерлоков Холмсов від фізики. Та й в економіці багато понять надаються через функції та їх похідні і тому, наприклад, можна за продуктивністю праці у певний момент часу (похідної) відновити обсяг продукції, випущений у відповідний час.

Щоб знайти невизначений інтеграл, потрібна досить невелика кількість основних формул інтегрування. Але процес його знаходження значно важче, ніж лише застосування цих формул. Вся складність відноситься не до інтегрування, а до приведення інтегрованого виразу до такого виду, що дає можливість знайти невизначений інтеграл за вищезазначеними основними формулами. Це означає, що для початку практики інтегрування потрібно активізувати отримані в середній школінавички перетворення виразів.

Вчитися знаходити інтеграли будемо, користуючись властивостями та таблицею невизначених інтегралівз уроку про основні поняття цієї теми (відкриється у новому вікні).

Існує кілька методів знаходження інтеграла, з яких метод заміни змінноїі метод інтегрування частинами- обов'язковий джентльменський набір кожного, хто успішно здав найвищу математику. Однак починати освоювати інтегрування корисніше і приємніше із застосуванням методу розкладання, заснованому на двох теоремах про властивості невизначеного інтеграла, які для зручності повторимо тут.

Теорема 3.Постійний множник у подинтегральном вираженні можна виносити за знак невизначеного інтеграла, тобто.

Теорема 4.Невизначений інтеграл суми алгебри кінцевого числафункцій дорівнює алгебраїчній суміневизначених інтегралів цих функцій, тобто.

(2)

Крім того, в інтегруванні може стати в нагоді наступне правило: якщо вираз підінтегральної функції містить постійний множник, то вираз первісної домножується на число, зворотне постійному множнику, тобто

(3)

Оскільки цей урок - вступний у вирішення завдань інтегрування, важливо відзначити дві речі, які або вже насправді початковому етапіабо трохи пізніше можуть вас здивувати. Здивування пов'язане з тим фактом, що інтегрування - операція, зворотна диференціюванню і невизначений інтеграл можна справедливо називати "антипохідною".

Перша річ, якою не слід дивуватися при інтегруванні.У таблиці інтегралів існують формули, які не мають аналогів серед формул похідної таблиці . Це такі формули:

Однак можна переконатися в тому, що похідні виразів, що стоять у правих частинах цих формул, збігаються з відповідними підінтегральними функціями.

Друга річ, якій не слід дивуватися при інтегруванні. Хоча похідна будь-якої елементарної функції є також елементарною функцією, невизначені інтеграли від деяких елементарних функцій не є елементарними функціями . Прикладами таких інтегралів можуть бути такі:

Для вироблення техніки інтегрування стануть у нагоді такі навички: скорочення дробів, розподіл багаточлена в чисельнику дробу на одночлен у знаменнику (для отримання суми невизначених інтегралів), перетворення коренів у ступені, множення одночлена на багаточлен, зведення в ступінь. Ці навички потрібні для перетворень підінтегрального виразу, у яких має вийти сума інтегралів, присутніх у таблиці інтегралів.

Знаходимо невизначені інтеграли разом

приклад 1.Знайти невизначений інтеграл

Рішення. Бачимо у знаменнику підінтегрального виразу багаточлен, у якому ікс у квадраті. Це майже вірна ознака того, що можна застосувати табличний інтеграл 21 (з арктангенсом у результаті). Виносимо із знаменника множник-двійку (є така властивість інтеграла - постійний множник можна виносити за знак інтеграла, вище воно було згадано як теорема 3). Результат всього цього:

Тепер у знаменнику є сума квадратів, а це означає, що можемо застосувати згаданий табличний інтеграл. Остаточно отримуємо відповідь:

приклад 2.Знайти невизначений інтеграл

Рішення. Знову застосовуємо теорему 3 - властивість інтеграла, на підставі якого постійний множник можна виносити за знак інтеграла:

Застосовуємо формулу 7 з таблиці інтегралів (змінна до ступеня) до підінтегральної функції:

Скорочуємо дроби і перед нами кінцева відповідь:

приклад 3.Знайти невизначений інтеграл

Рішення. Застосовуючи спочатку теорему 4, а потім теорему 3 про властивості знайдемо даний інтеграл як суму трьох інтегралів:

Усі три отримані інтеграли – табличні. Використовуємо формулу (7) з таблиці інтегралів при n = 1/2, n= 2 і n= 1/5, і тоді

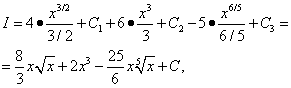
об'єднує всі три довільні постійні, які були введені при знаходженні трьохінтегралів. Тому в аналогічних ситуаціях слід запроваджувати лише одну довільну постійну (константу) інтегрування.

приклад 4.Знайти невизначений інтеграл

Рішення. Коли знаменнику подинтегральной дробу - одночлен, можемо почленно розділити чисельник на знаменник. Вихідний інтеграл перетворився на суму двох інтегралів:

Щоб застосувати табличний інтеграл, перетворимо коріння в міру і ось вже остаточна відповідь:

Продовжуємо знаходити невизначені інтеграли разом

Приклад 7.Знайти невизначений інтеграл

Рішення. Якщо ми перетворимо підінтегральну функцію, звівши двочлен у квадрат і розділивши почленно чисельник на знаменник, то вихідний інтеграл стане сумою трьох інтегралів.

А чи можна під знак диференціала підбивати нелінійну функцію? Так, якщо підінтегральний вираз є твір двох множників: один множник — складна функція від якоїсь нелінійної функції, а інший множник є похідною від цієї нелінійної функції. Розглянемо сказане на прикладах.

Знайти невизначені інтеграли.

Приклад 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6+C.

Що являє собою цей підінтегральний вираз? Твір статечної функціївід (х 2 + х + 2) та множника (2х + 1), який дорівнює похідній від основи ступеня: (х 2 + х + 2)" = 2х + 1.

Це дозволило нам підвести (2х + 1) під знак диференціала:

∫u 5 du=u 6 : 6+ C. (Формула 1). )

Перевірка. (F(x)+C)" =((x²+x+2) 6 : 6 + C) = 1/6 · 6 (x 2 + x + 2) 5 · (x 2 + x + 2)" =

= (x 2 + x + 2) 5 · (2x + 1) = (2x + 1) (x 2 + x + 2) 5 = f (x).

приклад 2.∫(3x 2 – 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6 + C

І чим цей приклад відрізняється від прикладу 1? Та нічим! Той самий п'ятий ступінь з основою (х 3 – х 2 + 3х + 1) множиться на тричлен (3х 2 – 2х + 3), який є похідною основи ступеня: (х 3 – х 2 + 3х + 1)" = 3х 2 - 2х + 3. Це підставу ступеня ми і підвели під знак диференціала, від чого значення підінтегрального виразу не змінилося, а потім застосували ту ж саму формулу 1). Інтеграли)

приклад 3.

Тут похідна від (2х3 – 3х) дасть (6х2 – 3), а у нас

є (12х 2 – 6), тобто вираз у 2 рази більше, значить, підіб'ємо (2х 3 – 3х) під знак диференціала, а перед інтегралом поставимо множник 2 . Застосуємо формулу 2) (лист ).

Ось що вийде:

Зробимо перевірку, враховуючи, що:

приклади. Знайти невизначені інтеграли.

1. ∫(6х+5) 3 dx. Як вирішуватимемо? Дивимося в лист і міркуємо приблизно так: підінтегральна функція є ступенем, а у нас є формула для інтеграла ступеня (формула 1) ), але в ній підстава ступеня uі змінна інтеграціятеж u.

А у нас змінна інтеграція х, а основа ступеня (6х+5). Зробимо заміну змінної інтегрування: замість dx запишемо d(6х+5). Що змінилося? Оскільки те, що стоїть після знака диференціала d, за замовчуванням, диференціюється,

то d(6x+5)=6dx, тобто. при заміні змінної х на змінну (6х+5) підінтегральна функція зросла у 6 разів, тому перед знаком інтеграла ставимо множник 1/6. Записати ці міркування можна так:

Отже, ми вирішили цей приклад запровадженням нової змінної (змінну х замінили на змінну 6х+5). А куди записали нову змінну (6х+5)? Під знак диференціалу. Тому, даний методвведення нової змінної часто називають методом (або способом ) підведення(новою змінною ) під знак диференціала.

У другому прикладі ми спочатку отримали ступінь з негативним показником, а потім підвели під знак диференціала (7х-2) і використали формулу інтеграла ступеня 1) (Інтеграли ).

Розберемо рішення прикладу 3.

Перед інтегралом стоїть коефіцієнт 1/5. Чому? Так як d (5x-2)=5dx, то, підвівши під знак диференціала функцію u=5x-2, ми збільшили підінтегральний вираз у 5 разів, тому, щоб значення даного виразуне змінилося — треба було поділити на 5, тобто. помножити на 1/5. Далі була використана формула 2) (Інтеграли) .

Усі найпростіші формули інтегралів матимуть вигляд:

∫f(x) dx=F(x)+C, причому, повинна виконуватись рівність:

(F(x)+C)"=f(x).

Формули інтегрування можна отримати зверненням відповідних формул диференціювання.

Справді,

Показник ступеня nможе бути і дрібним. Часто доводиться знаходити невизначений інтеграл від функції у=х. Обчислимо інтеграл від функції f(x)=√x, використовуючи формулу 1) .

Запишемо цей приклад у вигляді формули 2) .

Оскільки (х+С)"=1, то ∫dx=x+C.

3) ∫dx=x+C.

Замінюючи 1/х ² на х -2, обчислимо інтеграл від 1/х ².

А можна було отримати цю відповідь зверненням відомої формулидиференціювання:

Запишемо наші міркування у вигляді формули 4).

Помноживши обидві частини набутої рівності на 2, отримаємо формулу 5).

Знайдемо інтеграли від основних тригонометричних функційзнаючи їх похідні: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Отримуємо формули інтегрування 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

Після вивчення показової та логарифмічні функції, додамо ще кілька формул.

Основні характеристики невизначеного інтеграла.

I.Похідна невизначеного інтеграла дорівнює підінтегральній функції .

(∫f(x) dx)"=f(x).

ІІ.Диференціал невизначеного інтеграла дорівнює підінтегральному виразу.

d∫f(x) dx=f(x) dx.

ІІІ. Невизначений інтегралвід диференціалу (похідної) деякої функції дорівнює суміцієї функції та довільної постійної З.

∫dF(x)=F(x)+Cабо ∫F"(x) dx=F(x)+C.

Зверніть увагу: у I, II та III властивостізнаки диференціала та інтеграла (інтеграла та диференціала) «з'їдають» один одного!

IV.Постійний множник підінтегрального виразу можна винести знак інтеграла.

∫kf (x) dx=k·∫f (x) dx,де k - постійна величинане дорівнює нулю.

V.Інтеграл від алгебраїчної суми функцій дорівнює сумі алгебри інтегралів від цих функцій.

∫(f(x)±g(x)) dx=∫f(x) dx±∫g(x) dx.

VI.Якщо F(x) є первісною для f(x), а kі b- Постійні величини, причому, k≠0, то (1/k)·F (kx+b) є первісною для f (kx+b). Справді, за правилом обчислення похідної складної функціїмаємо:

Можна записати:

Для кожного математичної діїІснує зворотна йому дія. Для дії диференціювання (знаходження похідних функцій) також існує зворотна дія- Інтегрування. За допомогою інтегрування знаходять (відновлюють) функцію за заданою похідною або диференціалу. Знайдену функцію називають первісної.

Визначення.Диференційована функція F(x)називається первісною для функції f(x)на заданому проміжку, якщо для всіх хз цього проміжку справедлива рівність: F′(x)=f(x).

приклади. Знайти первісні для функцій: 1) f(x) = 2x; 2) f(x) = 3cos3x.

1) Оскільки (х²)′=2х, то, за визначенням, функція F(x)=x² буде першорядною для функції f(x)=2x.

2) (sin3x)′=3cos3x. Якщо позначити f(x)=3cos3x і F(x)=sin3x, то, за визначенням первісної, маємо: F′(x)=f(x), і, отже, F(x)=sin3x є первісною для f( x) = 3cos3x.

Зауважимо, що і (sin3x +5 )′= 3cos3xі (sin3x -8,2 )′= 3cos3x, ... у загальному виглядіможна записати: (sin3x +С)′= 3cos3x, де З- Деяка постійна величина. Ці приклади говорять про неоднозначність дії інтегрування, на відміну від дії диференціювання, коли в будь-якій функції, що диференціюється, існує єдина похідна.

Визначення.Якщо функція F(x)є первісною для функції f(x)на деякому проміжку, то безліч всіх первісних цієї функції має вигляд:

F(x)+Cде С - будь-яке дійсне число.

Сукупність всіх первісних F (x) + C функції f (x) на проміжку, що розглядається, називається невизначеним інтегралом і позначається символом ∫ (Знак інтеграла). Записують: ∫f(x) dx=F(x)+C.

Вираз ∫f (x) dxчитають: «інтеграл еф від ікс до де ікс».

f(x) dx- Підінтегральний вираз,

f(x)- Підінтегральна функція,

х- Змінна інтегрування.

F(x)- Первісна для функції f(x),

З- Деяка постійна величина.

Тепер розглянуті приклади можна записати так:

1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Що означає знак d?

d -знак диференціала - має подвійне призначення: по-перше, цей знак відокремлює підінтегральну функцію від змінної інтегрування; по-друге, все, що стоїть після цього знака, диференціюється за умовчанням і множиться на підінтегральну функцію.

приклади. Знайти інтеграли: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) Після піктограми диференціалу dстоїть хх, а р

∫ 2хрdx=рх²+С. Порівняйте з прикладом 1).

Зробимо перевірку. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) Після піктограми диференціалу dстоїть р. Отже, змінна інтеграція р, а множник хслід вважати деякою постійною величиною.

∫ 2хрdр=р²х+С. Порівняйте з прикладами 1) і 3).

Зробимо перевірку. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

Сторінка 1 з 1 1

Інтегральне обчислення.

Первісна функція.

Визначення: Функція F(x) називається первісною функцієюфункції f (x) на відрізку , якщо в будь-якій точці цього відрізка правильна рівність:

Слід зазначити, що первісних однієї й тієї функції може бути нескінченно багато. Вони відрізнятимуться один від одного на деяке постійне число.

F 1 (x) = F 2 (x) + C.

Невизначений інтеграл.

Визначення: Невизначеним інтеграломфункції f(x) називається сукупність первісних функцій, які визначені співвідношенням:

Записують:

Умовою існування невизначеного інтеграла на певному відрізку є безперервність функції цьому відрізку.

Властивості:

Приклад:

Знаходження значення невизначеного інтеграла пов'язане головним чином із знаходженням первісної функції. Для деяких функцій це досить складне завдання. Нижче буде розглянуто способи знаходження невизначених інтегралів для основних класів функцій – раціональних, ірраціональних, тригонометричних, показових та ін.

Для зручності значення невизначених інтегралів більшості елементарних функцій зібрані спеціальні таблиці інтегралів, які бувають іноді дуже об'ємними. У них включені різні комбінації функцій, що найчастіше зустрічаються. Але більшість представлених у цих таблицях формул є наслідками один одного, тому наведемо таблицю основних інтегралів, за допомогою якої можна отримати значення невизначених інтегралів різних функцій.

Інтеграл	Значення	Інтеграл	Значення

	lnsinx+ C



	ln

Методи інтегрування.

Розглянемо три основні методи інтегрування.

Безпосереднє інтегрування.

Метод безпосереднього інтегрування заснований на припущенні про можливе значенняпервісної функції з подальшою перевіркою цього значення диференціюванням. Загалом, зауважимо, що диференціювання є потужним інструментом перевірки результатів інтегрування.

Розглянемо застосування цього на прикладі:

Потрібно знайти значення інтегралу . На основі відомої формули диференціювання
можна зробити висновок, що шуканий інтеграл дорівнює
, де С - деяке постійне число. Однак, з іншого боку
. Таким чином, остаточно можна зробити висновок:

Зауважимо, що на відміну диференціювання, де знаходження похідної використовувалися чіткі прийоми і методи, правила знаходження похідної, нарешті визначення похідної, для інтегрування такі методи недоступні. Якщо при знаходженні похідної ми користувалися, так би мовити, конструктивними методами, які, базуючись на певних правилах, призводили до результату, то при знаходженні первісної доводиться переважно спиратися на знання таблиць похідних та первісних.

Що стосується методу безпосереднього інтегрування, то він застосовний тільки для деяких обмежених класів функцій. Функцій, для яких можна відразу знайти первинну дуже мало. Тому здебільшого застосовуються способи, описані нижче.

Спосіб підстановки (заміни змінних).

Теорема: Якщо потрібно знайти інтеграл
, але складно відшукати первісну, то за допомогою заміниx=(t) іdx=(t)dtвиходить:

Доказ : Продиференціюємо пропоновану рівність:

За розглянутою вище якістю №2 невизначеного інтеграла:

f(x) dx = f[  (t)]  (t) dt

що з урахуванням введених позначень є вихідним припущенням. Теорему доведено.

приклад.Знайти невизначений інтеграл
.

Зробимо заміну t = sinx, dt = cosxdt.

приклад.

Заміна
Отримуємо:

Нижче буде розглянуто інші приклади застосування методу підстановки для різних типів функцій.

Інтегрування частинами.

Спосіб заснований на відомій формулі похідної праці:

(uv)=uv+vu

де uіv - деякі функції від х.

У диференціальній формі: d(uv) = udv + vdu

Проінтегрувавши, отримуємо:
, а відповідно до наведених вище властивостей невизначеного інтеграла:

або
;

Отримали формулу інтегрування частинами, яка дозволяє знаходити інтеграли багатьох елементарних функцій.

приклад.

Як видно, послідовне застосування формули інтегрування частинами дозволяє поступово спростити функцію і привести інтеграл до табличного.

приклад.

Видно, що в результаті повторного застосування інтегрування частинами функцію не вдалося спростити до табличного виду. Однак останній отриманий інтеграл нічим не відрізняється від вихідного. Тому перенесемо його до лівої частини рівності.

Таким чином, інтеграл знайдено взагалі без застосування таблиць інтегралів.

Перш ніж докладно розглянути методи інтегрування різних класів функцій, наведемо ще кілька прикладів знаходження невизначених інтегралів приведенням їх до табличних.

приклад.

Інтегрування елементарних дробів.

Визначення: Елементарниминазиваються дроби наступних чотирьох типів:

I.
ІІІ.

ІІ.
IV.

m,n- натуральні числа(m2,n2) іb 2 – 4ac<0.

Перші два типи інтегралів від елементарних дробів досить просто наводяться до табличних підстановок t=ax+b.

Розглянемо спосіб інтегрування елементарних дробів виду III.

Інтеграл дробу виду III може бути представлений у вигляді:

Тут у загальному вигляді показано приведення інтеграла дробу виду III до двох табличних інтегралів.

Розглянемо застосування зазначеної формули на прикладах.

приклад.

Взагалі кажучи, якщо у тричлена ax 2 +bx+cвираз b 2 – 4ac>0, то дріб за визначенням не є елементарним, проте, проте його можна інтегрувати вказаним вище способом.

приклад.

Розглянемо тепер методи інтегрування найпростіших дробів IV типу.

Спочатку розглянемо окремий випадок при М = 0, N = 1.

Тоді інтеграл виду
можна шляхом виділення у знаменнику повного квадрата подати у вигляді
. Зробимо таке перетворення:

Другий інтеграл, що входить до цієї рівності, будемо брати частинами.

Позначимо:

Для вихідного інтеграла отримуємо:

Отримана формула називається рекурентної.Якщо застосувати її n-1 раз, то вийде табличний інтеграл
.

Повернемося тепер до інтегралу від елементарного дробу виду IV у загальному випадку.

В отриманій рівності перший інтеграл за допомогою підстановки t = u 2 + sнаводиться до табличного а до другого інтегралу застосовується розглянута вище рекурентна формула.

Незважаючи на складність інтегрування елементарного дробу виду IV, що здається, на практиці його досить легко застосовувати для дробів з невеликим ступенем n, А універсальність і спільність підходу уможливлює дуже просту реалізацію цього на ЕОМ.

приклад:

Інтегрування оптимальних функцій.

Інтегрування раціональних дробів.

Для того щоб проінтегрувати раціональний дріб необхідно розкласти його на елементарні дроби.

Теорема: Якщо
- правильний раціональний дріб, знаменник P(x) якого представлений у вигляді твору лінійних і квадратичних множників (зазначимо, що будь-який многочлен з дійсними коефіцієнтами може бути представлений у такому вигляді: P(x) = (x - a)  …(x - b)  (x 2 + px + q)  …(x 2 + rx + s)  ), то цей дріб може бути розкладений на елементарні за наступною схемою:

де A i, Bi, Mi, Ni, Ri, Si – деякі постійні величини.

При інтегруванні раціональних дробів вдаються до розкладання вихідного дробу елементарні. Для знаходження величинA i ,B i ,M i ,N i ,R i ,S i застосовують так званий метод невизначених коефіцієнтів, Суть якого полягає в тому, що для того, щоб два многочлена були тотожно рівні, необхідно і достатньо, щоб були рівні коефіцієнти при однакових ступенях х.

Застосування цього розглянемо на конкретному прикладі.

приклад.

Приводячи до спільного знаменника та прирівнюючи відповідні чисельники, отримуємо:

приклад.

Т.к. дріб неправильний, то попередньо слід виділити в неї цілу частину:

6x 5 - 8x 4 - 25x 3 + 20x 2 - 76x - 7 3x 3 - 4x 2 - 17x + 6

6x 5 - 8x 4 - 34x 3 + 12x 2 2x 2 + 3

9x 3 + 8x 2 – 76x - 7

9x 3 – 12x 2 – 51x +18

20x 2 – 25x – 25

Розкладемо знаменник отриманого дробу на множники. Видно, що за х = 3 знаменник дробу перетворюється на нуль. Тоді:

3x 3 – 4x 2 – 17x+ 6x-3

3x 3 – 9x 2 3x 2 + 5x-2

Таким чином, 3x 3 – 4x 2 – 17x+ 6 = (x– 3)(3x 2 + 5x– 2) = (x– 3)(x+ 2)(3x– 1). Тоді:

Для того, щоб уникнути при знаходженні невизначених коефіцієнтів розкриття дужок, угруповання та вирішення системи рівнянь (яка в деяких випадках може виявитися досить великою) застосовують так званий метод довільних значень . Суть методу у тому, що у отримане вище вираз підставляються почергово кілька (за кількістю невизначених коефіцієнтів) довільних значень x. Для спрощення обчислень прийнято як довільні значення приймати точки, у яких знаменник дробу дорівнює нулю, тобто. у разі – 3, -2, 1/3. Отримуємо:

Остаточно отримуємо:

приклад.

Знайдемо невизначені коефіцієнти:

Тоді значення заданого інтегралу:

Інтегрування деяких тригонометричних

функцій.

Інтегралів від тригонометричних функцій може бути дуже багато. Більшість із цих інтегралів взагалі не можна вирахувати аналітично, тому розглянемо деякі найголовніші типифункцій, які можуть бути інтегровані завжди.

Інтеграл виду
.

Тут R - позначення деякої раціональної функції від змінних sinxіcosx.

Інтеграли цього виду обчислюються за допомогою підстановки
. Ця підстановка дозволяє перетворити тригонометричну функцію на раціональну.

Тоді

Таким чином:

Описане вище перетворення називається універсальною тригонометричною підстановкою.

приклад.

Безперечною перевагою цієї підстановки є те, що з її допомогою завжди можна перетворити тригонометричну функцію в раціональну та обчислити відповідний інтеграл. До недоліків можна віднести те, що при перетворенні може вийти досить складна раціональна функція, інтегрування якої займе багато часу та сил.

Однак при неможливості застосувати раціональнішу заміну змінної цей метод є єдино результативним.

приклад.

Інтеграл виду
якщо

функціяRcosx.

Незважаючи на можливість обчислення такого інтеграла за допомогою універсальної тригонометричної підстановки, раціональніше застосувати підстановку t = sinx.

Функція
може містити cosx тільки в парних ступенях, а, отже, може бути перетворена на раціональну функцію щодо sinx.

приклад.

Взагалі кажучи, для застосування цього методу необхідна лише непарність функції щодо косинуса, а ступінь синуса, що входить у функцію, може бути будь-якою, як цілою, так і дробовою.

Інтеграл виду
якщо

функціяRє непарною щодоsinx.

За аналогією з розглянутим вище випадком робиться підстановка t = cosx.

приклад.

Інтеграл виду

функціяRпарна щодоsinxіcosx.

Для перетворення функції Rв раціональну використовується підстановка

t = tgx.

приклад.

Інтеграл твору синусів та косинусів

різних аргументів.

Залежно від типу твору застосовується одна з трьох формул:

приклад.

Іноді при інтегруванні тригонометричних функцій зручно використовувати загальновідомі тригонометричні формули зниження порядку функцій.

приклад.

Іноді застосовують деякі нестандартні прийоми.

приклад.

Інтегрування деяких ірраціональних функций.

Далеко не кожна ірраціональна функціяможе мати інтеграл, виражений елементарними функціями. Для знаходження інтеграла від ірраціональної функції слід застосувати підстановку, яка дозволить перетворити функцію на раціональну, інтеграл від якої може бути знайдений як відомо завжди.

Розглянемо деякі прийоми для інтегрування різних типів ірраціональних функций.

Інтеграл виду
деn- Натуральне число.

За допомогою підстановки
функція раціоналізується.

приклад.

Якщо до складу ірраціональної функції входять коріння різних ступенів, то як нова змінна раціонально взяти корінь ступеня, що дорівнює найменшому загальному кратному ступенів коренів, що входять у вираз.

Проілюструємо це з прикладу.

приклад.

Інтегрування біномінальних диференціалів.

Визначення: Біномінальним диференціаломназивається вираз

x m (a + bx n ) p dx

де m, n, і p- Раціональні числа.

Як було підтверджено академіком Чебишевим П.Л. (1821-1894), інтеграл від біномінального диференціала може бути виражений через елементарні функції лише у наступних трьох випадках:

Якщо р- ціле число, то інтеграл раціоналізується за допомогою підстановки

, де - спільний знаменник mі n.