Знаходження координат вектора досить часто зустрічається умова багатьох завдань у математиці. Вміння знаходити координати вектора допоможе вам в інших, більше складних завданняхзі схожою тематикою. У цій статті ми розглянемо формулу знаходження координат вектора та кілька завдань.
Знаходження координат вектора у площині
Що таке площину? Площиною вважається двовимірний простір, простір з двома вимірами (вимір x і вимір y). Наприклад, папір – площина. Поверхня столу – площина. Якась необ'ємна фігура (квадрат, трикутник, трапеція) теж є площиною. Таким чином, якщо за умови завдання потрібно знайти координати вектора, що лежить на площині, відразу згадуємо про x та y. Знайти координати такого вектора можна наступним чином: Координати AB вектора = (xB - xA; yB - xA). З формули видно, що від координат кінцевої точкиНеобхідно відібрати координати початкової точки.
Приклад:
- Вектор CD має початкові (5; 6) та кінцеві (7; 8) координати.
- Знайти координати вектора.
- Використовуючи вищезгадану формулу, отримаємо такий вираз: CD = (7-5; 8-6) = (2; 2).
- Таким чином, координати CD вектор = (2; 2).
- Відповідно, x координата дорівнює двом, y координата - теж двом.
Знаходження координат вектора у просторі
Що таке місце? Простір це вже тривимірне вимір, де дано 3 координати: x, y, z. Якщо потрібно знайти вектор, який лежить у просторі, формула практично не змінюється. Додається лише одна координата. Для знаходження вектора потрібно від координат кінця відібрати координати початку. AB = (xB - xA; yB - yA; zB - zA)
Приклад:
- Вектор DF має початкові (2; 3; 1) та кінцеві (1; 5; 2).
- Застосовуючи вищезазначену формулу, отримаємо: Координати вектора DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Пам'ятайте, значення координат може бути негативним, у цьому немає жодної проблеми.
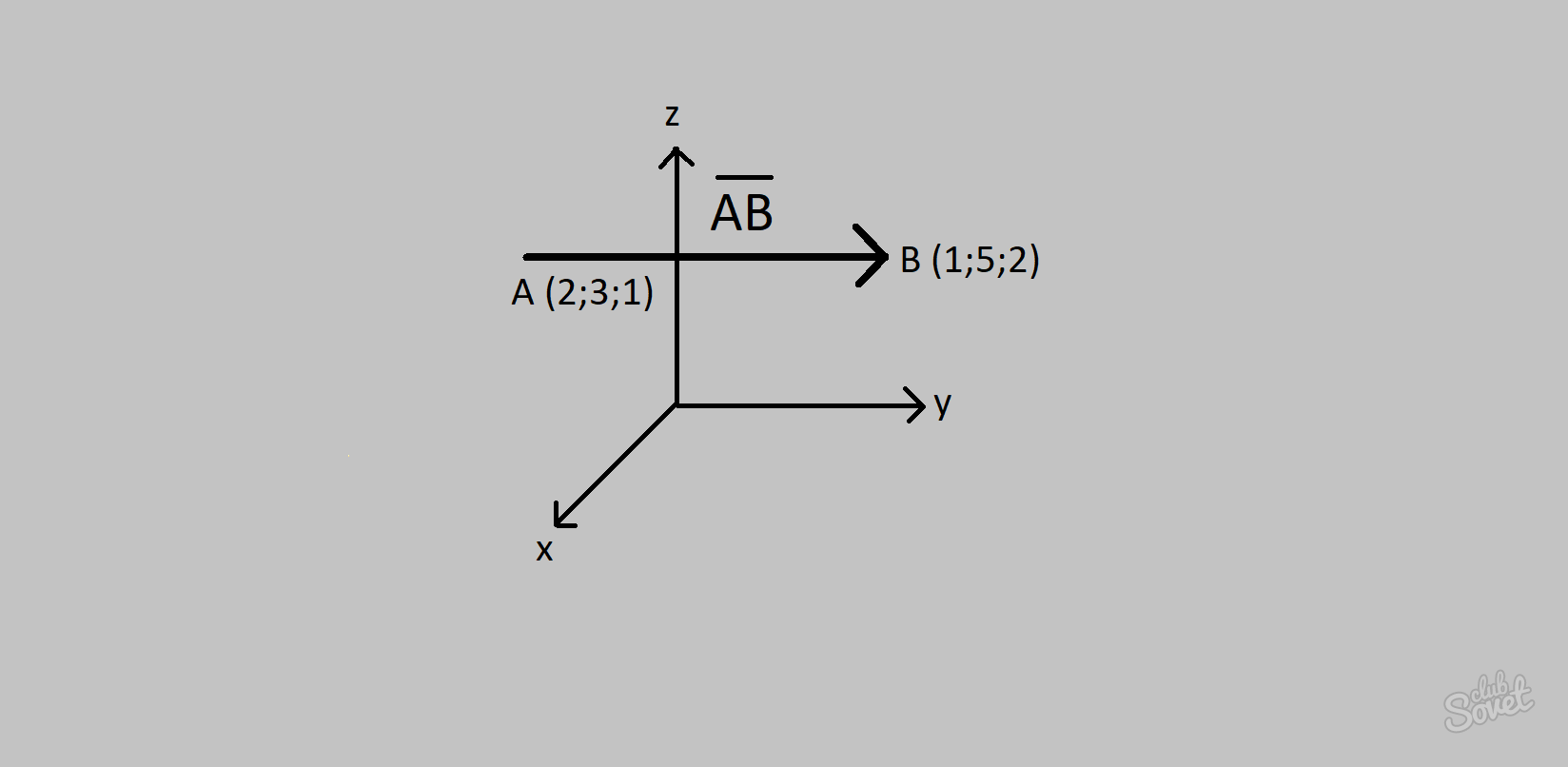
Як знайти координати вектора онлайн?
Якщо з якихось причин вам не хочеться знаходити координати самостійно, можна скористатися калькулятором онлайн . Для початку виберіть розмірність вектора. Розмірність вектора відповідає за його виміри. Розмірність 3 означає, що вектор перебуває у просторі, розмірність 2 — що у площині. Далі вставте координати точок у відповідні поля та програма визначить вам координати самого вектора. Все дуже просто.
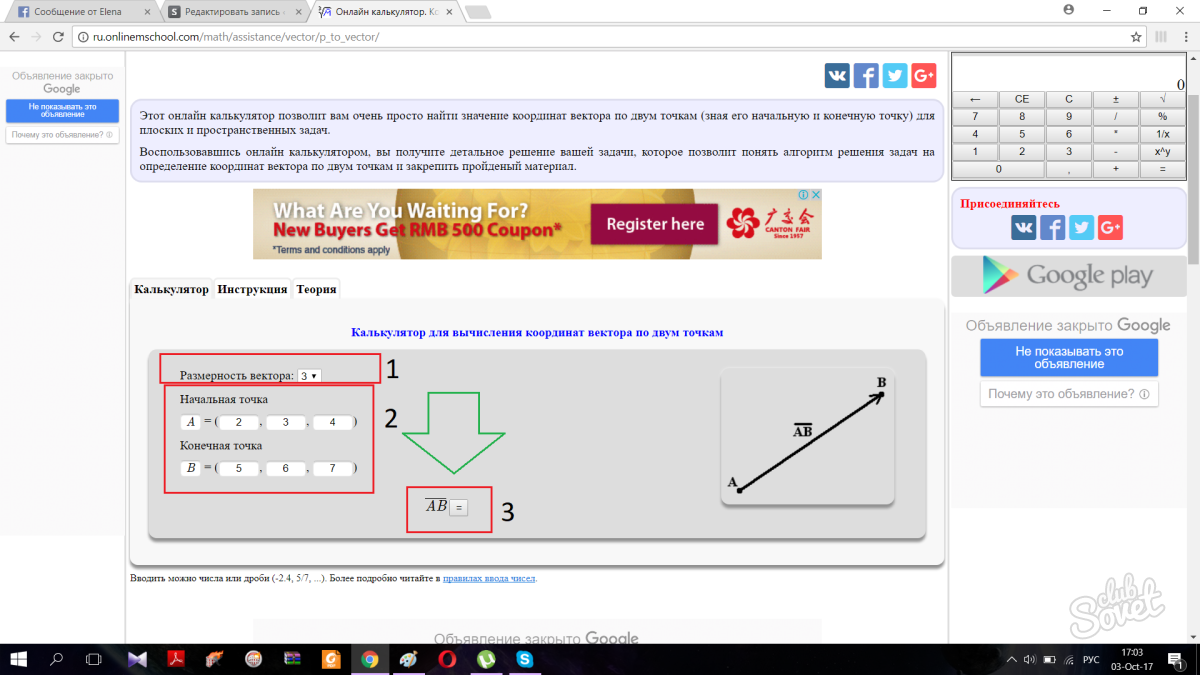
Натиснувши кнопку, сторінка автоматично прокрутиться вниз і видасть вам правильну відповідь разом з етапами рішення.
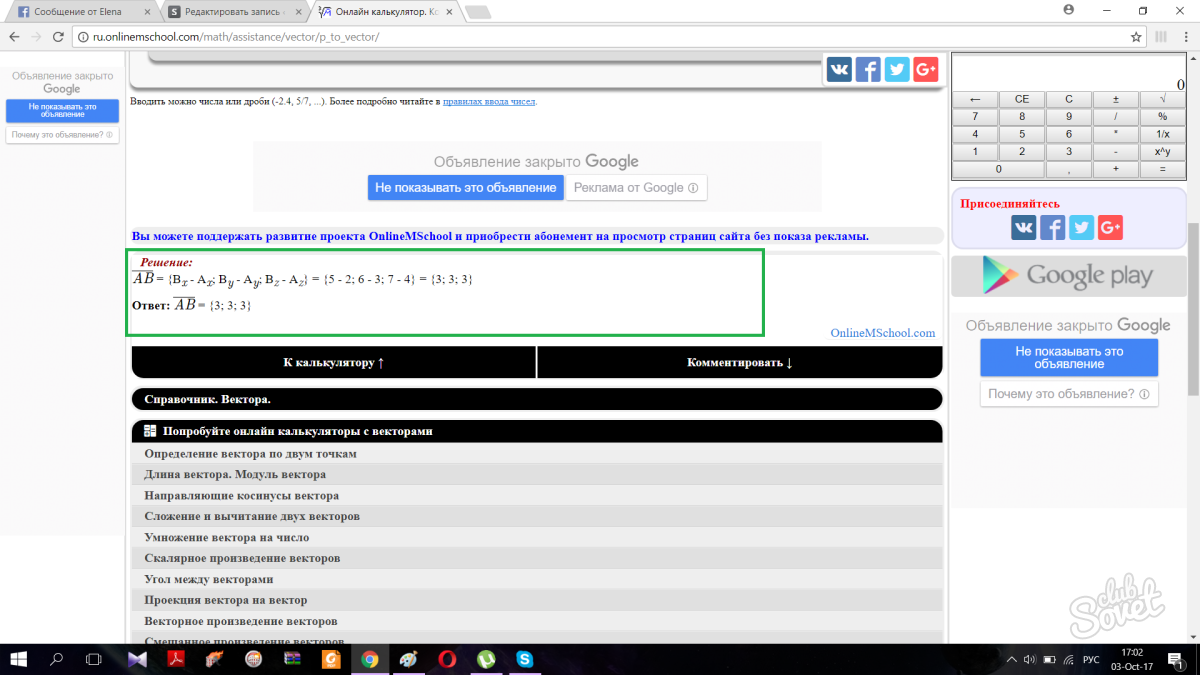
Рекомендовано добре вивчити цю тему, тому що поняття вектора зустрічається не тільки в математиці, а й у фізиці. Студенти факультету Інформаційних технологійтеж вивчають тему векторів, але більш складному рівні.
Якщо дані дві точки площини і , то вектор має такі координати:
Якщо дані дві точки простору і , то вектор має такі координати:
Тобто, з координат кінця векторапотрібно відняти відповідні координати початку вектора.
Завдання:Для тих самих точок запишіть формули знаходження координат вектора. Формули наприкінці уроку.
Приклад 1
Дано дві точки площини і . Знайти координати вектора
Рішення:за відповідною формулою:
Як варіант, можна було використати наступний запис:
Естети вирішать і так:
Особисто я звик до першої версії запису.
Відповідь:
За умовою не потрібно будувати креслення (що характерно для завдань аналітичної геометрії), але з метою пояснення деяких моментів чайникам, не полінуюся:
Обов'язково потрібно розуміти відмінність між координатами точок та координатами векторів:
Координати точок- Це звичайні координати у прямокутній системі координат. Відкладати крапки на координатної площиниДумаю, всі вміють ще з 5-6 класу. Кожна точка має суворе місце на площині, і переміщати їх кудись не можна.
Координати ж вектора- Це його розкладання по базису, в даному випадку. Будь-який вектор є вільним, тому за потреби ми легко можемо відкласти його від будь-якої іншої точки площини. Цікаво, що для векторів можна взагалі не будувати осі, прямокутну системукоординат, потрібен лише базис, у разі ортонормований базис площині .
Записи координат точок і координат векторів начебто схожі: , а сенс координатабсолютно різний, і вам слід добре розуміти цю різницю. Ця відмінність, зрозуміло, справедлива і для простору.
Пані та панове, набиваємо руку:
Приклад 2
а) Дані точки та . Знайти вектори та .
б) Дані точки та . Знайти вектори та .
в) Дані точки та . Знайти вектори та .
г) Дані точки. Знайти вектори.
Мабуть, достатньо. Це приклади для самостійного рішення, Постарайтеся ними не нехтувати, окупиться;-). Креслення робити не потрібно. Рішення та відповіді наприкінці уроку.
Що важливо під час вирішення завдань аналітичної геометрії?Важливо бути гранично уважним, щоб не припуститися майстерної помилки «два плюс два і нулю». Відразу перепрошую, якщо де помилився =)
Як знайти довжину відрізка?
Довжина, як зазначалося, позначається знаком модуля.
Якщо дані дві точки площини і , то довжину відрізка можна обчислити за формулою
Якщо дані дві точки простору і , то довжину відрізка можна обчислити за формулою
Примітка: Формули залишаться коректними, якщо переставити місцями відповідні координати: і , але стандартніший перший варіант
Приклад 3
Рішення:за відповідною формулою:
Відповідь:
Для наочності виконаю креслення 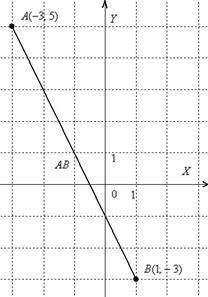
Відрізок – це не вектор, і переміщати його кудись, звичайно, не можна. Крім того, якщо ви виконаєте креслення в масштабі: 1 од. = 1 см (дві зошити), то отриману відповідь можна перевірити звичайною лінійкою, безпосередньо вимірявши довжину відрізка.
Так, рішення коротке, але в ньому є ще пара важливих моментів, які хотілося б пояснити:
По-перше, у відповіді ставимо розмірність: «одиниці». В умові не сказано, ЩО це, міліметри, сантиметри, метри чи кілометри. Тому математично грамотним рішенням буде загальне формулювання: «одиниці» – скорочено «од.».
По-друге, повторимо шкільний матеріал, Корисний не тільки для розглянутої задачі:
Зверніть увагу на важливий технічний прийом – винесення множника з-під кореня. В результаті обчислень у нас вийшов результат і хороший математичний стиль передбачає винесення множника з-під кореня (якщо це можливо). Докладніше процес виглядає так: . Звичайно, залишити відповідь у вигляді не буде помилкою - але недоліком точно і вагомим аргументом для причіпки з боку викладача.
Ось інші поширені випадки: 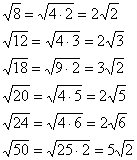
Нерідко під коренем виходить достатньо велике числонаприклад. Як бути у таких випадках? На калькуляторі перевіряємо, чи число ділиться на 4: . Так, розділилося націло, таким чином: ![]() . А може, число ще раз вдасться поділити на 4? . Таким чином:
. А може, число ще раз вдасться поділити на 4? . Таким чином: ![]() . У числа остання цифра непарна, тому розділити втретє на 4 явно не вдасться. Пробуємо поділити дев'ять: . В результаті:
. У числа остання цифра непарна, тому розділити втретє на 4 явно не вдасться. Пробуємо поділити дев'ять: . В результаті:
Готово.
Висновок:якщо під коренем виходить невитягне націло число, то намагаємося винести множник з-під кореня - на калькуляторі перевіряємо, чи число на: 4, 9, 16, 25, 36, 49 і т.д.
У ході рішення різних завданькоріння зустрічаються часто, завжди намагайтеся витягувати множники з-під кореня, щоб уникнути нижчої оцінки і непотрібних проблем з доопрацюванням ваших рішень за зауваженням викладача.
Давайте заразом повторимо зведення коренів у квадрат та інші ступені:
Правила дій зі ступенями в загальному виглядіможна знайти в шкільному підручникуз алгебри, але, гадаю, з наведених прикладів все чи майже все вже ясно.
Завдання для самостійного вирішення з відрізком у просторі:
Приклад 4
Дано крапки і . Знайти довжину відрізка.
Рішення та відповідь наприкінці уроку.
Як знайти довжину вектора?
Якщо дано вектор площини, його довжина обчислюється за такою формулою.
Якщо дано вектор простору, то його довжина обчислюється за формулою ![]() .
.
Дані формули (як і формули довжини відрізка) легко виводяться за допомогою відомої теореми Піфагора.
Приклад 5
Дано крапки і . Знайти довжину вектора.
Я взяв ті ж точки, що й у Прикладі 3.
Рішення:Спочатку знайдемо вектор:
За формулою обчислимо довжину вектора:
Відповідь:
Не забуваймо вказувати розмірність – «одиниці»! Чи завжди, до речі, потрібно розраховувати наближене значення (у даному прикладі 8,94), якщо це не потрібно в умові? На мою думку, зайвим не буде, відсутність наближеного значення тягне на причіпку. Округлення доцільно проводити до 2-3 знаків після коми.
Виконаємо креслення до завдання:
У чому принципова відмінність від Прімера 3? Відмінність полягає в тому, що тут йдеться про вектор, а не про відрізок. Вектор можна перемістити у будь-яку точку площини.
А в чому подібність Прімера 3 і Прімера 5? Геометрично очевидно, що довжина відрізка дорівнює довжині вектора. Так само очевидно, що довжина вектора буде такою самою. За підсумками: ![]() .
.
б) Дано вектори , , і . Знайти їх довжину.
Рішення та відповіді наприкінці уроку.
У цій статті ми з тобою почнемо обговорення однієї палички-виручалочки, яка дозволить тобі звести багато завдань з геометрії до простої арифметики. Ця «паличка» може суттєво полегшити тобі життя особливо у тому випадку, коли ти невпевнено почуваєшся у побудові просторових фігур, перерізів і т. д. Все це вимагає певної уяви та практичних навичок. А метод, який ми тут почнемо розглядати, дозволить тобі практично повністю абстрагуватися від усілякого роду. геометричних побудовта міркувань. Метод має назву "метод координат". У цій статті ми з тобою розглянемо такі питання:
- Координатна площина
- Точки та вектори на площині
- Побудова вектора по двох точках
- Довжина вектора (відстань між двома точками)
- Координати середини відрізка
- Скалярний добуток векторів
- Кут між двома векторами
Я гадаю, ти вже здогадався, чому метод координат так називається? Мабуть, він отримав таку назву, тому що він оперує не з геометричними об'єктами, а з них числовими характеристиками(координатами). А саме перетворення, що дозволяє перейти від геометрії до алгебри, полягає у запровадженні системи координат. Якщо вихідна фігура була плоскою, то координати двовимірні, а якщо об'ємна фігура, то координати тривимірні. У цій статті ми розглядатимемо лише двовимірний випадок. А основна мета статті – навчити тебе користуватися деякими базовими прийомамиметоду координат (вони іноді виявляються корисними під час вирішення завдань із планіметрії у частині B ЄДІ). Обговоренню методів вирішення завдань С2 (завдання по стереометрії) присвячені наступні два розділи з цієї тематики.
З чого було б логічно розпочати обговорення методу координат? Напевно, із поняття системи координат. Згадай, коли ти з нею вперше зіткнувся. Мені здається, що у 7 класі, коли ти дізнався про існування лінійної функціїнаприклад. Нагадаю, ти будував її по точках. Пам'ятаєш? Ти вибирав довільне число, підставляв її у формулу та обчислював таким чином. Наприклад, якщо, те, якщо ж, те й т.д. Що ж ти отримував у результаті? А отримував ти крапки з координатами: і. Далі ти малював "хрестик" (систему координат), вибирав на ній масштаб (скільки клітин у тебе буде одиничним відрізком) і відзначав на ній отримані тобою точки, які потім з'єднував прямою лінією, отримана лінія і є графік функції.
Тут є кілька моментів, які варто пояснити тобі трохи докладніше:
1. Одиничний відрізок ти вибираєш з міркувань зручності, так, щоб все красиво та компактно вміщалося на малюнку
2. Прийнято, що вісь йде зліва направо, а вісь - знизу вгору
3. Вони перетинаються під прямим кутом, а точка їхнього перетину називається початком координат. Вона позначається літерою.
4. У записі координати точки, наприклад, ліворуч у дужках стоїть координата точки по осі, а праворуч, по осі. Зокрема, просто означає, що у точки
5. Для того, щоб задати будь-яку точку на координатної осі, потрібно вказати її координати (2 числа)
6. Для будь-якої точки, що лежить на осі,
7. Для будь-якої точки, що лежить на осі,
8. Вісь називається віссю абсцис
9. Вісь називається віссю ординат
Тепер давай із тобою зробимо наступний крок: відзначимо дві точки З'єднаємо ці дві точки відрізком. І поставимо стрілочку так, ніби ми проводимо відрізок з точки до точки: тобто зробимо наш відрізок спрямованим!

Згадай, як називається спрямований відрізок? Мабуть, він називається вектором!
Таким чином, якщо ми з'єднаємо точку з точкою, причому початком у нас буде точка A, а кінцем - точка B,ми отримаємо вектор. Цю побудову ти теж робив у 8 класі, пам'ятаєш?
Виявляється, вектори, як точки, можна позначати двома цифрами: ці цифри називаються координатами вектора. Питання: як ти думаєш, чи достатньо нам знати координати початку та кінця вектора, щоб знайти його координати? Виявляється, що так! І робиться це дуже просто:
Таким чином, так як у векторі точка - початок, а - кінець, вектор має наступні координати:
Наприклад, якщо, то координати вектора
Тепер давай зробимо навпаки, знайдемо координати вектора. Що нам для цього потрібно змінити? Так, потрібно поміняти місцями початок і кінець: тепер початок вектора буде у точці, а кінець – у точці. Тоді:
Подивися уважно, чим відрізняються вектори та? Єдина їхня відмінність - це знаки в координатах. Вони протилежні. Цей факт прийнято записувати так:
Іноді, якщо спеціально не обговорюється, яка точка є початком вектора, а яка - кінцем, то вектори позначають не двома великими літерами, а однієї малої, наприклад: , і т.д.
Тепер трохи потренуйсясам і знайди координати наступних векторів:
Перевірка:
А тепер виріши завдання трохи складніше:
Век-тор з початком у точці має ко-ор-ді-на-ти. Знай-діте абс-цис-су точки.
Усе те досить прозаїчно: Нехай - координати точки. Тоді
Систему я склав визначення того, що таке координати вектора. Тоді точка має координати. Нас цікавить абсцис. Тоді
Відповідь:
Що ще можна робити із векторами? Та майже все те ж саме, що і з звичайними числами(Хіба що ділити не можна, зате множити можна аж двома способами, один з яких ми тут обговоримо трохи пізніше)
- Вектори можна складати один з одним
- Вектори можна віднімати один з одного
- Вектори можна множити (або ділити) на довільне ненульове число
- Вектори можна множити один на одного
Всі ці операції мають цілком наочне геометричне уявлення. Наприклад, правило трикутника (або паралелограма) для складання та віднімання:
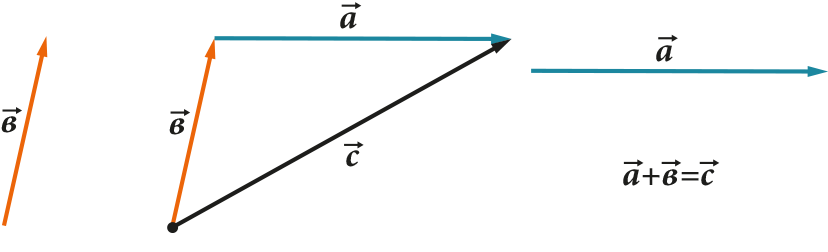
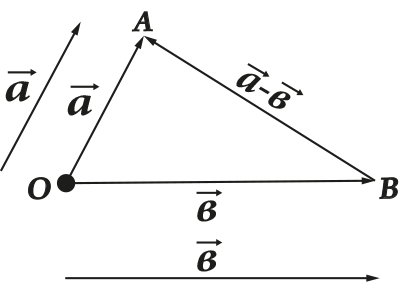
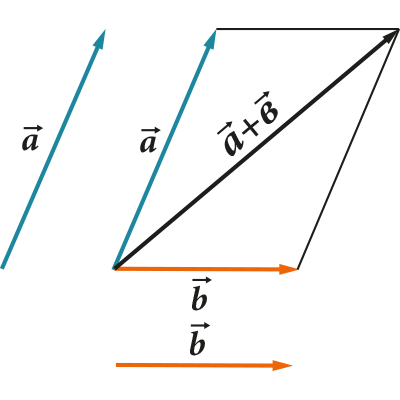
Вектор розтягується або стискається або змінює напрямок при множенні або розподілі на число:

Однак тут нас цікавитиме питання, що ж відбувається з координатами.
1. При складанні (відніманні) двох векторів, ми складаємо (віднімаємо) поелементно їх координати. Тобто:
2. При множенні (розподілі) вектора на число всі його координати множаться (діляться) на це число:
Наприклад:
· Знайди суму ко-ор-ді-нат вік-то-ра.
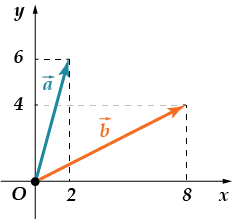
Давай спочатку знайдемо координати кожного вектора. Обидва вони мають однаковий початок – точку початку координат. Кінці вони різні. Тоді, . Тепер обчислимо координати вектора. Тоді сума координат отриманого вектора дорівнює.
Відповідь:
Тепер виріши сам наступне завдання:
· Знайти суму координат вектора
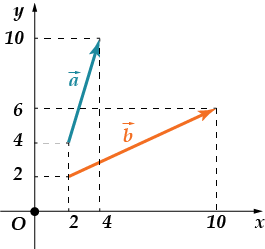
Перевіряємо:
Давайте розглянемо тепер таке завдання: у нас є дві точки на координатній площині. Як знайти відстань між ними? Нехай перша точка буде, а друга. Позначимо відстань між ними через. Давай зробимо для наочності наступне креслення:
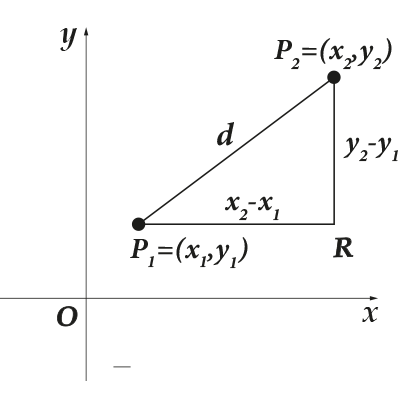
Що я зробив? Я, по-перше, поєднав точки і,також з точки провів лінію, паралельну осі, А з точки провів лінію, паралельну осі. Вони перетнулися в точці, утворивши при цьому чудову фігуру? Чим вона чудова? Та ми з тобою майже всі знаємо про прямокутний трикутник. Ну теорему Піфагора - точно. Шуканий відрізок – це гіпотенуза цього трикутника, а відрізки – катети. Чому рівні координати точки? Так, їх нескладно знайти за картинкою: Так як відрізки паралельні осям і відповідно, то їх довжини легко знайти: якщо позначити довжини відрізків відповідно через, то
Тепер скористаємося теоремою Піфагора. Довжини катетів нам відомі, гіпотенузу ми знайдемо:
Таким чином, відстань між двома точками - це корінь із суми квадратів різниць з координат. Або ж - відстань між двома точками - це довжина відрізка, що їх з'єднує. Легко помітити, що відстань між точками залежить від напрямку. Тоді:
Звідси робимо три висновки:
Давай трохи повправляємось у обчисленні відстані між двома точками:
Наприклад, якщо, то відстань між і дорівнює
Або підемо інакше: знайдемо координати вектора
І знайдемо довжину вектора:
Як бачиш, одне й те саме!
Тепер трохи потренуйся сам:
Завдання: знайти відстань між вказаними точками:
Перевіряємо:
Ось ще пара завдань на ту ж формулу, щоправда звучать вони трохи інакше:
1. Знайди квад-рат довжини століття.

2. Знай-ді-те квад-рат довжини вік-то-ра

Я так думаю, ти з ними легко справився? Перевіряємо:
1. А це на уважність) Ми вже знайшли координати векторів і раніше: . Тоді вектор має координати. Квадрат його довжини дорівнюватиме:
2. Знайдемо координати вектора
Тоді квадрат його довжини дорівнює
Нічого складного, правда? Звичайна арифметика, не більше.
Наступні завдання не можна однозначно класифікувати, вони скоріш загальну ерудицію і вміння малювати прості картинки.
1. Знай-ді-те синус кута на-кло-на від-різ-ка, з'єд-ня-ю-ще-го крапки, з віссю абсцис.
 і
і
Як ми будемо чинити тут? Потрібно знайти синус кута між і віссю. Де ми вміємо шукати синус? Правильно, в прямокутному трикутнику. То що нам потрібно зробити? Побудувати цей трикутник!
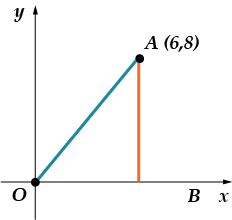
Оскільки координати точки і то відрізок дорівнює, а відрізок. Нам потрібно знайти синус кута. Нагадаю тобі, що синус – це відношення протилежного катетадо гіпотенузи, тоді
Що нам лишилося зробити? Знайти гіпотенузу. Ти можеш зробити це двома способами: за теоремою Піфагора (катети відомі!) або за формулою відстані між двома точками (насправді одне й те саме, що і перший спосіб!). Я піду другим шляхом:
Відповідь:
Наступне завдання здасться тобі ще простіше. Вона – на координати точки.
Завдання 2.З точки опущений пер-пен-ді-куляр на вісь абс-цис. Най-ді-те абс-цис-су ос-но-ва-ня пер-пен-ді-ку-ля-ра.
Давай зробимо малюнок:
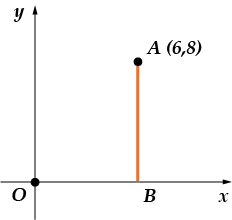
Основа перпендикуляра - це та точка, в якій він перетинає вісь абсцис (вісь), у мене це точка. На малюнку видно, що має координати: . Нас цікавить абсциса – тобто «іксова» складова. Вона рівна.
Відповідь: .
Завдання 3.В умовах попереднього завданнязнайти суму відстаней від точки до осей координат.
Завдання - взагалі елементарне, якщо знати, що таке відстань від точки до осей. Ти знаєш? Я сподіваюся, але все ж таки нагадаю тобі:
Отже, на моєму малюнку, розташованому трохи вище, я вже зобразив такий перпендикуляр? До якої він осі? До осі. І чому ж дорівнює його довжина? Вона рівна. Тепер сам проведи перпендикуляр до осі та знайди його довжину. Вона дорівнюватиме, адже так? Тоді їхня сума дорівнює.
Відповідь: .
Завдання 4.В умовах задачі 2 знайдіть ординату точки, симетричній точціщодо осі абсцис.
Я думаю, тобі інтуїтивно зрозуміло, що таке симетрія? Дуже багато об'єктів нею мають: багато будинків, столів, літаків, багато геометричні фігури: куля, циліндр, квадрат, ромб і т. д. Грубо кажучи, симетрію можна розуміти ось як: фігура складається з двох (або більше) однакових половинок. Така симетрія називається осьовою. А що тоді таке вісь? Це якраз та лінія, за якою фігуру можна, умовно кажучи, «розрізати» на однакові половинки (на цій картинці вісь симетрії - пряма):

Тепер давай повернемося до нашого завдання. Нам відомо, що ми шукаємо точку, симетричну щодо осі. Тоді ця вісь – вісь симетрії. Отже, нам треба зазначити таку точку, щоб вісь розрізала відрізок на рівні частини. Спробуй сам наголосити на такій точці. А тепер порівняй із моїм рішенням:
![]()
У тебе вийшло так само? Добре! У знайденої точки нас цікавить ордината. Вона дорівнює
Відповідь:
А тепер скажи мені, подумавши секунд, чому дорівнюватиме абсцис точки, симетричній точці A щодо осі ординат? Яка твоя відповідь? Правильну відповідь: .
У загальному випадкуправило можна записати ось так:
Крапка, симетрична точці щодо осі абсцис, має координати:
Крапка, симетрична точці щодо осі ординат, має координати:
Ну і тепер зовсім страшна завдання: знайти координати точки, симетричної точки щодо початку координат. Ти спочатку подумай сам, а потім подивися на мій малюнок!
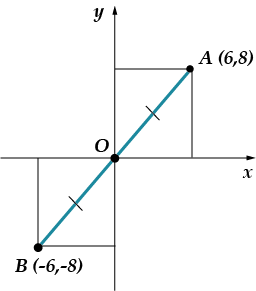
Відповідь:
Тепер Завдання на паралелограм:
Завдання 5: Крапки яв-ля-ють-ся вер-ши-на-ми парал-ле-ло-ло-грам-ма. Знайди ор-ді-на-ту точки.
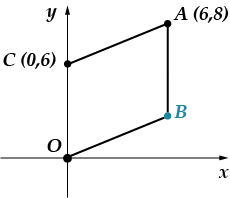
Можна вирішувати це завдання двома способами: логікою та методом координат. Я спочатку застосую метод координат, а потім розповім тобі як можна вирішити інакше.
Цілком зрозуміло, що абсцис точки дорівнює. (Вона лежить на перпендикулярі, проведеній з точки до осі абсцис). Нам треба знайти ординату. Скористаємося тим, що наша фігура – паралелограм, це означає, що. Знайдемо довжину відрізка, використовуючи формулу відстані між двома точками:
Опускаємо перпендикуляр, що з'єднує крапку з віссю. Точку перетину позначу буквою.
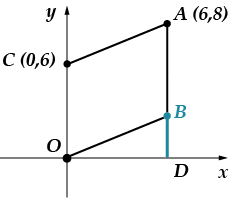
Довжина відрізка дорівнює. (Знайди саму задачу, де ми обговорювали цей момент), тоді знайдемо довжину відрізка по теоремі Піфагора:
Довжина відрізка - точно збігається з його ординатою.
Відповідь: .
Інше рішення (я просто наведу малюнок, що його ілюструє)
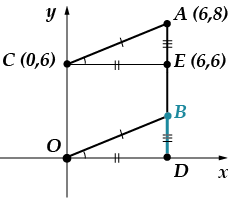
Хід рішення:
1. Провести
2. Знайти координати точки та довжину
3. Довести, що.
Ще одна Завдання на довжину відрізка:
Крапки яв-ля-ють-ся вер-ши-на-ми трикутника. Знайдіть довжину його середньої лінії, параллельної.

Ти пам'ятаєш, що таке середня лініятрикутника? Тоді тобі це завдання елементарна. Якщо не пам'ятаєш, то я нагадаю: середня лінія трикутника – це лінія, яка з'єднує середини протилежних сторін. Вона паралельна до основи і дорівнює його половині.
Підстава – це відрізок. Його довжину нам доводилося шукати раніше, воно рівне. Тоді довжина середньої лінії вдвічі менша і дорівнює.
Відповідь: .
Коментар: це завдання можна вирішити і в інший спосіб, до якого ми звернемося трохи пізніше.
А поки що - ось тобі кілька завдань, потренуйся на них, вони дуже прості, але допомагають «набивати руку», на використанні способу координат!
1. Крапки яв-ля-ють-ся вер-ши-на-ми тра-пе-ції. Знайдіть довжину її середньої лінії.

2. Крапки і яв-ля-ють-ся вер-ши-на-ми парал-ле-ло-грам-ма. Знайди ор-ді-на-ту точки.

3. Знай-ди-те довжину від-різ-ка, з'єд-ня-ю-ще-го точки і

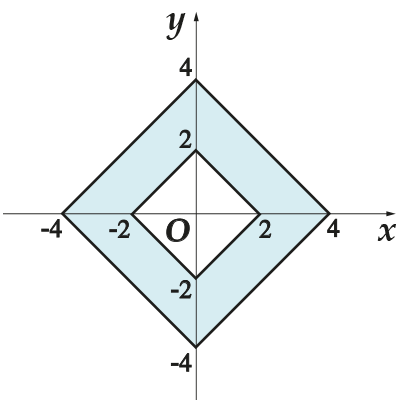
4. Най-ді-те пло-ща за-кра-шен-ної фі-гу-ри на ко-ор-ді-нат-ної плос-ко-сті.
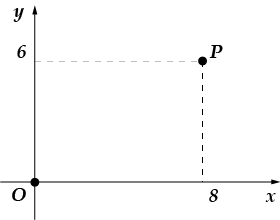
5. Окруж-ність з центром в на-ча-ле ко-ор-ді-нат про-хо-дить через точку. Знай-діть її ра-ді-ус.
6. Най-ді-те ра-ді-ус окруж-ності, опи-сан-ної біля пря-мо-кут-ні-ка, вер-ши-ни ко-то-ро-го мають ко-ор -ді-на-ти зі-від-віт-ствен-но

Рішення:
1. Відомо, що середня лінія трапеції дорівнює напівсумі її основ. Основа рівна, а основа. Тоді
Відповідь:
2. Найпростіше вирішити це завдання так: помітити, що (правило паралелограма). Обчислити координати векторів і легко: . При складанні векторів координати складаються. Тоді має координати. Ці координати має і точка, оскільки початок вектора - це точка з координатами. Нас цікавить ордината. Вона рівна.
Відповідь:
3. Діємо відразу за формулою відстані між двома точками:
Відповідь:
4. Подивися на картинку і скажи, між якими двома фігурами затиснута заштрихована область? Вона затиснута між двома квадратами. Тоді площа шуканої фігури дорівнює площі великого квадрата мінус площа маленького. Сторона маленького квадрата- це відрізок, що з'єднує точки і його довжина дорівнює
Тоді площа маленького квадрата дорівнює
Так само чинимо і з великим квадратом: його сторона - це відрізок, що з'єднує точки і Його довжина дорівнює
Тоді площа великого квадрата дорівнює
Площу шуканої фігури знайдемо за формулою:
Відповідь:
5. Якщо коло має як центр початок координат і проходить через точку, то її радіус буде в точності дорівнює довжинівідрізка (зроби малюнок і ти зрозумієш, чому це очевидно). Знайдемо довжину цього відрізку:
Відповідь:
6. Відомо, що радіус описаного біля прямокутника кола дорівнює половинійого діагоналі. Знайдемо довжину будь-якої з двох діагоналей (адже у прямокутнику вони рівні!)
Відповідь:
Ну що, ти справився з усім? Було не дуже складно розібратися, адже так? Правило тут одне – вміти зробити наочну картинку і просто «рахувати» з неї всі дані.
Нам залишилося зовсім небагато. Є ще буквально два моменти, які мені хотілося б обговорити.
Давай спробуємо вирішити ось таке нехитре завдання. Нехай дані дві точки в. Знайти координати середини відрізка. Розв'язання цього завдання таке: нехай точка - шукана середина, тоді має координати:
Тобто: координати середини відрізка = середнє арифметичне відповідних координат кінців відрізка.
Це дуже просте і зазвичай викликає труднощів в учнів. Давай подивимося, в яких завданнях і як воно використовується:
1. Най-ді-те ор-ді-на-ту се-ре-ді-ни від-різ-ка, зі-є-ня-ю-щ-го точки і

2. Крапки яв-ля-ють-ся вер-ши-на-ми че-ти-рех-вугі-ни-ка. Най-ді-те ор-ді-на-ту точки пе-ре-се-че-ня його діа-го-на-лей.

3. Знай-ді-те абс-цис-су цен-тра окруж-ності, опи-сан-ної біля прямо-вуго-ни-ка, вер-ши-ни ко-то-ро-го мають ко-ор-ді-на-ти со-від-віт-но.

Рішення:
1. Перше завдання - просто класика. Діємо відразу за визначенням середини відрізка. Вона має координати. Ордината дорівнює.
Відповідь:
2. Легко бачити, що цей чотирикутник є паралелограмом (навіть ромбом!). Ти й сам можеш це довести, вирахувавши довжини сторін і порівнявши їх між собою. Що я знаю про паралелограм? Його діагоналі точкою перетину діляться навпіл! Ага! Значить точка перетину діагоналей – це що? Це середина будь-якої з діагоналей! Виберу, зокрема, діагональ. Тоді точка має координати Ординату точки, що дорівнює.
Відповідь:
3. З чим збігається центр описаного біля прямокутника кола? Він збігається з точкою перетину його діагоналей. А що ти знаєш про діагоналі прямокутника? Вони рівні і точкою перетину діляться навпіл. Завдання звелося до попереднього. Візьму, наприклад, діагональ. Тоді якщо – центр описаного кола, то – середина. Шукаю координати: Абсцисса рівна.
Відповідь:
Тепер потренуйся трохи самостійно, я лише наведу відповіді до кожного завдання, щоб ти міг себе перевірити.
1. Най-ді-те ра-ді-ус окруж-ності, опи-сан-ної біля трикутника, вер-ши-ни ко-то-ро-го мають ко-ор-ди -на ти

2. Най-ді-те ор-ді-на-ту цен-тра окруж-ності, опи-сан-ної біля трикутника, вер-ши-ни ко-то-ро-го мають ко-ор-ді-на-ти
3. Якого ра-ді-у-са має бути коло з центром у точці щоб вона торкалася осі абс-цис?
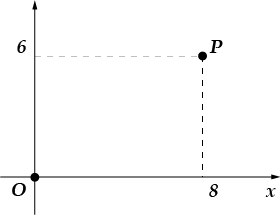
4. Най-ді-те ор-ді-на-ту точки пе-ре-се-че-ня осі і від-різ-ка, со-є-ня-ю-ще-го точки і

Відповіді:
Чи все вдалося? Дуже на це надіюсь! Тепер – останній ривок. Зараз будь особливо уважним. Той матеріал, який я зараз поясню, має безпосереднє відношення не тільки до простим завданнямна метод координат з частини B, але також зустрічається повсюдно і в задачі С2.
Яку зі своїх обіцянок я ще не дотримав? Згадай, які операції над векторами я обіцяв запровадити і які зрештою ввів? Я нічого не забув? Забув! Забув пояснити, що означає збільшення векторів.
Існують два способи помножити вектор на вектор. Залежно від обраного способу у нас виходитимуть об'єкти різної природи:
Векторний твір виконується досить хитро. Як його робити і навіщо воно потрібне, ми з тобою обговоримо в наступній статті. А в цій ми зупинимося на скалярному творі.
Є аж два способи, які дозволяють нам його обчислити:
Як ти здогадався, результат має бути той самий! Отже, давай спочатку розглянемо перший спосіб:
Скалярний твір через координати
Знайти: - загальноприйняте позначення скалярного твору
Формула для обчислення така:
Тобто скалярний добуток= Сума творів координат векторів!
Приклад:
Знайди-те
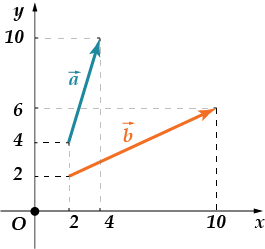
Рішення:
Знайдемо координати кожного із векторів:
Обчислюємо скалярний твір за такою формулою:
Відповідь:
Бачиш абсолютно нічого складного!
Ану, тепер спробуй сам:
· Най-ді-те ска-ляр-не про-з-ве-де-ние вік-то-рів і
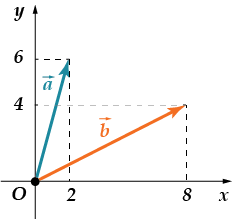
Впорався? Може, й підступ невеликий помітив? Давай перевіримо:
Координати векторів, як у минулому завданні! Відповідь: .
Крім координатного, є й інший спосіб обчислити скалярний твір, а саме через довжини векторів і косинус кута між ними:
Позначає кут між векторами та.
Тобто скалярний добуток дорівнює добутку довжин векторів на косинус кута між ними.
Навіщо нам ця друга формула, якщо в нас є перша, яка набагато простіше, в ній принаймні немає жодних косінусів. А потрібна вона для того, що з першої та другої формул ми з тобою зможемо вивести, як знаходити кут між векторами!
Нехай тоді згадуй формулу для довжини вектора!
Тоді якщо я підставлю ці дані до формули скалярного твору, то я отримаю:
Але з іншого боку:
Отже, що ми з тобою отримали? У нас тепер є формула, яка дає змогу обчислювати кут між двома векторами! Іноді її для стислості записують ще й так:
Тобто алгоритм обчислення кута між векторами наступний:
- Обчислюємо скалярний твір через координати
- Знаходимо довжини векторів та перемножуємо їх
- Ділимо результат пункту 1 на результат пункту 2
Давай потренуємось на прикладах:
1. Знай-ді-те кут між вік-то-ра-ми і. Відповідь дайте у гра-ду-сах.
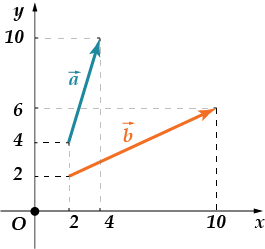
2. В умовах попереднього завдання знайдіть косинус між векторами
Вчинимо так: перше завдання я допоможу тобі вирішити, а друге спробуй зробити сам! Згоден? Тоді починаємо!
1. Ці вектори - наші старі знайомі. Їх скалярний твір ми вже вважали і він був рівний. Координати вони такі: , . Тоді знайдемо їх довжини:
Тоді шукаємо косинус між векторами:
Косинус якого кута дорівнює? Це кут.
Відповідь:
Ну а тепер сам розв'яжи друге завдання, а потім порівняємо! Я наведу лише дуже коротке рішення:
2. має координати, має координати.
Нехай - кут між векторами і тоді
Відповідь:
Слід зазначити, що завдання безпосередньо на векторі та метод координат у частині B екзаменаційної роботидосить рідкісні. Однак переважна більшість завдань C2 можна легко вирішити, вдавшись до введення системи координат. Тож ти можеш вважати цю статтю фундаментом, на основі якого ми робитимемо досить хитрі побудови, які знадобляться нам для вирішення складних завдань.
