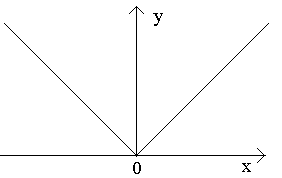
Definitsioon. Kui funktsioon f(x) on määratletud intervallil [ a, b], on pidev igas intervalli punktis ( a, b), punktis a pidev paremal, punktis b on vasakul pidev, siis ütleme, et funktsioon f(x) pidev segmendil [a, b].
Teisisõnu, funktsioon f(x) on pidev intervallil [ a, b], kui on täidetud kolm tingimust:
1) "x 0 Î( a, b): f(x) = f(x 0);
2) f(x) = f(a);
3) f(x) = f(b).
Funktsioonide puhul, mis on intervallil pidevad, arvestame mõningaid omadusi, mille sõnastame järgnevate teoreemide kujul ilma tõestusi tegemata.
1. teoreem. Kui funktsioon f(x) on pidev intervallil [ a, b], siis saavutab see selle segmendi minimaalse ja maksimaalse väärtuse.
See teoreem väidab (joonis 1.15), et lõigul [ a, b] on selline punkt x 1 see f(x 1) £ f(x) iga x alates [ a, b] ja et sellel on mõte x 2 (x 2 О[ a, b]) selline, et " xÎ[ a, b] (f(x 2)³ f(x)).
Tähendus f(x 1) on antud funktsiooni jaoks suurim [ a, b], A f(x 2) – väikseim. Tähistame: f(x 1) = M, f(x 2) =m. Kuna jaoks f(x) ebavõrdsus kehtib: " xÎ[ a, b] m£ f(x) £ M, siis saame teoreemist 1 järgmise järelduse.
Tagajärg. Kui funktsioon f(x) on intervallil pidev, siis on see selle intervalliga piiratud.
2. teoreem. Kui funktsioon f(x) on pidev intervallil [ a,b] ja segmendi otstes võtab erinevate märkide väärtused, siis on selline sisemine punkt x 0 segment [ a, b], milles funktsioon muutub 0-ks, s.t. $ x 0 Î ( a, b) (f(x 0) = 0).
See teoreem väidab, et funktsiooni graafik y = f(x), pidev intervallil [ a, b], lõikub teljega Ox väärtuste korral vähemalt üks kord f(a) Ja f(b) on vastupidised märgid. Niisiis, (joonis 1.16) f(a) > 0, f(b) < 0 и функция f(x) muutub punktides 0-ks x 1 , x 2 , x 3 .
3. teoreem. Laske funktsioonil f(x) on pidev intervallil [ a, b], f(a) = A, f(b) = B Ja A¹ B. (Joon. 1.17). Siis suvalise numbri jaoks C, mis on numbrite vahel A Ja B, on selline sisepunkt x 0 segment [ a, b], Mida f(x 0) = C.
Tagajärg. Kui funktsioon f(x) on pidev intervallil [ a, b], m – väikseim väärtus f(x), M – kõrgeim väärtus funktsioonid f(x) segmendil [ a, b], siis võtab funktsioon (vähemalt korra) mis tahes väärtuse m vahel sõlmitud m Ja M ja seetõttu segment [ m, M] on kõigi funktsiooni väärtuste kogum f(x) segmendil [ a, b].
Pange tähele, et kui funktsioon on pidev intervallil ( a, b) või on segmendis [ a, b] katkestuspunktid, siis sellise funktsiooni teoreemid 1, 2, 3 lakkavad olemast tõesed.
Kokkuvõtteks vaatleme pöördfunktsiooni olemasolu teoreemi.
Tuletagem meelde, et intervalli all peame silmas lõiku või intervalli või poolintervalli, lõplikku või lõpmatut.
 |
4. teoreem. Lase f(x) on intervallil pidev X, suureneb (või väheneb) võrra X ja sellel on väärtuste vahemik Y. Siis funktsiooni jaoks y = f(x) on pöördfunktsioon x= j(y), mis on määratletud intervallil Y, pidev ja suurenev (või kahanev) võrra Y mitme tähendusega X.
Kommenteeri. Laske funktsioonil x= j(y) on funktsiooni pöördväärtus f(x). Kuna argumenti tähistatakse tavaliselt tähisega x, ja funktsioon läbi y, siis kirjutame pöördfunktsioon nagu y =j(x).
Näide 1. Funktsioon y = x 2 (joonis 1.8, a) komplektis X= a, b[ ja on pidev selle intervalli igas punktis. Siis nimetatakse seda intervallis pidevaks ] a, b[ . Funktsiooni pidevuse mõiste vormi ]-∞ intervallidel on defineeritud sarnaselt, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Olgu nüüd funktsioon y = f(x) määratletud intervallil [ a, b] . Intervalli ja lõigu erinevus: intervalli piiripunktid ei sisaldu intervallis, küll aga lõigu piiripunktid. Siin tuleks mainida nn ühekülgset järjepidevust: punktis a, jääb segmendile [ a, b] , saame läheneda ainult paremalt ja punktini b- ainult vasakul. Funktsioon on pidev intervallil [ a, b], kui see on kokkuvõttes pidev sisemised punktid selle lõigu, on pidev punktis paremal a ja jäetakse punktis pidevaks b.
Pideva funktsiooni näiteks võib olla mis tahes elementaarfunktsioon. Iga elementaarne funktsioon on pidev igal intervallil, millel see on määratletud. Näiteks funktsioonid ja on pidevad mis tahes intervalli [ a, b], funktsioon on pidev intervallil [ 0 , b] , on funktsioon pidev igal lõigul, mis ei sisalda punkti a = 2 .
Näide 4. Kontrollige funktsiooni järjepidevust.
Lahendus. Kontrollime esimest tingimust. Funktsioon ei ole defineeritud punktides - 3 ja 3. Vähemalt üks funktsiooni järjepidevuse tingimus tervel arvujoonel ei ole täidetud. Sellepärast seda funktsiooni on intervallidega pidev
.Näide 5. Määrake, millisel parameetri väärtusel a pidev kogu ulatuses määratluspiirkond funktsiooni 
Lahendus.
Leiame parempoolse piirangu aadressilt:
![]() .
.
Ilmselgelt väärtus punktis x= 2 peaks olema võrdne kirves :
![]()
a = 1,5 .
Näide 6. Määrake, milliste parameetrite väärtustel a Ja b pidev kogu ulatuses määratluspiirkond funktsiooni 
Lahendus.
Leiame punktis funktsiooni vasakpoolse piiri:
![]() .
.
Seetõttu peab punkti väärtus olema 1:
Leiame vasakpoolse funktsiooni punktist:
Ilmselt peaks funktsiooni väärtus punktis olema võrdne:
Vastus: funktsioon on pidev kogu määratluspiirkonnas millal a = 1; b = -3 .
Pidevate funktsioonide põhiomadused
Matemaatika jõudis pideva funktsiooni mõisteni, uurides ennekõike erinevaid liikumisseadusi. Ruum ja aeg on lõpmatud ning sõltuvus näiteks teed s ajast t, mida väljendab seadus s = f(t) , toob näite pidevast funktsioonid f(t) . Ka soojendatava vee temperatuur muutub pidevalt, see on ka aja pidev funktsioon: T = f(t) .
IN matemaatiline analüüs mõned omadused on tõestatud pidevad funktsioonid. Toome välja nendest omadustest kõige olulisemad.
1. Kui intervallil pidev funktsioon võtab intervalli lõpus erinevate märkide väärtused, siis selle intervalli mingil hetkel omandab see väärtuse võrdne nulliga. Formaalsemas avalduses on see omadus antud teoreemis, mida tuntakse esimese Bolzano-Cauchy teoreemina.
2. Funktsioon f(x) pidev intervallil [ a, b], võtab kõik vahepealsed väärtused lõpp-punktide väärtuste vahel, st vahel f(a) Ja f(b) . Formaalsemas avalduses on see omadus antud teoreemis, mida tuntakse teise Bolzano-Cauchy teoreemina.
Funktsiooni pidevus intervallil
| Parameetri nimi | Tähendus |
| Artikli teema: | Funktsiooni pidevus intervallil |
| Rubriik (temaatiline kategooria) | Matemaatika |
Definitsioon. Funktsiooni nimetatakse tavaliselt intervalli pidevaks, kui see on pidev selle intervalli igas punktis.
Kui funktsioon on määratletud aadressil X=A ja kus f(X) = f(A),
siis nad ütlevad seda f(X) punktis ja paremal pool on pidev. Samamoodi, kui f(X) = f(b), siis nad ütlevad seda hetkel b seda funktsiooni jäetud pidevaks.
Definitsioon. Funktsiooni nimetatakse tavaliselt pidevaks intervallil [ a, b], kui see on pidev igas punktis (punktis A pidev paremal, punktis b– pidev vasakul).
Kõrgeim väärtus funktsioonid juures = f(x) segmendil [ a, b f(x 1) see f(x) £ f(x 1) kõigile X Î [ a, b].
Madalaim väärtus funktsioonid juures = f(x) segmendil [ a, b] on tavaks nimetada seda selle tähenduseks f(x 2) seda f(x) ³ f(x 2) kõigile X Î [ a, b].
Funktsioonidel, mis on intervallil pidevad, on mitmeid olulised omadused, mida väljendatakse järgmiste teoreemidega.
Teoreem 3.3.1. Funktsioon, mis on pidev intervallil [ a, b], saavutab sellel oma minimaalse väärtuse m ja suurim väärtus M, see tähendab, et selliseid punkte on x 1 ja x 2 sellest segmendist, see f(x 1) = m, f(x 2) = M.
Teoreemil on lihtne geomeetriline tähendus (vt joonis 2).
 |
Teoreem 3.3.2. Juhul kui funktsioon juures = f(x) on pidev intervallil [ a, b] ja selle otstes on ebavõrdsed väärtused f(A) = A, f(b) = B, A ¹ B, siis ükskõik milline arv C on A ja B vahel, on punkt Koos Î [ a, b] selline, et f(Koos) = S.
Geomeetriline tähendus Teoreem on illustreeritud joonisel 3. Mis tahes sirgjoon juures= C, kus A< C < B (или A >C > B), lõikub funktsiooni graafikuga juures = f(x).
Tagajärg. Kui funktsioon on segmendil pidev ja omandab selle otstes erinevate märkide väärtused, siis sellel lõigul on vähemalt üks punkt, kus funktsioon kaob.
Tagajärje geomeetriline tähendus on illustreeritud joonisel 4.

Küsimused enesekontrolliks
1. Millist funktsiooni nimetatakse tavaliselt punktis pidevaks?
2. Andke teine samaväärne definitsioon funktsiooni ja argumentide juurdekasvu osas.
3. Mida saab öelda kahe pideva funktsiooni summa, erinevuse, korrutise ja jagatise kohta?
4. Milliste argumendi väärtuste jaoks on kogu ratsionaalne ja murdosa-ratsionaalfunktsioonid pidev?
5. Millal on kompleksfunktsioon punktis pidev?
6. Mida nimetatakse tavaliselt funktsioonide katkestuspunktiks?
7. Milliseid punkte nimetatakse esimest tüüpi katkestuspunktideks?
8. Millist suurust nimetatakse tavaliselt funktsioonihüppeks?
9. Selgitage mõiste "eemaldatav katkestuspunkt". Too näiteid.
10. Milliseid punkte nimetatakse teist tüüpi katkestuspunktideks? Too näiteid.
11. Selgitage mõisteid: "järjepidevus intervallil", "järjepidevus paremal", "järjepidevus vasakul", "järjepidevus lõigul".
12. Määratlege funktsioonide suurimad ja väikseimad väärtused.
13. Sõnasta teoreem segmendi pidevuse ja funktsiooni suurima ja väikseima väärtuse vahelise seose kohta. Selgitage seda joonisega.
14. Sõnasta teoreem intervalli funktsioonide pidevuse ja funktsiooni väärtuste intervalli vahelise seose kohta. Illustreerige selle geomeetrilist tähendust joonisel.
15. Esitage ülaltoodud teoreemi ja selle geomeetrilise tõlgenduse järeldus.
LOENG nr 4
Loengu teema: Funktsiooni tuletis
Loengu ülevaade: Tuletise mõiste, selle geomeetriline ja füüsiline tähendus. Eristamise põhireeglid. Tuletis keeruline funktsioon. Mõned rakendused on tuletatud.
4.1. Tuletise mõiste, selle geomeetriline ja füüsikaline tähendus
Mõelge funktsioonile juures = f(x), määratud intervallis ] a, b[. Lase XÎ ] a, b[Ja X Î ] a, b[, siis funktsiooni juurdekasv punktis X 0 väljendatakse valemiga D juures = f(x 0+D X) – f(x 0).
Definitsioon. Tuletisfunktsioon y = f(x) punktis X 0 nimetatakse tavaliselt selle funktsiooni juurdekasvu ja argumendi juurdekasvu suhte piiriks, kui viimane kipub olema null:
f'(x 0) = ![]() või y"(x 0) =.
või y"(x 0) =.
Tuletise geomeetriline tähendus: antud funktsiooni tuletis punktis on võrdne Ox-telje vahelise nurga puutujaga ja selle funktsiooni graafiku puutujaga punktis vastav punkt(vt joonis 1):
f"(x 0) = punakaspruun a.
INTERVJUUL PIDEVATE FUNKTSIOONIDE OMADUSED
Vaatleme mõningaid intervallil pidevate funktsioonide omadusi. Esitame need omadused ilma tõenditeta.
Funktsioon y = f(x) helistas pidev segmendil [a, b], kui see on pidev selle lõigu kõigis sisemistes punktides ja selle otstes, s.o. punktides a Ja b, on vastavalt paremal ja vasakul pidev.
1. teoreem. Funktsioon, mis on pidev intervallil [ a, b], on selle lõigu vähemalt ühes punktis suurim väärtus ja vähemalt ühes punktis väikseim väärtus.
Teoreem väidab, et kui funktsioon y = f(x) on pidev intervallil [ a, b], siis on vähemalt üks punkt x 1 Î [ a, b] nii, et funktsiooni väärtus f(x) sel hetkel on selle segmendi kõigist väärtustest suurim: f(x 1) ≥ f(x). Samamoodi on selline punkt x 2, milles funktsiooni väärtus on segmendi kõigist väärtustest väikseim: f(x 1) ≤ f(x).
On selge, et selliseid punkte võib olla mitu, näiteks jooniselt on näha, et funktsioon f(x) võtab kahes punktis väikseima väärtuse x 2 Ja x 2 ".
Kommenteeri. Teoreemi väide võib muutuda valeks, kui arvestada funktsiooni väärtust intervallil ( a, b). Tõepoolest, kui arvestada funktsiooni y = x(0, 2), siis on see sellel intervallil pidev, kuid ei saavuta selles ei suurimat ega väikseimat väärtust: see jõuab nende väärtusteni intervalli otstes, kuid otsad ei kuulu meie domeenile.
Samuti lakkab teoreem kehtimast katkendlike funktsioonide puhul. Too näide.
Tagajärg. Kui funktsioon f(x) on pidev [ a, b], siis on see selles segmendis piiratud.
2. teoreem. Laske funktsioonil y = f(x) on pidev intervallil [ a, b] ja selle lõigu lõpus võtab erinevate märkide väärtused, siis on segmendi sees vähemalt üks punkt x = C, milles funktsioon läheb nulli: f(C)= 0, kus a< C< b

Sellel teoreemil on lihtne geomeetriline tähendus: kui pideva funktsiooni graafiku punktid y = f(x), mis vastab segmendi otstele [ a, b] valetama kaasa erinevad küljed teljelt Ox, siis see graafik lõikub teljega vähemalt ühes lõigu punktis Ox. Katkestatud funktsioonidel ei pruugi see omadus olla.
See teoreem lubab järgmist üldistust.
Teoreem 3 (vaheväärtuste teoreem). Laske funktsioonil y = f(x) on pidev intervallil [ a, b] Ja f(a) = A, f(b) = B. Siis suvalise numbri jaoks C vahel sõlmitud A Ja B, selles segmendis on selline punkt CÎ [ a, b], Mida f(c) = C.

See teoreem on geomeetriliselt ilmne. Vaatleme funktsiooni graafikut y = f(x). Lase f(a) = A, f(b) = B. Siis mis tahes sirgjoon y = C, Kus C– mis tahes arv nende vahel A Ja B, lõikub funktsiooni graafikuga vähemalt ühes punktis. See väärtus on lõikepunkti abstsiss x = C, mille juures f(c) = C.
Seega läbib pidev funktsioon, liikudes ühelt väärtuselt teisele, tingimata läbi kõik vaheväärtused. Eriti:
Tagajärg. Kui funktsioon y = f(x) on pidev teatud intervalli jooksul ja võtab suurima ja väikseima väärtuse, siis sellel intervallil võtab see vähemalt korra mis tahes väärtuse, mis jääb selle väikseima ja suurima väärtuse vahele.
TULETISED JA SELLE RAKENDUSED. TULETISE MÄÄRATLUS
Olgu meil mingi funktsioon y=f(x), määratletud teatud intervalliga. Iga argumendi väärtuse jaoks x sellest intervallist funktsioon y=f(x) omab teatud tähendust.
Mõelge kahele argumendi väärtusele: esialgne x 0 ja uus x.

Erinevus x–x 0 kutsutakse suurendades argumendi x punktis x 0 ja on tähistatud Δx. Seega Δx = x – x 0 (argumendi juurdekasv võib olla kas positiivne või negatiivne). Sellest võrdsusest järeldub, et x=x 0 +Δx, st. algne tähendus muutuja sai veidi juurdekasvu. Siis, kui punktis x 0 funktsiooni väärtus oli f(x 0 ), siis sisse uus punkt x funktsioon võtab väärtuse f(x) = f(x 0 +Δx).
Erinevus y-y 0 = f(x) – f(x 0 ) helistas funktsiooni juurdekasv y = f(x) punktis x 0 ja seda tähistab sümbol Δy. Seega
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) . | (1) |
Tavaliselt argumendi algväärtus x 0 loetakse fikseerituks ja uus väärtus x- muutuv. Siis y 0 = f(x 0 ) osutub konstantseks ja y = f(x)- muutuv. Kasvu Δy Ja Δx on ka muutujad ja valem (1) näitab seda Dy on muutuja funktsioon Δx.
Loome funktsiooni juurdekasvu ja argumendi juurdekasvu suhte
Leiame selle suhte piiri Δx→0. Kui see piir on olemas, nimetatakse seda selle funktsiooni tuletiseks f(x) punktis x 0 ja tähistada f "(x 0). Niisiis,
Tuletis seda funktsiooni y = f(x) punktis x 0 nimetatakse funktsiooni juurdekasvu suhte Δ piiriks y argumendi juurdekasvule Δ x, kui viimane kipub suvaliselt nulli.
Pange tähele, et sama funktsiooni korral on tuletis in erinevaid punkte x võib omandada erinevaid väärtusi, s.t. tuletist võib pidada argumendi funktsiooniks x. See funktsioon on määratud f "(x)
Tuletist tähistatakse sümbolitega f "(x),y ", . Konkreetne tähendus tuletis at x = a tähistatud f "(a) või y "| x=a.
Funktsiooni tuletise leidmise tehte f(x) nimetatakse selle funktsiooni diferentseerimiseks.
Tuletise definitsiooni järgi otse otsimiseks võite kasutada järgmist. pöidlareegel:
Näited.
DERIVAATI MEHAANILINE TUNNE
Füüsikast on teada, et seadus ühtlane liikumine paistab nagu s = v t, Kus s– tee, mis kulges ajahetke t, v- ühtlase liikumise kiirus.
Siiski, kuna Enamik looduses toimuvaid liikumisi on ebaühtlased, siis üldiselt kiirus ja sellest tulenevalt ka vahemaa s oleneb ajast t, st. saab olema aja funktsioon.
Niisiis, las materiaalne punkt liigub sirgjooneliselt ühes suunas vastavalt seadusele s=s(t).
Märgime teatud ajahetke t 0 . Sel hetkel on punkt rajast mööda läinud s=s(t 0 ). Määrame kiiruse v materiaalne punkt ajahetkel t 0 .
Selleks kaalume mõnda teist ajahetke t 0 + Δ t. See vastab läbitud teele s =s(t 0 + Δ t). Seejärel teatud aja jooksul Δ t punkt on läbinud tee Δs =s(t 0 + Δ t)–s(t).
Mõelgem suhtumisele. Seda nimetatakse keskmiseks kiiruseks ajavahemikus Δ t. Keskmine kiirus ei suuda hetkel täpselt iseloomustada punkti liikumiskiirust t 0 (kuna liikumine on ebaühtlane). Selle tõelise kiiruse täpsemaks väljendamiseks kasutage keskmine kiirus, peate võtma lühema aja Δ t.
Niisiis, liikumise kiirus sisse Sel hetkel aega t 0 (hetkkiirus) on keskmise kiiruse piirväärtus vahemikus alates t 0 kuni t 0 +Δ t, kui Δ t→0:
![]() ,
,
need. ebaühtlane kiirus see on läbitud vahemaa tuletis aja suhtes.

TULETISE GEOMEETRILINE TÄHENDUS
Tutvustame esmalt kõvera puutuja määratlust antud punktis.
Olgu meil kõver ja sellel fikseeritud punkt M 0(vt joonist) Mõelge veel ühele punktile M see kõver ja joonestada sekant M 0 M. Kui punkt M hakkab mööda kõverat liikuma ja punkt M 0 jääb liikumatuks, siis sekant muudab oma asukohta. Kui, punkti piiramatu lähendusega M mööda kõverat punktini M 0 igal pool kaldub sekant hõivama teatud sirge positsiooni M 0 T, siis otse M 0 T nimetatakse kõvera puutujaks antud punktis M 0.
See., puutuja kõverale antud punktis M 0 nimetatakse sekandi piirpositsiooniks M 0 M millal punkt M kaldub piki kõverat punkti M 0.
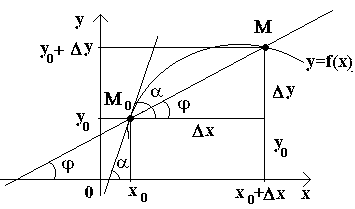
Vaatleme nüüd pidevat funktsiooni y=f(x) ja sellele funktsioonile vastav kõver. Mingil väärtusel X Funktsioon 0 võtab väärtuse y 0 =f(x 0). Need väärtused x 0 ja y 0 kõveral vastab punktile M 0 (x 0 ; y 0). Esitame argumendi x 0 juurdekasv Δ X. Argumendi uus väärtus vastab funktsiooni suurendatud väärtusele y 0 +Δ y=f(x 0 –Δ x). Saame asjast aru M(x 0+Δ x; y 0+Δ y). Joonistame sekanti M 0 M ja tähistage φ-ga nurka, mille moodustab sekant telje positiivse suunaga Ox. Loome suhte ja paneme seda tähele.
Kui nüüd Δ x→0, siis funktsiooni Δ pidevuse tõttu juures→0 ja seega ka punkt M, liikudes mööda kõverat, läheneb punktile piiranguteta M 0. Siis sekant M 0 M kipub võtma punktis kõvera puutuja positsiooni M 0, ja nurk φ→α punktis Δ x→0, kus α tähistab puutuja ja telje positiivse suuna vahelist nurka Ox. Kuna funktsioon tan φ sõltub pidevalt φ-st φ≠π/2 korral, siis φ→α tan φ → tan α korral on puutuja kalle:
![]()
need. f "(x)= tg α .
Seega geomeetriliselt y "(x 0) tähistab selle funktsiooni graafiku puutuja kalle punktis x 0, st. juures antud väärtus argument x, on tuletis võrdne funktsiooni graafiku puutuja poolt moodustatud nurga puutujaga f(x) sobivas kohas M 0 (x; y) positiivse telje suunaga Ox.
Näide. Otsi kalle kõvera puutuja y = x 2 punktis M(-1; 1).
Oleme juba varem näinud, et ( x 2)" = 2X. Kuid kõvera puutuja nurgakoefitsient on tan α = y"| x=-1 = – 2.
FUNKTSIOONIDE ERINEVUS. ERINEVATE FUNKTSIOONIDE JÄDEVASUS
Funktsioon y=f(x) helistas eristatav mingil hetkel x 0, kui sellel on selles punktis teatud tuletis, st. kui suhte piir on olemas ja on lõplik.
Kui funktsioon on diferentseeruv teatud lõigu igas punktis [ A; b] või intervall ( A; b), siis nad ütlevad, et ta eristatav segmendil [ A; b] või vastavalt intervallis ( A; b).
Kehtib järgnev teoreem, mis loob seose diferentseeruvate ja pidevate funktsioonide vahel.
Teoreem. Kui funktsioon y=f(x) mingil hetkel eristuvad x 0, siis on see selles punktis pidev.
Seega tuleneb funktsiooni diferentseeritavusest selle järjepidevus.
Tõestus. Kui ![]() , See
, See
![]() ,
,
kus α on lõpmata väike suurus, st. suurus, mis kaldub nulli kui Δ x→0. Kuid siis
Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 juures Δ x→0, st. f(x) – f(x 0)→0 kl x→x 0 , mis tähendab, et funktsioon f(x) pidev mingis punktis x 0 . Q.E.D.
Seega ei saa funktsioonil olla tuletist katkestuspunktides. Vastupidine pole tõsi: on pidevaid funktsioone, mis ei ole mõnes punktis diferentseeruvad (st neil ei ole nendes punktides tuletist).
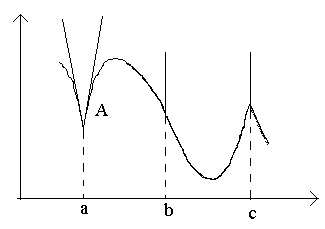
Mõelge joonisel olevatele punktidele a, b, c.
Punktis a kell Δ x→0 suhtarvul pole piirangut (kuna Δ ühepoolsed piirid on erinevad x→0–0 ja Δ x→0+0). Punktis A graafikul pole defineeritud puutujat, kuid on kaks erinevat ühesuunalist puutujat, millel on tõusud To 1 ja To 2. Seda tüüpi punkti nimetatakse nurgapunktiks.
Punktis b kell Δ x→0 seos on konstantse märgiga lõputult suur suurus. Funktsioonil on lõpmatu tuletis. Sellel hetkel on graafikul vertikaalne puutuja. Punktitüüp – vertikaalse puutuja “käänupunkt”.
Punktis cühepoolsed tuletised on lõpmata suured kogused erinevaid märke. Selles punktis on graafikul kaks ühendatud vertikaalset puutujat. Tüüp - "tagasipunkt" vertikaalse puutujaga - erijuhtum nurgapunkt.