Sections of geometric figures have different shapes. The cross-section of a parallelepiped is invariably a rectangle or square. It has a number of parameters that can be detected by an analytical method.
Instructions
1. It is possible to draw four sections through the parallelepiped, which are squares or rectangles. Each it has two diagonal and two cross sections. As usual, they have different sizes. The exception is the cube, in which they are identical. Before constructing a section of a parallelepiped, get an idea of what this figure represents. There are two types of parallelepipeds - ordinary and rectangular. In an ordinary parallelepiped, the faces are located at a certain angle to the base, while in a rectangular one they are perpendicular to it. All faces rectangular parallelepiped are rectangles or squares. It follows from this that a cube is special case rectangular parallelepiped.
2. Every section of a parallelepiped has certain collations. The main ones are area, perimeter, and lengths of diagonals. If from these problems the sides of the section or some of its other parameters are known, this is enough to determine its perimeter or area. The diagonals of the sections are also determined along the sides. The first of these parameters is the area of the diagonal section. In order to determine the area of the diagonal section, it is necessary to know the height and sides of the base of the parallelepiped. If the length and width of the base of the parallelepiped are given, then find the diagonal using the Pythagorean theorem: d=?a^2+b^2. Having found the diagonal and knowing the height of the parallelepiped, calculate the cross-sectional area of the parallelepiped: S=d*h.
3. The perimeter of the diagonal section can also be calculated using two values - the diagonal of the base and the height of the parallelepiped. In this case, first find two diagonals (upper and lower bases) using the Pythagorean theorem, and then add them with twice the height.
4. If you draw a plane, parallel to the ribs parallelepiped, it is possible to obtain a rectangular section, the sides of which are one of the sides of the base of the parallelepiped and the height. Find the area of this section in the following way: S = a * h. Find the perimeter of this section in a similar way using the following formula: p = 2 * (a + h).
5. The final case occurs when the section runs parallel to the two bases of the parallelepiped. Then its area and perimeter are equal to the value of the area and perimeter of the bases, i.e.: S=a*b - cross-sectional area; p=2*(a+b).
Before moving on to finding the height of a parallelepiped, it is necessary to clarify what a height is and what a parallelepiped is. In geometry, height is a perpendicular from the top of a figure to its base, or a segment that connects the upper and lower bases using the shortest method. A parallelepiped is a polyhedron that has two parallel and equal polygon as bases whose corners are united by segments. The parallelepiped is made up of six parallelograms, parallel in pairs and equal to each other.
Instructions
1. There can be three heights in a parallelogram, depending on the location of the figure in space; by turning the parallelepiped on its side, you will swap its bases and faces. The upper and lower parallelograms are invariably bases. If the lateral edges of the figure are perpendicular to the bases, then the parallelepiped is straight, and each of its edges is a ready height. Allowed to measure.
2. In order to get a straight parallelepiped of the same size from an inclined parallelepiped, you need to extend the side faces in one direction. After this, build perpendicular section, from the corners of which, set aside the length of the edge of the parallelepiped, and at this distance construct a second perpendicular section. The two parallelograms you constructed will bound the new parallelepiped, which is equal in area to the first. For the future, it should be noted that the volumes equal-sized figures identical.
3. Frequently asked question We encounter heights in problems. We are always given data that allows us to calculate it. This can be the volume, linear dimensions of the parallelepiped, the lengths of its diagonals. So the volume of the parallelepiped equal to the product its base by its height, that is, knowing the volume and size of the base, it is easy to find out the height by dividing the first by the second. If you are dealing with a rectangular parallelepiped, that is, one whose base is a rectangle, they may try to complicate your task due to its special qualities. So in a rectangular parallelepiped, every square of its diagonal equal to the sum squares of 3 dimensions of a parallelepiped. If the “given” for the problem of a rectangular parallelepiped indicates the length of its diagonal and the lengths of the sides of the base, then this information is enough to find out the size of the desired height.
A parallelepiped is a special case of a prism, in which all six faces are parallelograms or rectangles. Parallelepiped with rectangular edges also called rectangular. A parallelepiped has four intersecting diagonals. If three edges a, b, c are given, you can find all the diagonals of a rectangular parallelepiped by performing additional constructions.
Instructions
1. Draw a rectangular parallelepiped. Write down the known data: three edges a, b, c. First construct one diagonal m. To determine it, we use the quality of a rectangular parallelepiped, according to which all its angles are right.
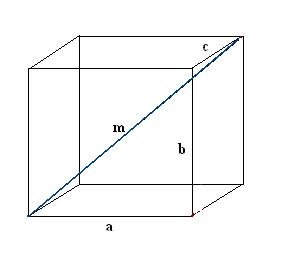
2.
Construct the diagonal n of one of the faces of the parallelepiped. Carry out the construction so that the desired edge, the desired diagonal of the parallelepiped and the diagonal of the face together form a right triangle a, n, m.
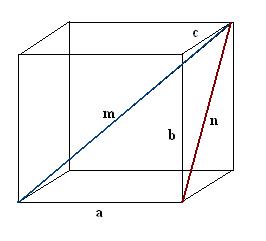
3. Find the constructed diagonal of the face. She is the hypotenuse of another right triangle b, c, n. According to the Pythagorean theorem, n² = c² + b². Calculate this expression and take the square root of the resulting value - this will be the diagonal of face n.
4. Find the diagonal of the parallelepiped m. To do this, in the right triangle a, n, m, find the unknown hypotenuse: m² = n² + a². Substitute the known values, then calculate the square root. The resulting result will be the first diagonal of the parallelepiped m.
5. Similarly, draw all the other three diagonals of the parallelepiped in steps. Also, for all of them, perform additional construction of diagonals of adjacent faces. By looking at the right triangles formed and applying the Pythagorean theorem, discover the values of the remaining diagonals of the cuboid.
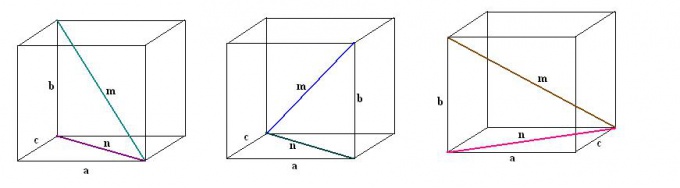
Video on the topic
Many real objects have a parallelepiped shape. Examples are the room and the pool. Parts with this shape are not uncommon in industry. For this reason, the task of finding the volume of a given figure often arises.
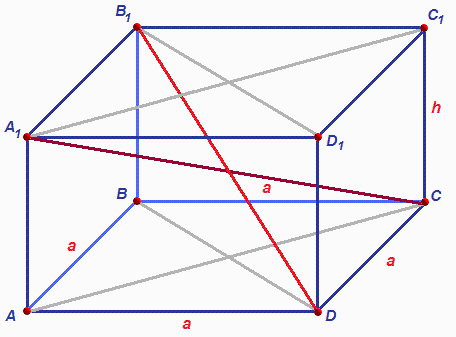
Instructions
1. A parallelepiped is a prism whose base is a parallelogram. A parallelepiped has faces - all the planes that form this figure. Each of them has six faces, and all of them are parallelograms. Its opposite sides are equal and parallel to each other. In addition, it has diagonals that intersect at one point and bisect at it.
2. There are 2 types of parallelepiped. For the first, all faces are parallelograms, and for the second, they are rectangles. The final one is called a rectangular parallelepiped. All its faces are rectangular, and the side faces are perpendicular to the base. If a rectangular parallelepiped has faces whose bases are squares, then it is called a cube. In this case, its faces and edges are equal. An edge is a side of any polyhedron, which includes a parallelepiped.
3. In order to find the volume of a parallelepiped, you need to know the area of its base and height. The volume is found based on which particular parallelepiped appears in the conditions of the problem. An ordinary parallelepiped has a parallelogram at its base, while a rectangular one has a rectangle or a square, which invariably has right angles. If there is a parallelogram at the base of a parallelepiped, then its volume is found as follows: V = S * H, where S is the area of the base, H is the height of the parallelepiped. The height of a parallelepiped is usually its side rib. At the base of a parallelepiped there can also be a parallelogram that is not a rectangle. From the course of planimetry it is known that the area of a parallelogram is equal to: S = a*h, where h is the height of the parallelogram, a is the length of the base, i.e. :V=a*hp*H
4. If the 2nd case occurs, when the base of the parallelepiped is a rectangle, then the volume is calculated using the same formula, but the area of the base is found in a slightly different way: V = S * H, S = a * b, where a and b are the sides, respectively rectangle and parallelepiped edge.V=a*b*H
5. To find the volume of a cube, one should be guided by primitive logical methods. Since all the faces and edges of the cube are equal, and at the base of the cube there is a square, guided by the formulas indicated above, we can derive the following formula: V = a^3
In many textbooks there are tasks related to the construction of sections of various geometric figures, including parallelepipeds. In order to cope with such a task, you should arm yourself with some knowledge.
You will need
- - paper;
- - pen;
- - ruler.
Instructions
1. Draw a parallelepiped on a piece of paper. If your problem says that the parallelepiped should be rectangular, then make its corners right. Remember that opposite edges must be parallel to each other. Name its vertices, say S1, T1, T, R, P, R1, P1 (as shown in the picture).
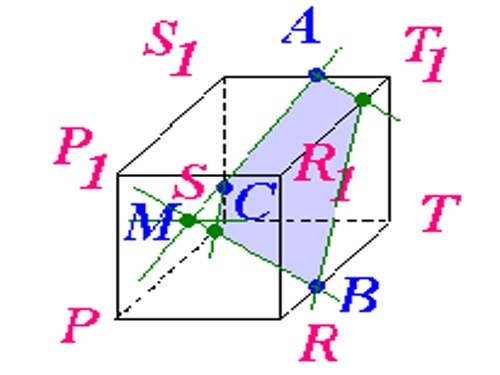
2. On the edge of SS1TT1 put 2 points: A and C, let point A be on the segment S1T1, and point C on the segment S1S. If your problem does not say where exactly these points must be, and the distance from the vertices is not indicated, place them arbitrarily. Draw a straight line through points A and C. Continue this line until it intersects with segment ST. Mark the place of intersection, let it be point M.
3. Place a point on the segment RT, designate it as point B. Draw a straight line through points M and B. Designate the point of intersection of this line with the edge SP as point K.
4. Combine points K and C. They must lie on the same face PP1SS1. Later, draw a straight line through point B, parallel to the segment KS, continue the line until it intersects with edge R1T1. Designate the intersection point as point E.
5. Combine points A and E. Later, highlight the resulting polygon ACKBE with a different color - this will be the section behind of this parallelepiped.
Note!
Remember that when constructing a section of a parallelepiped, you are allowed to connect only those points that lie in the same plane; if the points you have are not sufficient for constructing the section, complete them by extending the segments until they intersect with the face on which the point is needed.
Helpful advice
Each parallelepiped can have 4 sections: 2 diagonal and 2 transverse. For greater clarity, select the resulting polygon-section; for this, you can simply outline it or shade it with a different color.
Tip 6: How to find the length of the diagonals of a parallelepiped
A parallelepiped is a prism whose base is a parallelogram. The parallelograms that make up a parallelepiped are called its faces, their sides are called edges, and the vertices of the parallelepiped are called the vertices of the parallelepiped.
Instructions
1. U parallelepiped it is allowed to construct four intersecting diagonals. If the given 3 edges a, b and c are known, find the lengths diagonals rectangular parallelepiped It won’t be difficult to perform additional formations.
2. First draw a rectangular parallelepiped. Sign all the data you know, there should be three of them: edges a, b and c. Draw the first diagonal m. To construct it, use the property of rectangular parallelepipeds, according to which all angles of similar figures are right.
3. Construct the diagonal n of one of the faces parallelepiped. Make the construction in such a way that the famous edge(s), the unfamiliar diagonal parallelepiped and the diagonal of the adjacent face (n) formed a right triangle a, n, m.
4. Look at the constructed diagonal of the face (n). It is the hypotenuse of another right triangle b, c, n. Following the Pythagorean theorem, which states that the square of the hypotenuse is equal to the sum of the squares of the legs (n? = c? + b?), find the square of the hypotenuse, then take the square root of the resulting value - this will be the length of the diagonal of the face n.
5. Find the diagonal of the parallelepiped m. In order to find its value, in a right triangle a, n, m, calculate the hypotenuse using the same formula: m? = n? + a?. Calculate the square root. The discovered total will be the first diagonal of your parallelepiped. Diagonal m.
6. Correctly, draw all the other diagonals in steps as well. parallelepiped, for all of which perform additional constructions diagonals adjacent edges. Using the Pythagorean theorem, discover the values of the remaining diagonals given parallelepiped .
7. There is another method that can be used to determine the length of the diagonal. According to one of the properties of a parallelogram, the square of the diagonal is equal to the sum of the squares of its 3 sides. It follows from this that the length can be found by adding the squares of the sides parallelepiped and extract the square from the resulting value.
Helpful advice
Properties of a parallelepiped: - a parallelepiped is symmetrical about the middle of its diagonal; - any segment with ends belonging to the surface of a parallelepiped and passing through the middle of its diagonal is divided in half by it, in particular, all diagonals of a parallelepiped intersect at one point and are divided in half by it; - opposite faces of a parallelepiped parallel and equal; - the square of the diagonal length of a rectangular parallelepiped is equal to the sum of the squares of its three dimensions.
A parallelepiped is a three-dimensional geometric figure with three measuring dimensions: length, width and height. All of them are involved in finding the area of both surfaces parallelepiped: full and side.
Instructions
1. A parallelepiped is a polyhedron built on the basis of a parallelogram. It has six faces, which are also these two-dimensional shapes. Depending on how they are located in space, a distinction is made between straight and inclined parallelepiped. This difference is expressed in the equality of the angle between the base and the side edge of 90°.
2. Based on which particular case of a parallelogram the base belongs to, we can distinguish a rectangular parallelepiped and its especially common variety - the cube. These forms are especially common in Everyday life and are called standard. They are inherent in household appliances, pieces of furniture, electronic devices, etc., as well as in human dwellings themselves, the dimensions of which are of significant importance for residents and realtors.
3. Usually it is believed square both surfaces parallelepiped, side and full. The first numerical collation represents the common area of its faces, the second is the same value plus the areas of both bases, i.e. the sum of all two-dimensional figures that make up a parallelepiped. The following formulas bear the name of the main ones along with the volume: Sb = P h, where P is the perimeter of the base, h is the height; Sp = Sb + 2 S, where So is square grounds.
4. For special cases, cube and figure with rectangular bases, the formulas are simplified. Now it is no longer necessary to determine the height, which is equal to the length of the vertical edge, but square and the perimeter is much easier to detect due to the presence of right angles; only length and width are involved in their determination. It turns out that for a rectangular parallelepiped:Sb = 2 c (a + b), where 2 (a + b) is the double sum of the sides of the base (perimeter), c is the length of the side edge; Sp = Sb + 2 a b = 2 a c + 2 b c + 2 a b = 2 (a c + b c + a b).
5. All edges of a cube have identical lengths, therefore: Sb = 4 a a = 4 a?; Sp = Sb + 2 a? = 6 a?.
The question relates to analytical geometry. It is solved using the equations of spatial lines and planes, the representation of the cube and its geometric properties, as well as using vector algebra. Methods for solving systems of linear equations may be required.
Instructions
1. Select these tasks so that they are comprehensive, but not redundant. Cutting plane? should be given by a general equation of the form Ax+By+Cz+D=0, which the best way consistent with his arbitrary choice. To define a cube, the coordinates of any 3 of its vertices are absolutely enough. Take, say, points M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), according to Figure 1. This figure illustrates a cross section of a cube. It intersects two side ribs and three base ribs.
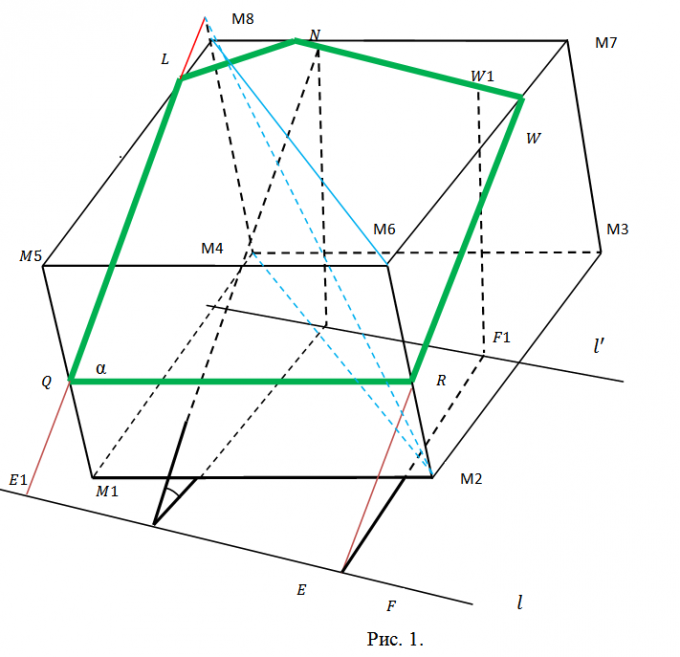
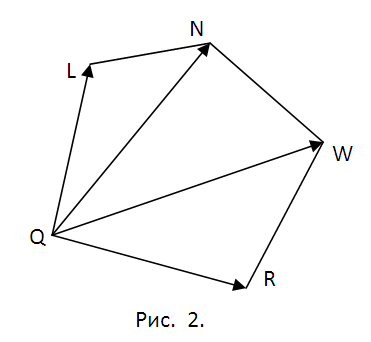
2. Decide on a plan for subsequent work. We have to look for the coordinates of the points Q, L, N, W, R where the section intersects with the corresponding edges of the cube. To do this, you will have to find the equations of the lines containing these edges and look for the points of intersection of the edges with the plane?. Later this will be followed by partitioning the pentagon QLNWR into triangles (see Fig. 2) and calculating the area of all of them using the properties of the vector product. The methodology is the same every time. Consequently, we can limit ourselves to the points Q and L and the area of the triangle?QLN.
3. The direction vector h of the straight line, containing the edge M1M5 (and point Q), is found as the vector product M1M2=(x2-x1, y2-y1, z2-z1) and M2M3=(x3-x2, y3-y2, z3-z2), h=(m1, n1, p1)=. The resulting vector is a guide for all other side edges. Find the length of the edge of the cube as, say, ?=?((x2-x1)^2+(y2-y1)^2+(z2-z1)^2). If the modulus of the vector h |h|??, then replace it with the corresponding collinear vector s=(m, n, p)=(h/|h|)?. Now write down the equation of the straight line containing M1M5 parametrically (see Fig. 3). After substituting the corresponding expressions into the equation of the cutting plane, you get A(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Determine t, substitute it into the equations for M1M5 and write down the coordinates of the point Q(qx, qy, qz) (Fig. 3).
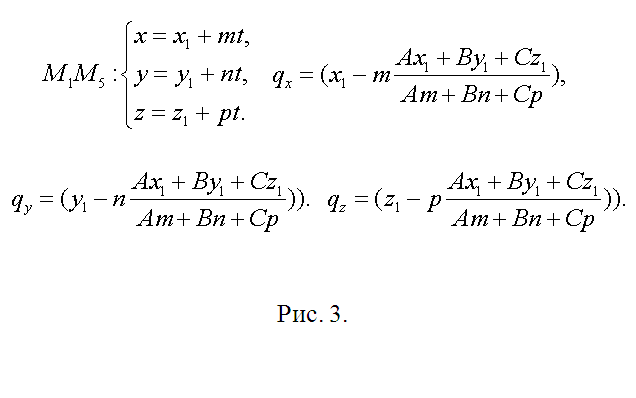
4. Apparently, point M5 has coordinates M5(x1+m, y1+n, z1+p). The direction vector for the straight line containing the edge M5M8 coincides with M2M3=(x3-x2, y3-y2,z3-z2). After this, repeat the previous reasoning regarding the point L(lx, ly, lz) (see Fig. 4). Everything that follows for N(nx, ny, nz) is an exact copy of this step.
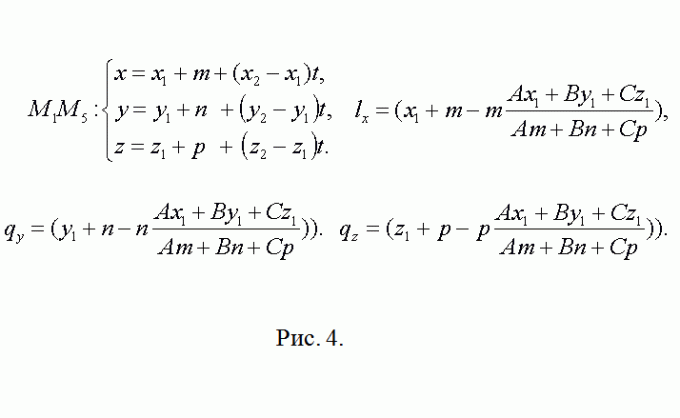
5. Write down the vectors QL=(lx-qx, ly-qy, lz-qz) and QN=(nx-qx, ny-qy, nz-qz). The geometric meaning of their vector product is that its modulus equal to area parallelogram built on vectors. Consequently, the area?QLN S1=(1/2)||. Follow the suggested method and calculate the areas of the triangles ?QNW and ?QWR - S1 and S2. Vector artwork It’s more comfortable to find everyone with the support of the determinant vector (see Fig. 5). Write down the final result S=S1+S2+S3.
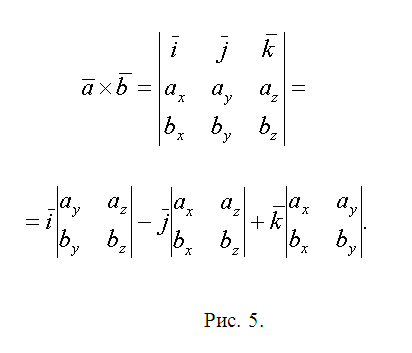
Tip 9: How to find the diagonal cross-sectional area of a prism
A prism is a polyhedron with two parallel bases and side faces in the shape of a parallelogram and in number, equal to the number sides of the base polygon.
Instructions
1. In an arbitrary prism, the side ribs are located at an angle to the plane of the base. A special case is a straight prism. In it sides lie in planes perpendicular to the bases. In a straight prism, the side faces are rectangles, and the side edges are equal to the height of the prism.
2. The diagonal section of a prism is a part of the plane entirely contained in the internal space of the polyhedron. The diagonal section can be limited by two side ribs geometric body and diagonals of the bases. Apparently, the number of permissible diagonal sections is determined by the number of diagonals in the base polygon.
3. Or the boundaries of the diagonal section can be the diagonals of the side faces and opposite sides prism bases. The diagonal cross-section of a rectangular prism has the shape of a rectangle. In the general case of an arbitrary prism, the shape of the diagonal section is a parallelogram.
4. IN rectangular prism The area of the diagonal section S is determined by the formulas: S=d*Hwhere d is the diagonal of the base, H is the height of the prism. Or S=a*Dwhere a is the side of the base that simultaneously belongs to the section plane, D is the diagonal of the side face.
5. In an arbitrary indirect prism, the diagonal section is a parallelogram, one side of which is equal to the lateral edge of the prism, the other is equal to the diagonal of the base. Or the sides of the diagonal section can be the diagonals of the side faces and the sides of the bases between the vertices of the prism, from where the diagonals of the side surfaces are drawn. The area of a parallelogram S is determined by the formula: S=d*hwhere d is the diagonal of the base of the prism, h is the height of the parallelogram - the diagonal section of the prism. Or S=a*hwhere a is the side of the base of the prism, which is also the boundary of the diagonal section, h is the height of the parallelogram.
6. To determine the height of the diagonal section, it is unsatisfactory to know the linear dimensions of the prism. We need data on the inclination of the prism to the base plane. The subsequent problem comes down to a stepwise solution of several triangles depending on the initial data on the angles between the elements of the prism.
“Golden Section” - Purpose of the study: To derive the law of beauty of the world from the point of view of mathematics. Admiralty. Window. Completed by 10th grade student Yulia Smetanina. Intercession Cathedral (St. Basil's Cathedral). Golden ratio in architecture. In mathematics, a proportion is the equality of two ratios: a: b = c: d. Egyptian pyramids.
“Construction of sections” - Sections are performed on the same scale as the image to which it relates. Features of making sections. Applying dimensions. Designation of sections. The outline of the exposed sections is performed solid line. Rules for making sections. Sections. Sections in the drawings are divided into extended and superimposed.
“Parallelepiped grade 10” - The angle is 60?. 3.Four, if the parallelepiped is a cube. The angle is 60?. 3.Equal squares, angles 90?. Iceland spar crystals have a rhombohedron shape. Option 2. Given parallelepiped ABCDA1B1C1D1. Diagonals of a parallelepiped. Prove that lines B1C and A1D are parallel. 2. The diagonals of the parallelepiped are equal. Parallelepiped.
“Volume of a parallelepiped” - We are doing the same now. IN Ancient Babylon The units of volume were cubes. Now let's define what volume units are? This means, according to the rule for calculating volume, we get: 3x3x3=27 (cm3). Task No. 2. Find the volume of a cube whose edge is 3 cm. A unit of volume equal to 1 dm3 is called a liter. Task No. 1.
“Lesson Rectangular parallelepiped” - Lesson goal: Length. Reflection. Find the area of the base of the rectangular parallelepiped. Construct a rectangle given length(a) and height (h). Scan. Edges. Ribs. Physical education minute. Algorithm for constructing a rectangular parallelepiped. Three times the length less height, and the width is 6 times less than the height.
“Volume of a rectangular parallelepiped” - T e s t. ( Geometric figure). 6. All faces of a parallelepiped are rectangles. 3. All faces of a cube are squares. Reply to next questions: Squares. Name the edges that have vertex E. Increase. Volumetric. Problem 2: The dimensions of a rectangular parallelepiped are 3cm, 6cm and 6cm.
With. 1
Lesson-based developments 11th grade using the textbook “Geometry” L. S. Atanasyan
LESSON No. 1. RECTANGULAR COORDINATE SYSTEM B SPACES !:
primary goal : introduce the concept of a Rectangular coordinate system, teach how to construct a point, knowing its coordinates, and determine it. coordinates of a point constructed in a rectangular coordinate system.
I . Oral work .
II build in in accordance with p. 42 textbooks.
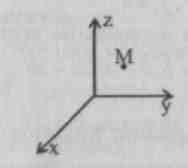The problem is whether the position of the point is set M.
V space? No. It is necessary to construct projections of the point M per plane (Ooh), (Oxz) (Ozy).
TO 
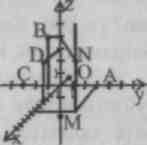test questions
Using the picture, find the coordinates of the points A, B, C,D, M, N.
Draw a coordinate system Oxyz and plot the points
Solving problems: No. 400 (oral), 401 (oral), 402.
Homework: theory (clause 42), No. 501.
LESSON No. 2. VECTOR COORDINATES
primary goal : introduce the concept of vector coordinates
I . Explanation of new material build in accordance with paragraph 43 of the textbook.
II . Problem solving : No. 403, 404,407(a, b, g, i, j, l) 410, 408, 412.
III
. Homework
: theory (item 13), repeat (item 38, 39), No. 405, 407 (d, e, f, g, h), 409 (c, d, e, f, h, m), 411.
LESSON No. 3. RELATIONSHIP BETWEEN VECTOR COORDINATES AND POINT COORDINATES
Primary goal: prove that the coordinates of any point are equal to the corresponding coordinates of its radius vector; teach how to find the coordinates of a vector, knowing the coordinates of its beginning and end.
I . Explanation of new material build in accordance with paragraph 44 of the textbook.
II. Problem solving : No. 416.417, 418 (a), 419.420.
III. Homework : theory (item 44), No. 418 (b, c), 421.
LESSON No. 4. THE SIMPLE PROBLEMS IN COORDINATES
Primary goal: derive formulas for finding the coordinates of the middle of a segment, the length of a vector from its coordinates, and the distance between two points.
Checking homework. No. 421. Solve No. 422.
III. Explanation of new material build in accordance with paragraph 45 of the textbook.
IV. Solving problems: No. 424, 426, 427, 430.
V. Homework: theory (item 45), No. 425, 429, 431.
LESSON No. 5.6 ANGLE BETWEEN VECTORS
Primary goal: generalize the concept of “angle between vectors”, teach you to find the angle between vectors in space.
Sh. Explanation of new material construct in accordance with paragraph 46. Show an example of finding angles between vectors on stereometric models (pay attention to the vectors lying on intersecting straight lines).
IV. Problem solving № 442,507,508
V. Homework: theory (clause 46), No. 441, for repetition - No. 490, 491 (oral), 492, 501.
№
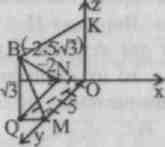501.
Find VM,BN, VH.
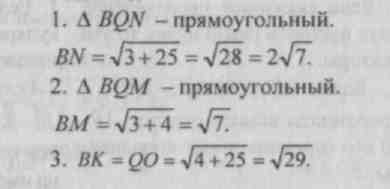Solution.
Explanation of new material.
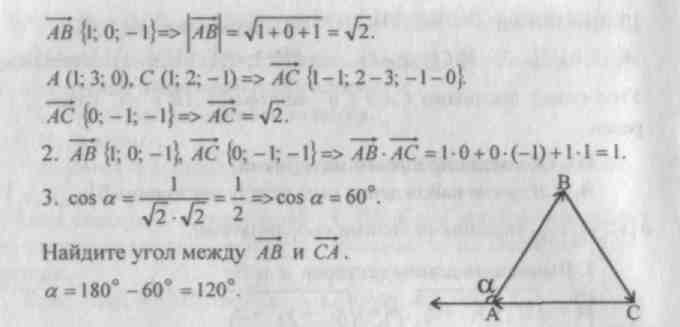
Homework: theory (clause 48), No. 451, 453, 464 (b, c, d), 469 (b, c).
Dictation
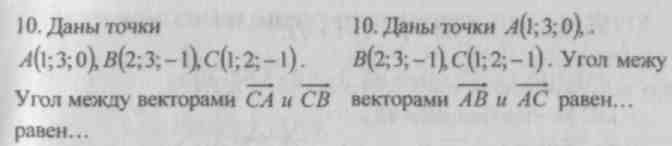
LESSON No. 7 SCALAR PRODUCT OF VECTORS
Primary goal: develop the skill of solving problems on finding an angle with vectors, straight lines, a straight line and a plane.
I. Checking homework ( at the board): No. 451 (b, d), No. 464 (c; d).
II. Problem solving(according to finished drawings).
Algorithm for solving problems:
Enter rectangular system coordinate"1
Write down the coordinates of all points.
Use an algorithm for finding the angle between straight lines, between a straight line and a plane.
III. Problem solving.
(vector method)
III. (Vector coordinate method).
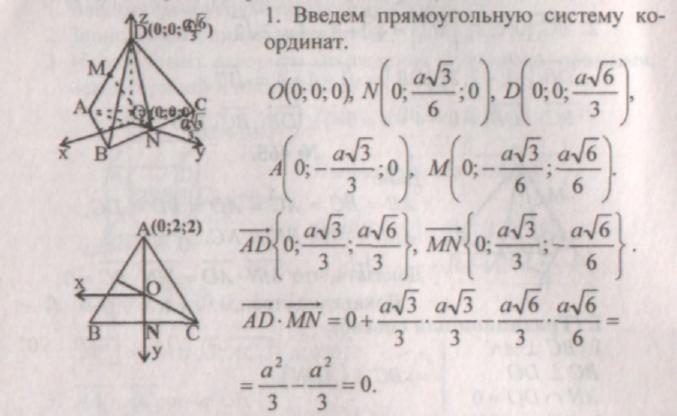
Homework:№ 455, 457, 462.
LESSON No. 8 SCALAR PRODUCT OF VECTORS
Primary goal: develop the skill of finding angles between straight lines, between a straight line and a plane.
№ 455.
(The drawing has been prepared in advance. Students speak out or someone writes the answers on the board.) 
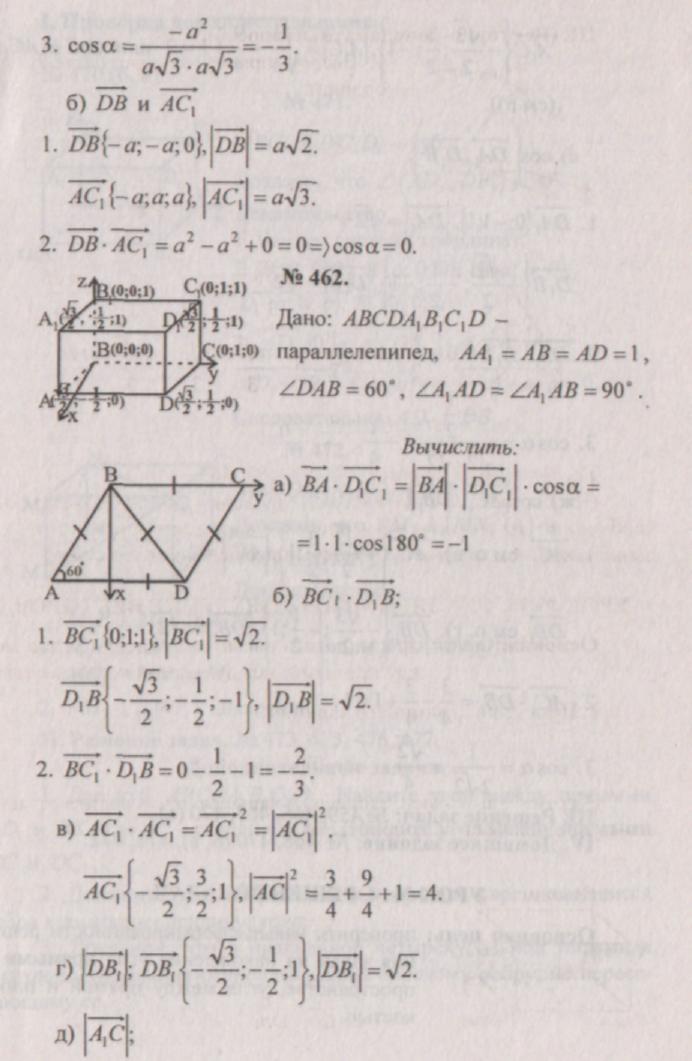
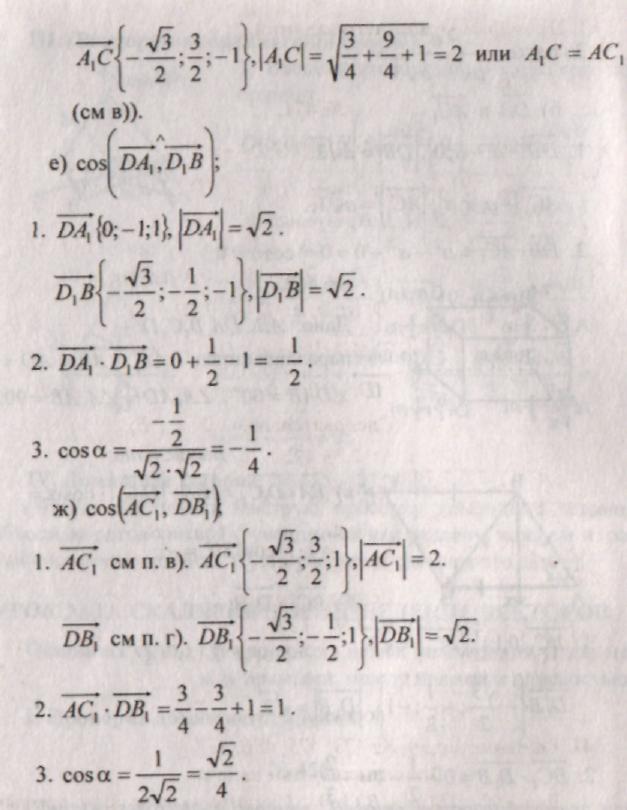
III. Problem solving: No. 459, 466, 467, 470 (a).
IV. Homework: No. 468, 470 (b, c), 471, 472.
LESSON No. 9 TEST No. 1
Tests for self-testing and correction of students' knowledge
|
Option |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
I |
V |
G |
V |
b |
A |
b |
G |
V |
|
II |
b |
A |
V |
G |
V |
b |
G |
G |
|
Option |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
I |
b |
G |
b |
V |
V |
G |
V |
b |
|
II |
b |
A |
G |
V |
G |
A |
V |
b |
LESSON #10. CYLINDER
Primary goal: introduce the concept of a cylinder, elements of a cylinder.
I. Explanation of new material build according to plan:
1. Concept cylindrical surface, cylinder.
Consider various items surrounding environment, giving an idea of the cylinder - a circular pencil, a glass, a penny, a pan, a piece of pipe, etc. (The cylinders shown must have different ratios between height and diameter.) Give an image of a cylinder, show in the drawing - axis, height, radius, generators, bases of the cylinder.
2. Enter concept of axial section of a cylinder, set its properties:
a) the axial section of the cylinder is a rectangle;
b) any two axial sections of the cylinder are equal to each other.
Introduce the concept of an equilateral cylinder with an axial section
which is a square.
3. Consider the section of a square by a plane
A) parallel axis cylinder;
b) perpendicular to the cylinder axis.
4. Introduce the concept of a tangent plane of a cylinder as a plane passing through the generatrix of the cylinder and perpendicular to the axial section drawn through this generatrix. (An analogy with a tangent to a circle).
II. Problem solving:№ 521, 522, 526, 529.
III. Homework:№ 523, 525, 530.
LESSON #11. CYLINDER
Primary goal: to formulate the skill of solving problems of finding the elements of a cylinder.
I. Checking homework(at the blackboard).
II. Oral work.
Identify objects in nature, technology, architecture, and among the objects around you that have a cylindrical shape.
Explain what is called a cylinder, a circular cylinder. Name its main elements and give them a definition.
Give the definition of a straight cylinder.
How many axial sections of the cylinder pass through each of its generatrices?
Determine the type of axial section of the cylinder. Justify your answer.
Can the axial section of a cylinder be: a) a rectangle; b) square; c) trapezoid?
Does the cylinder have: a) a center of symmetry; b) axis of symmetry; c) plane of symmetry? Please indicate them in each case. How many are there? Show on the model.
Let AA 1 IN 1 IN And MM1 N 1 N - two axial sections of the cylinder. Compare their areas.
A cylinder rolls along a plane. What figure is obtained when its axis moves?
Which of the following statements are true:
b) any section of a cylinder by a plane is a circle equal to the circumference of the base;
c) a plane perpendicular to the axis of the cylinder intersects it in a circle, equal basis cylinder;
d) the section of a cylinder by plane can be a circle, a rectangle and an ellipse?
12. Formulate and prove a theorem about the section of a cylinder by a plane perpendicular to its axis.
III. Problem solving: No. 527 (b), 532, 534.
IV. Homework: No. 527 (a), 531, 535.
LESSON #12. CONE
Primary goal: check the level of formulation of the problem solving skill of finding the elements of a cylinder. Introduce the concepts of a cone and elements of a cone.
Independent work (15 min).
The section of the cylinder with a plane parallel to the axis is a square, the area of which is 20 dm. Find the axial cross-sectional area of the cylinder if its diagonal is 10 dm.
Option II
The height of the cylinder is 16 cm, the radius of the base is 10 cm. The cylinder is crossed by a plane parallel to the axis so that the cross-section is square. Find the distance from the cylinder axis to this section.
The development of the lateral surface of the cylinder is a rectangle, the diagonal of which, equal to 12l, makes an angle of 30° on one side. Find the total surface area of the cylinder if its height is equal to the shorter side of the development.
1. Concepts of a cone, its elements (top, axis, generators, base, side surface cone). Cone image
N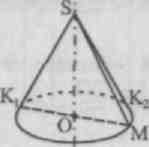 
in the figure we draw tangents from the point S
to the ellipse representing the base of the cone. Let us denote by TO 1
And TO 2
touch points. A common mistake is that students assume the triangle S.K. 1
K 2
for the image of the axial section of the cone. However, the chord TO 1
TO 2
does not pass through the center ABOUT base of the cone. To construct an image of an axial section passing through the generatrix S.K. 1
it is enough to construct an image of the diameter TO 1
M and connect the resulting point M with top S
cone S.K. 1
And S.K. 2
- images of extreme generators, i.e. they separate the visible generators (their images are obtained by connecting arbitrary point arcs TO 1
MK 2
ellipse with vertex S) from invisible.
2. Consider the cross section of a cone with various planes, highlighting two cases:
Cutting plane through the vertex of a cone;
The cutting plane is parallel to the base of the cone.
1(a). If they intersect at two points, then in the cross section of the cone we get isosceles triangle, the base of which is a segment with ends at these points. From axial section. It is obtained if the intersection points under consideration are the ends of the diameter of the base of the cone. Among the cones, an equilateral one stands out (its axial section is equilateral triangle). If R is the radius of its base, then the generatrix of an equilateral cone is equal to 2 R .
1(b). If they only have one common point, then the plane under consideration is tangent to the cone.
The tangent plane to a cone can be defined in different ways.
Definition 1. The plane passing through the generatrix of the cone is perpendicular to the axial section drawn through this generatrix.
Definition 2. A plane that has only one common generatrix with a cone.
The interpretation of a plane tangent to a cone and a plane tangent to a cylinder should be the same in the same textbook. It should be noted that by accepting one of propositions 1 or 2 in as a definition, it is necessary to familiarize students with the other as a property of a tangent plane to a cone.
1 (c). Continuing our consideration of the plane passing through the vertex of the cone, we come to the case: if the plane and the circle of the base do not have common points, then the plane in question with the cone have only one common point - the vertex of the cone.
2. When proving the theorem about the section of a cone by a plane parallel to its base (No. 556), it is advisable to obtain the following conclusions:
1. The section under consideration is a circle.
2. Designated by R And r - respectively, the radius of the cone and the section under consideration and through N And h the height of the given and cut off cone, we obtain that, ,where k is the similarity coefficient of the given and cut off cones. Prove that
Generalize by solving problem No. 557.
Consideration of the section, perpendicular to the axis cone, allows effective use homothety method similar to cross section of the pyramid by plane, parallel to the base. Having established the shape and location of the section, the concept of a truncated cone is introduced.
When depicting a truncated cone, it is convenient to first draw the cone from which the truncated cone is obtained.
Problem solving: No. 548 (a), 549.
Homework: theory (p. 55, 56), No. 547, 548 (b, c), 550.
LESSON #13. CONE
Primary goal: introduce the concept of the area of the lateral surface of a cone as the area of its development.
I. Checking homework(at the blackboard).
II
Introduce the concept of lateral surface area using the development of a cone.
The total surface area of a cone.
Derive a formula for calculating the area of the lateral surface of a truncated cone.
V. Homework: No. 560 (b, c), 561, 563, 568.
LESSON No. 14. SPHERE AND BALL. SPHERE EQUATION. RELATIVE POSITION OF SPHERE AND PLANE. TANGENT PLANE TO THE SPHERE. AREA OF THE SPHERE
Primary goal: enter concepts of sphere and ball, derive the equation of the sphere, consider the relative position of the sphere and the plane, define the tangent plane to the sphere, write down the formula for calculating the area of the sphere.
I. Explanation of new material construct in a lecture manner in accordance with paragraphs 58 - 62 of the textbook.
For examples, use problems: No. 575 to understand the definitions of the sphere; No. 576, 578 for working out the equation of the sphere; No. 586 for illustration relative position spheres and planes; No. 593 (a), 594 to practice the formula for the area of a sphere.
Problem solving:
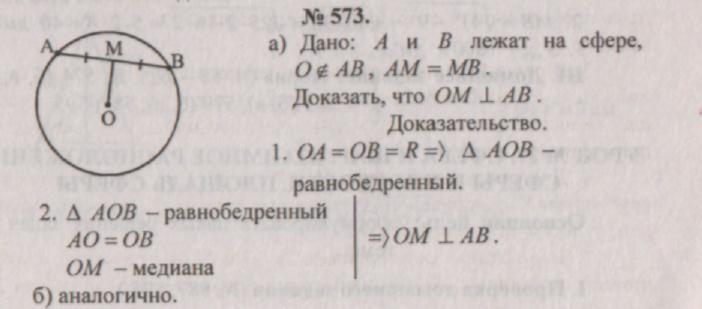
III. Homework: theory (p. 58 - 62), No. 574 (b, c, d).
577 (b, c), 579 (6, c), 587, 595.
LESSON No. 15. SPHERE AND BALL. RELATIVE POSITION OF SPHERE AND PLANE. AREA OF THE SPHERE
Primary goal: formulate the skill of solving problems on a topic.
Examination home tasks (No. 587, 595.)
Problem solving
III. Homework: No. 582, 584, 585, 592, 597.
LESSON No. 16. PREPARATION FOR THE TEST
Primary goal: repeat, systematize, generalize the studied material.
I. Checking homework(at the blackboard): No. 582, 584, 585.
II. Oral work- on questions to Chapter VI.
III. Problem solving.
Lesson #17 Test № 2
LESSON No. 18. VOLUME OF A RECTANGULAR PARALLELEPIPED
Primary goal: introduce the concept of body volume.
I. Explanation of new material.
A. The concept of volume of a body is introduced by analogy with the concept of area flat figure. Possible together with students fill out the second half tables.
Control questions.
What is the volume of a body?
What does it mean to measure body volume?
4. How to get 
unit cube?
5. The unit cube fits into the part of space occupied by the octahedron, 2 times and 2 times - the fraction of the unit cube, which number is characterized V octahedron?
B. Volume of a cube equal to cube his ribs. V= a 3 .
Derive the formula for calculation V cube, if its diagonal is known
II. Problem solving.
1. The total surface area of a cube is 6 m 2 . Find its volume. (1 m 3)
The volume of the cube is 8 m. Find the total surface area.
If each edge of a cube is increased by 1 m, then its volume will increase 125 times. Find the edge of the cube.
Three cubes made of lead have edges of 3, 4 and 5 cm. They are melted into one cube. Find his rib
The volume of a cube is A. Find the area of its diagonal
III. Two bodies whose volumes are equal are called equal-sized.
(When proving the following theorem, use a model or a previously prepared drawing.)
Theorem. An inclined prism is equal in size to a straight prism, the base of which is perpendicular to the inclined section, and the side edge is equal to the side edge inclined prism.
Control questions.
Which two bodies are called equal in size?
Two bodies are equal. Are they the same size?
The two bodies are equal in size. Are they equal?
LESSON No. 19. VOLUME OF A RECTANGULAR PARALLELEPIPED
Primary goal: develop the skill of solving problems to find the volume of a parallelepiped.
I. Oral work.
What is the volume of a body?
What is the volume of a cube? A tenth of it?
The cube is intersected by two diagonal sections. What is the volume of each part?
In a cube with an edge of 2 cm diagonal section made. What is the volume of each of the resulting parts?
The total surface area of the cube is 24 cm2. What is the volume of a cube?
The diagonal of the cube is A. Find its volume.
Volume of a cube V. Find its diagonal.
The diagonal of a cube's face is 8. What is the volume of the cube?
The volume of the inclined prism is 27 cm 3 . What is the size of an edge of a cube of equal size?
Explanation of new material.
The volume of a rectangular parallelepiped is equal to the product of its three dimensions. V = abc . Or the volume of a rectangular parallelepiped is equal to the product of the area of the base and the height. V= S basic H
III. Problem solving.
Homework: theory (vol. 64), no. 648,650,651,652
IV. Independent work.
OPTION I
1. The volume of a rectangular parallelepiped is 96 cm, the side edge is 8 cm. What is the area of the base?
The base of a rectangular parallelepiped is a square with side A. The diagonal of the side face forms an angle α with the plane of the base.
In a rectangular parallelepiped, the diagonals of adjacent lateral faces emanating from the same vertex form angles α and β with common side rib emanating from the same vertex. The lateral edge of the parallelepiped is equal to b . Find the volume of the parallelepiped.
The volume of a rectangular parallelepiped is 100 cm 3, the base area is 25 cm 2. Find the height of the parallelepiped.
In a rectangular parallelepiped, the base is a square. The diagonal of the parallelepiped is d and forms an angle α with the side edge having general beginning. Find the volume of the parallelepiped.
LESSON No. 20. VOLUME OF A DIRECT PRISM
Primary goal: derive a formula for calculating the volume of a straight prism.
I. Checking homework.
P. Explanation of new material.
The base of a straight prism is a right triangle. Its volume is equal to the product of the area of the base and the height.
The base of a straight prism - arbitrary triangle. Its volume is equal to the product of the area of the base and the height.
Arbitrary straight prism. Prove that its volume is equal to the product of the area of the base and the height.
THAT. The volume of a straight prism is equal to the product of the area of the base and the height. 
Sh. Problem solving.№ 659, 661, 662, 729.
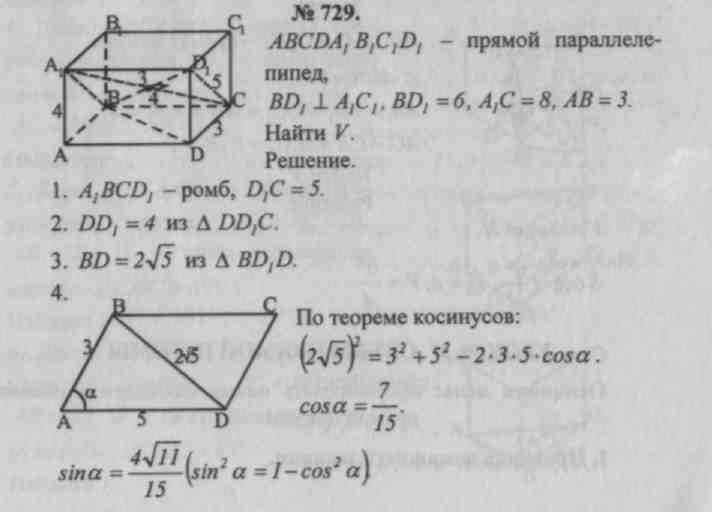
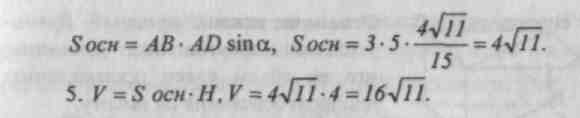
Homework: theory (item 65), No. 660, 728, 730, 731.
LESSON No. 21. CYLINDER VOLUME
Primary goal: derive a formula for calculating the volume of a cylinder.
I . Explanation of the new build in accordance with paragraph 66 of the textbook.
II. Problem solving. No. 671, 672.
Sh. Homework: theory (item 66), No. 666, 667, 668, 699, 670.
Additional tasks.
A section of the cylinder with a plane parallel to the axis cuts off an arc of 60° from the base circumference. The cross-sectional area is S, and the diagonal of the section makes an angle α with the plane of the base of the cylinder. Find the volume of the cylinder.
A section of a cylinder by a plane parallel to the axis cuts off an arc of 90° from the base circumference. The cross-sectional area is S, and the diagonal of the section makes an angle α with the generatrix of the cylinder. Find the volume of the cylinder.
A cube is inscribed in a cylinder. The volume of the cube is F. Find the volume of the cylinder.
LESSON No. 22. VOLUME OF A PYRAMID
Maintarget: develop the skill of finding the volume of a pyramid, whose vertex is projected to the center inscribed in the base of a circle or circumscribed around the base of a circle.
I. Checking homework.
Continue with the sentences.
If all the lateral edges of the pyramid are equal, then the vertex is projected onto the base in...
If all the apothems of the pyramid are equal, then the apex is projected onto the base in...
If all dihedral angles when the base is equal, then the vertex is projected onto the base in...
If all the side ribs are aligned with the plane of the base equal angles, then the vertex is projected onto the base in...
Sh. Problem solving.№ 691, 693, 695, 740.
IV. Homework:№ 692, 694.
P. Dictation.
LESSON No. 23,24. PREPARATION FOR THE TEST TEST TEST No. 4
Primary goal: check the level of development of problem solving skills to find the volume of a cylinder, inclined prism, pyramid and cone.
LESSON No. 25 VOLUME OF THE BALL AND ITS PARTS
Maintarget: derive the formula for the volume of a sphere and its parts.
I. Explanation of new material.
1. Volume of a sphere of radius R equals
For proof, see paragraph 71.
2. A spherical segment is the part of the ball cut off from it by a plane (Fig. a, c).
ABOUT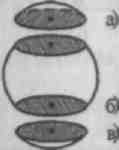 
volume ball segment is determined by the formula 
, where H is the height of the spherical segment
3. The spherical layer is the part of the ball located between two parallel planes, intersecting the ball (Fig. 323, b). 
4. A spherical sector is a body that is obtained from a spherical segment and a cone. The volume of the spherical sector is determined by the formula, where H is the height of the corresponding spherical segment
II. Problem solving.
Problem 1. What is the volume of a spherical sector if the radius of its base circle is 60 cm and the radius of the ball is 75 cm?
Solution. 1. Under the base of the sector in the task is understood as the basis segment corresponding to the sector. Let R - radius of the ball, r - radius of the segment base.
2. Our task comes down to finding the height of this segment: N – RO 1 . OR - the radius of the ball perpendicular to the base of the segment.
3. From a right triangle O.O. l M(˂ M.O. 1 O= 90°) let's find: OO 1 = √OM 2 - O 1 M 2 = √75 2 +60 2 =40, therefore H = P.O. l = OP- O.O. l = R-00 ] =75-45 = 30.
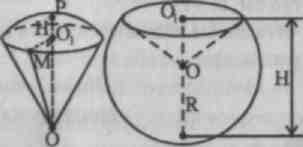
4. Volume of the spherical sector. =112500π
5. Note. The problem has two solutions:
1) The spherical sector that we considered is called convex, and its height is equal to R – OO 1 , is called non-convex.
Let's find its volume.
6. Consider the second case, where the sector height N =R + O.O. 1 = 120, so the resulting volume will be 4 times greater than the calculated volume: V = π45 10 4 cm 3
7. Thus, the required volume is either 112,500π cm or 450,000π cm 3.
III. Homemade assignment: theory (p. 71, 72), No. 710, 711, 717.
LESSON№ 26 . VOLUME OF THE BALL AND ITS PARTS
Primary goal: formulate the skill of finding the volume of a ball and its parts.
I. Checking homework.
Sh. Problem solving.
A. 1. The outer diameter of a hollow ball is 18 cm, the wall thickness is 3 cm. Find the volume of the material from which the ball is made.
[b84πcm 3.]
The diameter of a lead ball is 30 cm. How many balls with a diameter of 3 cm can be made from this lead?
The radii of the three balls are 3, 4, 5 cm. Find the radius of a ball whose volume is equal to the sum of their volumes,
The largest ball is carved from a cube. What percentage of the material is removed? [≈ 47.6%.]
Ball sector radius R, angle in axial section 120°. Find the volume.
Prove that if the radii of three balls are in the ratio 1:2:3, then the volume of the larger ball is 3 times more than the amount volumes of smaller balls.
The height of the ball segment is 0.4 times the radius of the ball. What part is the volume of this segment from the volume of a cylinder having the same base and height? 13\24
Two equal ball arranged so that the center of one lies on the surface of the other. How does the volume of the total part of the balls relate to the volume of the whole ball?
The diameter of the ball, equal to 30 cm, serves as the axis of a cylinder whose base radius is 12 cm. Find the volume of the part of the ball,
Which figure has a larger volume: a sphere with a radius of 1 dm or a regular one? triangular prism, each edge of which is equal to 2 dm? [The volume of the ball is larger.]
A section of a ball by a plane perpendicular to its radius divides the radius in half. Find the ratio of the volumes of the parts of the ball.
A section of a ball by a plane perpendicular to its diameter divides the diameter in a ratio of 1:2. Find the ratio of the volumes of the parts of the ball.
LESSON No. 27. AREA OF A SPHERE
Primary goal: derive a formula for calculating the surface area of a ball.
I. Explanation of new material build in accordance with paragraph 73 of the textbook.
II. Problem solving: No. 722, 723, 724; for repetition - No. 761, 762, 763.
III. Homework: cards.
LESSON No. 28. PREPARATION FOR THE TEST
I. Questions to review the topic.
Ball and its elements.
Volume of the ball and its parts.
Bodies of revolution and their volumes.
Polyhedra and their volumes.
Surface area of the ball.
Surface area of polyhedra.
III. Problem solving.
Volume of a sphere radius R equals V. Find the volume of a sphere with radius: 2 R; 0,5R.
Surface area regular tetrahedron equal to the surface area of the sphere. Find the ratio of the volumes of the tetrahedron and the sphere.
The diameter of a ball of radius 12 cm is divided into 3 parts, the lengths of which are in the ratio 3:3:2. Planes perpendicular to the diameter are drawn through the division points. Find the volume of each formed parts of the ball.
5. To the right one quadrangular pyramid a ball is inscribed so that the side faces of the pyramid touch the surface of the ball, and its big circle lies at the base of the pyramid. Side faces pyramids are inclined to the plane of the base at an angle A, and the volume of the ball is equal to V . Find the volume of the pyramid.
Home test
Option 1
The volume of the ball is 400 cm3. Another ball is built on the radius as on the diameter. Find the volume of the small sphere.
3. The diagonal section of a rectangular parallelepiped inscribed in a ball is a square with area S. Find the volume of the sphere.
4. The diameter of a ball with a radius of 12 cm is divided into 3 parts, the lengths of which are in the ratio 1:3:4. Planes perpendicular to the diameter are drawn through the division points. Find the volume of the resulting spherical layer.
MO "Senkinskaya Secondary School"
With. 1