The video course “Get an A” includes all the topics necessary for successful passing the Unified State Exam in mathematics for 60-65 points. Completely all problems 1-13 Profile Unified State Examination mathematics. Also suitable for passing the Basic Unified State Examination in mathematics. If you want to pass the Unified State Exam with 90-100 points, you need to solve part 1 in 30 minutes and without mistakes!
Preparation course for the Unified State Exam for grades 10-11, as well as for teachers. Everything you need to solve Part 1 of the Unified State Exam in mathematics (the first 12 problems) and Problem 13 (trigonometry). And this is more than 70 points on the Unified State Exam, and neither a 100-point student nor a humanities student can do without them.
All necessary theory. Quick ways solutions, pitfalls and secrets of the Unified State Exam. All current tasks of part 1 from the FIPI Task Bank have been analyzed. The course fully complies with the requirements of the Unified State Exam 2018.
The course contains 5 big topics, 2.5 hours each. Each topic is given from scratch, simply and clearly.
Hundreds of Unified State Exam tasks. Word problems and probability theory. Simple and easy to remember algorithms for solving problems. Geometry. Theory, reference material, analysis of all types of Unified State Examination tasks. Stereometry. Tricky solutions, useful cheat sheets, development spatial imagination. Trigonometry from scratch to problem 13. Understanding instead of cramming. Visual explanation complex concepts. Algebra. Roots, powers and logarithms, function and derivative. Basis for solution complex tasks 2 parts of the Unified State Exam.
Lesson objectives:
- Introduce the concept of parallel planes.
- Consider and prove theorems expressing the sign of parallelism of planes and the properties of parallel planes.
- Trace the application of these theorems in solving problems.
Lesson plan (write on the board):
I. Preparatory oral work.
II. Learning new material:
1. The relative position of two planes in space.
2. Determination of parallel planes.
3. Sign of parallel planes.
4. Property of parallel planes.
III. Lesson summary.
IV. Homework.
DURING THE CLASSES
I. Oral work
I would like to start the lesson with a quote from Chaadaev’s philosophical letter:
“Where does this miraculous power of analysis in mathematics come from? The fact is that the mind here acts in complete submission to this rule.”
We will look at this obedience to the rule in the next task. To learn new material, you need to repeat some questions. To do this, you need to establish a statement that follows from these statements and justify your answer:
II. Learning new material
1. How can two planes be located in space? What is the set of points belonging to both planes?
Answer:
a) coincide (then we will be dealing with one plane, it’s not satisfactory);
b) intersect, ;
c) do not intersect ( common points absolutely not).
2. Definition: If two planes do not intersect, then they are called parallel
3. Designation:
4. Give examples of parallel planes from the environment
5. How to find out if any two planes in space are parallel?
Answer:
You can use the definition, but this is inappropriate, because It is not always possible to establish the intersection of planes. Therefore, it is necessary to consider a condition sufficient to assert that the planes are parallel.
6. Let's consider the situations:
b) if 
?
c) if 
?
Why is the answer in a) and b) “not always”, but in c) “yes”? (Intersecting lines define a plane in a unique way, which means they are uniquely defined!)
Situation 3 is a sign of parallelism of two planes.
7. Theorem: If two intersecting lines of one plane are respectively parallel to two lines of another plane, then these planes are parallel.
Given:
Prove:
Proof:
(Students apply designations to the drawing.)
1. Note: . Likewise:
2. Let: .
3. We have: Similarly:
4. We get: through M there is a contradiction with the axiom of planimetry.
5. So: incorrect, means , etc.
8. Solve No. 51 (Students apply symbols to the drawing).
Given:
Prove:
Proof:
1 way
1. Let's build 
Method 2
Enter via via .
9. Let's consider two properties of parallel planes:
Theorem: If two parallel planes are intersected by a third, then the lines of their intersection are parallel.
(The students themselves complete the construction and mark it on the drawing).
Given:
In this lesson we will define parallel planes and recall the axiom about the intersection of two planes. Next, we will prove a theorem - a sign of parallelism of planes and, relying on it, we will solve several problems on the parallelism of planes.
Topic: Parallelism of lines and planes
Lesson: Parallel Planes
In this lesson we will define parallel planes and recall the axiom about the intersection of two planes.
Definition. Two planes are called parallel if they do not intersect.
Designation: .
Illustration of parallel planes(Fig. 1.)
1. What planes are called parallel?
2. Can planes passing through nonparallel lines be parallel?
3. What it could be mutual arrangement two straight lines, each of which lies in one of two different parallel planes?
4. Geometry. Grades 10-11: textbook for students educational institutions(basic and profile levels) / I. M. Smirnova, V. A. Smirnov. - 5th edition, corrected and expanded - M.: Mnemosyne, 2008. - 288 pp.: ill.
Tasks 1, 2, 5 p. 29
The relation of parallelism of planes, its properties and applications is considered.
A visual representation of the location of the two
planes gives modeling using the planes of the surfaces of adjacent walls, the ceiling and floor of the room, bunk beds, two fastened sheets of paper
magicians, etc. (Fig. 242–244).
Although there is infinite set options for the relative arrangement of various planes, to establish and characterize which measurements of angles and distances will be used in the future, we will first focus on those where the classification (as well as straight lines with planes) is based on the number of their common points.
1. Two planes have at least three common points that do not lie on the same line. Such planes coincide (axiom C 2, §7).
2. The common points of two planes are located on one straight line, which is the line of intersection of these planes (axiom C 3, §7). Such planes intersect.
3. The two planes have no common points.
IN in this case they are called parallel-
Two planes are called parallel if they have no common points.
The parallelism of planes is indicated by the sign ||: α || β.
As always, when introducing geometric concepts arose-
There is no problem with their existence. The existence of intersecting-
Xia planes is characteristic feature space,
and we have already used this many times. Less obvious is
The existence of parallel planes is confirmed. There is no
doubts that, for example, planes of opposite graphs
The cubes are parallel, that is, they do not intersect. But directly
Indeed, by definition, this cannot be established. For solving
understanding of the question posed, as well as other issues related to
parallelism of planes, it is necessary to have a sign of parallelism.
To search for a sign, it is advisable to consider a plane,
“woven” from straight lines. It is obvious that each straight line is one of
parallel planes must be parallel to the other.
IN otherwise the planes will have a common point. Enough
Is the plane β exactly parallel to the same straight line α
so that planes α and β are parallel? Absolutely
but, no (justify this!). Practical experience shows that
two such intersecting lines are sufficient. To secure
on the mast there is a platform parallel to the ground, just place it
on two beams attached to the mast, parallel |
||
earthly (Fig. 245). There are many more |
||
examples of the use of this provision technique |
||
parallelism of real flat surfaces |
||
objects (try this!). |
||
The above considerations allow us to formulate |
||
lyrate the following statement. |
||
(a sign of parallel planes). |
||
intersecting straight lines of one plane |
||
If the planes are parallel to the second plane, then these planes are parallel.
Let the intersecting lines a and b of the plane α be parallel to the plane β. Let us prove that the planes α and β are parallel by contradiction. To do this, let us assume that the planes α and β intersect along a straight line
t (Fig. 246). Lines a and b cannot intersect lines according to the condition. However, then in the plane α two straight lines are drawn through one point that do not intersect with the straight line, that is, parallel to it. This is a contradiction
and completes the proof of the theorem.
The sign of parallelism of planes is used when horizontally placing flat structures (concrete slabs, floors, disk of goniometer devices, etc.) using two levels placed in the plane of the structure on intersecting straight lines. Based on this feature, it is possible to construct a plane parallel to this one.
Problem 1. Through a point lying outside a given plane, draw a plane parallel to the given one.
Let the plane β and a point M outside the plane be given (Fig. 247, a). Let us draw through point M two intersecting lines a and b, parallel to the plane β. To do this, you need to take two intersecting straight lines c and d in the β plane (Fig. 247, b). Then through point M draw lines a and b parallel to lines c and d, respectively.
but (Fig. 247, c).
Intersecting lines a and b parallel to the plane β, based on the parallelism of the line and the plane (Theorem 1 §11). They uniquely define the plane α. According to the proven criterion, α || β.
Example 1. Given a cube ABCDA 1 B 1 C 1 D 1 , points M , N , P are the midpoints of the edges BC , B 1 C 1 , A 1 D 1 , respectively. Establish the relative position of the planes: 1) ABB 1 and PNM; 2) NMA and A 1 C 1 C ; 3)A 1 NM
and PC 1 C; 4) MAD 1 and DB 1 C.
1) The planes ABB 1 and РNM (Fig. 248) are parallel, based on the parallelism of the planes (Theorem 1). Indeed, the lines РN and NM intersect and are parallel to the plane ABB 1, based on the parallelism of the line and the plane (Theorem 1 §11), because the segments РN and NM connect the midpoints opposite sides squares, so they are parallel to the sides of the squares:
РN ||A 1 B 1 ,NM ||В 1 B.
2) Planes NMA and A 1 C 1 C intersect along straight line AA 1 (Fig. 249). Indeed, the lines AA 1 and CC 1 are parallel, based on the parallelism of the lines (AA 1 ||ВB 1,ВB 1 ||СC 1). Therefore, straight line AA 1 lies in the plane A 1 C 1 C. The belonging of straight line AA 1 to the plane NMA is similarly justified.
3) Planes A 1 NM and РС 1 C (Fig. 250) are parallel, based on the parallelism of the planes. Indeed, NM ||С 1 C . Therefore, the straight line NM is parallel to the plane PC 1 C. The segments PC 1 and A 1 N are also parallel, since the quadrilateral PC 1 NA 1 is a parallelogram (A 1 P ||NC 1, A 1 P =NC 1). Thus, line A 1 N is parallel to plane PC 1 C. Lines A 1 N and NM intersect.
4) The planes MAD 1 and DB 1 C intersect (Fig. 251). Although the line of their intersection is not easy to construct, it is not difficult to indicate one point of this line. Indeed, the lines A 1 D and B 1 C are parallel, since the quadrilateral A 1 B 1 CD is a parallelogram (A 1 B 1 = AB = CD , A 1 B 1 || AB , AB || CD ). Therefore, line A 1 D belongs to the plane DB 1 C. Lines A 1 D and AD 1 intersect at a point common to the planes MAD 1 and DB 1 C.
The given sign of parallelism of planes |
||
sometimes it is more convenient to use in a slightly different |
||
1′ (sign of parallel planes). |
||
If two intersecting lines of one plane are respectively parallel to two lines of another plane, then these planes are parallel.
Using the criterion of parallelism of a line and a plane (Theorem 1 §11), it is easy to establish that the condition of Theorem 1 follows from the conditions of Theorem 1. The application of the theorem inverse to the criterion of parallelism of a line and a plane (Theorem 2 §11) completes the justification for the equivalence of the conditions of Theorems 1 and 1 ′.
Naturally, the question arises about the uniqueness of the construction given in Problem 1. Since we will have to use this property more than once, we will highlight it as a separate theorem. However, let's look at another statement first.
Theorem 2 (about the intersection of two parallel planes with a third).
If two parallel planes are intersected by a third plane, then the lines of intersection of the planes are parallel.
Let parallel planes α, β and a plane γ intersecting them be given (Fig. 252). Let us denote the intersection lines
through a and b. These lines lie in the γ plane and do not intersect, since the α and β planes do not have common points. Therefore, directly
a and b are parallel.
Theorem 3 (on the existence and uniqueness of a plane parallel to this one).
Through a point located outside a given plane, one can draw a single plane parallel to the given one.
The construction of such a plane was carried out in problem 1. We will prove the uniqueness of the construction by contradiction. Let us assume that two different planes α and γ are drawn through point M, pa-
parallel planes β (Fig. 253), and straight line t is the line of their intersection. Let us draw a plane δ through the point M, intersecting the line
m and the β plane (how can this be done?). Let us denote by a and b
the line of intersection of the plane δ with the planes α and γ, and through c - the line of intersection of the planes δ and β (Fig. 253). According to Theorem 2,a ||c
and b ||s. That is, in the δ plane through
two straight lines parallel to straight lines pass through point M. A contradiction indicates that the assumption is incorrect.
The relation of parallelism of planes has a number of properties that have analogues in planimetry.
Theorem 4 (on segments of parallel lines between parallel planes).
Segments of parallel lines cut off by parallel planes are equal to each other.
Let two parallel planes α and β and segments be given AB
and CD of parallel straight lines a and d, cut off by these planes (Fig. 254, a). Let us draw the plane γ through straight lines a and d (Fig. 254, b). It intersects the planes α and β along straight lines AC and BD, which, according to Theorem 2, are parallel. Therefore, quadrilateral ABCD is a parallelogram; its opposite sides AC and BD are equal.
From the above property it follows that if we plot from all points of the plane
on one side of the plane parallel lines same length, then the ends of these segments form two parallel planes. It is on this property that the construction of a parallelepiped using the deposition of segments is based (Fig. 255).
Theorem 5 (on the transitivity of the relation of parallelism of planes).
If each of two planes is parallel to a third, then the two planes are parallel to each other.
Let the planes α and β be parallel to the plane γ. Let's assume that
α and β are not parallel. Then the planes α and β have a common point, and through this point there pass two different planes parallel to the plane γ, which contradicts Theorem 3. Therefore, the planes α and β do not have common points, that is, they are parallel.
Theorem 5 is another sign of parallelism of planes. It is widely used in both geometry and practical activities. For example, in a multi-story building, the parallelism of the floor and ceiling planes on each floor guarantees their parallelism on different floors.
Problem 2. Prove that if a straight line intersects the plane α, then it also intersects every plane parallel to the plane α.
Let planes α and β be parallel, and straight line a intersects plane α at point A. Let us prove that it also intersects the plane
β. Let's assume that this is not the case. Then straight line a is parallel to plane β. Let us draw the plane γ through the straight line and arbitrary point plane β (Fig. 256).
This plane intersects parallel planes α and β along straight lines b is. Co-
according to Theorem 2, b || c, that is, in the plane γ, two lines a and b pass through point A, parallel to line c . This contradiction proves the statement.
Try to prove on your own that if the plane α intersects the plane β, then it also intersects every plane parallel to the plane β.
Example 2. In the tetrahedron ABCD, points K, F, E are the midpoints of edges DA, DC, DB, aM and P - the centers of mass of faces ABD and ВСD, respectively.
1) Establish the relative position of the planes KEF and ABC;
DEF and ABC.
2) Construct the intersection line of the AFB and KEC planes.
3) Find the cross-sectional area of the tetrahedron by a plane parallel to the plane ABD and passing through point P if all the edges of the tetrahedron are equal.
Let’s construct a drawing that meets the condition (Fig. 257, a). 1) The planes KEF and ABC are parallel, based on the parallelism of the planes (Theorem 1’): the intersecting lines KE and KF of the KEF plane are parallel to the intersecting lines AB and AC of the ABC plane (the midlines of the corresponding
existing triangles).
Planes DEF and ABC intersect along straight line BC, since straight line BC belongs to both planes, and they cannot coincide - points A, B, C, D do not lie in the same plane.
2) Plane AFB intersects with plane KEC along a straight line containing point P, since lines CE and BF lying in these planes are in the plane BCD and intersect at point P. Another point is the point of intersection Q of straight lines AF and CK in the plane ACD (Fig. 257, b). Obviously, this point is the center of mass of the ACD face. The required intersection is the line PQ.
3) Construct the section specified in the condition, using the sign of parallelism of planes. Let us draw lines through points P and Q parallel to lines DB and DA, respectively (Fig. 257, c). These lines intersect the segment CD at point L. The latter follows from the property of the center of mass of a triangle - it divides the medians of the triangle in a ratio of 2: 1, counting from the vertex. It remains to apply Thales' theorem. Thus, the PLQ and BDA planes are parallel. The required section is triangle LSN.
By construction, triangles BCD and SCL are similar with similarity coefficient CE CP =3 2. Therefore LS =3 2 BD . Similar to the established
the following equalities are added: LN =3 2 AD,NS =3 2 AB. It follows that the triangles LSN and ABD are similar with a similarity coefficient of 3 2. According to the properties of the areas of similar triangles,
S LNS =4 9 S ABD . It remains to find the area of triangle ABD. By-
since, by condition, all edges of the tetrahedron are equal to a, then S ABD =4 3 a 2.
The required area is 3 1 3 a 2 .
It is appropriate to note that the answer depends only on the area of the face ABD. Therefore, the equality of all edges is only a means of finding this area. Thus, this task can be significantly generalized.
Answer. 1)KEF ||ABC ; 3)3 1 3 a 2 .
Test questions
1. Is it true that two planes are parallel if every line lying in one plane is parallel to the other plane?
2. Planes α and β are parallel. Are there skew lines lying in these planes?
3. Two sides of a triangle are parallel to a certain plane. Is the third side of the triangle parallel to this plane?
4. Two sides of a parallelogram are parallel to a certain plane. Is it true that the plane of a parallelogram is parallel to the given plane?
5. Can segments of two straight lines cut off by parallel planes be unequal?
6. Can the cross section of a cube be isosceles trapezoid? Can the cross section of a cube be regular pentagon? Is it true that two planes parallel to the same line are parallel to each other?
The lines of intersection of planes α and β with plane γ are parallel to each other. Are planes α and β parallel?
Can three faces of a cube be parallel to the same plane?
Graphic exercises
1. Fig. 258 shows the cube ABCDA 1 B 1 C 1 D 1, points M, N, K, L, P are the midpoints of the corresponding edges. Fill out the table according to the example given by selecting required location planes α and β.
Mutual
location
α || β α = β
α × β α || β α = β
A1 B1 C1 | D 1 KP |
||
and ADC | and BB1 D | and MNP | and BMN |
B 1 KP | A1 DC1 | A1 C1 C |
|
and PLN | and DMN | and AB1 C | and MKP |
2. In Fig. 259 shows a tetrahedron ABCD, points K, F, M, N, Q are the midpoints of the corresponding edges. Please indicate:
1) a plane passing through point K parallel to plane ABC;
2) a plane passing through the line BD parallel to the plane MNQ.
3. Determine what is the section of a figure by a plane passing through the given three points shown in the figure.
kah 260, a)–e) and 261, a)–d).
4. Construct a drawing based on the given data.
1) From the vertices of a parallelogram ABCD lying in one of two parallel planes, parallel lines are drawn that intersect the second plane at points A 1 , B 1 , C 1 , D 1 , respectively.
2) Triangle A 1 B 1 C 1 is the projection of triangle ABC onto the plane α parallel to it. Point M is the middle of the sun, M 1 is the projection of point M onto the plane α.
207. In the cube ABCDA 1 B 1 C 1 D 1 points O, O 1 are the centers of faces ABCD and A 1 B 1 C 1 D 1, respectively, M is the middle of edge AB.
1°) Determine the relative position of the planes MO 1 O
and ADD 1, ABD 1 and CO 1 C 1.
2°) Construct the point of intersection of the plane DCC 1 and straight line MO 1 and the line of intersection of the planes MCC 1 and A 1 D 1 C 1.
3) Find the cross-sectional area of a cube by a plane parallel to the plane AD 1 C 1 and passing through the point O 1 if the edge of the cube is equal to a.
208. In the tetrahedron ABCD, the points K, L, P are the centers of mass of the faces ABD, BDC, ABC, respectively, and aM is the middle of the edge AD.
1°) Determine the relative position of the ACD planes
and KLP ; MLK and ABC .
2°) Construct the point of intersection of plane ABC and line ML and the line of intersection of planes MKL and ABC.
3) Find the cross-sectional area of the tetrahedron by a plane passing through the points K, L and M parallel to the straight line AD, if all the edges of the tetrahedron are equal.
209. Given a cube ABCDA 1 B 1 C 1 D 1 . Points L, M, M 1 are the midpoints of edges AB, AD and A 1 D 1, respectively.
1°) Determine the relative position of the planes B 1 D 1 D
and LMM1.
2) Construct a plane passing through point M parallel to the plane ACC 1.
3) Construct a section of the cube with a plane passing through point M 1 parallel to the plane CDD 1.
4) Determine the relative position of the planes MA 1 B 1
and CDM1.
5) Construct a plane passing through the line C 1 D 1 parallel to the plane CDM 1.
210. In a regular quadrangular pyramidSABCD, all edges are equal to each other. Points L, M and N are the midpoints of the edges AS, BS, CS, respectively.
1°) Determine the relative position of: straight lines LM and BC; straight line LN and plane ABD; planes LMN and BDC.
2°) Prove that triangles ABC and LMN are similar.
3) Construct a section of the pyramid using the plane AMN; plane LMN; planeLBC.
4*) Which of the sections of the pyramid passing through the vertex S has the largest area?
Parallelism of lines and planes
In the SABC tetrahedron all faces are regular triangles. Points L, M and N are the midpoints of the edges AS, BS, CS, respectively. 1°) Determine the relative position of straight lines LM and BC. 2°) Determine the relative position of straight line LN and plane ABC.
3) Prove that triangles LMN and ABC are similar.
From the vertices of a parallelogram ABCD lying in one of |
|||
two parallel planes, drawn in pairs parallel |
|||
linear straight lines intersecting the second plane corresponding |
|||
specifically at points A 1, B 1, C 1, D 1. | |||
1°) Prove that the quadrilateral A 1 B 1 C 1 D 1 is parallel |
|||
2°) Prove that parallelograms ABCD and A 1 B 1 C 1 D 1 |
|||
are equal to each other. | |||
3°) Determine the relative position of the planes ABC 1 |
|||
and DD1 C1. | |||
4) Draw plane 1 through the middle of segment AA so |
|||
so that it intersects these lines at points that are |
|||
vertices of a parallelogram equal to the parallelogram |
|||
mu ABCD. | |||
Given two parallel planes and a point O, not belonging to |
|||
pressing against any of these planes and not lying between |
|||
them. From point O | three rays are drawn intersecting the plane |
||
bones, respectively, at points A, B, C and A 1, B 1, C 1 and not lying |
|||
lying in the same plane. | |||
1°) Determine the relative position of these planes |
|||
and the plane passing through the midpoints of the segments AA 1, BB 1, CC 1. |
|||
2) Find the perimeter of triangle A 1 B 1 C 1 ifOA = m, |
|||
AA 1 = n, AB = c, AC = b, BC = a. | |||
Triangle A 1 B 1 C 1 is the projection of triangle ABC |
|||
onto the plane α parallel to it. Point M - middle of hundred |
|||
ron BC ;M 1 - projection of point M | onto the α plane. Point N |
||
divides side AB | in a ratio of 1:2. | plane M 1 MN and straight |
|
1) Construct the intersection point N 1 |
|||
my A 1 B 1 . | |||
2) Determine the shape of the quadrilateral M 1 N 1 NM. |
|||
M lies outside the plane of the trapezoid ABCB from the base- |
|||
mi AD | and B.C. Construct the line of intersection of the planes: |
||
1°) ABM and CDM; | 2) CBM and ADM. |
||
Construct a section of the cube that is: 1°) equilateral triangle; 2) a pentagon.
217. Construct a section of a tetrahedron that is a parallelogram.
218°. Prove that opposite faces of a parallelepiped are parallel.
219. Prove that the set of all lines passing through this point and parallel to a given plane, forms a plane parallel to the given one.
220. Given four points A, B, C, D, not lying in the same plane. Prove that each plane parallel to the lines AB and CD intersects the lines AC, AD, BD, BC at the vertices of the parallelogram.
221. Prove that a plane and a line not belonging to this plane are parallel to each other if both of them are parallel to the same plane.
222. Through the point O of the intersection of the diagonals of the cube ABCDA 1 B 1 C 1 D 1 a plane is drawn parallel to the face ABCD. This plane intersects edges BB 1 and CC 1 at points M and N, respectively. Prove that angle MON is a right angle.
223. Prove that two planes are parallel to each other if and only if every straight line intersecting one of the planes also intersects the second.
224*. In a triangular pyramid SABC, through segments AD and CE, where D is the midpoint SB, and E is the midpoint SA, draw sections of the pyramid parallel to each other.
225. Find geometric places:
1) the midpoints of all segments with ends on two data parallel planes; 2*) midpoints of segments with ends on two given intersecting lines.
226*. Side AB of triangle ABC lying in plane α is parallel to plane β. Equilateral triangle 1 B 1 C 1 is parallel projection triangle ABC on the plane β;AB = 5, BC = 6, AC = 9.
1) Establish the relative position of straight lines AB and A 1 B 1,
BC and B1 C1, A1 C1 and AC.
2) Find the area of triangle A 1 B 1 C 1.
227*. Given two intersecting lines. Indicate the set of all points in space through which a line can be drawn intersecting each of two given lines.
Basic definition
The two planes are called
are parallel,
if they do not have common points.
Main statements
Parallel sign - If two intersecting straight lines of one plane of the plane are respectively parallel to two straight lines of the second plane, then these planes
the bones are parallel.
Theorem on intersecting If two parallel-intersecting two non-parallel planes are intersected by a third plane, then the lines of the third intersection of the plane
they are parallel.
a α,b α,a ×b ,c β,d β,a ||c ,b ||d α || β
α || β, a = γ∩α,b = γ∩βa ||b
M α
β: α || β,M β
Getting ready for thematic
for assessment on the topic “Parallelism of lines and planes”
Self-control tasks
1. The four points do not belong to the same plane. Can some three of them lie on the same straight line?
2. Can three different planes have exactly two points in common?
3. Can two skew lines be parallel to a third line at the same time?
4. Is it true that straight a and b are not parallel if there is no line c parallel to a and b?
5. Can they equal segments have unequal projections?
6. Can a ray be a parallel projection of a line?
7. Can a square be an image of a cube?
8. Is it true that through a given point in space only one plane can be drawn parallel to a given line?
9. Is it always possible to draw a line through a given point parallel to two given planes that do not contain this point?
10. Is it possible to draw parallel planes through two intersecting lines?
Answers to tasks for self-control
Test sample
Two parallelograms ABCD and ABC 1 D 1 lie in different planes.
1°) Determine the relative position of straight lines CD and C 1 D 1.
2°) Determine the relative position of the straight line C 1 D 1 and the plane
3°) Construct the line of intersection of the planes DD 1 C 1 and ВСС 1.
4°) Determine the relative position of the planes ADD 1 and BCC 1.
5) Through point M, dividing segment AB in a ratio of 2:1, counting from point A, draw a plane α parallel to plane C 1 BC. 6) Construct the point of intersection of the straight line AC with the plane α and find the ratio in which this point divides the segment AC.
Parallelism of lines and planes |
|||
The relative position of lines in space |
|||
Table 21 |
|||
Number of common points | |||
At least two | |||
lie in one | do not lie in one |
||
plane | plane |
||
Relative position of straight lines and planes in space
Table 22 |
||||
Number of common points | ||||
At least two | None |
|||
a lies in α | and intersects α | and i α - parallel |
(a α) | (a × α) | ny (a || α) |
Mutual arrangement of planes in space |
||
Table 23 |
||
Number of common points | ||
At least three | At least one, but | None |
not lying on | there are no common points, no le- |
|
one straight line | pressing on one straight line | |
Trigonometric
You have already dealt with trigonometric functions in geometry lessons. Until now, their applications were mainly limited to solving triangles, that is, we were talking about finding some elements of a triangle from others. From the history of mathematics it is known that the emergence of trigonometry is associated with the measurement of lengths and angles. However, now the sphere
her applications are much wider than in ancient times.
The word "trigonometry" comes from the Greek τριγωνον
(trigonon) – triangle and µετρεω (metreo) – measure, measure-
I bark. Literally it means measuring triangles.
IN This chapter systematizes the material already known to you from the geometry course, and continues the study trigonometric functions and their applications to characterize batch processes, in particular rotational movement, oscillatory processes and so on.
Most applications of trigonometry relate specifically to periodic processes, that is, processes that repeat at regular intervals of time. Sunrise and sunset, changes in seasons, rotation of the wheel - these are the simplest examples of such processes. Mechanical and electromagnetic vibrations are also important examples of periodic processes. Therefore, the study of periodic processes is an important task. And the role of mathematics in its solution is decisive.
getting ready to study the topic “Trigonometric functions”
It is advisable to begin studying the topic “Trigonometric functions” by reviewing the definitions and properties of trigonometric functions of angles of triangles and their applications for solving both right and arbitrary triangles.
Sine, cosine, tangent, cotangent of rectangular angles
triangle
Table 24
The sine of an acute angle is the ratio opposite leg to the hypotenuse:
sin α = a c .
The cosine of an acute angle is the ratio adjacent leg to the hypotenuse:
cosα = b c .
The tangent of an acute angle is the ratio of the opposite side to the adjacent side:
tg α =a b .
The cotangent of an acute angle is the ratio of the adjacent side to the opposite side:
ctgα = a b .
Sine, cosine, tangent, cotangent of angles from 0° to 180°
Table 25
sin α = R y ; cosα = R x ;
tg α = x y ; cotgα = x y.
(X;at) - point coordinates A located on the upper semicircle, α - the angle formed by the radius OA circle with axis X.
Values of sine, cosine, tangent, cotangent
some corners
Table 26
Corner t
0° | 90° | 180° |
||||||||||
sin t | ||||||||||||
cos t | ||||||||||||
tg t | ||||||||||||
ctg t | ||||||||||||
Trigonometric functions |
Solving arbitrary triangles
Table 27
Theorem of sines
The sides of a triangle are proportional to the sines of opposite angles:
sin aα = sin bβ = sin cγ .
Cosine theorem
The square of an arbitrary side of a triangle is equal to the sum of the squares of the other two sides without twice the product of these sides by the cosine of the angle between them:
c2 = a2 + b2 − 2 ab cos γ ,b2 = a2 + c2 − 2 ac cos β , a2 = b2 + c2 − 2 bc cos α .
The area of a triangle is equal to half the product of its two sides and the sine of the angle between them:
S=1 2 absinγ = 1 2 acsinβ = 1 2 bcsinα .
Basic trigonometric identities
Table 28 |
||||||||||||||||
0 ° ≤ α ≤ 180° | sin 2 α + cos 2 α = 1 |
|||||||||||||||
0 ° ≤ α ≤ 180°, α ≠ 90° | ||||||||||||||||
1 +tgα = cos2 α |
||||||||||||||||
0 ° < α < 180° | 1 + ctg 2 α = | |||||||||||||||
sin 2 α |
||||||||||||||||
Given a triangle ABC,WITH= 90°, Sun=3 ,AB= 2. What is equal to |
||||||||||||||||
IN ? | B. 45 °. | IN. 60 °. | ||||||||||||||
A. 30 °. | ||||||||||||||||
G. It is impossible to calculate without computing tools. |
||||||||||||||||
Given a triangle | ABC , WITH | Sun= 3, | IN= 60°. What is equal to |
|||||||||||||
AB ? | ||||||||||||||||
A. 3 | B. 6. | 3 . |
||||||||||||||
According to these parties right triangle find |
||||||||||||||||
cosine of its smaller angle: A= 3,b= 4,c | ||||||||||||||||
A. 0,8. | ||||||||||||||||
Which of the given values cannot take the skew- |
||||||||||||||||
nus of an acute angle? | ||||||||||||||||
7 − 1 | 7 2 | |||||||||||||||
A. | ||||||||||||||||
5. Compare the sum of sines sharp corners arbitrary right triangle (we denote it byA) with one.
< 1. B.A= 1.
> 1. G. It's impossible to compare. Arrange the numbers in ascending order: A= sin 30°, b= cos 30°,
= tg 30°.
<
b<c.B.a<c<b Trigonometric functions For which acute angles is sine less than cosine? For all. For smaller ones 45°. For large 45°. G. Not for anyone. What is cos equal to? α, if α is an acute angle of a rectangular triangle square and sinα = 12
.
The length of the shadow of a tree is 15 m. The rays of the Sun form an angle 30° with the Earth's surface. What is the approximate height? tree? Select the most accurate result. B. 13 m. IN. 7m. What is the value of the expression 1 −
x2
at X= – 0,8? B. –0,6. G.≈ 1,34. From the formula a2
+b2
=4
express b< 0 черезa. A.b=4
−a2
. B.b=a2
−4
. b= −a2
− 4
. b= −4
−a2
. Dot A located in the third quarter at a distance of 3 from the axis X And on distance 10
from the origin. What are the coordinates has a point A?
B.(−1; 3). IN.(−1; −3). G.(−3; −1). next points belongs circle x 2+
y 2 =
1? B.(0,5; 0,5). . G. 15.
Specify the coordinates of the pointA, lying on a circle of radius 1 (see figure). (−1; 0).B.(1; 0). (0; − 1). G.(0; 1).A.IN.
Parallelism of planes. If two intersecting lines of one plane are respectively parallel to two intersecting lines of another plane, then these planes are parallel.
Proof. Let a And b- plane data, a 1 And a 2– straight lines in a plane a, intersecting at point A, b 1 And
b 2 correspondingly, the lines parallel to them in the plane b. Let us assume that the planes a And b not parallel, that is, they intersect along some straight line With. Straight A 1 is parallel to the line b 1, which means it is parallel to the plane itself b(a sign of parallelism between a line and a plane). Straight A 2 is parallel to the line b 2, this means it is parallel to the plane itself b(a sign of parallelism between a line and a plane). Straight With belongs to the plane a, which means at least one of the straight lines a 1 or a 2 intersects a line With, that is, it has a common point with it. But straight With also belongs to the plane b, which means crossing the line With, straight a 1 or a 2 intersects the plane b, which cannot be, since they are straight a 1 And a 2 parallel to the plane b. It follows from this that the planes a And b do not intersect, that is, they are parallel.
Theorem 1
. If two parallel planes intersect in thirds, then the straight lines of intersection are parallel. 
Proof. Let a And b- parallel planes, and g
- the plane intersecting them. Plane a intersected with the plane g
in a straight line A. Plane b intersected with the plane g in a straight line b. Intersection lines A And b lie in the same plane g
and therefore can be either intersecting or parallel lines. But, belonging to two parallel planes, they cannot have common points. Therefore they are parallel.
Theorem 2.
The segments of parallel lines enclosed between two parallel planes are equal.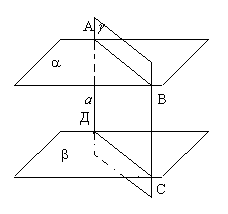 
Proof. Let a And b- parallel planes, and A
And b- parallel lines intersecting them. Through straight lines A And b we will conduct plane g
(these lines are parallel, which means define a plane, and only one). Plane a intersected with the plane g
in a straight line AB .
Plane b intersected with the plane g along the straight line SD. According to the previous theorem, the straight line With parallel to the line d. Direct A,b, AB
And
SD belong to the plane g A quadrilateral bounded by these lines is a parallelogram (its opposite sides are parallel). And since this is a parallelogram, then its opposite sides are equal, that is, AD = BC