General information about straight prism
The lateral surface of a prism (more precisely, the lateral surface area) is called sum areas of the side faces. The total surface of the prism is equal to the sum of the lateral surface and the areas of the bases.
Theorem 19.1. The lateral surface of a straight prism is equal to the product of the perimeter of the base and the height of the prism, i.e., the length of the side edge.
Proof. The lateral faces of a straight prism are rectangles. The bases of these rectangles are the sides of the polygon lying at the base of the prism, and the heights are equal to the length of the side edges. It follows that the lateral surface of the prism is equal to
S = a 1 l + a 2 l + ... + a n l = pl,
where a 1 and n are the lengths of the base edges, p is the perimeter of the base of the prism, and I is the length of the side edges. The theorem has been proven.
Practical task
Problem (22) . In an inclined prism it is carried out section, perpendicular to the side ribs and intersecting all the side ribs. Find the lateral surface of the prism if the perimeter of the section is equal to p and the side edges are equal to l.
Solution. The plane of the drawn section divides the prism into two parts (Fig. 411). Let us subject one of them to parallel translation, combining the bases of the prism. In this case, we obtain a straight prism, the base of which is the cross-section of the original prism, and the side edges are equal to l. This prism has the same lateral surface as the original one. Thus, the lateral surface of the original prism is equal to pl.
Summary of the covered topic
Now let’s try to summarize the topic we covered about prisms and remember what properties a prism has.

Prism properties
Firstly, a prism has all its bases as equal polygons;
Secondly, in a prism all its lateral faces are parallelograms;
Thirdly, in such a multifaceted figure as a prism, all lateral edges are equal;
Also, it should be remembered that polyhedra such as prisms can be straight or inclined.
Which prism is called a straight prism?
If the side edge of a prism is located perpendicular to the plane of its base, then such a prism is called a straight one.
It would not be superfluous to recall that the lateral faces of a straight prism are rectangles.
What type of prism is called oblique?
But if the side edge of a prism is not located perpendicular to the plane of its base, then we can safely say that it is an inclined prism.
Which prism is called correct?

If a regular polygon lies at the base of a straight prism, then such a prism is regular.
Now let us remember the properties that a regular prism has.
Properties of a regular prism
Firstly, regular polygons always serve as the bases of a regular prism;
Secondly, if we consider the side faces of a regular prism, they are always equal rectangles;
Thirdly, if you compare the sizes of the side ribs, then in a regular prism they are always equal.
Fourthly, a correct prism is always straight;
Fifthly, if in a regular prism the lateral faces have the shape of squares, then such a figure is usually called a semi-regular polygon.
Prism cross section
Now let's look at the cross section of the prism:

Homework
Now let's try to consolidate the topic we've learned by solving problems.
Let's draw an inclined triangular prism, the distance between its edges will be equal to: 3 cm, 4 cm and 5 cm, and the lateral surface of this prism will be equal to 60 cm2. Having these parameters, find the side edge of this prism.
Do you know that geometric figures constantly surround us, not only in geometry lessons, but also in everyday life there are objects that resemble one or another geometric figure.

Every home, school or work has a computer whose system unit is shaped like a straight prism.
If you pick up a simple pencil, you will see that the main part of the pencil is a prism.
Walking along the central street of the city, we see that under our feet lies a tile that has the shape of a hexagonal prism.
A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions
Different prisms are different from each other. At the same time, they have a lot in common. To find the area of the base of the prism, you will need to understand what type it has.
General theory
A prism is any polyhedron whose sides have the shape of a parallelogram. Moreover, its base can be any polyhedron - from a triangle to an n-gon. Moreover, the bases of the prism are always equal to each other. What does not apply to the side faces is that they can vary significantly in size.
When solving problems, not only the area of the base of the prism is encountered. It may require knowledge of the lateral surface, that is, all the faces that are not bases. The complete surface will be the union of all the faces that make up the prism.
Sometimes problems involve height. It is perpendicular to the bases. The diagonal of a polyhedron is a segment that connects in pairs any two vertices that do not belong to the same face.
It should be noted that the base area of a straight or inclined prism does not depend on the angle between them and the side faces. If they have the same figures on the top and bottom faces, then their areas will be equal.
Triangular prism
It has at its base a figure with three vertices, that is, a triangle. As you know, it can be different. If so, it is enough to remember that its area is determined by half the product of the legs.
The mathematical notation looks like this: S = ½ av.
To find out the area of the base in general, the formulas are useful: Heron and the one in which half of the side is taken by the height drawn to it.
The first formula should be written as follows: S = √(р (р-а) (р-в) (р-с)). This notation contains a semi-perimeter (p), that is, the sum of three sides divided by two.
Second: S = ½ n a * a.
If you want to find out the area of the base of a triangular prism, which is regular, then the triangle turns out to be equilateral. There is a formula for it: S = ¼ a 2 * √3.

Quadrangular prism
Its base is any of the known quadrangles. It can be a rectangle or square, parallelepiped or rhombus. In each case, in order to calculate the area of the base of the prism, you will need your own formula.
If the base is a rectangle, then its area is determined as follows: S = ab, where a, b are the sides of the rectangle.
When it comes to a quadrangular prism, the area of the base of a regular prism is calculated using the formula for a square. Because it is he who lies at the foundation. S = a 2.
In the case when the base is a parallelepiped, the following equality will be needed: S = a * n a. It happens that the side of a parallelepiped and one of the angles are given. Then, to calculate the height, you will need to use an additional formula: n a = b * sin A. Moreover, angle A is adjacent to side “b”, and height n is opposite to this angle.
If there is a rhombus at the base of the prism, then to determine its area you will need the same formula as for a parallelogram (since it is a special case of it). But you can also use this: S = ½ d 1 d 2. Here d 1 and d 2 are two diagonals of the rhombus.

Regular pentagonal prism
This case involves dividing the polygon into triangles, the areas of which are easier to find out. Although it happens that figures can have a different number of vertices.
Since the base of the prism is a regular pentagon, it can be divided into five equilateral triangles. Then the area of the base of the prism is equal to the area of one such triangle (the formula can be seen above), multiplied by five.

Regular hexagonal prism
Using the principle described for a pentagonal prism, it is possible to divide the hexagon of the base into 6 equilateral triangles. The formula for the base area of such a prism is similar to the previous one. Only it should be multiplied by six.
The formula will look like this: S = 3/2 a 2 * √3.

Tasks
No. 1. Given a regular straight line, its diagonal is 22 cm, the height of the polyhedron is 14 cm. Calculate the area of the base of the prism and the entire surface.
Solution. The base of the prism is a square, but its side is unknown. You can find its value from the diagonal of the square (x), which is related to the diagonal of the prism (d) and its height (h). x 2 = d 2 - n 2. On the other hand, this segment “x” is the hypotenuse in a triangle whose legs are equal to the side of the square. That is, x 2 = a 2 + a 2. Thus it turns out that a 2 = (d 2 - n 2)/2.
Substitute the number 22 instead of d, and replace “n” with its value - 14, it turns out that the side of the square is 12 cm. Now just find out the area of the base: 12 * 12 = 144 cm 2.
To find out the area of the entire surface, you need to add twice the base area and quadruple the side area. The latter can be easily found using the formula for a rectangle: multiply the height of the polyhedron and the side of the base. That is, 14 and 12, this number will be equal to 168 cm 2. The total surface area of the prism turns out to be 960 cm 2.
Answer. The area of the base of the prism is 144 cm 2. The entire surface is 960 cm 2.
No. 2. Given At the base there is a triangle with a side of 6 cm. In this case, the diagonal of the side face is 10 cm. Calculate the areas: the base and the side surface.
Solution. Since the prism is regular, its base is an equilateral triangle. Therefore, its area turns out to be equal to 6 squared, multiplied by ¼ and the square root of 3. A simple calculation leads to the result: 9√3 cm 2. This is the area of one base of the prism.
All side faces are the same and are rectangles with sides of 6 and 10 cm. To calculate their areas, just multiply these numbers. Then multiply them by three, because the prism has exactly that many side faces. Then the area of the lateral surface of the wound turns out to be 180 cm 2.
Answer. Areas: base - 9√3 cm 2, lateral surface of the prism - 180 cm 2.
Prism elements
| Name | Definition | Designations on the drawing | Drawing |
| Reasons | Two faces that are congruent polygons lying in parallel planes. | ABCDE , KLMNP | |
| Side faces | All edges except the bases. Each side face is necessarily a parallelogram. | ABLK , BCML , CDNM , DEPN , EAKP | |
| Side surface | Merging side faces. | ||
| Full surface | Combining the bases and side surface. | ||
| Side ribs | Common sides of the side faces. | AK , BL , CM , DN , EP | |
| Height | A segment connecting the bases of a prism and perpendicular to them. | KR | |
| Diagonal | A segment connecting two vertices of a prism that do not belong to the same face. | BP | |
| Diagonal plane | A plane passing through the lateral edge of the prism and the diagonal of the base. | ||
| Diagonal section | The intersection of a prism and a diagonal plane. A parallelogram is formed in the cross-section, including its special cases - rhombus, rectangle, square. | EBLP | |
| Perpendicular section | The intersection of a prism and a plane perpendicular to its side edge. |
Prism properties
- 1. The bases of the prism are equal polygons.
- 2. The lateral faces of the prism are parallelograms.
- 3. The lateral edges of the prism are parallel and equal.
- 4. Prism volume equal to the product of its height and the area of its base:
- 5. The total surface area of the prism is equal to the sum of the area of its lateral surface and twice the area of the base.
Types of prisms
There are prisms straight And inclined.
Straight prism- a prism in which all lateral edges are perpendicular to the base.
Lateral surface area the straight line of the prism is equal to the product of the perimeter of the base and the height.Oblique prism- a prism in which at least one side edge is not perpendicular to the base.
Lateral surface area of an inclined prism is equal to the product of the perpendicular section perimeter and the length of the side edge. Volume of an inclined prism equal to the product of the perpendicular cross-sectional area and the lateral edge.Correct prism- a straight prism whose base is a regular polygon.
Properties of a regular prism
- 1. The bases of a regular prism are regular polygons.
- 2. The lateral faces of a regular prism are equal rectangles.
- 3. The lateral edges of a regular prism are equal.
see also
Links
| Polyhedra | |
|---|---|
| Correct (Platonic solids) |
|
| Regular non-convex | Stellated polyhedron (Stellated octahedron, Stellated dodecahedron, Stellated icosahedron, Stellated icosidodecahedron) |
| Convex | |
| Formulas, theorems, theories | |
| Other | |
Wikimedia Foundation. 2010.
See what “Prism (mathematics)” is in other dictionaries:
- (beginning) “Mathematics in Nine Books” (Chinese trad. 九章算術 ... Wikipedia
A branch of mathematics that deals with the study of the properties of various figures (points, lines, angles, two-dimensional and three-dimensional objects), their sizes and relative positions. For ease of teaching, geometry is divided into planimetry and stereometry. IN… … Collier's Encyclopedia
Zemlyakov, Alexander Nikolaevich File:Zemlyakov.jpg Alexander Nikolaevich Zemlyakov (April 17, 1950 (19500417), Bologoye January 1, 2005, Chernogolovka) mathematician, outstanding Soviet and Russian teacher, author of educational pedagogical ... ... Wikipedia
Alexander Nikolaevich Zemlyakov (April 17, 1950 (19500417), Bologoye January 1, 2005, Chernogolovka) mathematician, outstanding Soviet and Russian teacher, author of educational literature. Biography Graduated in 1967 with a gold medal... ... Wikipedia
Dodecahedron A regular polyhedron or Platonic solid is a convex polyhedron consisting of identical regular polygons and having spatial symmetry ... Wikipedia
This term has other meanings, see Pyramidatsu (meanings). The reliability of this section of the article has been questioned. You must verify the accuracy of the facts stated in this section. There may be explanations on the talk page... Wikipedia
In spatial geometry, when solving problems with prisms, the problem often arises with calculating the area of the sides or faces that form these volumetric figures. This article is devoted to the issue of determining the area of the base of the prism and its lateral surface.
Prism figure
Before moving on to considering formulas for the base area and surface of a prism of one type or another, you should understand what kind of figure we are talking about.
A prism in geometry is a spatial figure consisting of two parallel polygons that are equal to each other and several quadrangles or parallelograms. The number of the latter is always equal to the number of vertices of one polygon. For example, if a figure is formed by two parallel n-gons, then the number of parallelograms will be n.
The parallelograms connecting n-gons are called the lateral sides of the prism, and their total area is the area of the lateral surface of the figure. The n-gons themselves are called bases.
The picture above shows an example of a prism made from paper. The yellow rectangle is its top base. The figure stands on a second similar base. The red and green rectangles are the side faces.
What types of prisms are there?
There are several types of prisms. They all differ from each other in only two parameters:
- the type of n-gon forming the base;
- the angle between the n-gon and the side faces.
For example, if the bases are triangles, then the prism is called triangular, if it is quadrilateral, as in the previous figure, then the figure is called a quadrangular prism, and so on. In addition, an n-gon can be convex or concave, then this property is also added to the name of the prism.
The angle between the side faces and the base can be either straight, acute or obtuse. In the first case they speak of a rectangular prism, in the second - of an inclined or oblique one.
Regular prisms are classified as a special type of figures. They have the highest symmetry among other prisms. It will be regular only if it is rectangular and its base is a regular n-gon. The figure below shows a set of regular prisms in which the number of sides of an n-gon varies from three to eight.

Prism surface
The surface of the figure of arbitrary type under consideration is understood as the set of all points that belong to the faces of the prism. It is convenient to study the surface of a prism by examining its development. Below is an example of such a development for a triangular prism.

It can be seen that the entire surface is formed by two triangles and three rectangles.
In the case of a general prism, its surface will consist of two n-gonal bases and n quadrangles.
Let us consider in more detail the issue of calculating the surface area of prisms of different types.
The base area of a regular prism
Perhaps the simplest problem when working with prisms is the problem of finding the area of the base of the regular figure. Since it is formed by an n-gon whose angles and side lengths are all the same, it can always be divided into identical triangles whose angles and sides are known. The total area of the triangles will be the area of the n-gon.
Another way to determine the portion of the surface area of a prism (base) is to use a well-known formula. It looks like this:
S n = n/4*a 2 *ctg(pi/n)
That is, the area S n of an n-gon is uniquely determined based on knowledge of the length of its side a. Some difficulty when calculating using the formula can be the calculation of the cotangent, especially when n>4 (for n≤4 the cotangent values are tabular data). It is recommended to use a calculator to determine this trigonometric function.
When posing a geometric problem, you should be careful, since you may need to find the area of the base of the prism. Then the value obtained from the formula should be multiplied by two.
Base area of a triangular prism
Using the example of a triangular prism, let's look at how you can find the area of the base of this figure.
Let's first consider a simple case - a regular prism. The area of the base is calculated using the formula given in the paragraph above; you need to substitute n=3 into it. We get:
S 3 = 3/4*a 2 *ctg(pi/3) = 3/4*a 2 *1/√3 = √3/4*a 2
It remains to substitute the specific values of the length of side a of the equilateral triangle into the expression to obtain the area of one base.
Now suppose that there is a prism whose base is an arbitrary triangle. Its two sides a and b and the angle between them α are known. This figure is shown below.

How in this case to find the area of the base of a triangular prism? It is necessary to remember that the area of any triangle is equal to half the product of the side and the height lowered to this side. In the figure, height h is drawn to side b. The length h corresponds to the product of the sine of the angle alpha and the length of the side a. Then the area of the entire triangle is:
S = 1/2*b*h = 1/2*b*a*sin(α)
This is the base area of the triangular prism shown.
Side surface
We looked at how to find the area of the base of a prism. The lateral surface of this figure always consists of parallelograms. For straight prisms, parallelograms become rectangles, so their total area is easy to calculate:
S = ∑ i=1 n (a i *b)
Here b is the length of the side edge, a i is the length of the side of the i-th rectangle, which coincides with the length of the side of the n-gon. In the case of a regular n-gonal prism, we obtain a simple expression:
If the prism is inclined, then to determine the area of its lateral surface, one should make a perpendicular cut, calculate its perimeter P sr and multiply it by the length of the lateral edge.

The picture above shows how this cut should be made for an inclined pentagonal prism.
There are a few more simple prism problems for you to solve. Consider a right prism with a right triangle at its base. The question is raised about finding the volume or surface area. Prism volume formula:
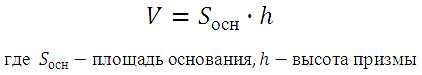
Prism surface area formula (general):

*For a straight prism, the lateral surface consists of rectangles and is equal to the product of the perimeter of the base and the height of the prism. You need to remember the formula for the area of a triangle. In this case, we have a right triangle - its area is equal to half the product of the legs. Let's consider the tasks:
The base of a right triangular prism is a right triangle with legs 10 and 15, the side edge is 5. Find the volume of the prism.

The base area is the area of a right triangle. It is equal to half the area of a rectangle with sides 10 and 15).
Thus, the required volume is equal to:
Answer: 375
The base of a right triangular prism is a right triangle with legs 20 and 8. The volume of the prism is 400. Find its side edge.
The task is the opposite of the previous one.
Prism volume:
The base area is the area of a right triangle:

Thus

Answer: 5
The base of a right triangular prism is a right triangle with legs 5 and 12, the height of the prism is 8. Find its surface area.
The surface area of a prism is the sum of the areas of all faces - these are two bases of equal area and a side surface.
In order to find the areas of all faces, it is necessary to find the third side of the base of the prism (the hypotenuse of the right triangle).
According to the Pythagorean theorem:
Now we can find the base area and lateral surface area. The area of the base is:

The area of the lateral surface of the prism with the perimeter of the base is equal to:
*You can do without the formula and simply add up the areas of three rectangles:
