The main methods for solving trigonometric equations are: reducing the equations to the simplest (using trigonometric formulas), introducing new variables, and factoring. Let's look at their use with examples. Pay attention to the format of writing solutions to trigonometric equations.
A necessary condition for successfully solving trigonometric equations is knowledge of trigonometric formulas (topic 13 of work 6).
Examples.
1. Equations reduced to the simplest.
1) Solve the equation
Solution:
Answer:
2) Find the roots of the equation
(sinx + cosx) 2 = 1 – sinxcosx, belonging to the segment.
Solution:
Answer:
2. Equations that reduce to quadratic.
1) Solve the equation 2 sin 2 x – cosx –1 = 0.
Solution: Using the formula sin 2 x = 1 – cos 2 x, we get
Answer:
2) Solve the equation cos 2x = 1 + 4 cosx.
Solution: Using the formula cos 2x = 2 cos 2 x – 1, we get
Answer:
3) Solve the equation tgx – 2ctgx + 1 = 0
Solution:
Answer:
3. Homogeneous equations
1) Solve the equation 2sinx – 3cosx = 0
Solution: Let cosx = 0, then 2sinx = 0 and sinx = 0 – a contradiction with the fact that sin 2 x + cos 2 x = 1. This means cosx ≠ 0 and we can divide the equation by cosx. We get
Answer:
2) Solve the equation 1 + 7 cos 2 x = 3 sin 2x
Solution:
We use the formulas 1 = sin 2 x + cos 2 x and sin 2x = 2 sinxcosx, we get
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Let cosx = 0, then sin 2 x = 0 and sinx = 0 – a contradiction with the fact that sin 2 x + cos 2 x = 1.
This means cosx ≠ 0 and we can divide the equation by cos 2 x .
We get
tg 2 x – 6 tgx + 8 = 0
Let us denote tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2 = 2
a) tgx = 4, x= arctan4 + 2 k, k
b) tgx = 2, x= arctan2 + 2 k, k .
Answer: arctg4 + 2 k, arctan2 + 2 k, k
4. Equations of the form a sinx + b cosx = s, s≠ 0.
1) Solve the equation.
Solution:
Answer:
5. Equations solved by factorization.
1) Solve the equation sin2x – sinx = 0.
Root of the equation f (X) = φ ( X) can only serve as the number 0. Let's check this:
cos 0 = 0 + 1 – the equality is true.
The number 0 is the only root of this equation.
Answer: 0.
Methods for solving trigonometric equations.Solving a trigonometric equation consists of two stages: equation transformation to get it simplest type (see above) and solutionthe resulting simplest trigonometric equation. There are seven basic methods for solving trigonometric equations.
1. Algebraic method.
(variable replacement and substitution method).
2. Factorization.
Example 1. Solve the equation: sin x+cos x = 1 .
Solution. Let's move all the terms of the equation to the left:
Sin x+cos x – 1 = 0 ,
Let us transform and factorize the expression in
Left side of the equation:

Example 2. Solve the equation: cos 2 x+ sin x cos x = 1.
Solution: cos 2 x+ sin x cos x– sin 2 x– cos 2 x = 0 ,
Sin x cos x– sin 2 x = 0 ,
Sin x· (cos x– sin x ) = 0 ,

Example 3. Solve the equation: cos 2 x–cos 8 x+ cos 6 x = 1.
Solution: cos 2 x+ cos 6 x= 1 + cos 8 x,
2 cos 4 x cos 2 x= 2cos² 4 x ,
Cos 4 x · (cos 2 x– cos 4 x) = 0 ,
Cos 4 x · 2 sin 3 x sin x = 0 ,
1). cos 4 x= 0, 2). sin 3 x= 0, 3). sin x = 0 ,

3. Reduction to homogeneous equation.The equation called homogeneous from regarding sin And cos , If all of it terms of the same degree relative to sin And cos same angle. To solve a homogeneous equation, you need: A) move all its members to the left side; b) put all common factors out of brackets; V) equate all factors and brackets to zero; G) parentheses equal to zero give homogeneous equation of lesser degree, which should be divided into cos(or sin) in the senior degree; d) solve the resulting algebraic equation with respect totan . sin 2 x+ 4 sin x cos x+ 5cos 2 x = 2. Solution: 3sin 2 x+ 4 sin x cos x+ 5 cos 2 x= 2sin 2 x+ 2cos 2 x , Sin 2 x+ 4 sin x cos x+ 3 cos 2 x = 0 , Tan 2 x+ 4 tan x + 3 = 0 , from here y 2 + 4y +3 = 0 , The roots of this equation are:y 1 = - 1, y 2 = - 3, hence 1) tan x= –1, 2) tan x = –3, |
4. Transition to half angle.
Let's look at this method using an example:
EXAMPLE Solve equation: 3 sin x– 5 cos x = 7.
Solution: 6 sin ( x/ 2) cos ( x/ 2) – 5 cos² ( x/ 2) + 5 sin² ( x/ 2) =
7 sin² ( x/ 2) + 7 cos² ( x/ 2) ,
2 sin² ( x/ 2) – 6 sin ( x/ 2) cos ( x/ 2) + 12 cos² ( x/ 2) = 0 ,
tan² ( x/ 2) – 3 tan ( x/ 2) + 6 = 0 ,
. . . . . . . . . .
5. Introduction of an auxiliary angle.
Consider an equation of the form:
a sin x + b cos x = c ,
Where a, b, c– coefficients;x– unknown.
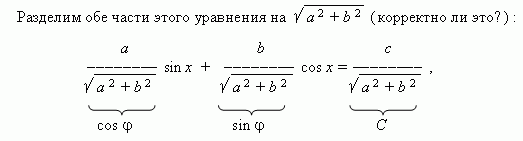
Now the coefficients of the equation have the properties of sine and cosine, namely: modulus (absolute value) of each of which no more than 1, and the sum of their squares is 1. Then we can denote them accordingly How cos and sin (here - so-called auxiliary angle), Andtake our equation
Subject:"Methods for solving trigonometric equations."
Lesson objectives:
educational:
Develop skills to distinguish between types of trigonometric equations;
Deepening understanding of methods for solving trigonometric equations;
educational:
Cultivating cognitive interest in the educational process;
Formation of the ability to analyze a given task;
developing:
To develop the skill of analyzing a situation and then choosing the most rational way out of it.
Equipment: poster with basic trigonometric formulas, computer, projector, screen.
Let's start the lesson by repeating the basic technique for solving any equation: reducing it to standard form. Through transformations, linear equations are reduced to the form ax = b, quadratic equations are reduced to the form ax 2 +bx +c =0. In the case of trigonometric equations, it is necessary to reduce them to the simplest, of the form: sinx = a, cosx = a, tgx = a, which can be easily solved.
First of all, of course, for this you need to use the basic trigonometric formulas that are presented on the poster: addition formulas, double angle formulas, reducing the multiplicity of the equation. We already know how to solve such equations. Let's repeat some of them:
At the same time, there are equations whose solution requires knowledge of some special techniques.
The topic of our lesson is to consider these techniques and systematize methods for solving trigonometric equations.
Methods for solving trigonometric equations.
1. Conversion to a quadratic equation with respect to some trigonometric function followed by a change of variable.
Let's look at each of the listed methods with examples, but let's dwell in more detail on the last two, since we have already used the first two when solving equations.
1. Conversion to a quadratic equation with respect to some trigonometric function.
2. Solving equations using the factorization method.
3. Solving homogeneous equations.
Homogeneous equations of the first and second degrees are equations of the form:
respectively (a ≠ 0, b ≠ 0, c ≠ 0).
When solving homogeneous equations, divide both sides of the equation term by cosx for (1) equation and by cos 2 x for (2). This division is possible because sinx and cosx are not equal to zero at the same time - they become zero at different points. Let's consider examples of solving homogeneous equations of the first and second degrees.
Let's remember this equation: when considering the next method - introducing an auxiliary argument, let's solve it in a different way.
4. Introduction of an auxiliary argument.
Let's consider the equation already solved by the previous method:
As you can see, the same result is obtained.
Let's look at another example:
In the examples considered, it was generally clear what needed to be divided into the original equation in order to introduce an auxiliary argument. But it may happen that it is not obvious which divisor to choose. There is a special technique for this, which we will now consider in general terms. Let an equation be given.
