Rectangular (other names - flat, two-dimensional) coordinate system, named after the French scientist Descartes (1596-1650) " Cartesian system coordinates on the plane” is formed by the intersection on the plane at right angles (perpendicular) of two numerical axes so that the positive semi-axis of one is directed to the right (x-axis, or abscissa axis), and the second is directed upward (y-axis, or ordinate axis).
The intersection point of the axes coincides with the 0 point of each of them and is called the origin of coordinates.
For each of the axes, an arbitrary scale (a single length segment) is selected. Each point on the plane corresponds to one pair of numbers, called the coordinates of this point on the plane. Conversely, any ordered pair of numbers corresponds to one point on the plane for which these numbers are coordinates.
The first coordinate of a point is called the abscissa of that point, and the second coordinate is called the ordinate.
The entire coordinate plane is divided into 4 quadrants (quarters). Quadrants are located from the first to the fourth counterclockwise (see figure).
To determine the coordinates of a point, you need to find its distance to the abscissa and ordinate axis. Since the distance (shortest) is determined by the perpendicular, then from the point two perpendiculars (auxiliary lines on the coordinate plane) are lowered onto the axis so that the point of their intersection is the location given point in the coordinate plane. The points of intersection of perpendiculars with axes are called projections of the point on the coordinate axes.
The first quadrant is limited by the positive semi-axes of abscissa and ordinate. Therefore, the coordinates of the points in this quarter of the plane will be positive
(signs "+" and
For example, point M (2; 4) in the figure above.
The second quadrant is limited by the negative x-axis and the positive y-axis. Consequently, the coordinates of points along the abscissa axis will be negative (sign “-”), and along the ordinate axis they will be positive (sign “+”).
For example, point C (-4; 1) in the figure above.
The third quadrant is limited by the negative x-axis and the negative y-axis. Consequently, the coordinates of the points along the abscissa and ordinate axis will be negative (signs “-” and “-”).
For example, point D (-6; -2) in the figure above.
The fourth quadrant is limited by the positive x-axis and the negative y-axis. Consequently, the coordinates of the points along the abscissa axis will be positive (the “+” sign). and along the ordinate axis - negative (sign “-”).
For example, point R (3; -3) in the figure above.
Constructing a point using its specified coordinates
we will find the first coordinate of the point on the x-axis and draw an auxiliary line through it - a perpendicular;
we find the second coordinate of the point on the ordinate axis and draw an auxiliary line through it - a perpendicular;
the point of intersection of two perpendiculars (auxiliary lines) will correspond to the point with the given coordinates.
primary vocational education
"Vocational School No. 5" Belgorod
Lesson summary
in mathematics on the topic:
Rectangular system coordinates in space
for 11th grade students
teacher of computer science and mathematics
GOU NPO PU No. 5
Belgorod 2010
Lesson topic
: Rectangular coordinate system in space. Vector coordinates
Lesson Objectives: - develop logical and spatial thinking
Introduce the concept of a coordinate system in space, vector coordinates
Literature: Geometry 10-11 grade L. S. Atanasyan, M.: Education, 2006
During the classes:
Org. Moment
Explanation of new material
If three pairwise perpendicular lines are drawn through a point in space, a direction is selected on each of them (it is indicated by an arrow) and the unit of measurement for segments is selected, then they say that rectangular coordinate system in space (Fig. 121). Straight lines with directions chosen on them are called coordinate axes, and their common point - origin. It is usually denoted by the letter O. The coordinate axes are designated as follows: Ox, Oy, Oz - and have names: abscissa axis, ordinate axis, applicate axis. The entire coordinate system is designated Oxyz. The planes passing through the coordinate axes Ox and Oy, Oy and Oz, Oz and Ox, respectively, are called coordinate planes and are designated Oxy, Oyz, Ozx.
Point O divides each of the coordinate axes into two rays. A ray whose direction coincides with the direction of the axis is called positive semi-axis, and the other beam negative semi-axis.
IN 
in a rectangular coordinate system, each point M of space is associated with a triple of numbers, which are called its coordinates. They are determined similarly to the coordinates of points on the plane. Let us draw three planes through point M, perpendicular to the coordinate axes, and denote by M 1, M 2 and M 3 the intersection points of these planes, respectively, with the abscissa, ordinate and applicate axes (Fig. 122). The first coordinate of point M (it is called abscissa and is usually denoted by the letter x) is defined as follows: x = OM 1, if M 1 is the point of the positive semi-axis; x = - OM 1, if M 1 is the point of the negative semi-axis; x = 0 if M 1 coincides with point O. Similarly, using point M 2 the second coordinate ( ordinate) y point M, and using point M 3 the third coordinate ( applicate) z point M. The coordinates of point M are written in parentheses after the designation of the point: M (x; y; z), with the abscissa indicated first, the ordinate indicated second, and the applicate third indicated. Figure 123 shows six points A (9; 5; 10), B (4; -3; 6), C (9; 0; 0), E (4; 0; 5), E (0; 3; 0 ), F (0; 0; -3).
E 
If point M (x; y; z) lies on coordinate plane or on the coordinate axis, then some of its coordinates are equal to zero. So, if M € Oxy, then the applicate of the point M is equal to zero: z = 0. Similarly, if M with Oxz, then y = 0, and if M € Oyz, then x = 0. If M € Ox, then the ordinate and applicate of the point M are equal to zero: y = 0 and z = 0 (for example, at point C in Figure 123). If M € Oy, then x = 0 and z = 0; if M€ Oz, then x = 0 and y = 0. All three coordinates of the origin are equal to zero: 0 (0; 0; 0).
Vector coordinates
Z 
Let us define a rectangular coordinate system Oxyz in space. On each of the positive semi-axes we plot from the origin of coordinates unit vector
, i.e. a vector whose length is equal to one. i unit vector of the x-axis, through j is the unit vector of the ordinate axis and through k unit vector of the applicate axis (Fig. 124). Let's call vectors i, j, k coordinate vectors. Obviously, these vectors are not coplanar. That's why any vectoraand can be decomposed into coordinate vectors, i.e., represent it in the form
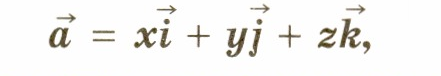
and the expansion coefficients x, y,z are determined in a unique way.
TO 
the coefficients x, y and z in the expansion of vector a in coordinate vectors are called vector coordinatesain this coordinate system. We will write the coordinates of the vector a in curly brackets after the vector designation: a (x; y; z). Figure 125 shows cuboid, having the following dimensions: OA 1 = 2, OA 2 = 2, OA 3 =4. The coordinates of the vectors shown in this figure are: a (2; 2; 4), b(2; 2; -1), A 3 A (2; 2; 0), i(1; 0; 0), j (0; 1; 0), k(0; 0; 1).
Since the zero vector can be represented as 0 = oi+ oj+ 0k, then all coordinates of the zero vector are equal to zero. Further, coordinates equal vectors respectively equal, i.e. if the vectors a(x 1, y 1, z 1) and b(x 2, y 2, z 2) are equal, then x 1 = x 2, y 1 = y 2 and z 1 = z 2 (explain why).
Let's consider rules, which allow using the coordinates of these vectors to find the coordinates of their sum and difference, as well as the coordinates of the product given vector for this number.
1 0 . Each coordinate of the sum of two or more vectors is equal to the sum of the corresponding coordinates of these vectors. In other words, if a (x 1, y 1, z 1) and b(x 2, y 2, z 2) are given vectors, then the vector a + b has coordinates (x 1 + x 2, y 1 + y 2 , z 1 + z 2 ).
2 0 . Each coordinate of the difference of two vectors is equal to the difference of the corresponding coordinates of these vectors. In other words, if a (x 1, y 1, z 1) and b(x 2 y 2; z 2) are given vectors, then the vector a- b has coordinates (x 1 - x 2, y 1 – y 2, z 1 - z 2 ).
3 ABOUT. Each coordinate of the product of a vector and a number is equal to the product of the corresponding coordinate of the vector and this number. In other words, if a(x;y;x) -
To determine the position of a point in space we will use Cartesian rectangular coordinates(Fig. 2).
The Cartesian rectangular coordinate system in space is formed by three mutually perpendicular coordinate axes OX, OY, OZ. The coordinate axes intersect at point O, which is called the origin, on each axis a positive direction is selected, indicated by arrows, and a unit of measurement for the segments on the axes. The units of measurement are usually (not necessarily) the same for all axes. The OX axis is called the abscissa axis (or simply abscissa), the OY axis is the ordinate axis, and the OZ axis is the applicate axis.
The position of point A in space is determined by three coordinates x, y and z. The x coordinate is equal to the length of the segment OB, the y coordinate is the length of the segment OC, the z coordinate is the length of the segment OD in the selected units of measurement. The segments OB, OC and OD are defined by planes drawn from a point parallel to the planes YOZ, XOZ and XOY, respectively.
The x coordinate is called the abscissa of point A, the y coordinate is called the ordinate of point A, and the z coordinate is called the applicate of point A.
Symbolically it is written like this:
or link a coordinate record to a specific point using an index:
x A , y A , z A ,
Each axis is considered as a number line, i.e., has a positive direction, and points lying on the negative ray are assigned negative values coordinates (distance is taken with a minus sign). That is, if, for example, point B lay not as in the figure - on the ray OX, but on its continuation in reverse side from point O (on the negative part of the axis OX), then the x abscissa of point A would be negative (minus the distance OB). Likewise for the other two axes.
Coordinate axes OX, OY, OZ, shown in Fig. 2, form a right-handed coordinate system. This means that if you look at the YOZ plane along the positive direction of the OX axis, then the movement of the OY axis towards the OZ axis will be clockwise. This situation can be described using the gimlet rule: if the gimlet (screw with a right-hand thread) is rotated in the direction from the OY axis to the OZ axis, then it will move along the positive direction of the OX axis.
Vectors of unit length directed along coordinate axes, are called coordinate unit vectors. They are usually designated as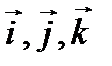 
(Fig. 3). There is also the designation 
The unit vectors form the basis of the coordinate system.
In the case of a right-handed coordinate system, valid following formulas With vector works ortov:
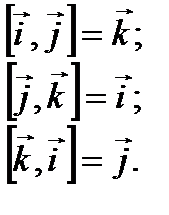
A rectangular coordinate system in space is a triple mutually perpendicular axes, intersecting at one point O, called the origin.
Coordinate axes are usually designated by letters and are called, respectively, the abscissa axis, the ordinate axis, the applicate axis, or the Oy axis, axis (Fig. 33).
The unit vectors of the coordinate axes Ox, Oy, Oz are designated respectively or. We will mainly use the latter designation.
There are right and left coordinate systems.
The coordinate system is called right if from the end of the third ort to the turn from the first ort to the second ort is seen to occur counterclockwise (Fig. 34, a).
The coordinate system is called left-handed if, from the end of the third ort, the rotation from the first ort to the second ort is visible as occurring clockwise (Fig. 34, b).
Thus, if you screw in the screw in the direction of vector k, rotating it away, then in the case of a right-handed system, the thread should be right-handed, and in the case of a left-handed system, left-handed (Fig. 35).
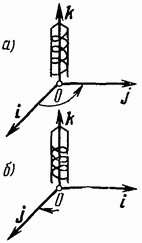
Many provisions of vector algebra do not depend on whether we use a right-handed or left-handed coordinate system. However, sometimes this circumstance matters. In what follows, we will always use the right-handed coordinate system, as is customary in physics.