TEXT TRANSCRIPT OF THE LESSON:
If three pairwise perpendicular lines are drawn through a point in space, on each of which a direction and a unit segment are chosen, then they say that a rectangular coordinate system in space is specified.
Straight lines with directions chosen on them are called coordinate axes and are designated as follows: Ox, Oy, Oz, have their own names: abscissa axis, ordinate axis and applicate axis, respectively, and their common point- origin of coordinates. It is usually denoted by the letter O.
The entire coordinate system is designated Oxyz.
If planes are drawn through the coordinate axes Ox and Oy, Oy and Oz, Oz and Ox, then such planes will be called coordinate planes and denoted: Oxy, Oyz, Ozx, respectively.
Point O divides each of the coordinate axes into two rays. The ray whose direction coincides with the direction of the axis is called the positive semi-axis, and the other ray is called the negative semi-axis.
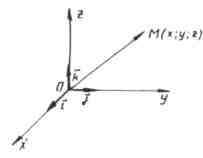
In a rectangular coordinate system, each point M in space is associated with a triple of numbers, which are called its coordinates. They are determined similarly to the coordinates of points on the plane.
Let's see how it's done.
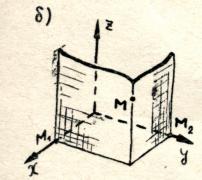
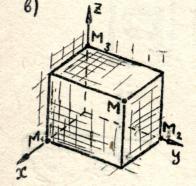
Let us draw three planes through point M, perpendicular to the axes coordinates, and denote by M₁, M₂ and M₃ the intersection points of these planes, respectively, with the abscissa, ordinate and applicate axes.
The first coordinate of point M (it is called the abscissa and is usually denoted by the letter x) is defined as follows: x = OM₁, if M₁ is the point of the positive semi-axis;
x= - OM₁, if M₁ is the point of the negative semi-axis; x =0 if M₁ coincides with point O.
Similarly, using the point M₂, the second coordinate (ordinate) at the point M is determined,
and using the point M₃ - the third coordinate (applicate) z of the point M.
The coordinates of point M are written in parentheses after the designation of point M (x; y; z).
Remember that the abscissa is indicated first, the ordinate is second, and the applicate is third.
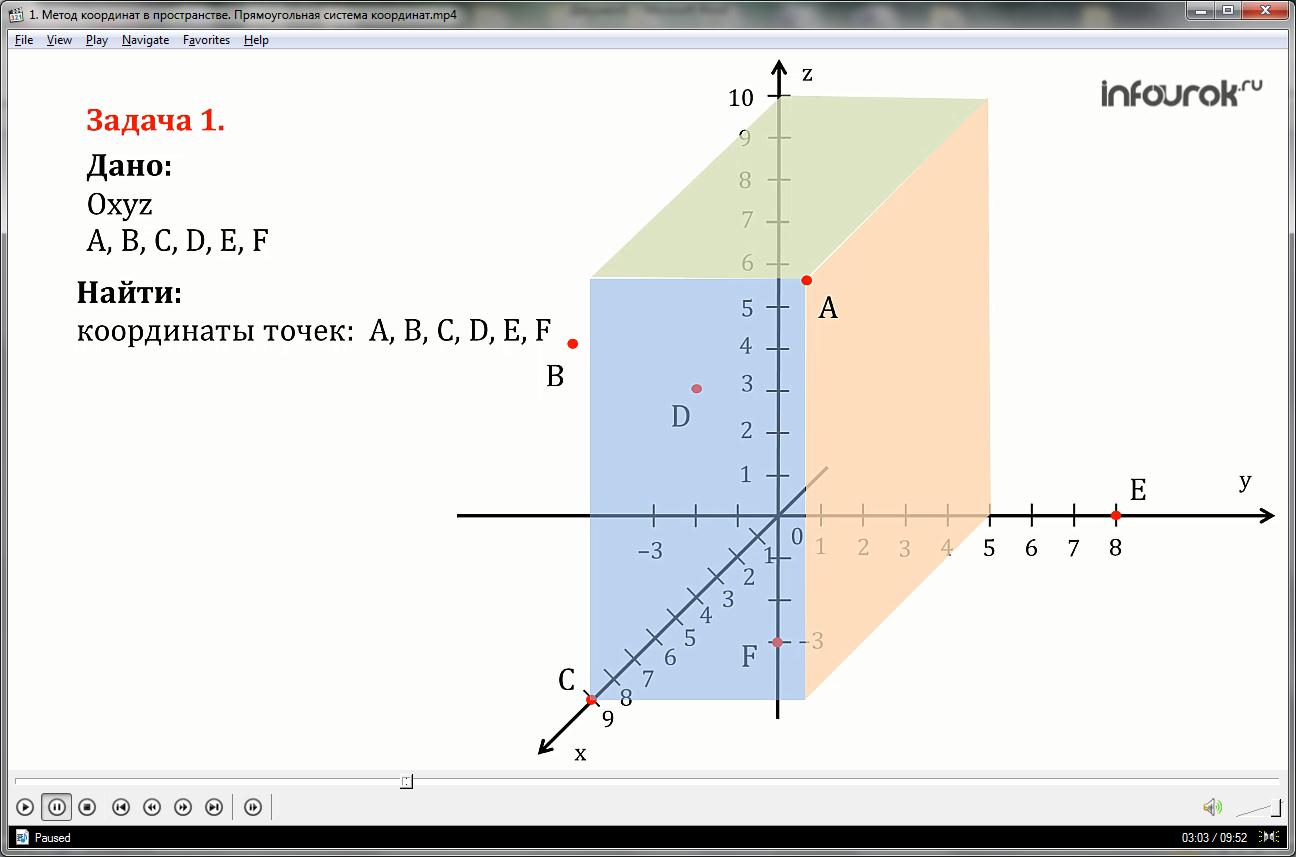
Let's find the coordinates of points A, B, C, D, E, F, shown in the figure.
Let us draw three planes through point A, perpendicular to the coordinate axes, then the points of intersection of these planes with the abscissa, ordinate and applicate axes, respectively, will be the coordinates of point A. Point A has the coordinates: abscissa = 9, ordinate = 5, applicate = 10 and it is written like this : A (9; 5; 10).
The coordinates of the following points are written similarly:
Point B has coordinates: abscissa = 4, ordinate = -3, applicate = 6
Point C has coordinates: abscissa = 9, ordinate = 0, applicate = 0
The point has D coordinates: abscissa = 4, ordinate = 0, applicate = 5
Point E has coordinates: abscissa = 0, ordinate = 8, applicate = 0
Point F has coordinates: abscissa = 0, ordinate = 0, applicate = -3
If a point M (x; y; z) lies on the coordinate plane on the coordinate axis, then some of its coordinates are equal to zero.
If MЄОху (point M belongs to the Oxy plane), then the applicate of point M is equal to zero: z=0.
Similarly, if МЄОхz (point M belongs to the Oxz plane), then y = 0, and if МЄОуz (point M belongs to the Oyz plane), then x = 0.
If МЄОх (point M lies on the abscissa axis), the ordinate and applicate of point M are equal to zero: y=o and z=0. In our example, this is point C.
If МЄОу (point M lies on the ordinate), then x=0 and z=0. In our example, this is point E.
If МЄОz (point M lies on the applicate axis), then x = 0 and y = 0. In our example, this is point F.
If all three coordinates of point M are equal to zero, then this means that M=O (0; 0; 0) is the origin of coordinates.
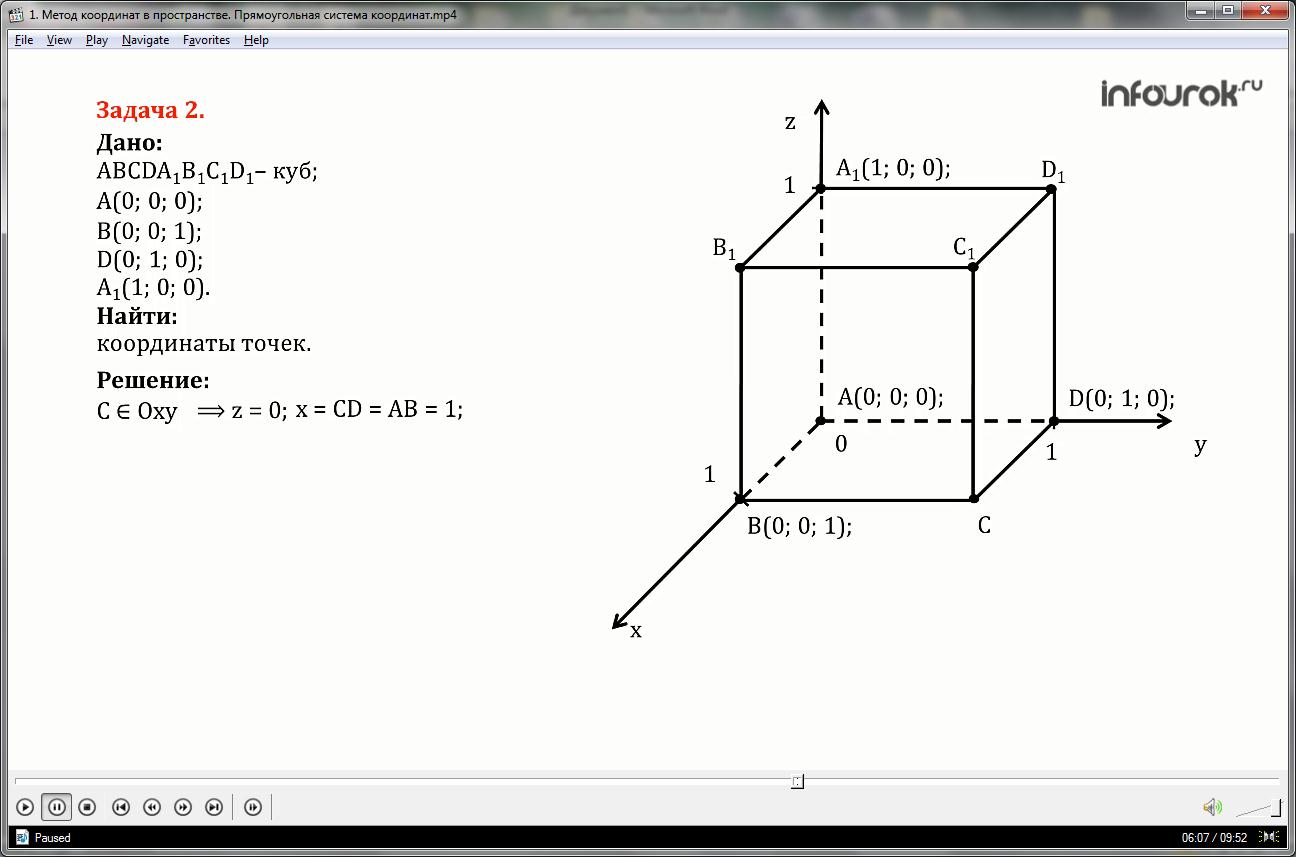
Given the coordinates of the four vertices of the cube ABCDA 1 B 1 C 1 D 1: A(0; 0; 0); B(0; 0; 1); D(0; 1; 0); A 1 (1; 0; 0). Find the coordinates of the remaining vertices of the cube.
Since the figure is a cube, all sides are equal to one, all faces are squares.
Point C belongs to the Oxy plane, that is, its z coordinate is equal to zero, the x coordinate is equal to the side CD and is equal to AB, which means it is equal to one, the coordinate Y is equal to the side of the cube CB, which means it is equal to AD and is equal to one.
Similarly, Point B 1 belongs to the Oxz plane, that is, its y coordinate is equal to zero, the x coordinate is equal to the side, the x coordinate is equal to the side A1B1 and is equal to AB, which means equal to one, the z coordinate is equal to the side of the cube B B1, which means equal to AA1 and equal to one.
Point D 1 belongs to the Oyz plane, that is, its x coordinate is equal to zero, the y coordinate is equal to side A 1 D 1 and is equal to AD, which means it is equal to one, the z coordinate is equal to the side of the cube A 1 B 1, which means it is equal to AB and is equal to one.
Point C 1 does not belong to any plane, that is, all coordinates are different from zero, the x coordinate is equal to the side C 1 D 1 and is equal to AB, which means it is equal to one, the coordinate y is equal to the side of the cube B 1 C 1, which means it is equal to AD and is equal to one, and the z coordinate is equal to the side CC 1, that is, AA 1 and is also equal to one.
Find the coordinates of the projections of point C(; ;) onto the coordinate planes Oxy, Oxz, Oyz and the coordinate axes Ox, Oy, Oz.
1) drop perpendiculars to the Oxy plane - this is CN, to the Oxz plane - CL, and to the Oyz plane - line CR.
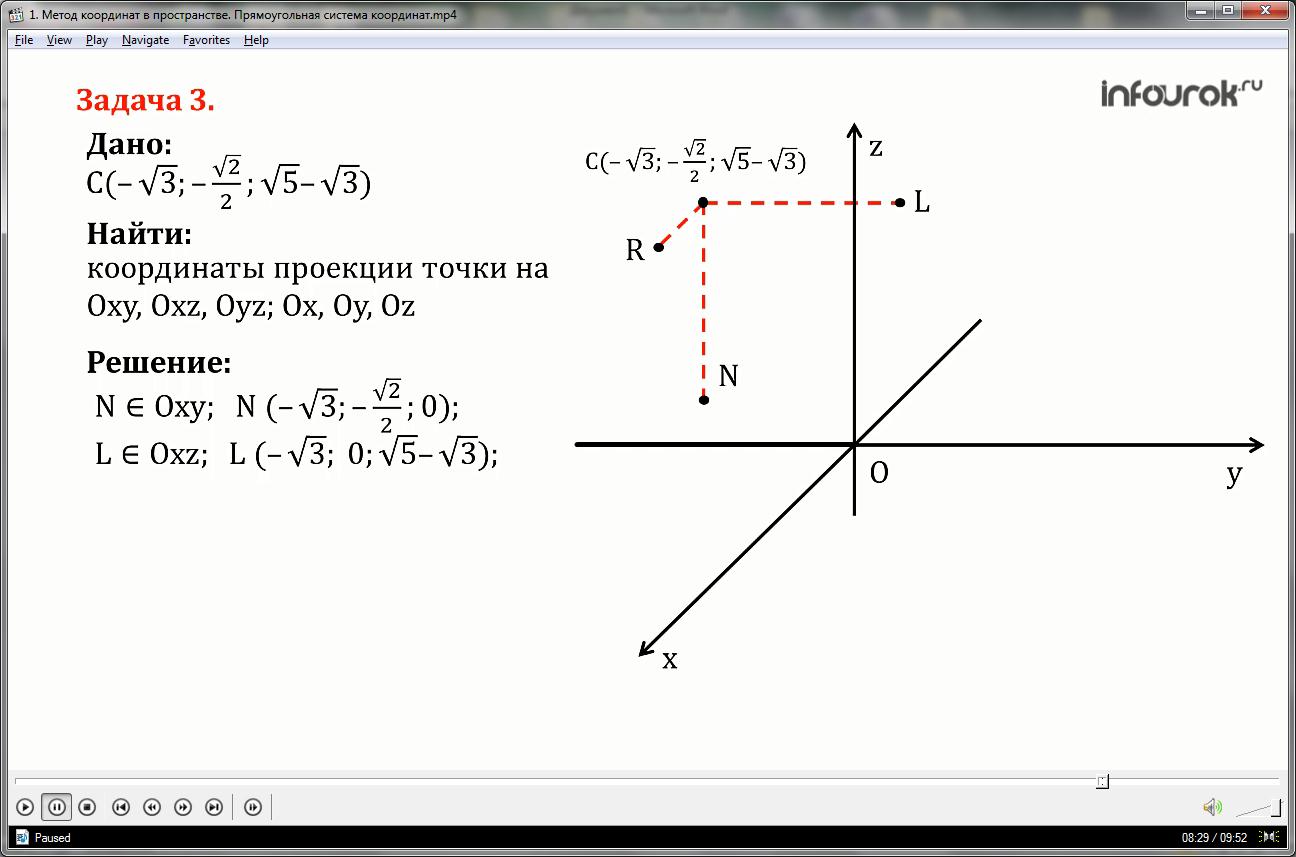
Thus, the projection of point C onto the Oxy plane is point N and it has coordinates x equal to minus root of three, y equal to minus root of two by two, z equal to zero.
The projection of point C onto the Oxz plane is point L and it has coordinates x equals minus root of three, i equal to zero, z equal to the root of five minus the root of three.
The projection of point C onto the plane Oyz is point R and it has coordinates x is equal to zero, y is equal to minus root of two by two, z is equal to root of five minus root of three.
2) From point N we draw perpendiculars to the Ox axis - straight line NK, and to Oy - straight line NG, and to the Oz axis we draw a perpendicular from point R - this is straight line RP.
The projection of point C onto the Ox axis - point K has coordinates x equal to minus the root of three, and y and z equal to zero.
The projection of point C onto the Oy axis - point G has coordinates x and z equal to zero, i is equal to minus the root of two by two.
The projection of point C onto the Oz axis - point P has coordinates x and y equal to zero, z equal root of five minus the root of three.
Ministry of Education Russian Federation
Municipal educational institution"Average secondary school No. 18"
ABSTRACT
BY GEOMETRY
TOPIC: METHOD OF COORDINATES IN SPACE
Completed by 11th grade student “C”
Melnik Roman
Supervisor
mathematics teacher Baksheeva I.K.
Biysk - 2008
Content
Introduction……………………………………………………………..… 3.
Chapter 1.
Coordinate method: history of development…………………………………4
Coordinates of a point in space……………………………….…...5
Defining figures in space………………………………….……...8
Chapter 2.
Decomposition of a vector into coordinate vectors. Coordinates
vector………………………………………………………………..……..10
Linear operations over vectors in coordinates…………..………12
Condition for collinearity of two vectors in coordinates……………..13
The simplest problems in coordinates………………………………….....14
Scalar product vectors and calculating the angle between vectors through their coordinates…………………………………….………15
Calculation of angles between straight lines and planes…………………..16
4. Chapter 3.
4.1. Application coordinate method to solving stereometric
tasks ………………………………………………………..…………….. 19
Conclusion. ……………………………………………………………..26
Bibliography……………………………………………………... 27
Introduction
The topic of my work is “Method of coordinates in space.” This topic relevant today for any graduate high school because:
Goal of the work: systematize knowledge on this topic and consider application this method when solving various stereometric problems.
To achieve the goal, the following were set tasks:
allows many exams geometric problems solve analytically, which requires less knowledge of geometry and significantly reduces execution time;
This method underlies analytical geometry, which is studied in the course of higher mathematics.
study theoretical material on the topic;
systematize and summarize the studied material;
identify the features of using the method;
consider the application of the coordinate method to solving stereometric problems;
compare the application of the coordinate method with other methods for solving stereometric problems.
Methods used :
method of analysis and synthesis,
comparison method.
Chapter 1
1. Coordinate method: history of development.
The coordinate method is a way to determine the position of a point or body using numbers or other symbols.
The numbers used to determine the position of a point are called point coordinates.
Well known to us geographical coordinates determine the position of a point on the Earth’s surface - each point on earth's surface has two coordinates: latitude and longitude.
To determine the position of a point in space, three numbers are needed. For example, to determine the position of a satellite, you can specify its height above the Earth's surface, as well as the latitude and longitude of the point over which it is located.
Using the coordinate method, you can present almost the entire school geometry course without a single drawing, using only numbers and algebraic operations. For example, a circle can be defined as a set of points that satisfy the equation, and a straight line can be defined as a set of points that satisfy the equation  . Thus, with the help of this method it was possible to connect together seemingly completely various sciences algebra and geometry. This connection was, in essence, a revolution in mathematics. It restored mathematics as a unified science.
. Thus, with the help of this method it was possible to connect together seemingly completely various sciences algebra and geometry. This connection was, in essence, a revolution in mathematics. It restored mathematics as a unified science.
The creator of the coordinate method is considered to be the French philosopher and mathematician Rene Descartes (1596-1650), who in the last part of Descartes’s large philosophical treatise, published in 1637, described the coordinate method and its application to solving geometric problems.
The development of Descartes' ideas led to the emergence of a special branch of mathematics, which is now called analytical geometry.
This name itself expresses the basic idea of the theory. Analytical geometry is that part of mathematics that solves geometric problems analytically (i.e., algebraically) by means.
Along with Descartes, the founder of analytical geometry is the remarkable French mathematician P. Fermat. Using the coordinate method, Fermat studied straight lines and second-order curves. The study of analytical geometry in three-dimensional space was significantly advanced in the 18th century by A. Clairaut. Explicitly and consistently analytical geometry on the plane and in three-dimensional space outlined by L. Euler in 1748 in the textbook “Introduction to the Analysis of Infinites”.
IN XIXcentury, another step was taken in the development of geometry - multidimensional spaces were studied. The main idea for the creators of the theory was the analogy with Descartes’ “Geometry”. His point on the plane is a pair of numbers 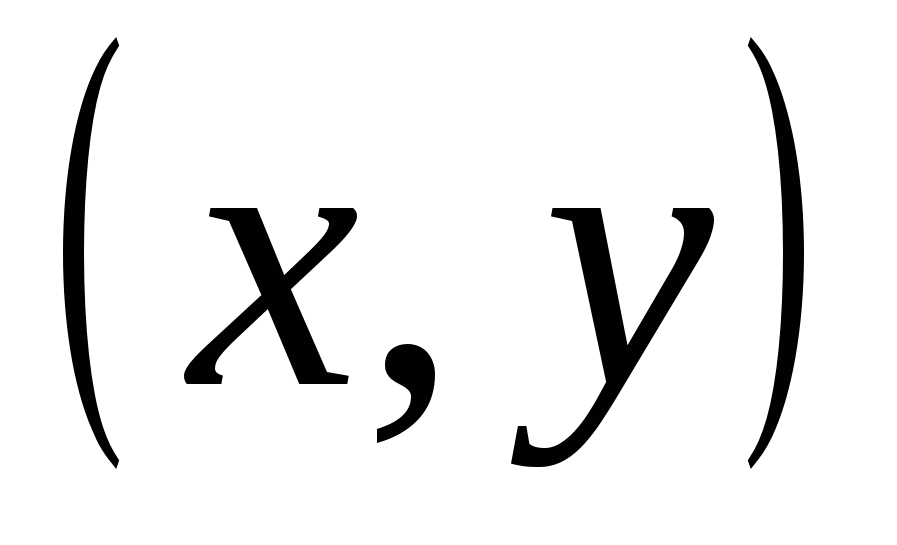 , a point in three-dimensional space – a triple of numbers
, a point in three-dimensional space – a triple of numbers 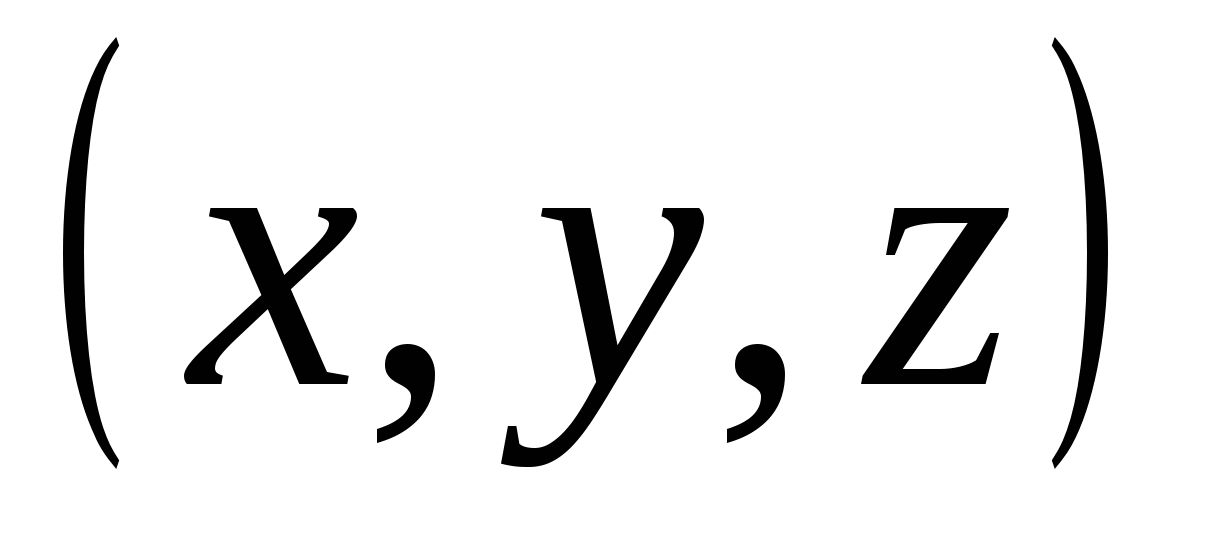 ; V new theory a point in four-dimensional space is a quadruple of numbers
; V new theory a point in four-dimensional space is a quadruple of numbers 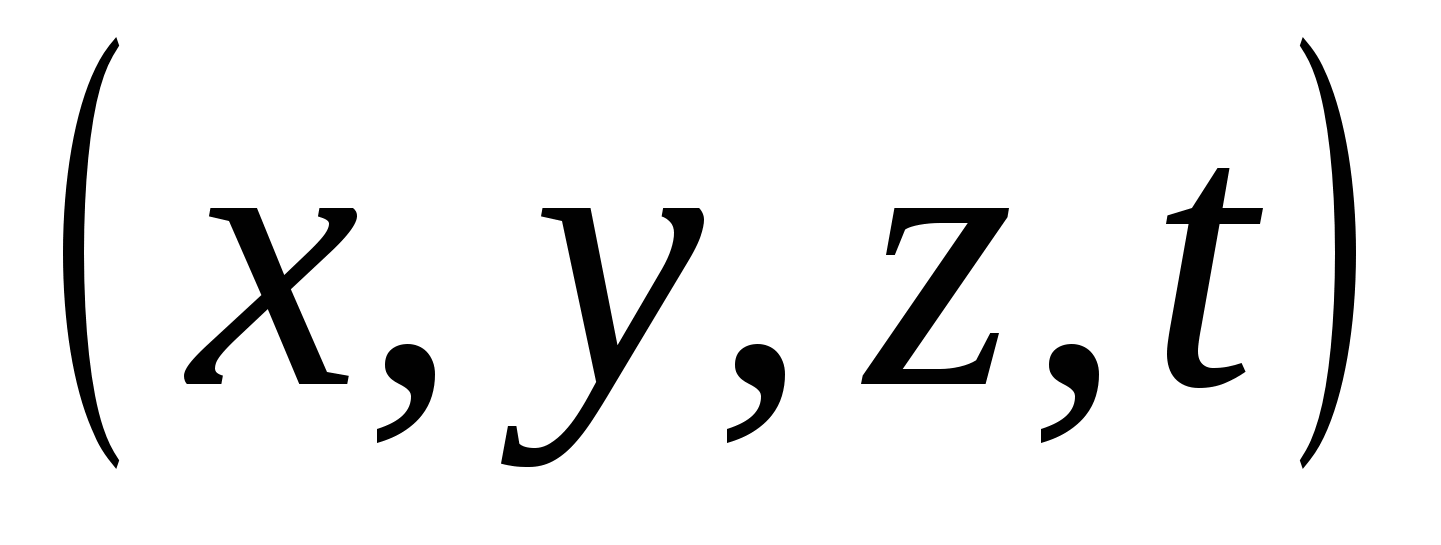 . In Descartes
. In Descartes 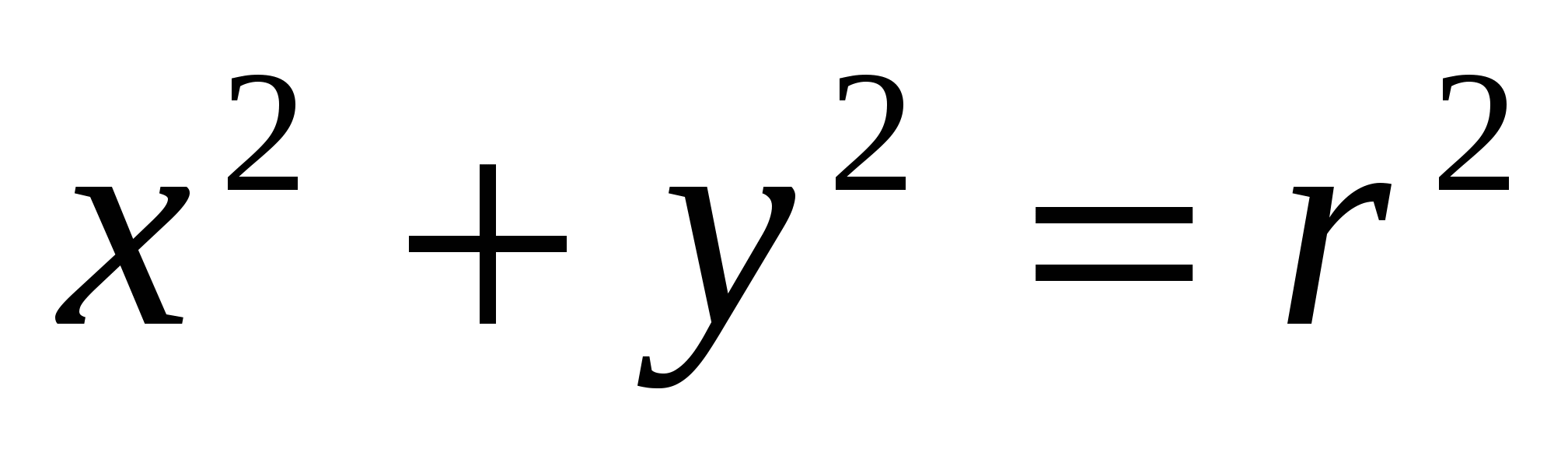 - equation of a circle on a plane,
- equation of a circle on a plane,  - equation of the surface of a ball in three-dimensional space; in the new theory
- equation of the surface of a ball in three-dimensional space; in the new theory 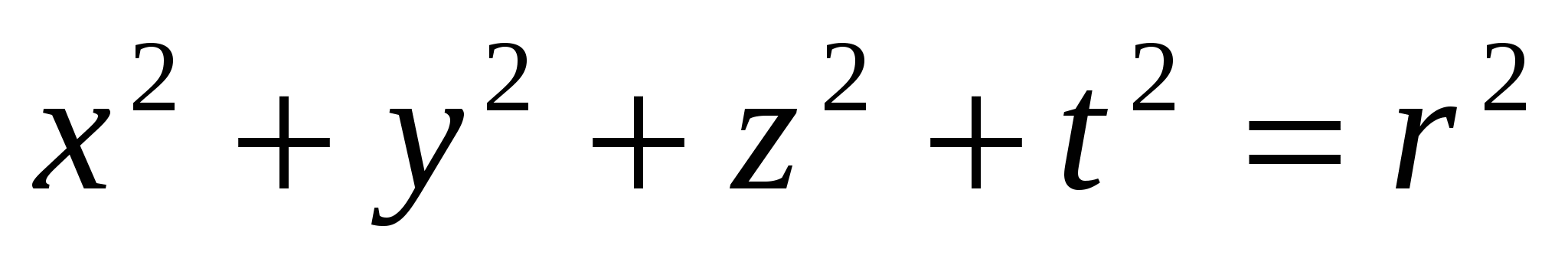 the surface of a sphere in four-dimensional space. Similarly inn
-
dimensional geometry considers planes, straight lines, distances between points, angles between straight lines, etc.
the surface of a sphere in four-dimensional space. Similarly inn
-
dimensional geometry considers planes, straight lines, distances between points, angles between straight lines, etc.
The ideas of multidimensional geometry became firmly established in mathematics at the endXIXcenturies, and at the very beginningXXcenturies, they have found application in special theory relativity, where to three spatial coordinates a fourth is added – time. Thus, the ideas of Descartes' geometry, developed by scientists of subsequent generations, lie at the basis of modern science.
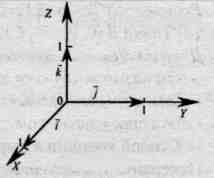
2. Coordinates of a point in space .
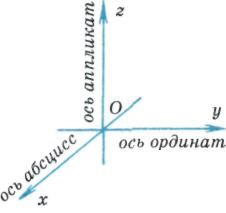 They say that a rectangular (Cartesian) coordinate system is given if three pairwise perpendicular lines are drawn through a point in space, a direction is selected on each of them, and a unit of measurement for the segments is selected. Planes passing through the coordinate axes, respectively
They say that a rectangular (Cartesian) coordinate system is given if three pairwise perpendicular lines are drawn through a point in space, a direction is selected on each of them, and a unit of measurement for the segments is selected. Planes passing through the coordinate axes, respectively 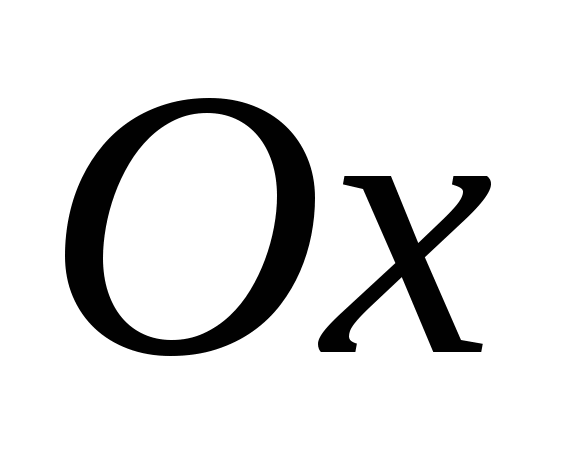 And
And 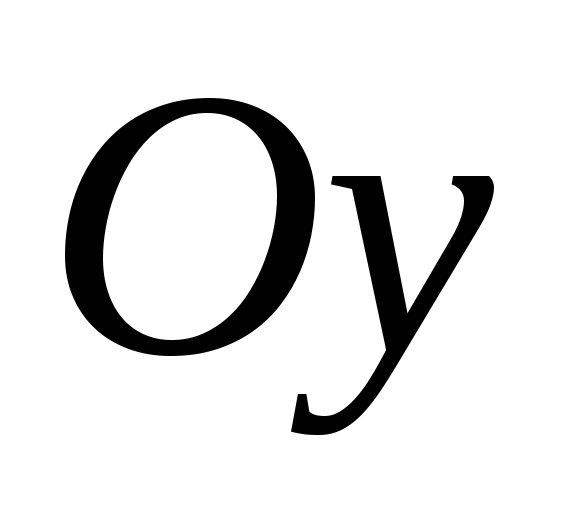 ,
, 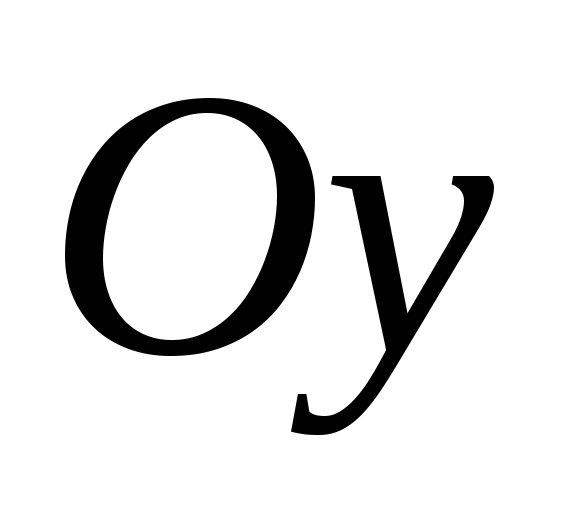 And
And  ,
,  And
And 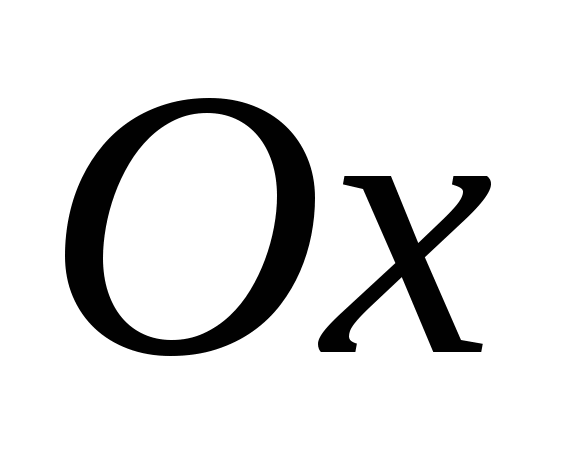 , are calledcoordinate planes
and are designated
, are calledcoordinate planes
and are designated 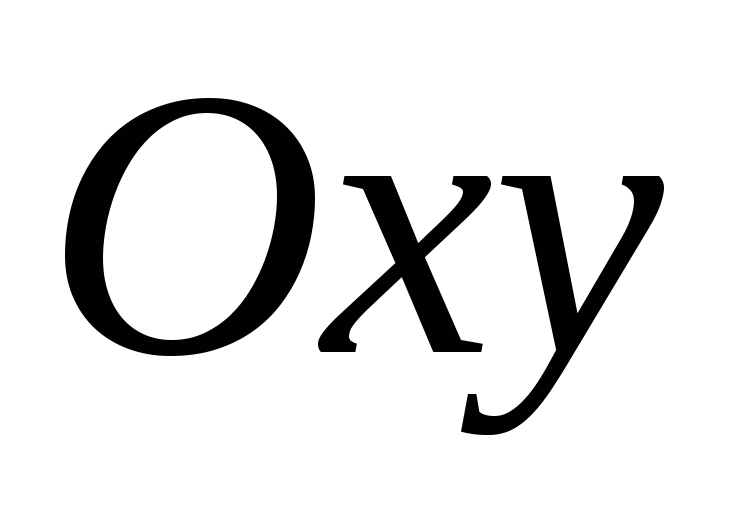 ,
, 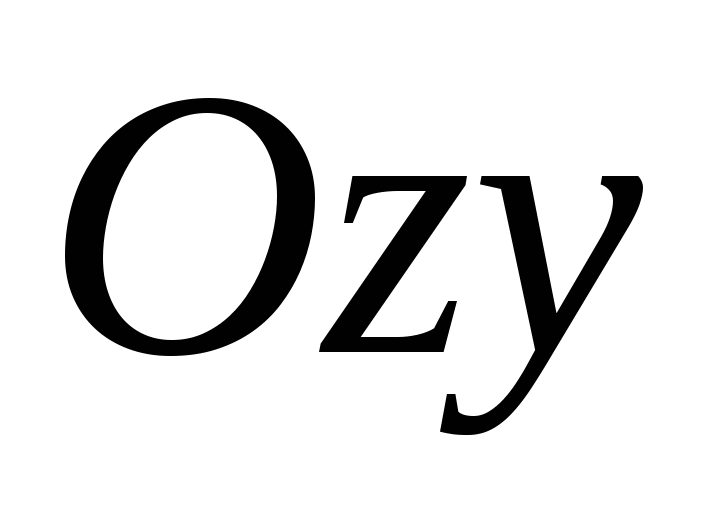 ,
,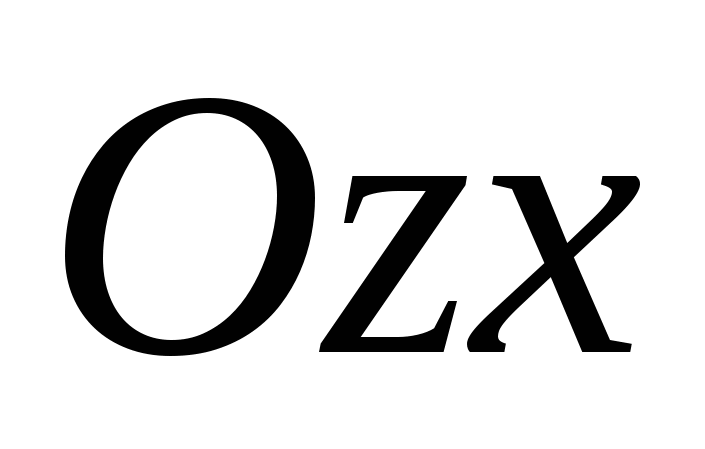 .
.
TO  The coordinates of a point in space are the coordinates of the projections of this point onto the coordinate axes.
The coordinates of a point in space are the coordinates of the projections of this point onto the coordinate axes.
Point coordinates: 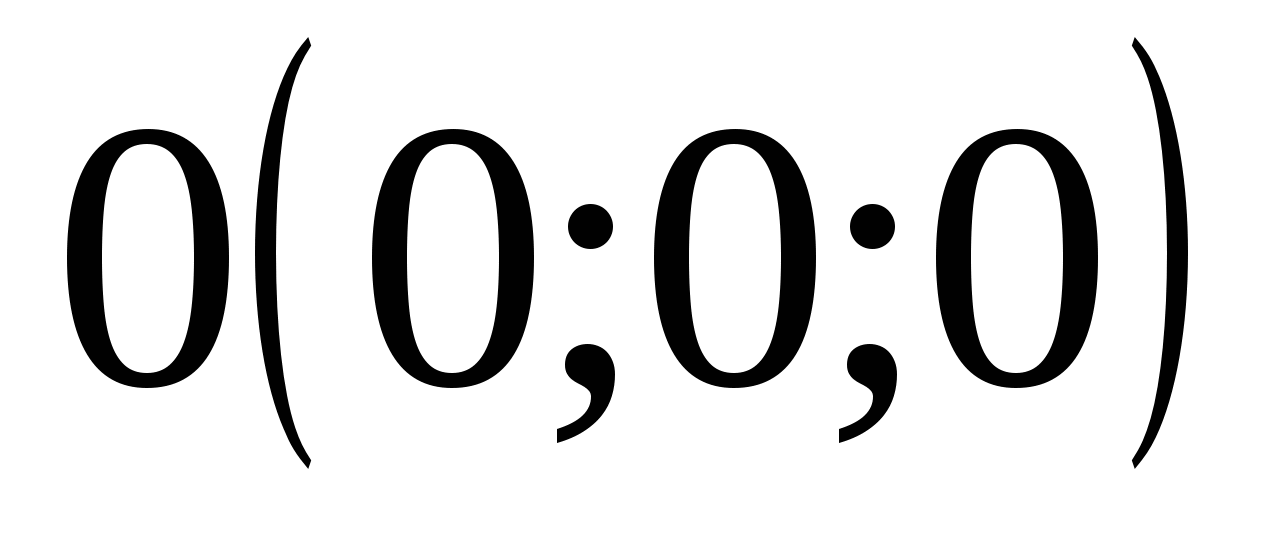 ,
, 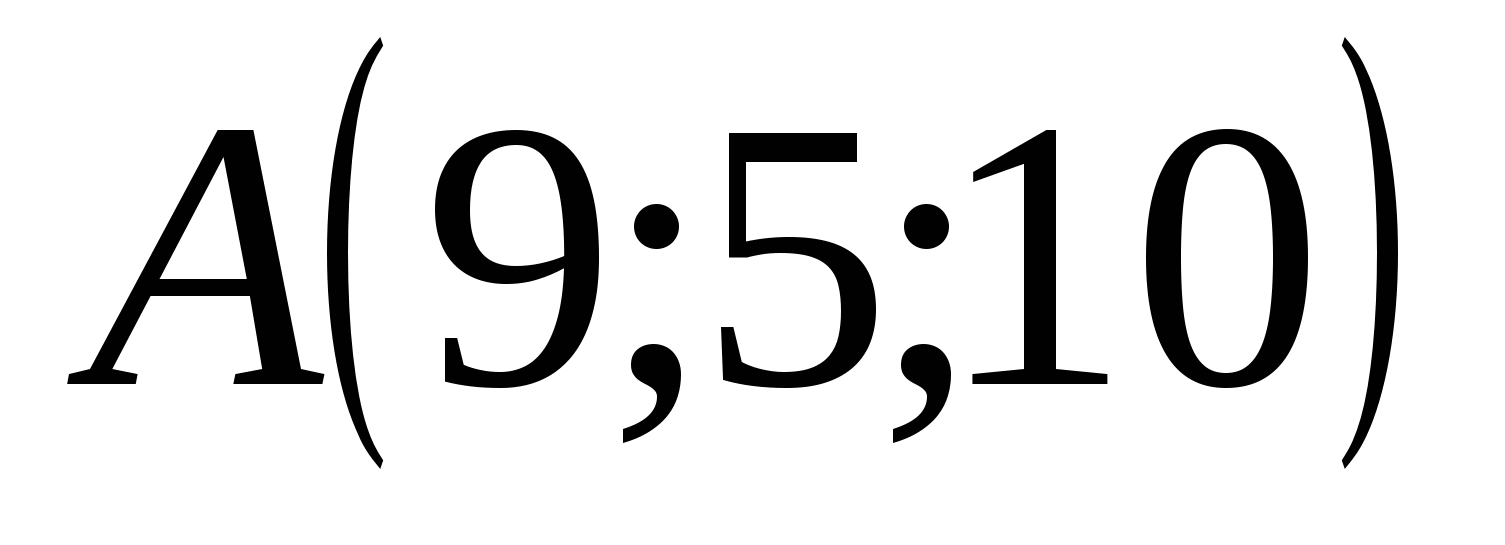 ,
, 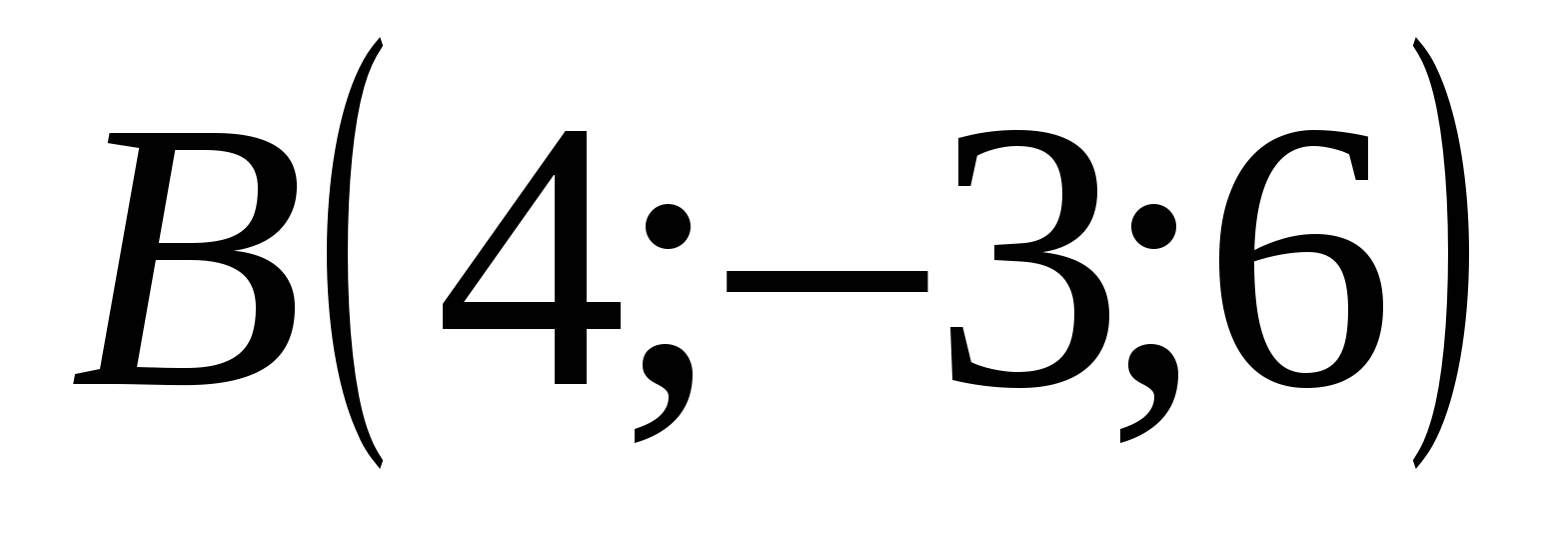 ,
, 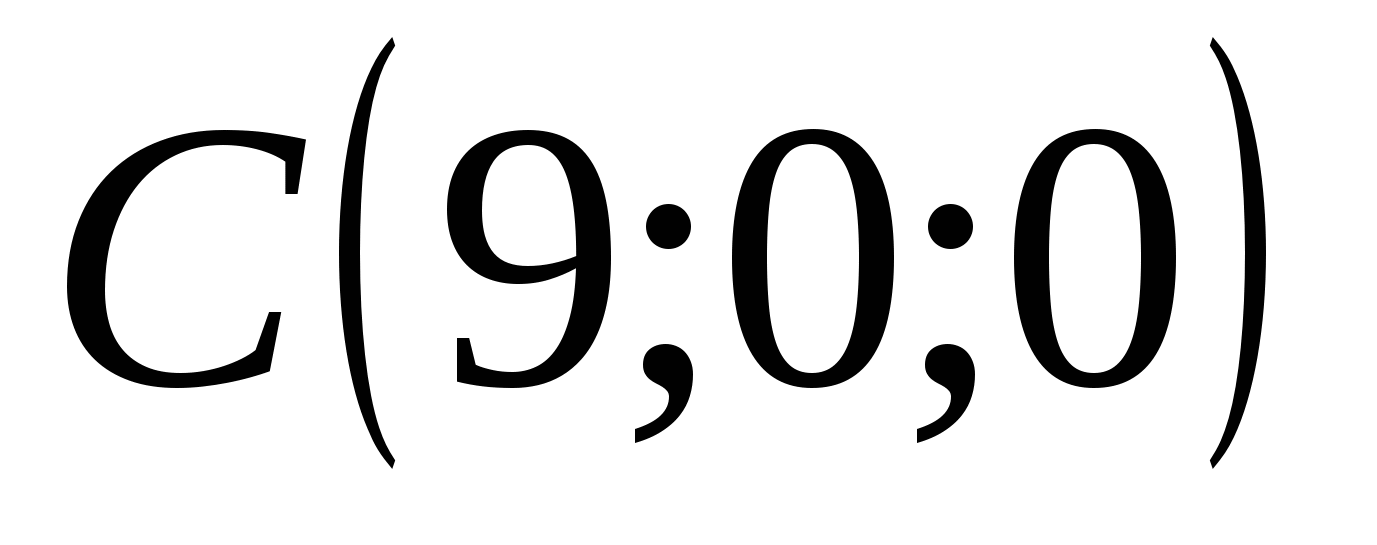 ,
, 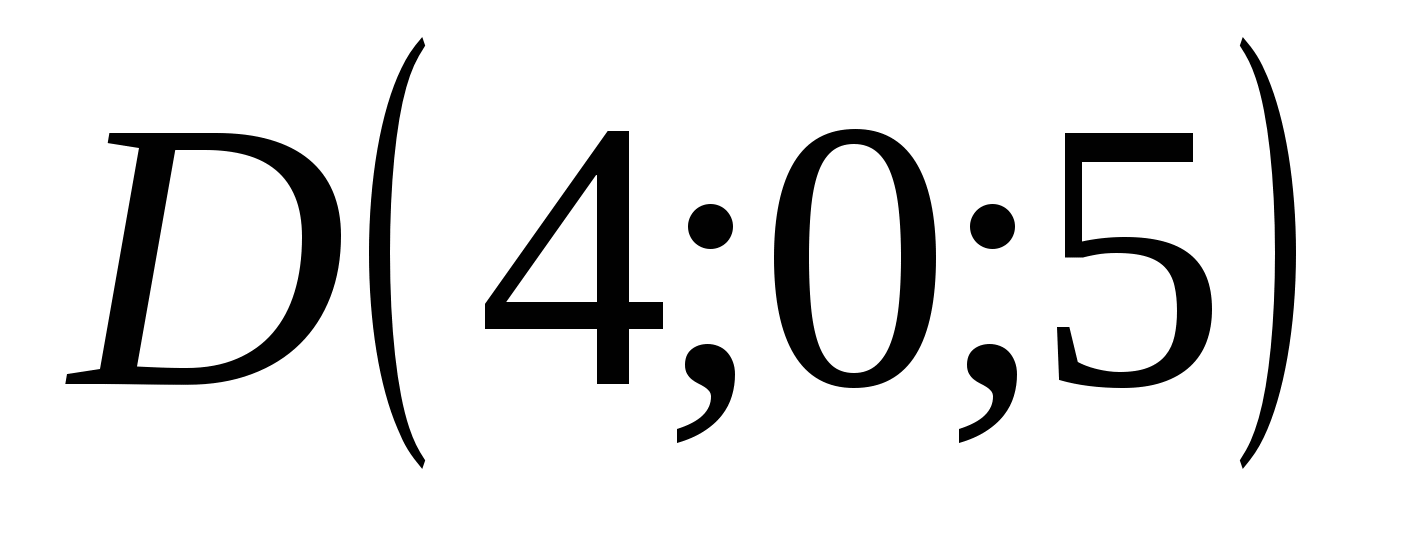 ,
, 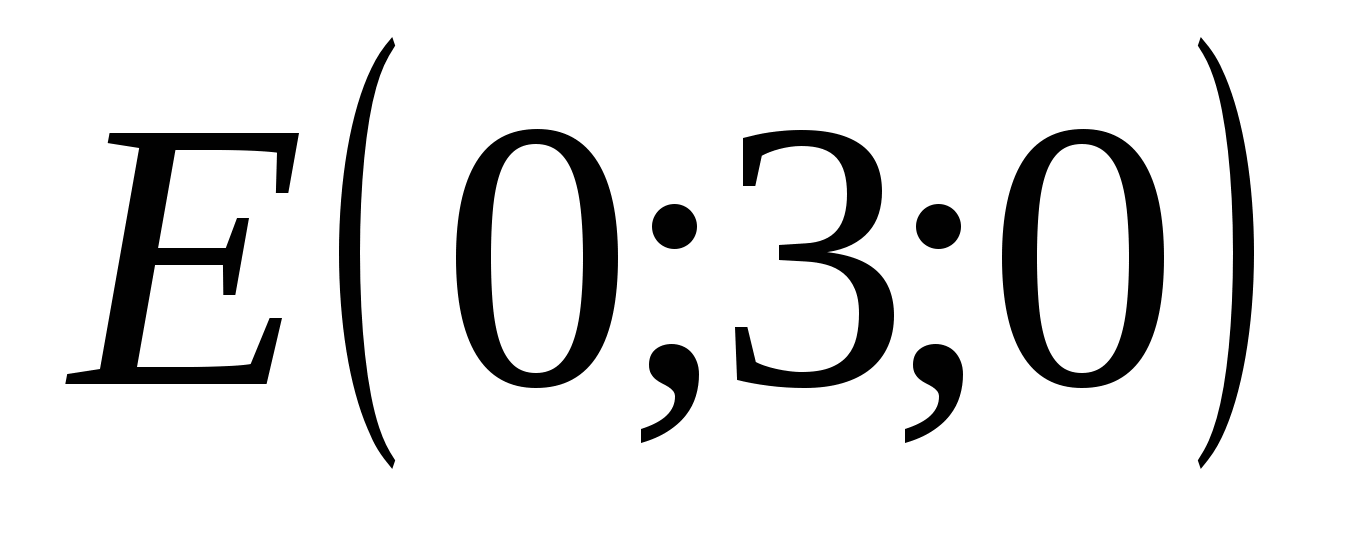 ,
, 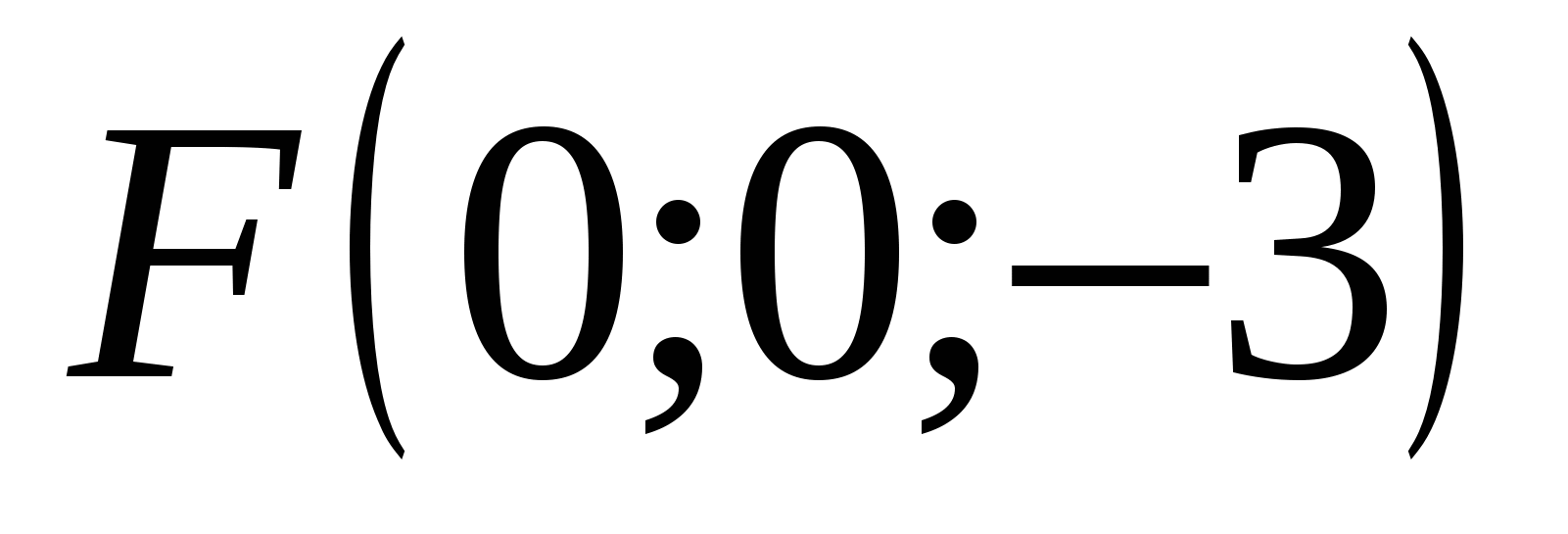 .
.
In space, except coordinate axes, it is convenient to also consider coordinate planes, i.e. planes passing through any two axes. There are three such planes:
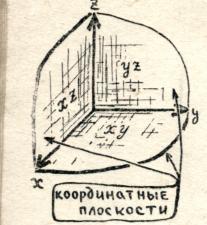
Plane ![]() (passing through the axes
(passing through the axes 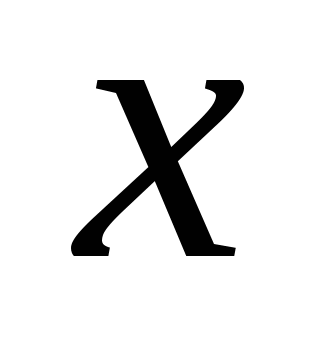 And
And 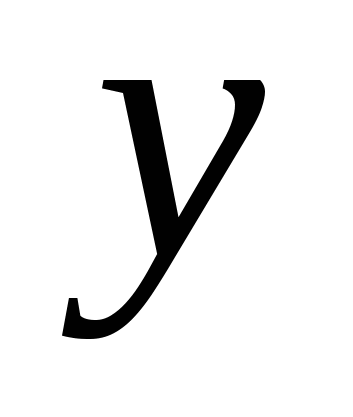 ) - set of points of the form
) - set of points of the form  , Where
, Where 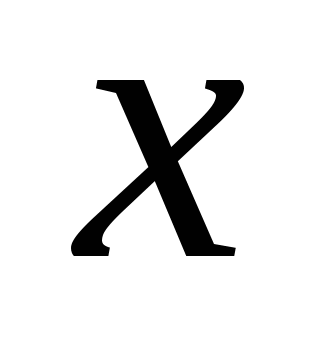 And
And 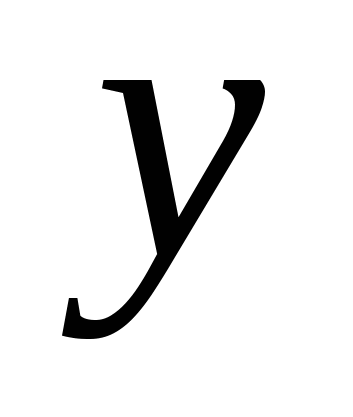 - any numbers;
- any numbers;
Plane  (passing through the axes
(passing through the axes  And
And  ) - set of points of the form
) - set of points of the form 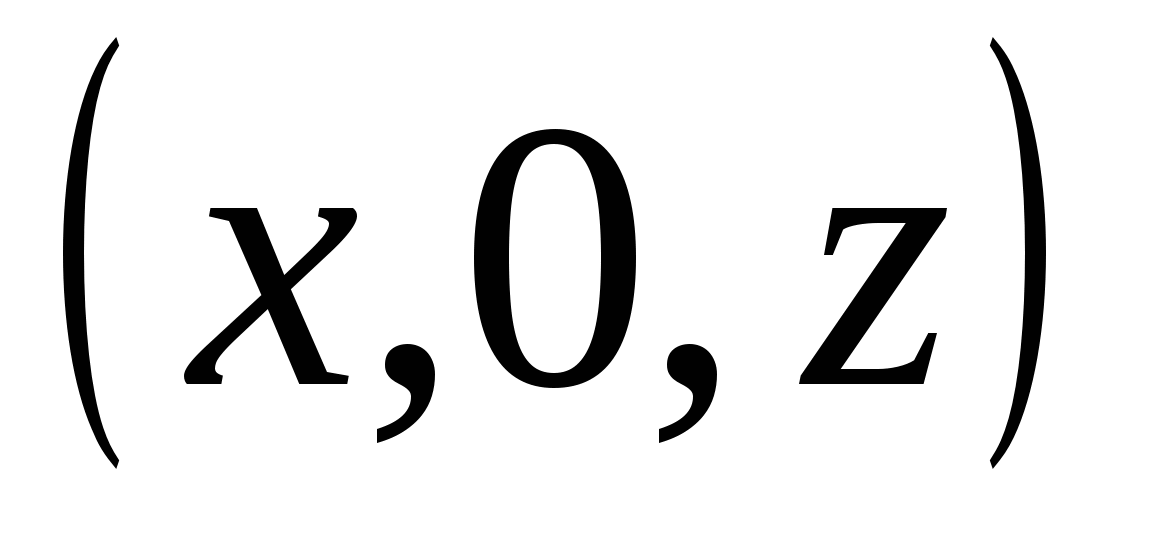 , Where
, Where  And
And  - any numbers;
- any numbers;
Plane  (passing through the axes
(passing through the axes 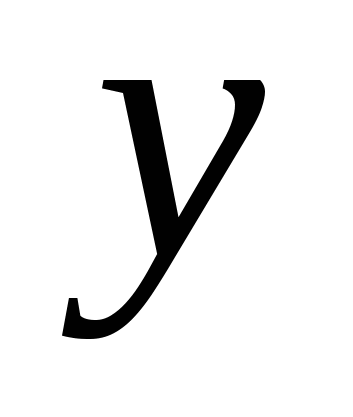 And
And  ) - set of points of the form
) - set of points of the form 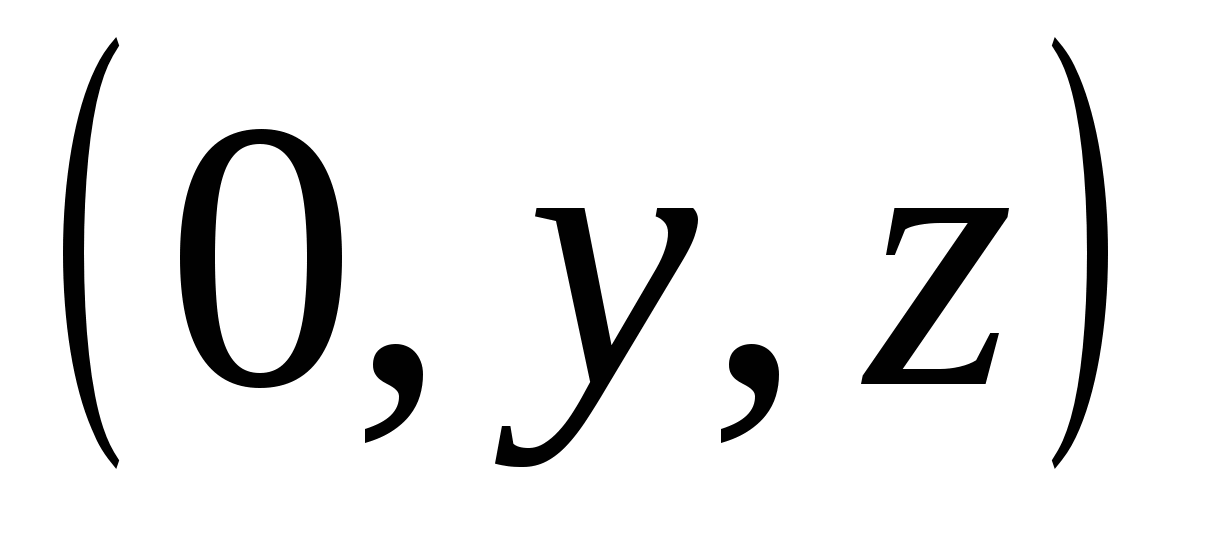 , Where
, Where 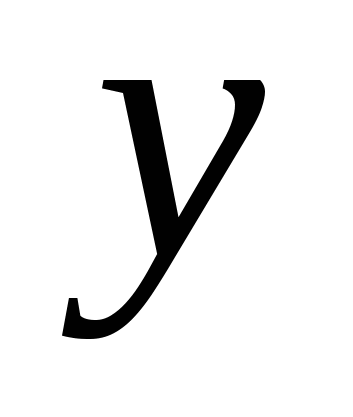 And
And  - any numbers.
- any numbers.
For any point M in space you can find three numbers 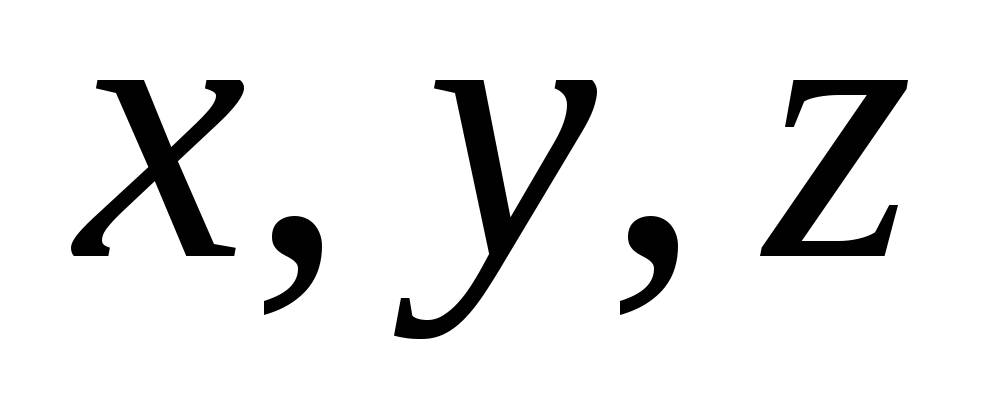 , which will serve as its coordinates.
, which will serve as its coordinates.
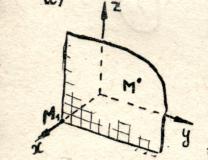 To find the first number
To find the first number 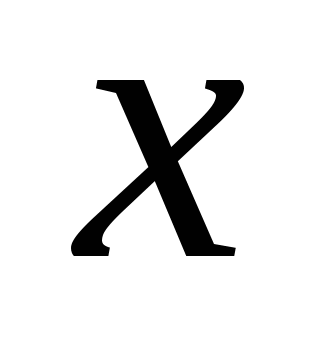 , let us draw a plane parallel to the point M coordinate plane
, let us draw a plane parallel to the point M coordinate plane  (perpendicular to the axisx).The point of intersection of this plane with the axis
(perpendicular to the axisx).The point of intersection of this plane with the axis 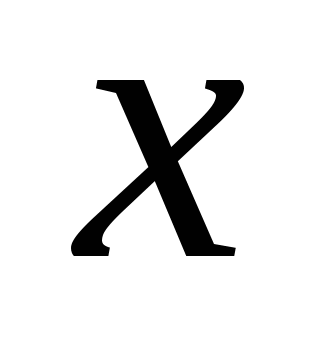 (point M 1
) has a coordinate on this axis
(point M 1
) has a coordinate on this axis 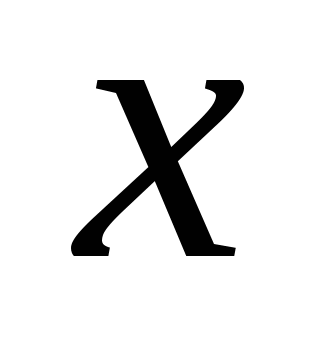 .This is the number
.This is the number 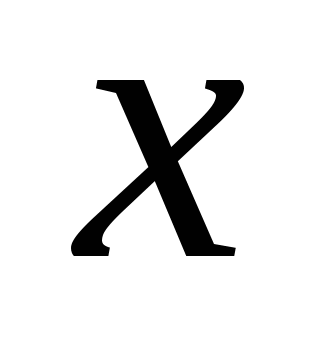 - coordinate of point M 1
on the axis
- coordinate of point M 1
on the axis 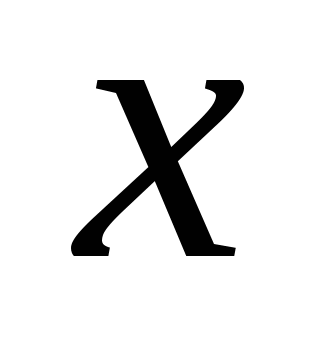 - calledabscissa points M.
- calledabscissa points M.
 To find the second coordinate, draw a plane through point M parallel to the plane
To find the second coordinate, draw a plane through point M parallel to the plane  (perpendicular to the axisy), found on the axis y point M 2. Number y– coordinate of point M 2 per axis y- called ordinate points M.
(perpendicular to the axisy), found on the axis y point M 2. Number y– coordinate of point M 2 per axis y- called ordinate points M.
 We will find the third coordinate of point M by carrying out similar constructions, but perpendicular to the z axis. Let's call the resulting number z applicate points M.
We will find the third coordinate of point M by carrying out similar constructions, but perpendicular to the z axis. Let's call the resulting number z applicate points M.
3. Defining figures in space.
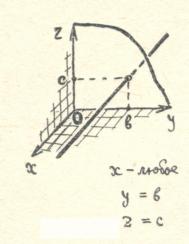
Just like on a plane, coordinates in space make it possible to specify using numbers and numerical ratios not only points, but also lines, surfaces and other sets of points. Let's see, for example, what set of points will be obtained if we specify only two coordinates and consider the third to be arbitrary.
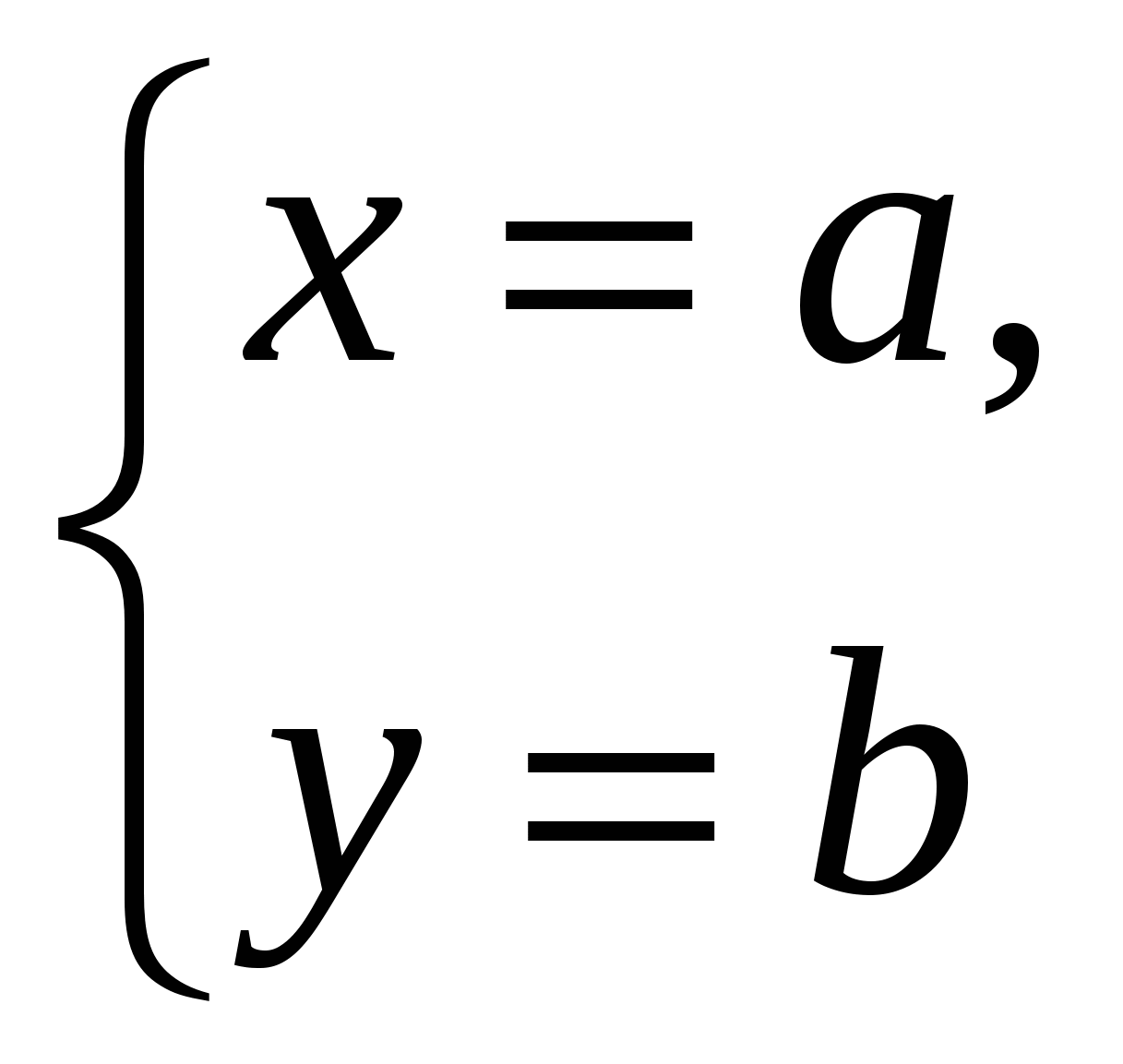
(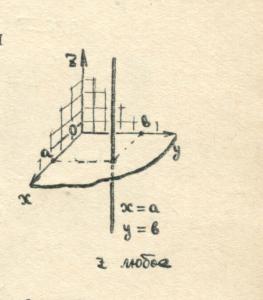 For example,
For example, 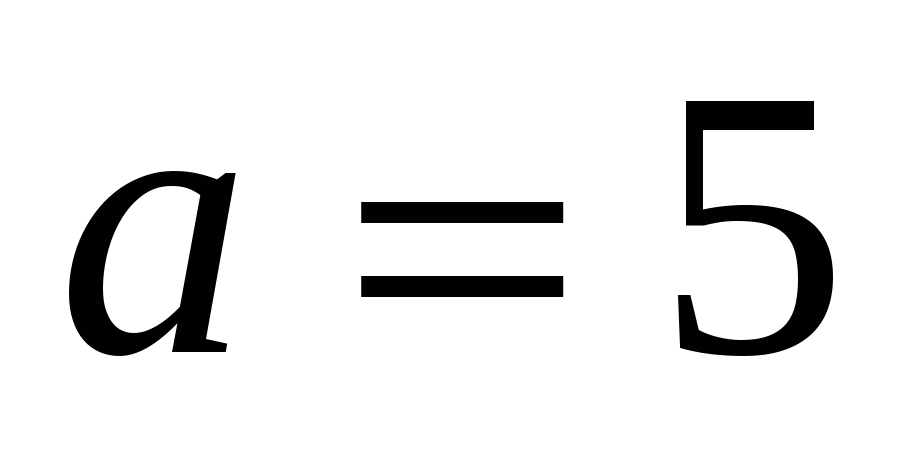
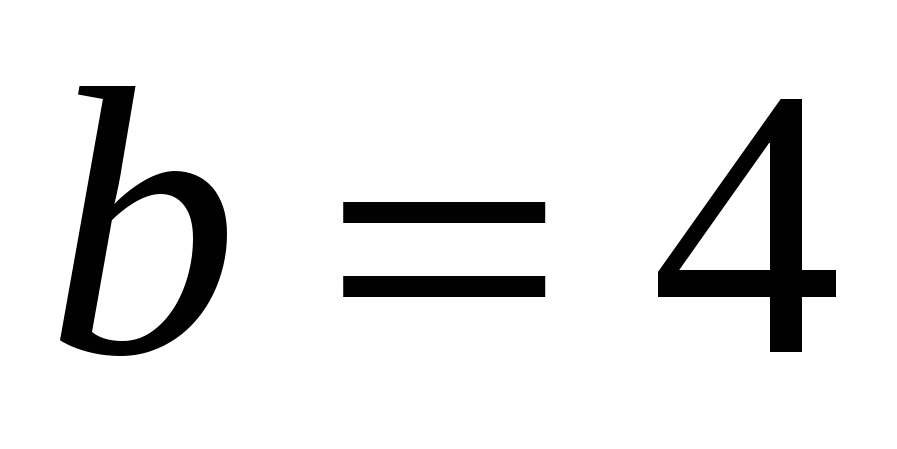 ), define a straight line in space, parallel to the axis
), define a straight line in space, parallel to the axis  .
.
All points on such a line have the same abscissa and the same ordinate. Coordinate  can take any value.
can take any value.


Let's look at a few more examples showing how you can set in
space various sets using equations and other relationships between coordinates.
1). Consider the equation.
Since the distance of the point 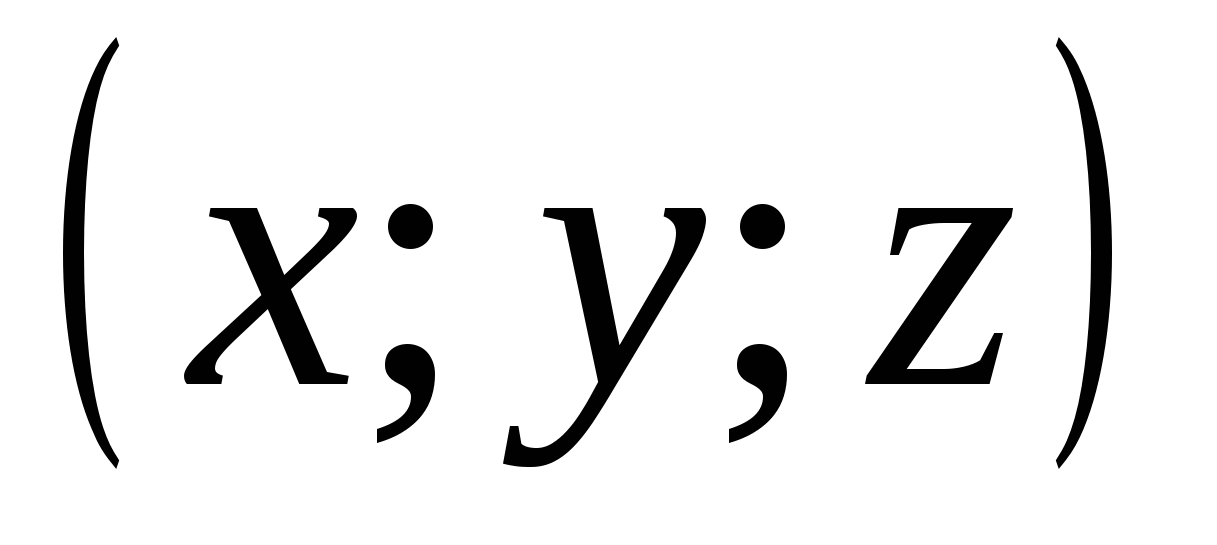 from the origin is given by the expression
from the origin is given by the expression 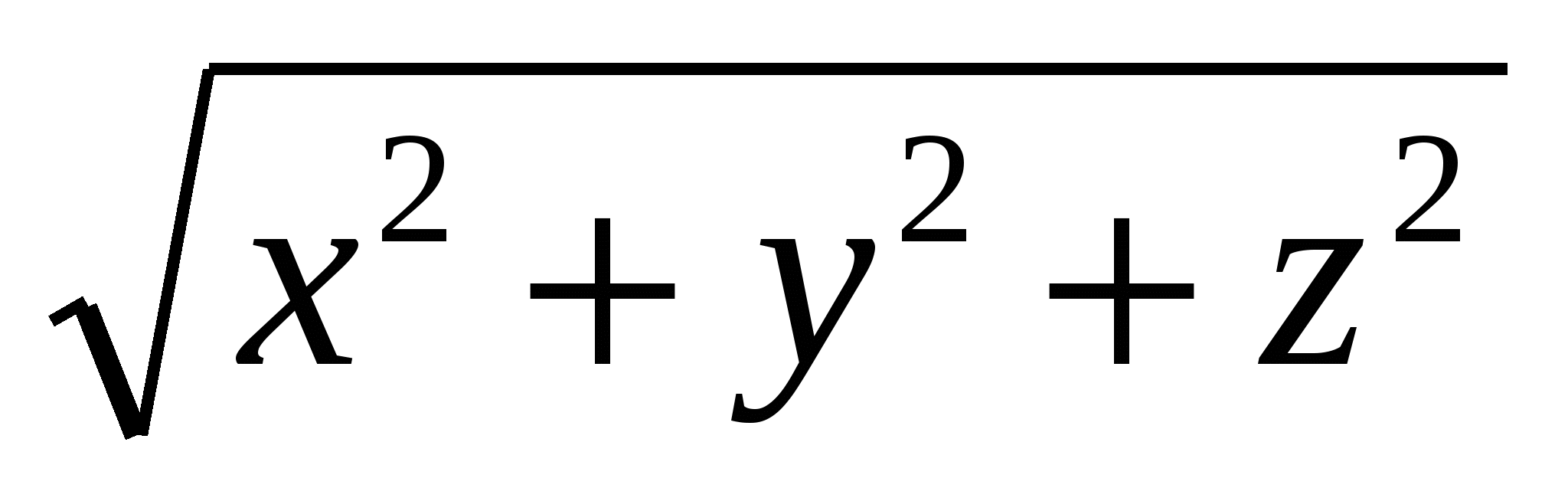 , then it is clear that translated into geometric language the relation
, then it is clear that translated into geometric language the relation 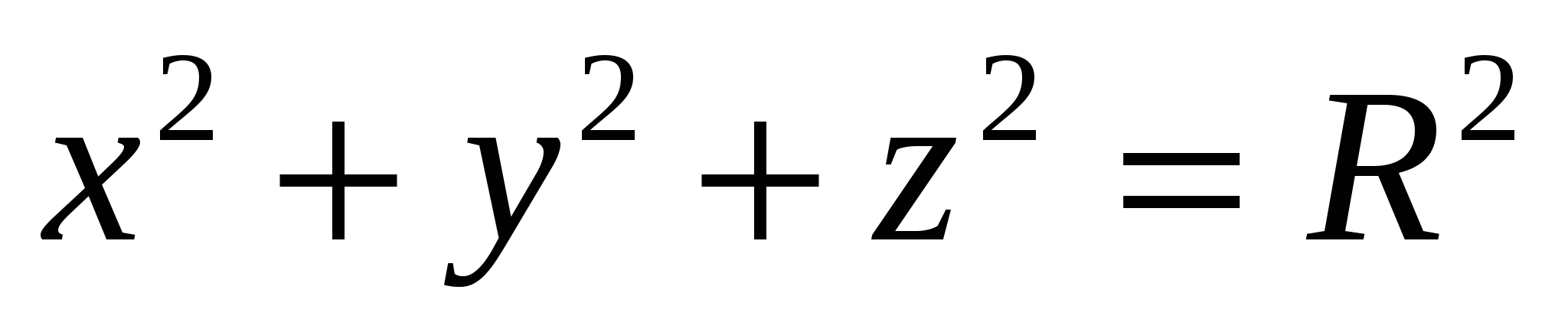 means that the point with coordinates
means that the point with coordinates 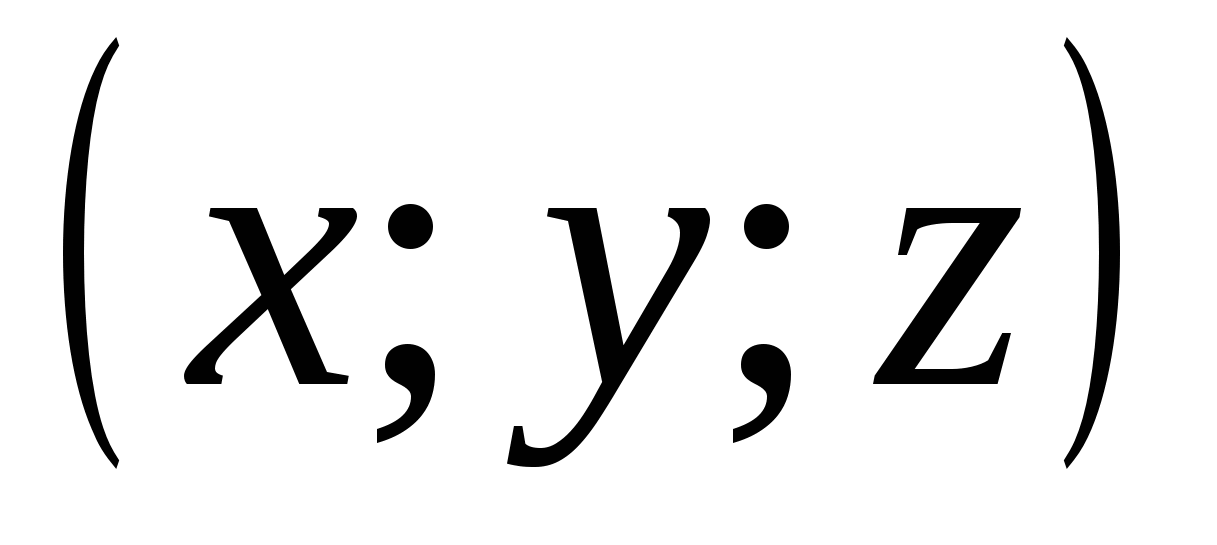 , is at a distanceR
from the origin. This means that the set of all points for which the relation holds
, is at a distanceR
from the origin. This means that the set of all points for which the relation holds 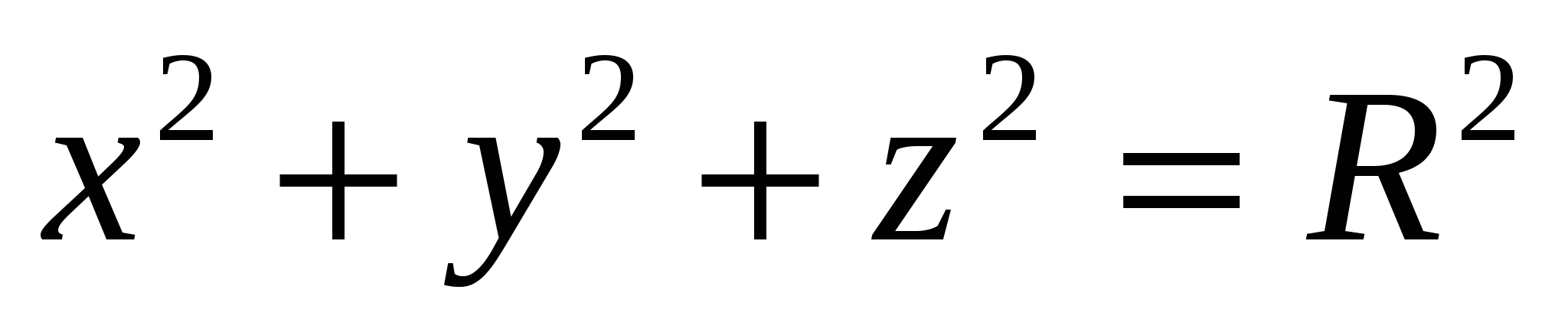 , is the surface of a ball - a sphere with center at the origin and radiusR
.
, is the surface of a ball - a sphere with center at the origin and radiusR
.
2). Let us consider where the points are located whose coordinates satisfy the relation  .
.
Since this relationship means that the distance of the point 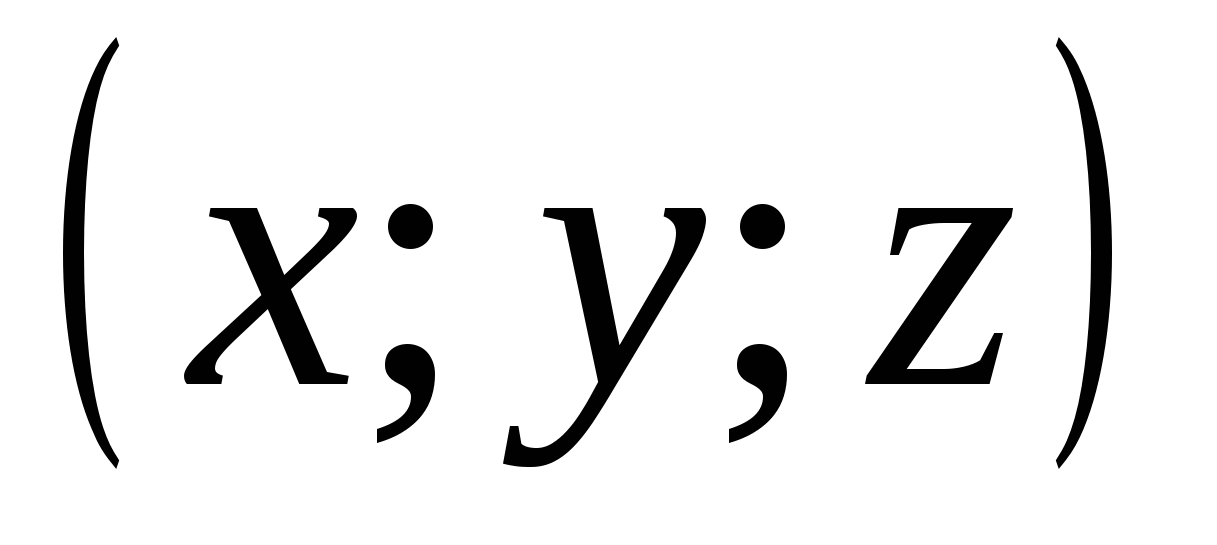 from the origin of coordinates is less than one, then the required set is the set of points lying inside a ball with a center at the origin of coordinates and a radius equal to one.
from the origin of coordinates is less than one, then the required set is the set of points lying inside a ball with a center at the origin of coordinates and a radius equal to one.
Chapter 2
1. Decomposition of a vector into coordinate vectors. Vector coordinates.
The basis of a space is any ordered triple of non-coplanar vectors 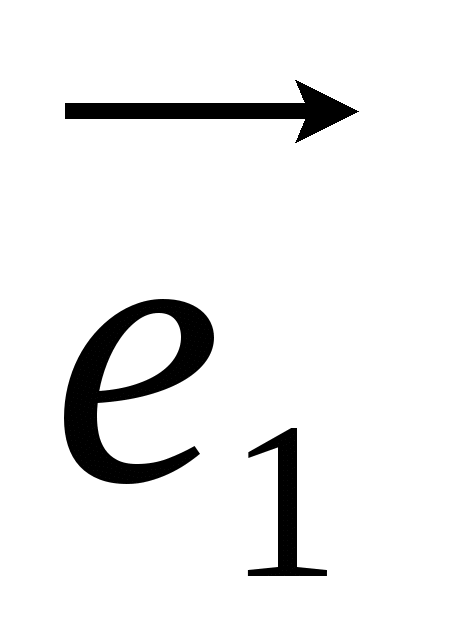 ,
, 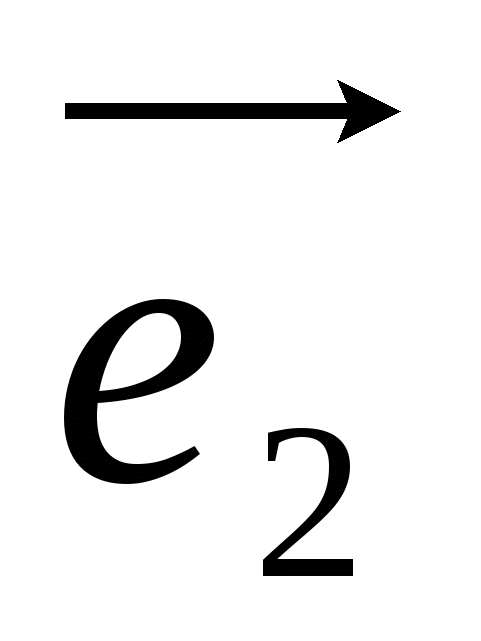 ,
, 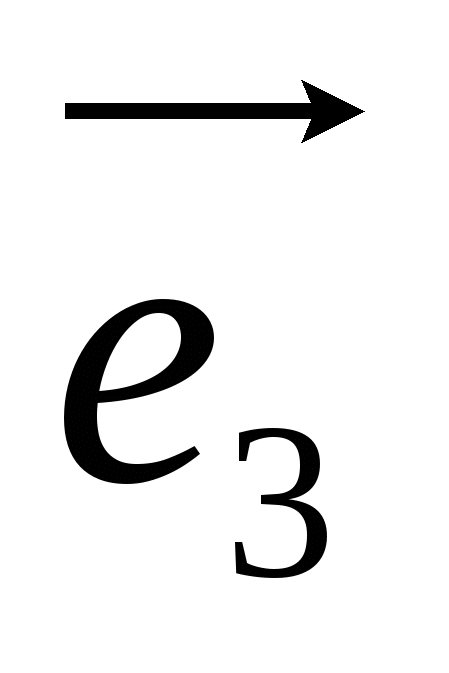 , denoted by the symbol
, denoted by the symbol 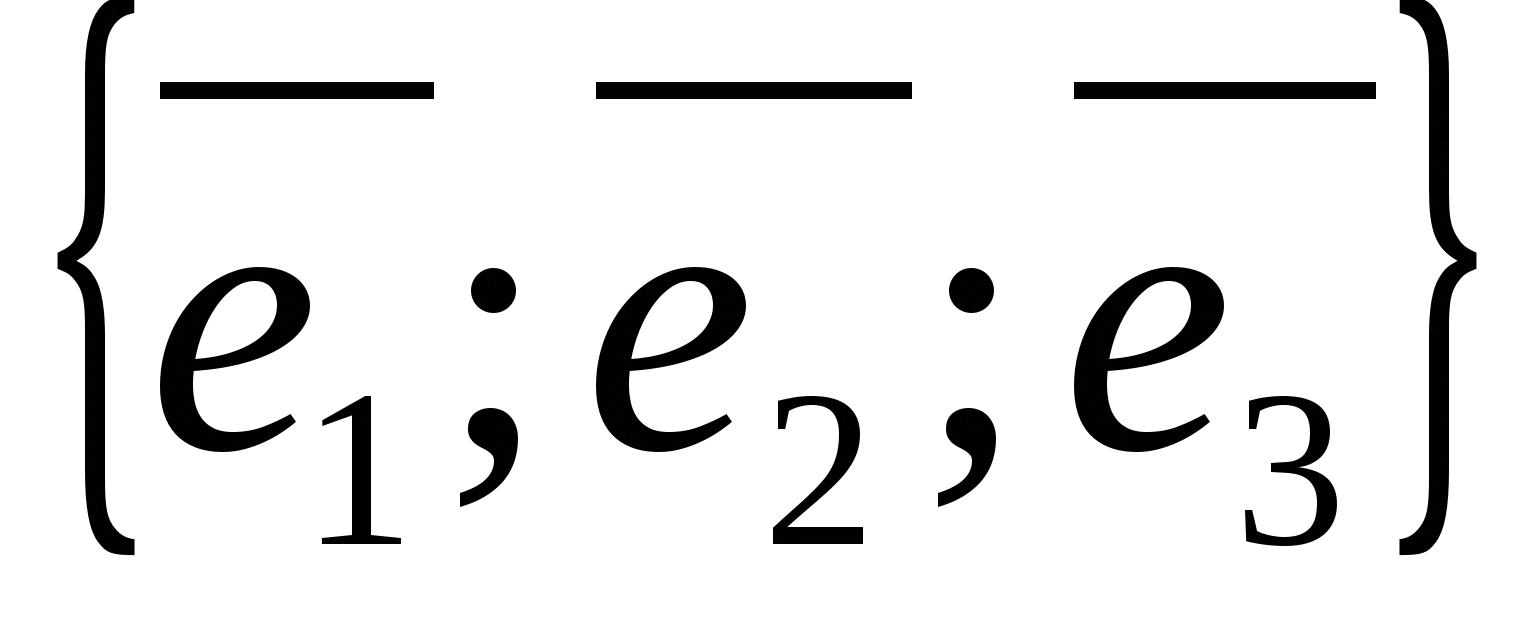 .
.
A special case is the rectangular orthonormal basis 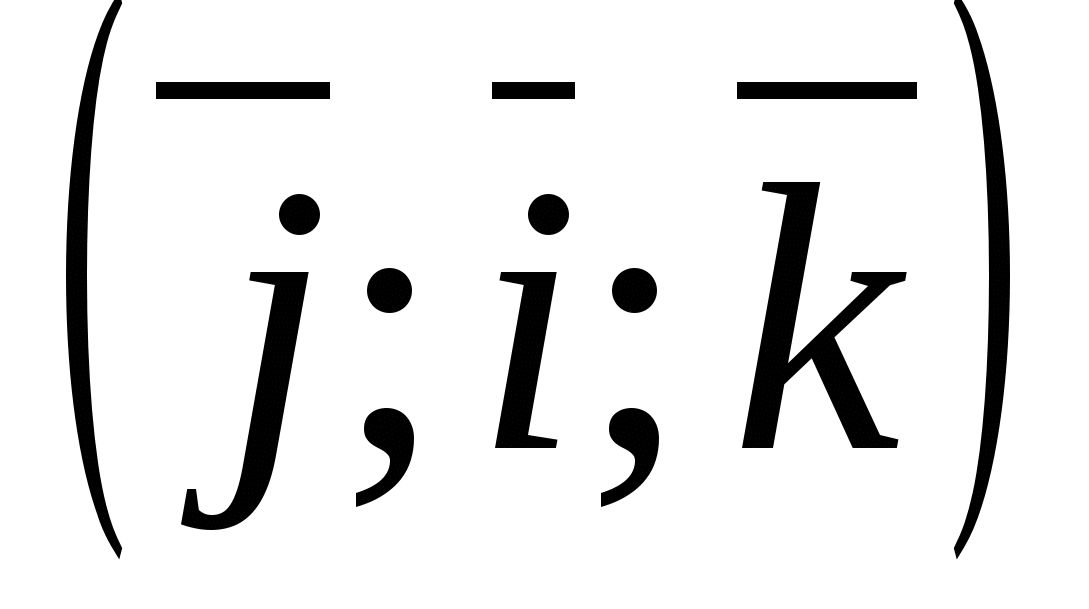 , Where
, Where 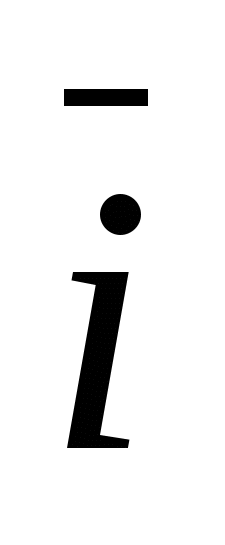 - unit vector of the x-axis, through -
- unit vector of the x-axis, through -  unit vector of the ordinate axis and through
unit vector of the ordinate axis and through 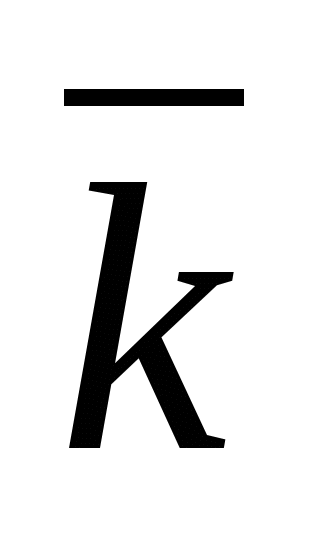 -unit vector axis applicate, i.e.
-unit vector axis applicate, i.e. 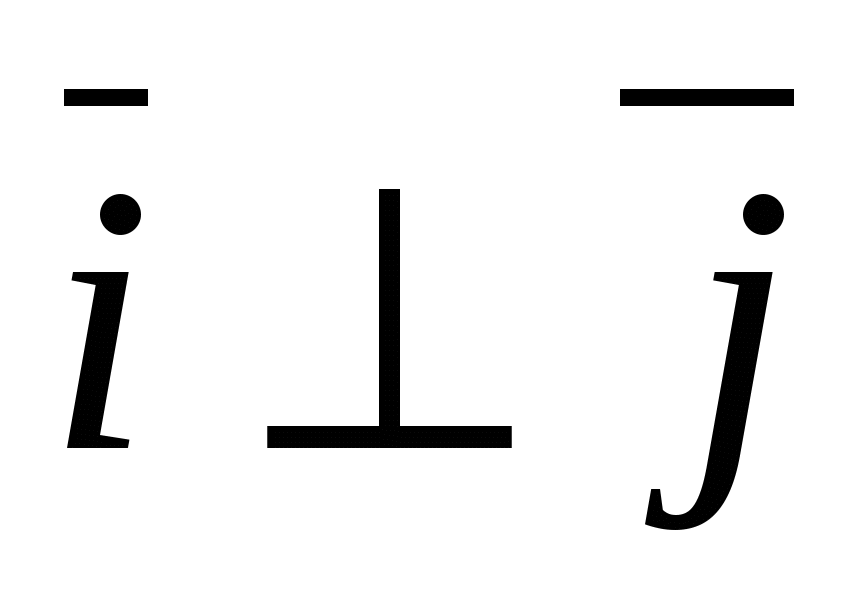 ,
, 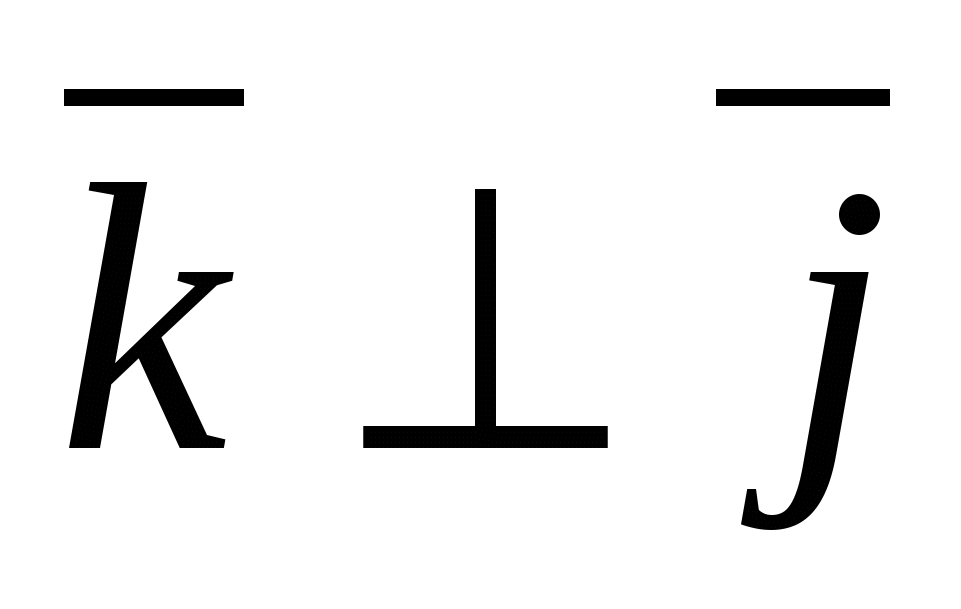 ,
, 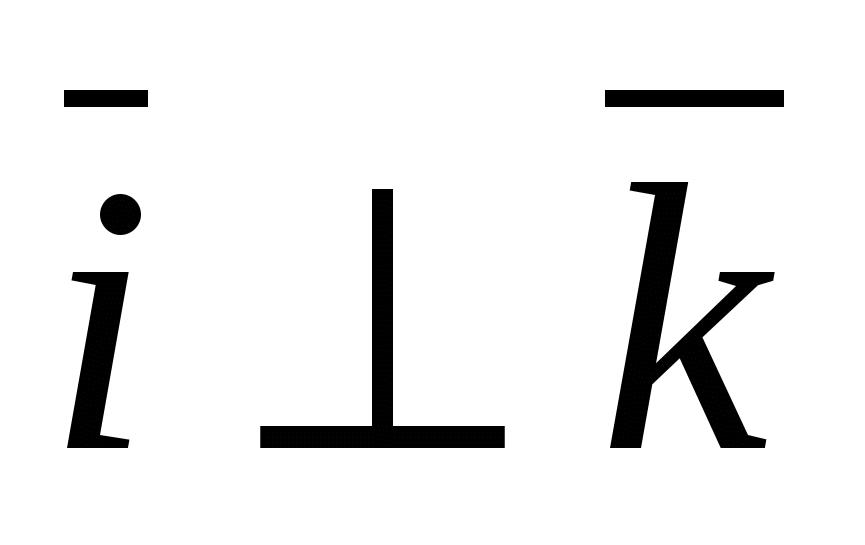 ,
,  .
.
This basis 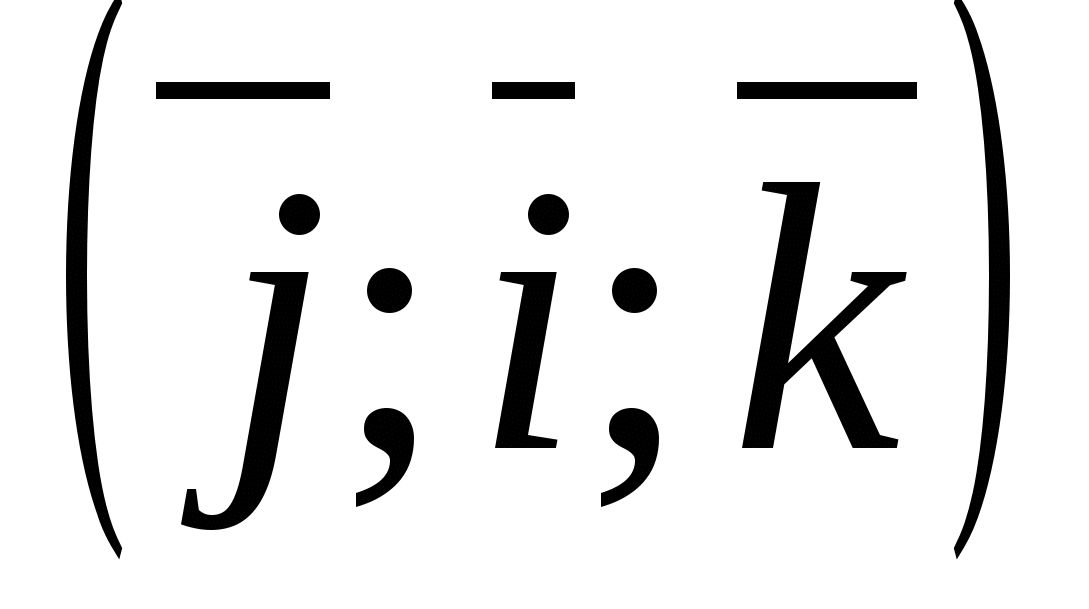 and the beginning of the countdown ABOUT define a rectangular Cartesian coordinate system
and the beginning of the countdown ABOUT define a rectangular Cartesian coordinate system  in space.
in space.
Theorem 1
Any space vector
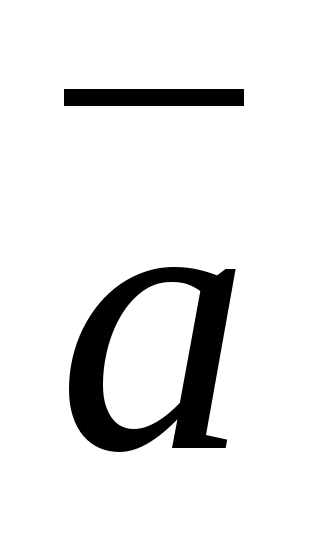 can be expanded into coordinate vectors, i.e. present in the form -
can be expanded into coordinate vectors, i.e. present in the form -
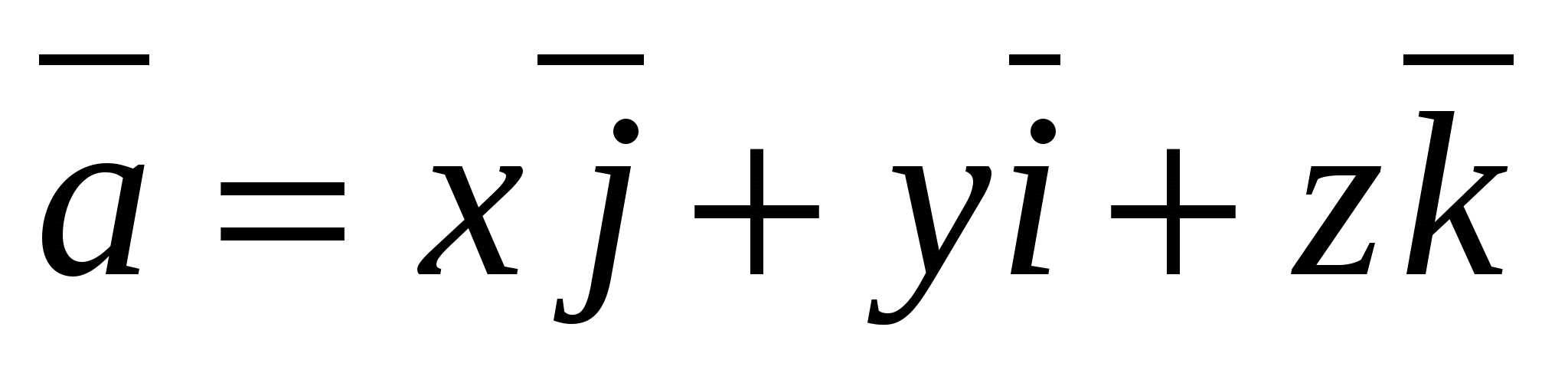 ,
,
and the expansion coefficients  are determined in a unique way.
are determined in a unique way.
H 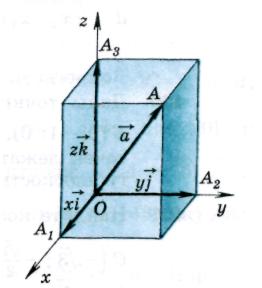 isla
isla 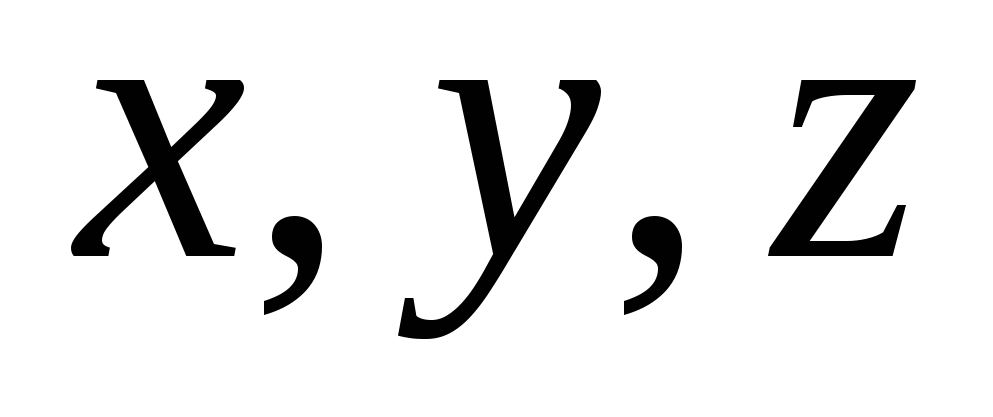 are called vector coordinates
are called vector coordinates 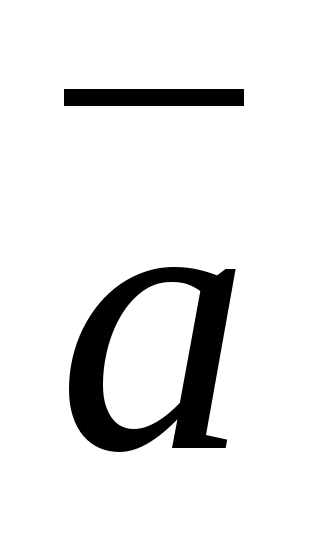 , i.e.
, i.e. 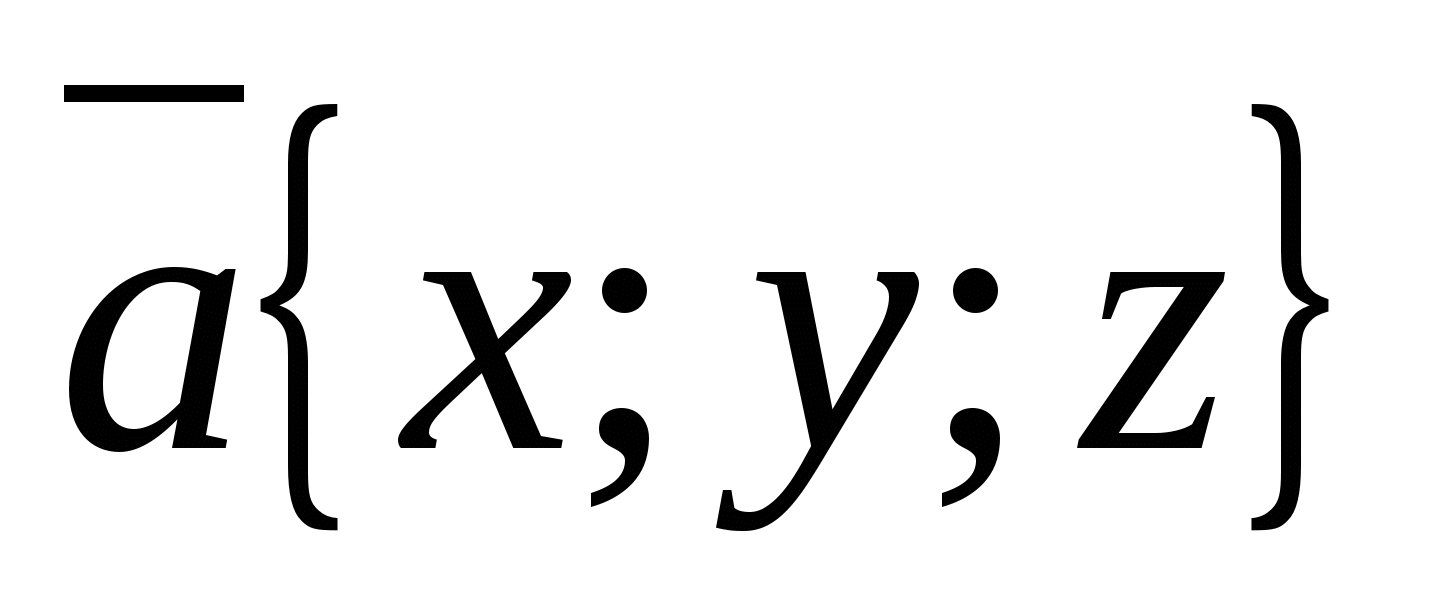 . Since the zero vector can be represented as
. Since the zero vector can be represented as 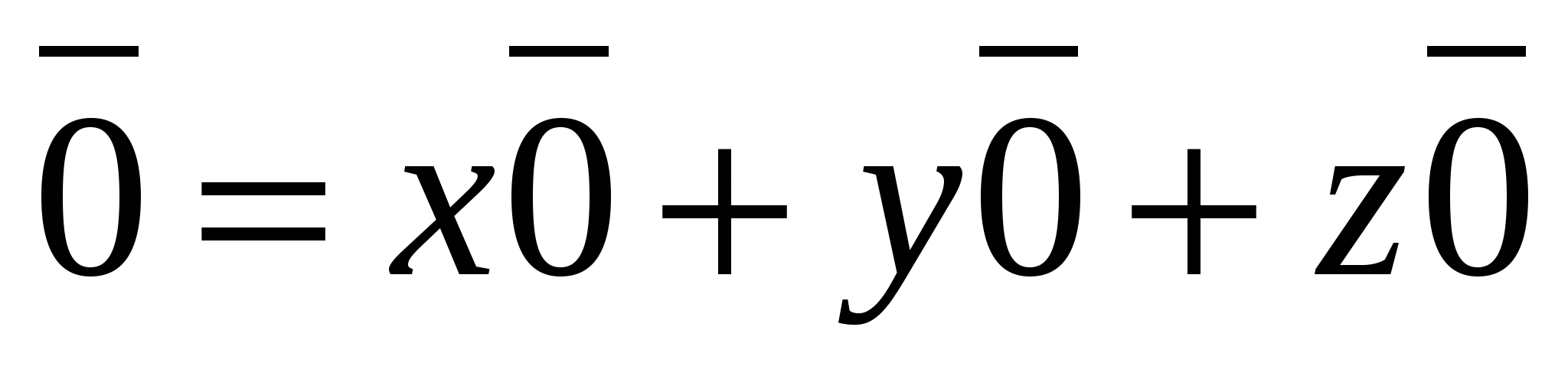 , then all coordinates of the zero vector are equal to zero,
, then all coordinates of the zero vector are equal to zero, 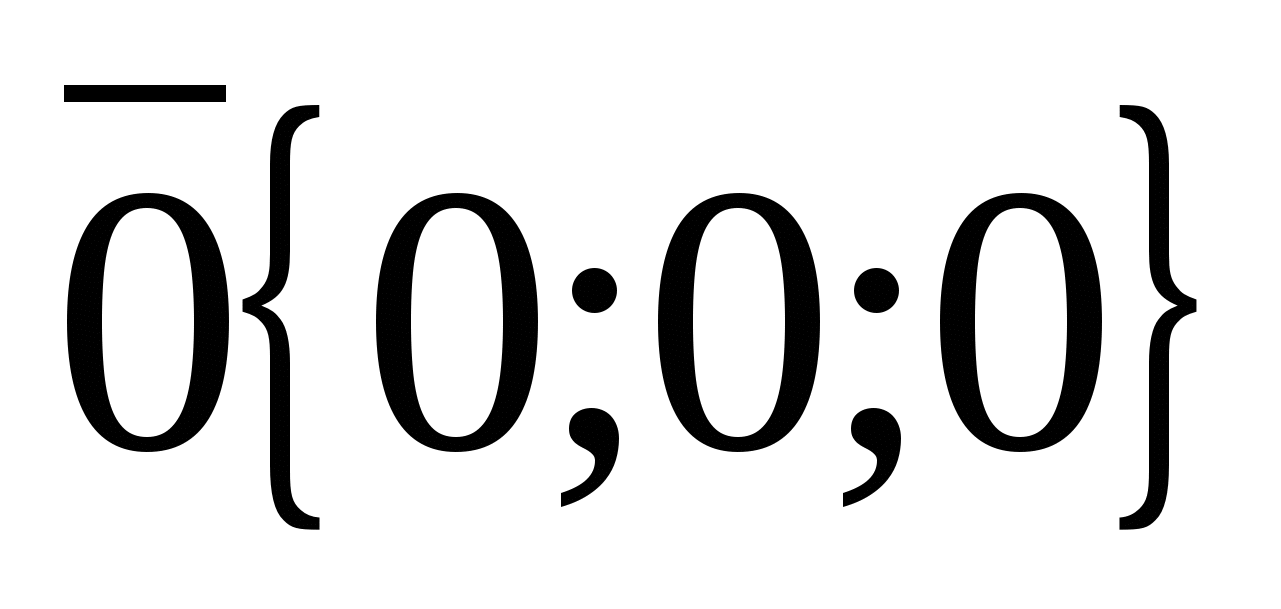 .
.
2. Linear operations on vectors in coordinates.
Rule 1.
Coordinates of equals
vectors are respectively equal,
those. if vectors 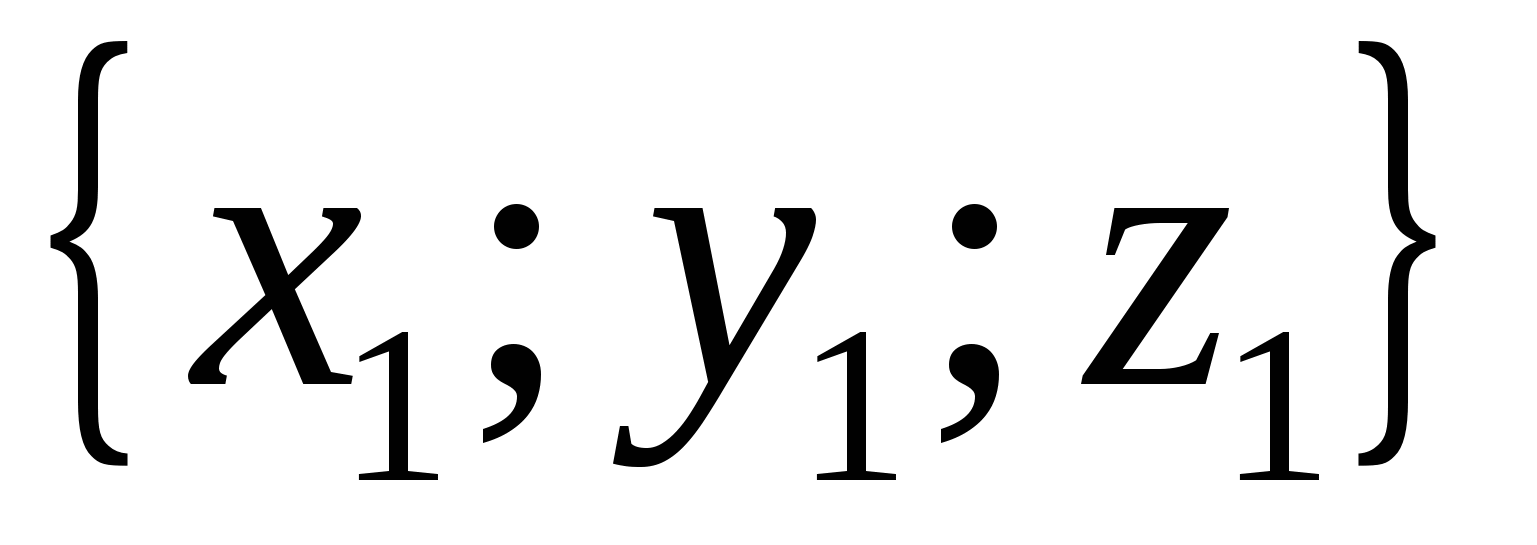 And
And 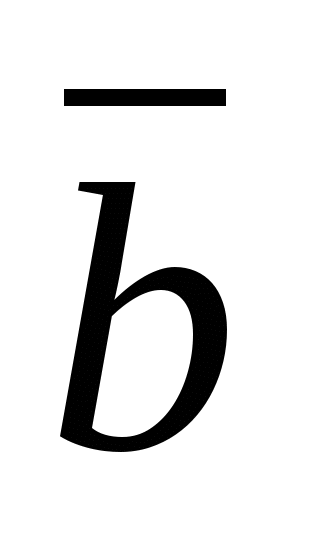
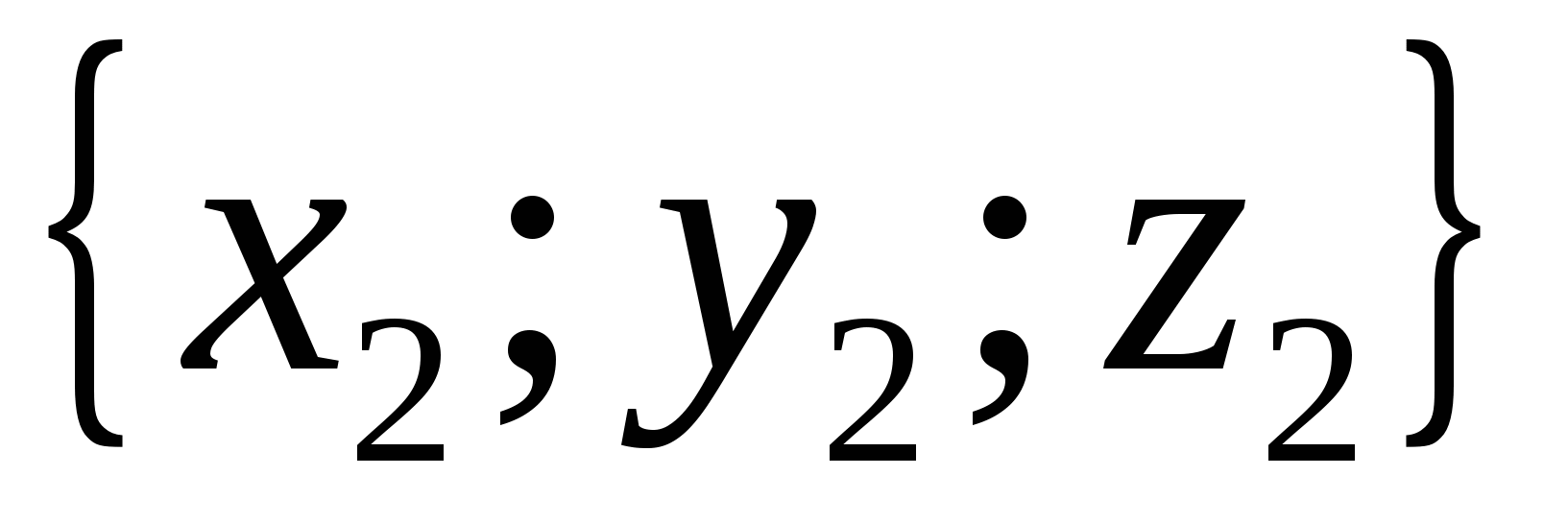 are equal, then
are equal, then 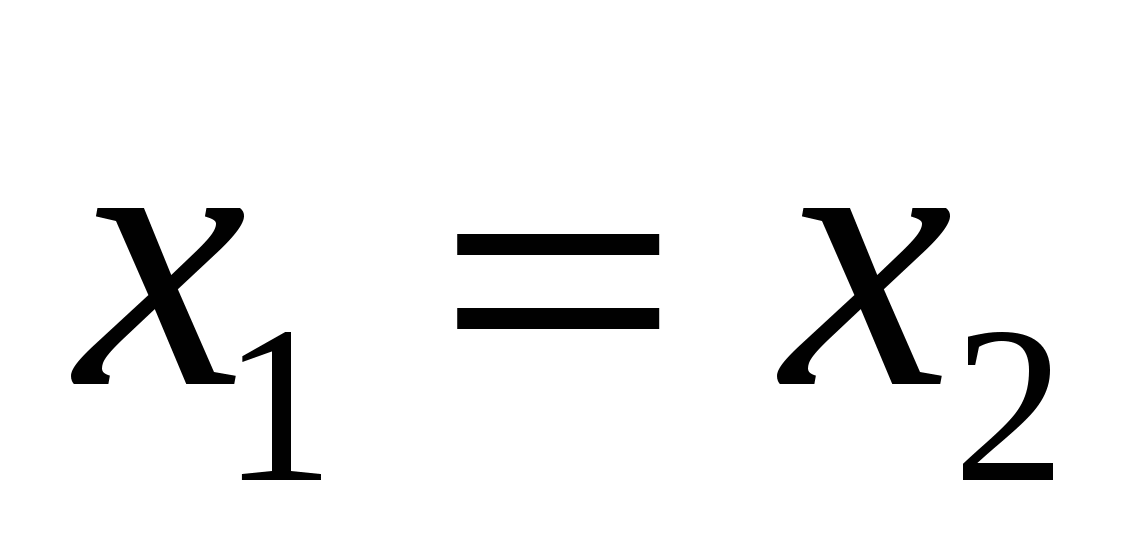 ,
,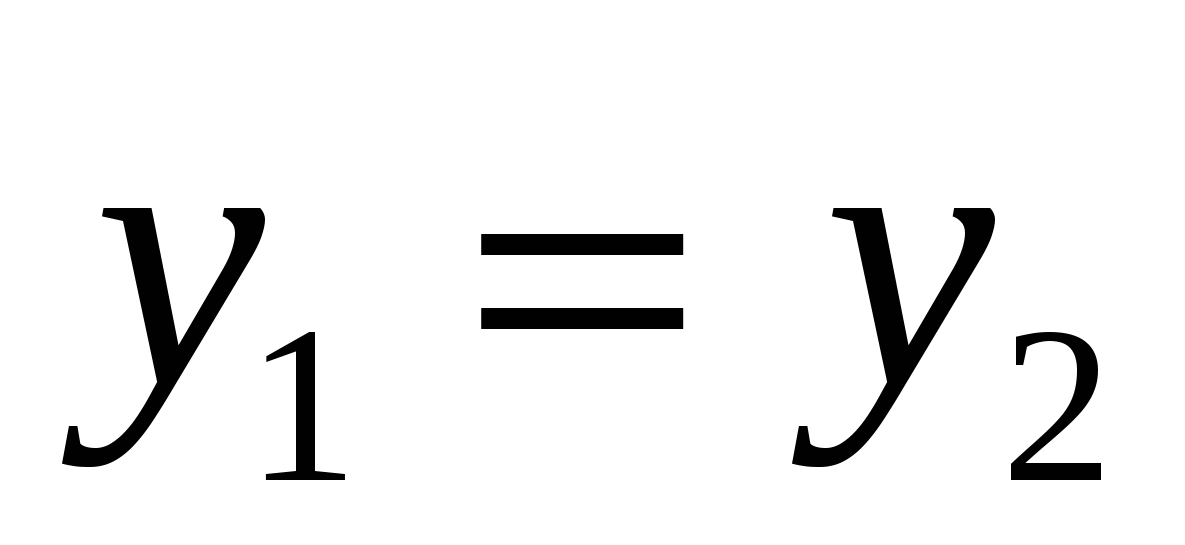 And
And 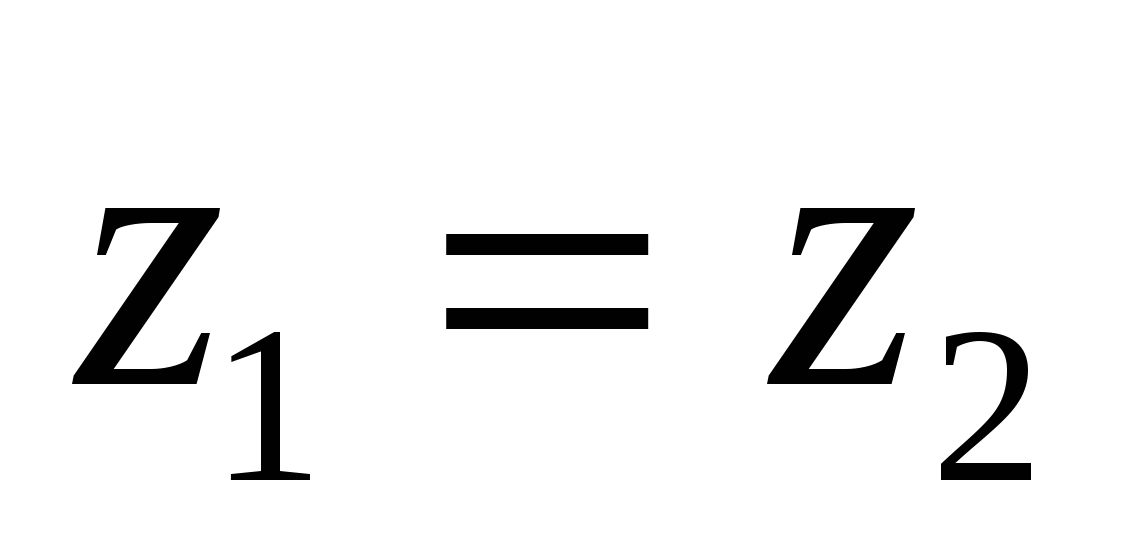 .
.
Rule 2.
Each coordinate of the sum of two or more vectors is equal to the sum of the corresponding coordinates of these vectors.
In other words, if 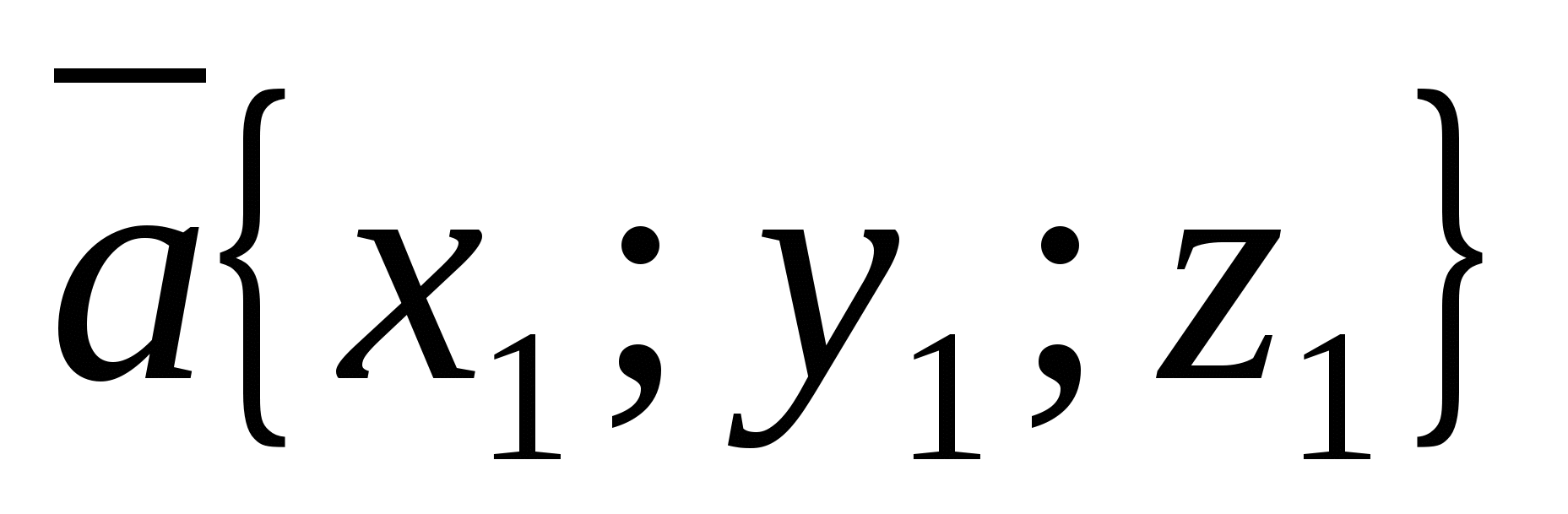 And
And 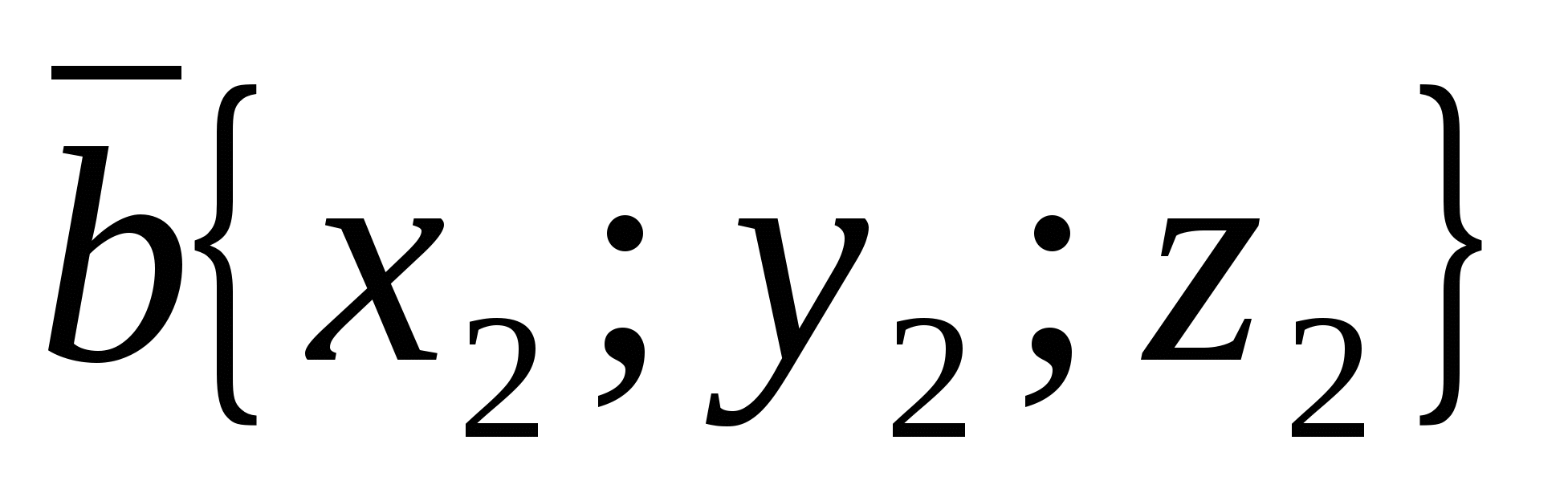 -given vectors, then vector
-given vectors, then vector 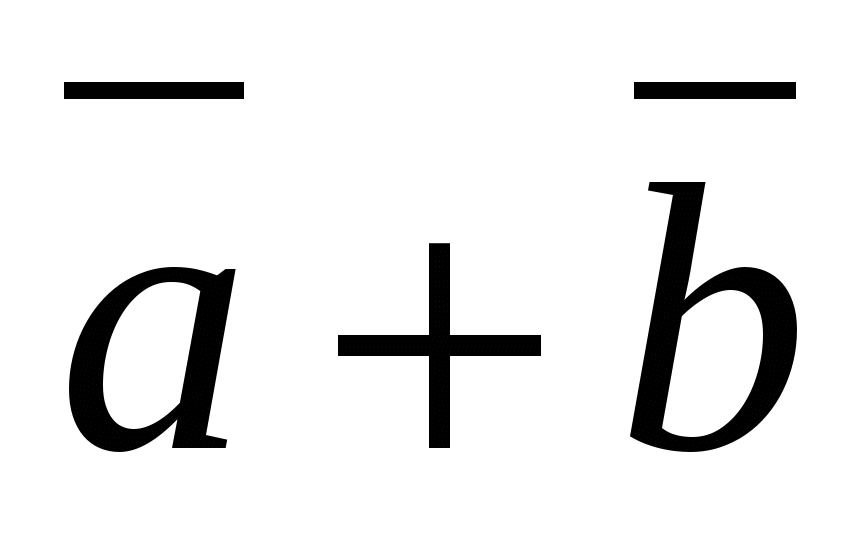 has coordinates.
has coordinates.
Rule 3.
Each coordinate of the difference of two vectors is equal to the difference of the corresponding coordinates of these vectors.
In other words, if 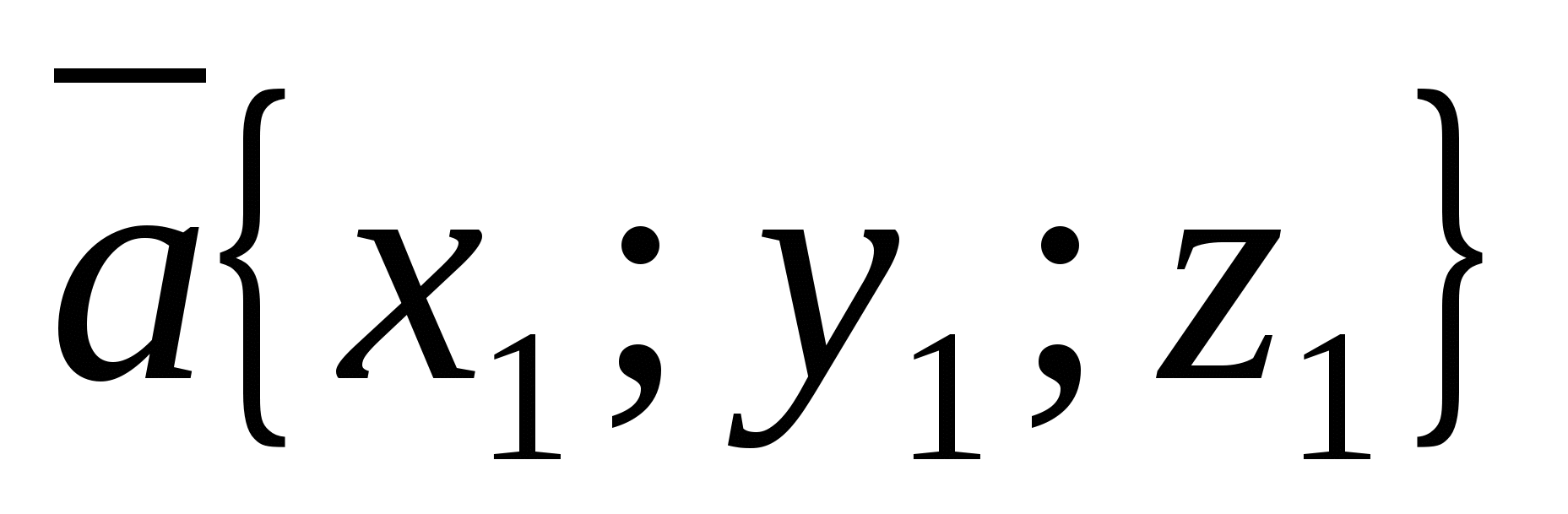 And
And 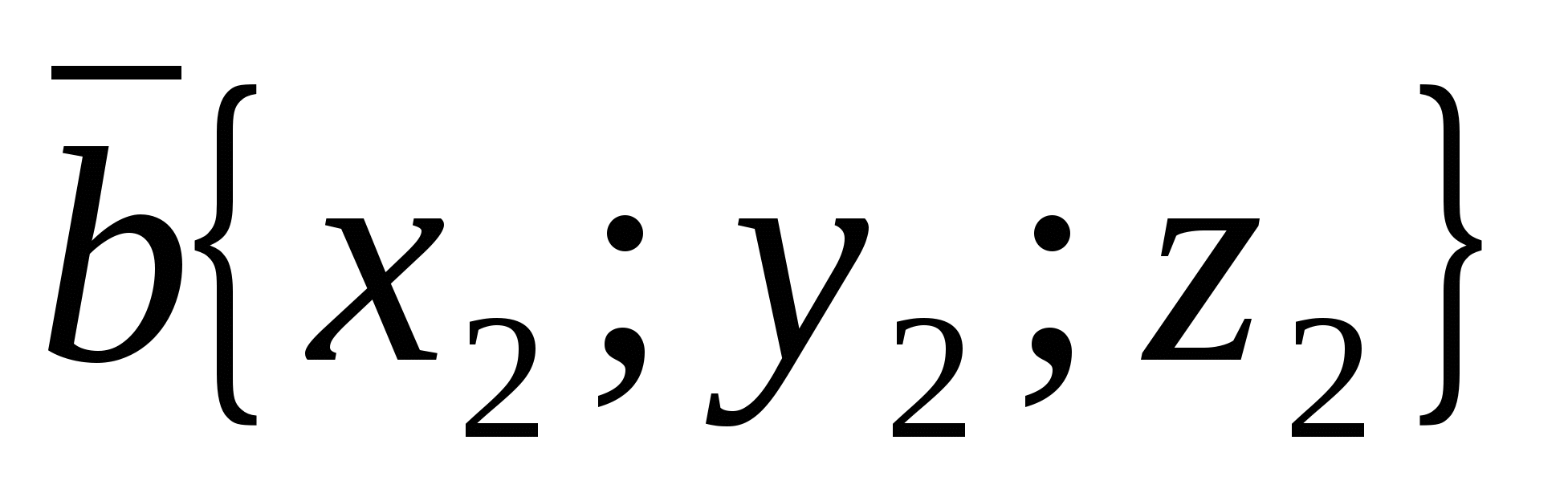 -given vectors, then vector
-given vectors, then vector 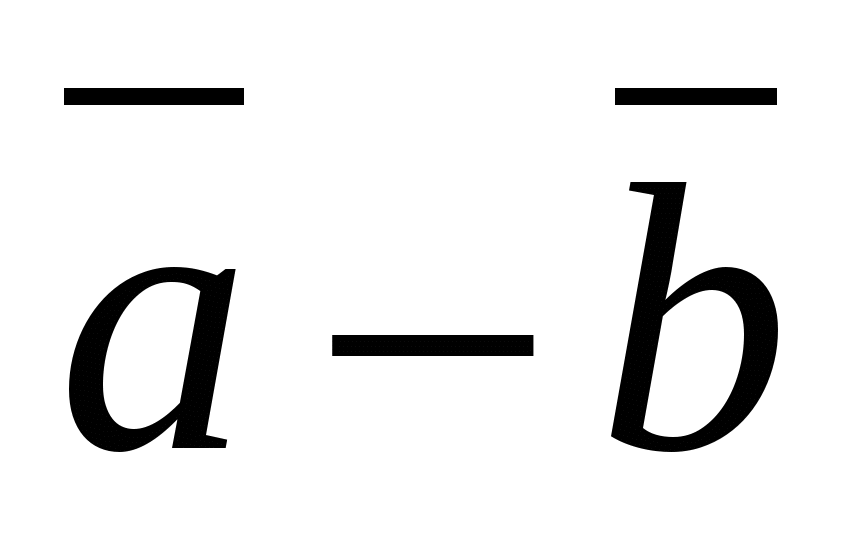 has coordinates
has coordinates
Rule 4.
Each coordinate of the product of a vector and a number is equal to the product of the corresponding coordinates of the vector and this number.
In other words, if 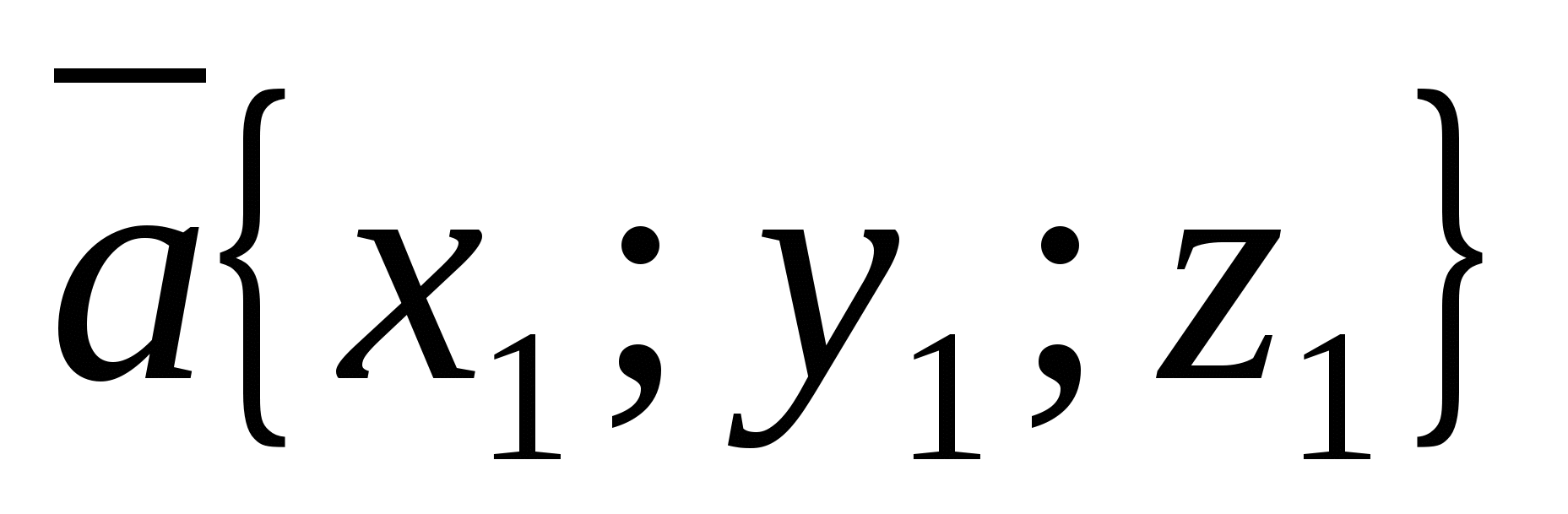 -given vector,
-given vector, ![]() -given number, then the vector
-given number, then the vector 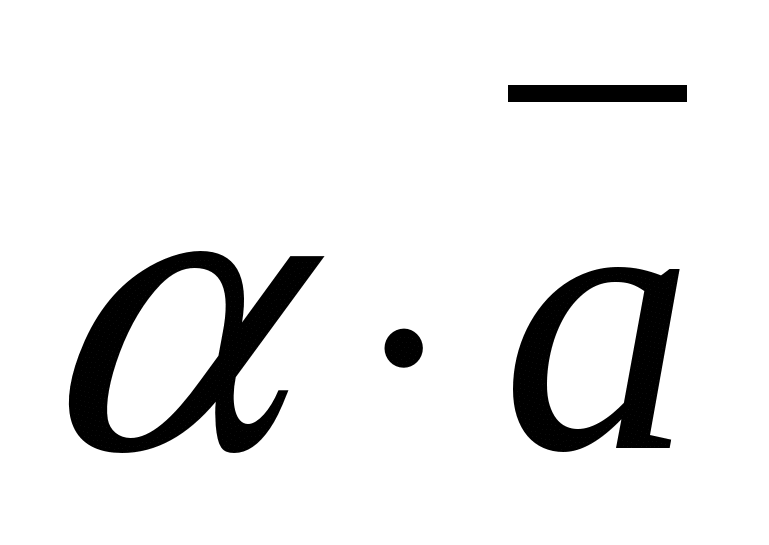 has coordinates.
has coordinates. 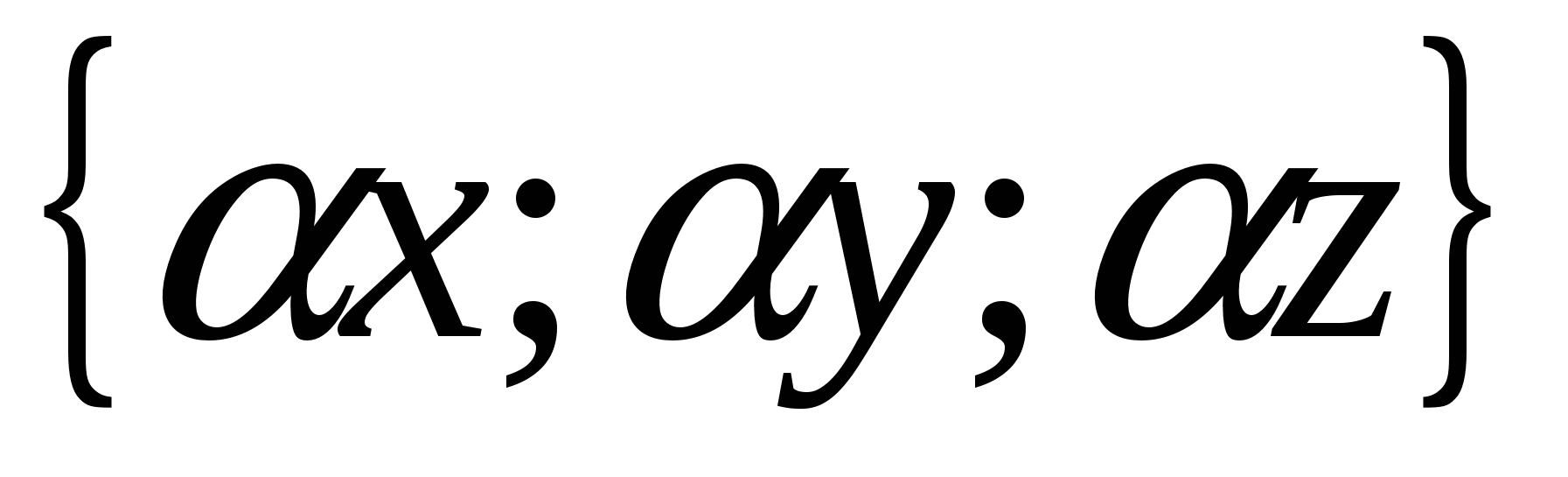 .
.
Example.
Find vector coordinates 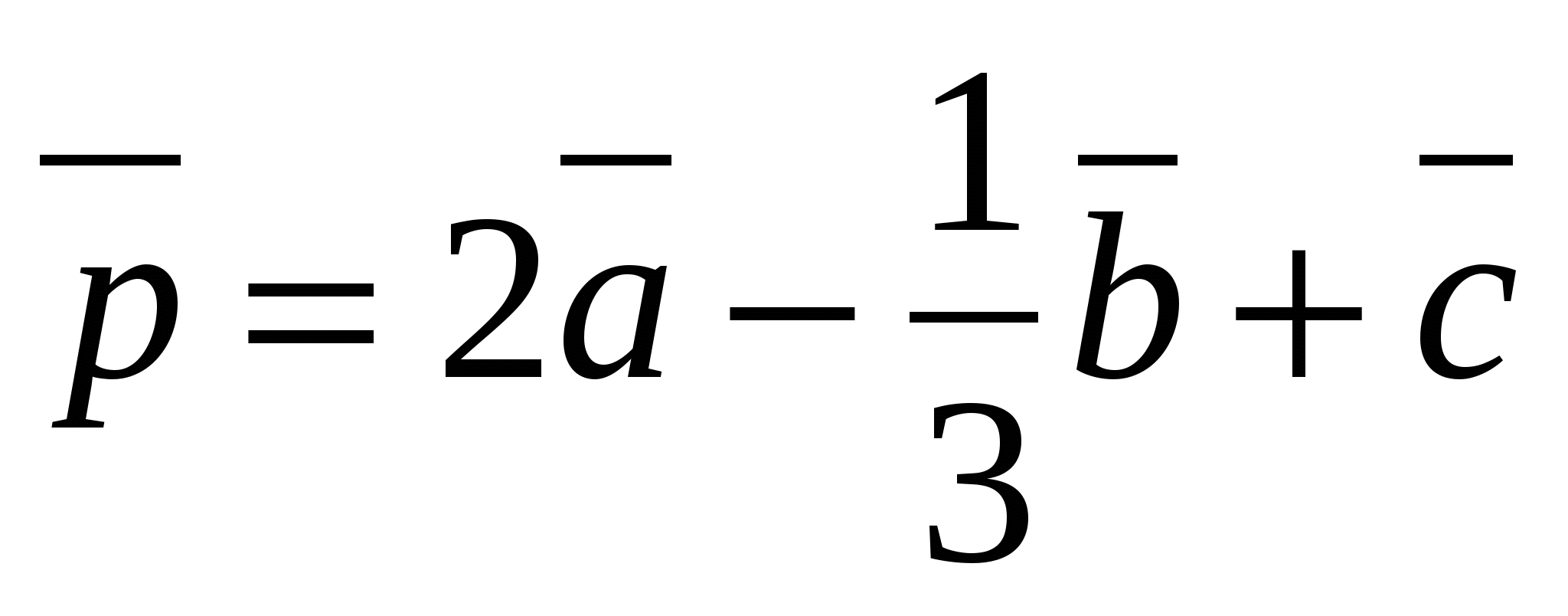 , If
, If 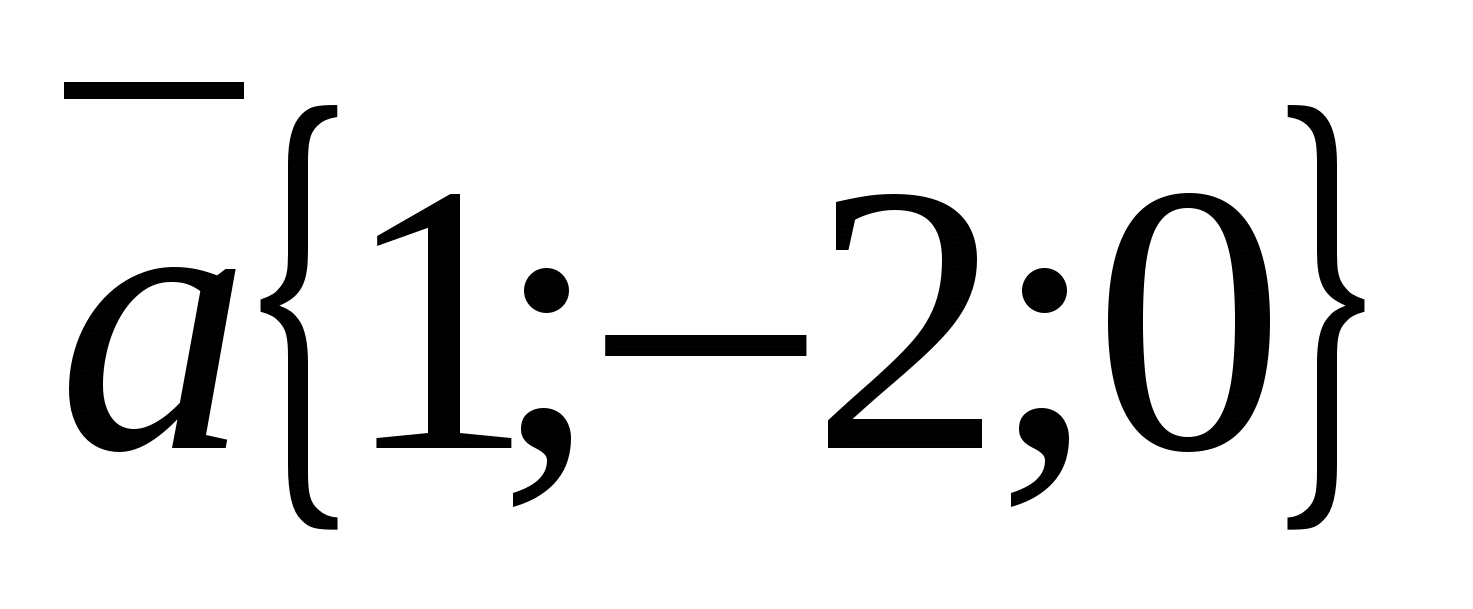 ,
, 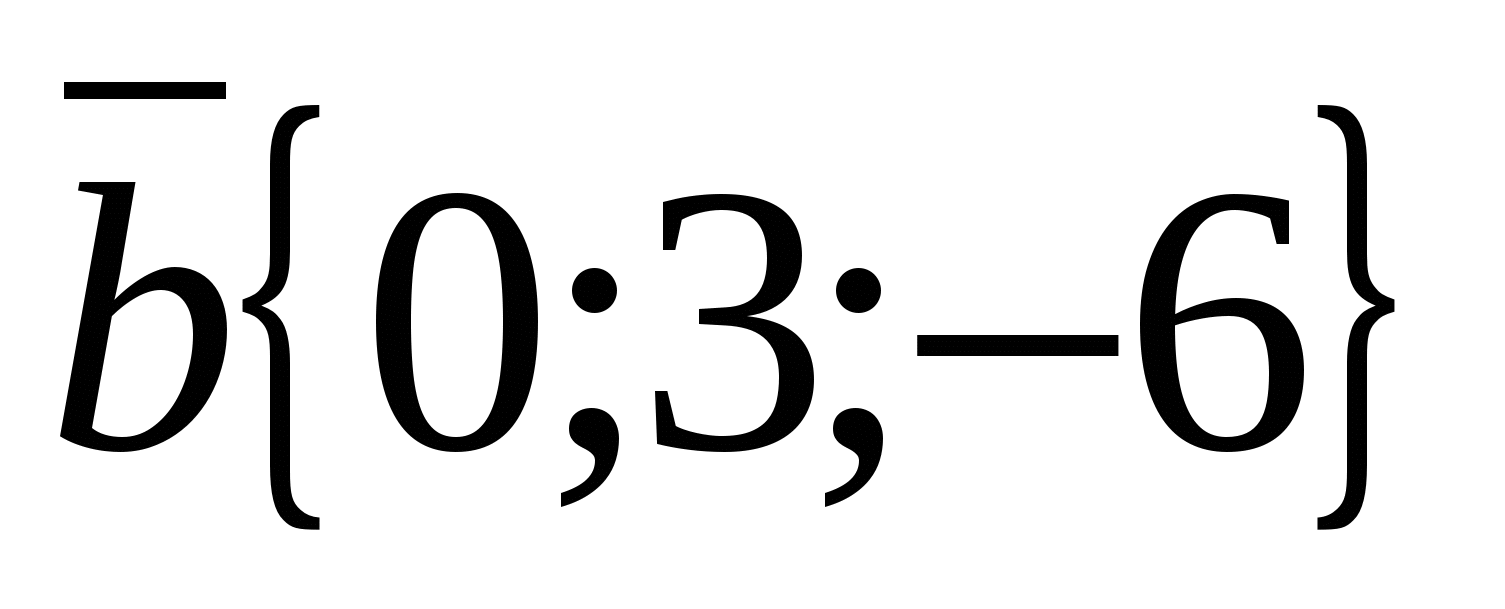 ,
, 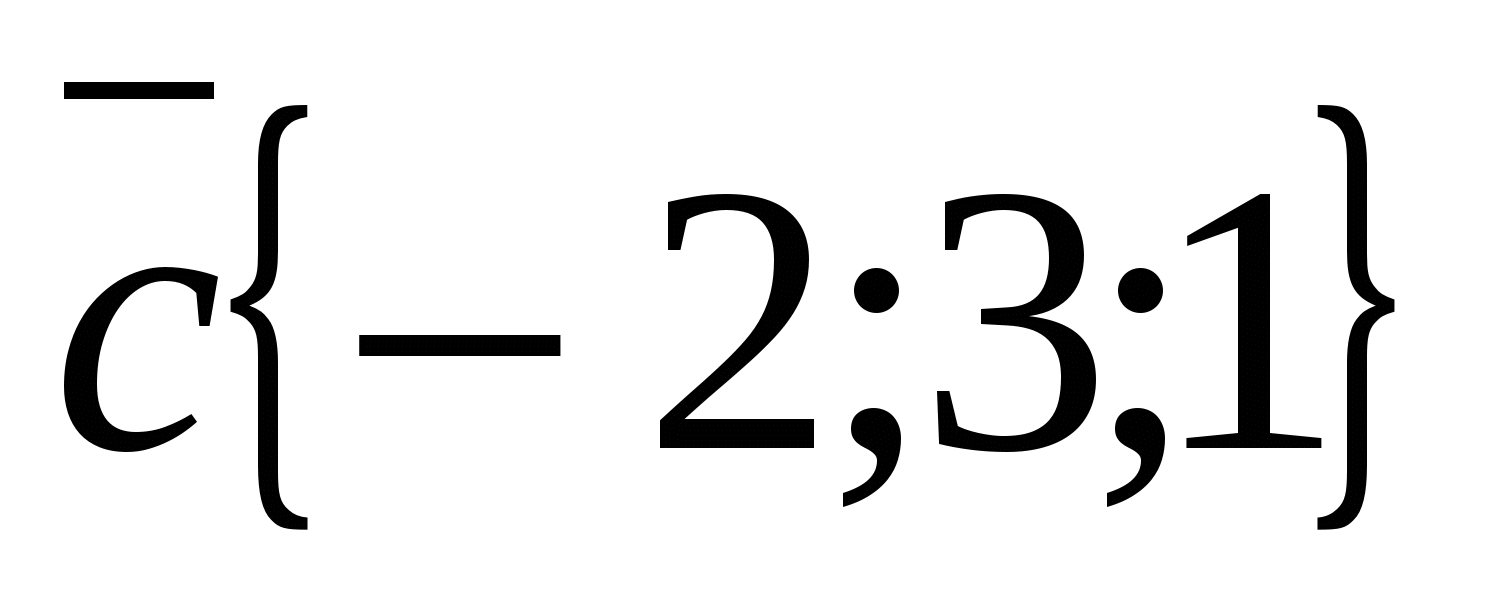 .
.
Solution.
Vector 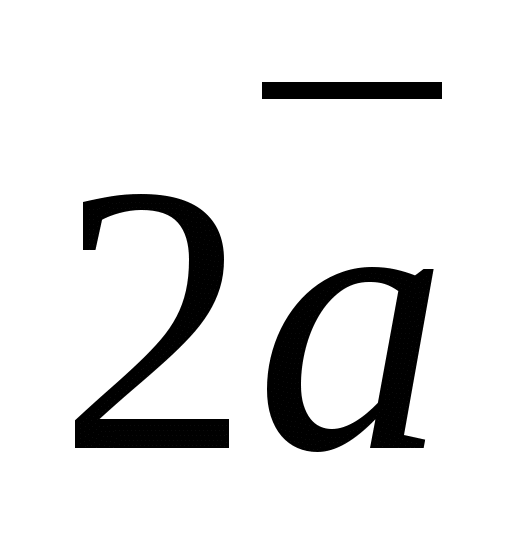 has coordinates
has coordinates 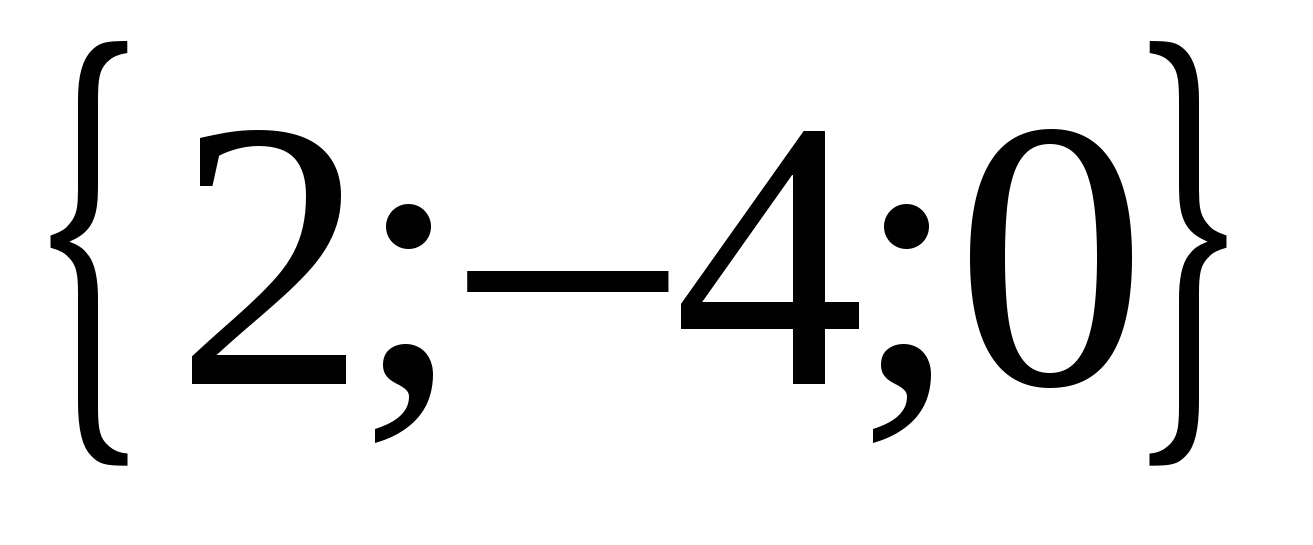 , and the vector
, and the vector  - coordinates
- coordinates 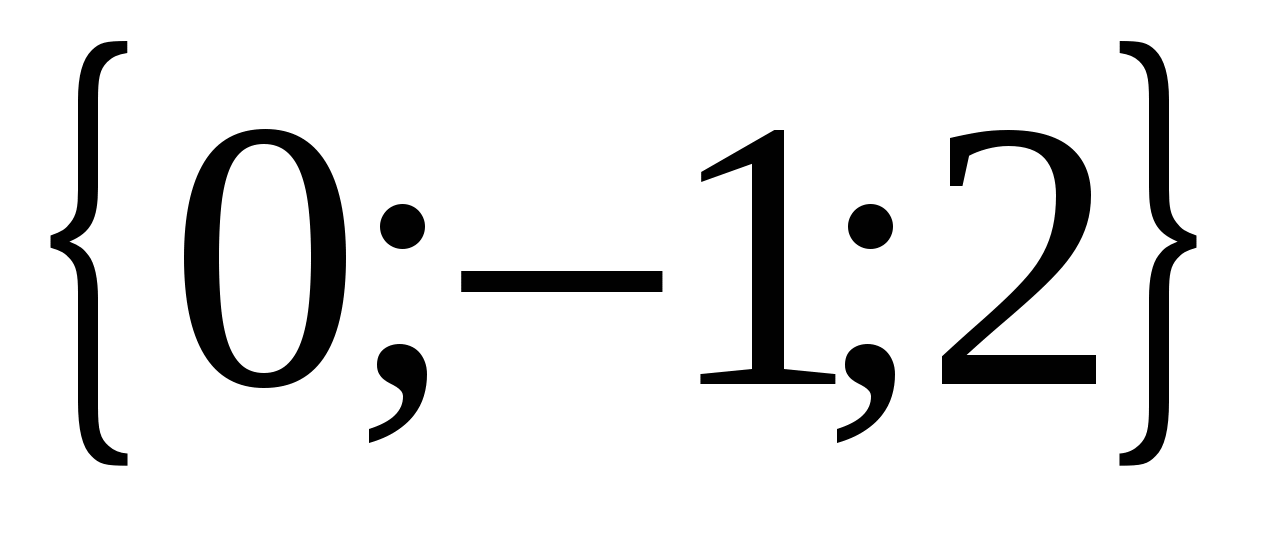 .
.
Because 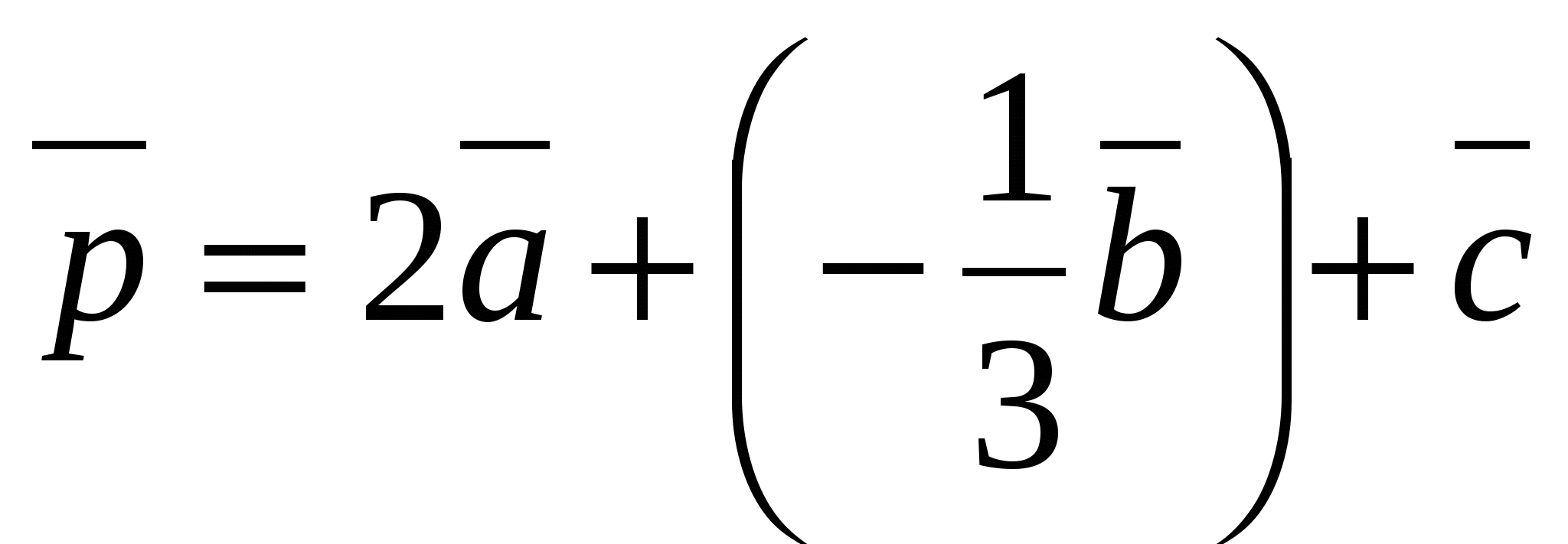 , then its coordinates
, then its coordinates  can be calculated as:
can be calculated as:  ,
, 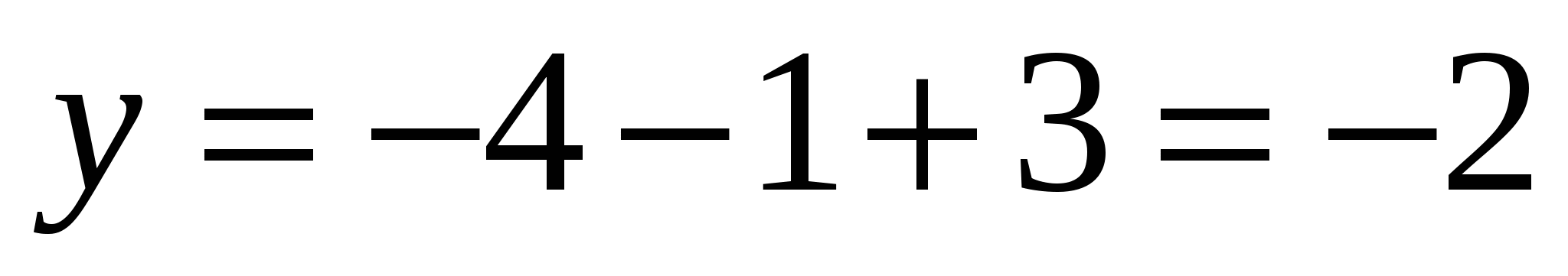 ,
, 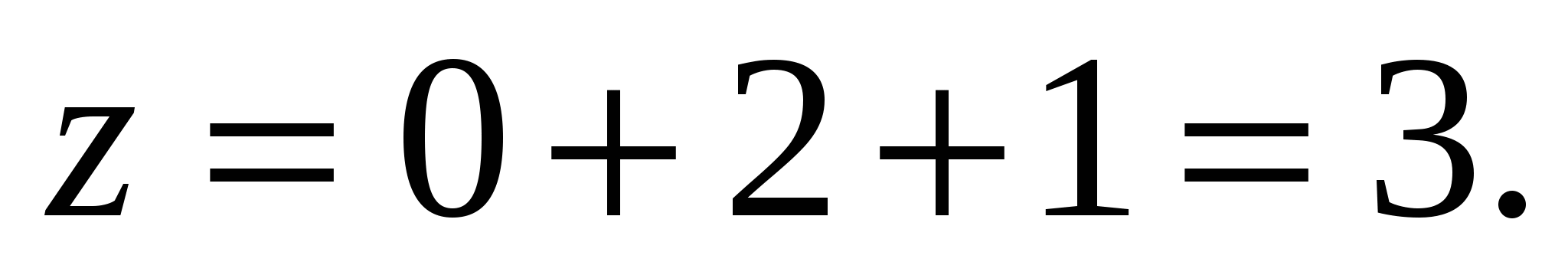 So it's a vector
So it's a vector 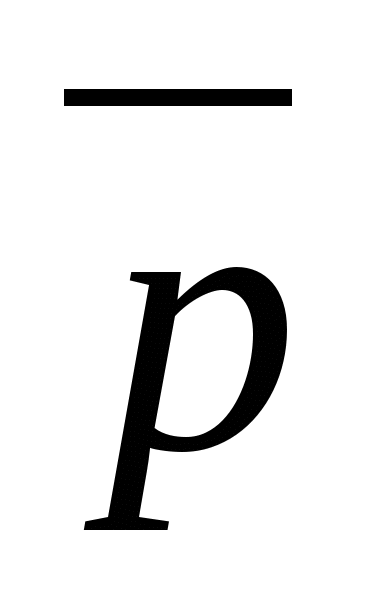 has coordinates
has coordinates 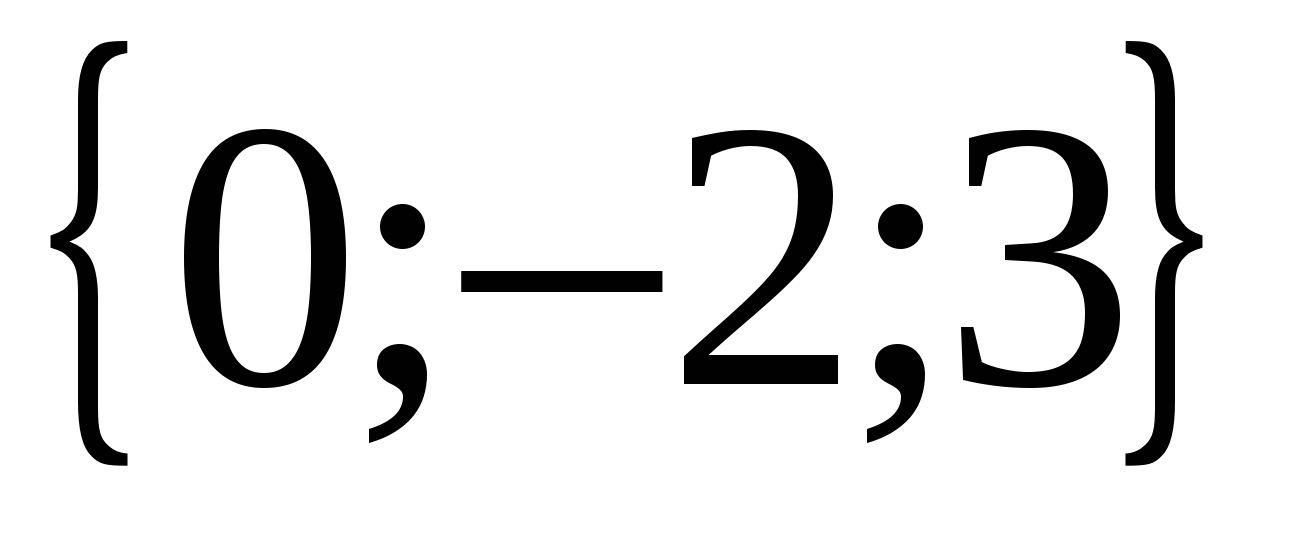 .
.
3. Relationship between vector coordinates and point coordinates.
Definition.
A vector whose end coincides with a given point, and whose beginning coincides with the origin of coordinates, is called radius vector this point.
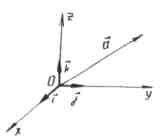
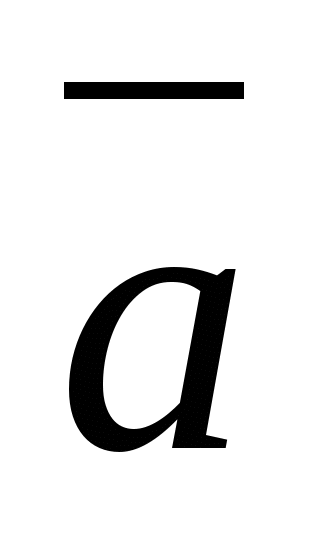
 - radius vector
- radius vector
 ,
,
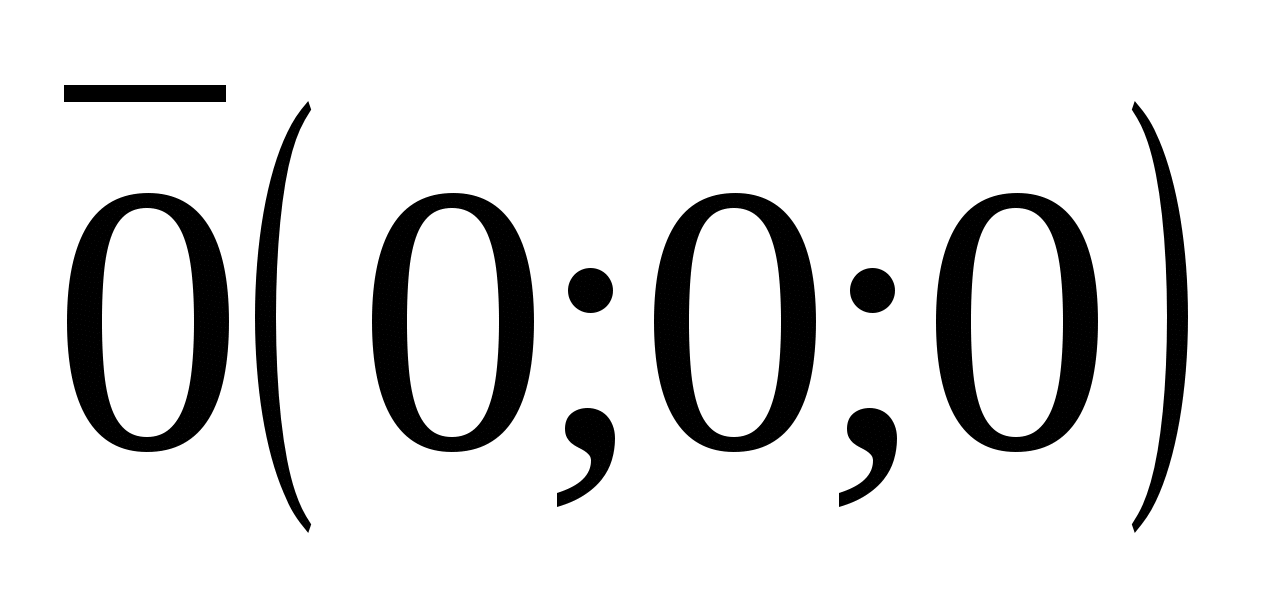 ;
;
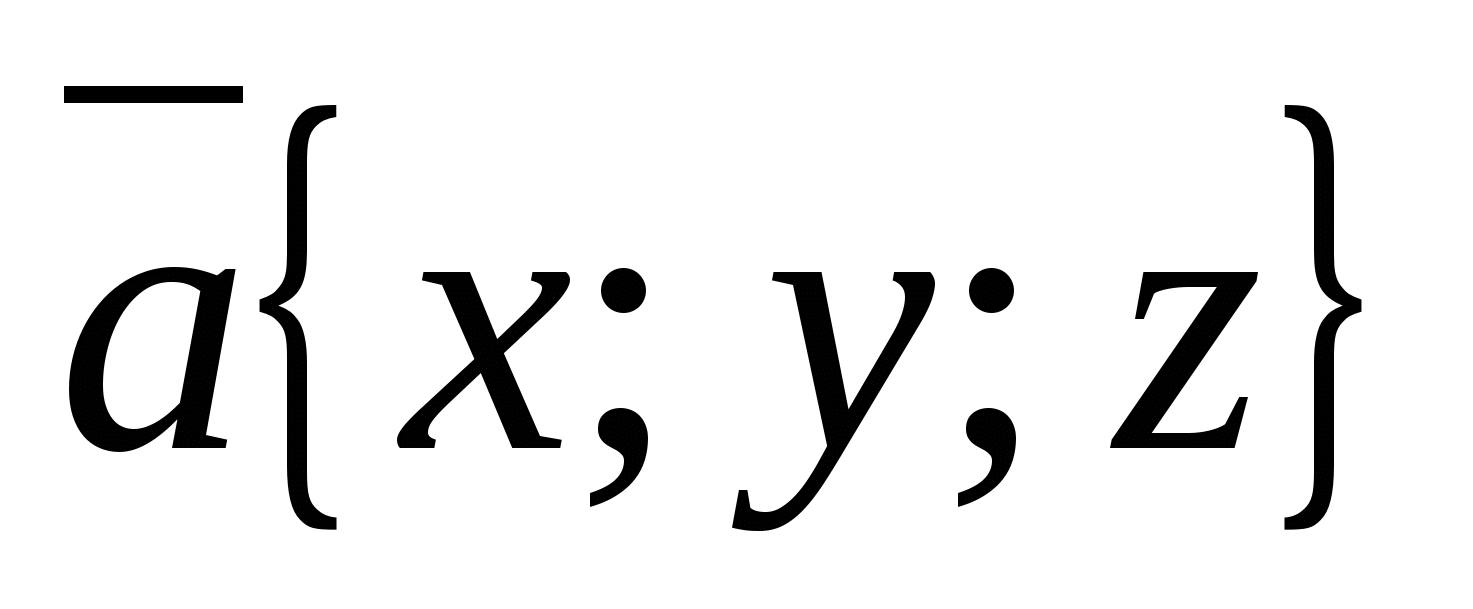
Rule 5.
The coordinates of any point are equal to the corresponding coordinates of its radius vector. ,.

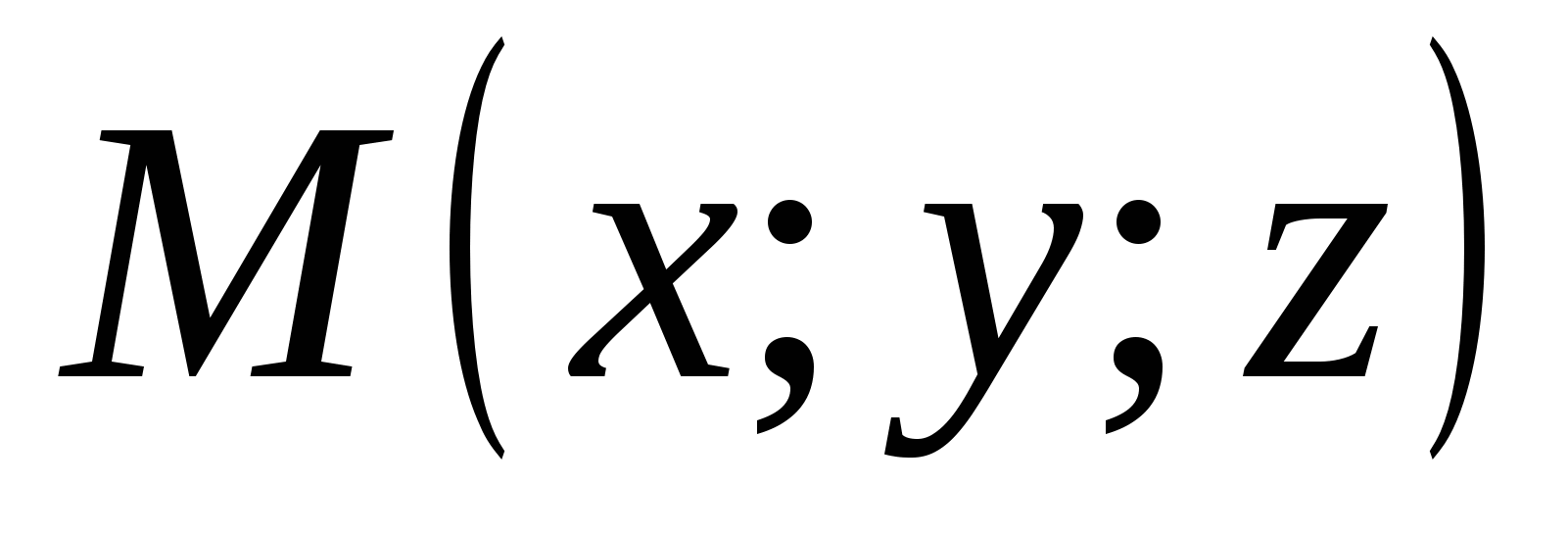
Rule 6.
Each vector coordinate is equal to the difference between the corresponding coordinates of its end and beginning.
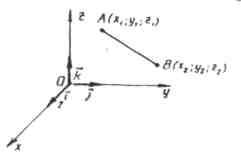 .
.
4. Condition for collinearity of two vectors in coordinates.
Let in the coordinate system  two vectors are given their coordinates
two vectors are given their coordinates  And
And 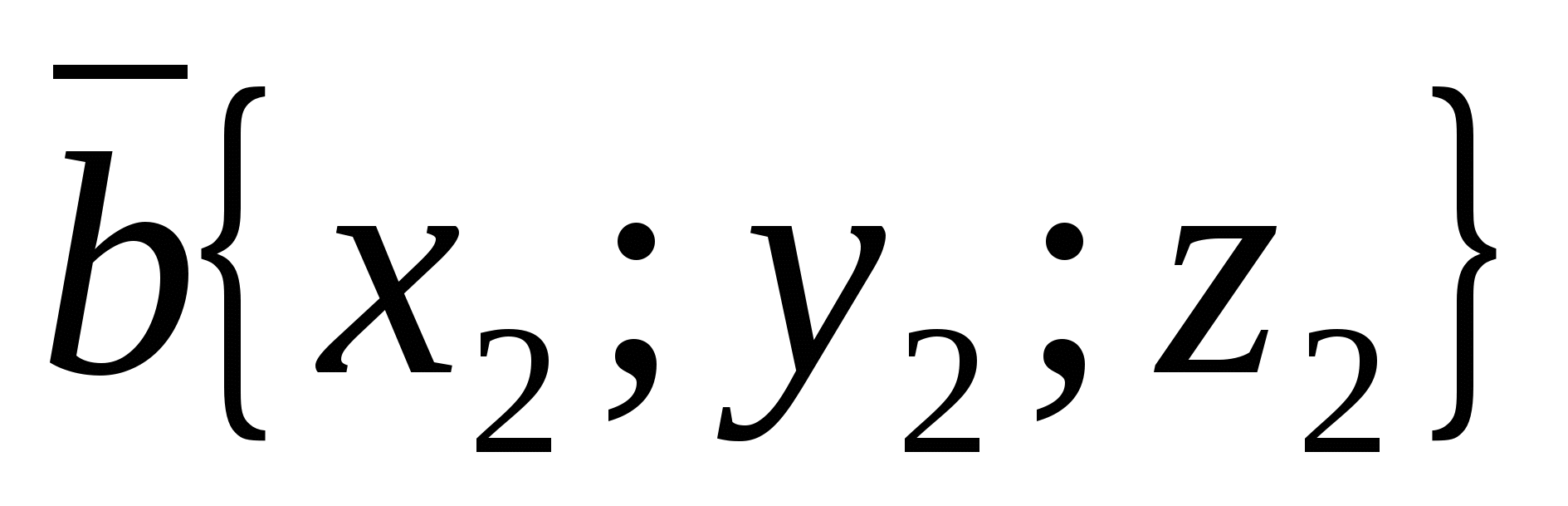 .
.
Rule 7.
Vectors
 And
And 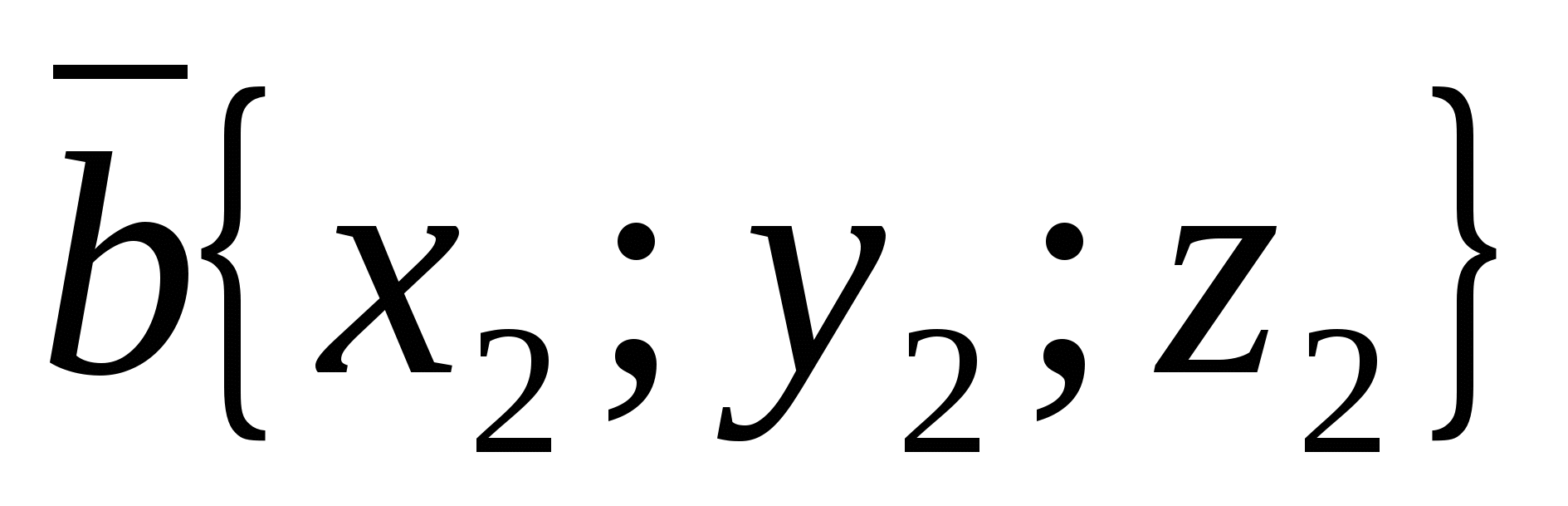 are collinear if and only if their corresponding coordinates are proportional,
are collinear if and only if their corresponding coordinates are proportional, 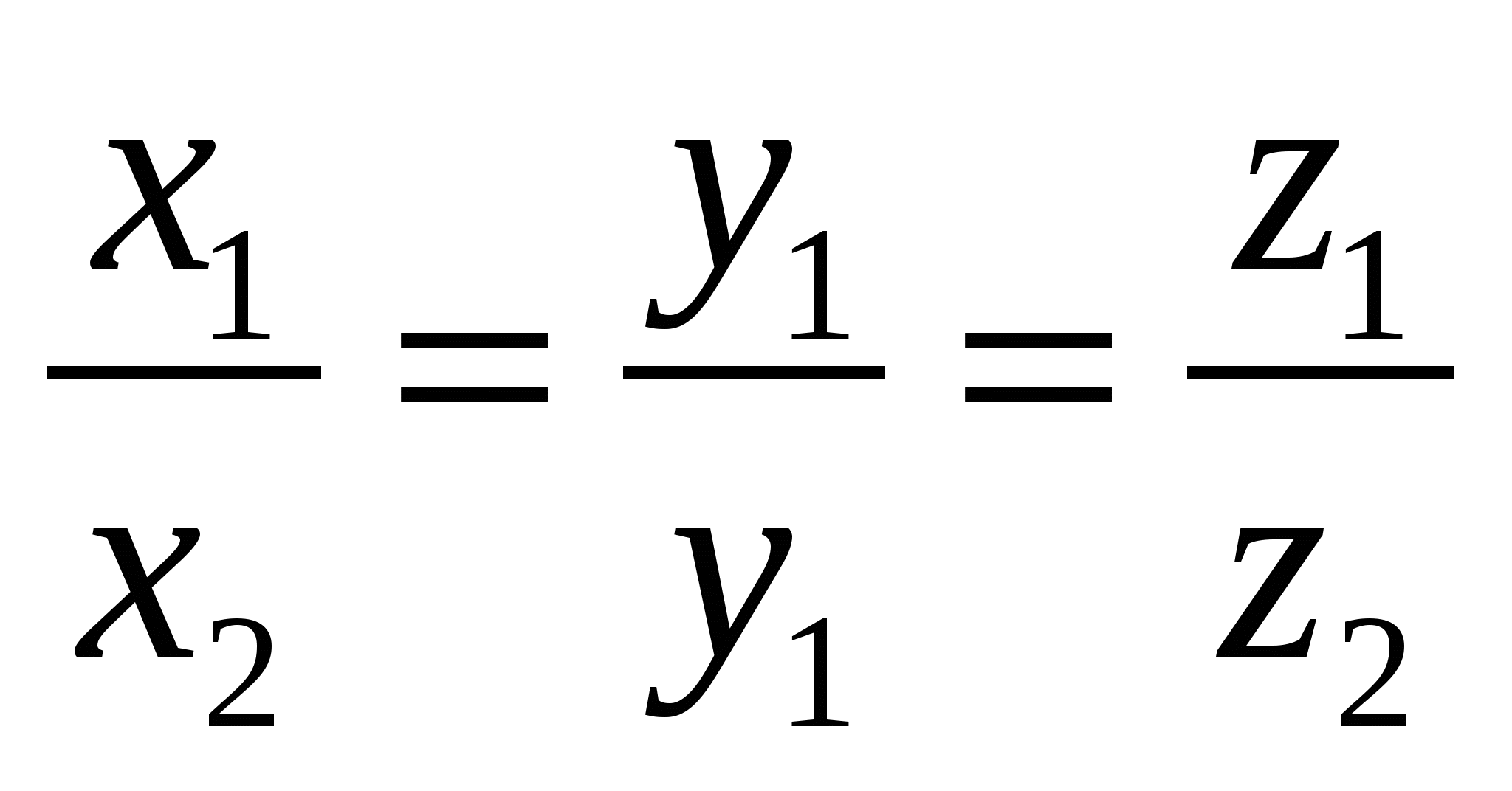 .
.
Example.
a) Consider the vectors 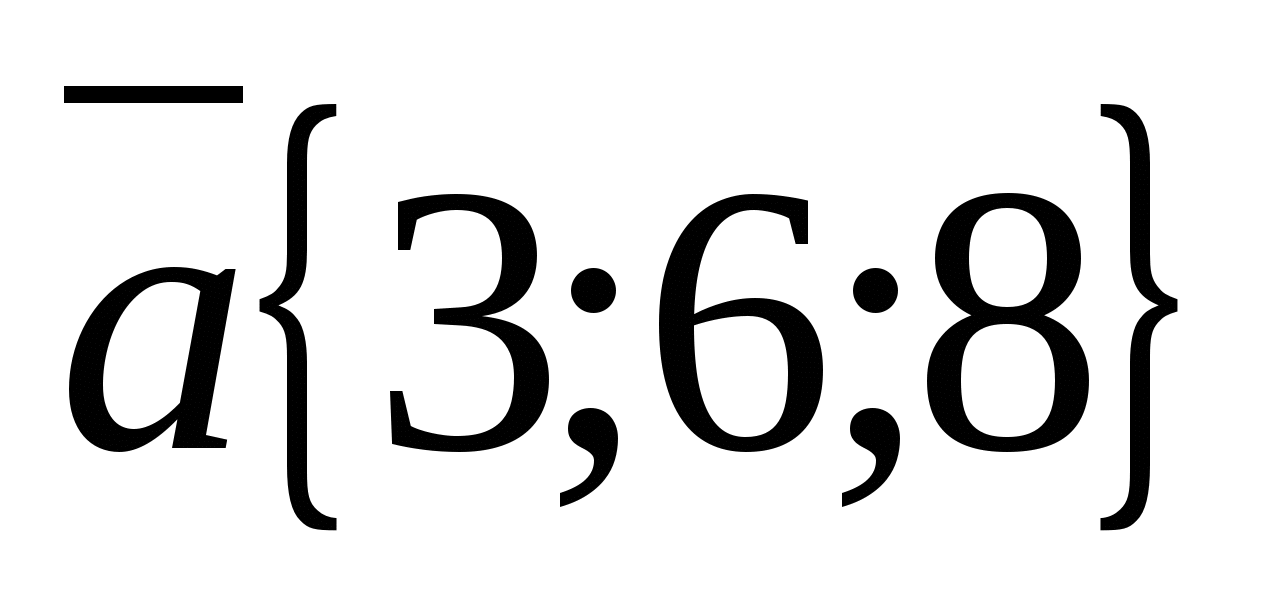 And
And 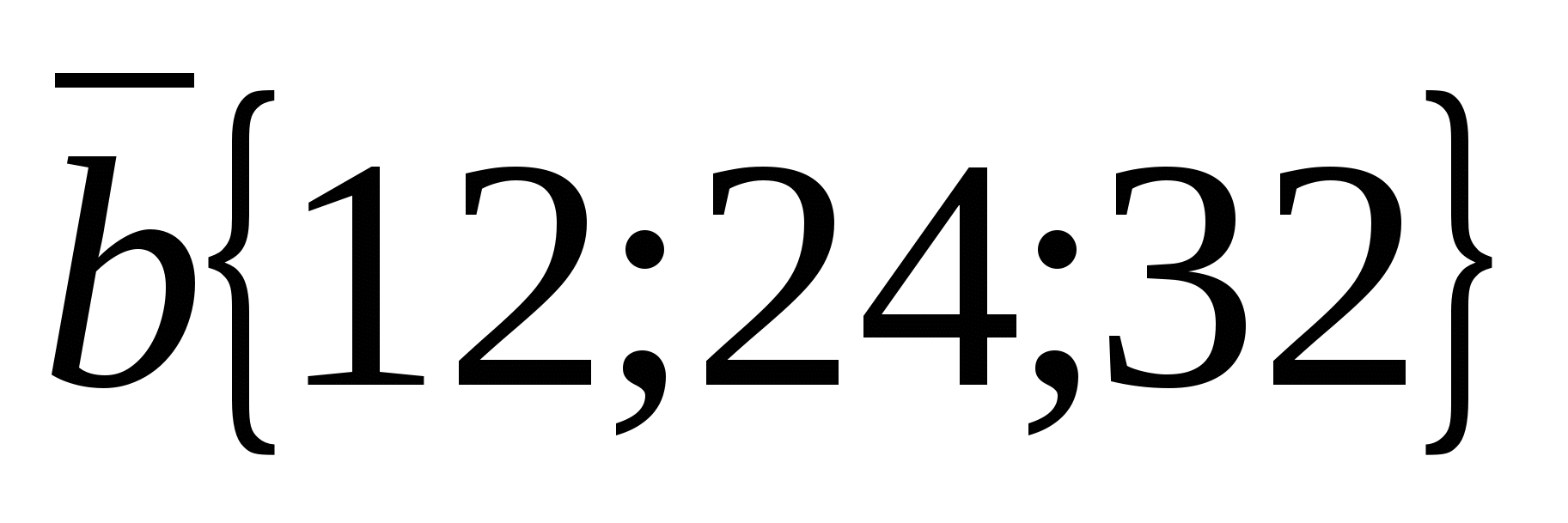 .
.
Vector coordinates 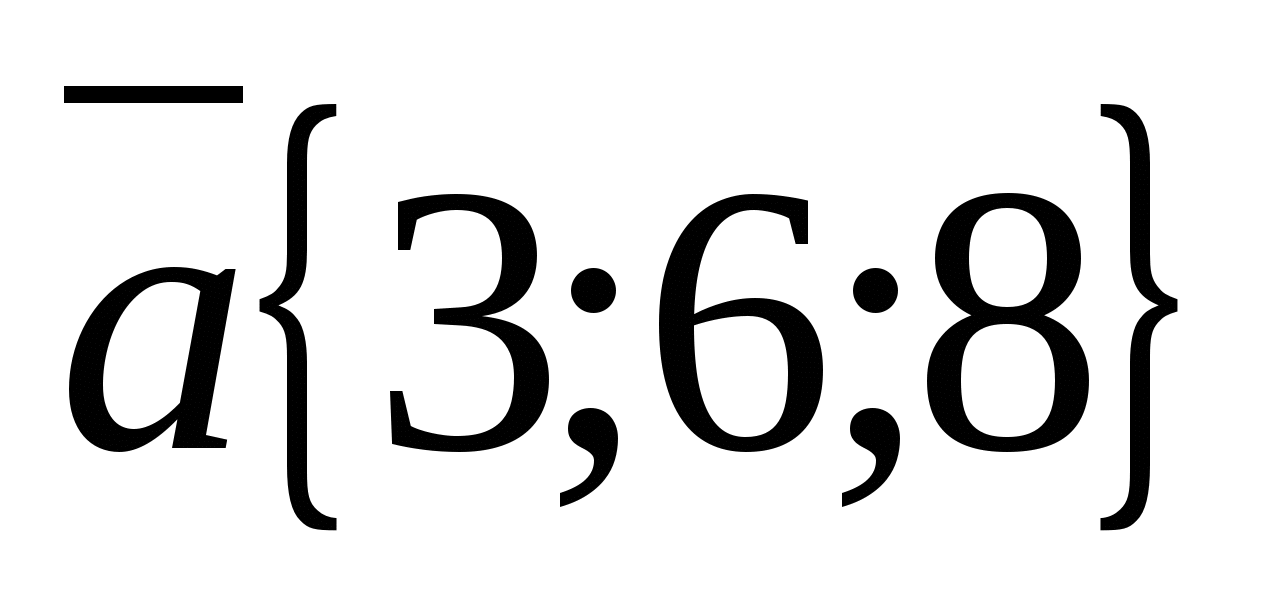 are proportional to the corresponding vector coordinates
are proportional to the corresponding vector coordinates 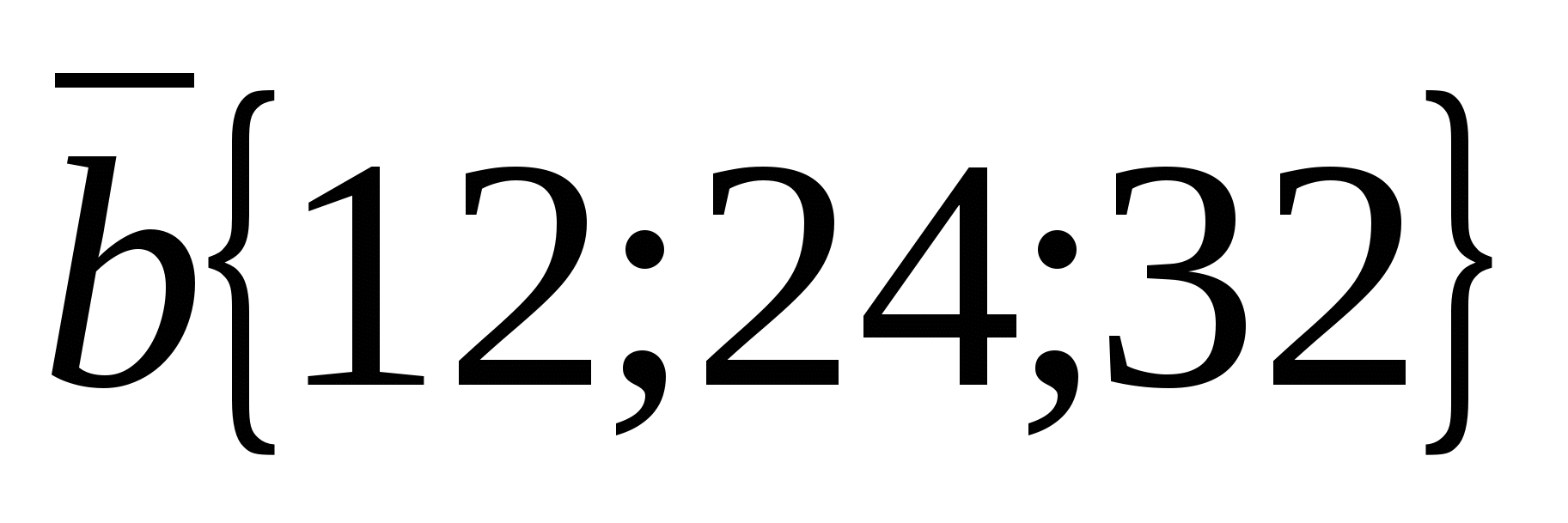 :
: 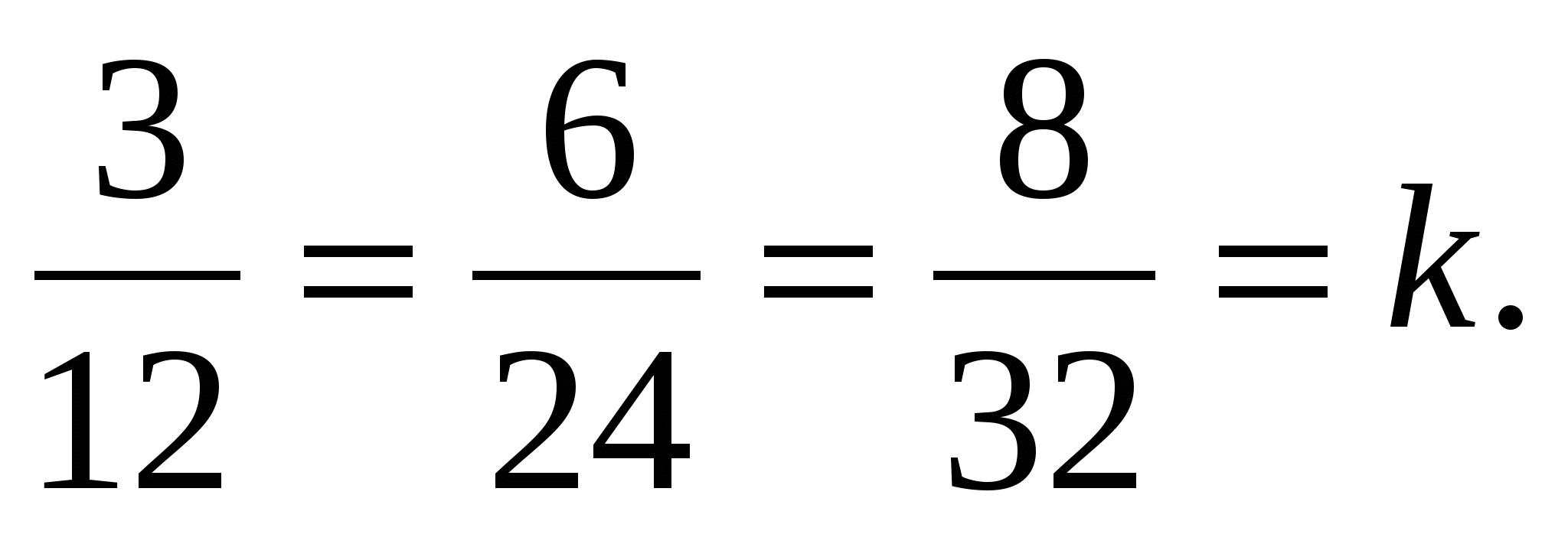 That's why
That's why 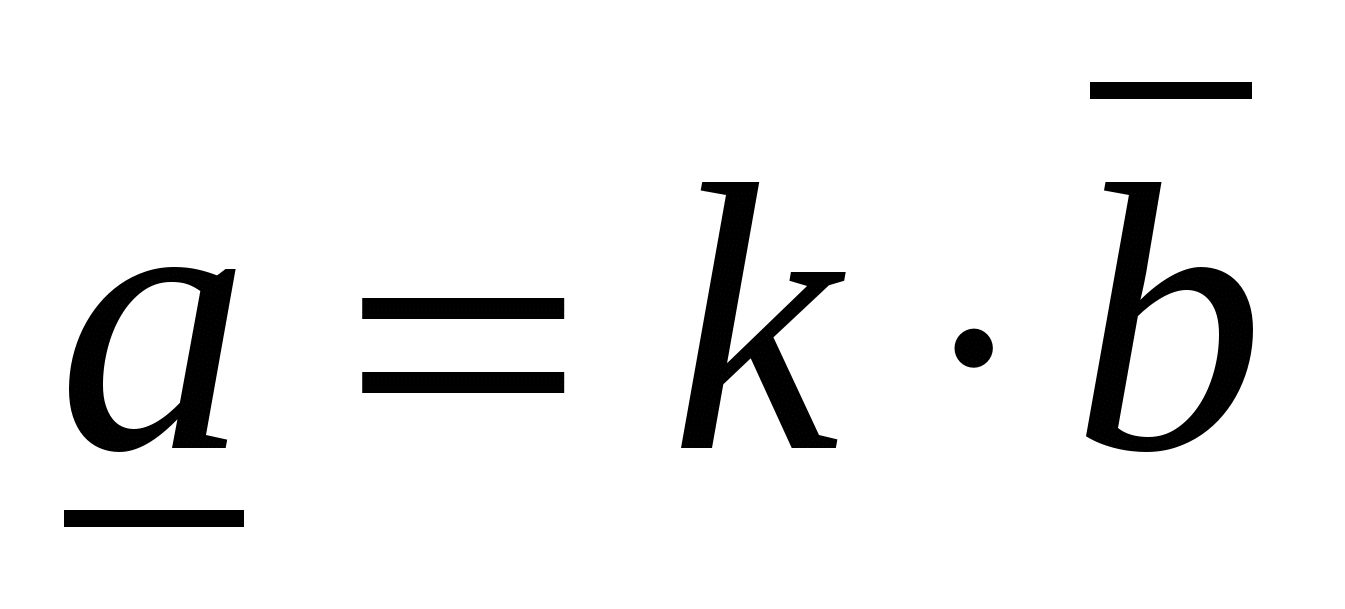 , and therefore the vectors are collinear.
, and therefore the vectors are collinear.
b) Consider the vectors 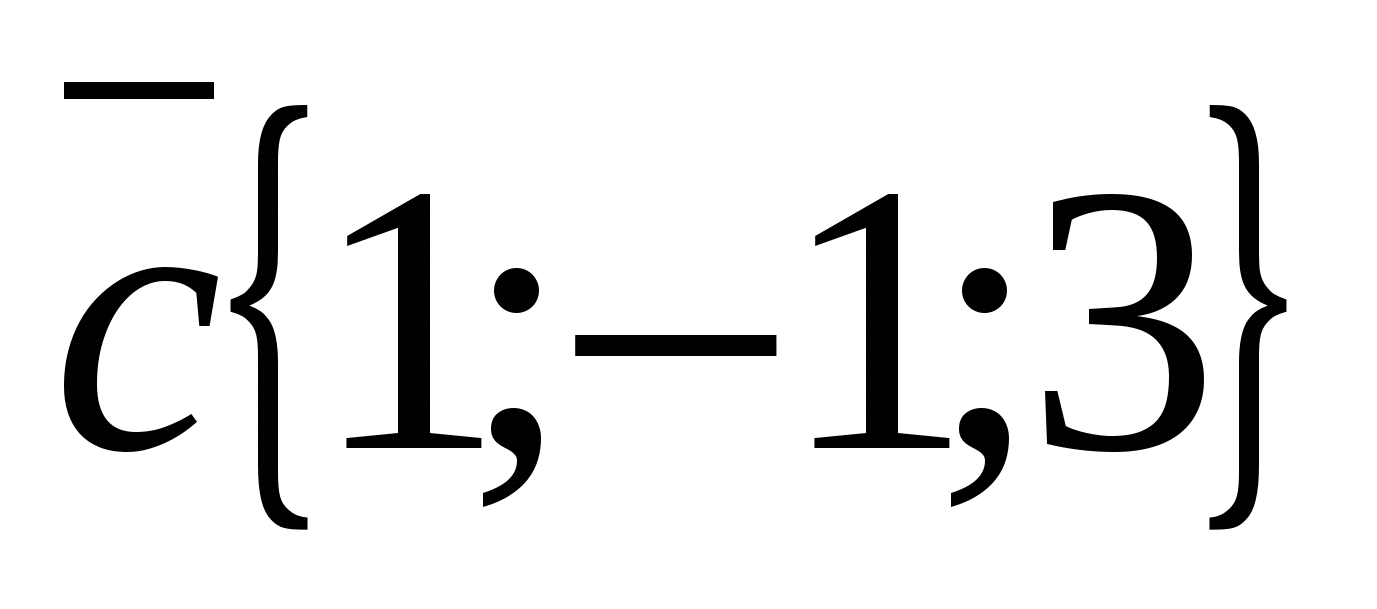 And
And 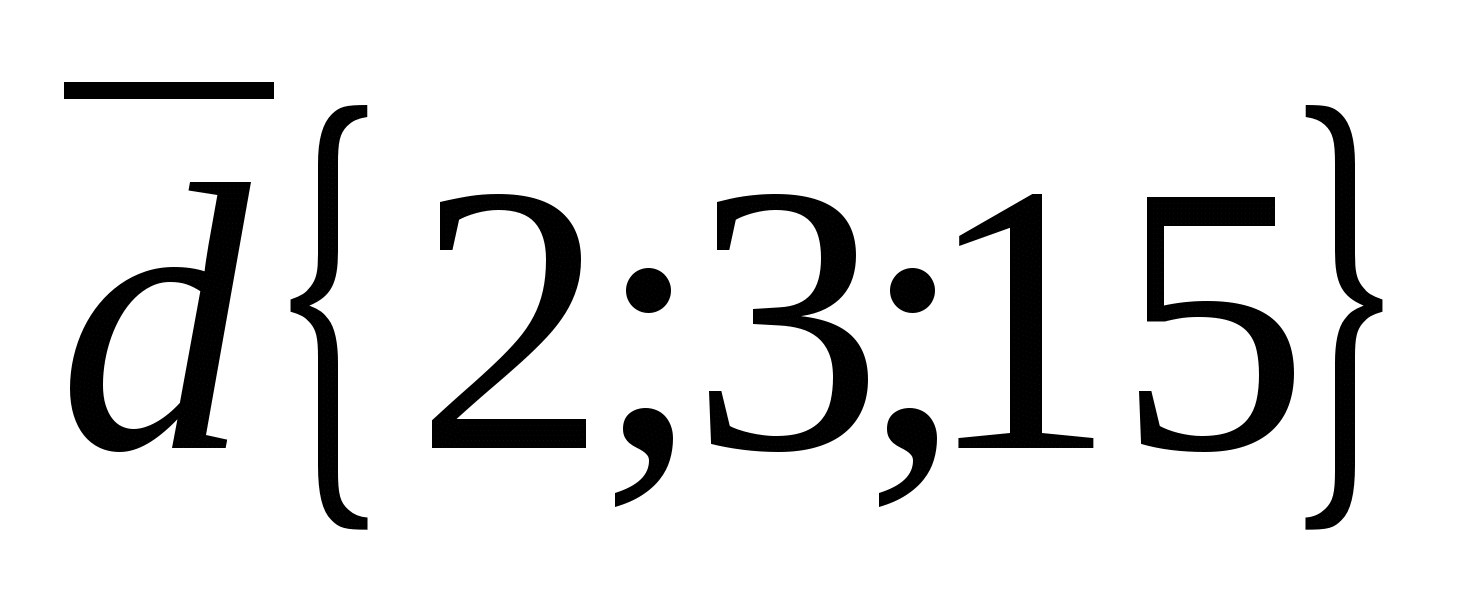 .
.
Vector coordinates 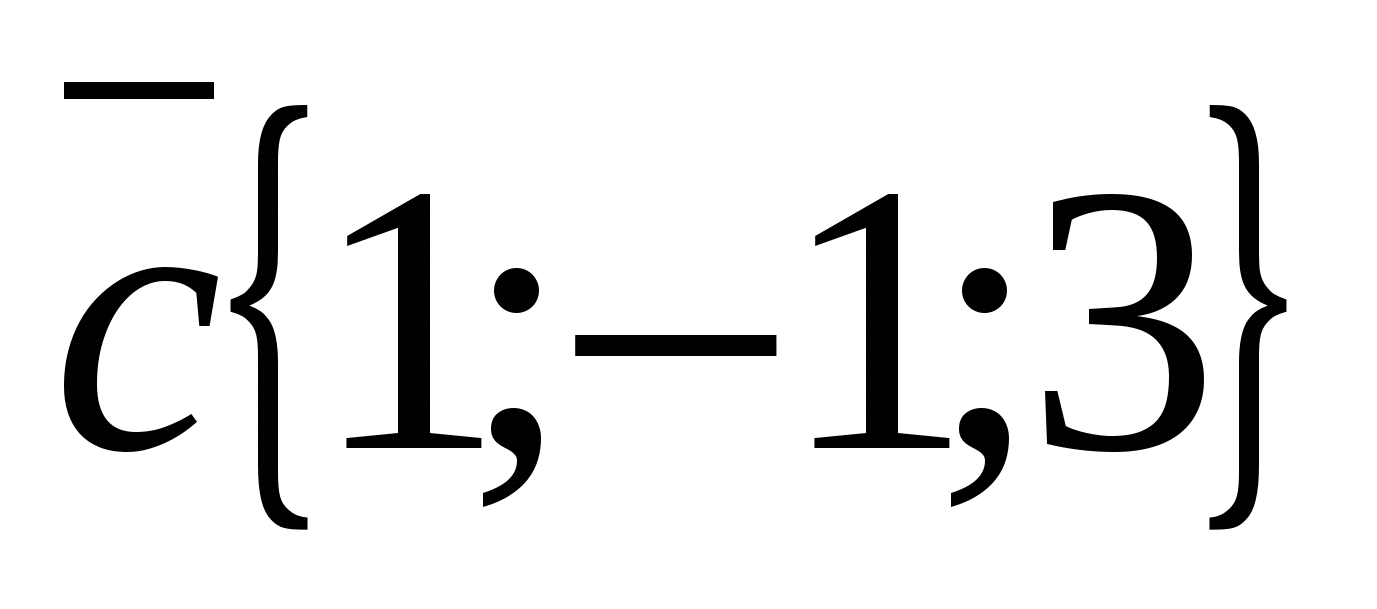 are not proportional to the corresponding vector coordinates
are not proportional to the corresponding vector coordinates 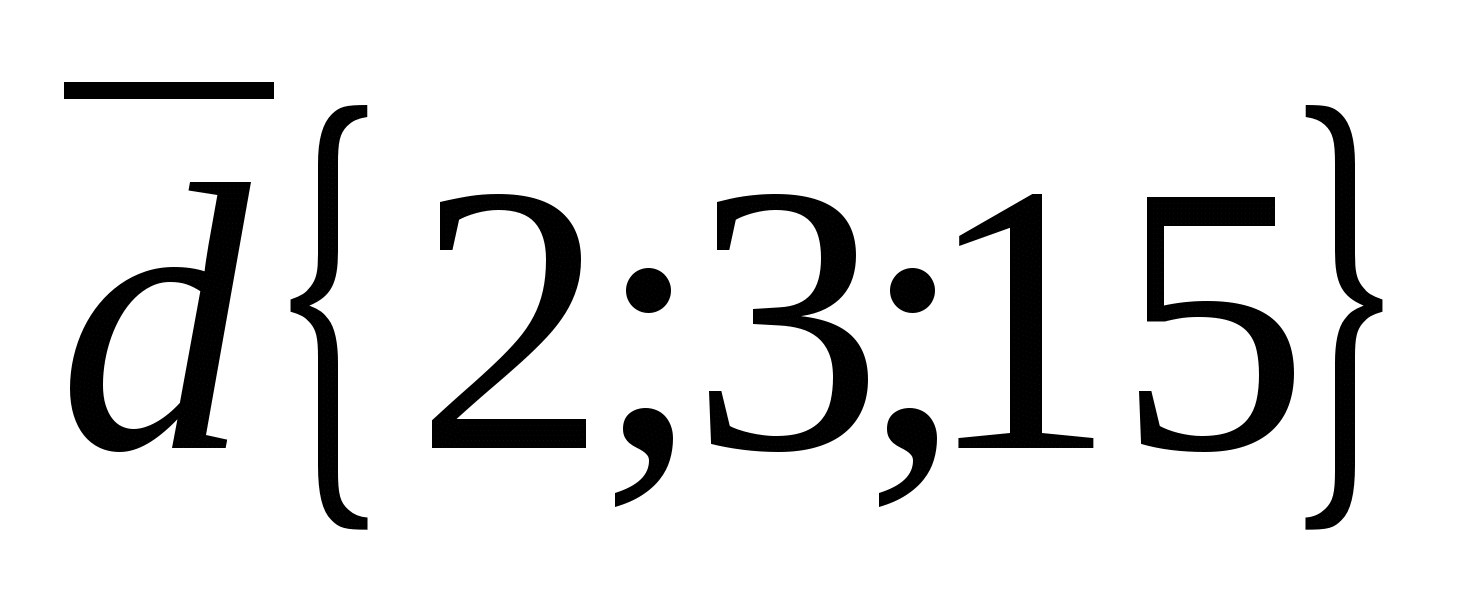 , For example
, For example 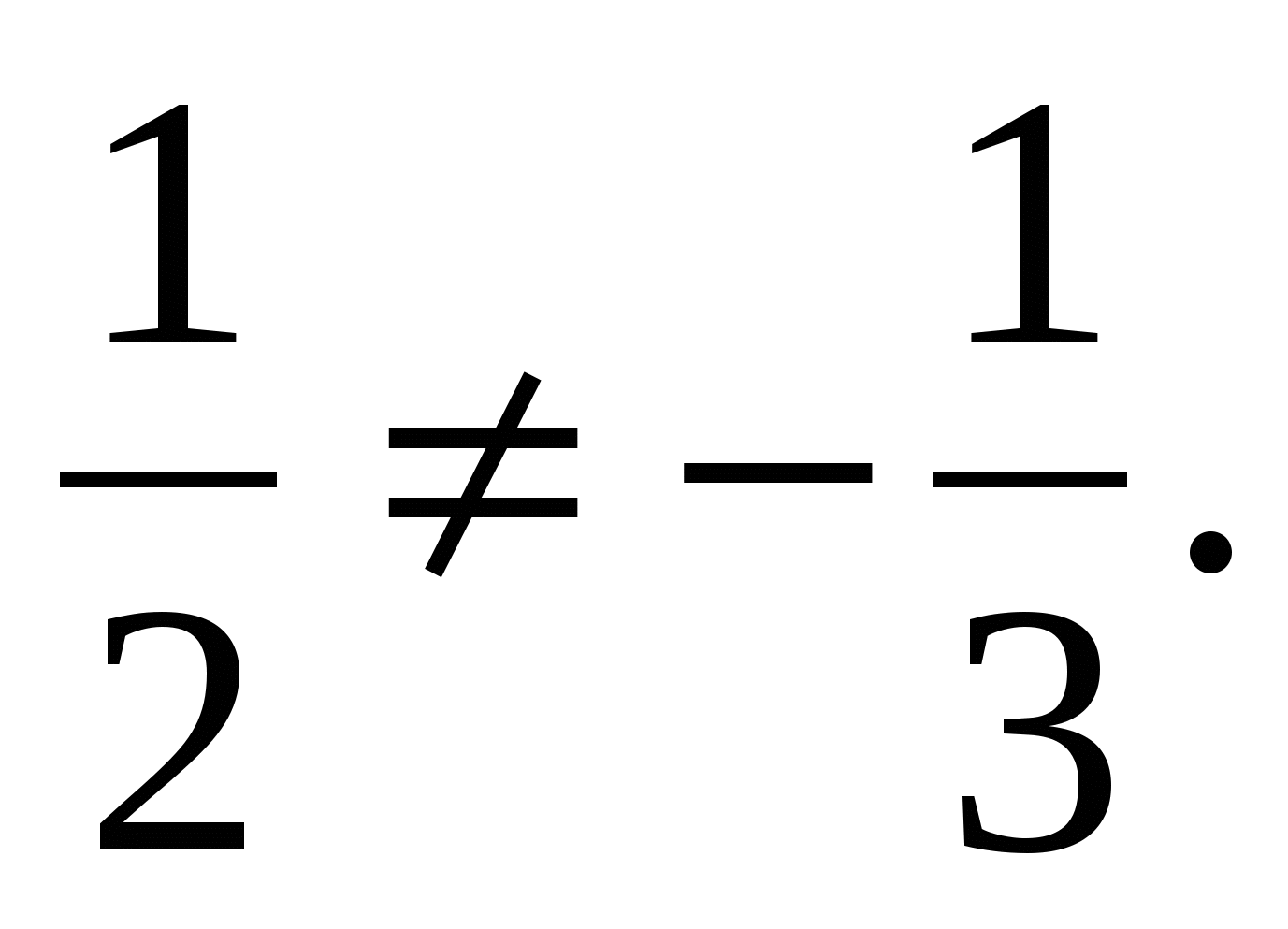 This means the vectors are not collinear.
This means the vectors are not collinear.
5. The simplest problems in coordinates.
Task 1.
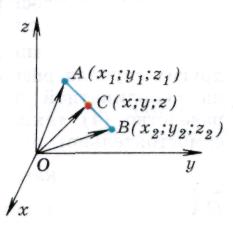 Each coordinate of the middle of a segment is equal to half the sum of the corresponding coordinates of its ends.
Each coordinate of the middle of a segment is equal to half the sum of the corresponding coordinates of its ends.
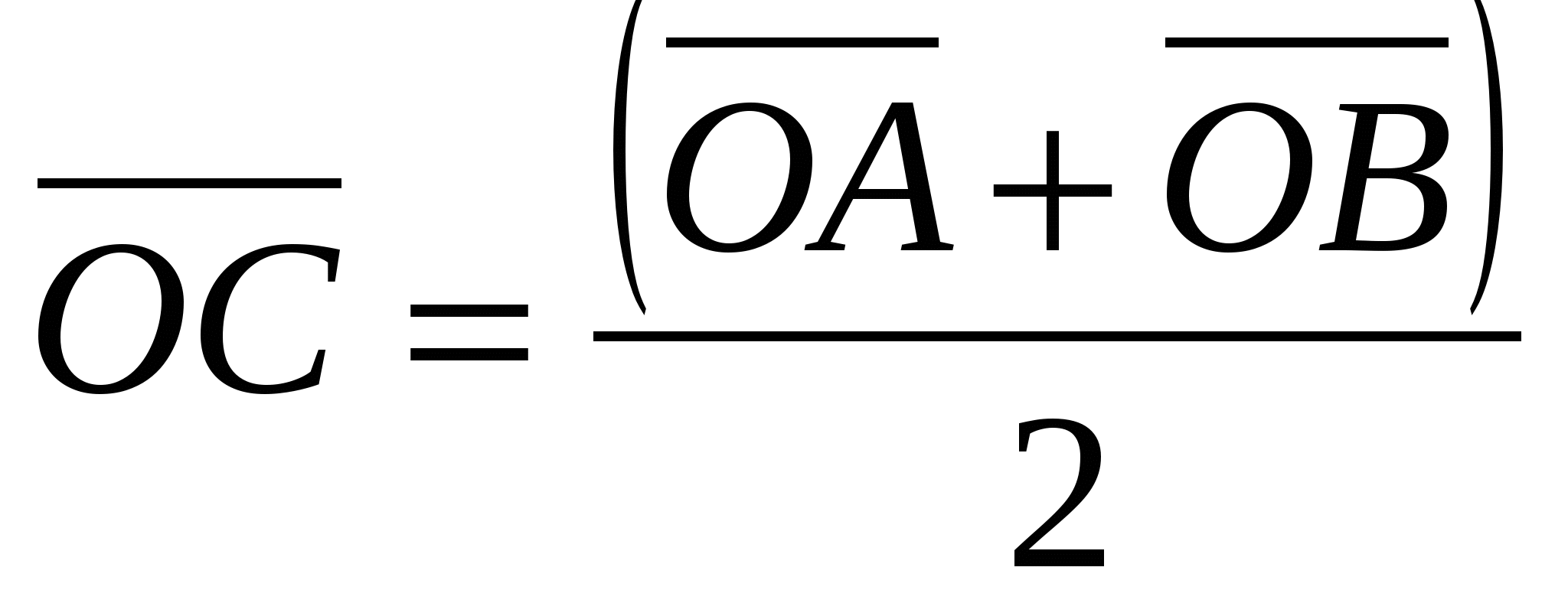 , Where
, Where 
 ,
, 
 And
And 
 .
.
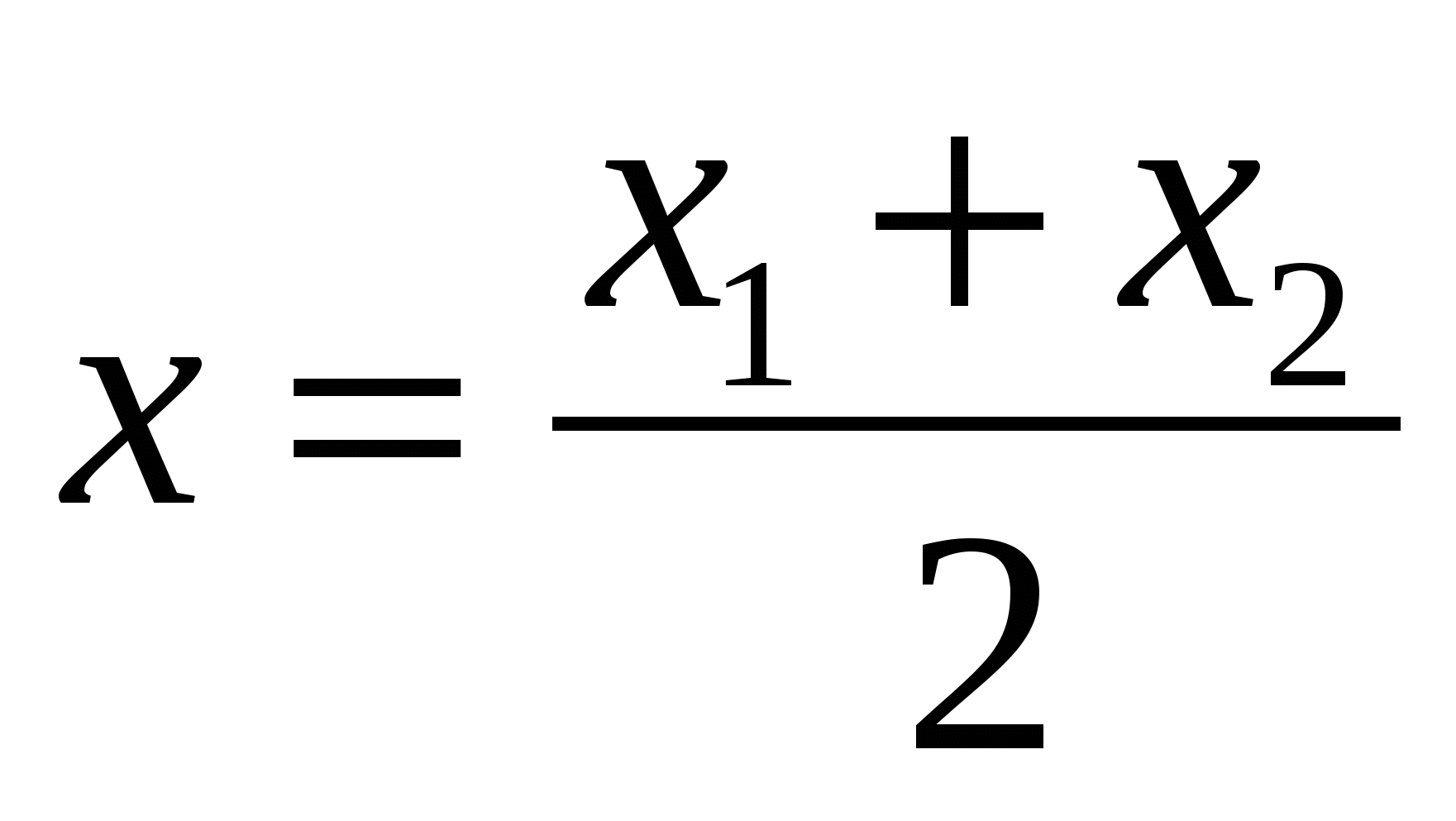 ,
,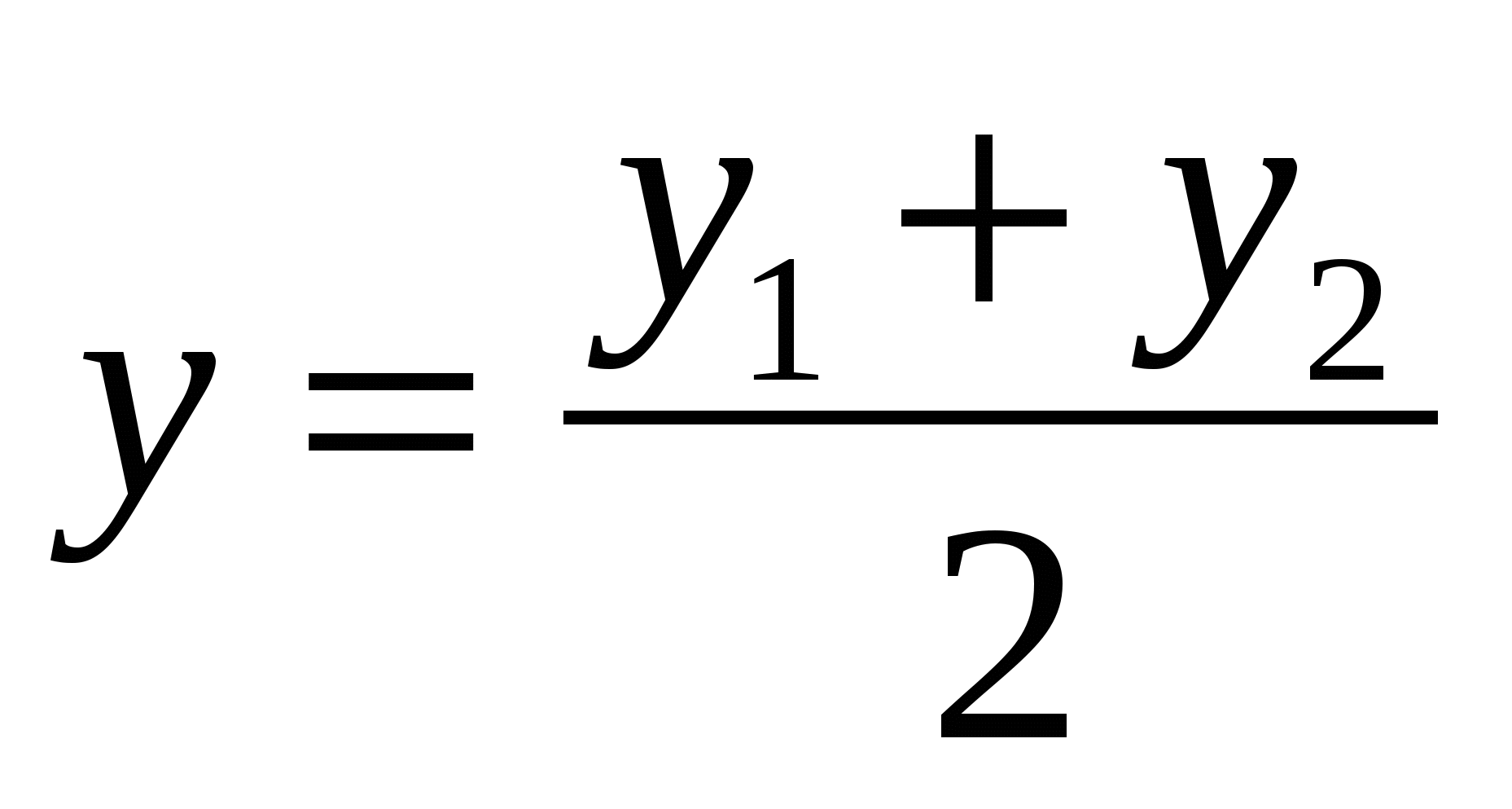 ,
, 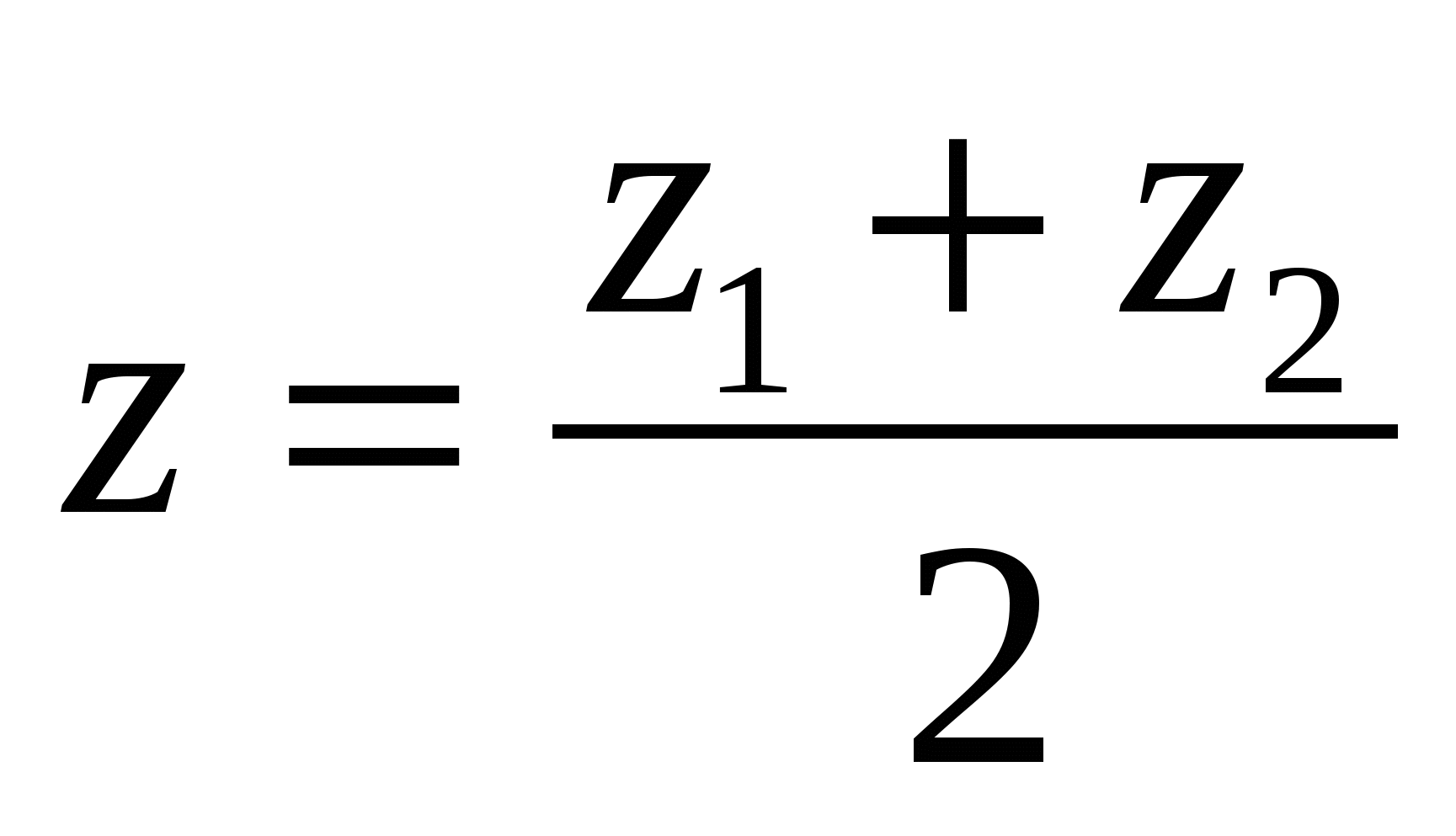 ,
,
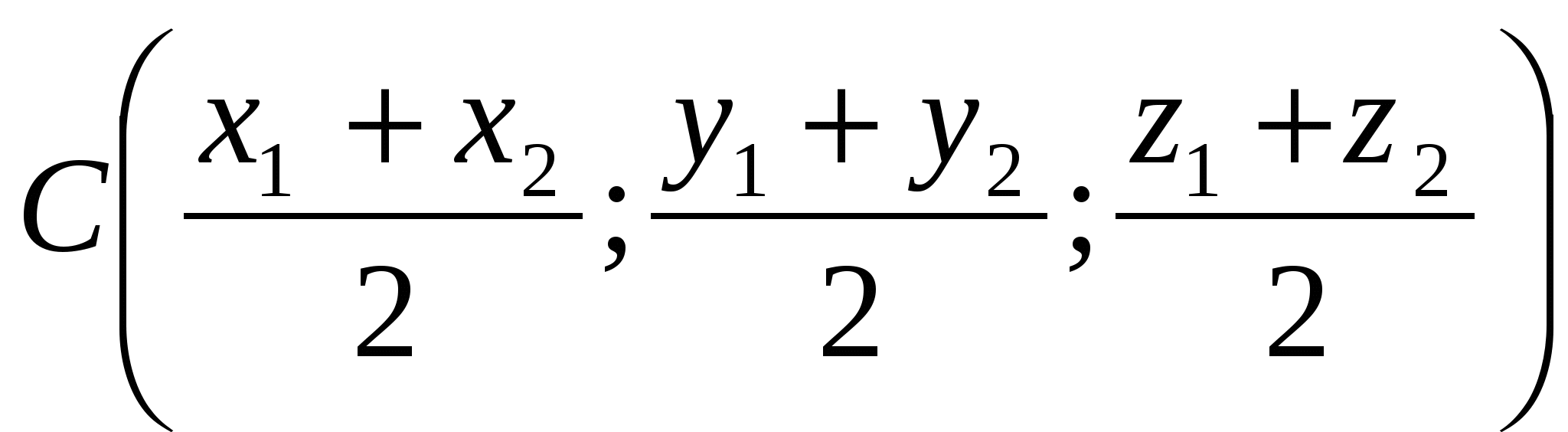
b) Calculation of the length of a vector from its coordinates.
Consider a vector 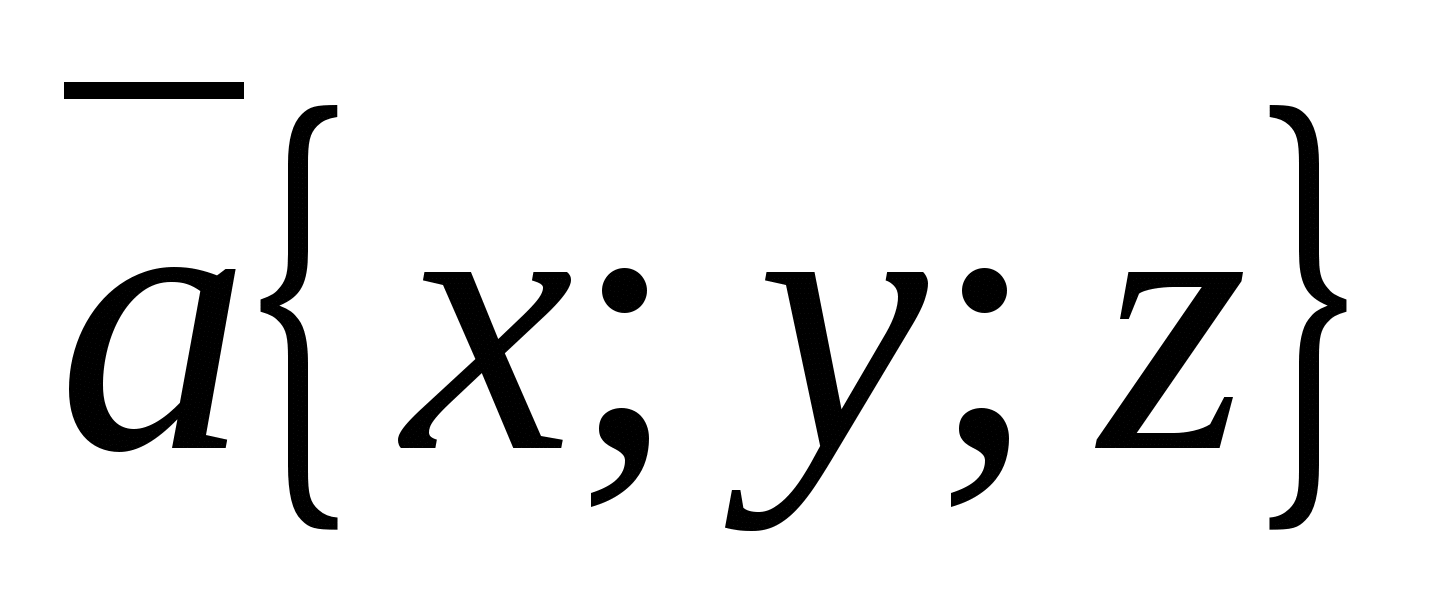 ,
,
the vector length is calculated by the formula
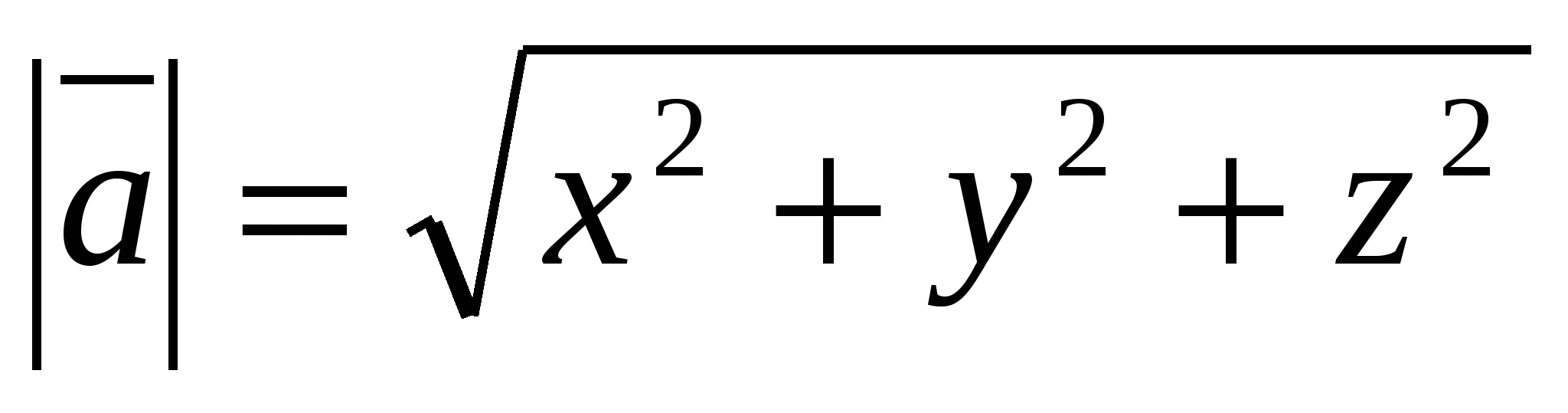 .
.
Because  =
=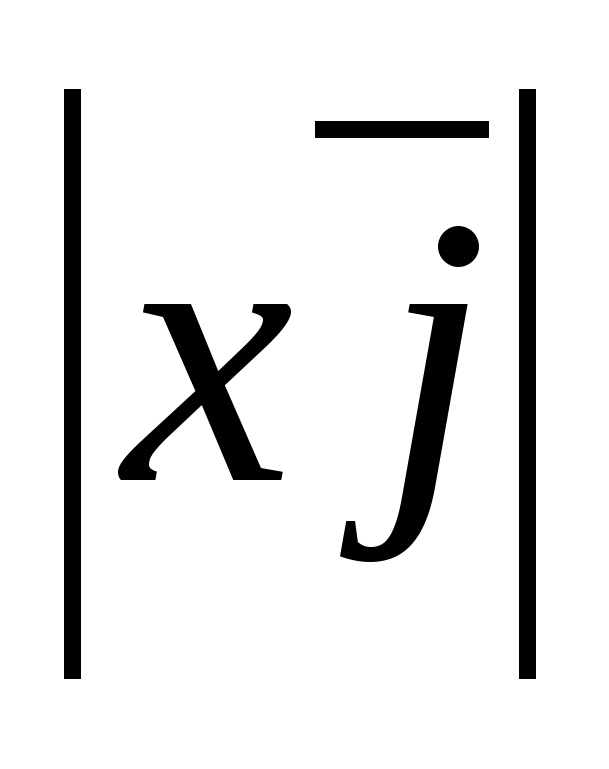 =
=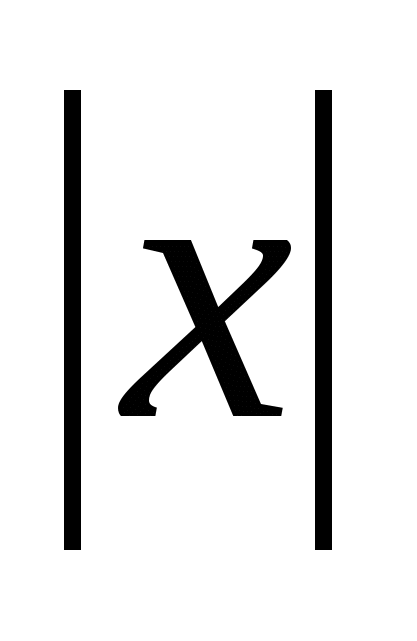 ,
,
 =
= =
=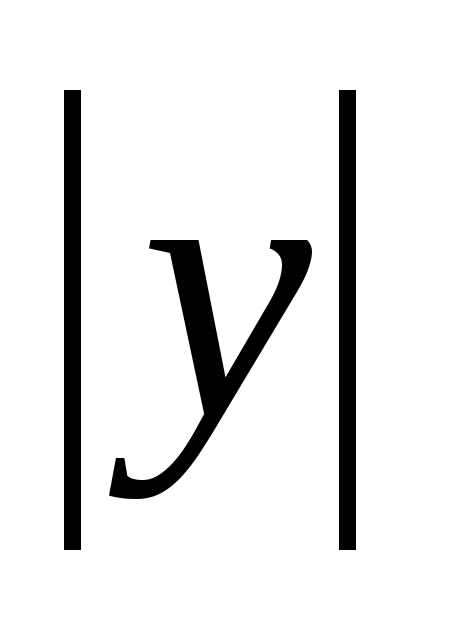 ,
,
 =
= =
= , And
, And 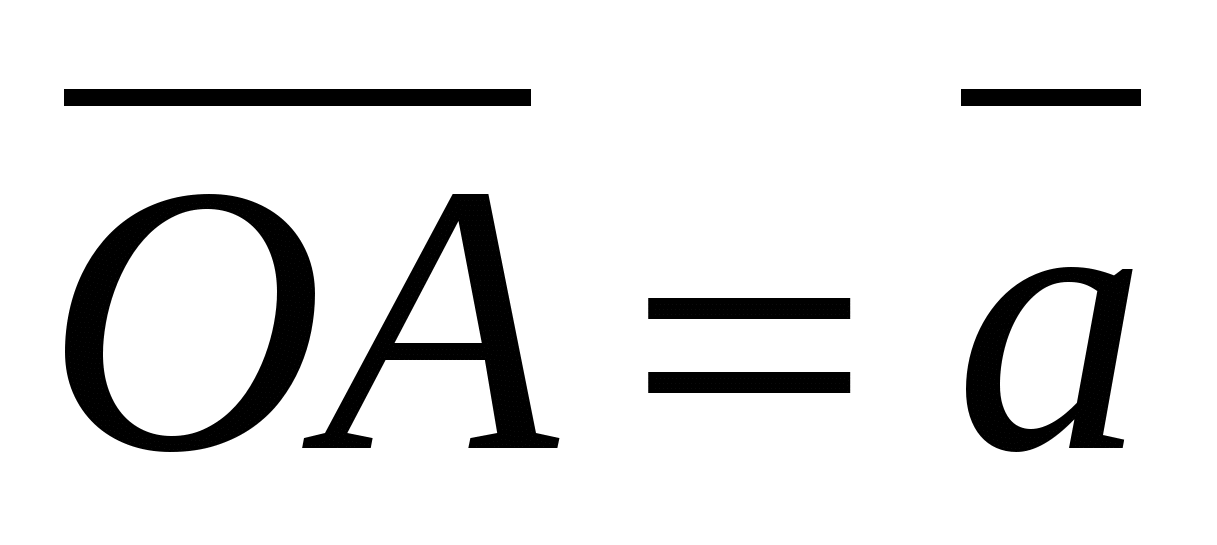 , then from the equality
, then from the equality 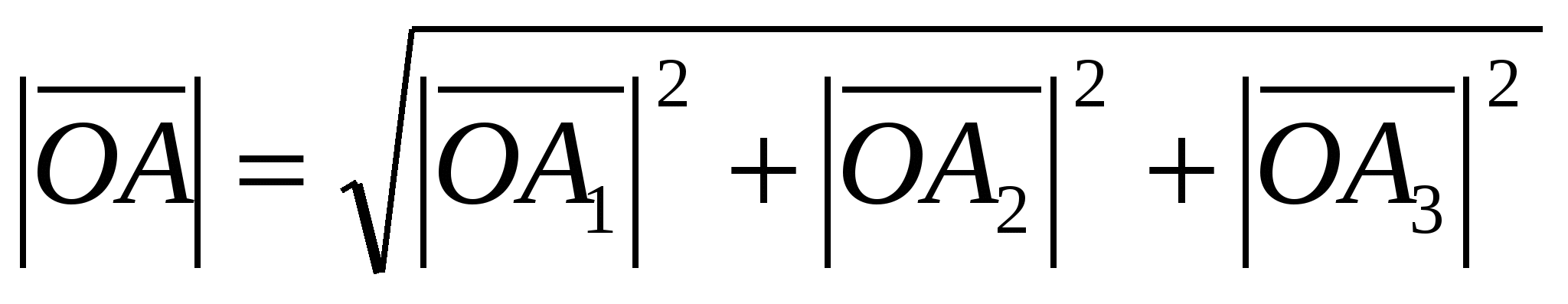 we get the formula: .
we get the formula: .
V) The distance between two points.
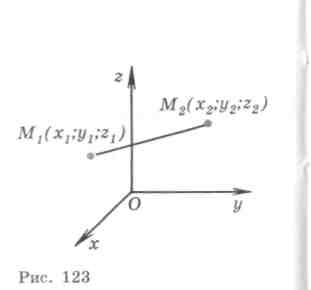 Let's consider two arbitrary points: point
Let's consider two arbitrary points: point  and period
and period 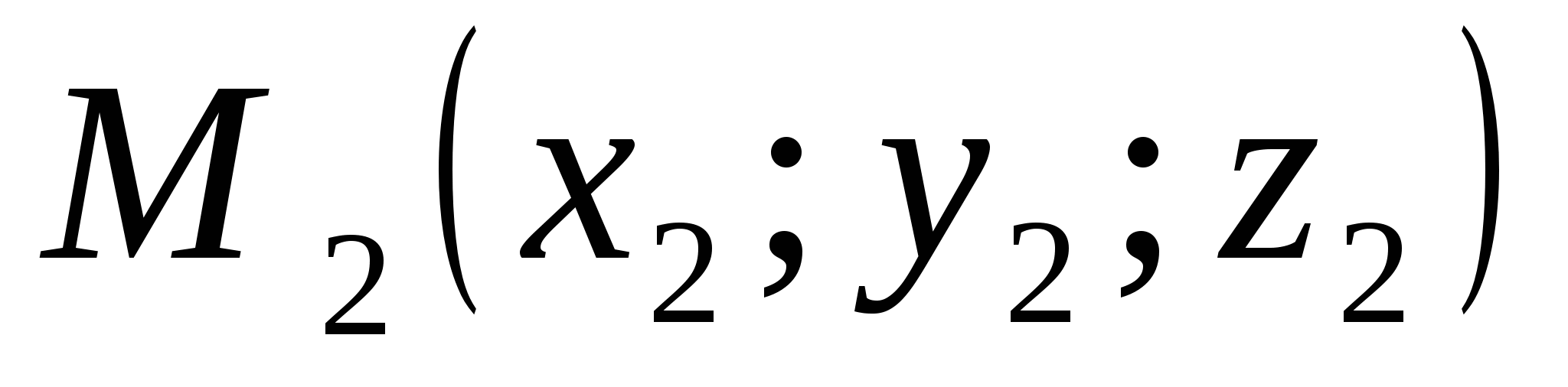 . Let's express the distanced
between points
. Let's express the distanced
between points 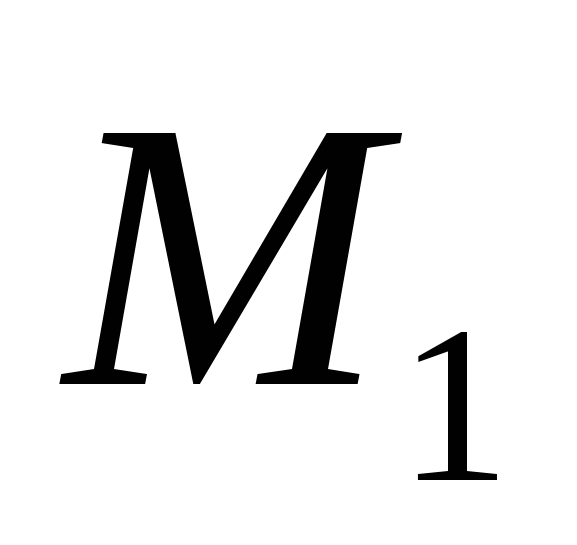 And
And 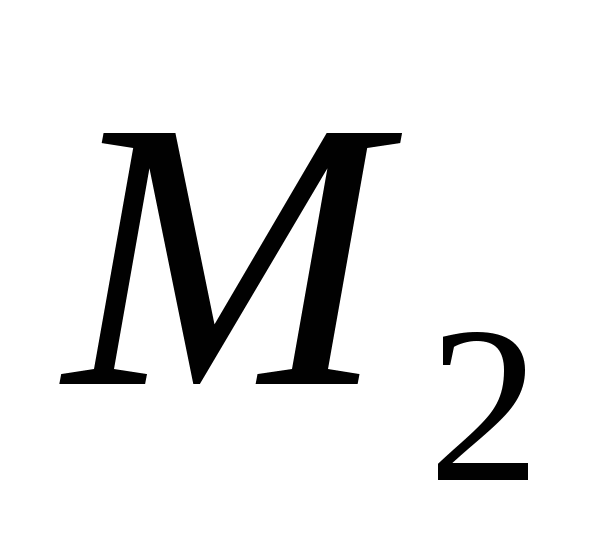 through their coordinates.
through their coordinates.
Consider the vector where .
But 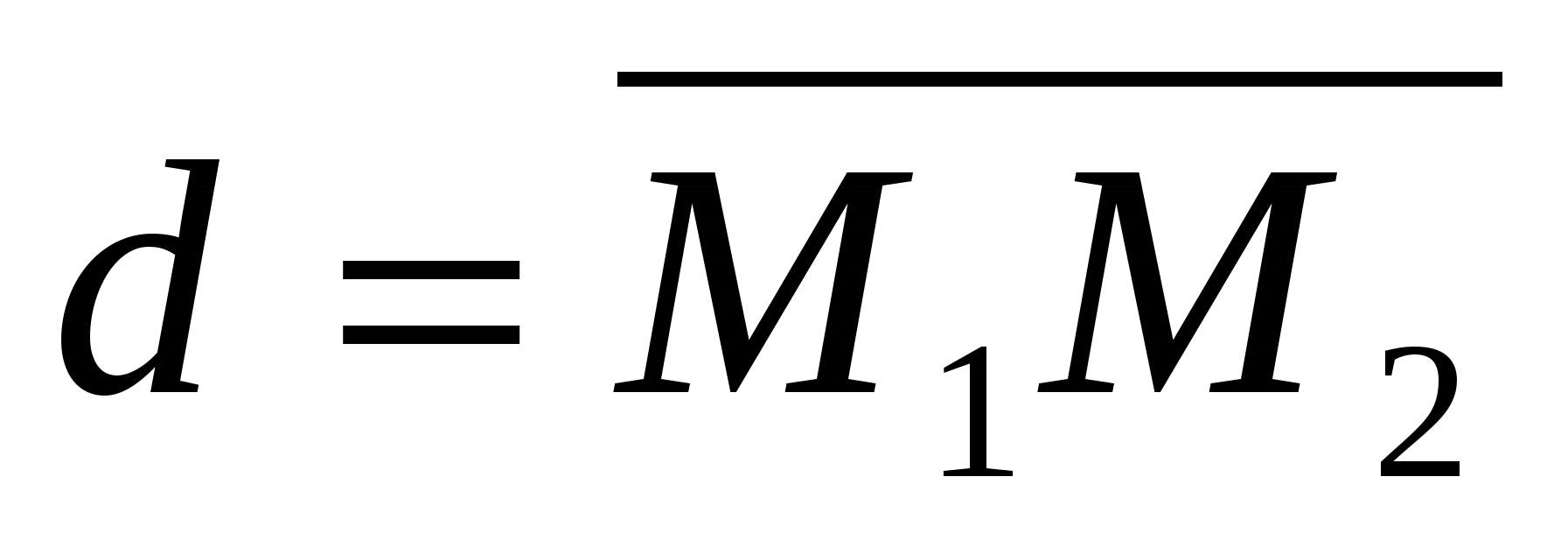 . Thus,distance between points
. Thus,distance between points 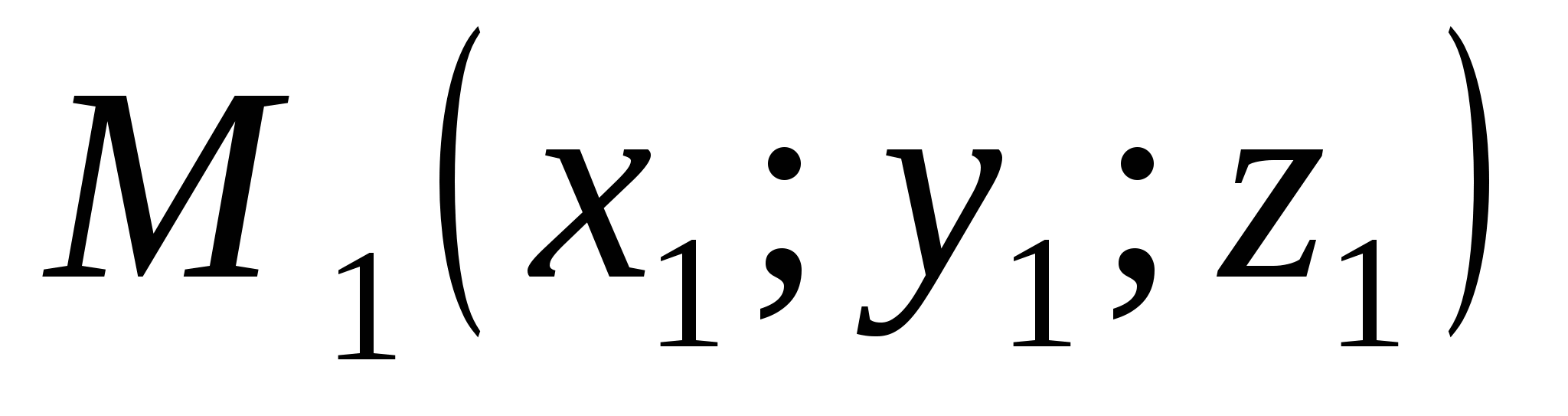 And
And 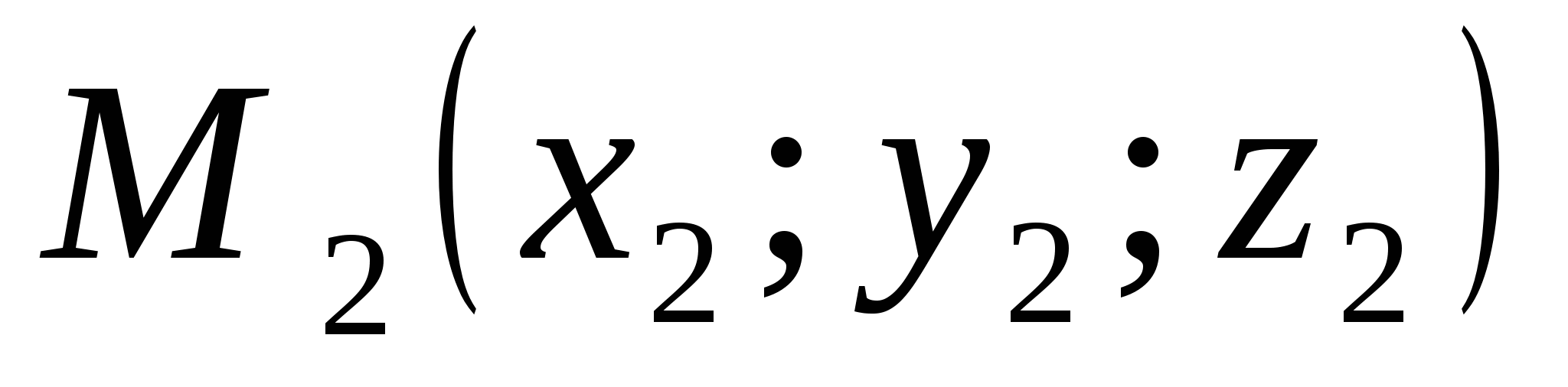
calculated by the formula .
6. Dot product of vectors and calculation of the angle between vectors through their coordinates.
1) Dot product of vectors
The scalar product of two vectors is the product of their lengths and the cosine of the angle between them.
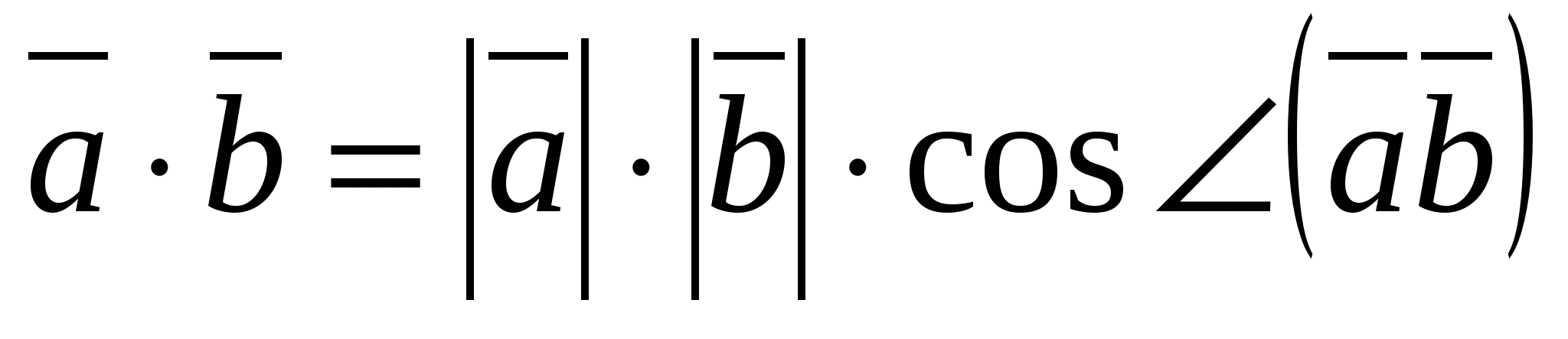
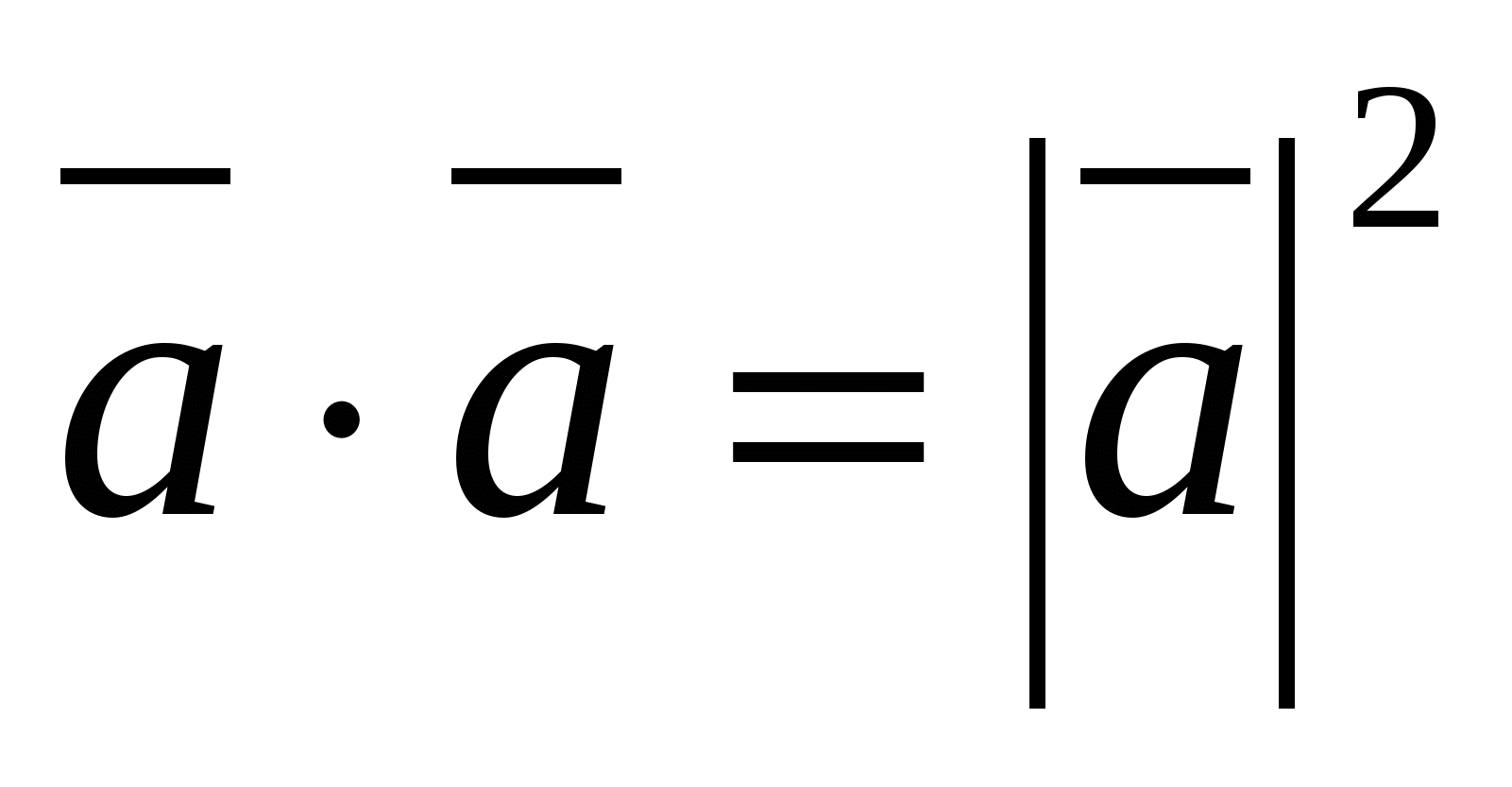
those.
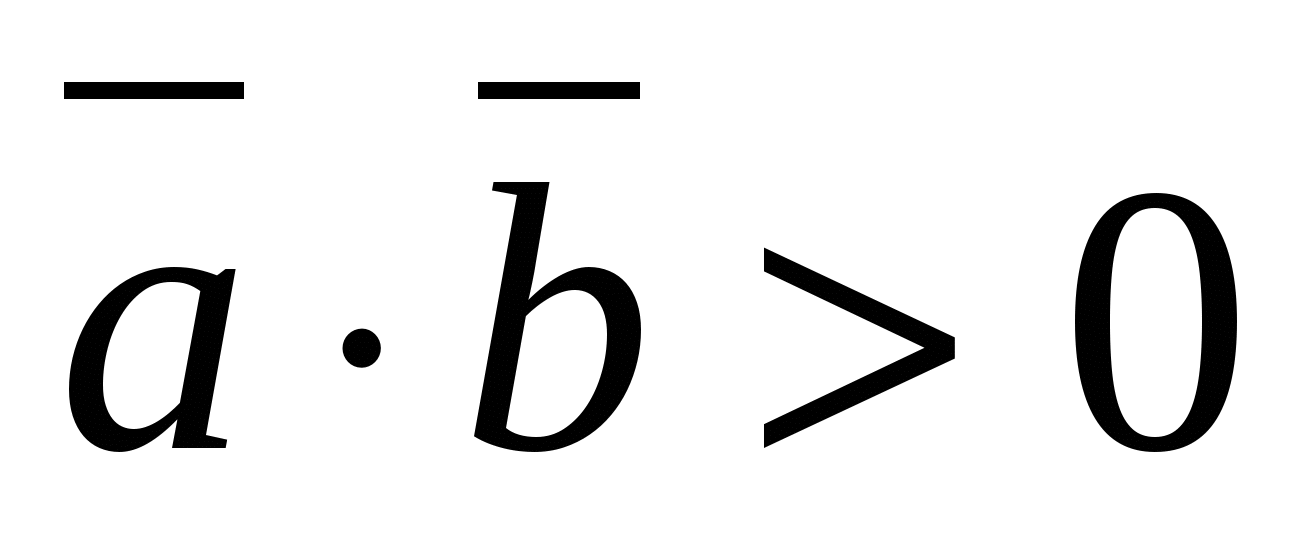

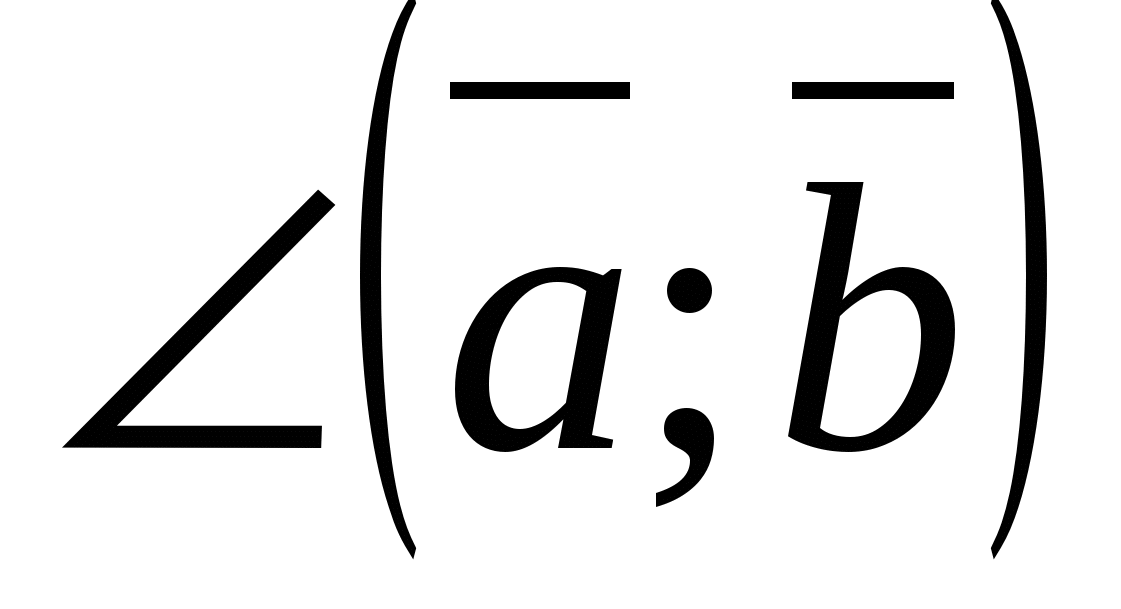 - spicy.
- spicy.
The scalar product of nonzero vectors is negative if and only if the angle between the vectors is obtuse,
those.
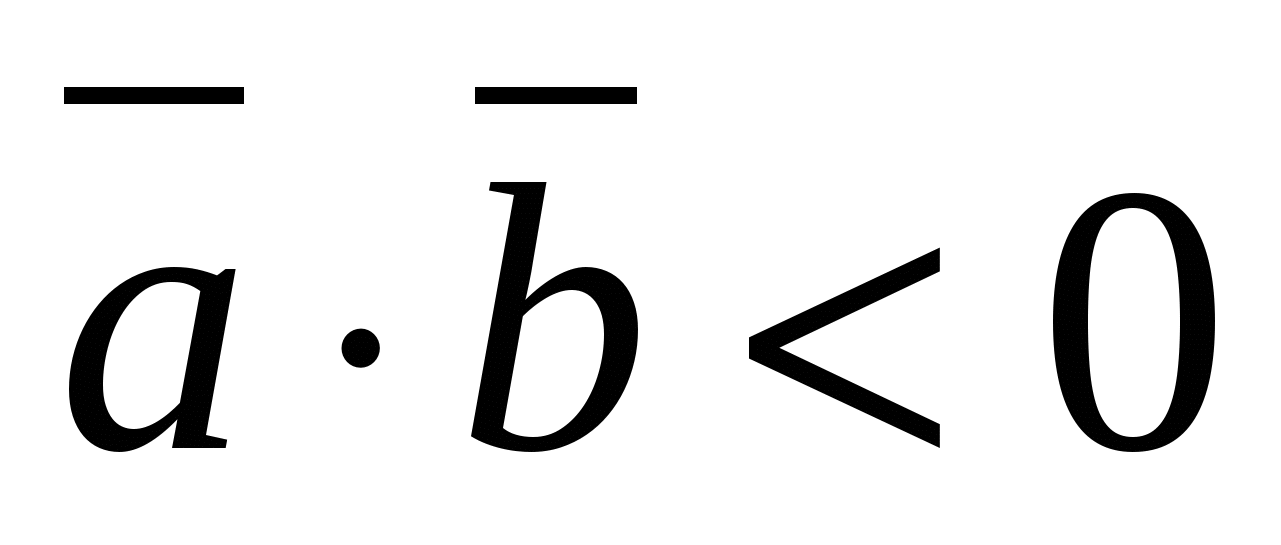

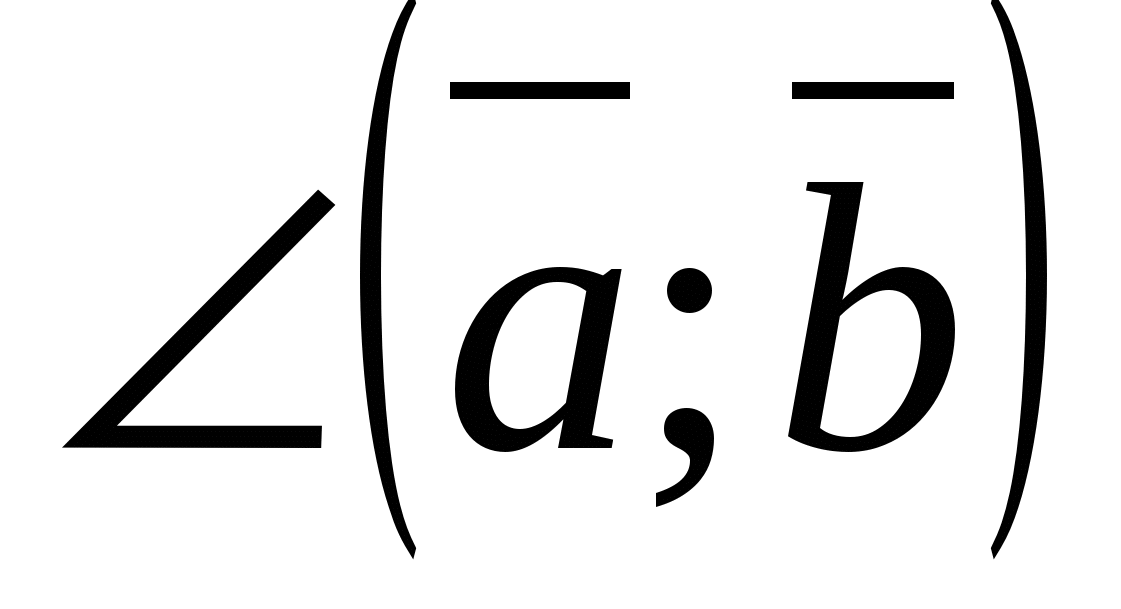 - blunt.
- blunt.
For any vectors, 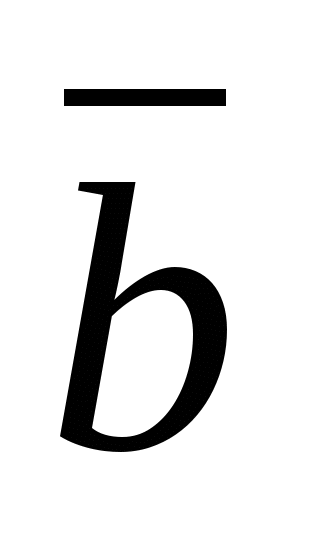 ,
, 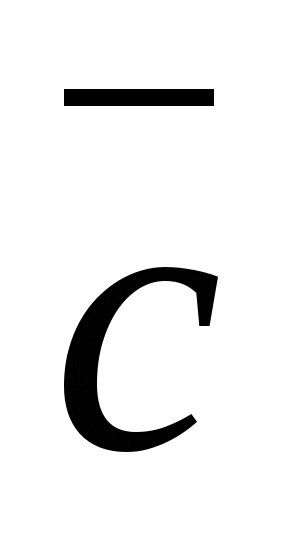 , and any numberk
the equalities are valid:
, and any numberk
the equalities are valid:
1. 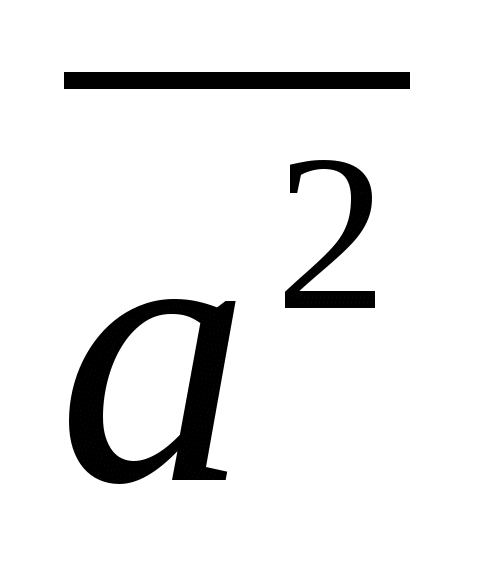
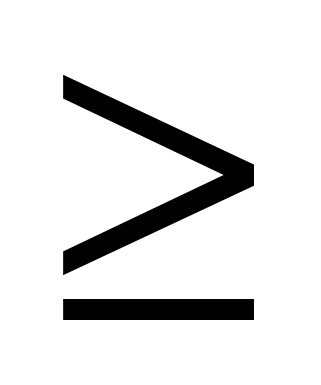 0, and
0, and 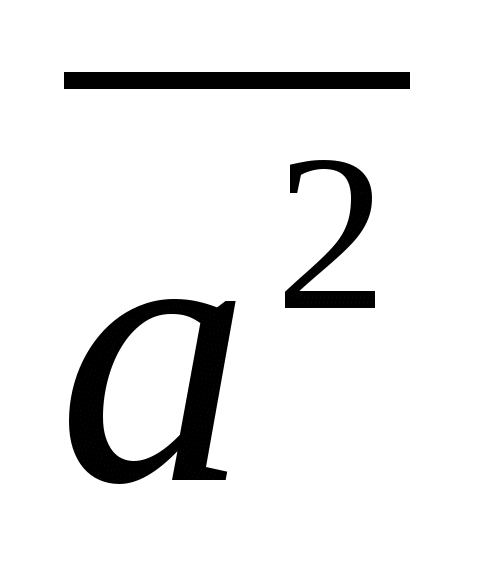 >0 at
>0 at 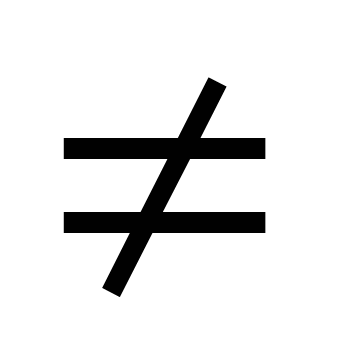 0.
0.
2. 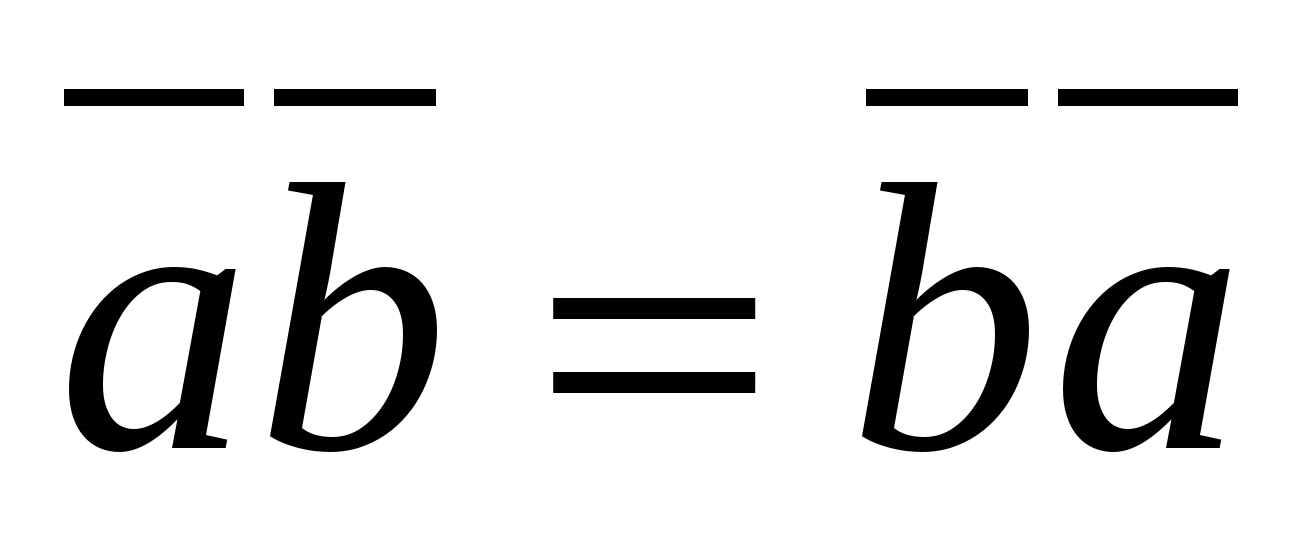 (transfer law).
(transfer law).
3.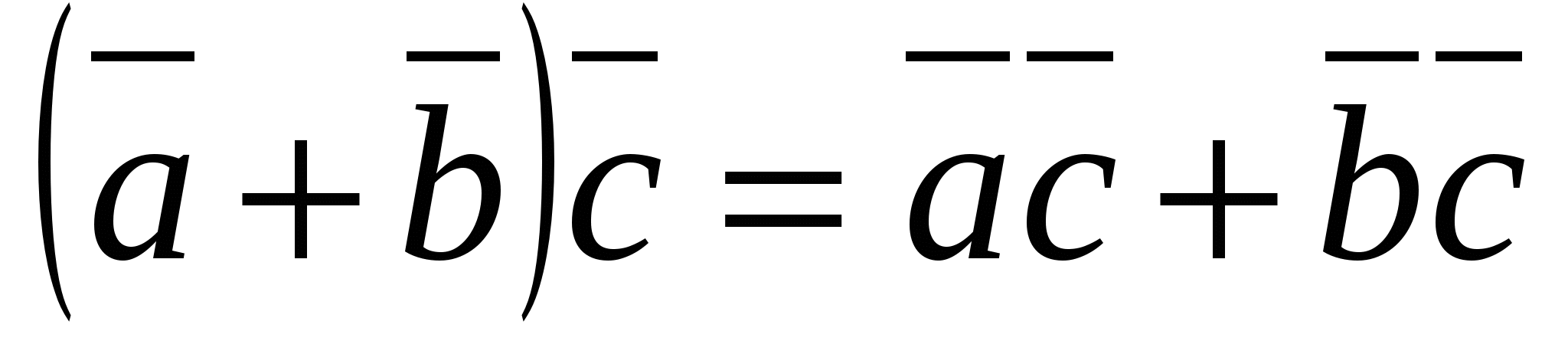 (distributive law).
(distributive law).
4. 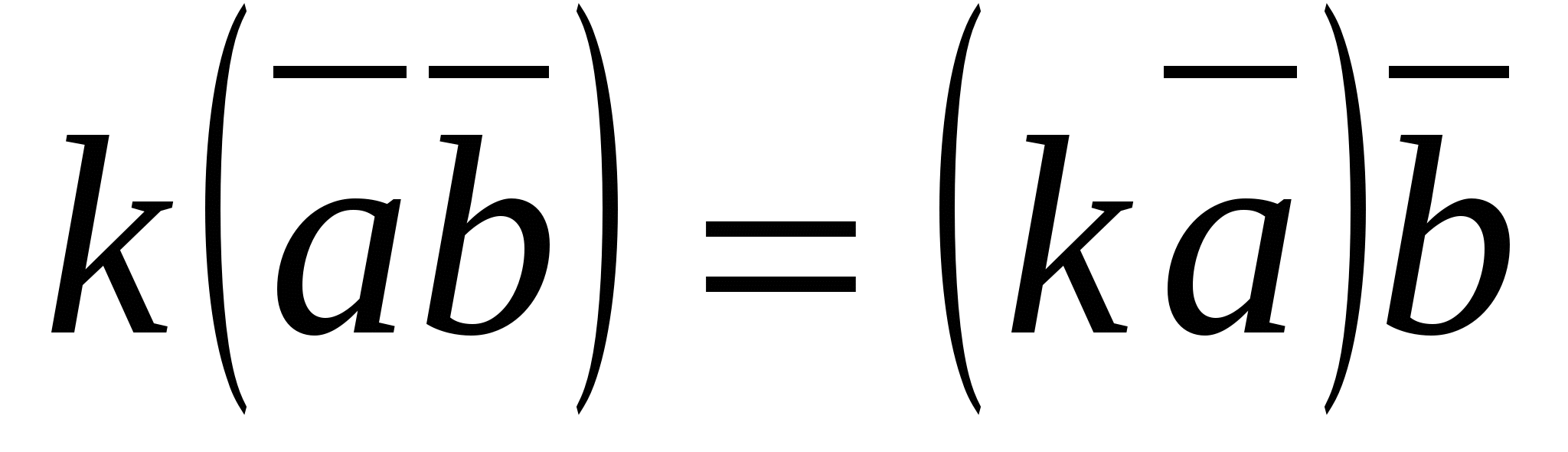 (combinative law).
(combinative law).
2) Calculation of the angle between vectors using their coordinates.
Cosine of angle  between non-zero vectors
between non-zero vectors 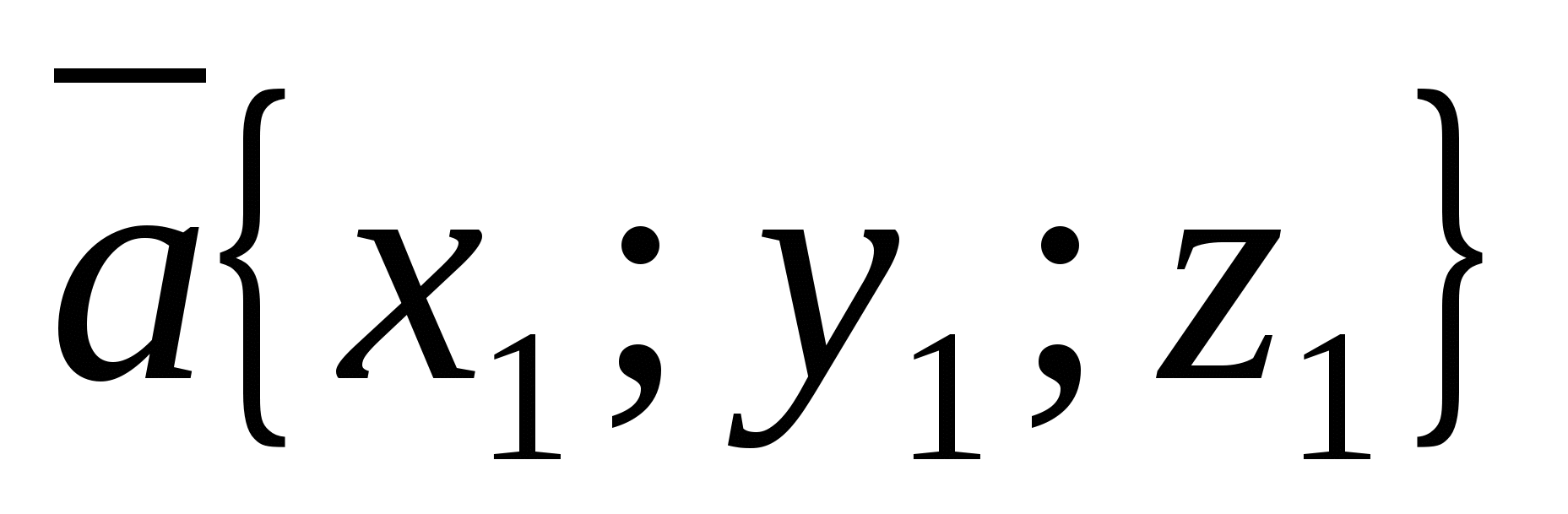 And
And 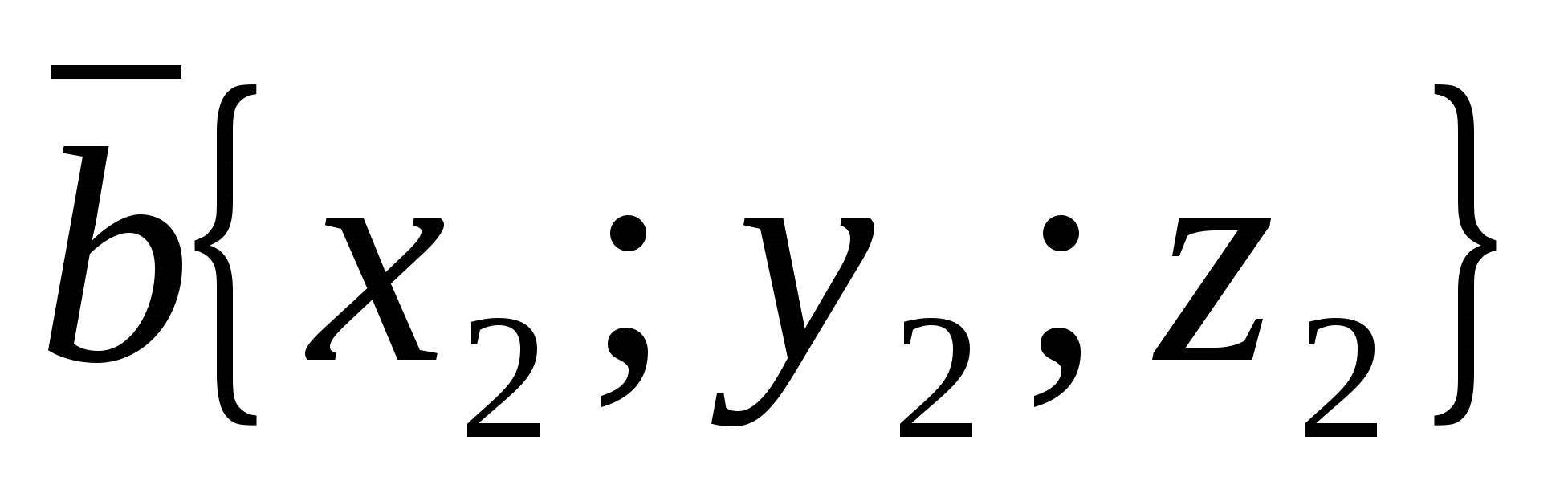 calculated by the formula
calculated by the formula
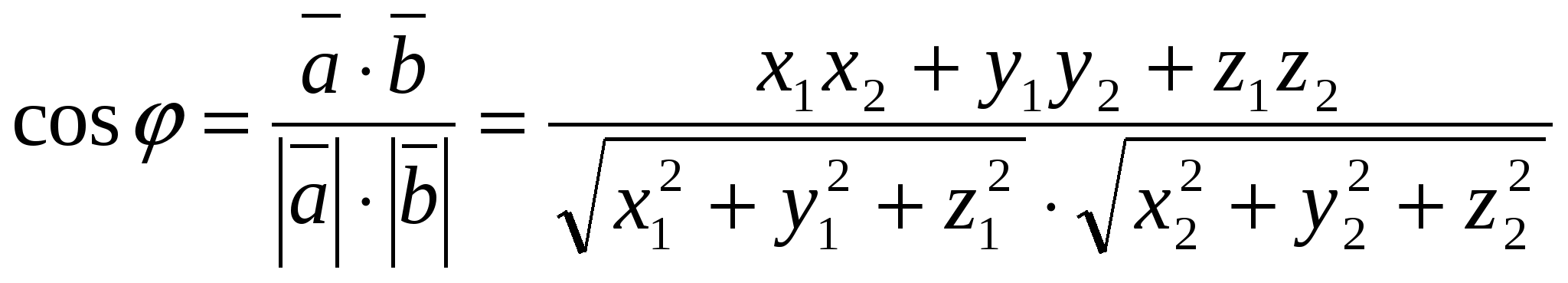 ,
,
Where 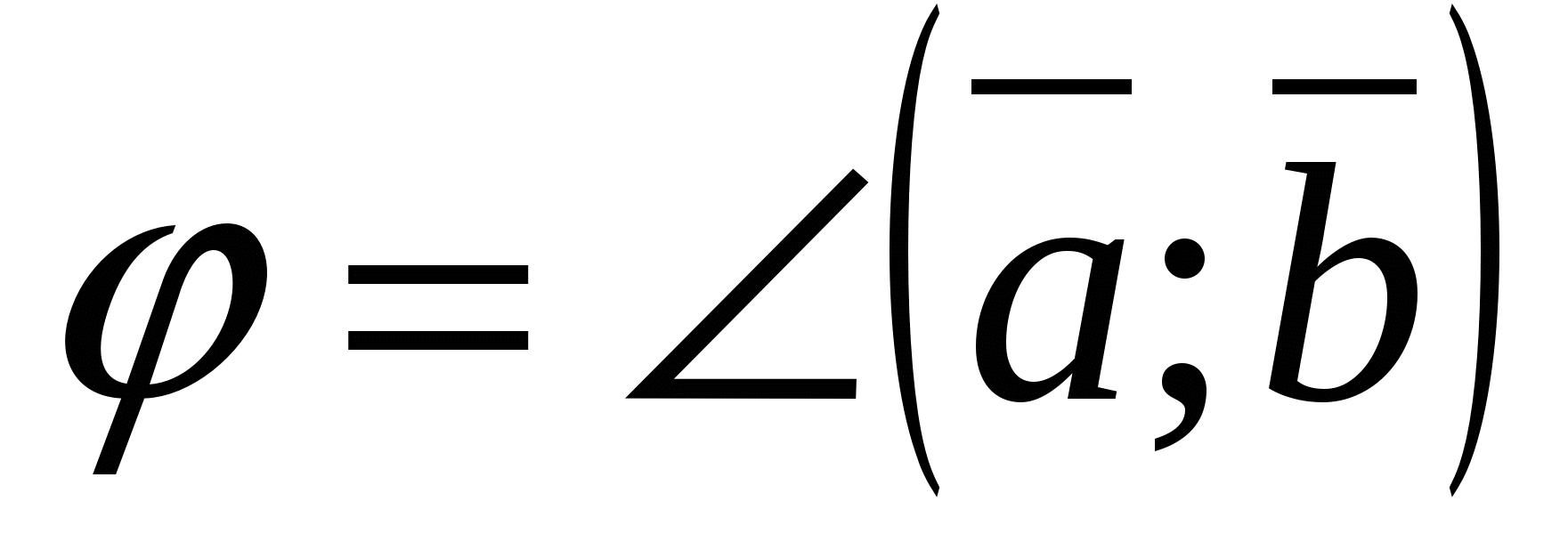
7. Calculation of angles between straight lines and planes.
1) Angle between straight lines.
To solve this problem, we introduce the concept of a directing vector of a straight line.
Definition.
A nonzero vector is called a direction vector of a line a if it lies either on a line a or on a line parallel to a.
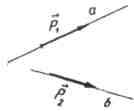 Example
Example
Vectors 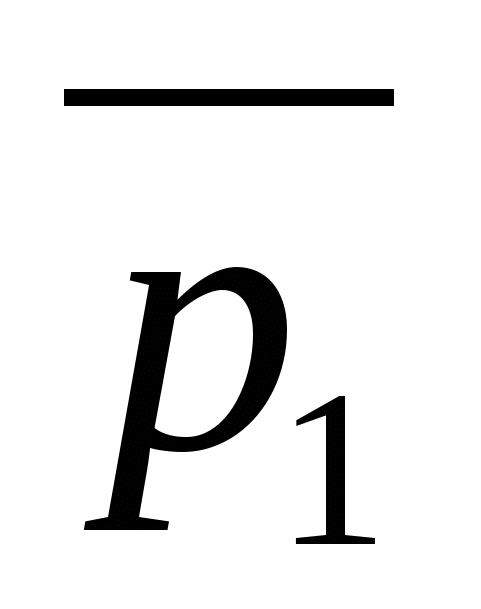 And
And  straight guidesa
And b
, respectively.
straight guidesa
And b
, respectively.
Definition.
The angle between lines is the angle between the direction vectors of these lines.
Angle between straight linesa
And b
equal to angle between the direction vectors of the straight lines, 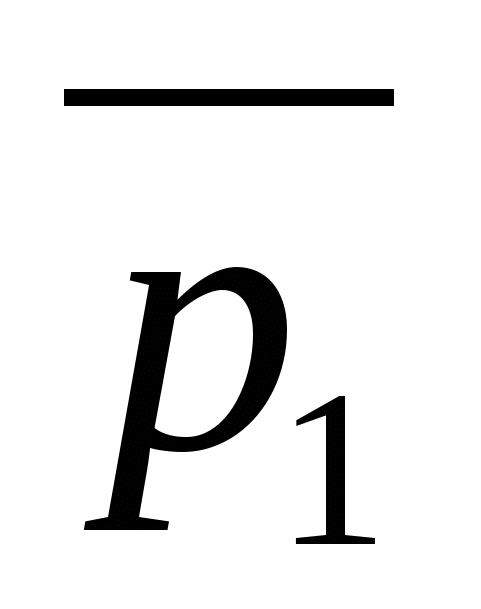 And
And 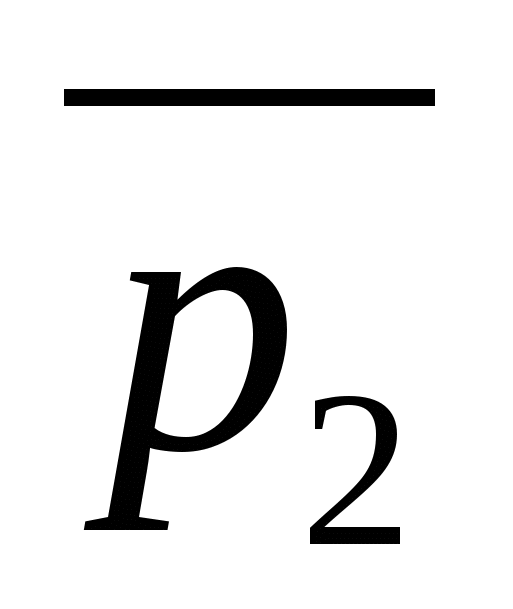 .
.
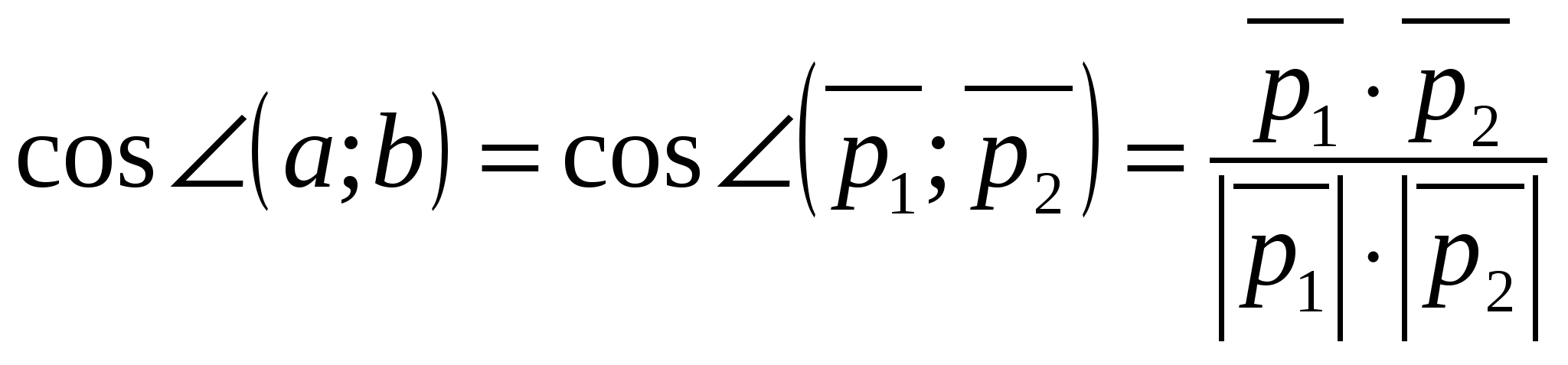 .
.
2).Angle between a straight line and a plane.
Definition.
The angle between a line and a plane is the angle between the direction vector of a given line and a non-zero vector perpendicular to the plane(normal).
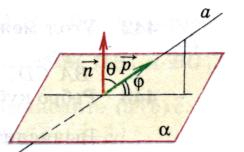
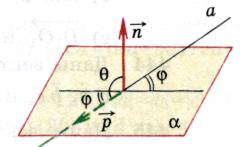
Let 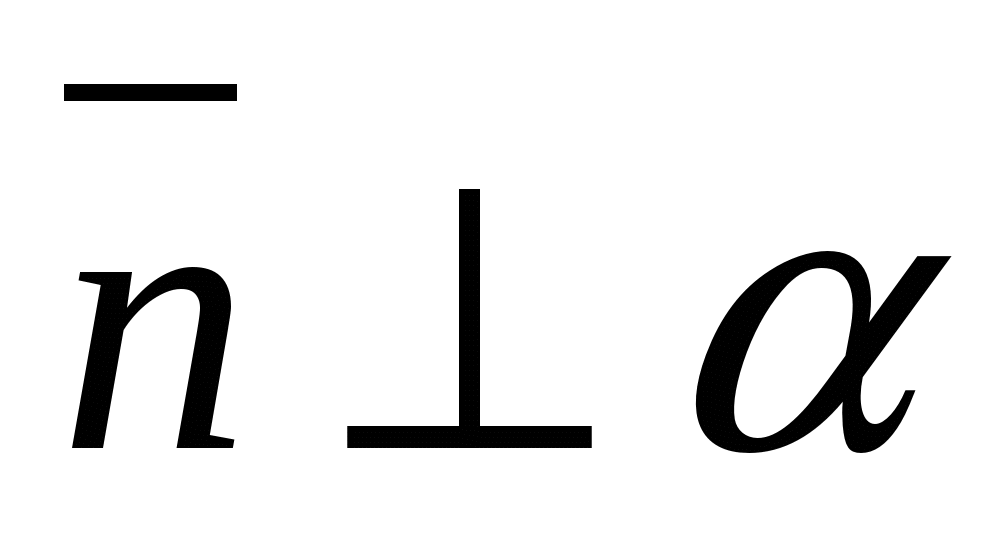 , (
, (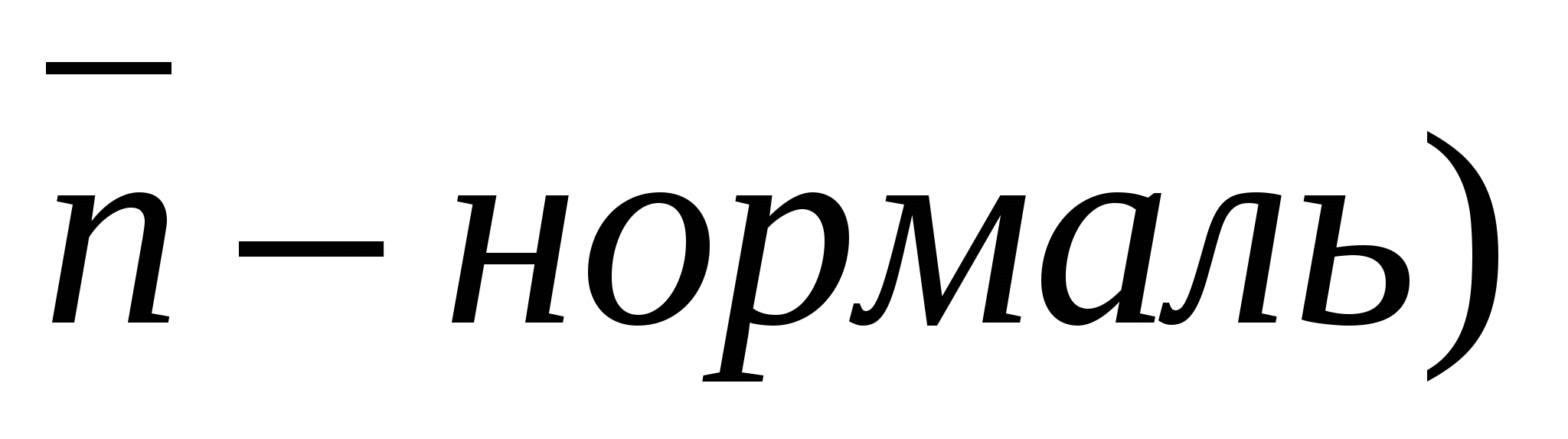
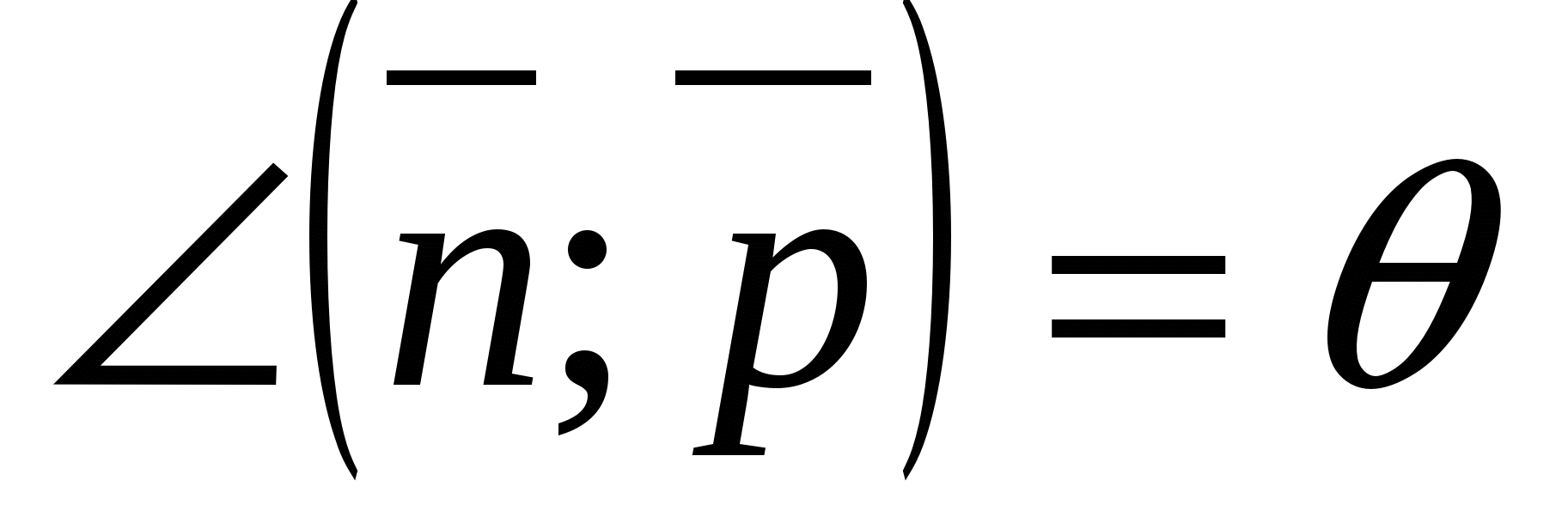 , A
, A 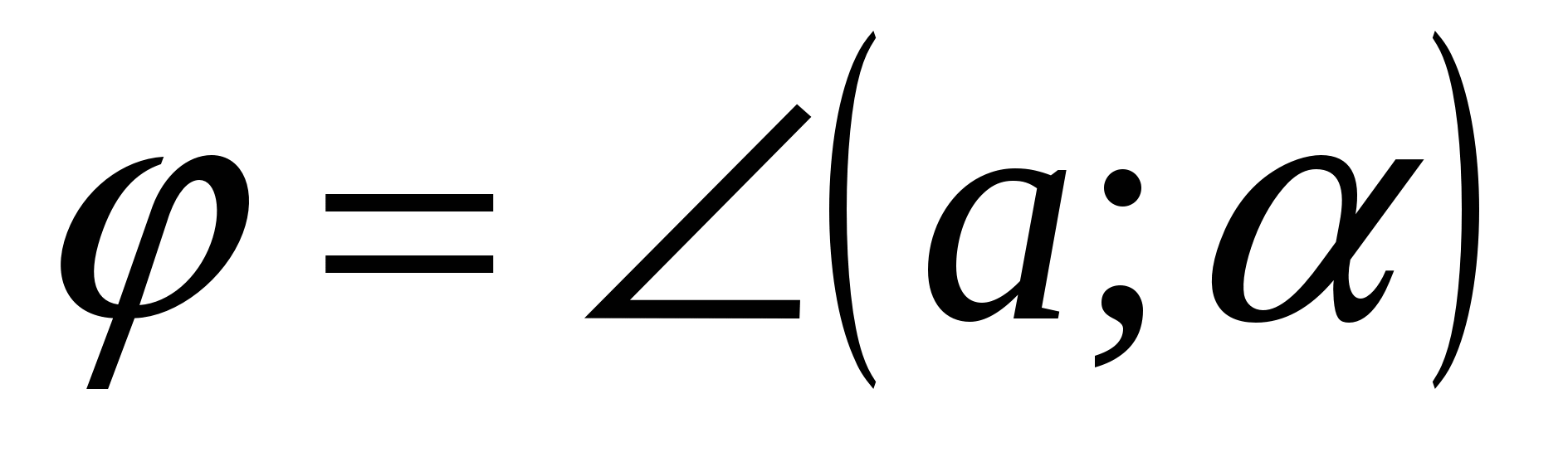 - desired angle (
- desired angle ( 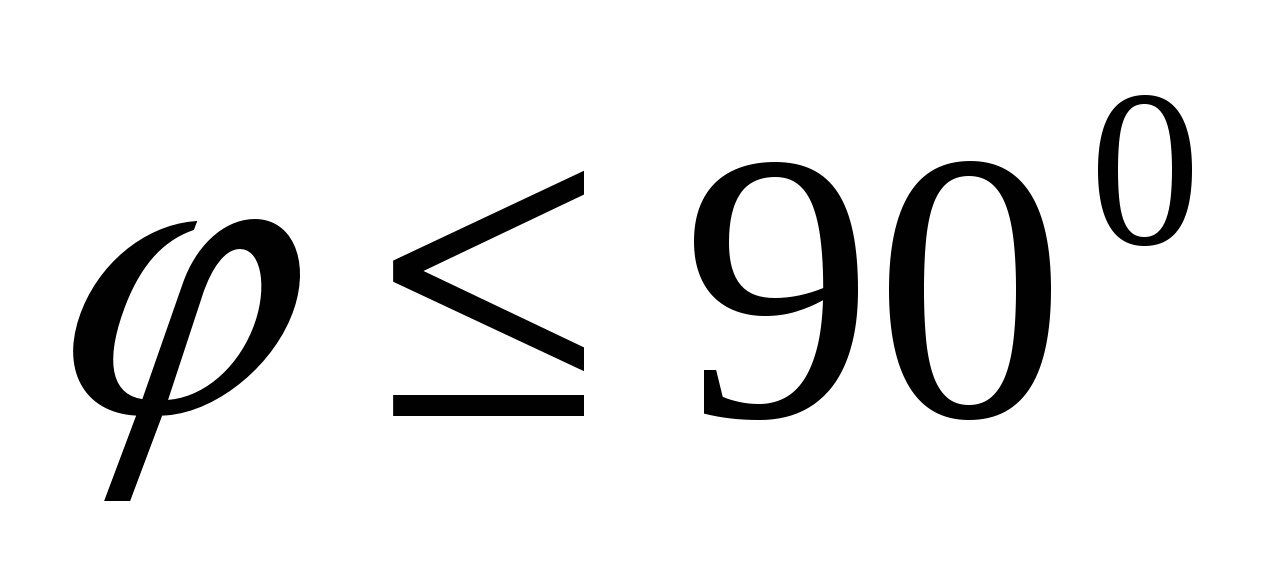 ).
).
Then

Means  .
.
Chapter 3.
Application of the coordinate method to solving stereometric problems.
Problem.1
At the base of the MABC pyramid lies right triangle ABC. 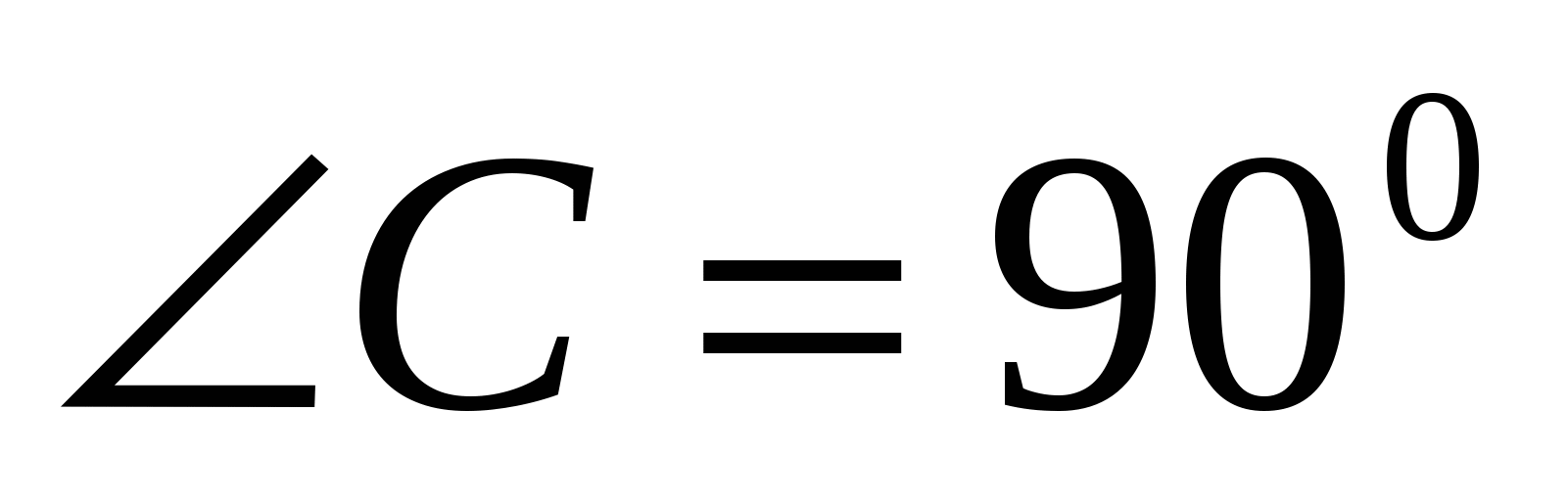 ,
A.C.=3,
B.C.=5. Edge AM is perpendicular to AC, AM=4,
,
A.C.=3,
B.C.=5. Edge AM is perpendicular to AC, AM=4, 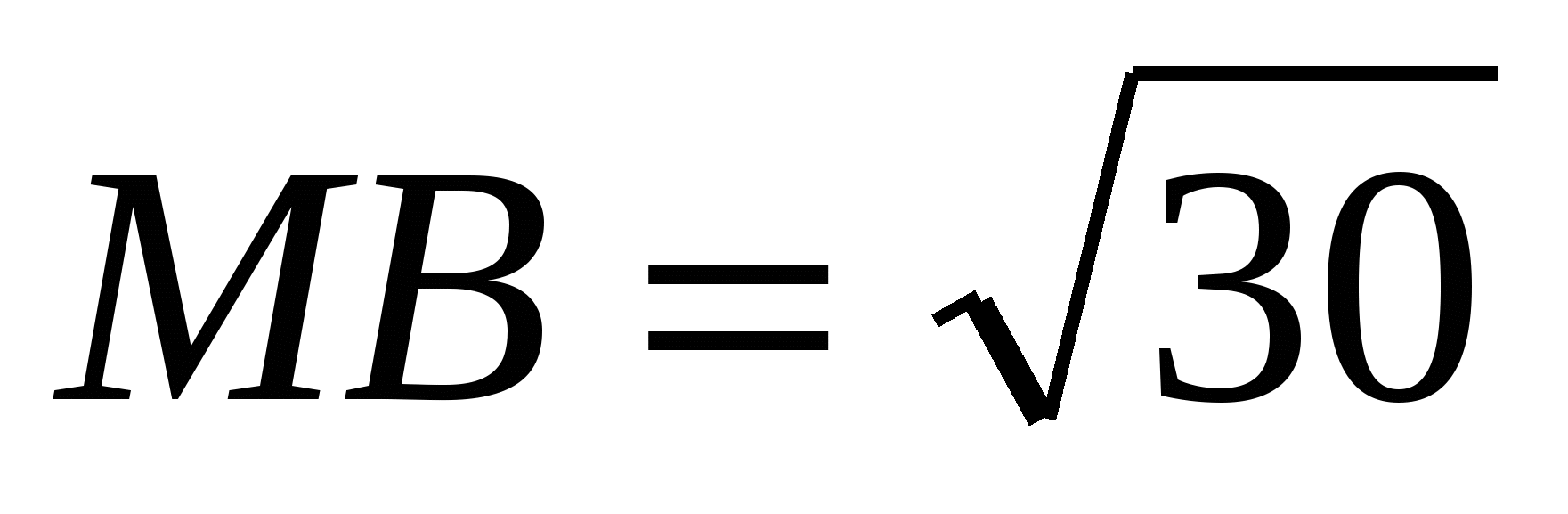 . Find the volume of the pyramid.
. Find the volume of the pyramid.
R 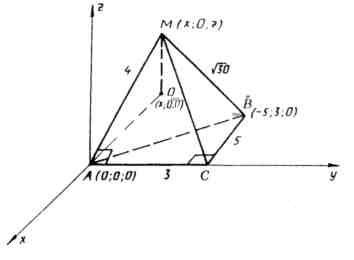 decision.
decision.
1) Let us introduce a rectangular coordinate system with the origin at the point  . Axis
. Axis 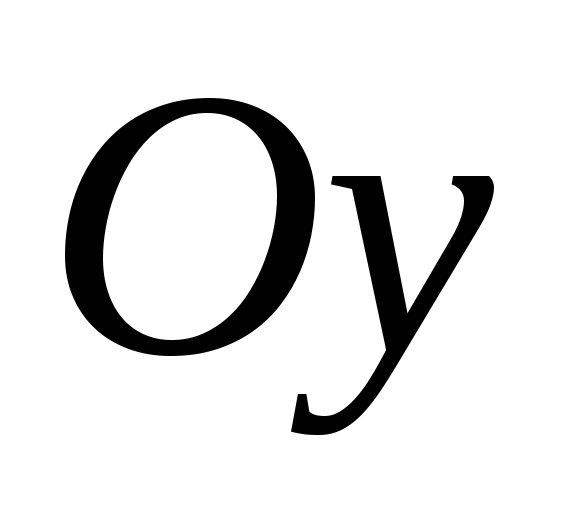 let's direct along the edgeAC, and the plane Oh
y
along the base of the pyramidABC.
let's direct along the edgeAC, and the plane Oh
y
along the base of the pyramidABC.
In this coordinate system: 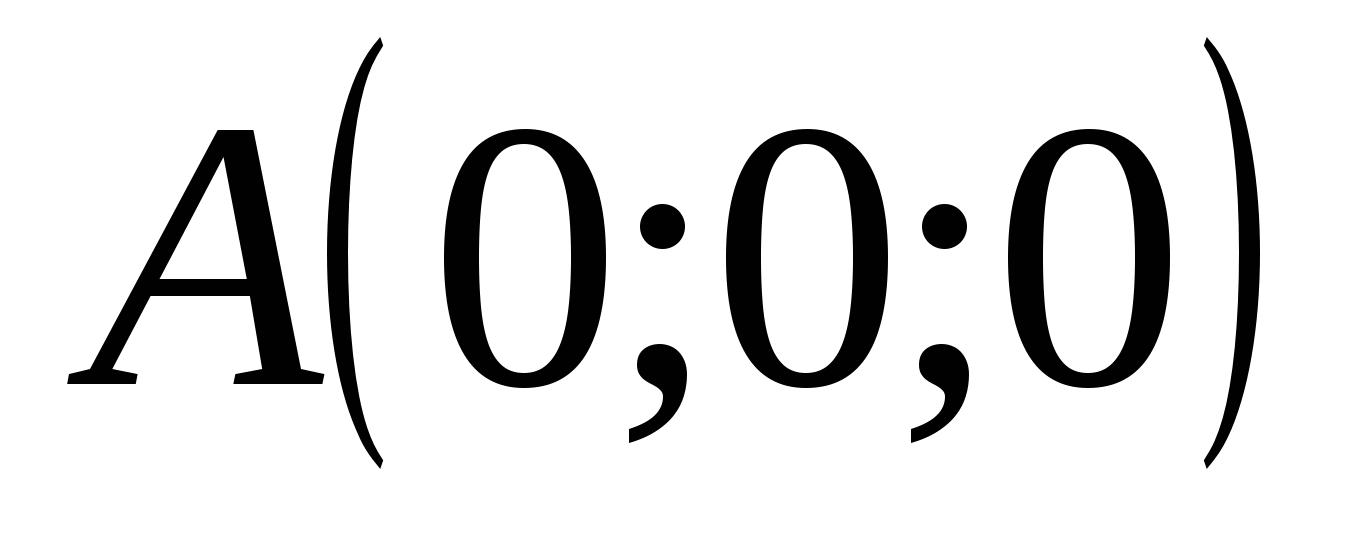 ,
, 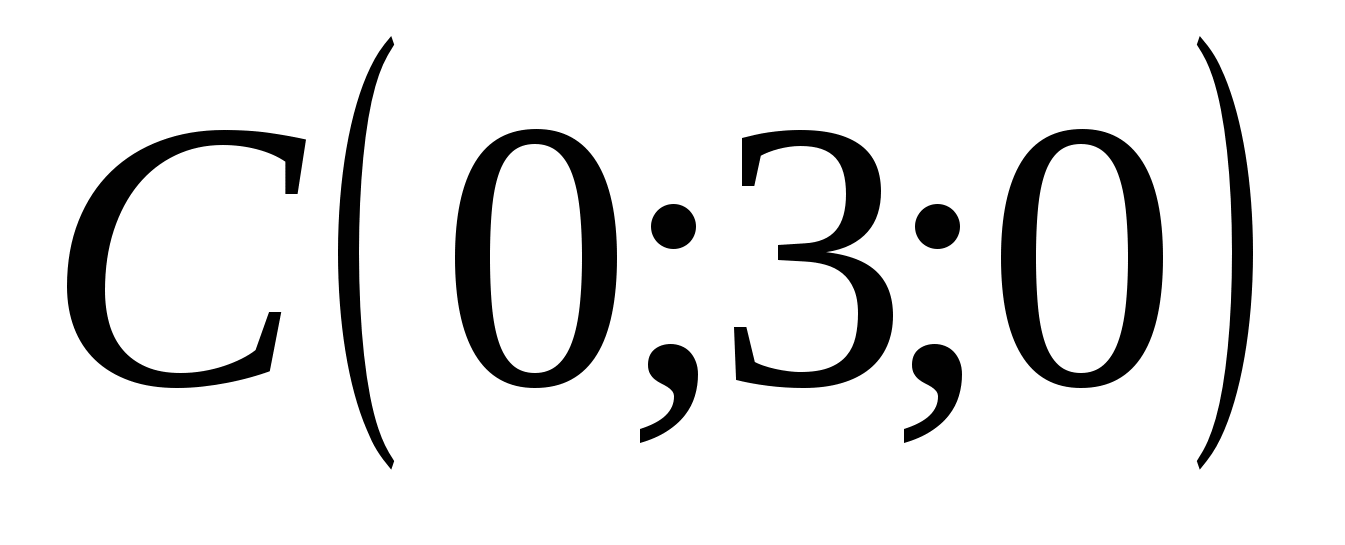 ,
, 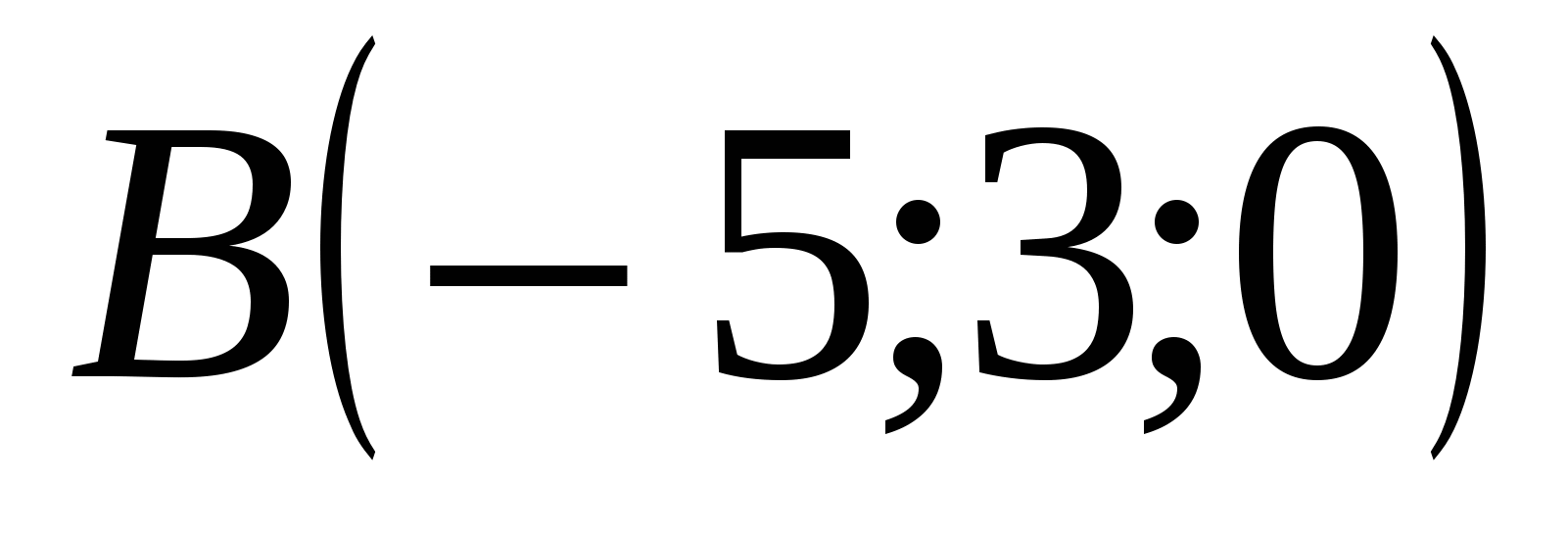 . Since by condition
. Since by condition 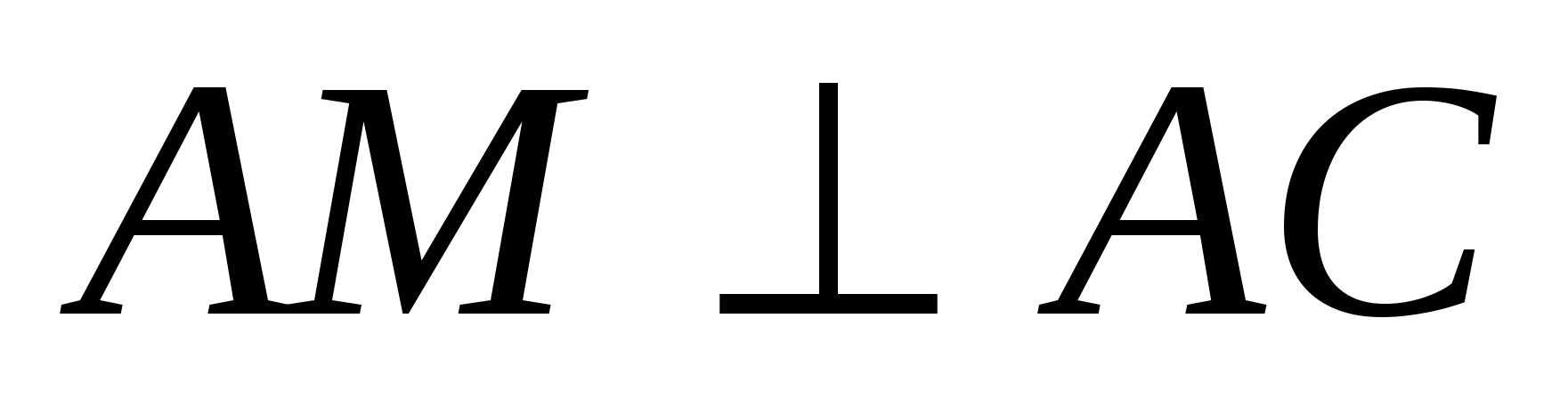 , then point M lies in the planexz
and has coordinates
, then point M lies in the planexz
and has coordinates
 .
.
2) 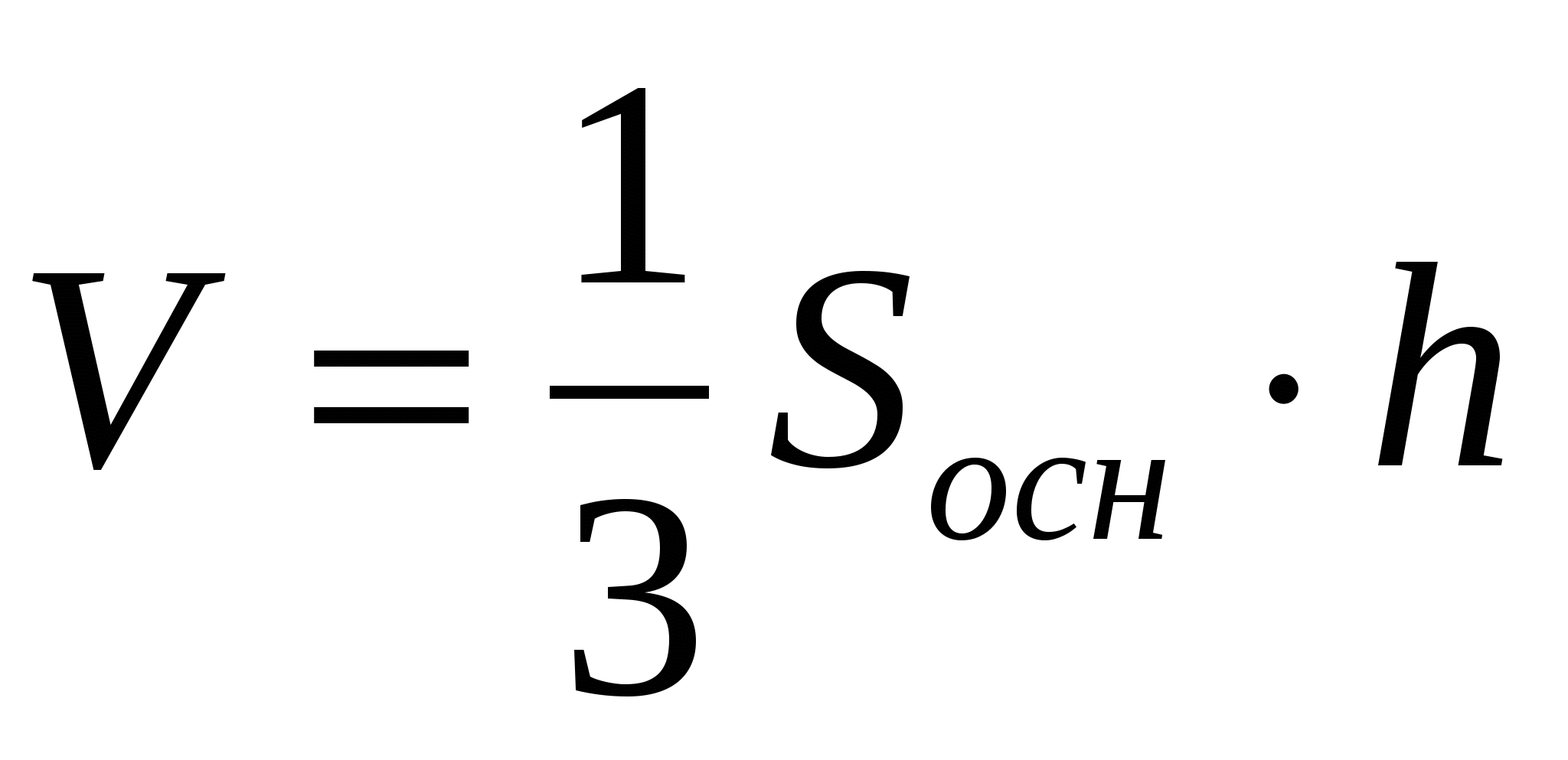 ,
, 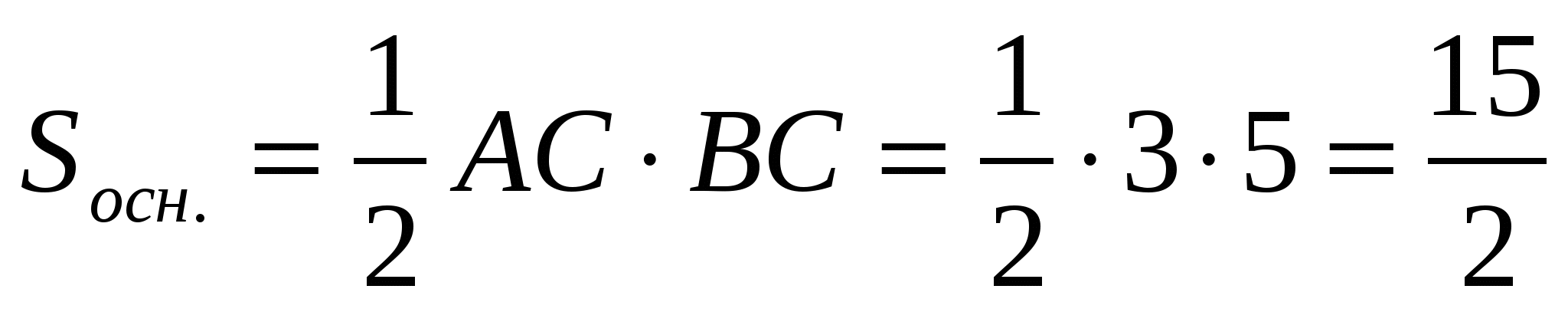 .
.
Let's find the height of the pyramid. Let's drop from the pointM perpendicular M
D
to the plane (ABC),
Then  , because
, because 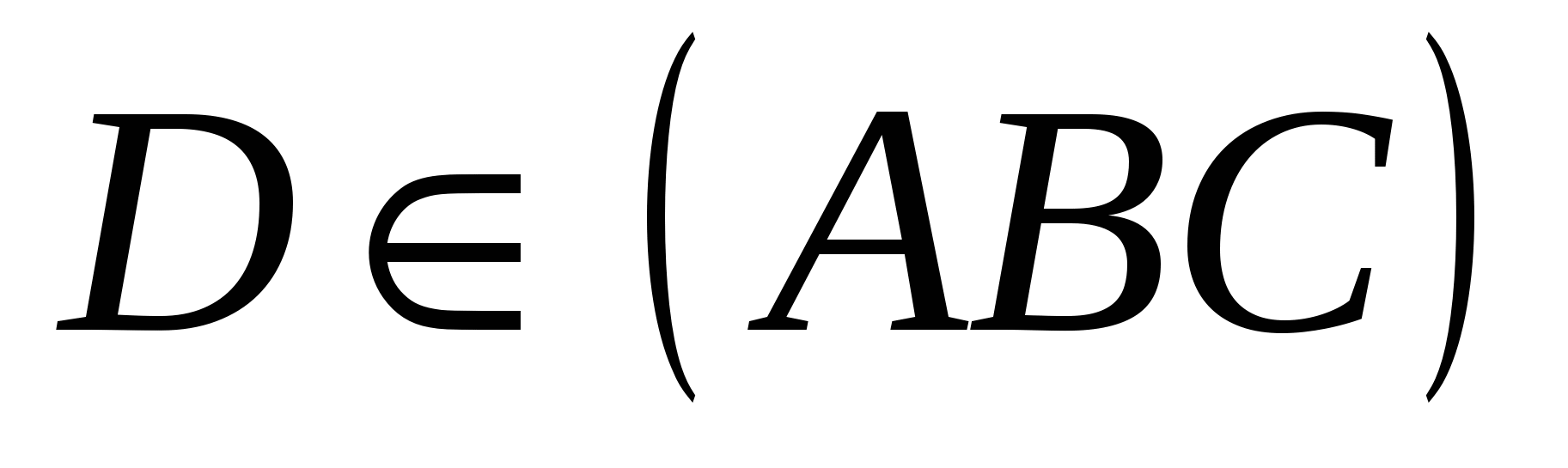 . Hence,
. Hence,  and distance between pointsM And Dequals , because
and distance between pointsM And Dequals , because 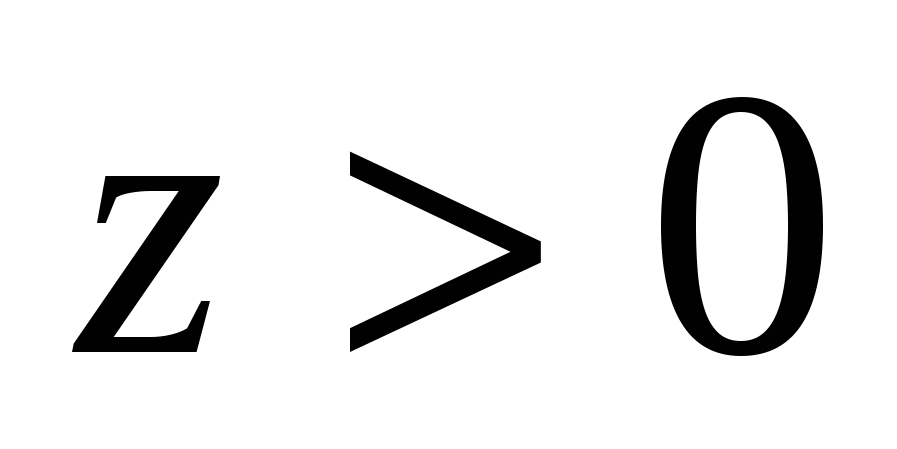 .
.
Let's find the coordinate valuez
using the distances between points containing given coordinate: 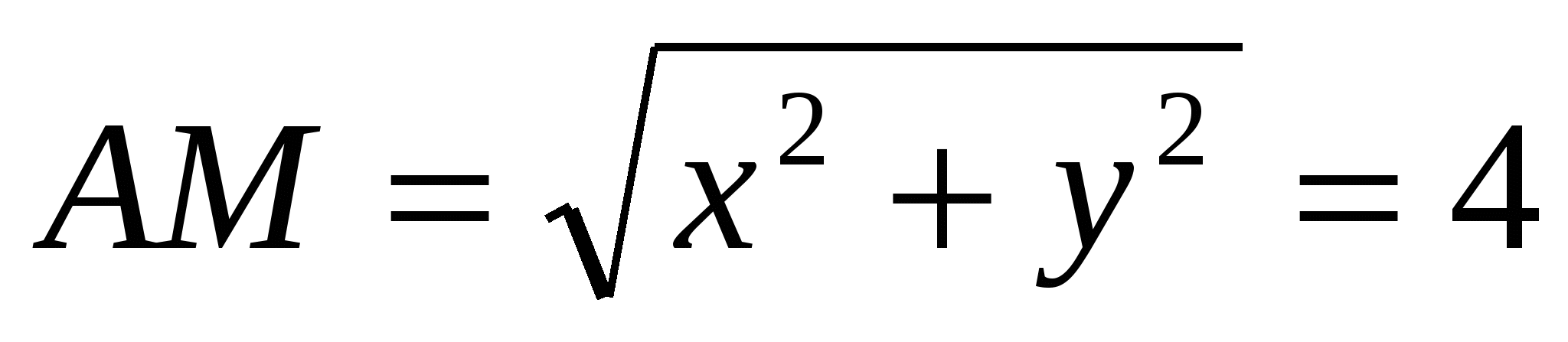 ,
,  . , i.e.
. , i.e. 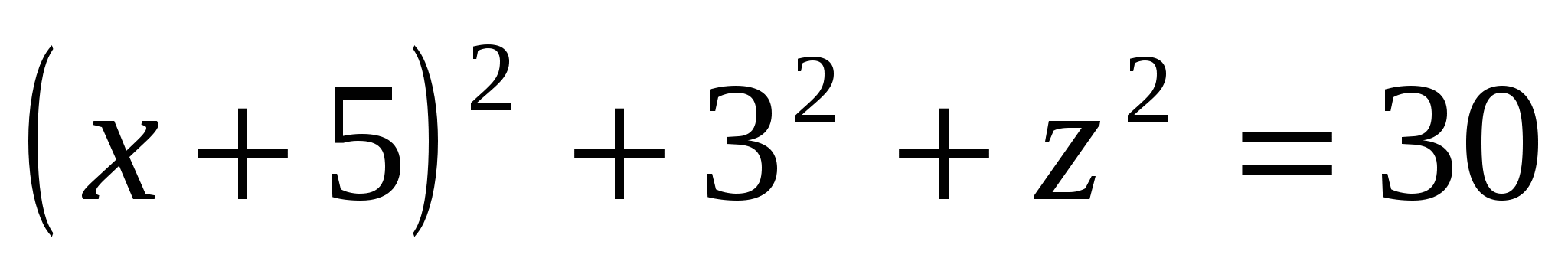 .
.
We have: 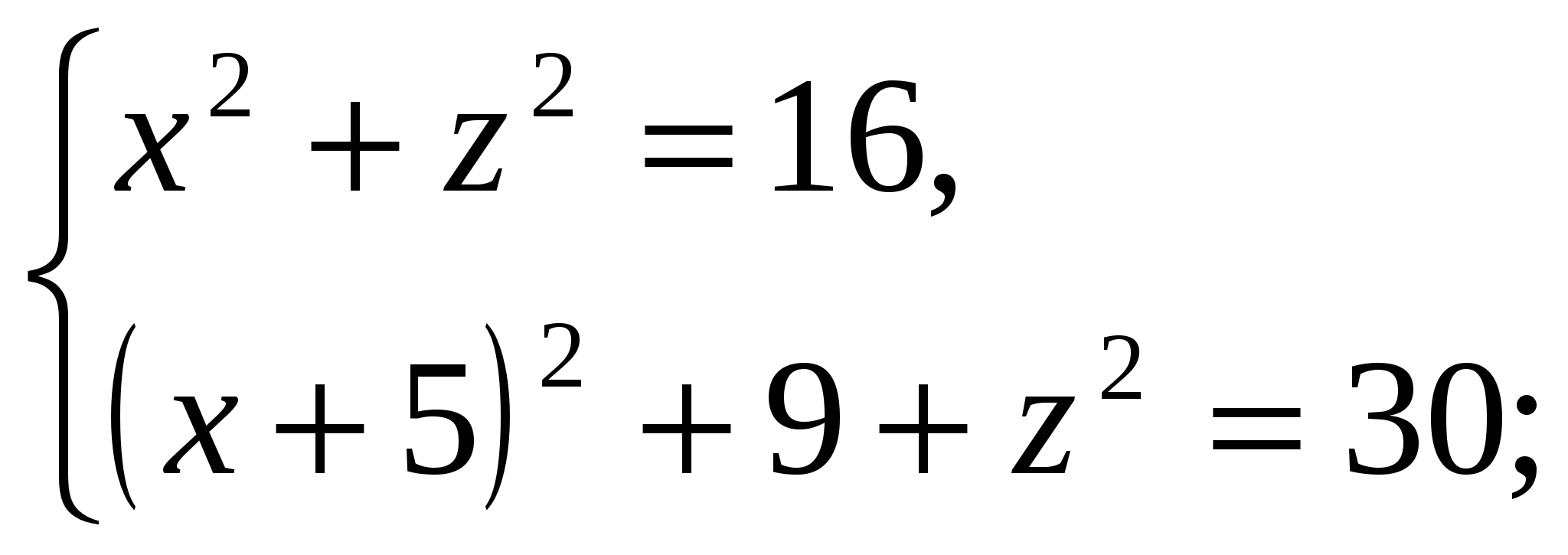
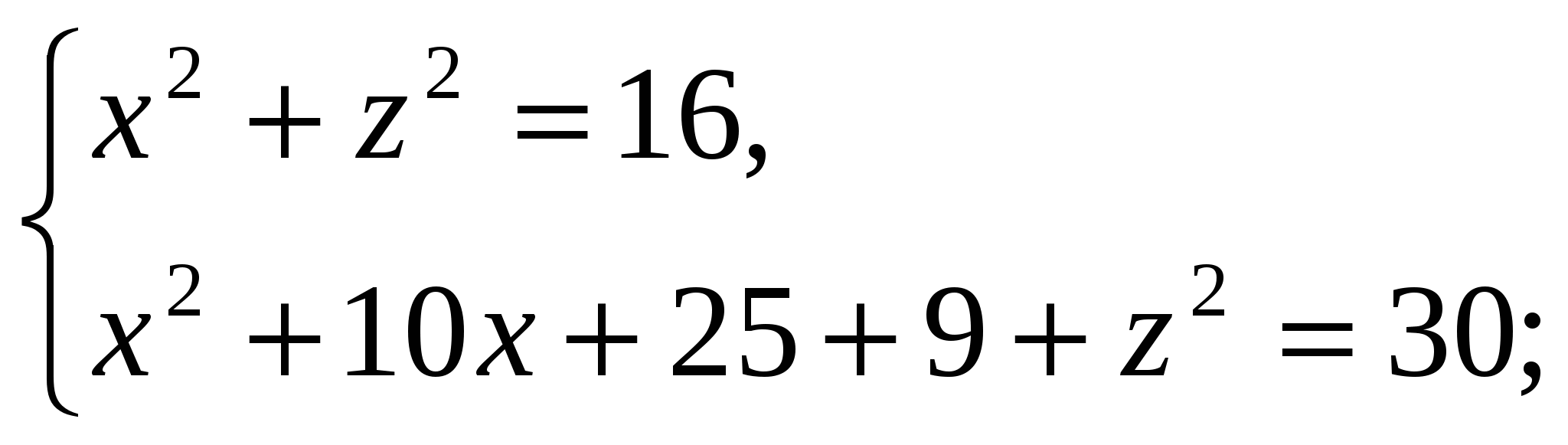
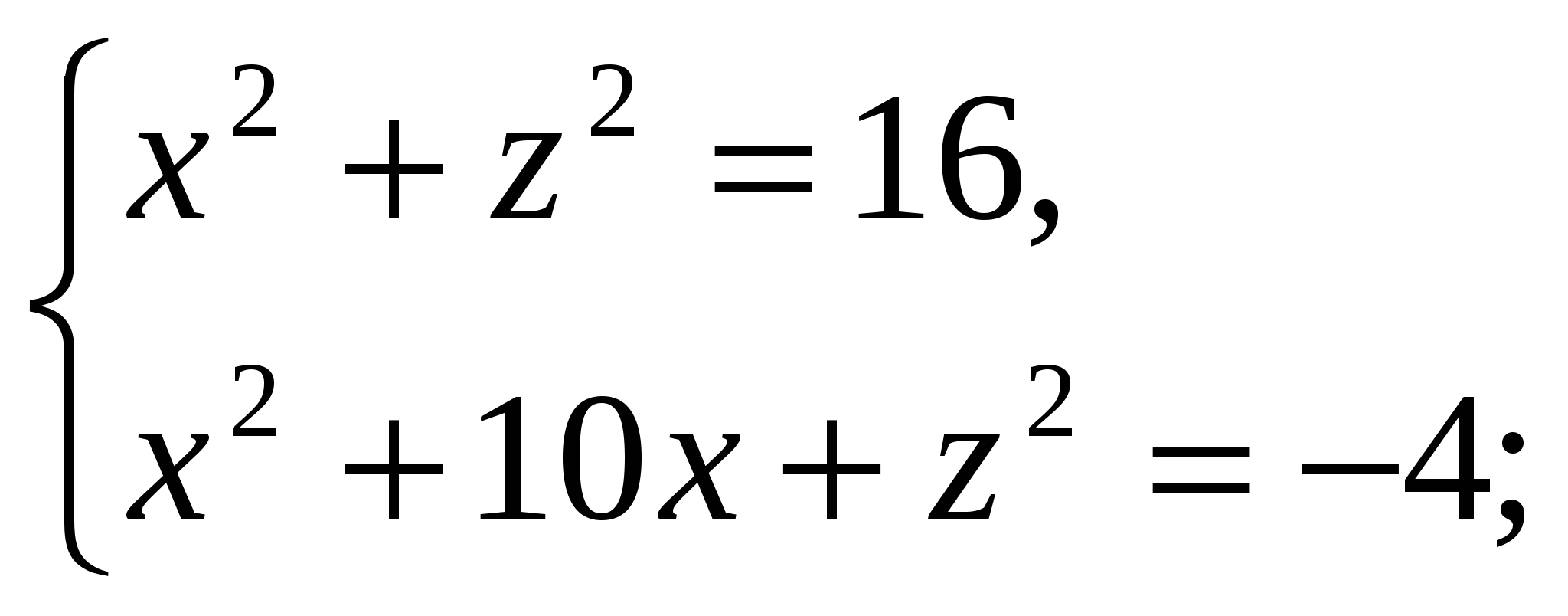
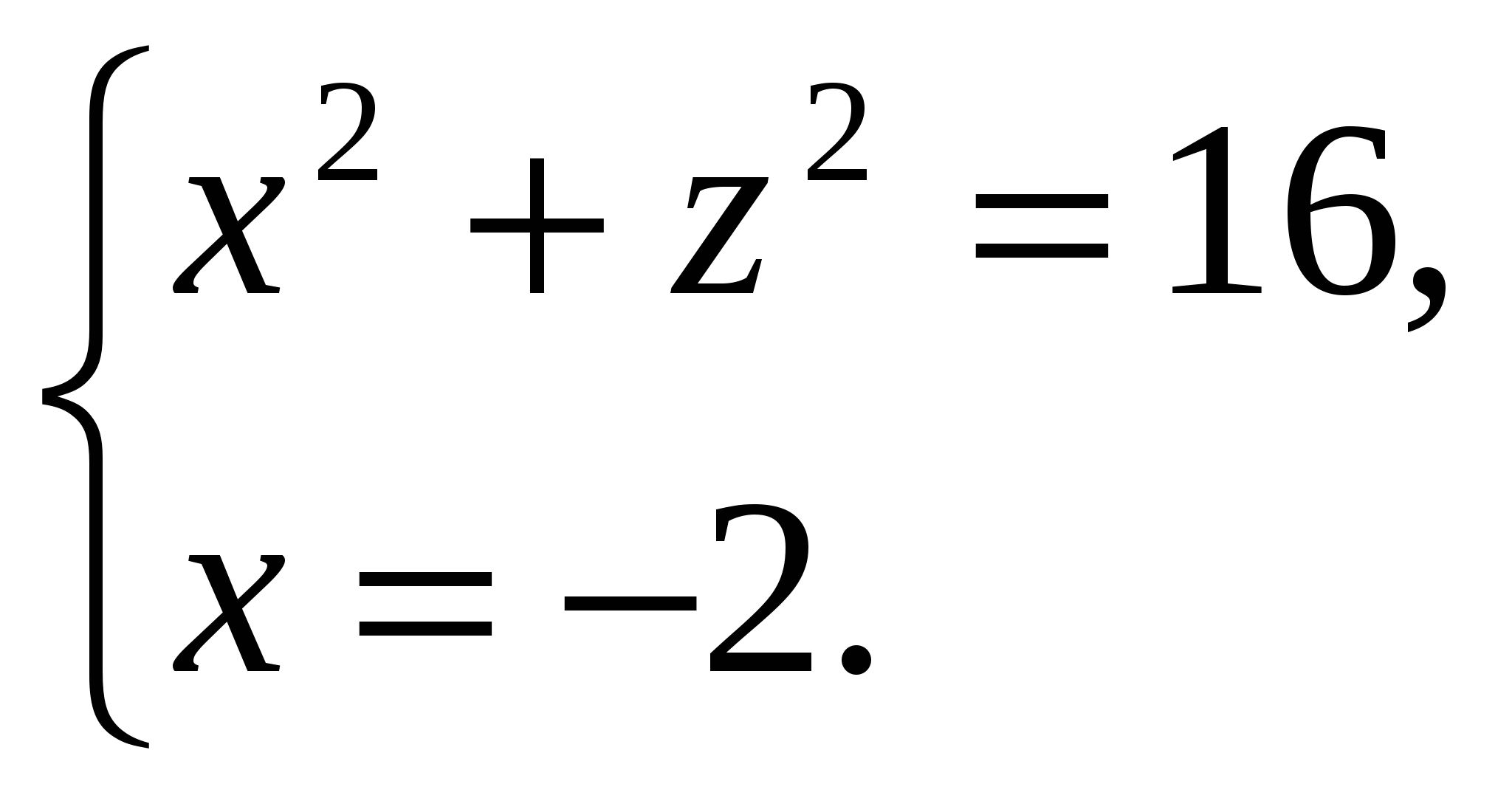
Because 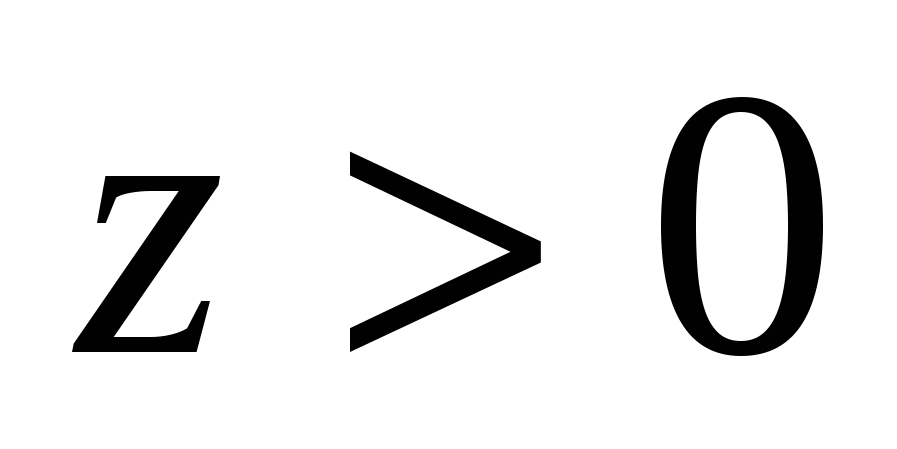 , then the height of the pyramid is equal to
, then the height of the pyramid is equal to 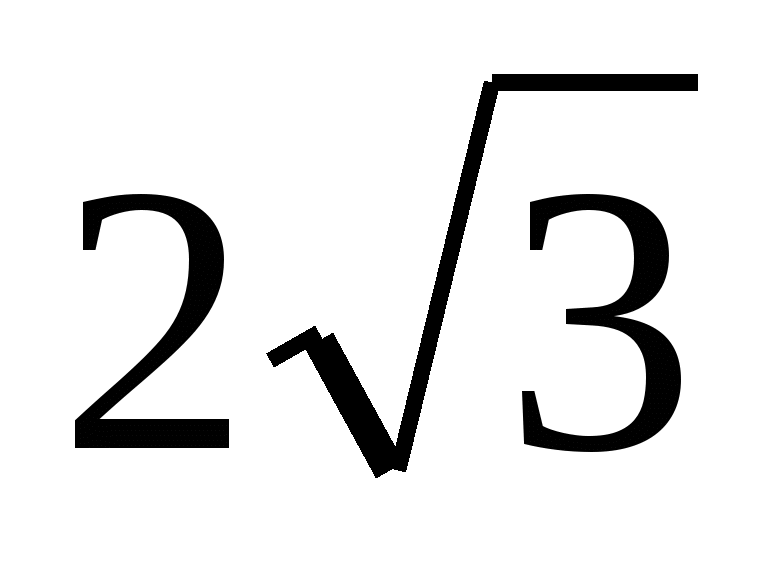 . Hence
. Hence 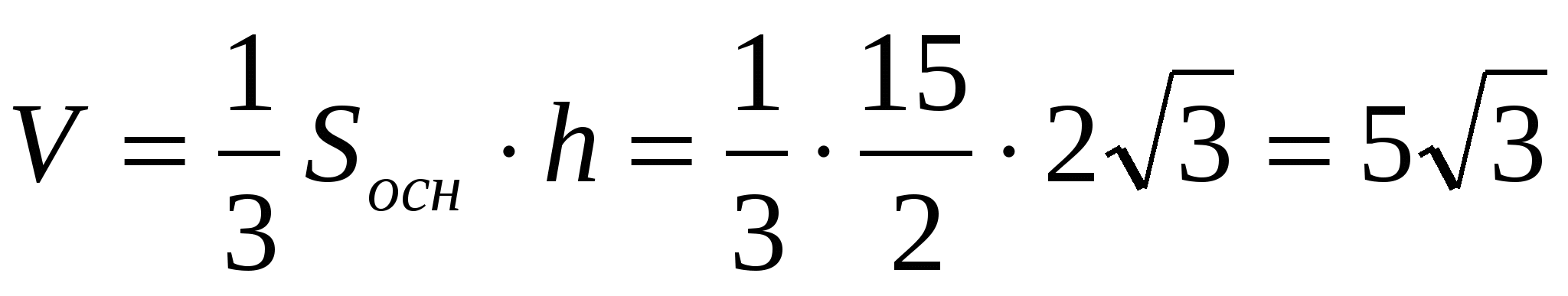 .
.
Answer: 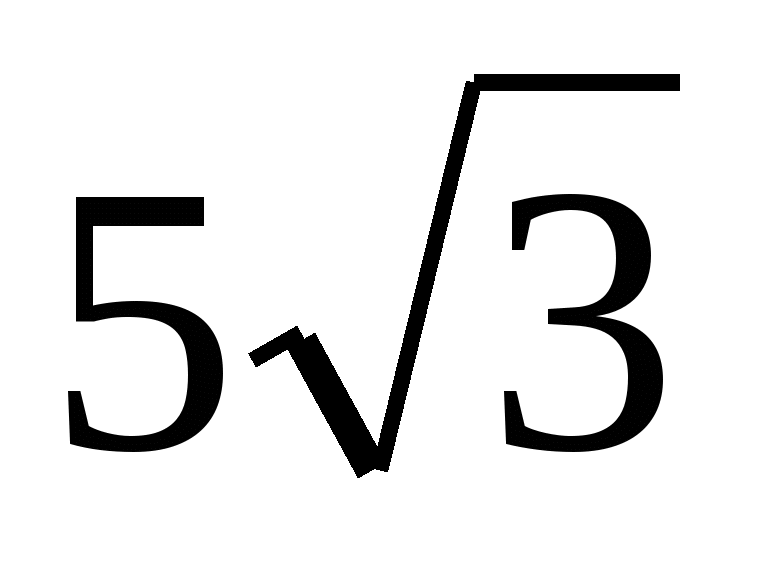 .
.
Problem.2.
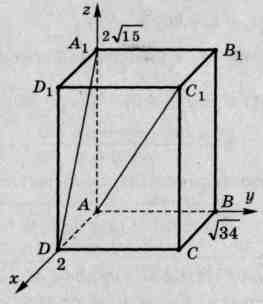
In a rectangular parallelepiped 
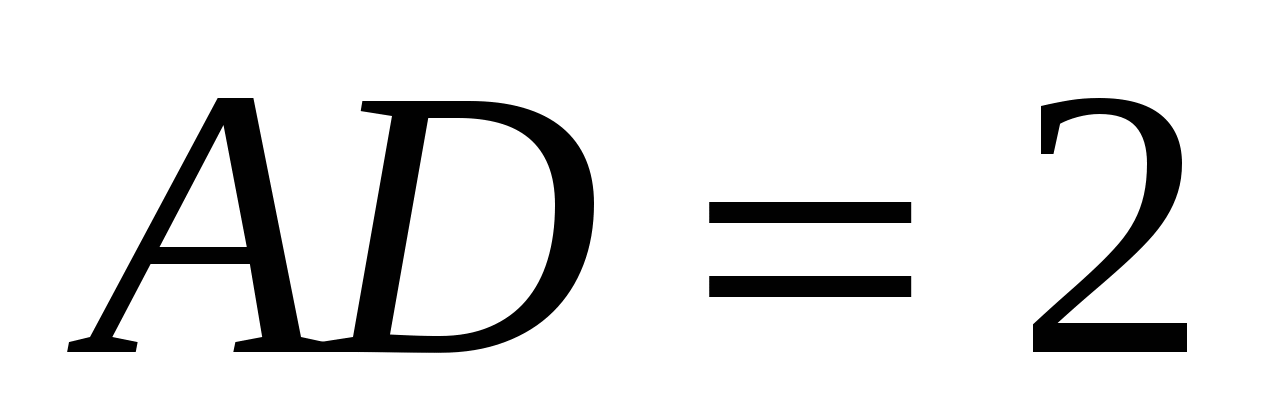 ,
, 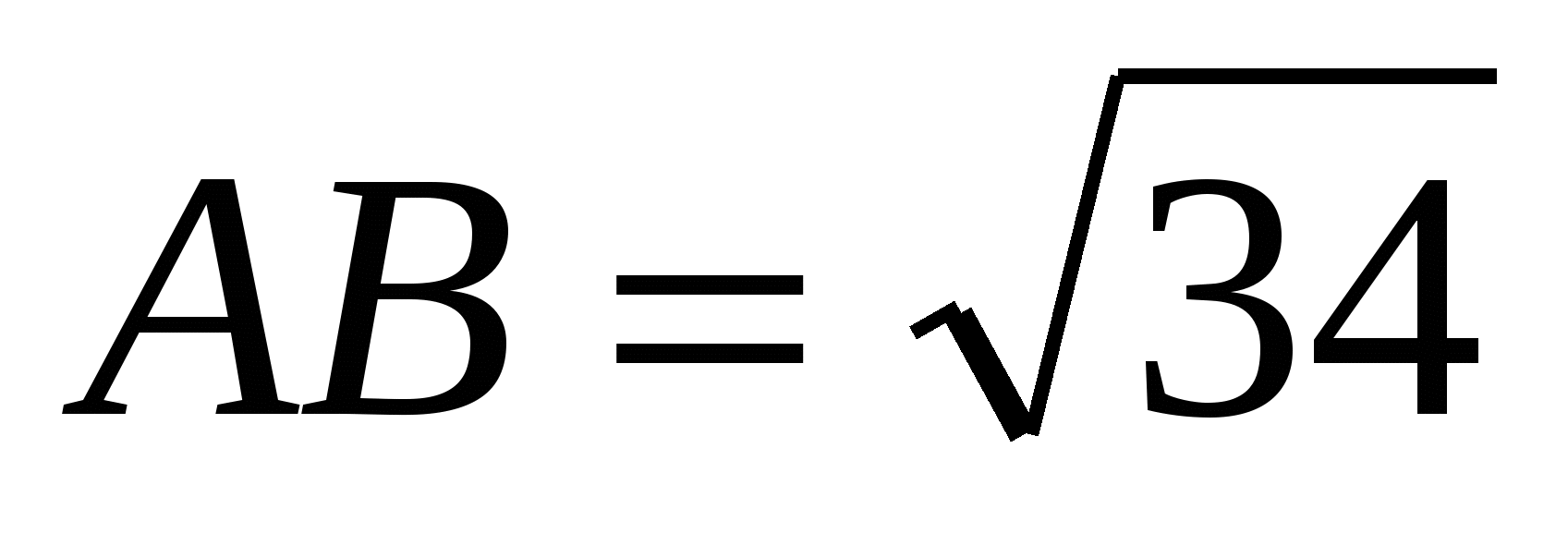 ,
,  . Find:
angle between straight lines
. Find:
angle between straight lines  And
And  .
.
 Solution.
Solution.
1). Let's introduce a coordinate system with the origin at the point 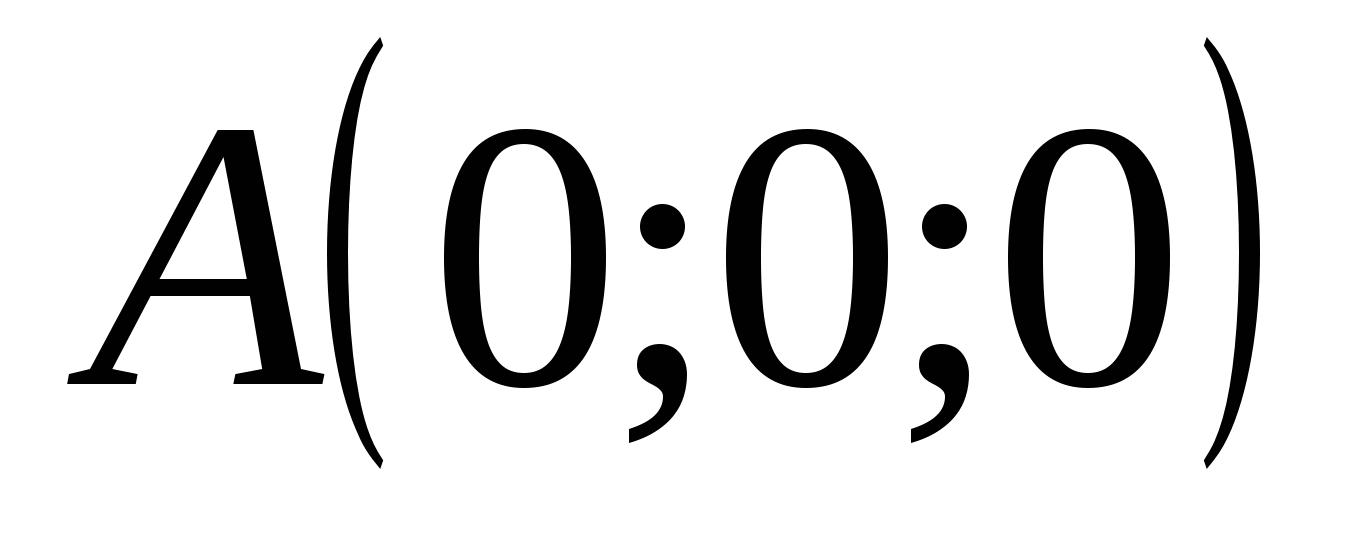 . Axles
. Axles  ,
,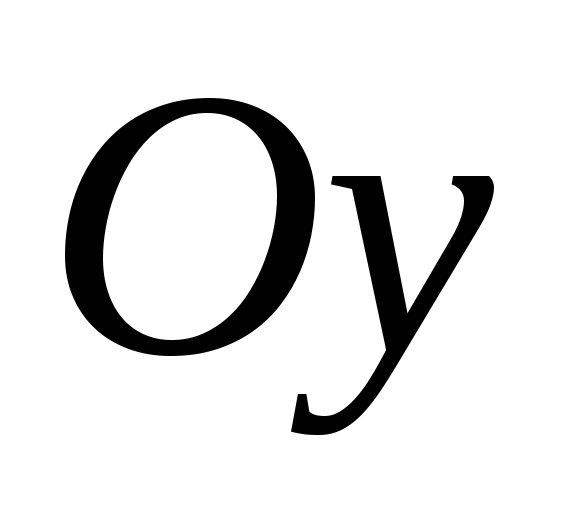 And
And  let's direct along the ribs
let's direct along the ribs  ,
, 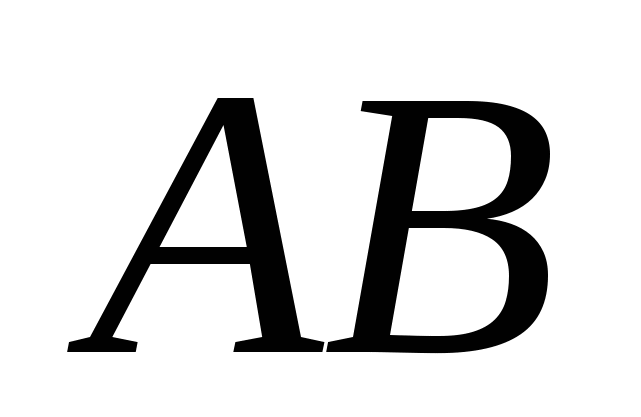 And
And 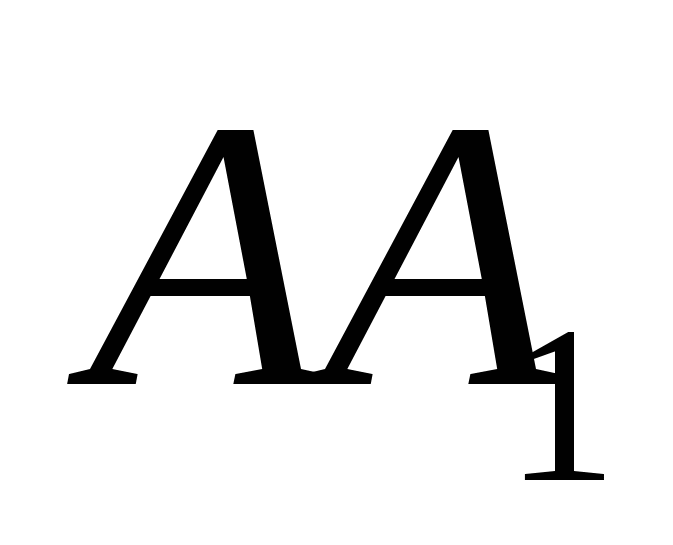 respectively. Since the angle between straight lines varies from
respectively. Since the angle between straight lines varies from 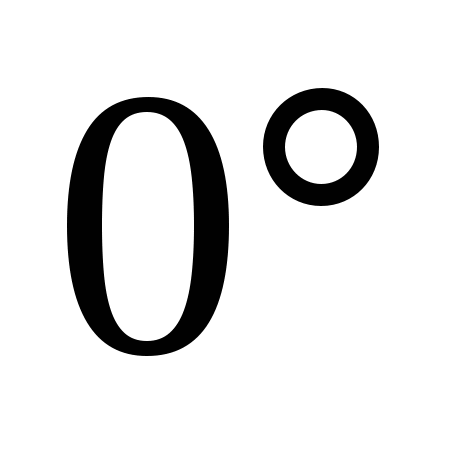 before
before  , and the angle between the vectors from
, and the angle between the vectors from 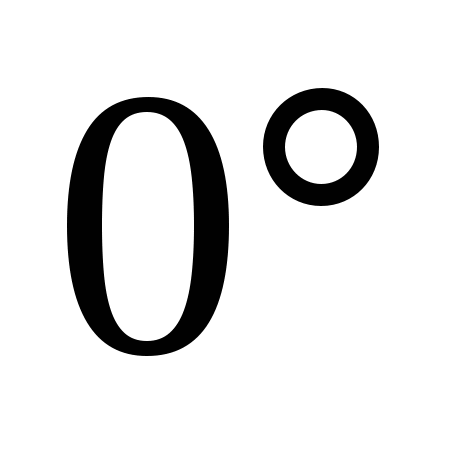 before
before 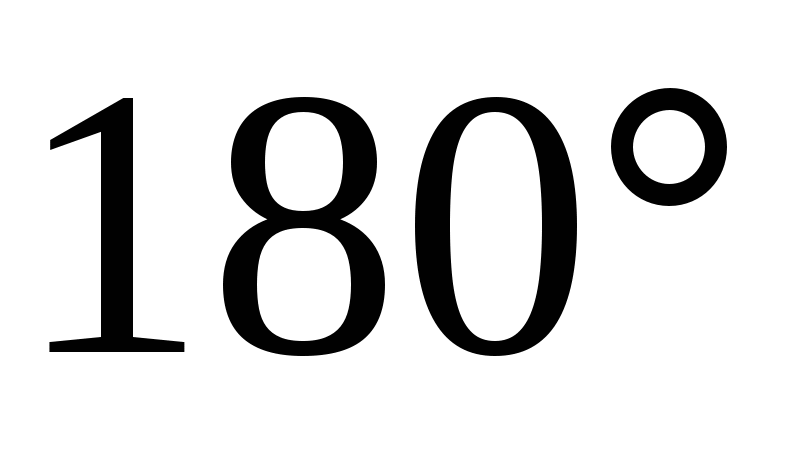 , then the angle between the lines
, then the angle between the lines  And
And  equal to the angle between the vectors
equal to the angle between the vectors 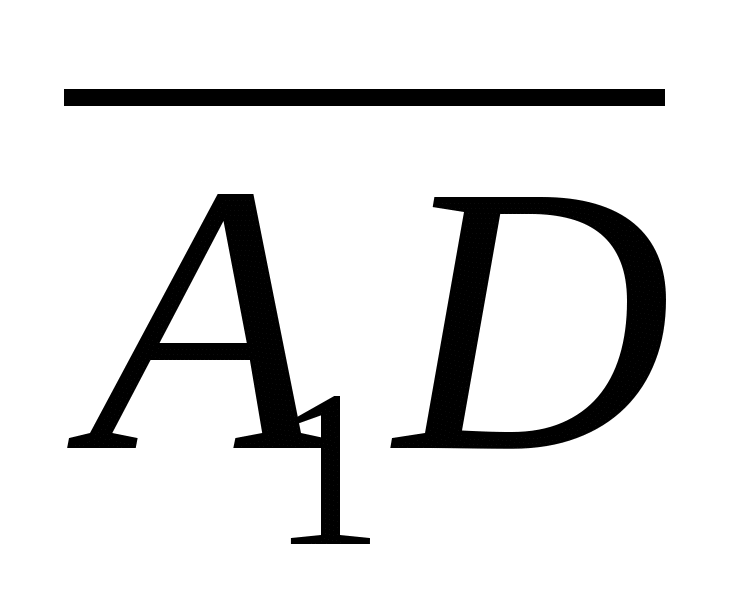 And
And 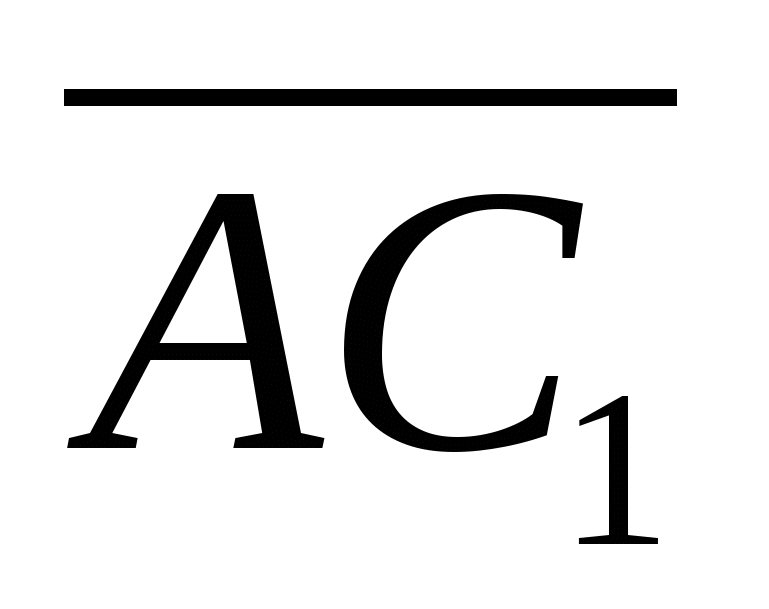 , if it is acute, or adjacent to it, if the angle between the vectors is obtuse.
, if it is acute, or adjacent to it, if the angle between the vectors is obtuse.
Thus,
2).Calculate the angle between the vectors 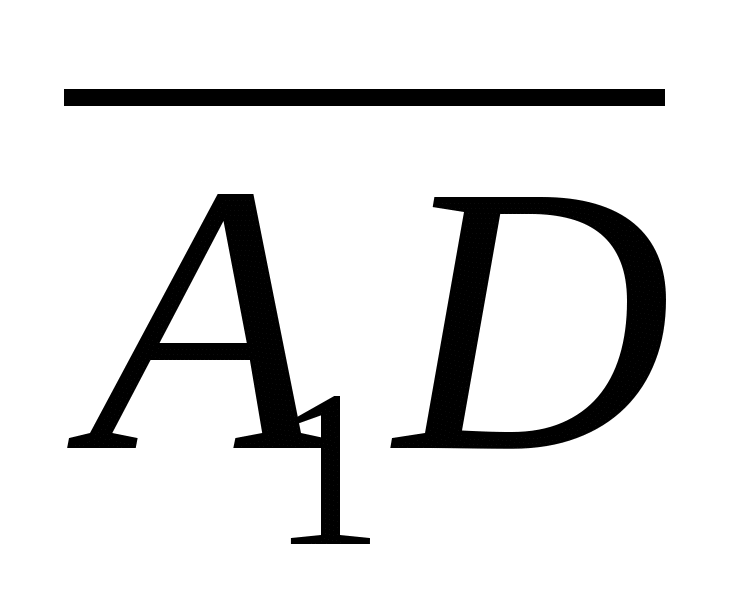 And
And 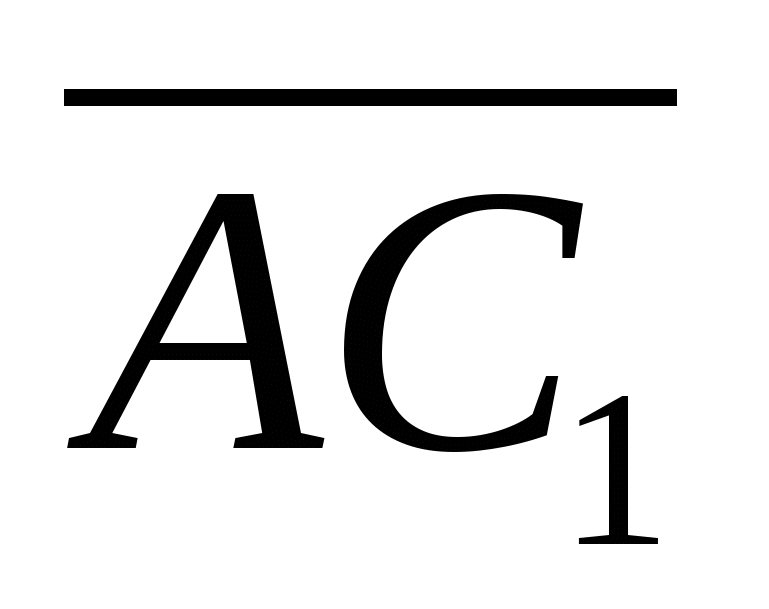 .
.
Find the coordinates of the vectors using the coordinates of the points  And
And  :
:
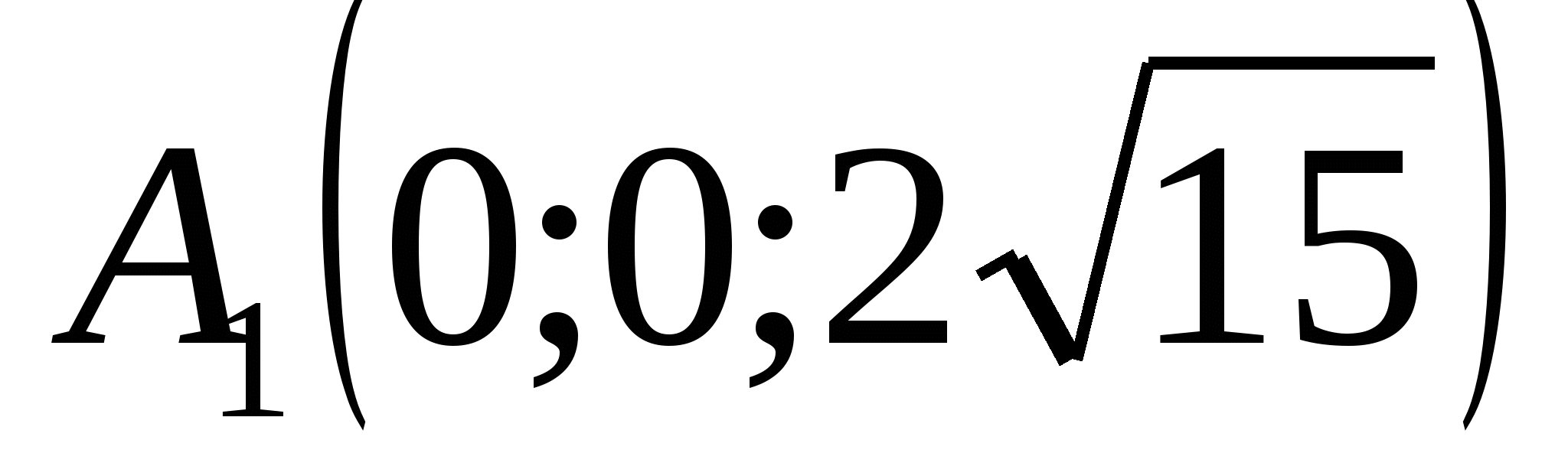 ,
, 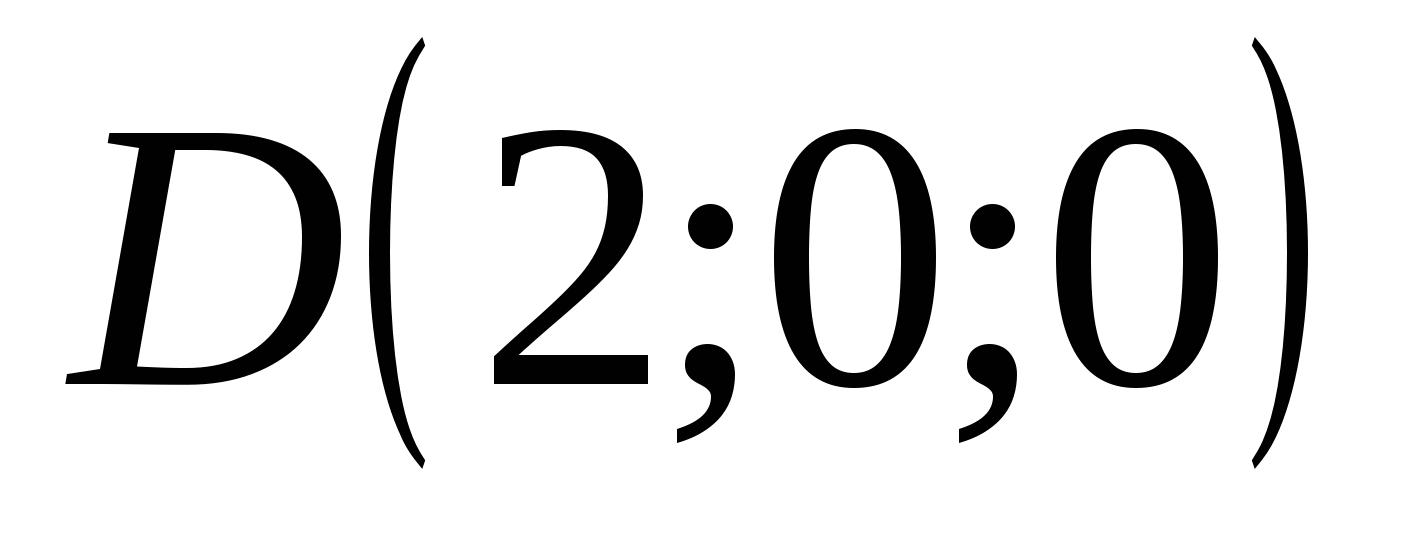 ,
,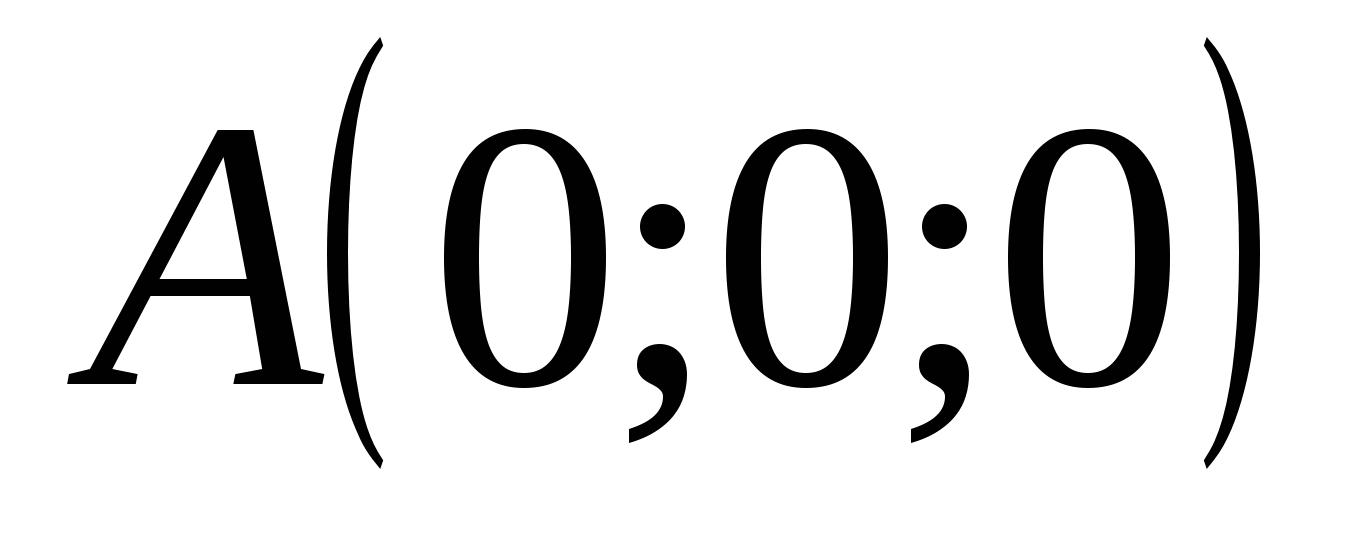 ,
,  .
.
Then the coordinates of the vectors 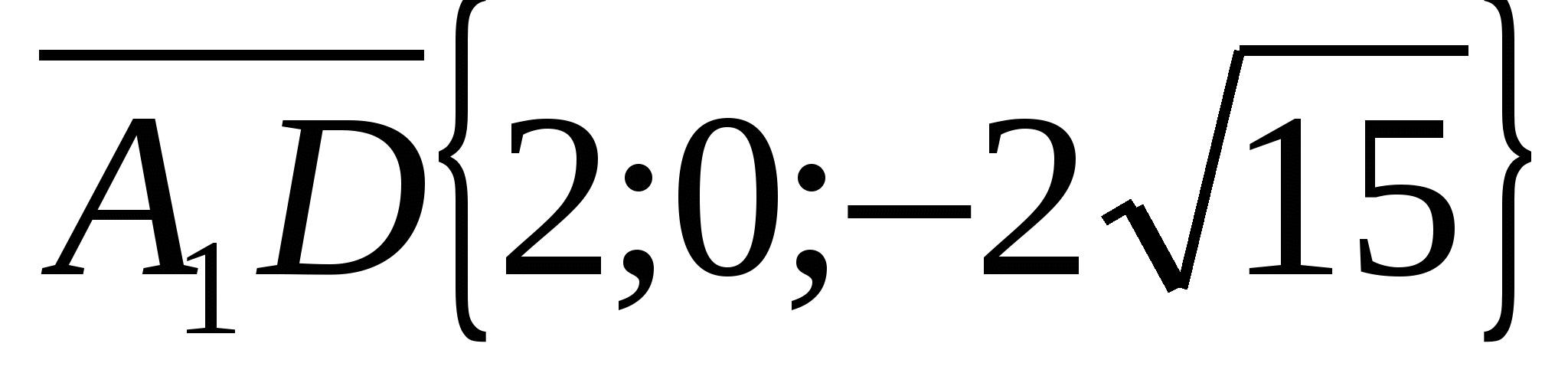 And
And 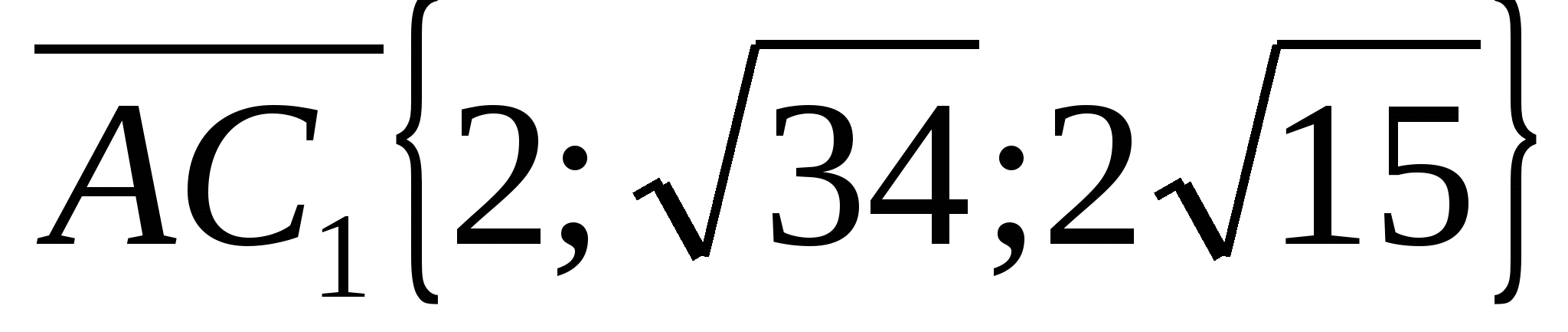 .
.
=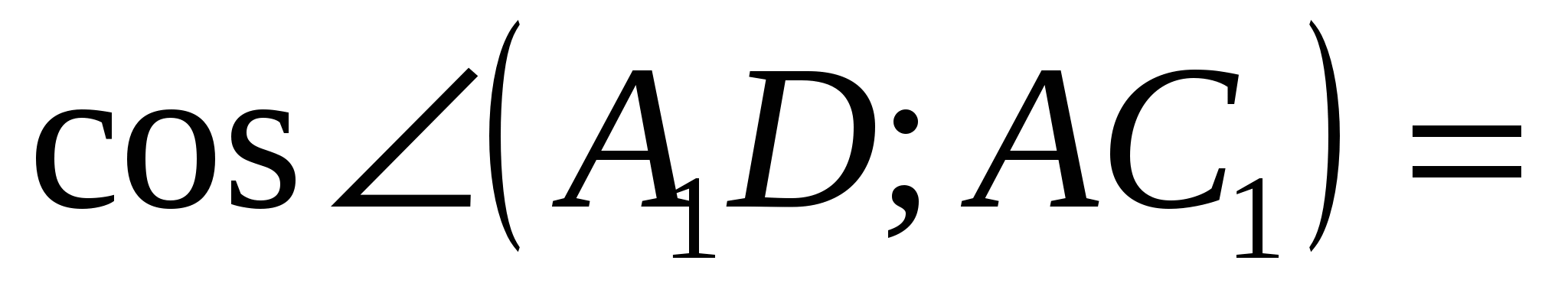
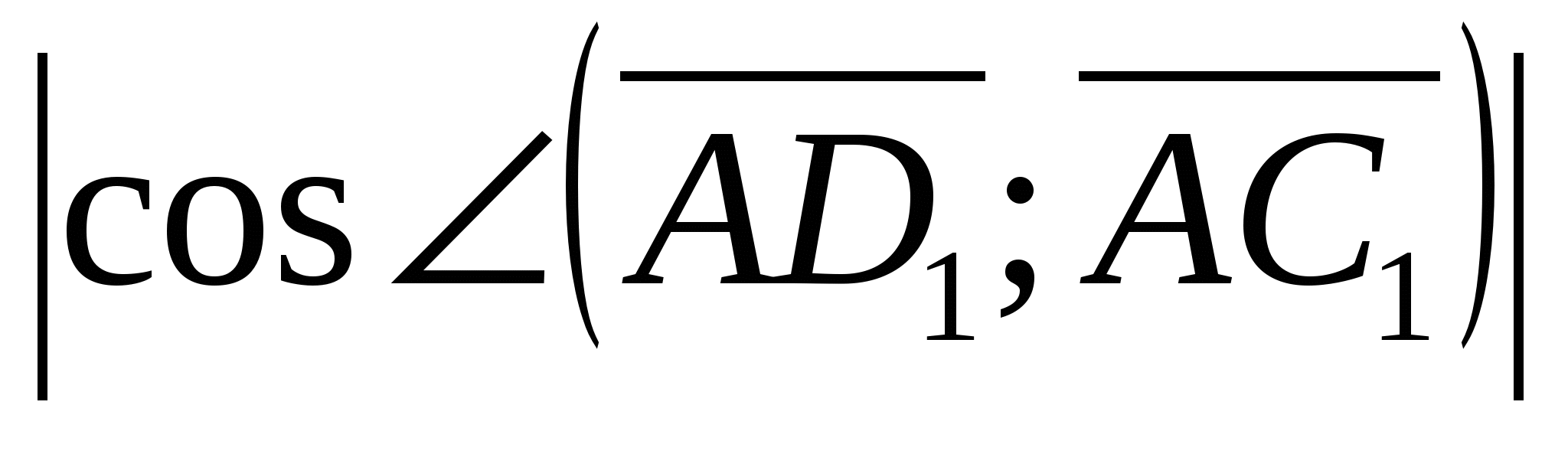 =
= =
=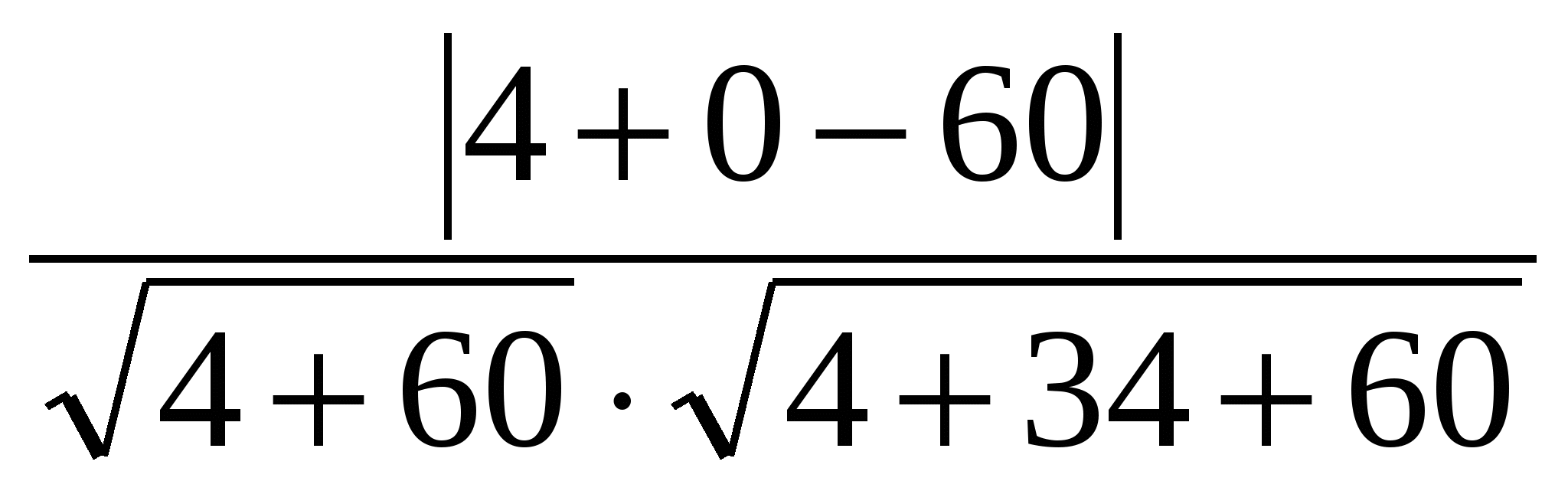
=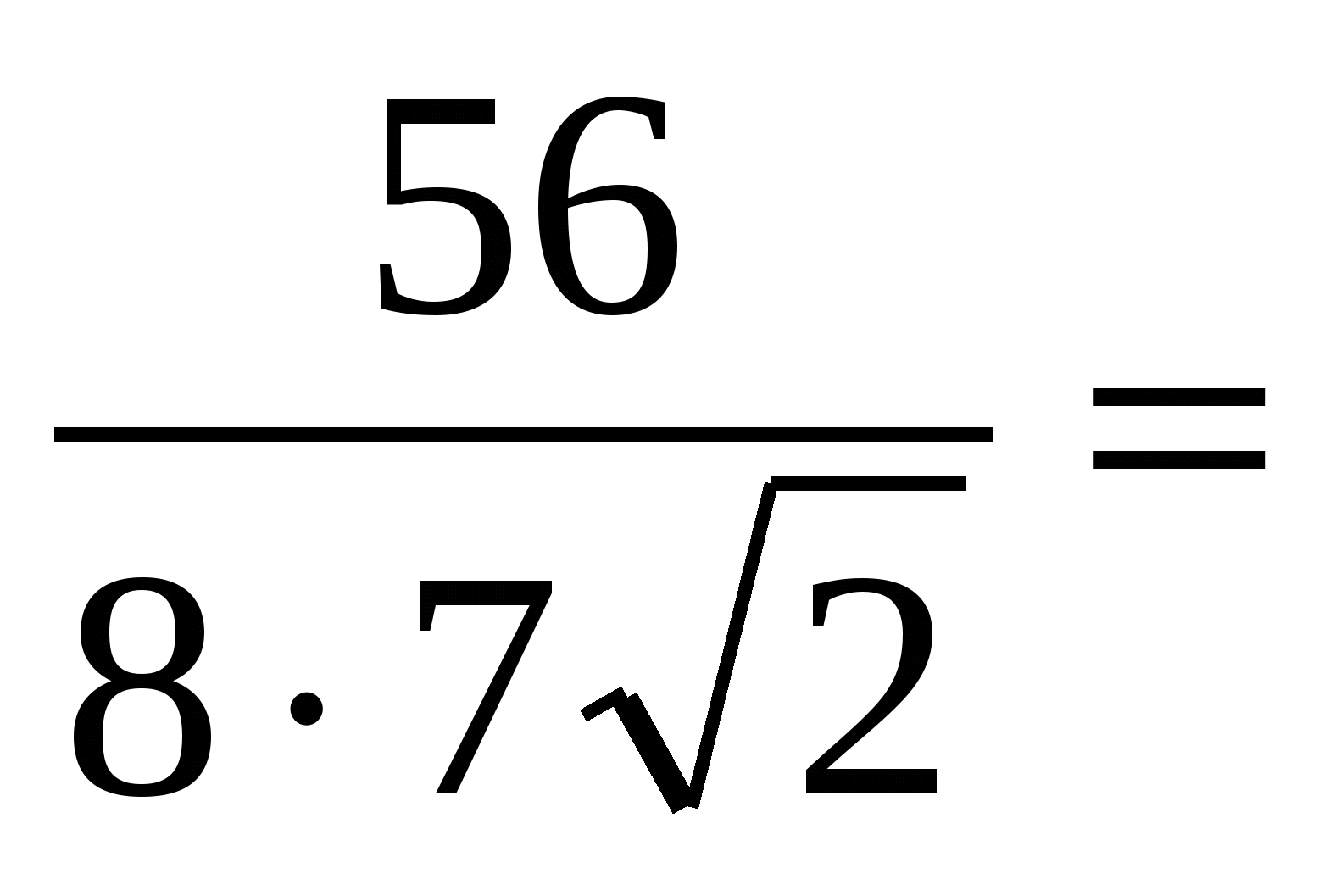
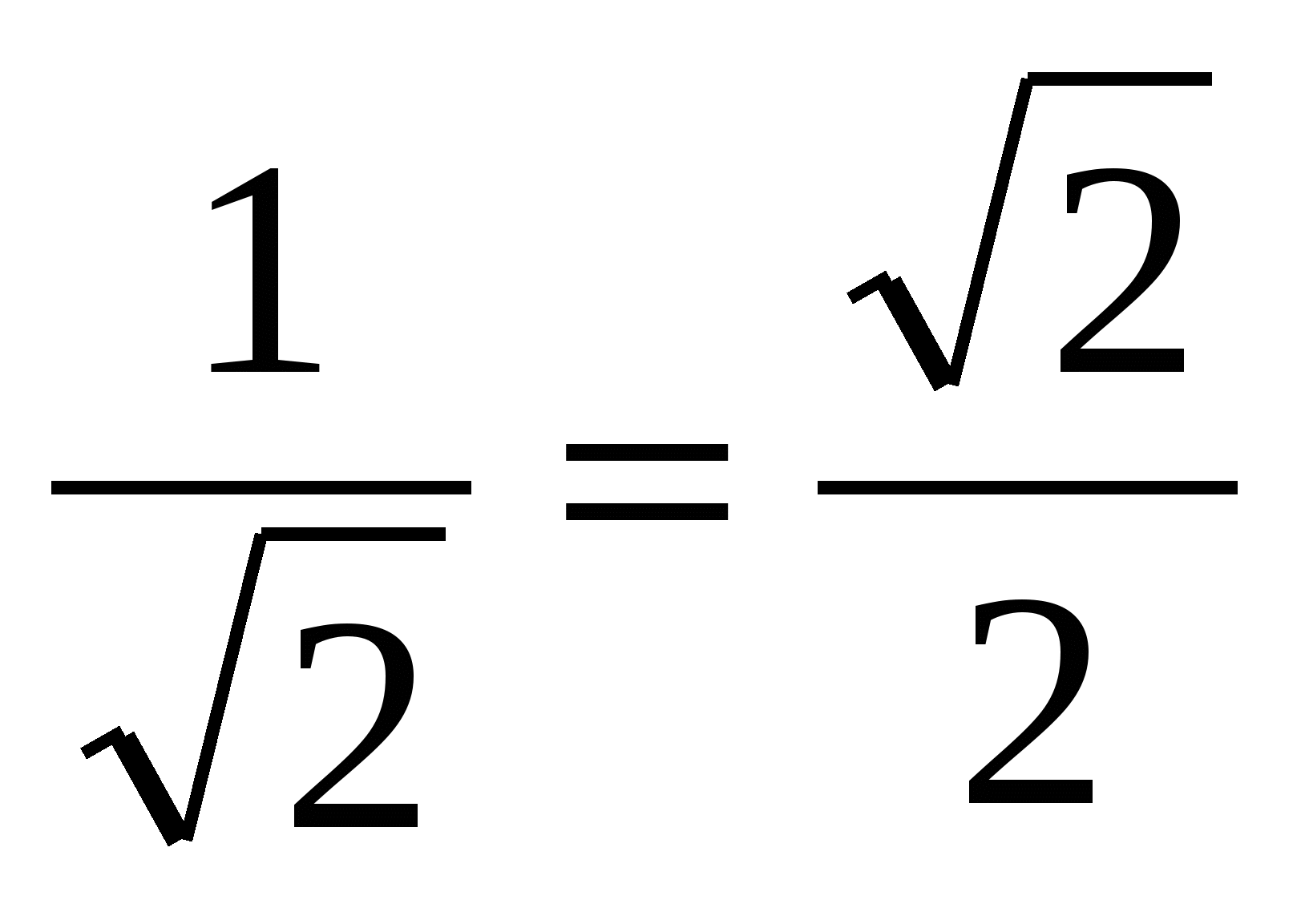 .
.
Hence, 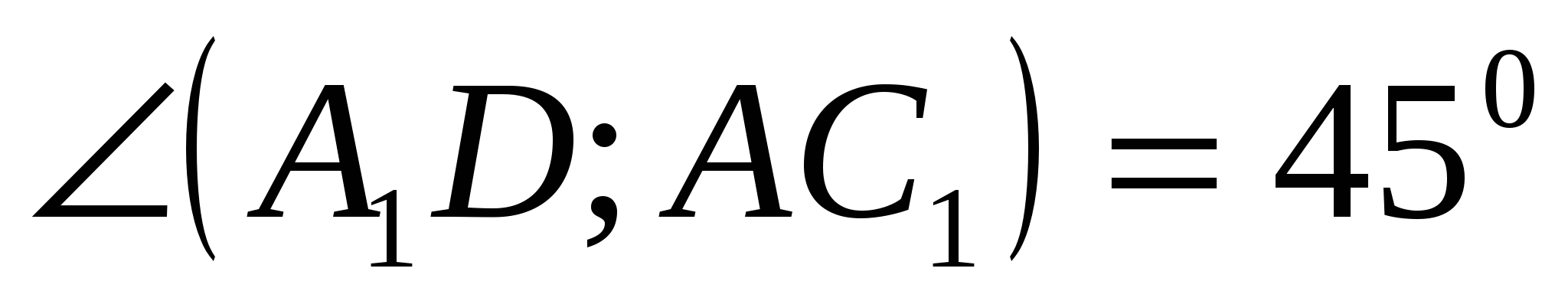
Answer:
 .
.
Task 3.
Dan cuboid  . Find the angle between a straight line
. Find the angle between a straight line 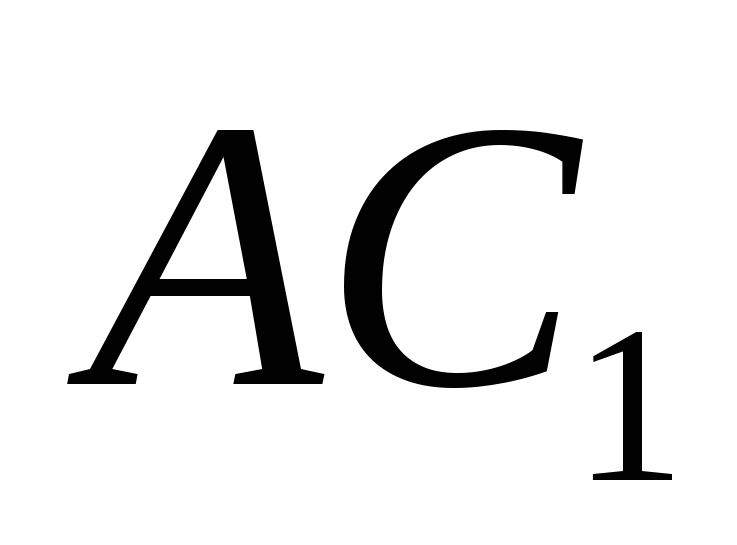 and the plane of the base
and the plane of the base 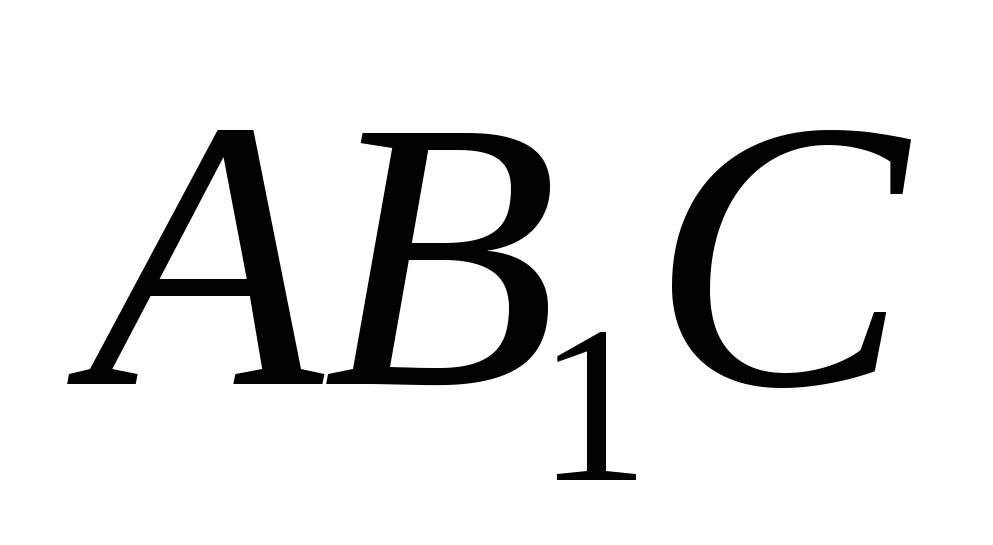 .
.
Solution.
1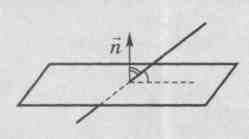 ) Angle between straight line
) Angle between straight line 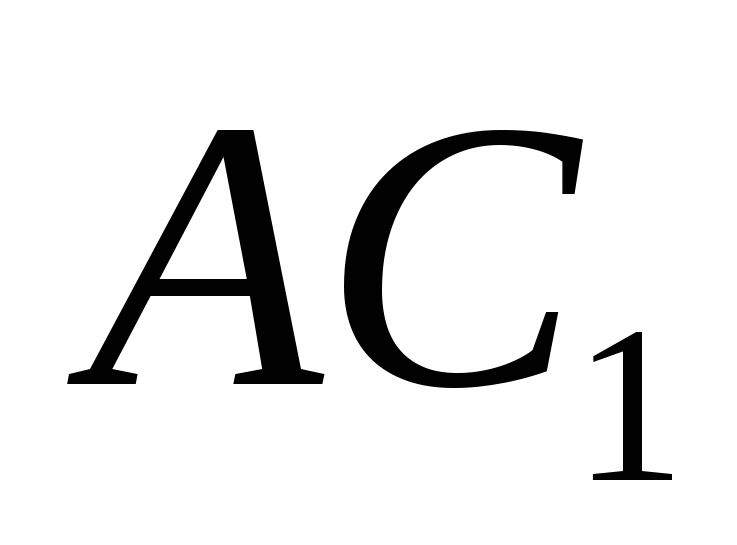 and planeAB
1
WITH- This
the angle between a straight line and its projection onto a plane. Angle between normal
and planeAB
1
WITH- This
the angle between a straight line and its projection onto a plane. Angle between normal 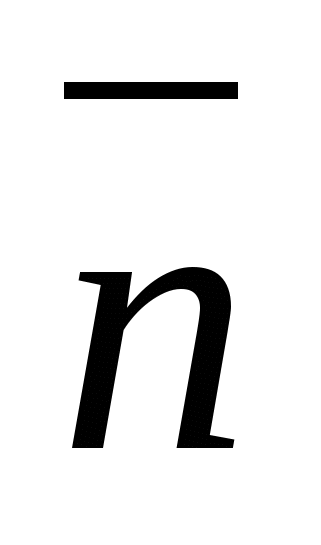 to a plane and a straight line
to a plane and a straight line 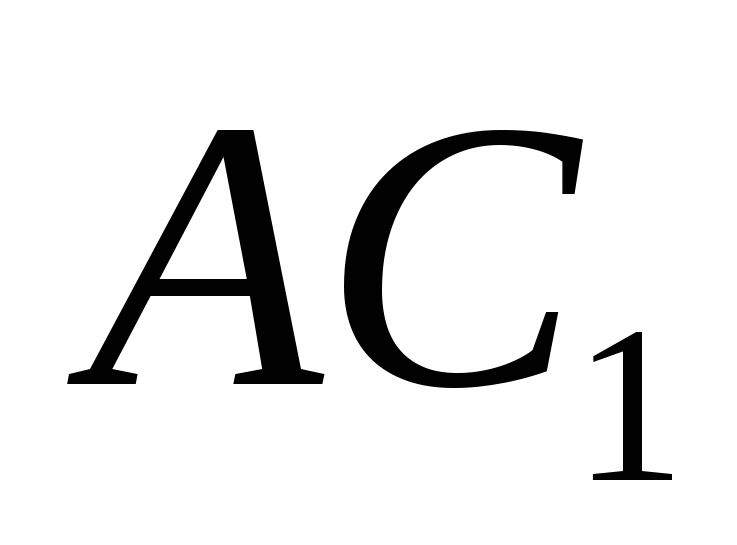 complements it to 90 0, therefore.
complements it to 90 0, therefore.
So, in order to find the angle between a straight line 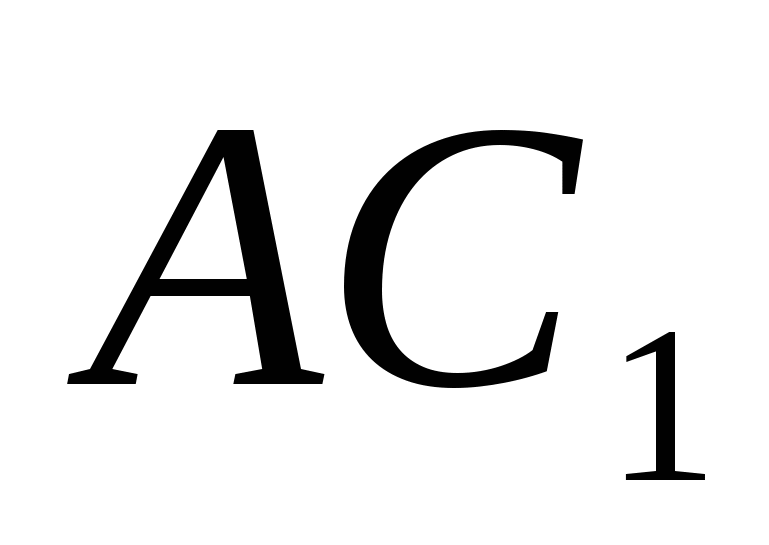 and plane (
and plane (  ), you should find the angle between the straight line
), you should find the angle between the straight line 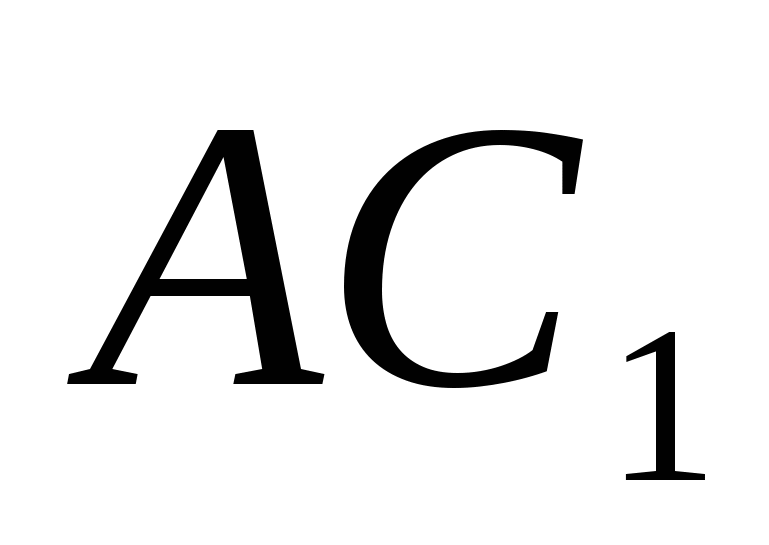 and normal
and normal 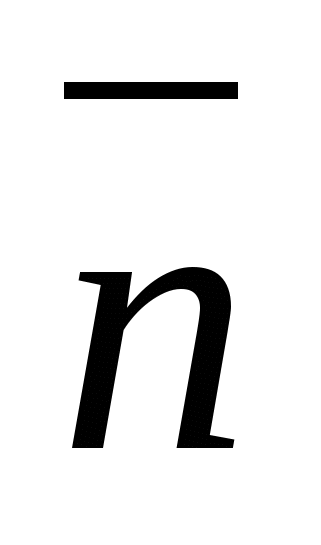 to the plane (
to the plane ( 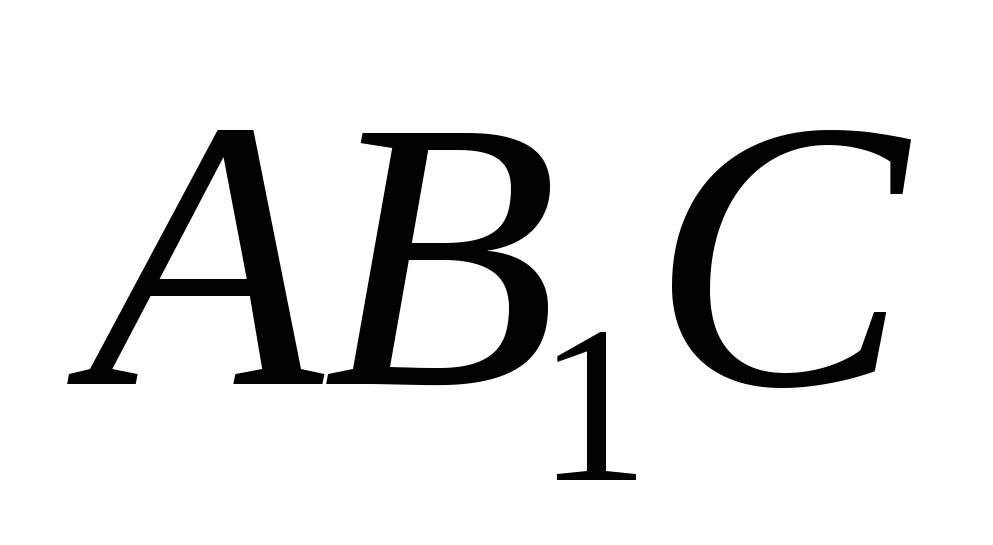 )
.
)
.
2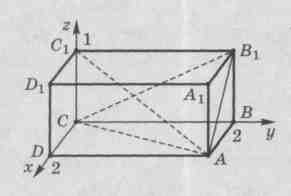 ) Let us introduce a coordinate system with the origin at the point
) Let us introduce a coordinate system with the origin at the point 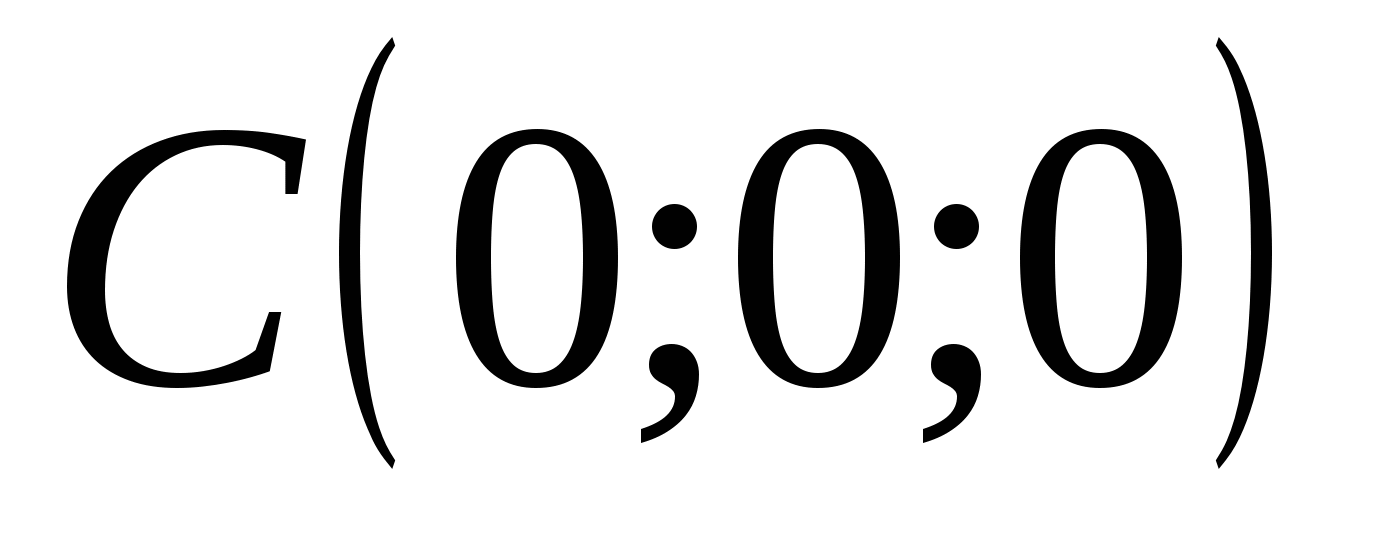 . Axles
. Axles 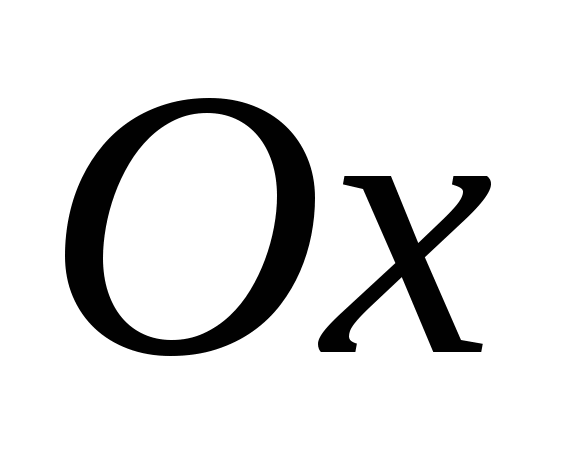 ,
,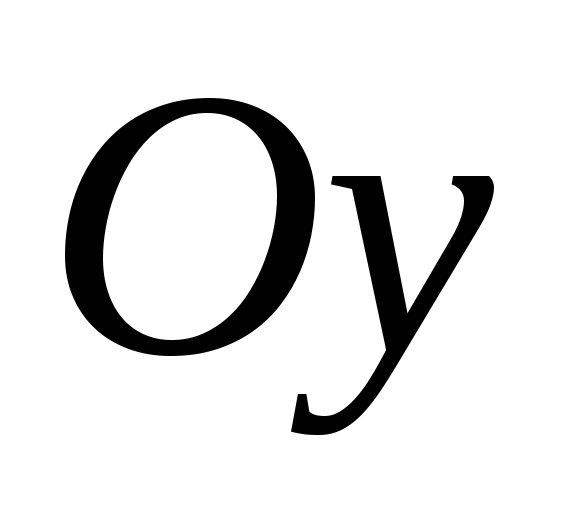 And
And  let's direct along the ribs
let's direct along the ribs  ,
, 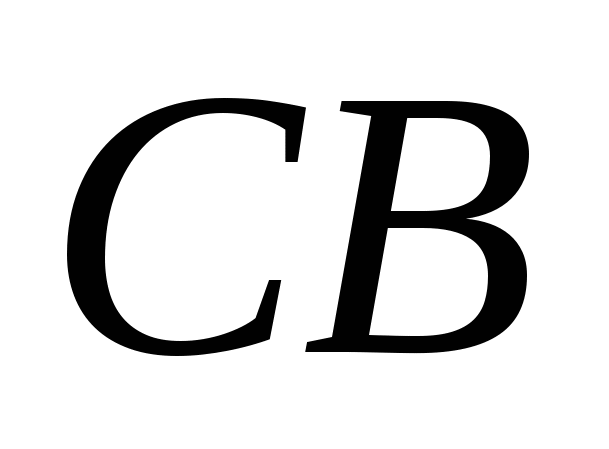 And
And 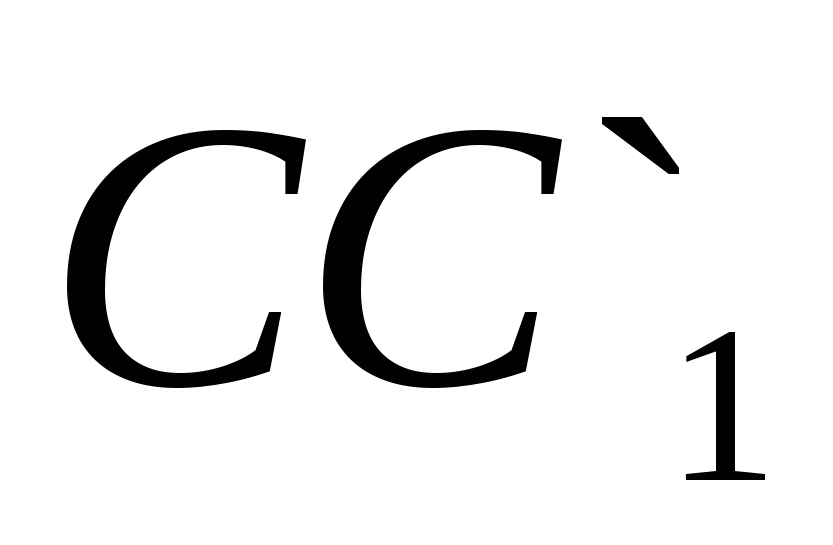 respectively.
respectively.
Point coordinates:
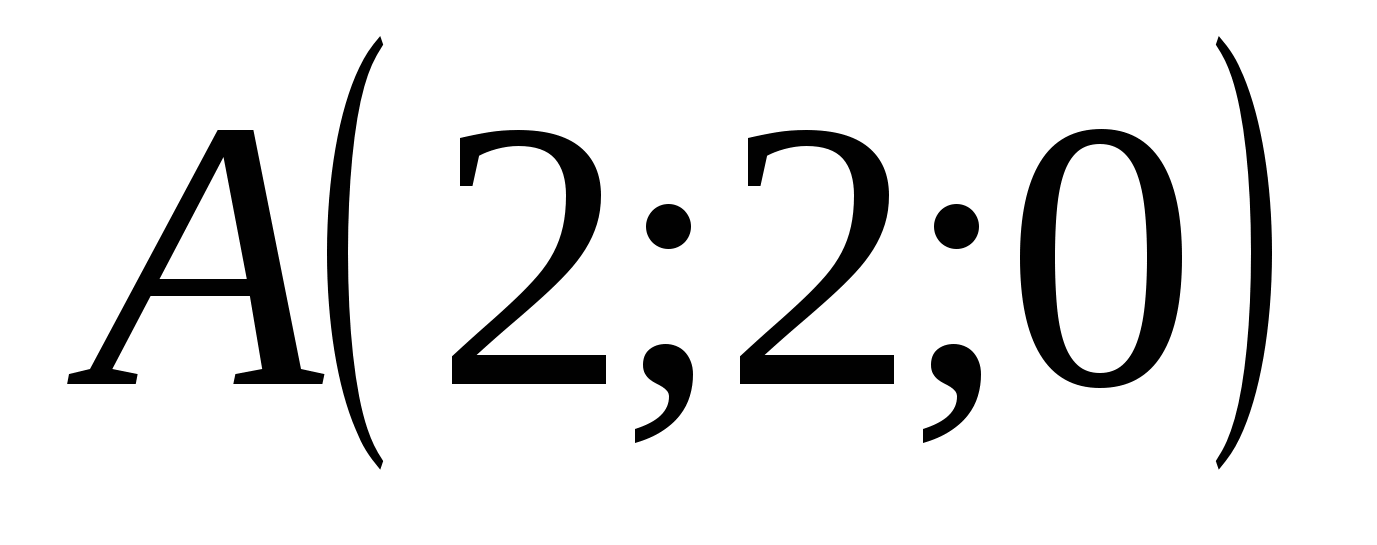 ,
, 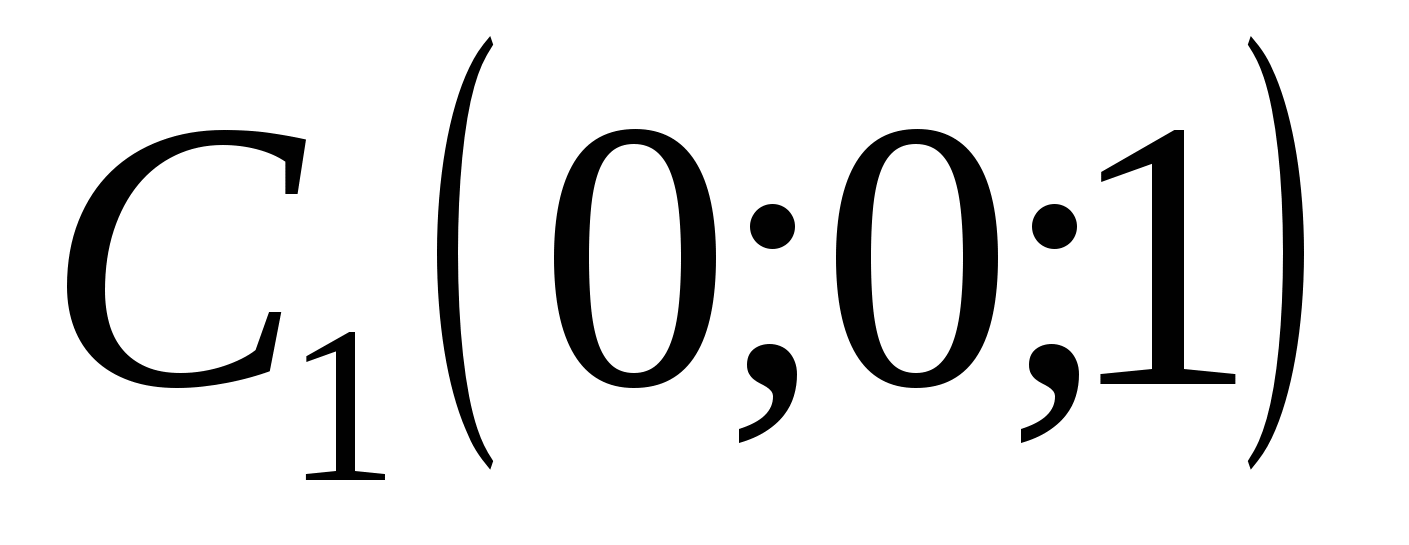 ,
, 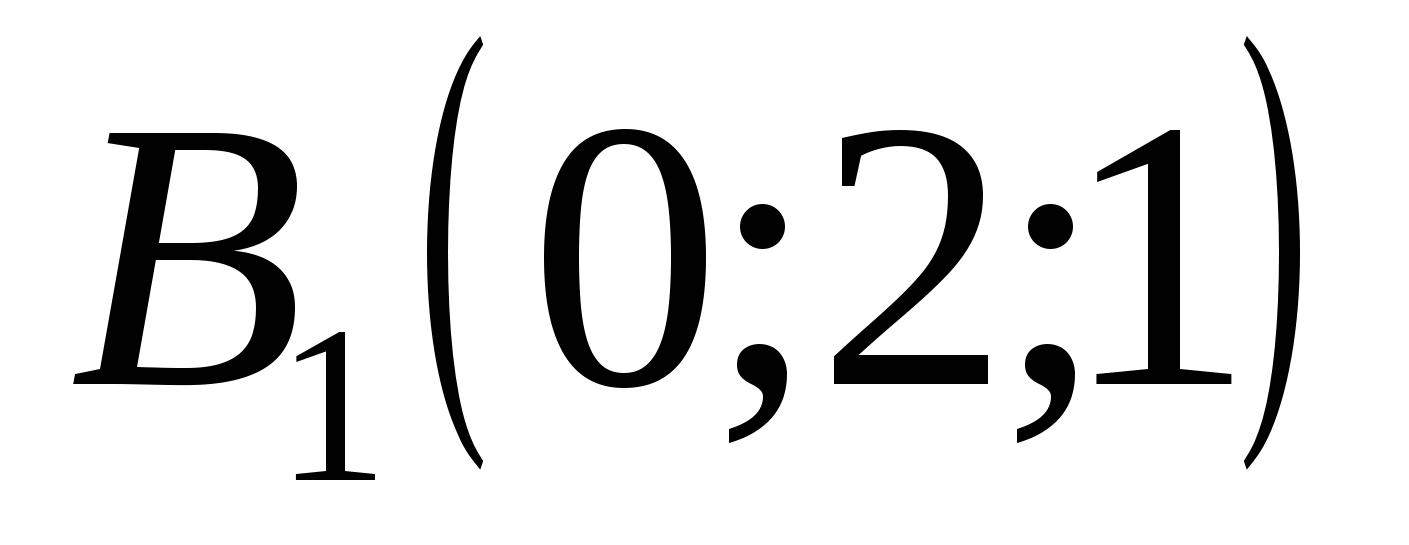 ,
,
A 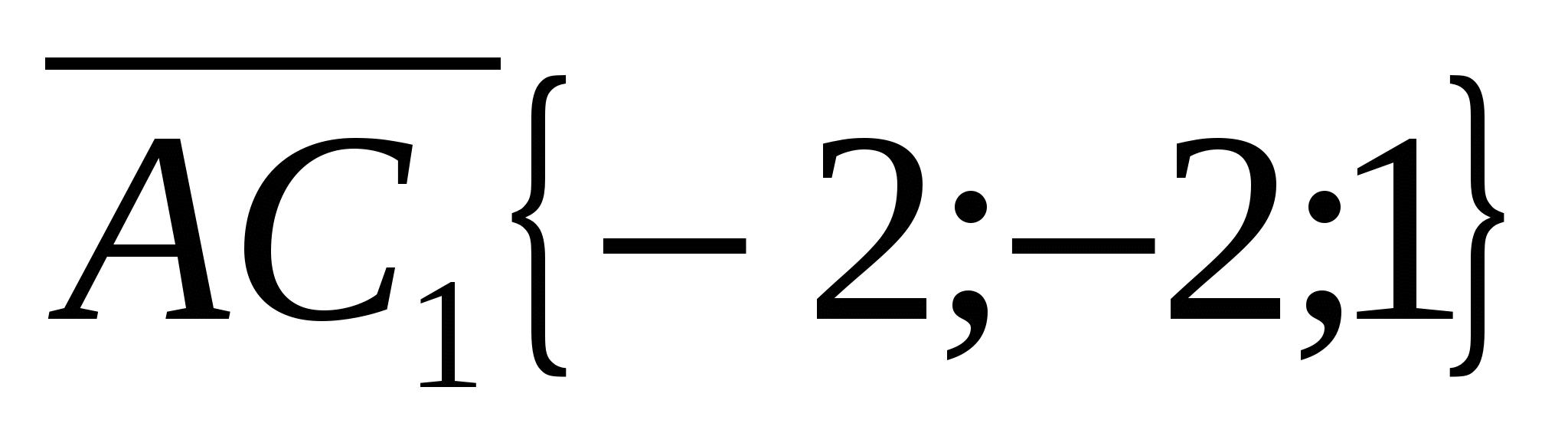 .
.
3) Find the coordinates of the normal plane ( 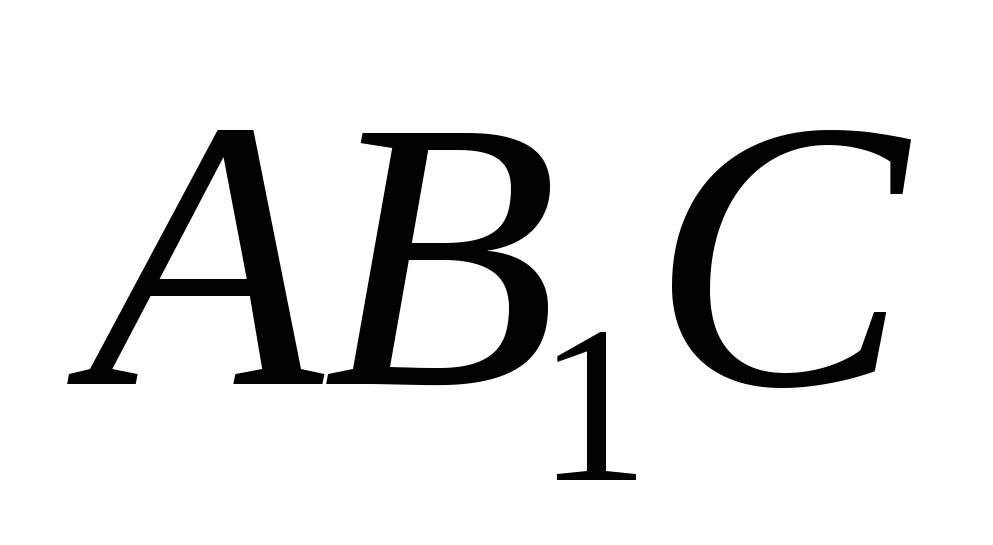 ). Let us write the equation of the plane (
). Let us write the equation of the plane ( 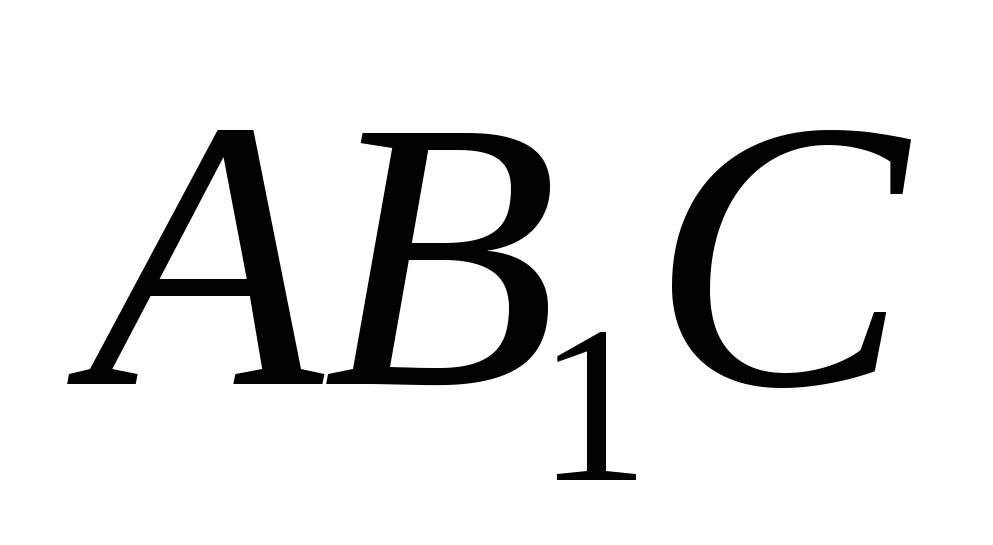 ), substituting the coordinates of the pointsA
,
B
1
And WITH V
plane equation
.
), substituting the coordinates of the pointsA
,
B
1
And WITH V
plane equation
.
We obtain a system of linear equations:
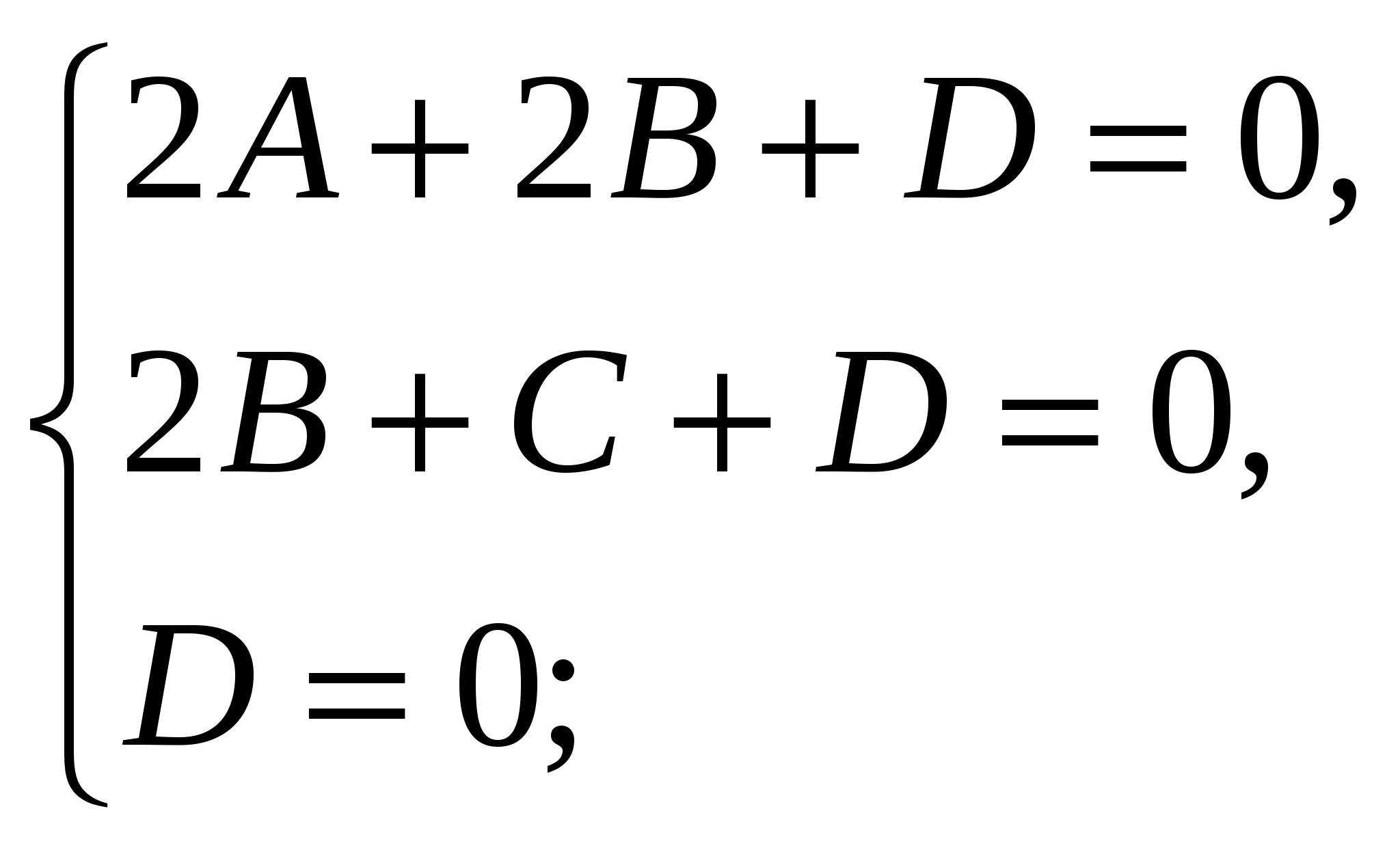
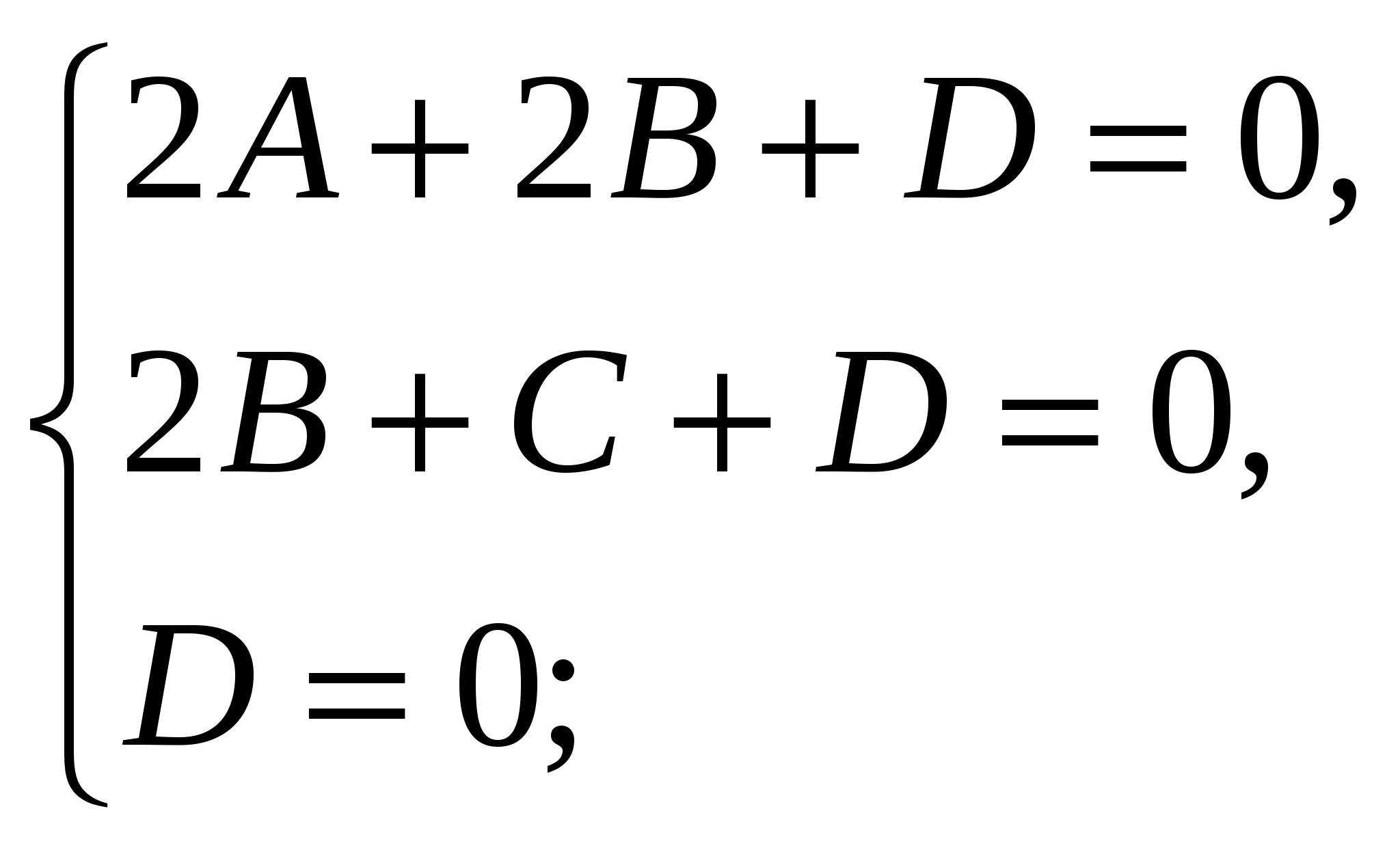
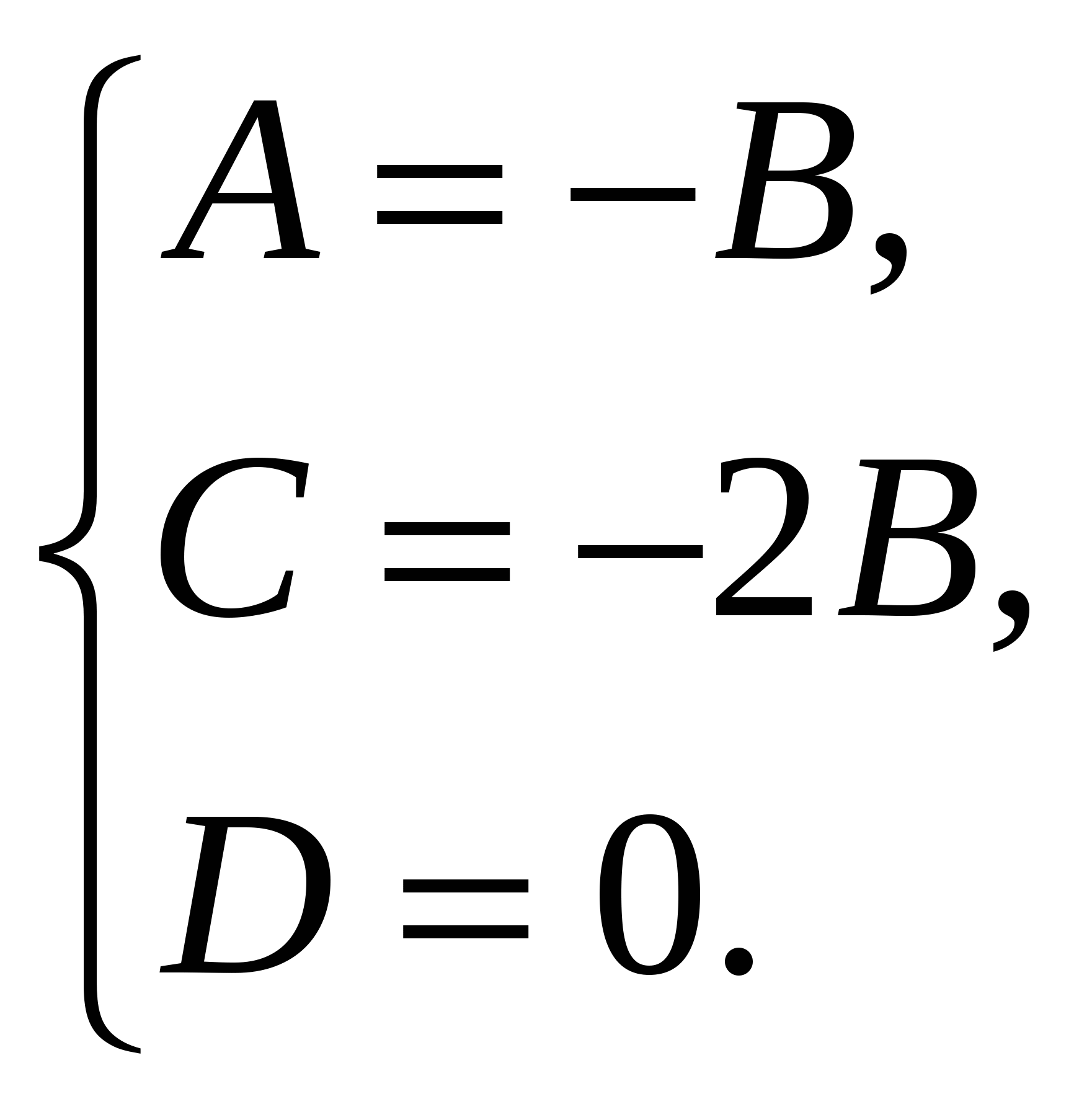
Therefore, the equation of the plane ( 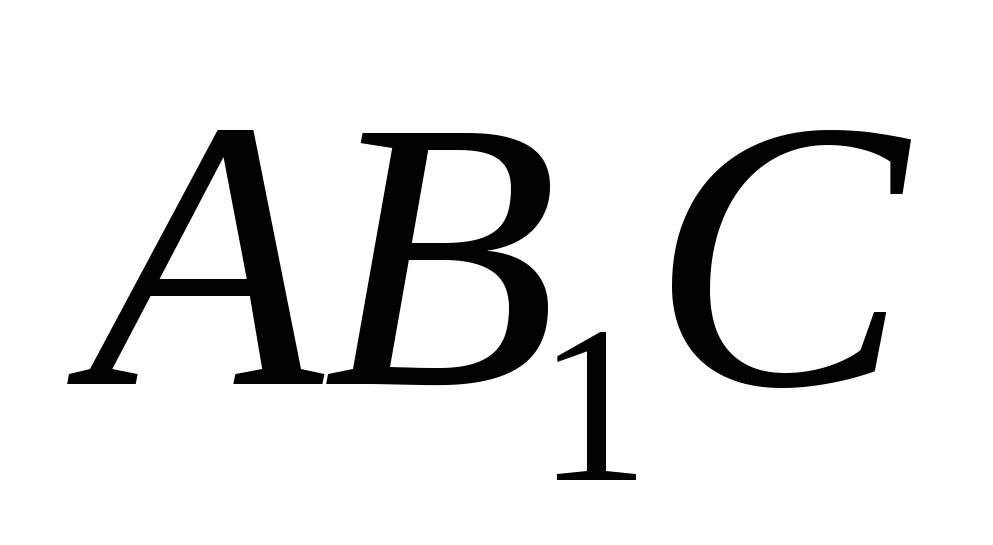 ) has the form , or
) has the form , or  , and the normal vector has coordinates
, and the normal vector has coordinates  .
.
Means
AND 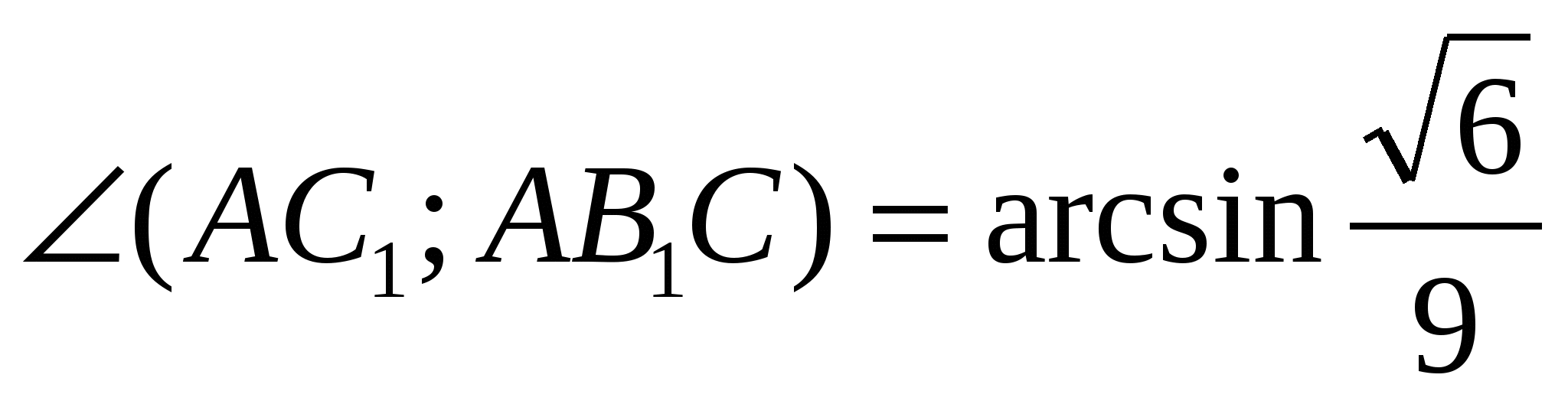 .
.
Answer:
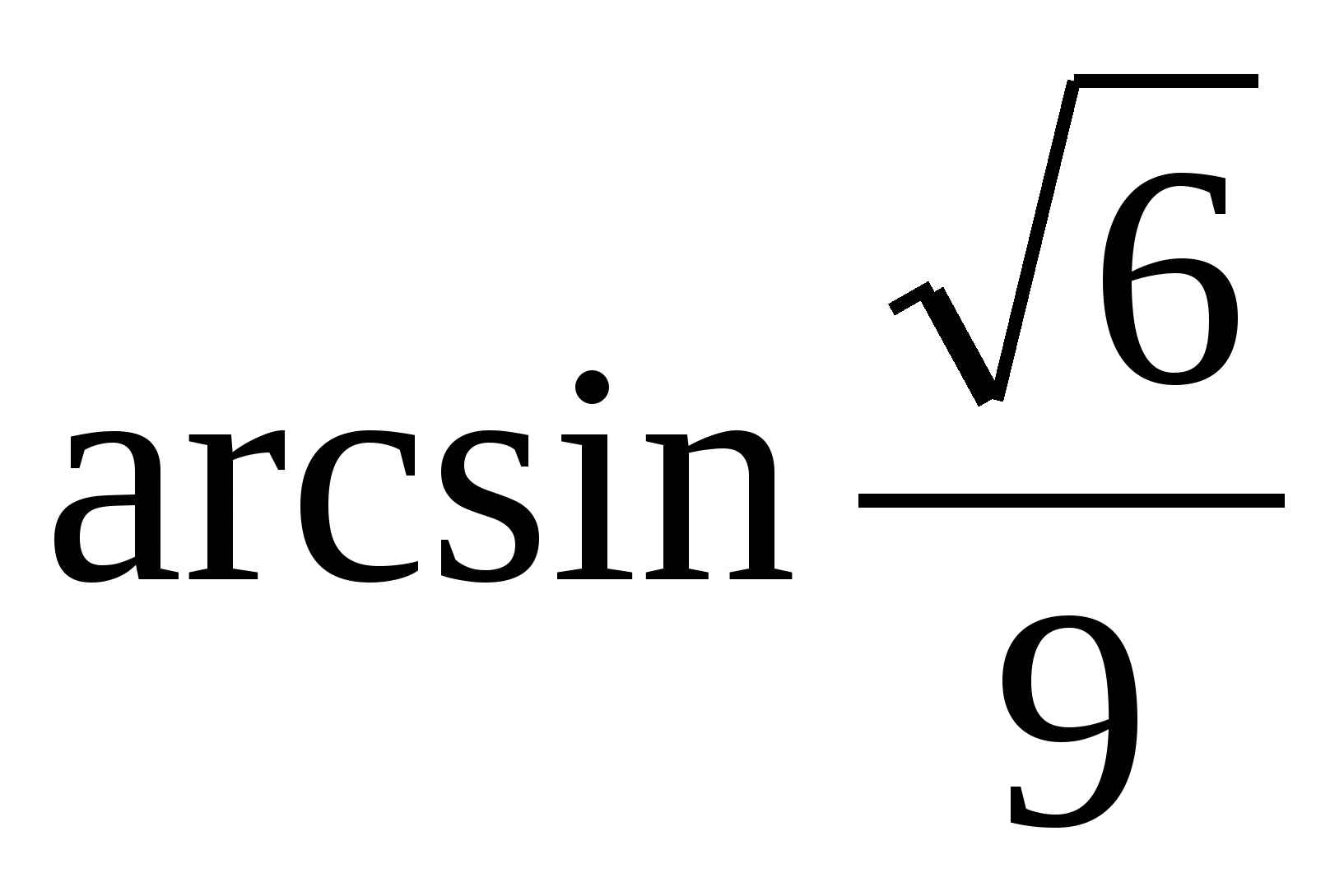 .
.
Let's consider solving the problem in two ways.
Task 4. Method 1: geometric.
On the ribs 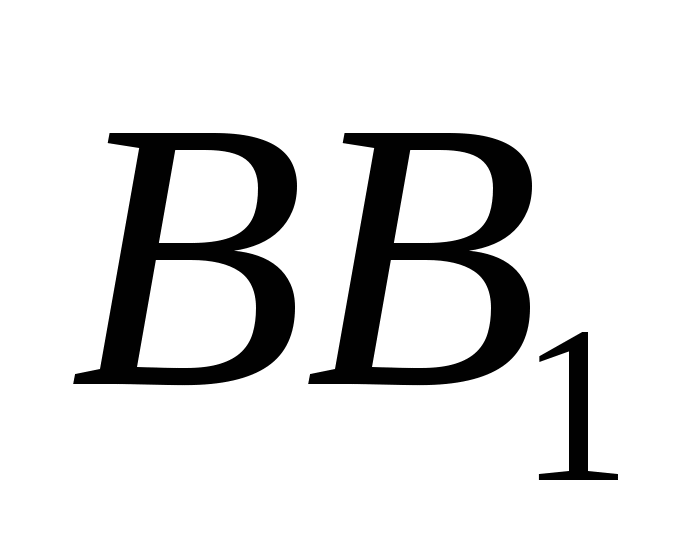 ,
,  And. . Let's go straight - middle line triangle and, i.e. And,
And. . Let's go straight - middle line triangle and, i.e. And,
The studied theoretical material was systematized.
When using the method to solve problems, the following features of the method were identified:
skill correct administration coordinate systems,
correct determination of point coordinates,
knowledge of the analytical apparatus of the method.
The application of the method was considered as a solution various types tasks, and in comparison with other methods.
I encountered some difficulties while doing the work:
when setting goals and objectives;
insufficient volume theoretical material in a school textbook;
when identifying the peculiarities of using the method,
when selecting material for the presentation of an abstract.
Bibliography.
L S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, L. S. Kiseleva, E. G. Poznyak. Geometry, 10-11.M., Education, 2003.
V.N.Litvinenko. Workshop on elementary mathematics. Stereometry: Tutorial.-M.: Verbum-M, 2000.
THEM.Gelfand, E.G. Glagoleva, A.A. Kirillov. Coordinate method. - M.: Nauka, 1968.
S.G. Grigoriev. Vector algebra and analytic geometry. Textbook on higher mathematics.-M.: Information and Implementation Center “Marketing”, 2000.
I. Ivanova, Z. Ilchenkova. Application coordinate vector to solving stereometric problems.//Mathematics, 2007, No. 2.
A.V. Dorofeev. Descartes and his geometry.//Mathematics, 1992, No. 4.
