CHAPTER THREE
POLYhedra
II VOLUME OF PRISM AND PYRAMID
82. Basic assumptions in volumes. The amount of space occupied geometric body, is called the volume of this body.
We set the task - to find an expression for this quantity in the form of a certain number that measures this quantity. In doing so, we will be guided by the following starting points:
1) Equal bodies have equal volumes.
2) The volume of a body(for example, each parallelepiped shown in Fig. 87), consisting of parts(P and Q), equal to the sum volumes of these parts.
Two bodies having the same volumes are called equal in size.
83. Unit of volume. When measuring volumes, the unit of volume is taken to be the volume of a cube in which each edge is equal to a linear unit. So, cubic meters (m 3), cubic centimeters (cm 3), etc. are used.
Volume of a parallelepiped
84. Theorem.Volume of a rectangular parallelepiped equal to the product its three dimensions.
In such short expressions This theorem must be understood as follows: the number expressing the volume of a rectangular parallelepiped in a cubic unit is equal to the product of numbers expressing its three dimensions in the corresponding linear unit, that is, in a unit that is an edge of a cube, the volume of which is taken as a cubic unit. So, if X is a number expressing the volume of a rectangular parallelepiped in cubic centimeters, And a, b And With-numbers expressing its three dimensions in linear centimeters, then the theorem states that x = abc.
In the proof, we will especially consider the following three cases:
1) Measurements are expressed integers.
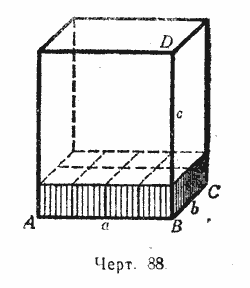
Let, for example, the measurements be (Fig. 88): AB = A, sun = b and BD = c,
Where a, b And With- some integers (for example, as shown in our drawing: A = 4, b= 2 and With= 5). Then the base of the parallelepiped contains ab such squares, each of which represents a corresponding square unit. Each of these squares can obviously accommodate one cubic unit. Then you get a layer (shown in the drawing) consisting of ab cubic units. Since the height of this layer is equal to one linear unit, and the height of the entire parallelepiped contains With such units, then inside the parallelepiped we can place With such layers. Therefore, the volume of this parallelepiped is equal to abc cubic units.
2) Measurements are expressed fractional numbers . Let the dimensions of the parallelepiped be:
m / n , p / q , r / s
. (some of these fractions may equal a whole number). Reducing the fractions to same denominator, will have:
mqs / nqs , pns / nqs , rnq / nqs
Let's take 1 / nqs the share of a linear unit for a new (auxiliary) unit of length. Then in this new unit of measurement of this parallelepiped they will be expressed in integers, namely: mqs, pns And rnq, and therefore, according to what has been proven (in case 1), the volume of the parallelepiped is equal to the product ( mqs) (pns) (rnq), if we measure this volume with a new cubic unit, corresponding to a new linear unit. One cubic unit corresponding to the previous linear unit contains ( nqs) 3 ; this means the new cubic unit is 1/( nqs) 3 former. Therefore, the volume of the parallelepiped, expressed in the previous units, is equal to:
3) Measurements are expressed irrational numbers. Let this parallelepiped (Fig. 89), which for brevity we denote by one letter Q, have the dimensions:
AB = α; AC = β; AD = γ,
where all numbers α, β and γ or only some of them are irrational.
Each of the numbers α, β and γ can be represented as an infinite decimal. Let's take approximate values of these fractions with P in decimal places, first with a deficit and then with an excess. Values with a disadvantage will be denoted by α n , β n , γ n, values with excess α" n , β" n , γ" n. Let us lay down on the edge AB, starting from point A, two segments AB 1 = α n and AB 2 = α" n.
On the edge AC from the same point A we plot the segments AC 1 = β n and AC 2 = β" n and on the edge AD from the same point-segment AD 1 = γ n and AD 2 = γ" n.
In this case we will have:
AB 1< АВ < АВ 2 ; АС 1 < АС < АС 2 ; AD 1 < AD < AD 2 .
Let us now construct two auxiliary parallelepipeds; one (let's call it Q 1) with measurements AB 1, AC 1 and AD 1 and the other (let's call it Q 2) with measurements AB 2, AC 2 and AD 2. The parallelepiped Q 1 will fit entirely inside the parallelepiped Q, and the parallelepiped Q 2 will contain the parallelepiped Q inside it.
By what has been proven (in case 2) we will have:
volume Q 1 = α n β n γ n (1)
volume Q 2 = α" n β" n γ" n (2)
Let's define the volume Q 1< объёма Q 2 .
Let's now start increasing the number P. This means that we take approximate values of the numbers α, β, γ increasingly larger and to a greater extent accuracy.
Let's see how the volumes of parallelepipeds Q 1 and Q 2 change.
With unlimited increase P volume Q 1 obviously increases due to equality (1) with an infinite increase n has as its limit the limit of the product (α n β n γ n). The volume Q 2 obviously decreases and, due to equality (2), has the limit of the product (α" n β" n γ" n). But it is known from algebra that both products
α n β n γ n and α" n β" n γ" n with unlimited magnification P have a common limit, which is the product irrational numbers αβγ.
We take this limit as a measure of the volume of the parallelepiped Q: volume Q = αβγ.
It can be proven that the volume thus determined satisfies the conditions established for volume (§ 82). In fact, with this definition of volume equal parallelepipeds, obviously have equal volumes. Therefore, the first condition (§ 82) is satisfied. Let's break it down now this parallelepiped Q with a plane parallel to its base, in two: Q 1 and Q 2 (Fig. 90).
Then we will have:
volume Q = AB AC AD,
volume Q 1 = AB AA 1 AD,
volume Q 2 = A 1 B 1 A 1 C A 1 D 1.
Adding the last two equalities term by term and noting that A 1 B 1 = AB and A 1 D 1 = AD, we obtain:
volume Q 1 + volume Q 2 = AB AA 1 AD + AB A 1 C AD = AB AD (AA 1 + A 1 C) = AB AD AC, from here we get:
volume Q 1 + volume Q 2 = volume Q.
Consequently, the second condition of § 82 is also satisfied if the parallelepiped is folded from two parts obtained by cutting it with a plane parallel to one of the faces.
85. Consequence. Let the dimensions of a rectangular parallelepiped, which serve as the sides of its base, be expressed by numbers A And b, and the third dimension (height) is a number With. Then, denoting its volume in the corresponding cubic units by the letter V, we can write:
V= abc.
Since the work ab expresses the area of the base, then we can say that The volume of a rectangular parallelepiped is equal to the product of the area of the base and the height .
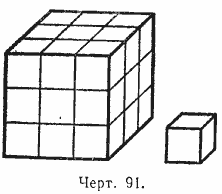
Comment. Ratio of two cubic units different names equal to the third power of the ratio of those linear units which serve as edges for these cubic units. Yes, attitude cubic meter to a cubic decimeter is equal to 10 3, i.e. 1000. Therefore, for example, if we have a cube with an edge length A linear units and another cube with an edge of length 3 A linear units, then the ratio of their volumes will be equal to 3 3, i.e. 27, which is clearly seen from drawing 91.
86. Lemma. An inclined prism is equal in size to a straight prism, the base of which is equal to the perpendicular section of the inclined prism, and the height is equal to its side edge.
Let the inclined prism ABCDEA 1 B 1 C 1 D 1 E 1 be given (Fig. 92).
Let's continue it all side ribs And side faces in one direction.
Let's take some edge on the continuation arbitrary pointA and let's walk through it perpendicular section abcde. Then, putting aside ahh 1 = AA 1, let's draw through A 1 perpendicular section a 1 b 1 c 1 d 1 e 1 . Since the planes of both sections are parallel, then bb 1 = ss 1 =dd 1 = her 1 = aa 1 = AA 1 (§17). As a result, the polyhedron a 1 d, for which the sections we have drawn are taken as the base, is a straight prism, which is discussed in the theorem.
Let us prove that this inclined prism is equal in size to this straight line. To do this, let us first make sure that the polyhedra a D and a 1 D 1 are equal. Their reasons abcde And a 1 b 1 c 1 d 1 e 1 are equal as the bases of a prism a 1 d; on the other hand, adding to both sides of the equality A 1 A = A 1 A along the same line segment A 1 A, we get: A A = A 1 A 1; like this b B = b 1 In 1, With C = With 1 C 1, etc. Let us now imagine that the polyhedron a D is embedded in a polyhedron a 1 D 1 so that their bases coincide; then the side ribs, being perpendicular to the bases and correspondingly equal, will also coincide; therefore polyhedron a D will be compatible with the polyhedron a 1 D 1 ; This means that these bodies are equal. Now note that if to a straight prism a 1 d add a polyhedron a D, and to inclined prism A 1 D add a polyhedron a 1 D 1 equal a D, then we get the same polyhedron a 1 D. From this it follows that two prisms A 1 D and a 1 d equal in size.
87. Theorem. The volume of a parallelepiped is equal to the product of the area of the base and the height.
Previously, we proved this theorem for a rectangular parallelepiped, now we will prove it for a straight parallelepiped, and then for an inclined one.
1). Let (Fig. 93) AC 1 be a right parallelepiped, i.e., one whose base ABCD is some kind of parallelogram, and all the side faces are rectangles.
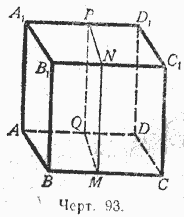
Let us take the side face AA 1 B 1 B as the base; then the parallelepiped will be
slanted. Looking at it like special case inclined prism, based on the lemma of the previous paragraph, we can assert that this parallelepiped is equal in size to a right parallelepiped whose base is a perpendicular section MNPQ, and the height is BC. The quadrilateral MNPQ is a rectangle because its angles serve linear angles direct dihedral angles; therefore, a right parallelepiped with a base of rectangle MNPQ must be rectangular and, therefore, its volume is equal to product of three its measurements, for which the segments MN, MQ and BC can be taken. Thus,
volume AC 1 = MN MQ BC = MN (MQ BC).
But the product MQ BC expresses the area of parallelogram ABCD, therefore
volume ACX = (area ABCD) MN = (area ABCD) BB 1.
2) Let (Fig. 94) AC 1 be an inclined parallelepiped.
It is equal in size to a straight line whose base is the perpendicular section MNPQ (i.e., perpendicular to the edges AD, BC, ...), and the height is the edge BC. But, according to proven evidence, the volume right parallelepiped equal to the product of the area of the base and the height; Means,
volume AC 1 = (area MNPQ) BC.
If RS is the height of the section MNPQ, then the area MNPQ = MQ RS, therefore
volume AC 1 = MQ RS BC = (BC MQ) RS.
The product BC MQ expresses the area of the parallelogram ABCD; therefore, volume AC 1 = (area ABCOD) RS.
It now remains to prove that the segment RS represents the height of the parallelepiped. Indeed, the section MNPQ, being perpendicular to the edges BC, B 1 C 1, .. . , must be perpendicular to the faces ABCD, BB 1 C 1 C, .... passing through these edges (§ 43). Therefore, if we construct a perpendicular to the ABCD plane from point S, then it must lie entirely in the MNPQ plane (§ 44) and, therefore, must merge with the straight line RS, which lies in this plane and is perpendicular to MQ. This means that the segment SR is the height of the parallelepiped. Thus, the volume and inclined parallelepiped equal to the product of the area of the base and the height.
Consequence. If V, B and H are numbers expressing in the corresponding units the volume, base area and height of the parallelepiped, then we can write.
Volume formulas
Volumes simple bodies. Rectangular parallelepiped, Cylinder, Pyramid, Cone, Sphere, Parallelepiped.Volumes and surface areas of regular bodies.
General information about the volumes and surface areas of regular bodies is given in the table.
| Name of the figure | Area and volume of figure S | Name of the figure | Area and volume of figure S |
| Rectangular parallelepiped | Cylinder |  |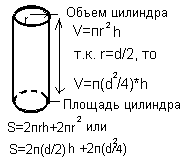
|
 |
 |
||
| Sphere |  |
Parallelepiped |  |
Example 1. Calculation of the volume of a rectangular tank.
The water tank has the shape of a rectangular parallelepiped 1 m long, 65 cm wide and 30 cm high. Determine the volume of the tank in m 3, cm 3, liters
The volume of a rectangular parallelepiped is l*b*h
a) V tank = 1 * 0.65 * 03 = 0.195 m 3
b) 1 m 315000 mm 2 =315000/100=3150 cm 2
1 m 3 =10 6 cm 3, which means 0.195 m 3 =0.195*10 6 =195000 cm 3
c) 1 liter = 1000 cm 3, which means 195000 cm 3 = 195 l
Example 2. Calculation of the volume and surface area of a trapezoidal prism.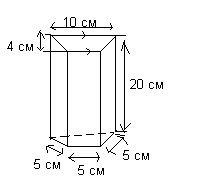
Calculate volume and total area surface of the prism shown in Fig.
The body shown in Fig. - This is a trapezoidal prism.
Since volume = area cross section* height, then
V=1/2*(10+5)*4*20=30*20=600 cm 3
Since the surface area is calculated by adding the sum of the areas of two trapezoids and the sum of the areas of four rectangles, then
S=(2*30)+3(5*20)+(10*20)=560 cm 2
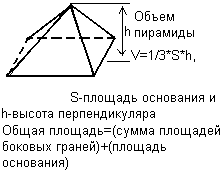
Example 3: Calculation of volume and total surface area regular pyramid.
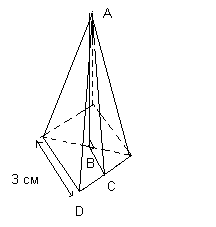
Determine the volume and total surface area of a regular pyramid with a square base, shown in the figure, if its height is 15 cm.
Since the volume of the pyramid = 1/3 (base area) * height, then
V=1/3*(5*5)*15=125 cm 3
Total surface area includes area square base and the area of four equal triangles.
Area of the triangle ADE=1/2*base*(side height).
The height of the AC face can be found using the Pythagorean theorem from triangle ABC, where AB=15 cm, BC=1/2*3=1.5 cm, and AC 2 =AB 2 +BC 2 =225+2.25=227.25
Therefore, the area of triangle ADE
S ADE =1/2*3*15.07=22.605 cm 2
The total area of the pyramid is S=(3*3)+4*22.605=99.42 cm 2.
Example 4. Calculation of the volume and total surface area of a cone.
Determine the volume and total surface area of a cone of radius 4 cm and height 10 cm.
Cone volume V=1/3πr 2 h =1/3*π4 2 *10=167.5cm 3
The total surface area is equal to the sum of the area conical surface and base area, i.e. S=πrl+πr 2
The figure shows that the length of the generatrix l can be found using the Pythagorean theorem.
l 2 =10 2 +4 2 =116 cm
Therefore, the total surface area is
S=π*4*10.8)+(π*4 2 =185.89 cm 2
Example 5. Calculation of the volume and total surface area of a prism.
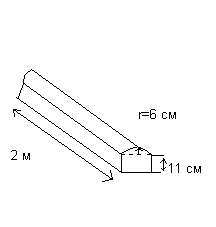
In Fig. wood profile shown. Let's find: a) its volume in m3
b) its total surface area
The profile is a prism, the cross section of which consists of a rectangle and a semicircle. Since the radius of the semicircle is 6 cm, the diameter is 12 cm.
Then the dimensions of the rectangle are 12*11 cm
Cross-sectional area S. =(11*12)+1/2* π 6 2 =188.52 cm 2
Since the volume of a wooden part is equal to the product of the cross-sectional area and the length, then
a) V=188.52*200=37704 cm 3 =37704 cm 3 /10 6 = 0.037704 m 3
b) The total area includes two ends (each area is 188.52 cm 2), three rectangles and a curved surface (which is a half-cylinder). Therefore, the total surface area
S=(2*188.52)+2*(11*200)+(12*200)+1/2*(2π*6*200)=377.04+4400+2400+3768=10945.04 cm 2 =1.094504 m2.
Example 6. Calculation of the volume and total surface area of a complex boiler.
The boiler consists of a cylindrical section 9 m long and 5 m in diameter, to one end of which is attached a hemispherical section with a diameter of 5 m, and to the other end a conical section 3 m high and a base diameter of 5 m. Calculate the volume of the boiler and its total surface area.
V hemisphere P =2/3*πr 3 =2/3*π*2.5 3 =10.42 π m 3
V cylinder Q = π r 2 h=π*2.5 2 *9=56.25 π m 3
V cone R =1/3 π r 2 =1/3*π*2.5 2 *3=6.25π m 3
Total boiler volume V= 10.42 π m 3 +56.25 π m 3 +6.25π m 3 =72.92π=228.97 m 3
S hemispheres P. =2*(πr 2)=2*π*2.5 2 =12.5π m 2
S side surface of the cylinder Q. =2πrh=2*π*2.5*9=45π m 2 (since this cylinder is a pipe without bases)
The length of the cone generatrix l is calculated using the Pythagorean theorem from triangle ABC;
l=(3 2 +2.5 2) 1/2 =3.9 m.
S cone R. =πrl=π*2.5*3.9=9.75 π m 2
Total surface area of the boiler
S= 12.5π+45π+9.75 π=67.25π=211.2 m2
Everyone good day! My name is Ivan, and I am the father of a schoolboy who is not very good at mathematics. Recently my son was given a task - to find the volume of a parallelepiped and after tinkering with it a little and not being able to solve the problem, he turned to me. School knowledge There was not much left in my memory, and therefore I had to take up the textbooks, re-read them and then explain the material I had studied to my son. Surely my experience will be useful for other parents, and that’s why I wrote this article, which provides detailed information on solving problems on the volume of this geometric figure.
A little theory
Before I tell you how to actually find the volume and area of a parallelepiped, and using what formula, let’s remember together what it is. This geometric figure has three equivalent interpretations:
- A parallelepiped is a polyhedron with 6 faces, the peculiarity of which is that each one is a parallelogram.
- The term also includes a hexagon with 3 pairs of faces that will be parallel to each other.
- A prism based on a parallelogram is also called a parallelepiped.
Most often, it is necessary to calculate the volume of parallelepipeds of several different types. Each case has its own formula and its own solution, and below I will explain in detail how to solve typical tasks by calculating the volumes of different types of this geometric figure.
Let's move on to practice
How to solve the problem of finding the volume of a rectangular parallelepiped? The peculiarity of this type of figure is that each of its faces is a rectangle. If you want to understand what a rectangular parallelepiped looks like, look at the most ordinary shoebox.
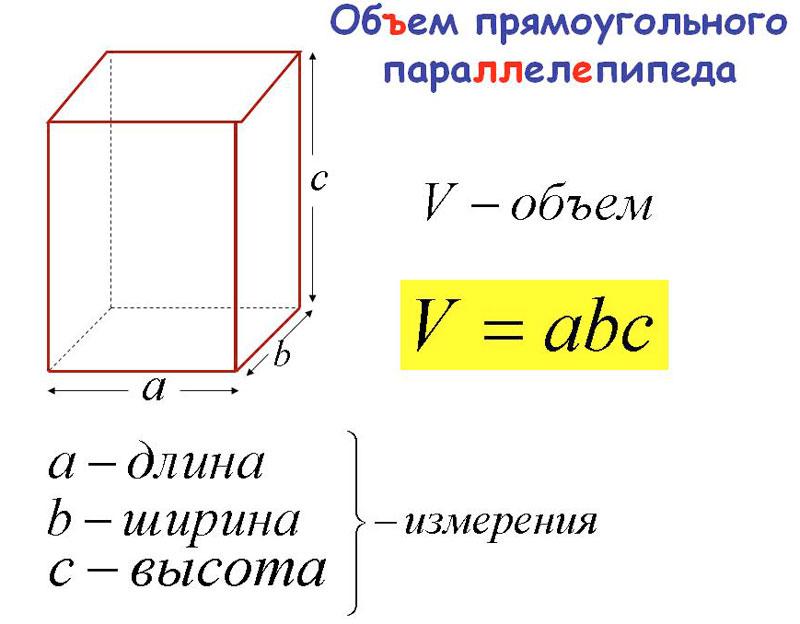To solve the problem, we first look for the values of the two sides of the base of the figure. The parties have perpendicular arrangement to each other and are found according to the formula: P-AxB, where A is the length, and B is the width. Next we find out one more key parameter, namely, we find the height. And then we move on to calculating the volume in which the following formula will work: V = PxH, that is, to obtain the volume you need to multiply the base area by the height. How to find the height - here it is worth looking into a geometry textbook and writing out a formula for finding the edge of a figure.
To find the volume of a right parallelepiped, let's look at what this particular figure looks like. Its side faces are rectangles perpendicular to the base, and therefore the volume will be calculated identical to the problem above, but you should only take into account that the height will not be the edge of the figure, but a segment connecting the faces opposite to each other and perpendicular to the base. The base here is a parallelogram and therefore the formula will be a little more complicated: P=AxBxsin(a). A, B are the length and width of the base, and “a” is the angle they will form when intersecting.
Volume of a parallelepiped
Let's figure out the volume of an inclined type of figure. The faces of this type of figure are not perpendicular to its base, and therefore calculations should begin by finding the height. We multiply the height by the area of the base and get the volume, that is, our formula looks like in the following way: V=PxN.
It remains to find out how to calculate the volume of a figure whose sides are square. This figure is more often called a cube, but at the same time it is a parallelepiped, each face of which is a square. Therefore, all its edges will be equal to each other. The formula for calculating the volume will be as simple as possible: you need to measure the ribs and raise the result of the calculations to the 3rd power.
This is how the volume of such an interesting geometric figure as a parallelepiped is found. I hope that the short cheat sheet I wrote will be a good help for schoolchildren and parents in solving geometry problems, and your student will not write a single test with a bad grade!