Definition
Pyramide er et polyhedron sammensat af en polygon \(A_1A_2...A_n\) og \(n\) trekanter med et fælles toppunkt \(P\) (ikke liggende i polygonens plan) og sider modsat det, der falder sammen med sider af polygonen.
Betegnelse: \(PA_1A_2...A_n\) .
Eksempel: femkantet pyramide \(PA_1A_2A_3A_4A_5\) .
Trekanter \(PA_1A_2, \PA_2A_3\) osv. hedder sideflader pyramider, segmenter \(PA_1, PA_2\) osv. – laterale ribben, polygon \(A_1A_2A_3A_4A_5\) – basis, punkt \(P\) – top.
Højde pyramider er en vinkelret nedadgående fra toppen af pyramiden til bundens plan.
En pyramide med en trekant ved sin base kaldes tetraeder.
Pyramiden kaldes korrekt, hvis dens base er en regulær polygon, og en af følgende betingelser er opfyldt:
\((a)\) lateralt pyramidens kanter lige;
\((b)\) pyramidens højde passerer gennem midten af cirklen, der er omskrevet nær bunden;
\((c)\) sideribberne er skråtstillede til basens plan i samme vinkel.
\((d)\) sideflader hælder til basens plan i samme vinkel.
Regelmæssig tetraeder er en trekantet pyramide, hvis flader alle er ens ligesidede trekanter.
Sætning
Betingelser \((a), (b), (c), (d)\) er ækvivalente.
Bevis
Lad os finde højden af pyramiden \(PH\) . Lad \(\alpha\) være bunden af pyramidens plan.

1) Lad os bevise, at fra \((a)\) følger \((b)\) . Lad \(PA_1=PA_2=PA_3=...=PA_n\) .
Fordi \(PH\perp \alpha\), så er \(PH\) vinkelret på enhver linje, der ligger i dette plan, hvilket betyder, at trekanterne er retvinklede. Det betyder, at disse trekanter er ens i fælles ben \(PH\) og hypotenusen \(PA_1=PA_2=PA_3=...=PA_n\) . Dette betyder \(A_1H=A_2H=...=A_nH\) . Det betyder, at punkterne \(A_1, A_2, ..., A_n\) er i samme afstand fra punktet \(H\), derfor ligger de på samme cirkel med radius \(A_1H\) . Denne cirkel er per definition afgrænset omkring polygonen \(A_1A_2...A_n\) .
2) Lad os bevise, at \((b)\) indebærer \((c)\) .
\(PA_1H, PA_2H, PA_3H,..., PA_nH\) rektangulær og lige på to ben. Dette betyder, at deres vinkler også er ens, derfor \(\vinkel PA_1H=\vinkel PA_2H=...=\vinkel PA_nH\).
3) Lad os bevise, at \((c)\) indebærer \((a)\) .
Svarende til det første punkt, trekanter \(PA_1H, PA_2H, PA_3H,..., PA_nH\) rektangulær og langs benet og skarpt hjørne. Det betyder, at deres hypotenuser også er ens, det vil sige \(PA_1=PA_2=PA_3=...=PA_n\) .
4) Lad os bevise, at \((b)\) indebærer \((d)\) .
Fordi i en regulær polygon falder centrene for de omskrevne og indskrevne cirkler sammen (generelt set kaldes dette punkt for midten af en regulær polygon), så er \(H\) midten af den indskrevne cirkel. Lad os tegne vinkelrette fra punktet \(H\) til siderne af basen: \(HK_1, HK_2\) osv. Disse er radierne af den indskrevne cirkel (per definition). Så ifølge TTP (\(PH\) er en vinkelret på planet, \(HK_1, HK_2\), osv. er projektioner vinkelret på siderne) skrånende \(PK_1, PK_2\), osv. vinkelret på siderne \(A_1A_2, A_2A_3\) osv. henholdsvis. Altså per definition \(\vinkel PK_1H, \vinkel PK_2H\) lig med vinklerne mellem sidefladerne og basen. Fordi trekanter \(PK_1H, PK_2H, ...\) er lige store (som rektangulære på to sider), så vinklerne \(\vinkel PK_1H, \vinkel PK_2H, ...\) er lige.
5) Lad os bevise, at \((d)\) indebærer \((b)\) .
I lighed med det fjerde punkt er trekanterne \(PK_1H, PK_2H, ...\) lige store (som rektangulære langs benet og spidse vinkel), hvilket betyder, at segmenterne \(HK_1=HK_2=...=HK_n\) er lige. Dette betyder per definition \(H\) er midten af en cirkel indskrevet i basen. Men fordi på regulære polygoner centrene for de indskrevne og omskrevne cirkler falder sammen, så er \(H\) midten af den omskrevne cirkel. Chtd.
Følge
Sidefladerne af en regulær pyramide er lige store trekanter.
Definition
Højden af sidefladen af en regulær pyramide trukket fra dens toppunkt kaldes apotem.
Apotemerne for alle sideflader af en regulær pyramide er lig med hinanden og er også medianer og halveringslinjer.
Vigtige bemærkninger
1. Højden er korrekt trekantet pyramide falder i skæringspunktet mellem højderne (eller halveringslinjer eller medianer) af basen (grundlaget er en regulær trekant).
2. Højden er korrekt firkantet pyramide falder i skæringspunktet mellem basens diagonaler (basen er en firkant).
3. Højden er korrekt sekskantet pyramide falder i skæringspunktet for basens diagonaler (basen er en regulær sekskant).
4. Pyramidens højde er vinkelret på enhver ret linje, der ligger ved bunden.
Definition
Pyramiden kaldes rektangulær, hvis en af dens sidekanter er vinkelret på bundens plan.

Vigtige bemærkninger
1. I en rektangulær pyramide er kanten vinkelret på bunden pyramidens højde. Det vil sige, \(SR\) er højden.
2. Fordi \(SR\) er altså vinkelret på en hvilken som helst linje fra basen \(\triangle SRM, \triangle SRP\) – retvinklede trekanter.
3. Trekanter \(\triangle SRN, \triangle SRK\)- også rektangulær.
Det vil sige, at enhver trekant dannet af denne kant og diagonalen, der kommer ud fra toppen af denne kant, der ligger ved bunden, vil være rektangulær.
\[(\Large(\text(Volumen og overfladeareal af pyramiden)))\]
Sætning
Pyramidens volumen er lig med en tredjedel af produktet af bundens areal og pyramidens højde: \
Konsekvenser
Lad \(a\) være siden af basen, \(h\) være højden af pyramiden.
1. Volumenet af en regulær trekantet pyramide er \(V_(\text(ret trekant.pir.))=\dfrac(\sqrt3)(12)a^2h\),
2. Volumenet af en regulær firkantet pyramide er \(V_(\text(right.four.pir.))=\dfrac13a^2h\).
3. Rumfanget af en regulær sekskantet pyramide er \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).
4. Volumen almindelig tetraeder lige med \(V_(\text(højre tetr.))=\dfrac(\sqrt3)(12)a^3\).
Sætning
Arealet af den laterale overflade af en almindelig pyramide er lig med halvproduktet af omkredsen af basen og apotemet.
\[(\Large(\text(Frustum)))\]
Definition
Overvej en vilkårlig pyramide \(PA_1A_2A_3...A_n\) . Lad os tegne et plan parallelt med bunden af pyramiden gennem et bestemt punkt, der ligger på pyramidens sidekant. Dette fly vil opdele pyramiden i to polyedre, hvoraf den ene er en pyramide (\(PB_1B_2...B_n\) ), og den anden hedder afkortet pyramide(\(A_1A_2...A_nB_1B_2...B_n\) ).
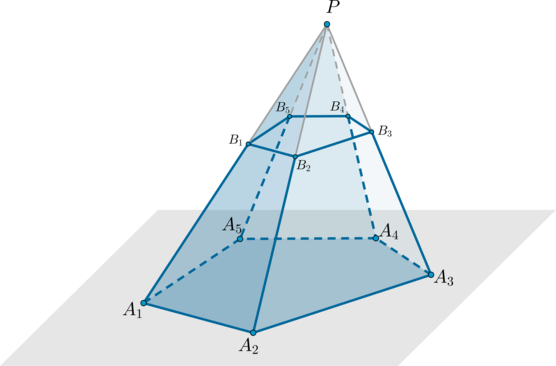
Den afkortede pyramide har to baser - polygoner \(A_1A_2...A_n\) og \(B_1B_2...B_n\), som ligner hinanden.
Højden af en afkortet pyramide er en vinkelret tegnet fra et eller andet punkt af den øvre base til planet for den nederste base.
Vigtige bemærkninger
1. Alle sideflader af en afkortet pyramide er trapezoider.
2. Segmentet, der forbinder centrene af baserne i en regulær afkortet pyramide (det vil sige en pyramide opnået ved tværsnit af en regulær pyramide) er højden.
Lad os overveje, hvilke egenskaber pyramider har, hvor sidefladerne er vinkelrette på bunden.
Hvis to tilstødende sideflader af pyramiden er vinkelrette på bunden, At den fælles sidekant af disse flader er højden af pyramiden. Hvis problemet siger det kanten af en pyramide er dens højde, At vi taler om specifikt om denne type pyramide.
Pyramidens flader vinkelret på basen er retvinklede trekanter.
Hvis bunden af pyramiden er en trekant
Sidefladen af en sådan pyramide i almindelig sag vi ser efter det som summen af arealerne af alle sideflader.
Pyramidens bund er ortogonal projektion ansigt ikke vinkelret på bunden (in I dette tilfælde, SBC). Dette betyder ifølge sætningen om arealet af ortogonal projektion, at arealet af basen er lig med produktet af arealet af denne flade og cosinus af vinklen mellem den og basens plan .
Hvis bunden af pyramiden er en retvinklet trekant

I dette tilfælde alle flader af pyramiden er retvinklede trekanter.
Trekanterne SAB og SAC er rektangulære, da SA er pyramidens højde. Trekant ABC rektangulær efter tilstand.
At trekanten SBC er retvinklet, følger af sætningen om tre perpendikulære (AB er projektionen af den skrå SB på grundplanet. Da AB er vinkelret på BC af betingelse, så er SB vinkelret på BC).
Vinklen mellem sidefladen af SBC og basen er i dette tilfælde vinkel ABS.
Det laterale overfladeareal er lig med summen af arealer af retvinklede trekanter:
Siden i dette tilfælde
![]()
Hvis bunden af pyramiden er en ligebenet trekant
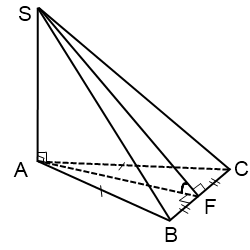
I dette tilfælde er vinklen mellem sidefladeplanet BCS og basisplanet vinkel AFS, hvor AF er højden, medianen og halveringslinjen ligebenet trekant ABC.
Tilsvarende, hvis i bunden af pyramiden ligger ligesidet trekant ABC.
Hvis bunden af pyramiden er et parallelogram
 I dette tilfælde er bunden af pyramiden en ortogonal projektion af sidefladerne, der ikke er vinkelrette på bunden.
I dette tilfælde er bunden af pyramiden en ortogonal projektion af sidefladerne, der ikke er vinkelrette på bunden.
Hvis vi deler basen i to trekanter, så
hvor α og β er vinklerne mellem henholdsvis ADS- og CDS-planerne og basisplanet.

Hvis BF og BK er højderne af parallelogrammet, så er vinkel BFS hældningsvinklen af sidefladen CDS til grundplanet, og vinkel BKS er hældningsvinklen af siden ADS.
(tegningen er lavet til tilfældet, hvor B er en stump vinkel).
Hvis bunden af pyramiden er en rombe ABCD, så er vinklerne BFS og BKS ens. Trekanter ABS og CBS samt ADS og CDS er også lige i dette tilfælde.
Hvis bunden af pyramiden er et rektangel
 I dette tilfælde er vinklen mellem sidefladeplanet SAD og basisplanet vinkel SAB,
I dette tilfælde er vinklen mellem sidefladeplanet SAD og basisplanet vinkel SAB,
og vinklen mellem planet for sidefladen SCD og basens plan er vinkel SCB
(ved sætningen om tre perpendikulære).
Henholdsvis,
Herfra lateral overflade kan findes som
Her alle sideflader af pyramiden er retvinklede trekanter(vinkler SAD og SCD er rette vinkler ifølge sætningen om tre vinkelrette). Derfor kan sidefladen søges direkte:
Hvis bunden af pyramiden er en kvadratisk ABCD, så er problemet forenklet: trekanter ABS og BCS samt trekanter ADS og CDS er lige store i dette tilfælde.
15. december 2012
Anmeldelser (12) om “Pyramider, hvor kanterne er vinkelrette på bunden”
-
Hvis du googler "rektangulær pyramide" på russisk, så er dit materiale i top fem. Jeg kan se, at der kun er én rektangulær pyramide på denne side, den sidste, og betegnelserne er ikke helt korrekte. Google kom sammen med Wikipedia med en mærkelig definition - en vinkelret kant og den samme som i bunden af en pyramide. Forresten, videre engelsk sprog Generelt er en rektangulær pyramide en pyramide, ved hvilken der er et rektangel i bunden, og det er lige meget, hvor højden overhovedet er.
Der er ikke et ord i teksten om en rektangulær pyramide. Meget ofte, i problemer, der involverer pyramider, hvor der er to sideflader vinkelret på basen, taler vi om vinklen mellem sidefladens plan og basens plan.
I dette materiale overvej hvordan man bestemmer denne vinkel afhængigt af polygonen ved bunden. Hvis bunden indeholder et parallelogram (inklusive en rombe), skal du tegne højderne af parallelogrammet fra bunden af pyramiden til modsatte sider(eller en lige linje, der indeholder disse sider). Hvis basen er et rektangel (inklusive en firkant), er der ingen grund til at tegne højder, da rektanglets sider er indbyrdes vinkelrette. I dette tilfælde bestemmes vinklen mellem basen og sidekanten lineær vinkel, dannet af pyramidens kanter; sidefladerne er retvinklede trekanter.
De rette vinkler ved basen er fremhævet for at fremhæve denne forskel fra det tilfælde, hvor basen er et parallelogram, der ikke er et rektangel.Fordi du fjernede den "rektangulære pyramide", men teknikere, der ved og forstår, hvordan søgemaskiner fungerer, vil næppe blive overbevist af dine argumenter. Lær IT, ikke kun matematik.
Kære Natashok! Beskylder du mig for at lyve? Jeg fortalte dig, at jeg ikke bruger udtrykket "rektangulær pyramide" i mit arbejde.
P.S. Jeg er desværre ikke it-specialist. Jeg er enig i, at læsefærdigheder er nødvendig på alle områder: både i matematik og på Informationsteknologi, og i stavning.
Figuren illustrerer tilfældet, når der er et rektangel i bunden af pyramiden. Ved paralleldesign bevares vinkler ikke, så rektanglet tegnes som et parallelogram. Den anden rette vinkel i figuren er noteret i forbindelse med sætningen om tre perpendikulære.
For det første ikke en tegning, men en tegning. Man tegner tegninger i tegning, men i matematik er det stadig tegninger. For det andet, se på den sidste tegning. Der er ingen sætninger om tre perpendikulære. Jeg gentager, basen i den sidste tegning er ikke et rektangel. Det er lige meget, hvordan du fremstiller det. Jeg følger notationerne. Selvom jeg bemærkede, at den tredje tegning nedenfor heller ikke er tydelig for mig. Parallelogrammet er ikke markeret på tegningen. Bare en firkant! Dens udseende ligner et parallelogram, men betegnelserne lader meget tilbage at ønske.
1) Ja, i geometri laver vi en tegning, men illustrationen til teksten er en tegning. I enhver lærebog i geometri skriver de "i figur 1", ikke "i tegning 1".
2) Et rektangel i stereometri er afbildet som et parallelogram, da vinkler ikke bevares under parallel design. Men linjernes parallelitet er bevaret. De modsatte sider af firkanten er afbildet som liggende på parallelle linjer. Det følger heraf, at denne firkant er et parallelogram.De modsatte sider af firkanten er afbildet som liggende på parallelle linjer. Jeg kan ikke se nogen indikation af, at disse linjer er parallelle, og parallelt design var ikke angivet i teksten. Så for mig er grundlaget stadig på den sidste tegning vilkårlig firkant
Kære Natasha! Billede rumlige figurer på flyet udføres i overensstemmelse med reglerne parallelt design. Det betyder, at parallelle linjer på tegningen er afbildet som parallelle linjer, og ikke-parallelle linjer er ikke parallelle.
Jeg er ikke enig i definitionen af en rektangulær pyramide. Rektangulær pyramide er en pyramide, i det ene toppunkt, hvoraf der er tre rette vinkler. Skriv til mig, hvorfor du spreder fejlagtigt materiale på niveau med en uvidende Wikipedia.
Hvis bunden af pyramiden er et rektangel, hvorfor er to modstående hjørner så markeret på billedet for at angive det? På den sidste tegning kan denne base være en rhomboid og en anden firkant.
I hvilken en af sideribberne er vinkelret på bunden.
I dette tilfælde vil denne kant være højden af pyramiden.
Egenskaber af pyramiden.
1. Når alle sidekanter er af samme størrelse, så:
- nær bunden af pyramiden er let at beskrive cirkel, mens toppen af pyramiden vil blive projiceret ind i midten af denne cirkel;
- sideribberne er identiske vinkler ;
- Desuden er det modsatte også tilfældet, dvs. når sideribberne dannes med basens plan lige store vinkler, eller når en cirkel kan beskrives nær bunden af pyramiden og toppen af pyramiden vil blive projiceret ind i midten af denne cirkel, hvilket betyder at alle pyramidens sidekanter har samme størrelse.
2. Når sidefladerne har en hældningsvinkel til bundens plan med samme værdi, så:
- det er let at beskrive en cirkel nær bunden af pyramiden, og toppen af pyramiden vil blive projiceret ind i midten af denne cirkel;
- højden af sidefladerne er lige lang;
- arealet af sidefladen er lig med ½ produktet af bundens omkreds og højden af sidefladen.
3. Om pyramiden kan beskrives kugle i tilfælde af at der ved bunden af pyramiden ligger en polygon, omkring hvilken en cirkel kan beskrives (de nødvendige og tilstrækkelig stand). Kuglens centrum vil være prik skæringspunkter mellem fly, der passerer gennem midten af pyramidens kanter vinkelret på dem. Ud fra denne sætning konkluderer vi, at en kugle kan beskrives både omkring enhver trekantet og omkring enhver regulær pyramide;
4. En kugle kan indskrives i en pyramide, hvis halveringslinjerne af den indre dihedrale vinkler pyramiderne skærer hinanden i 1. punkt (en nødvendig og tilstrækkelig betingelse). Dette punkt bliver kuglens centrum.
5. Keglen vil blive indskrevet i pyramiden, når deres toppunkter falder sammen, og keglens bund vil være indskrevet i bunden af pyramiden. I dette tilfælde er det kun muligt at passe en kegle ind i en pyramide, hvis pyramidens apotemer har lige store størrelser (en nødvendig og tilstrækkelig betingelse);
6. Kegle vil blive beskrevet nær pyramiden, hvis deres toppunkter falder sammen, og keglens bund vil blive beskrevet nær pyramidens bund. I dette tilfælde er det kun muligt at beskrive en kegle nær pyramiden, hvis alle pyramidens sidekanter har samme værdier(nødvendig og tilstrækkelig betingelse). Højden af disse kegler og pyramider er de samme.
7. Cylinder vil blive indskrevet i en pyramide, hvis en af dens baser falder sammen med en cirkel, der er indskrevet i sektionen af pyramiden af et plan parallelt med basen, og den anden base hører til pyramidens basis.
8. Cylinderen vil blive beskrevet nær pyramiden, når toppen af pyramiden tilhører en af dens baser, og cylinderens anden base vil blive beskrevet nær pyramidens bund. I dette tilfælde er det kun muligt at beskrive en cylinder nær en pyramide, hvis bunden af pyramiden er en indskrevet polygon (en nødvendig og tilstrækkelig betingelse).
Formler til bestemmelse af volumen og arealet af en rektangulær pyramide.
V- volumen af pyramiden,
S- område af bunden af pyramiden,
h- pyramidens højde,
Sb- område af pyramidens laterale overflade,
-en- apotem (ikke at forveksle med α ) pyramider,
P- omkredsen af bunden af pyramiden,
n- antallet af sider af bunden af pyramiden,
b- længde lateral ribben pyramider,
α - flad vinkel i toppen af pyramiden.
