«Сечения параллелепипеда» - Задание: построить сечение через ребро параллелепипеда и точку К. Задание: построить сечение, проходящее через точки M, N, K. M ? (ABB’A’) N ? (ABCD) K ? CC’. Прямоугольник CKK’C’ - сечение ABCDA’B’C’D’. Прямоугольник ADKN - сечение ABCDA’B’C’D’. 1. Вступительное слово учителя – 3 мин 2. Активизация знаний учащихся.
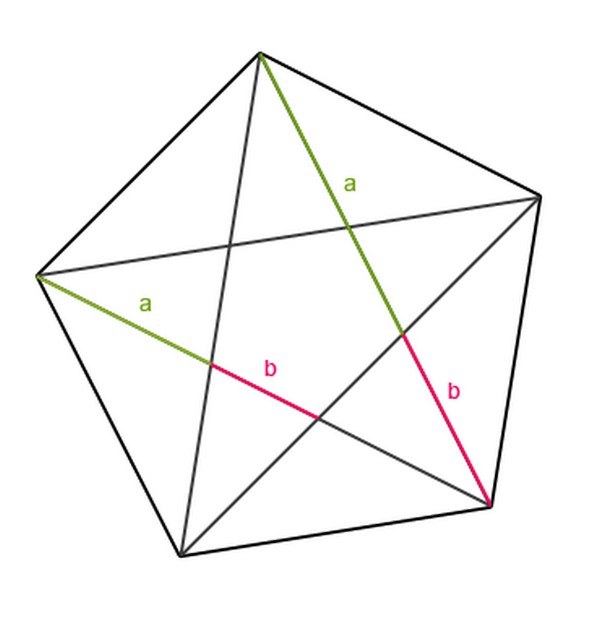
«Пропорции золотого сечения» - «Золотой пятиугольник». На числах основана гармония Вселенной. Температура наружного воздуха. Спиралевидные ураганы и галактики. Античные храмы. «Золотой прямоугольник». Сохранить землю- значит сохранить золотые пропорции. Например, соотношения суши и воды на поверхности Земли находятся в золотой пропорции.
«Объём призмы» - Как найти объем прямой призмы? Изучение теоремы об объеме призмы. Решение задачи. Проведение высоты треугольника ABC. Понятие призмы. Задача. Площадь S основания исходной призмы. Цели урока. Вопросы. Основные шаги при доказательстве теоремы прямой призмы? Объем исходной призмы равен произведению S · h.
«Золотое сечение» - Окно. Храм Василия Блаженного. Золотое сечение в природе. Золотое сечение – пропорция. Парфенон. Египетские пирамиды. В математике пропорцией называется равенство двух отношений: a: b = c: d. Цель исследования: Вывести закон красоты мира с точки зрения математики. г.Санкт – Петербург. Покровский собор (храм Василия Блаженного).
«Призма 10 класс» - Прямая. Правильная. Призма. Sп.п = Sбок.+2Sоснован. Геометрия. Призмой называется многогранник у которого грани находятся в параллельных плоскостях. Sбок.= Pоснован. + h Для прямой призмы: Sп.п = Pоснов. h + 2Sоснов. Наклонная. Формулы нахождения площади. Виды призм. Применение призмы в быту. Применение призмы в архитектуре.
«Понятие площади» - Зачетная система по геометрии в 8 классе. Использование на уроке разноуровневой технологии обучения. Основными принципами разноуровневой технологии являются: Материал по теме усвоен, настроение приподнятое. Тема: «Подобие фигур» №3(а). Тема: «Многоугольники» №1 (1час). Тематическое планирование зачетов.
Инструкция
Способ расчета площади сечения также зависит от данных, которые уже имеются в задаче. Кроме этого, решение определяется тем, что лежит в основании призмы. Если необходимо найти диагональное сечение призмы, найдите длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Например, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения найдите по формуле: диагональ основания умножить на высоту.
Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту.
В случае, если в основании находится круг, площадь сечения призмы найдите умножением числа «пи» на радиус заданной фигуры в квадрате.
Различают следующие виды призм - правильные и прямые. Если необходимо найти сечение правильной призмы, вам нужно знать длину только одной из сторон многоугольника, ведь в основании лежит квадрат, у которого все стороны равны. Найдите диагональ квадрата, которая равна произведению его стороны на корень из двух. После этого перемножив диагональ и высоту, вы получите площадь сечения правильной призмы.
Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где - периметр перпендикулярного сечения, - длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко всем боковым ребрам призмы, а его углы - это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко всем боковым граням.
Осевым называется сечение, которое проходит через ось геометрического тела, образованного при вращении некой геометрической фигуры. Цилиндр получается в результате вращения прямоугольника вокруг одной из сторон, и этим обусловлены многие его свойства. Образующие этого геометрического тела параллельны и равны между собой, что очень важно для определения параметров его осевого сечения, в том числе диагонали.
Вам понадобится
- - цилиндр с заданными параметрами;
- - лист бумаги;
- - карандаш;
- - линейка;
- - циркуль;
- - теорема Пифагора;
- - теоремы синусов и косинусов.
Инструкция
Постройте цилиндр согласно заданным условиям. Для того чтобы его начертить, вам необходимо знать радиус основания и высоту. Однако в задаче на определение диагонали могут быть указаны и другие условия - например, угол между диагональю и образующей или диаметром основания. В этом случае при создании чертежа используйте тот размер, который вам задан. Остальные возьмите произвольно и укажите, что именно вам дано. Обозначьте точки пересечения оси и оснований как О и О".
Начертите осевое сечение. Оно представляет собой прямоугольник, два стороны которого являются диаметрами оснований, а две другие - образующими. Поскольку и образующие перпендикулярны основаниям, они являются одновременно и высотами данного геометрического тела. Обозначьте получившийся прямоугольник как АВСD. Проведите диагонали АС и ВD. Вспомните свойства диагоналей прямоугольника. Они равны между собой и делятся в точке пересечения пополам.
Рассмотрите треугольник АDC. Он прямоугольный, поскольку образующая CD перпендикулярна основанию. Один катет представляет собой диаметр основания, второй - образующую. Диагональ является гипотенузой. Вспомните, как вычисляется длина гипотенузы любого прямоугольного треугольника. Она равна квадратному корню из суммы квадратов катетов. То есть в данном случае d=√4r2+h2, где d – диагональ, r – радиус основания, а h – высота цилиндра.
Если в задаче высота цилиндра не дана, но указан угол диагонали осевого сечения с основанием или образующей, используйте теорему синусов или косинусов. Вспомните, что означают данные тригонометрические функции. Это отношения противолежащего или прилежащего заданному угол катета к гипотенузе, которую вам и нужно найти. Допустим, вам заданы высота и угол CAD между диагональю и диаметром основания. В этом случае используйте теорему синусов, поскольку угол CAD находится напротив образующей. Найдите гипотенузу d по формуле d=h/sinCAD. Если же вам задан радиус и этот же угол, используйте теорему косинусов. В этом случае d=2r/cos CAD.
По тому же принципу действуйте и в тех случаях, когда заданы угол ACD между диагональю и образующей. В этом случае теорема синусов используется, когда дан радиус, а косинусов - если известна высота.
Видео по теме
Золотое сечение - пропорция, которую издревле считали наиболее совершенной и гармоничной. Она заложена в основу конструкций множества древних сооружений, от статуй до храмов, и очень часто встречается в природе. Вместе с тем эта пропорция выражается удивительно изящными математическими конструкциями.
Инструкция
Золотая пропорция определяется следующим образом: это такое разбиение отрезка на две части, что меньшая часть относится к большей так же, как большая часть - ко всему отрезку.
Если длину всего отрезка принять за 1, а длину большей части - за x, то искомая пропорция выразится уравнением:
(1 - x)/x = x/1.
Умножая обе части пропорции на x и перенося слагаемые, получаем квадратное уравнение:
x^2 + x - 1 = 0.
Уравнение имеет два действительных корня, из которых нас, естественно, интересует только положительный. Он равен (√5 - 1)/2, что примерно равняется 0,618. Это число и выражает золотое сечение. В математике его чаще всего обозначают буквой φ.
Число φ обладает рядом замечательных математических свойств. Например, даже из исходного уравнения видно, что 1/φ = φ + 1. Действительно, 1/(0,618) = 1,618.
Другой способ вычислить золотую пропорцию состоит в использовании бесконечной дроби. Начиная с любого произвольного x, можно последовательно построить дробь:
x
1/(x + 1)
1/(1/(x+1) + 1)
1/(1/(1/(x+1) + 1) +1)
Для облегчения вычислений эту дробь можно представить в виде итеративной процедуры, в которой для вычисления следующего шага нужно прибавить единицу к результату предыдущего шага и разделить единицу на получившееся число. Иными словами:
x0 = x
x(n + 1) = 1/(xn + 1).
Этот процесс сходится, и его предел равен φ + 1.
Если заменить вычисление обратной величины извлечением квадратного корня, то есть провести итеративный цикл:
x0 = x
x(n + 1) = √(xn + 1),
то результат останется неизменным: независимо от изначально выбранного x итерации сходятся к значению φ + 1.
Называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.
Грани призмы, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами
.
Все боковые ребра равны между собой как параллельные отрезки, ограниченные двумя параллельными плоскостями. Все боковые грани призмы являются параллелограммами. Соответствующие стороны оснований призмы равны и параллельны. Поэтому в основаниях лежат равные многоугольники.
Поверхность призмы
состоит из двух оснований и боковой поверхности.
Высотой призмы
называется отрезок, являющийся общим перпендикуляром плоскостей, в которых лежат основания призмы.
Высота призмы
равна расстоянию между плоскостями оснований.
Сечение призмы плоскостью, проведенной через два боковых ребра, не принадлежащих одной грани, называется диагональным сечением призмы
.
Прямой призмой
называется призма, у которой боковые ребра перпендикулярно плоскости основания, другие призмы называются наклонными.
Правильной призмой
называется прямая призма, основанием которой является правильный многоугольник.
Призма, основанием которой является параллелограмм, называется параллелепипедом
.
Пусть l
- боковое ребро; P
- периметр основания; S осн
- площадь основания;H
- высота; P сеч
- периметр перпендикулярного сечения; S сеч
– площадь перпендикулярного сечения; S б
- площадь боковой поверхности; V
- объем; S пп
- площадь полной поверхности призмы.
Произвольная призма
:
S б = P сеч ·l, V = S осн ·H, V = S сеч ·l
Прямая призма
:
S пп = S б + 2S осн, S б = P·H, V = S осн ·H
Решение задач
Пример 1
.
Площадь боковой поверхности правильной треугольной призмы равна площади основания. Вычислите длину бокового ребра, если сторона основания 7см.
Решение
.
Площадь основания призмы найдем по формуле: ![]() По условию эти площади равны, т.е.:
Ответ
: .
Пример 2
.
Найти площадь полной поверхности правильной треугольной призмы, сторона основания которой 6 см, а высота - 10 см.
Решение
.
Площадь основания призмы находится по формуле:
По условию эти площади равны, т.е.:
Ответ
: .
Пример 2
.
Найти площадь полной поверхности правильной треугольной призмы, сторона основания которой 6 см, а высота - 10 см.
Решение
.
Площадь основания призмы находится по формуле: ![]() Ответ
:
Пример 3
.
Основанием прямой призмы является равнобедренный треугольник, в котором высота, проведенная к основанию равна 8см, высота призмы равна 12см. Найдите полную поверхность призмы, если боковая грань что содержит основание треугольника - квадрат.
Решение
.
Ответ
:
Пример 3
.
Основанием прямой призмы является равнобедренный треугольник, в котором высота, проведенная к основанию равна 8см, высота призмы равна 12см. Найдите полную поверхность призмы, если боковая грань что содержит основание треугольника - квадрат.
Решение
.
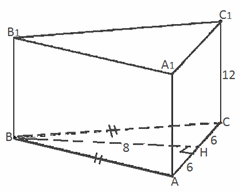 Площадь поверхности призмы будет равна сумме площадей оснований и сумме площадей боковых поверхностей, то есть
S = 2S ABC + S A1C1CA + 2S ABB1A1
.
Поскольку боковая грань, содержащая основание треугольника, является квадратом, то основание треугольника также равно 12 см (основание треугольника одновременно является стороной грани).
Ответ
: 480 см 2 .
Пример 4
.
Основание прямой призмы - треугольник со сторонами 5 и 3 см и углом 120 градусов между ними. Наибольшая из площадей боковых граней равна 35 см 2 , найти площадь боковой поверхности.
Решение
.
Площадь поверхности призмы будет равна сумме площадей оснований и сумме площадей боковых поверхностей, то есть
S = 2S ABC + S A1C1CA + 2S ABB1A1
.
Поскольку боковая грань, содержащая основание треугольника, является квадратом, то основание треугольника также равно 12 см (основание треугольника одновременно является стороной грани).
Ответ
: 480 см 2 .
Пример 4
.
Основание прямой призмы - треугольник со сторонами 5 и 3 см и углом 120 градусов между ними. Наибольшая из площадей боковых граней равна 35 см 2 , найти площадь боковой поверхности.
Решение
.
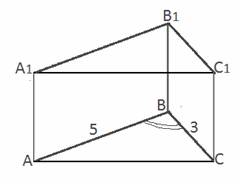 По теореме косинусов:a 2 = b 2 + c 2 - 2bc·cos
AC 2 = AB 2 + BC 2 - 2·AB·BC·cos120
AC 2 = 25 + 9 - 2·5·3·cos120
AC 2 = 34 - 30 ·(-0.5)
AC 2 = 49, AC = 7
см.
Каждая из граней боковой поверхности представляет собой прямоугольник с высотой, равной высоте призмы. Таким образом, боковая грань призмы наибольшей площади лежит на той стороне основания, длина стороны которого наибольшая.
То есть наибольшая из боковых граней имеет длину 7 см.
Тогда высота призмы равна 35/7 = 5
см.
S б = 5·5 + 3·5 + 7·5 = 75 см 2
Ответ
: 75 см 2 .
Пример 5
.
В правильной четырёхугольной призме площадь основания 144 см 2 , а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение
.
По теореме косинусов:a 2 = b 2 + c 2 - 2bc·cos
AC 2 = AB 2 + BC 2 - 2·AB·BC·cos120
AC 2 = 25 + 9 - 2·5·3·cos120
AC 2 = 34 - 30 ·(-0.5)
AC 2 = 49, AC = 7
см.
Каждая из граней боковой поверхности представляет собой прямоугольник с высотой, равной высоте призмы. Таким образом, боковая грань призмы наибольшей площади лежит на той стороне основания, длина стороны которого наибольшая.
То есть наибольшая из боковых граней имеет длину 7 см.
Тогда высота призмы равна 35/7 = 5
см.
S б = 5·5 + 3·5 + 7·5 = 75 см 2
Ответ
: 75 см 2 .
Пример 5
.
В правильной четырёхугольной призме площадь основания 144 см 2 , а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение
.
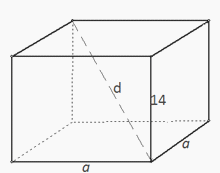 Sосн = a 2 = 144, a = 12 см.
d 2 = a 2 + a 2 + c 2 = 144 + 144 + 196 = 484 , d = 22 см.
S пп = 2S осн + 4S б.
S пп = 2· 144 + 4·12·14 = 288 + 336 = 624 см 2 .
Ответ
: диагональ 22 см, площадь полной поверхности 624 см 2 .
Пример 6
.
Определить полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение
.
Sосн = a 2 = 144, a = 12 см.
d 2 = a 2 + a 2 + c 2 = 144 + 144 + 196 = 484 , d = 22 см.
S пп = 2S осн + 4S б.
S пп = 2· 144 + 4·12·14 = 288 + 336 = 624 см 2 .
Ответ
: диагональ 22 см, площадь полной поверхности 624 см 2 .
Пример 6
.
Определить полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение
.
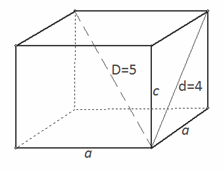 По теореме Пифагора:
d 2 = a 2 + c 2 , D 2 = a 2 + a 2 + c 2 = 2a 2 + c 2
.
Получим два уравнения с двумя неизвестными:
16 = a 2 + c 2 ,
25 = 2a 2 + c 2 .
Вычтем из второго уравнения первое: a 2 = 9, a = 3.
Тогда
По теореме Пифагора:
d 2 = a 2 + c 2 , D 2 = a 2 + a 2 + c 2 = 2a 2 + c 2
.
Получим два уравнения с двумя неизвестными:
16 = a 2 + c 2 ,
25 = 2a 2 + c 2 .
Вычтем из второго уравнения первое: a 2 = 9, a = 3.
Тогда
92. В правильной треугольной пирамиде ABCD (с вершиной D) сторона основания равна 2, а боковое ребро равно 4. Найдите площадь сечения пирамиды плоскостью KLM, где K, L, M середины рёбер AB, BC и CD соответственно.
93. В правильной треугольной призме ABCA1 B1 C1 боковое ребро равно 4, а сторона основания равна 6. Найдите площадь сечения призмы плоскостью, проходящей через точки A, B и середину ребра B1 C1 .
95. Ребро куба ABCDA1 B1 C1 D1 равно 4. Найдите площадь сечения куба плоскостью, проходящей через вершину D1 и середины рёбер AD и CD.
96. Ребро куба ABCDA1 B1 C1 D1 равно 4. Точка E середина ребра A1 D1 . Найдите площадь сечения куба плоскостью ACE.
97. В правильной четырёхугольной призме ABCDA1 B1 C1 D1 сторона основания равна 1, а высота равна 2. Точка M середина ребра AA1 . Найдите площадь сечения призмы плоскостью
BMD1 .
3 p
98. В прямоугольном параллелепипеде ABCDA1 B1 C1 D1 известны рёбра: AB = 3, AD = 3, AA1 = 5. Точка M расположена на ребре AA1 так, что AM = 4. а) Найдите площадь сечения параллелепипеда плоскостью BMD1 . б) Найдите угол между плоскостями BMD1 и ABC (указание: используйтетеорему о площади ортогональной проекции многоугольника ).
