Tanım. Eğer fonksiyon F(X) aralıkta tanımlanır [ a, b], aralığın her noktasında süreklidir ( a, b), noktada A sağda sürekli, bu noktada B solda sürekli ise fonksiyon deriz F(X) segmentte sürekli [a, b].
Başka bir deyişle, fonksiyon F(X) aralığında süreklidir [ a, b], eğer üç koşul karşılanırsa:
1) "X 0 Î( a, b): F(X) = F(X 0);
2) F(X) = F(A);
3) F(X) = F(B).
Bir aralıkta sürekli olan fonksiyonlar için, aşağıdaki teoremler şeklinde formüle ettiğimiz bazı özellikleri ispat yapmadan dikkate alıyoruz.
Teorem 1. Eğer fonksiyon F(X) aralığında süreklidir [ a, b], daha sonra bu segmentte minimum ve maksimum değerlerine ulaşır.
Bu teorem şunu belirtmektedir (Şekil 1.15) segmentte [ a, b] öyle bir nokta var ki X 1 şu F(X 1) £ F(X) herhangi biri için X itibaren [ a, b] ve bunun bir anlamı var X 2 (X 2 О[ a, b]) öyle ki " XÎ[ a, b] (F(X 2)³ F(X)).
Anlam F(X 1) belirli bir fonksiyon için en büyüğüdür [ a, b], A F(X 2) – en küçüğü. Şunu belirtelim: F(X 1) = M, F(X 2) =M. beri F(X) eşitsizlik geçerlidir: " XÎ[ a, b] M£ F(X) £ M, o zaman Teorem 1'den aşağıdaki sonucu elde ederiz.
Sonuçlar. Eğer fonksiyon F(X) bir aralıkta sürekli ise bu aralıkta sınırlıdır.
Teorem 2. Eğer fonksiyon F(X) aralığında süreklidir [ a,b] ve segmentin uçlarında farklı işaretlerin değerleri alınır, o zaman böyle bir iç nokta vardır X 0 bölüm [ a, b], burada fonksiyon 0'a döner, yani. $ X 0 Î ( a, b) (F(X 0) = 0).
Bu teorem, bir fonksiyonun grafiğinin y = f(X), aralıkta sürekli [ a, b], eksenle kesişiyor Öküz değerler en az bir kez F(A) Ve F(B) sahip olmak zıt işaretler. Yani, (Şekil 1.16) F(A) > 0, F(B) < 0 и функция F(X) bazı noktalarda 0 olur X 1 , X 2 , X 3 .
Teorem 3. Fonksiyona izin ver F(X) aralığında süreklidir [ a, b], F(A) = A, F(B) = B Ve A¹ B. (Şekil 1.17). Daha sonra herhangi bir sayı için C, sayıların arasına alınmış A Ve Böyle bir içsel nokta var ki X 0 bölüm [ a, b], Ne F(X 0) = C.
Sonuçlar. Eğer fonksiyon F(X) aralığında süreklidir [ a, b], M – en küçük değer F(X), M – en yüksek değer işlevler F(X) segmentte [ a, b] ise, işlev (en az bir kez) herhangi bir değeri alır M arasında sonuçlandırılmıştır M Ve M ve dolayısıyla segment [ m, M] tüm işlev değerlerinin kümesidir F(X) segmentte [ a, b].
Bir fonksiyonun aralıkta sürekli olup olmadığına dikkat edin ( a, b) veya segmentte [ a, b] süreksizlik noktaları varsa, böyle bir fonksiyon için Teorem 1, 2, 3'ün doğruluğu sona erer.
Sonuç olarak, ters bir fonksiyonun varlığına ilişkin teoremi düşünün.
Aralık derken, bir parçayı veya aralığı ya da yarım aralığı, sonlu veya sonsuzu kastettiğimizi hatırlayalım.
 |
Teorem 4. İzin vermek F(X) aralıkta süreklidir X, artar (veya azalır) X ve bir dizi değere sahiptir e. Daha sonra fonksiyon için y = f(X) ters bir fonksiyon var X= J(sen), aralıkta tanımlanmış e sürekli ve artan (veya azalan) e birden fazla anlamı olan X.
Yorum. Fonksiyona izin ver X= J(sen) fonksiyonun tersidir F(X). Argüman genellikle şu şekilde ifade edildiğinden X ve fonksiyon aracılığıyla sen, sonra yazacağız ters fonksiyon formda y =J(X).
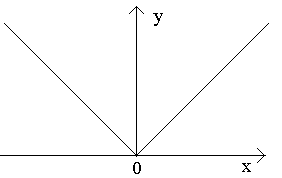
Örnek 1. İşlev y = x 2 (Şekil 1.8, a) sette X= A, B[ ve bu aralığın her noktasında süreklidir. O zaman aralıkta sürekli denir ] A, B[ . Bir fonksiyonun ]- ∞ formundaki aralıklarla süreklilik kavramı benzer şekilde tanımlanır, B[ , ]A, + ∞[ , ]- ∞, + ∞[ . Şimdi fonksiyona izin ver sen = F(X) aralıkta tanımlanır [ A, B] . Aralık ve doğru parçası arasındaki fark: Bir aralığın sınır noktaları aralığa dahil edilmez, ancak bir doğru parçasının sınır noktaları doğru parçasına dahil edilir. Burada tek taraflı süreklilik denilen şeyden bahsetmeliyiz: A, segmentte kalan [ A, B] , yalnızca sağdan ve noktaya yaklaşabiliriz B- yalnızca solda. Fonksiyonun aralıkta sürekli olduğu söylenir. A, B] eğer her şeyde sürekli ise iç noktalar bu segmentin sağ tarafında bu noktada süreklidir A ve noktada sürekli bırakılır B.
Sürekli bir fonksiyonun bir örneği, temel fonksiyonlardan herhangi biri olabilir. Her biri temel fonksiyon tanımlandığı herhangi bir aralıkta süreklidir. Örneğin, ve fonksiyonları herhangi bir aralıkta süreklidir [ A, B], fonksiyon [ aralığında süreklidir 0 , B] , fonksiyon nokta içermeyen herhangi bir parça üzerinde süreklidir A = 2 .
Örnek 4. Süreklilik açısından fonksiyonu inceleyin.
Çözüm. İlk koşulu kontrol edelim. Fonksiyon - 3 ve 3 noktalarında tanımlı değildir. Fonksiyonun tüm sayı doğrusu boyunca sürekliliği için şartlardan en az biri karşılanmamıştır. Bu yüzden bu fonksiyon aralıklarla süreklidir
.Örnek 5. Parametrenin hangi değerinde olduğunu belirleyin A boyunca sürekli tanım alanı işlev 
Çözüm.
Sağdan limiti şu şekilde bulalım:
![]() .
.
Açıkçası bu noktada değer X= 2 eşit olmalı balta :
![]()
A = 1,5 .
Örnek 6. Hangi parametre değerlerinde olduğunu belirleyin A Ve B boyunca sürekli tanım alanı işlev 
Çözüm.
Fonksiyonun sol taraftaki limitini şu noktada bulalım:
![]() .
.
Bu nedenle noktadaki değer 1 olmalıdır:
Bu noktada soldaki fonksiyonu bulalım:
Açıkçası, fonksiyonun bir noktadaki değeri şuna eşit olmalıdır:
Cevap: Fonksiyon tanım alanının tamamında süreklidir. A = 1; B = -3 .
Sürekli fonksiyonların temel özellikleri
Matematik sürekli fonksiyon kavramına öncelikle çeşitli hareket yasalarını inceleyerek ulaştı. Uzay ve zaman sonsuzdur ve bağımlılık, örneğin yollar S zaman zaman T kanunla ifade edilen S = F(T) sürekli bir örnek verir işlevler F(T). Isıtılan suyun sıcaklığı da sürekli olarak değişir; bu aynı zamanda zamanın sürekli bir fonksiyonudur: T = F(T) .
İÇİNDE matematiksel analiz bazı özellikleri kanıtlanmıştır sürekli fonksiyonlar. Bu özelliklerden en önemlilerini sunalım.
1. Bir aralıkta sürekli olan bir fonksiyon aralığın uçlarında farklı işaretlerin değerlerini alıyorsa, o zaman bu aralığın bir noktasında değeri alır sıfıra eşit. Daha resmi bir ifadeyle bu özellik, birinci Bolzano-Cauchy teoremi olarak bilinen bir teoremde verilmektedir.
2. İşlev F(X) , aralıkta sürekli [ A, B] , uç noktalardaki değerler arasındaki, yani arasındaki tüm ara değerleri alır. F(A) Ve F(B). Daha resmi bir ifadeyle bu özellik, ikinci Bolzano-Cauchy teoremi olarak bilinen bir teoremde verilmektedir.
Bir fonksiyonun aralıktaki sürekliliği
| Parametre adı | Anlam |
| Makale konusu: | Bir fonksiyonun aralıktaki sürekliliği |
| Puan anahtarı (tematik kategori) | Matematik |
Tanım. Bir fonksiyon genellikle bu aralığın her noktasında sürekli ise bu aralıkta sürekli olarak adlandırılır.
Fonksiyon şurada tanımlanmışsa X=A ve aynı zamanda F(X) = F(A),
sonra şunu söylüyorlar F(X) noktada ve sağda süreklidir. Aynı şekilde eğer F(X) = F(B), o zaman bunu söylüyorlar B bu fonksiyon sürekli sol.
Tanım. Bir fonksiyona genellikle [ aralığında sürekli denir. A, B], eğer her noktada sürekli ise (noktada) A sağda sürekli, bu noktada B– solda sürekli).
En yüksek değer işlevler en = F(X) segmentte [ A, B F(X 1) bu F(X) £ F(X 1) herkes için X Î [ A, B].
En düşük değer işlevler en = F(X) segmentte [ A, B] buna anlamı demek gelenekseldir F(X 2) bu F(X) ³ F(X 2) herkes için X Î [ A, B].
Bir aralıkta sürekli olan fonksiyonların bir takım özellikleri vardır. önemli özellikler aşağıdaki teoremlerle ifade edilir.
Teorem 3.3.1. Aralıkta sürekli bir fonksiyon [ A, B], minimum değerine ulaşır M ve en büyük değer M yani böyle noktalar var X 1 ve X Bu segmentin 2'si, yani F(X 1) = M, F(X 2) = M.
Teoremin basit bir geometrik anlamı vardır (bkz. Şekil 2).
 |
Teorem 3.3.2. Fonksiyonun olması durumunda en = F(X) aralığında süreklidir [ A, B] ve uçlarında eşit olmayan değerler alır F(A) = A, F(B) = B, A ¹ B ise A ile B arasında C sayısı ne olursa olsun bir nokta olacaktır İle Î [ A, B] öyle ki F(İle) = S.
Geometrik anlam Teorem Şekil 3'te gösterilmektedir. Herhangi bir düz çizgi en= C, burada A< C < B (или A >C > B), fonksiyonun grafiğiyle kesişir en = F(X).
Sonuçlar. Bir fonksiyon bir doğru parçası üzerinde sürekli ise ve uçlarında farklı işaretlerin değerlerini alıyorsa, o zaman bu parça üzerinde fonksiyonun sıfır olduğu en az bir nokta vardır.
Sonucun geometrik anlamı Şekil 4'te gösterilmektedir.

Kendini kontrol etmeye yönelik sorular
1. Hangi fonksiyona genellikle bir noktada sürekli denir?
2. Fonksiyonun artışı ve argümanlar açısından eşdeğer başka bir tanım verin.
3. İki sürekli fonksiyonun toplamı, farkı, çarpımı ve bölümü hakkında ne söylenebilir?
4. Argümanın hangi değerleri için bütünüyle rasyonel ve kesirli-rasyonel fonksiyonlar sürekli?
5. Karmaşık bir fonksiyon ne zaman bir noktada süreklidir?
6. Fonksiyonların kırılma noktası olarak adlandırılan şey nedir?
7. Hangi noktalara birinci türden süreksizlik noktaları denir?
8. Hangi niceliğe genellikle fonksiyon sıçraması denir?
9. "Çıkarılabilir kırılma noktası" kavramını açıklayınız. Örnekler verin.
10. Hangi noktalara ikinci türden süreksizlik noktaları denir? Örnekler verin.
11. “Aralıkta süreklilik”, “sağda süreklilik”, “solda süreklilik”, “doğru parçasında süreklilik” kavramlarını açıklayınız.
12. Fonksiyonların en büyük ve en küçük değerlerini tanımlayınız.
13. Bir fonksiyonun en büyük ve en küçük değerlerine sahip bir segment üzerindeki süreklilik arasındaki bağlantı hakkında bir teorem formüle edin. Bir çizimle açıklayınız.
14. Bir aralıktaki fonksiyonların sürekliliği ile fonksiyon değerlerinin aralığı arasındaki bağlantı hakkında bir teorem formüle edin. Geometrik anlamını şekilde gösterin.
15. Yukarıdaki teoremin ve onun geometrik yorumuna bir sonuç verin.
DERS No. 4
Ders konusu: Bir fonksiyonun türevi
Dersin özeti: Türev kavramı, geometrik ve fiziksel anlam. Farklılaşmanın temel kuralları. Türev karmaşık fonksiyon. Bazı uygulamalar türevdir.
4.1. Türev kavramı, geometrik ve fiziksel anlamı
İşlevi düşünün en = F(X), aralıkta belirtilir ] A, B[. İzin vermek XÎ ] A, B[ Ve X Î ] A, B[, ardından fonksiyonun o noktadaki artışı X 0, D formülüyle ifade edilir en = F(X 0+Gün X) – F(X 0).
Tanım. y fonksiyonunun türevi = F(X) noktada X 0'a genellikle bu fonksiyonun artışının argümanın artışına oranının, ikincisi sıfıra yaklaştığında oranının limiti denir:
F'(X 0) = ![]() veya sen"(X 0) =.
veya sen"(X 0) =.
Türevin geometrik anlamı: Belirli bir fonksiyonun bir noktadaki türevi, Ox ekseni arasındaki açının tanjantına ve bu fonksiyonun grafiğinin teğetine eşittir. karşılık gelen nokta(bkz. Şekil 1):
F"(X 0) = tan a.
BİR GÖRÜŞMEDE DEVAM EDEN FONKSİYONLARIN ÖZELLİKLERİ
Bir aralıkta sürekli olan fonksiyonların bazı özelliklerini ele alalım. Bu özellikleri kanıt olmadan sunuyoruz.
İşlev y = f(x) isminde segmentte sürekli [A, B], eğer bu parçanın tüm iç noktalarında ve uçlarında sürekli ise, yani. noktalarda A Ve B, sırasıyla sağda ve solda süreklidir.
Teorem 1. Aralıkta sürekli bir fonksiyon [ A, B], bu segmentin en az bir noktasında en büyük değeri alır ve en az bir noktasında en küçük değeri alır.
Teorem şunu belirtir: Eğer bir fonksiyon y = f(x) aralıkta süreklidir [ A, B], o zaman en az bir nokta var x 1 Î [ A, B] öyle ki fonksiyonun değeri f(x) bu noktada bu segmentteki tüm değerlerinin en büyüğü olacak: f(x 1) ≥ f(x). Benzer şekilde şöyle bir nokta var x 2, burada fonksiyon değeri segmentteki tüm değerlerin en küçüğü olacaktır: f(x 1) ≤ f(x).
Bu tür birkaç noktanın olabileceği açıktır; örneğin, şekil fonksiyonu göstermektedir; f(x) iki noktada en küçük değeri alır x 2 Ve X 2 ".
Yorum. Fonksiyonun değerini aralıkta düşünürsek, teoremin ifadesi yanlış olabilir ( A, B). Aslında fonksiyonu düşünürsek y = x(0, 2) üzerinde ise bu aralıkta süreklidir ancak içindeki en büyük veya en küçük değerlere ulaşmaz: aralığın uçlarında bu değerlere ulaşır ancak uçlar ait değildir bizim alanımıza.
Ayrıca teoremin süreksiz fonksiyonlar için geçerliliği sona erer. Bir örnek verin.
Sonuçlar. Eğer fonksiyon f(x) sürekli [ A, B], o zaman bu segmentte sınırlıdır.
Teorem 2. Fonksiyona izin ver y = f(x) aralıkta süreklidir [ A, B] ve bu parçanın uçlarında farklı işaretlerin değerleri alındığında, parçanın içinde en az bir nokta vardır x = C, burada fonksiyon sıfıra gider: f(C)= 0, burada a< C< b

Bu teoremin basit bir geometrik anlamı vardır: Sürekli bir fonksiyonun grafiğinin noktaları y = f(x), segmentin uçlarına karşılık gelir [ A, B] birlikte uzanmak farklı taraflar eksenden Öküz, bu durumda bu grafik, ekseni parçanın en az bir noktasında kesiyorsa Öküz. Süreksiz fonksiyonlar bu özelliğe sahip olmayabilir.
Bu teorem aşağıdaki genellemeyi kabul eder.
Teorem 3 (ara değer teoremi). Fonksiyona izin ver y = f(x) aralıkta süreklidir [ A, B] Ve f(a) = Bir, f(b) = B. Daha sonra herhangi bir sayı için C arasında sonuçlandırılmıştır A Ve B, bu segmentin içinde öyle bir nokta var ki CÎ [ A, B], Ne f(c) = C.

Bu teorem geometrik olarak açıktır. Fonksiyonun grafiğini düşünün y = f(x). İzin vermek f(a) = Bir, f(b) = B. Daha sonra herhangi bir düz çizgi y = C, Nerede C– arasında herhangi bir sayı A Ve B, fonksiyonun grafiğini en az bir noktada kesecektir. Kesişme noktasının apsisi bu değer olacaktır x = C, hangisinde f(c) = C.
Böylece, bir değerden diğerine hareket eden sürekli bir fonksiyon zorunlu olarak tüm ara değerlerden geçer. Özellikle:
Sonuçlar. Eğer fonksiyon y = f(x) Belirli bir aralıkta süreklidir ve en büyük ve en küçük değerleri alır, daha sonra bu aralıkta en küçük ve en büyük değerleri arasında yer alan herhangi bir değeri en az bir kez alır.
TÜREV VE UYGULAMALARI. TÜREV TANIMI
Biraz fonksiyonumuz olsun y=f(x), belirli bir aralıkta tanımlanır. Her bağımsız değişken değeri için X bu aralıktan fonksiyon y=f(x) belli bir anlamı vardır.
İki bağımsız değişken değerini düşünün: başlangıç X 0 ve yeni X.

Fark x–x 0 denir x argümanını artırarak bu noktada X 0 ve gösterilir Δx. Böylece, Δx = x – x 0 (bağımsız değişken artışı pozitif veya negatif olabilir). Bu eşitlikten şu sonuç çıkıyor x=x 0 +Δx, yani orijinal anlam değişken bir miktar artış aldı. O zaman eğer bu noktada X 0 fonksiyon değeri şuydu: f(x 0 ), sonra içeri yeni nokta X fonksiyon değeri alacak f(x) = f(x 0 +Δx).
Fark y-y 0 = f(x) – f(x) 0 ) isminde fonksiyon artışı y = f(x) bu noktada X 0 ve sembolüyle gösterilir Δy. Böylece,
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) . | (1) |
Genellikle argümanın başlangıç değeri X 0 sabit kabul edilir ve yeni değer X– değişken. Daha sonra sen 0 = f(x 0 ) sabit olduğu ortaya çıkıyor ve y = f(x)– değişken. Artışlar Δy Ve Δx aynı zamanda değişkenler olacaktır ve formül (1) şunu gösterir: Dy bir değişkenin fonksiyonudur Δx.
Fonksiyonun artışının argümanın artışına oranını oluşturalım
Bu oranın limitini bulalım. Δx→0. Bu limit mevcutsa buna bu fonksiyonun türevi denir. f(x) bu noktada X 0 ve belirtmek F "(X 0). Bu yüzden,
Türev bu fonksiyon y = f(x) bu noktada X 0, Δ fonksiyonunun artış oranının limiti olarak adlandırılır sen argüman artışına Δ X ikincisi keyfi olarak sıfıra yöneldiğinde.
Aynı fonksiyon için türevin çeşitli noktalar X farklı değerler alabilir, yani türev argümanın bir fonksiyonu olarak düşünülebilir X. Bu işlev belirlenmiş F "(X)
Türev sembollerle gösterilir F "(x),y ", . Özel anlam türev x = bir ile gösterilir F "(A) veya sen "| x=a.
Bir fonksiyonun türevini bulma işlemi f(x) bu fonksiyonun farklılaşması denir.
Türevi doğrudan tanım gereği bulmak için aşağıdakileri kullanabilirsiniz: temel kural:
Örnekler.
TÜREVİN MEKANİK ANLAMI
Fizikten kanunun olduğu bilinmektedir. düzgün hareket benziyor s = v t, Nerede S– zamanın anına kadar katedilen yol T, v– düzgün hareket hızı.
Ancak, çünkü Doğada meydana gelen hareketlerin çoğu eşitsizdir; genel olarak hız ve dolayısıyla mesafe S zamana bağlı olacak T, yani zamanın bir fonksiyonu olacaktır.
Öyleyse, yasaya göre maddi bir noktanın tek yönde düz bir çizgide hareket etmesine izin verin. s=s(t).
Zamanda belirli bir noktayı işaretleyelim T 0. Bu noktada nokta yolu geçti s=s(t 0 ). Hızı belirleyelim v zamanın bir anında maddi bir nokta T 0 .
Bunu yapmak için zamandaki başka bir noktayı ele alalım T 0 + Δ T. Katedilen yola karşılık gelir =s(t 0 + Δ T). Daha sonra belirli bir süre boyunca Δ T nokta Δs yolunu kat etti =s(t 0 + Δ T)–s(t).
Tutumu ele alalım. Δ zaman aralığındaki ortalama hıza denir. T. Ortalama hız şu anda bir noktanın hareket hızını doğru bir şekilde karakterize edemez T 0 (çünkü hareket düzensizdir). Bu gerçek hızı daha doğru bir şekilde ifade etmek için ortalama hız, daha kısa bir süre ayırmanız gerekir Δ T.
Yani hareket hızı şu anda zaman T 0 (anlık hız), aralıktaki ortalama hızın sınırıdır. T 0 ila T 0 +Δ T, ne zaman Δ T→0:
![]() ,
,
onlar. düzensiz hız bu zamana göre kat edilen mesafenin türevidir.

TÜREVİN GEOMETRİK ANLAMI
Öncelikle belirli bir noktadaki bir eğriye teğetin tanımını verelim.
Bir eğri ve üzerinde sabit bir nokta olsun M 0(şekle bakın). Başka bir noktayı düşünün. M bu eğri ve bir sekant çizin M 0 M. Eğer nokta M eğri boyunca hareket etmeye başlar ve nokta M 0 hareketsiz kalırsa sekant konumu değişir. Eğer noktanın sınırsız yaklaşımıyla M bir eğri boyunca bir noktaya M 0 herhangi bir tarafta sekant belirli bir düz çizginin konumunu işgal etme eğilimindedir M 0 T, sonra düz M 0 T belirli bir noktada eğrinin teğeti denir M 0.
O., teğet belirli bir noktadaki eğriye M 0 sekantın sınır konumu denir M 0 M ne zaman nokta M eğri boyunca bir noktaya doğru yönelir M 0.
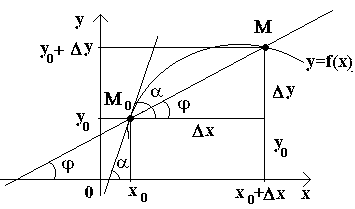
Şimdi sürekli fonksiyonu ele alalım y=f(x) ve bu fonksiyona karşılık gelen eğri. Bir miktar değerde X 0 fonksiyonu değer alır y 0 =f(x 0). Bu değerler X 0 ve sen Eğri üzerindeki 0 bir noktaya karşılık gelir M 0 (x 0; y 0). Argümanı verelim x 0Δ'yı artır X. Bağımsız değişkenin yeni değeri, işlevin artan değerine karşılık gelir sen 0 +Δ y=f(x 0 –Δ X). Ana noktayı anladık M(x 0+Δ X; y 0+Δ y). Haydi bir sekant çizelim M 0 M ve eksenin pozitif yönü ile bir sekantın oluşturduğu açıyı φ ile belirtin Öküz. Bir ilişki yaratalım ve bunu fark edelim.
Şimdi ise Δ X→0 ise Δ fonksiyonunun sürekliliğinden dolayı en→0 ve dolayısıyla nokta M Bir eğri boyunca hareket ederek sınırsız noktaya yaklaşır M 0. Daha sonra sekant M 0 M noktasındaki eğriye teğet konumunu alma eğiliminde olacaktır. M 0 ve Δ'daki φ→α açısı X→0, burada α, teğet ile eksenin pozitif yönü arasındaki açıyı belirtir Öküz. tan φ fonksiyonu φ≠π/2 için sürekli olarak φ'ye bağlı olduğundan, φ→α tan φ → tan α için ve dolayısıyla tanjantın eğimi şöyle olacaktır:
![]()
onlar. f "(x)= tgα.
Böylece geometrik olarak y "(x 0) noktada bu fonksiyonun grafiğine teğetin eğimini temsil eder x 0, yani en verilen değer argüman X türev, fonksiyonun grafiğine teğetin oluşturduğu açının teğetine eşittir f(x) uygun noktada M 0 (x; y) pozitif eksen yönü ile Öküz.
Örnek. Bulmak eğim eğriye teğet y = x 2 noktada M(-1; 1).
Bunu daha önce de görmüştük ( X 2)" = 2X. Ancak eğriye teğetin açısal katsayısı tan α = sen"| x=-1 = – 2.
FONKSİYONLARIN DİĞERLENEBİLİRLİĞİ. DİFERANSİYEL FONKSİYONUN SÜREKLİLİĞİ
İşlev y=f(x) isminde türevlenebilir bir noktada X 0 eğer bu noktada belirli bir türevi varsa, yani ilişkinin sınırı mevcut ve sonlu ise.
Bir fonksiyon belirli bir parçanın her noktasında türevlenebilirse [ A; B] veya aralık ( A; B), sonra diyorlar ki o türevlenebilir segmentte [ A; B] veya sırasıyla aralıkta ( A; B).
Türevlenebilir ve sürekli fonksiyonlar arasındaki bağlantıyı kuran aşağıdaki teorem geçerlidir.
Teorem. Eğer fonksiyon y=f(x) bir noktada farklılaşabilir x 0 ise bu noktada süreklidir.
Böylece bir fonksiyonun türevlenebilirliğinden sürekliliği ortaya çıkar.
Kanıt. Eğer ![]() , O
, O
![]() ,
,
burada α sonsuz küçük bir miktardır, yani Δ olarak sıfıra yaklaşan bir miktar X→0. Ama sonra
Δ sen=F "(x 0) Δ X+αΔ X=> Δ sen→ 0'da Δ X→0, yani f(x) – f(x 0)→0 saat X→X 0 , bu, işlevin olduğu anlamına gelir f(x) bir noktada sürekli X 0. Q.E.D.
Dolayısıyla fonksiyonun süreksizlik noktalarında türevi olamaz. Bunun tersi doğru değildir: Bazı noktalarda türevi alınamayan (yani bu noktalarda türevi olmayan) sürekli fonksiyonlar vardır.
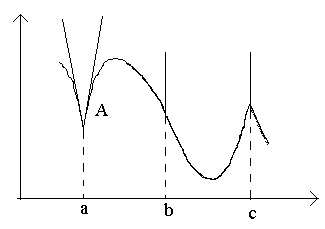
Şekildeki noktaları göz önünde bulundurun a, b, c.
bu noktada AΔ'da X→0 oranının limiti yoktur (çünkü tek taraflı limitler Δ için farklıdır) X→0–0 ve Δ X→0+0). bu noktada A grafiğin tanımlı bir teğeti yoktur ancak eğimleri olan iki farklı tek yönlü teğet vardır İle 1 ve İle 2. Bu tür noktalara köşe noktası denir.
bu noktada BΔ'da X→0 ilişkisi süresiz olarak sabit işaretlidir büyük boy. Fonksiyonun sonsuz türevi vardır. Bu noktada grafiğin dikey bir teğeti vardır. Nokta türü – dikey bir teğetin “bükülme noktası”.
bu noktada C Tek taraflı türevler sonsuz büyük miktarlarda farklı işaretlerden oluşur. Bu noktada grafiğin birleştirilmiş iki dikey teğeti vardır. Tip – dikey teğet ile “dönüş noktası” – özel durum köşe noktası.