Со помош на онлајн калкулатор можете да најдете точки на флексија и интервали на конвексност на функционалниот графиксо дизајнот на решението во Word. Дали функцијата од две променливи f(x1,x2) е конвексна се решава со помош на Хесијанската матрица.
Правила за внесување функции:
Насоката на конвексност на графикот на функцијата. Точки на флексија
Дефиниција: Кривата y=f(x) се нарекува конвексна надолу во интервалот (a; b) ако лежи над тангентата во која било точка од овој интервал.Дефиниција: За кривата y=f(x) се вели дека е конвексна нагоре во интервалот (a; b) ако лежи под тангентата во која било точка од овој интервал. 
Дефиниција: Интервалите во кои графикот на функцијата е конвексен нагоре или надолу се нарекуваат интервали на конвексност на графикот на функцијата.
Конвексноста надолу или нагоре на кривата која е график на функцијата y=f(x) се карактеризира со знакот на нејзиниот втор извод: ако во одреден интервал f''(x) > 0, тогаш кривата е конвексна надолу на овој интервал; ако f''(x)< 0, то кривая выпукла вверх на этом промежутке.
Дефиниција: Точка на графикот на функцијата y=f(x) која ги одвојува интервалите на конвексност спротивни насокина овој график се нарекува точка на флексија. 
Точките на флексија можат да послужат само критични точки II вид, т.е. точки кои припаѓаат на доменот на дефиниција на функцијата y = f(x) при што вториот извод f’’(x) исчезнува или има дисконтинуитет.
Правилото за наоѓање точки на флексија во графикот на функцијата y = f(x)
- Најдете го вториот извод f’’(x) .
- Најдете критични точки од вториот вид на функцијата y=f(x), т.е. точката во која f''(x) исчезнува или доживува дисконтинуитет.
- Истражете го знакот на вториот извод f’’(x) во интервалот во кој пронајдените критични точки го делат доменот на дефиниција на функцијата f(x). Ако критичната точка x 0 ги одвојува интервалите на конвексност на спротивни насоки, тогаш x 0 е апсциса на точката на флексија на функционалниот график.
- Пресметајте ги вредностите на функциите на точките на флексија.
Пример 1. Најдете ги интервалите на конвексност и точките на флексија на следнава крива: f(x) = 6x 2 –x 3.
Решение: Најдете f ‘(x) = 12x – 3x 2 , f ‘’(x) = 12 – 6x.
Да ги најдеме критичните точки на вториот извод со решавање на равенката 12-6x=0. x=2. 
f(2) = 6*2 2 – 2 3 = 16
Одговор: Функцијата е конвексна нагоре за x∈(2; +∞) ; функцијата е конвексна надолу при x∈(-∞; 2) ; точка на флексија (2;16) .
Пример 2. Дали функцијата има точки на флексија: f(x)=x 3 -6x 2 +2x-1
Пример 3. Најдете ги интервалите каде графикот на функцијата е конвексен и закривен: f(x)=x 3 -6x 2 +12x+4
График на функција y=f(x)повикани конвекснина интервалот (а; б), ако се наоѓа под некоја од неговите тангенти на овој интервал.
График на функција y=f(x)повикани конкавнана интервалот (а; б), ако се наоѓа над некоја од неговите тангенти на овој интервал.
Сликата покажува крива која е конвексна на (а; б)и конкавна на (б; в).
Примери.
Да разгледаме доволен критериум за да утврдиме дали графикот на функцијата ќе биде внатре даден интервалконвексни или конкавни.
Теорема. Нека y=f(x)диференцијабилна на (а; б). Ако во сите точки од интервалот (а; б)втор извод на функцијата y = f(x)негативно, т.е. ѓ ""(x) < 0, то график функции на этом интервале выпуклый, если же ѓ""(x) > 0 – конкавна.
Доказ. Да претпоставиме за дефинитивно тоа ѓ""(x) < 0 и докажем, что график функции будет выпуклым.
Да ги земеме функциите на графиконот y = f(x) произволна точка М0со апсциса x 0 Î ( а; б) и исцртај низ точката М0тангента. Нејзината равенка. Мора да покажеме дека графикот на функцијата на (а; б)лежи под оваа тангента, т.е. со иста вредност xордината на крива y = f(x)ќе биде помала од ординатата на тангентата.
Значи, равенката на кривата е y = f(x). Да ја означиме ординатата на тангентата што одговара на апсцисата x. Потоа. Следствено, разликата помеѓу ординатите на кривата и тангентата за иста вредност xќе .
Разлика f(x) – f(x 0)трансформираат според теоремата на Лагранж, каде впомеѓу xИ x 0.
Така,
Повторно ја применуваме теоремата на Лагранж на изразот во квадратни загради: , каде в 1помеѓу c 0И x 0. Според условите на теоремата ѓ ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Така, секоја точка на кривата лежи под тангентата на кривата за сите вредности xИ x 0 Î ( а; б), што значи дека кривата е конвексна. Вториот дел од теоремата се докажува на сличен начин.
Примери.
Графичка точка континуирана функција, одвојувајќи го својот конвексен дел од конкавниот дел, се нарекува точка на флексија.
Очигледно, во точката на флексија, тангентата, доколку постои, ја пресекува кривата, бидејќи на едната страна од оваа точка кривата лежи под тангентата, а од другата страна - над неа.
Да утврдиме доволни услови за тоа дадена точкакривата е точка на флексија.
Теорема. Нека кривата е дефинирана со равенката y = f(x). Ако ѓ ""(x 0) = 0 или ѓ ""(x 0) не постои дури и кога поминува низ вредноста x = x 0дериват ѓ ""(x) го менува знакот, па точката во графикот на функцијата со апсцисата x = x 0има точка на флексија.
Доказ. Нека ѓ ""(x) < 0 при x < x 0И ѓ ""(x) > 0 во x > x 0. Потоа во x < x 0кривата е конвексна, и кога x > x 0– конкавна. Затоа, поентата А, легнат на кривината, со апсциса x 0има точка на флексија. Слично може да се разгледа и вториот случај, кога ѓ ""(x) > 0 во x < x 0И ѓ ""(x) < 0 при x > x 0.
Така, точките на флексија треба да се бараат само меѓу оние точки каде што вториот извод исчезнува или не постои.
Примери.Најдете ги точките на флексија и определете ги интервалите на конвексност и конкавност на кривите.
АСИМПТОТИ НА ГРАФИКОТ НА ФУНКЦИЈАТА
Кога се проучува функцијата, важно е да се утврди обликот на нејзиниот график на неограничено растојание од точката на графиконот од потеклото.
Од особен интерес е случајот кога графикот на функцијата, кога нејзината променлива точка е отстранета до бесконечност, на неодредено време се приближува до одредена права линија.
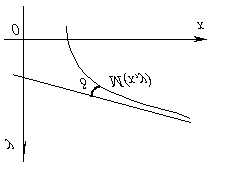
Правата линија се нарекува асимптотафункционална графика y = f(x), ако растојанието од променливата точка Мграфика на оваа линија кога се отстранува точка Мдо бесконечност се стреми кон нула, т.е. точка на графикот на функцијата, како што се стреми кон бесконечност, мора неодредено да се приближува до асимптотата.
Кривата може да се приближи до својата асимптота додека останува на едната страна од неа или со различни страни, бесконечно множествоеднаш преминувајќи ја асимптотата и движејќи се од едната на другата страна.
Ако со d го означиме растојанието од точката Мкрива до асимптота, тогаш е јасно дека d се стреми кон нула додека точката се оддалечува Мдо бесконечност.
Понатаму ќе правиме разлика помеѓу вертикални и коси асимптоти.
ВЕРТИКАЛНИ АСИМПТОТИ
Нека во x→ x 0од која било странична функција y = f(x)се зголемува неограничено во апсолутна вредност, т.е. или или 
. Потоа од дефиницијата за асимптота произлегува дека правата линија x = x 0е асимптота. Очигледно е и спротивното, ако линијата x = x 0е асимптота, т.е. .
Така, вертикалната асимптота на графикот на функцијата y = f(x)се нарекува права линија ако f(x)→ ∞ под барем еден од условите x→ x 0– 0 или x → x 0 + 0, x = x 0
Затоа, да се најдат вертикалните асимптоти на графикот на функцијата y = f(x)треба да се најдат тие вредности x = x 0, при што функцијата оди до бесконечност (трпи бесконечен дисконтинуитет). Потоа вертикална асимптотаја има равенката x = x 0.
Примери.
Косо АСИМПТОТИ
Бидејќи асимптотата е права линија, тогаш ако кривата y = f(x)има коси асимптота, тогаш нејзината равенка ќе биде y = kx + б. Наша задача е да ги најдеме коефициентите кИ б.
Теорема. Директно y = kx + бслужи како коси асимптота кај x→ +∞ за графикот на функцијата y
= f(x)тогаш и само кога 
. Слична изјава важи и за x → –∞.
Доказ. Нека пратеник- должина на сегментот, еднакво на растојаниетоод точка Мда асимптотира. По услов. Да го означиме со φ аголот на наклонетост на асимптотата кон оската Вол. Потоа од ΔMNPследува дека . Бидејќи φ е константен агол (φ ≠ π/2), тогаш , но
При проучување на функција и конструирање на нејзиниот график, во една фаза одредуваме точки на флексија и интервали на конвексност. Овие податоци, заедно со интервалите на зголемување и намалување, овозможуваат шематски да се прикаже графикот на функцијата што се проучува.
Понатамошната презентација претпоставува дека можете да направите до одреден ред и различни типови.
Да почнеме да го проучуваме материјалот со потребни дефинициии концепти. Следно, ќе ја изразиме врската помеѓу вредноста на вториот извод на функцијата на одреден интервал и насоката на неговата конвексност. По ова, ќе преминеме на условите што ни овозможуваат да ги одредиме точките на флексија на функционалниот график. Според текстот што ќе го дадеме типични примерисо детални решенија.
Навигација на страница.
Конвексност, конкавност на функција, точка на флексија.
Дефиниција.
конвексен надолуна интервалот X ако неговиот график се наоѓа не пониско од тангентата на него во која било точка од интервалот X.
Дефиниција.
Се нарекува функцијата што треба да се диференцира конвексен нагорена интервалот X ако неговиот график не се наоѓа повисоко од тангентата на него во која било точка од интервалот X.
Често се нарекува нагорна конвексна функција конвекснии конвексен надолу - конкавна.
Погледнете го цртежот што ги илустрира овие дефиниции.
Дефиниција.
Точката се нарекува точка на флексија на функционалниот график y=f(x) ако во дадена точка има тангента на графикот на функцијата (може да биде паралелна со оската Oy) и има соседство на точката во која лево и десно од точката М графикот на функцијата има различни насоки на конвексност.
Со други зборови, точката М се нарекува точка на флексија на графикот на функцијата ако во оваа точка има тангента и графикот на функцијата ја менува насоката на конвексноста, поминувајќи низ неа.
Доколку е потребно, погледнете го делот за да се потсетите на условите за постоење на невертикална и вертикална тангента.
Сликата подолу покажува неколку примери на точки на флексија (означени со црвени точки). Забележете дека некои функции може да немаат точки на флексија, додека други може да имаат една, неколку или бесконечно многу точки на флексија.
Наоѓање интервали на конвексност на функција.
Дозволете ни да формулираме теорема што ни овозможува да ги одредиме интервалите на конвексност на функцијата.
Теорема.
Ако функцијата y=f(x) има конечен втор извод на интервалот X и ако важи неравенството 
(), тогаш графикот на функцијата има конвексност насочена надолу (нагоре) од X.
Оваа теорема ви овозможува да ги пронајдете интервалите на конкавност и конвексност на функцијата; треба само да ги решите неравенките и, соодветно, доменот на дефиниција на оригиналната функција.
Треба да се забележи дека точките во кои е дефинирана функцијата y=f(x), а вториот извод не постои ќе бидат вклучени во интервалите на конкавност и конвексност.
Ајде да го разбереме ова со пример.
Пример.
Откријте ги интервалите на кои графикот на функцијата 
има конвексност насочена нагоре и конвексност насочена надолу.
Решение.
Доменот на функцијата е целото множество реални броеви.
Ајде да го најдеме вториот извод. 
Доменот на дефиниција на вториот извод се совпаѓа со доменот на дефиниција на оригиналната функција, затоа, за да се дознаат интервалите на конкавност и конвексност, доволно е да се реши и соодветно. 
Затоа, функцијата е конвексна надолу во интервалот и конвексна нагоре на интервалот.
Графичка илустрација.
Делот од графикот на функцијата во конвексниот интервал е прикажан со сина боја, а во интервалот на вдлабнатина – со црвена боја.
Сега да разгледаме пример кога доменот на дефиниција на вториот извод не се совпаѓа со доменот на дефиниција на функцијата. Во овој случај, како што веќе забележавме, точките од доменот на дефиниција во кои не постои конечен втор извод треба да бидат вклучени во интервалите на конвексност и (или) конкавност.
Пример.
Најдете ги интервалите на конвексност и конкавност на графикот на функцијата.
Решение.
Да почнеме со доменот на функцијата:
Ајде да го најдеме вториот дериват: 
Доменот на дефиниција на вториот извод е множеството 
. Како што можете да видите, x=0 припаѓа на доменот на оригиналната функција, но не припаѓа на доменот на вториот извод. Не заборавајте за оваа точка; ќе треба да се вклучи во интервалот на конвексност и (или) конкавност.
Сега решаваме неравенки на доменот на дефиниција на оригиналната функција. Ајде да аплицираме. Бројач на изразување 
оди на нула во 
или 
, именителот – на x = 0 или x = 1. Шематски ги исцртуваме овие точки на бројната права и го дознаваме знакот на изразот на секој од интервалите вклучени во доменот на дефиниција на оригиналната функција (тоа е прикажано како засенчена област на долната нумеричка линија). За позитивна вредност ставаме знак плус, за негативна вредност ставаме знак минус. 
Така,
И 
Затоа, со вклучување на точката x=0, го добиваме одговорот.
На 
графикот на функцијата има конвексност насочена надолу, кога 
- конвексност насочена нагоре.
Графичка илустрација.
Делот од графиконот на функцијата на интервалот на конвексност е прикажан со сина боја, на интервалите на вдлабнатина - со црвена боја, црната линија со точки е вертикална асимптота.
Потребни и доволни услови за флексија.
Неопходен услов за флексија.
Ајде да формулираме неопходен условфлексијафункционална графика.
Нека графикот на функцијата y=f(x) има флексија во точка и има континуиран втор извод, тогаш важи еднаквоста.
Од овој услов произлегува дека апсцисата на точките на флексија треба да се бара меѓу оние кај кои исчезнува вториот извод на функцијата. НО, овој услов не е доволен, односно не сите вредности во кои вториот дериват е еднаков на нула се апсциси на точките на флексија.
Исто така, треба да се забележи дека дефиницијата за точка на флексија бара постоење на тангента линија, или вертикална. Што значи тоа? А тоа значи следново: апсцисите на точките на флексија можат да бидат сè од доменот на дефинирање на функцијата за која 
И 
. Тоа се обично точките во кои исчезнува именителот на првиот извод.
Првиот доволен услов за флексија.
Откако ќе се најде сето она што може да биде абсциси на точки на флексија, треба да го користите првиот доволен услов за флексијафункционална графика.
Нека функцијата y=f(x) е непрекината во точката, има тангента (можеби вертикална) на неа и нека оваа функција има втор извод во некое соседство на точката. Потоа, ако во ова соседство лево и десно од , вториот извод има различни знаци, тогаш е точката на флексија на графикот на функцијата.
Како што можете да видите на првиот доволна состојбане бара постоење на вториот извод во самата точка, туку бара негово постоење во соседството на точката.
Сега да ги сумираме сите информации во форма на алгоритам.
Алгоритам за наоѓање точки на флексија на функција.
Ги наоѓаме сите апсциси на можни точки на флексија на графикот на функцијата (или И ) и дознај со поминување низ кој вториот извод го менува знакот. Таквите вредности ќе бидат апсцисата на точките на флексија, а соодветните точки ќе бидат точките на флексија на функционалниот график.
Ајде да погледнеме два примери за наоѓање точки на флексија за појаснување.
Пример.
Најдете точки на флексија и интервали на конвексност и конкавност на графикот на функцијата 
.
Решение.
Доменот на функцијата е целото множество од реални броеви.
Ајде да го најдеме првиот дериват: 
Доменот на дефиниција на првиот извод е и целото множество реални броеви, па затоа и еднаквостите И не се исполнува за ниту еден .
Ајде да го најдеме вториот дериват:
Ајде да дознаеме во кои вредности на аргументот x вториот извод оди на нула: 
Така, апсцисите на можните точки на флексија се x=-2 и x=3.
Сега останува да се провери, користејќи доволен знак на флексија, во која од овие точки вториот дериват го менува знакот. За да го направите ова, нацртајте ги точките x=-2 и x=3 на бројната оска и, како во метод на генерализиран интервал, ги поставуваме знаците на вториот извод над секој интервал. Под секој интервал, насоката на конвексност на функционалниот график е прикажана шематски со лакови. 
Вториот извод го менува знакот од плус во минус, поминувајќи низ точката x=-2 од лево кон десно и го менува знакот од минус во плус, поминувајќи низ x=3. Според тоа, и x=-2 и x=3 се апсциса на точките на флексија на функционалниот график. Тие одговараат на графичките точки и .
Погледнувајќи ја бројната права и знаците на вториот извод на неговите интервали, можеме да извлечеме заклучоци за интервалите на конвексност и конкавност. Графикот на функцијата е конвексен на интервалот и конкавен на интервалите и .
Графичка илустрација.
Делот од функционалниот графикон на конвексниот интервал е прикажан со сина боја, на интервалот на вдлабнатина – со црвена боја, а точките на флексија се прикажани како црни точки.
Пример.
Најдете ја апсцисата на сите точки на флексија на функционалниот график 
.
Решение.
Доменот на дефиниција на оваа функција е целокупното множество реални броеви.
Ајде да го најдеме дериватот. 
Првиот извод, за разлика од оригиналната функција, не е дефиниран на x=3. Но 
И 
. Според тоа, во точката со апсциса x=3 има вертикална тангента на графикот на првобитната функција. Така, x=3 може да биде апсциса на точката на флексија на функционалниот график.
Го наоѓаме вториот дериват, неговиот домен на дефиниција и точките во кои исчезнува: 
Добивме уште две можни апсциси на точки на флексија. Ги означуваме сите три точки на бројната права и го одредуваме знакот на вториот извод на секој од добиените интервали. 
Вториот дериват го менува знакот кога минува низ секоја од точките, затоа, сите тие се апсциси на точките на флексија.
Инструкции
Поени флексија функциимора да припаѓа на доменот на неговата дефиниција, кој мора прво да се најде. Распоред функциие линија која може да биде континуирана или да има прекини, монотоно да се намалува или зголемува, да има минимум или максимум поени(асимптоти), да бидат конвексни или конкавни. Острата промена во последните две состојби се нарекува точка на флексија.
Неопходен услов за постоење флексија функциисе состои во еднаквост на секунда до нула. Така, со диференцирање на функцијата двапати и изедначување на добиениот израз на нула, можеме да ја најдеме апсцисата на можни точки флексија.
Овој услов произлегува од дефиницијата на својствата на конвексност и конкавност на графикот функции, т.е. негативни и позитивна вредноствтор дериват. Во точката флексија ненадејна променаовие својства, што значи дека изводот ја поминува нултата ознака. Сепак, тоа што е еднакво на нула сè уште не е доволно за да укаже на флексија.
Постојат два доволни услови дека апсцисата пронајдена во претходната фаза припаѓа на точката флексија:Преку оваа точка можете да нацртате тангента на функции. Вториот дериват има различни знаци десно и лево од очекуваниот поени флексија. Така, неговото постоење во самата точка не е неопходно, доволно е да се утврди дека во неа таа го менува знакот. функциие еднаква на нула, а третата не е.
Решение: Најдете. ВО во овој случајнема ограничувања, затоа, тоа е целиот простор на реалните броеви. Пресметај го првиот извод: y’ = 3 ∛(x - 5) + (3 x + 3)/∛(x - 5)².
Обрни внимание на . Од ова произлегува дека доменот на дефинирање на изводот е ограничен. Точката x = 5 е пробиена, што значи дека низ неа може да помине тангента, што делумно одговара на првиот знак на доволност флексија.
Определи го добиениот израз за x → 5 – 0 и x → 5 + 0. Тие се еднакви на -∞ и +∞. Докажавте дека низ точката x=5 минува вертикална тангента. Оваа точка може да испадне да биде точка флексија, но прво пресметајте го вториот извод: Y'' = 1/∛(x - 5)² + 3/∛(x - 5)² – 2/3 (3 x + 3)/∛(x - 5)^5 = (2 x – 22)/∛(x - 5)^5.
Исфрлете го именителот бидејќи веќе сте ја земале предвид точката x = 5. Решете ја равенката 2 x – 22 = 0. Има еден корен x = 11. Последниот чекор е да се потврди дека поени x=5 и x=11 се точки флексија. Анализирајте го однесувањето на вториот дериват во нивна близина. Очигледно, во точката x = 5 го менува знакот од „+“ во „-“, а во точката x = 11 - обратно. Заклучок: и двете поенисе поени флексија. Првиот доволен услов е задоволен.