Теорема. Нека функцијата x=φ(t)континуирано во една точка а, и функцијата y=f(x)континуирано во една точка b=φ(a). Потоа комплексната функција y=f[φ(t)]=F(t)континуирано во една точка а.

Нека x=φ(t)И y=f(x)- наједноставните елементарни функции, со многу вредности (x)функции x=φ(t)е обемот на функцијата y=f(x). Како што знаеме, елементарните функции се континуирани во секоја точка од дадениот домен. Затоа, според претходната теорема, комплексната функција y=f(φ(t)), односно суперпозицијата на две елементарни функции е континуирана. На пример, функцијата е континуирана во која било точка x ≠ 0, како сложена функција од две елементарни функции x=t -1И y=sin x. Исто така функционира y=ln грев xконтинуирано во која било точка од интервалите (2kπ,(2k+1)π), k ∈ Z (грев x>0).

Дефиниција.Нека функцијата y = f(x) е дефинирана во точката x0 и некое нејзино соседство. Се повикува функцијата y = f(x). континуирано во точката x0, Ако:

1. постои
2. оваа граница е еднаква на вредноста на функцијата во точката x0:

При дефинирањето на границата беше нагласено дека f(x) не може да се дефинира во точката x0, а доколку е дефинирана во оваа точка, тогаш вредноста на f(x0) на никаков начин не учествува во одредувањето на границата. При одредување на континуитет, фундаментално е дека постои f(x0) и оваа вредност мора да биде еднаква на lim f(x).

Дефиниција.Нека функцијата y = f(x) е дефинирана во точката x0 и некое нејзино соседство. Функцијата f(x) се нарекува континуирана во точка x0 ако за сите ε>0 има позитивен број δ таков што за сите x во δ-соседството на точката x0 (т.е. |x-x0|
Овде се зема предвид дека вредноста на границата мора да биде еднаква на f(x0), затоа, во споредба со дефиницијата на границата, се отстранува состојбата на пункција на δ-соседството 0.
Да дадеме уште една (еквивалентна на претходната) дефиниција во однос на зголемувањата. Да означиме Δх = x - x0; оваа вредност ќе ја наречеме зголемување на аргументот. Бидејќи x->x0, тогаш Δx->0, т.е. Δx - b.m. (бесконечно мало) количество. Да означиме Δу = f(x)-f(x0), оваа вредност ќе ја наречеме зголемување на функцијата, бидејќи |Δу| треба да биде (за доволно мал |Δх|) помал од произволен број ε>0, тогаш Δу- е исто така b.m. вредност, затоа

Дефиниција.Нека функцијата y = f(x) е дефинирана во точката x0 и некое нејзино соседство. Се повикува функцијата f(x). континуирано во точката x0, ако бесконечно мало зголемување на аргументот одговара на бесконечно мало зголемување на функцијата.

Дефиниција.Функцијата f(x), која не е континуирана во точката x0, наречена дисконтинуиранаво оваа точка.

Дефиниција.Функцијата f(x) се нарекува непрекината на множеството X ако е непрекината во секоја точка од ова множество.

Теорема за континуитет на збир, производ, количник

Теорема за премин до граница под знакот на континуирана функција

Теорема за континуитет на суперпозиција на непрекинати функции

Нека функцијата f(x) е дефинирана на интервал и нека биде монотона на овој интервал. Тогаш f(x) може да има само точки на дисконтинуитет од првиот вид на овој сегмент.

Теорема за средна вредност.Ако функцијата f(x) е континуирана на отсечка и во две точки a и b (a е помала од b) зема нееднакви вредности A = f(a) ≠ B = f(b), тогаш за кој било број C лежи помеѓу A и B, постои точка c ∈ во која вредноста на функцијата е еднаква на C: f(c) = C.

Теорема за ограниченоста на непрекината функција на интервал.Ако функцијата f(x) е континуирана на интервал, тогаш таа е ограничена на овој интервал.

Теорема за постигнување минимални и максимални вредности.Ако функцијата f(x) е континуирана на интервал, тогаш таа ги достигнува долните и горните граници на овој интервал.

Теорема за континуитет на инверзната функција.Нека функцијата y=f(x) е континуирана и строго растечка (намалувачка) на интервалот [a,b]. Потоа на сегментот постои инверзна функција x = g(y), исто така монотоно растечка (намалувачка) на и континуирана.

Континуитет на функцијата. Точки на прекин.

Бикот оди, се ниша, воздивнува додека оди:
- О, таблата е при крај, сега ќе паднам!

Во оваа лекција ќе го испитаме концептот на континуитет на функцијата, класификацијата на точките на дисконтинуитет и заеднички практичен проблем студии на континуитет на функции. Од самото име на темата, многумина интуитивно погодуваат за што ќе се дискутира и сметаат дека материјалот е прилично едноставен. Ова е вистина. Но, тоа се едноставни задачи кои најчесто се казнуваат за запоставување и површен пристап кон нивно решавање. Затоа, препорачувам многу внимателно да ја проучувате статијата и да ги фатите сите суптилности и техники.

Што треба да знаете и да можете да правите?Не многу. За добро да ја научите лекцијата, треба да разберете што е тоа граница на функција. За читателите со низок степен на подготовка, доволно е да ја разберат статијата Ограничувања на функциите. Примери на решенијаи погледнете го геометриското значење на лимитот во прирачникот Графикони и својства на елементарните функции. Исто така, препорачливо е да се запознаете со геометриски трансформации на графикони, бидејќи практиката во повеќето случаи вклучува конструирање цртеж. Изгледите се оптимистички за секого, па дури и полн котел ќе може сам да се справи со задачата во следните час или два!

Континуитет на функцијата. Точки на прекин и нивна класификација

Концептот на континуитет на функција

Да разгледаме некоја функција која е континуирана на целата нумеричка права:

Или, попрецизно кажано, нашата функција е континуирана вклучена (множеството реални броеви).

Кој е „филистејскиот“ критериум на континуитет? Очигледно, графикот на континуирана функција може да се нацрта без да се подигне моливот од хартијата.

Во овој случај, треба јасно да се разликуваат два едноставни концепти: домен на функцијаИ континуитет на функцијата. Генерално не е иста работа. На пример:

Оваа функција е дефинирана на целата бројна линија, односно за ситеЗначењето на „x“ има свое значење на „y“. Конкретно, ако, тогаш. Забележете дека другата точка е интерпункирана, бидејќи според дефиницијата на функцијата, вредноста на аргументот мора да одговара на единствено нештовредност на функцијата. Така, доменнашата функција: .

Сепак оваа функција не е континуирана вклучена!Сосема е очигледно дека во моментот таа страда јаз. Терминот е исто така доста разбирлив и визуелен; навистина, овде моливот сепак ќе треба да се откине од хартијата. Малку подоцна ќе ја разгледаме класификацијата на точките на прекин.

Континуитет на функција во точка и на интервал

Во одреден математички проблем, можеме да зборуваме за континуитет на функција во точка, континуитет на функција на интервал, полуинтервал или континуитет на функција на сегмент. Тоа е, нема „обичен континуитет“– функцијата може да биде континуирана НЕКАДЕ. А фундаменталниот „градежник“ на сè друго е континуитет на функцијата во точката .

Теоријата на математичка анализа дава дефиниција за континуитет на функцијата во точка со користење на соседствата „делта“ и „епсилон“, но во пракса постои различна дефиниција во употреба, на која ќе обрнеме големо внимание.

Прво да се потсетиме еднострани границикои упаднаа во нашите животи на првата лекција за графиконите на функциите. Размислете за секојдневна ситуација:

Ако се приближиме до оската до точката лево(црвена стрелка), тогаш соодветните вредности на „игрите“ ќе одат по оската до точката (црвена стрелка). Математички, овој факт е фиксиран со користење граница на левата страна:

Обрнете внимание на записот (читај „x tends to ka лево“). „Адитивот“ „минус нула“ симболизира , во суштина тоа значи дека се приближуваме до бројката од левата страна.

Слично, ако се приближите до точката „ка“ десно(сина стрелка), тогаш „игрите“ ќе дојдат до истата вредност, но по зелената стрелка и граница на десната ракаќе биде форматирана на следниов начин:

„Адитив“ симболизира , а влезот гласи: „x има тенденција да ка на десната страна“.

Ако едностраните граници се конечни и еднакви(како во нашиот случај): , тогаш ќе кажеме дека има ОПШТА граница. Едноставно е, општата граница е нашата „вообичаена“ граница на функција, еднаков на конечен број.

Забележете дека ако функцијата не е дефинирана во (извадете ја црната точка на гранката на графикот), тогаш горенаведените пресметки остануваат валидни. Како што веќе беше забележано неколку пати, особено во статијата на бесконечно мали функции, изразите значат дека "x" бескрајно блискусе приближува кон точката, додека НЕ Е ВАЖНО, без разлика дали самата функција е дефинирана во дадена точка или не. Добар пример ќе се најде во следниот пасус, кога ќе се анализира функцијата.

Дефиниција: функцијата е континуирана во точка ако границата на функцијата во дадена точка е еднаква на вредноста на функцијата во таа точка: .

Дефиницијата е детална во следните термини:

1) Функцијата мора да биде дефинирана во точката, односно вредноста мора да постои.

2) Мора да постои општа граница на функцијата. Како што е наведено погоре, ова подразбира постоење и еднаквост на еднострани граници: .

3) Границата на функцијата во дадена точка мора да биде еднаква на вредноста на функцијата во оваа точка: .

Доколку се прекрши барем еденод трите услови, тогаш функцијата го губи својството на континуитет во точката .

Континуитет на функција во интервале формулирана генијално и многу едноставно: функцијата е континуирана на интервалот ако е непрекината во секоја точка од дадениот интервал.

Особено, многу функции се континуирани на бесконечен интервал, односно на множеството реални броеви. Ова е линеарна функција, полиноми, експоненцијални, синуси, косинусови итн. И воопшто, било кој елементарна функцијаконтинуирано на него домен на дефиниција, на пример, логаритамската функција е континуирана на интервалот . Се надеваме дека до сега имате прилично добра идеја за тоа како изгледаат графиконите на основните функции. Подетални информации за нивниот континуитет може да се добијат од еден љубезен човек по име Фихтенхолц.

Со континуитет на функција на сегмент и полуинтервали, сè исто така не е тешко, но посоодветно е да се зборува за ова на час. за наоѓање на минималните и максималните вредности на функцијата на сегмент, но засега да не се грижиме за тоа.

Класификација на точките на прекин

Фасцинантниот живот на функциите е богат со секакви посебни точки, а точките за прекин се само една од страниците на нивната биографија.

Забелешка : за секој случај, ќе се задржам на една елементарна точка: точката на прекин е секогаш единствена точка– нема „неколку точки на пауза по ред“, односно не постои нешто како „интервал на пауза“.

Овие точки, пак, се поделени во две големи групи: руптури од прв видИ руптури од втор вид. Секој тип на јаз има свои карактеристични карактеристики, кои ќе ги разгледаме токму сега:

Точка на дисконтинуитет од првиот вид

Ако во точка е нарушен условот за континуитет и еднострани граници конечни , тогаш се нарекува точка на дисконтинуитет од прв вид.

Да почнеме со најоптимистичкиот случај. Според првичната идеја на лекцијата, сакав да ја кажам теоријата „во општа смисла“, но за да ја покажам реалноста на материјалот, се решив на опцијата со специфични знаци.

Тажно е, како фотографија од младенци на позадината на Вечниот пламен, но следнава снимка е општо прифатена. Дозволете ни да го прикажеме графикот на функцијата на цртежот:


Оваа функција е континуирана на целата бројна права, освен точката. И всушност, именителот не може да биде еднаков на нула. Меѓутоа, во согласност со значењето на лимитот, можеме бескрајно блискупристапи кон „нула“ и од лево и од десно, односно, постојат еднострани граници и, очигледно, се совпаѓаат:
(Задоволен е условот бр. 2 на континуитет).

Но, функцијата не е дефинирана во точката, затоа, условот бр. 1 на континуитет е нарушен и функцијата претрпува дисконтинуитет во овој момент.

Прекин од овој тип (со постоечките општа граница) се нарекуваат јаз што може да се поправи. Зошто отстранлив? Бидејќи функцијата може редефинирана точката на прекин:

Дали изгледа чудно? Можеби. Но, таквата нотација на функцијата не противречи на ништо! Сега јазот е затворен и сите се среќни:


Ајде да извршиме формална проверка:

2) – постои општа граница;
3)

Така, сите три услови се задоволени, а функцијата е континуирана во точка со дефиниција за континуитет на функција во точка.

Како и да е, хејтерите на матан можат да ја дефинираат функцијата на лош начин, на пример :


Интересно е што тука се исполнети првите два услови за континуитет:
1) – функцијата е дефинирана во дадена точка;
2) – постои општа граница.

Но, третата граница не е помината: , односно границата на функцијата во точката не еднаквивредноста на дадена функција во дадена точка.

Така, во одреден момент функцијата претрпува дисконтинуитет.

Вториот, потажен случај се вика руптура од прв вид со скок. А тагата ја предизвикуваат едностраните граници што конечни и различни. Пример е прикажан во вториот цртеж на лекцијата. Таков јаз обично се јавува кога на делови дефинирани функции, кои веќе се споменати во статијата за трансформации на графикони.

Размислете за функцијата на парчиња и ќе го завршиме неговото цртање. Како да се изгради графикон? Многу едноставно. На полу-интервал цртаме фрагмент од парабола (зелена), на интервал - права линија (црвена) и на полу-интервал - права линија (сина).

Притоа, поради неравенството, вредноста се определува за квадратната функција (зелена точка), а поради неравенството вредноста се одредува за линеарната функција (сина точка):

Во најтешкиот случај, треба да прибегнете кон конструкција точка-по-точка на секое парче од графиконот (видете го првиот лекција за графикони на функции).

Сега ќе не интересира само поентата. Ајде да го испитаме за континуитет:

2) Ајде да пресметаме еднострани граници.

Лево имаме сегмент со црвена линија, така што границата од левата страна е:

На десната страна е сината права линија, а десната граница:

Како резултат на тоа, добивме конечни броеви, и тие не еднакви. Бидејќи едностраните граници конечни и различни: , тогаш нашата функција толерира дисконтинуитет од првиот вид со скок.

Логично е дека јазот не може да се елиминира - функцијата навистина не може дополнително да се дефинира и „залепи заедно“, како во претходниот пример.

Точки на дисконтинуитет од втор вид

Обично, сите други случаи на руптура се паметно класифицирани во оваа категорија. Нема да набројувам сè, бидејќи во пракса, во 99% од проблемите ќе наидете бескраен јаз– кога се левак или деснак, а почесто и двете граници се бесконечни.

И, се разбира, најочигледната слика е хиперболата во точката нулта. Овде и двете еднострани граници се бесконечни: , затоа, функцијата трпи дисконтинуитет од вториот вид во точката .

Се обидувам да ги пополнам моите написи со што е можно поразновидна содржина, па да го погледнеме графикот на функцијата што сè уште не е сретната:

според стандардната шема:

1) Функцијата не е дефинирана во овој момент бидејќи именителот оди на нула.

Се разбира, веднаш можеме да заклучиме дека функцијата трпи дисконтинуитет во точката , но би било добро да се класифицира природата на дисконтинуитетот, што често го бара условот. За ова:

Да потсетам дека под снимање мислиме бесконечно мал негативен број, и под записот - бесконечно мал позитивен број.

Едностраните граници се бесконечни, што значи дека функцијата претрпува дисконтинуитет од вториот вид во точката. y-оската е вертикална асимптотаза графиконот.

Не е невообичаено да постојат и еднострани граници, но само една од нив е бесконечна, на пример:

Ова е графикот на функцијата.

Ја испитуваме точката за континуитет:

1) Функцијата не е дефинирана во овој момент.

2) Ајде да пресметаме еднострани граници:

За начинот на пресметување на ваквите еднострани граници ќе зборуваме во последните два примери од предавањето, иако многу читатели веќе виделе и погодиле сè.

Границата од левата страна е конечна и еднаква на нула (ние „не одиме до самата точка“), но десната граница е бесконечна и портокаловата гранка на графикот се приближува бесконечно блиску до нејзината вертикална асимптота, дадена со равенката (црна линија со точки).

Така, функцијата страда втор вид дисконтинуитетво точка.

Што се однесува до дисконтинуитет од првиот вид, функцијата може да се дефинира во самата точка на дисконтинуитет. На пример, за деловна функција Слободно ставете црна задебелена точка на почетокот на координатите. На десната страна е гранка на хипербола, а десната граница е бесконечна. Мислам дека скоро секој има идеја за тоа како изгледа овој график.

Она што сите го очекуваа:

Како да се испита функцијата за континуитет?

Проучувањето на функцијата за континуитет во точка се врши според веќе воспоставена рутинска шема, која се состои од проверка на три услови на континуитет:

Пример 1

Функција за истражување

Решение:

1) Единствената точка во опсегот е местото каде што функцијата не е дефинирана.

2) Ајде да пресметаме еднострани граници: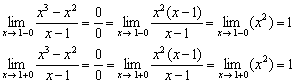

Едностраните граници се конечни и еднакви.

Така, во точката функцијата претрпува отстранлив дисконтинуитет.

Како изгледа графикот на оваа функција?

Би сакал да поедноставам , и се чини дека е добиена обична парабола. НОоригиналната функција не е дефинирана во точката, па затоа е потребна следната клаузула:

Ајде да го направиме цртежот:

Одговори: функцијата е континуирана на целата бројна права освен точката во која претрпува отстранлив дисконтинуитет.

Функцијата може дополнително да се дефинира на добар или не толку добар начин, но според условот тоа не е потребно.

Велиш дека ова е пресилен пример? Воопшто не. Ова се случило десетици пати во пракса. Речиси сите задачи на страницата доаѓаат од вистинска независна работа и тестови.

Ајде да се ослободиме од нашите омилени модули:

Пример 2

Функција за истражување за континуитет. Да се ​​определи природата на функционалните дисконтинуитети, доколку постојат. Извршете го цртежот.

Решение: Поради некоја причина, студентите се плашат и не ги сакаат функциите со модул, иако нема ништо комплицирано во нив. Веќе малку допревме такви работи во лекцијата. Геометриски трансформации на графикони. Бидејќи модулот не е негативен, тој се проширува на следниов начин: , каде што „алфа“ е некој израз. Во овој случај, и нашата функција треба да се напише на парче: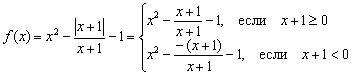

Но, фракциите на двете парчиња мора да се намалат за . Намалувањето, како и во претходниот пример, нема да се одвива без последици. Оригиналната функција не е дефинирана во точката бидејќи именителот оди на нула. Затоа, системот треба дополнително да го специфицира условот и да ја направи првата нееднаквост строга:

Сега за една МНОГУ КОРИСНА техника за одлучување: пред да се финализира задачата на нацрт, поволно е да се направи цртеж (без разлика дали тоа го бараат условите или не). Ова ќе помогне, прво, веднаш да ги видите точките на континуитет и точките на дисконтинуитет, и, второ, 100% ќе ве заштити од грешки при наоѓање еднострани граници.

Ајде да го направиме цртежот. Во согласност со нашите пресметки, лево од точката потребно е да се нацрта фрагмент од парабола (сина боја), а десно - парче парабола (црвена боја), додека функцијата не е дефинирана на самата точка:

Ако се сомневате, земете неколку x вредности и приклучете ги во функцијата (сеќавајќи се дека модулот го уништува можниот знак минус) и проверете го графикот.

Да ја испитаме функцијата за континуитет аналитички:

1) Функцијата не е дефинирана во точката, така што веднаш можеме да кажеме дека во неа не е континуирана.

2) Да ја утврдиме природата на дисконтинуитетот; за да го направиме ова, пресметуваме еднострани граници:

Едностраните граници се конечни и различни, што значи дека функцијата претрпува дисконтинуитет од 1-виот вид со скок во точката. Повторно забележете дека при наоѓање граници, не е важно дали функцијата во точката на прекин е дефинирана или не.

Сега останува само да се пренесе цртежот од нацртот (тој е направен како со помош на истражување ;-)) и да се заврши задачата:

Одговори: функцијата е континуирана на целата бројна права, освен точката во која претрпува дисконтинуитет од првиот вид со скок.

Понекогаш тие бараат дополнителна индикација за скокот на дисконтинуитет. Се пресметува едноставно - од десната граница треба да ја одземете левата граница: , односно во точката на прекин нашата функција скокна 2 единици надолу (како што ни кажува знакот минус).

Пример 3

Функција за истражување за континуитет. Да се ​​определи природата на функционалните дисконтинуитети, доколку постојат. Направете цртеж.

Ова е пример за да го решите сами, примерок од решението на крајот од часот.

Ајде да преминеме на најпопуларната и најраспространета верзија на задачата, кога функцијата се состои од три дела:

Пример 4

Испитајте ја функцијата за континуитет и нацртајте график на функцијата .

Решение: очигледно е дека сите три дела од функцијата се континуирани на соодветните интервали, па останува да се проверат само две точки на „спој“ меѓу парчињата. Прво, ајде да направиме нацрт-цртеж; јас ја коментирав техниката на градење доволно детално во првиот дел од статијата. Единственото нешто е што треба внимателно да ги следиме нашите еднини точки: поради нееднаквоста, вредноста и припаѓа на правата линија (зелена точка), а поради нееднаквоста, вредноста припаѓа на параболата (црвена точка):


Па, во принцип, сè е јасно =) Останува само да се формализира одлуката. За секоја од двете точки на „спојување“, стандардно проверуваме 3 услови за континуитет:

јас)Ја испитуваме точката за континуитет

1)

Едностраните граници се конечни и различни, што значи дека функцијата претрпува дисконтинуитет од 1-виот вид со скок во точката.

Дозволете ни да го пресметаме скокот на дисконтинуитет како разлика помеѓу десната и левата граница:
, односно, графикот отскокна една единица.

II)Ја испитуваме точката за континуитет

1) – функцијата е дефинирана во дадена точка.

2) Најдете еднострани граници:

– едностраните граници се конечни и еднакви, што значи дека постои општа граница.

3) – границата на функцијата во точка е еднаква на вредноста на оваа функција во дадена точка.

Во последната фаза, го пренесуваме цртежот во финалната верзија, по што го ставаме последниот акорд:

Одговори: функцијата е непрекината на целата бројна права, освен точката во која претрпува дисконтинуитет од првиот вид со скок.

Пример 5

Испитајте ја функцијата за континуитет и конструирајте го нејзиниот график .

Ова е пример за независно решение, кратко решение и приближен примерок на проблемот на крајот од часот.

Може да добиете впечаток дека во еден момент функцијата мора да биде континуирана, а во друга да има дисконтинуитет. Во пракса, тоа не е секогаш случај. Обидете се да не ги занемарите преостанатите примери - ќе има неколку интересни и важни карактеристики:

Пример 6

Дадена функција . Истражете ја функцијата за континуитет во точките. Изградете графикон.

Решение: и повторно веднаш извршете го цртежот на нацртот:

Особеноста на овој график е што функцијата на парчиња е дадена со равенката на оската на апсцисата. Овде оваа област е нацртана со зелена боја, но во тетратка обично се истакнува со задебелени букви со едноставен молив. И, се разбира, не заборавајте за нашите овни: вредноста припаѓа на тангентата гранка (црвена точка), а вредноста припаѓа на права линија.

Сè е јасно од цртежот - функцијата е континуирана по целата нумеричка линија, останува само да се формализира решението, кое е доведено до целосна автоматизација буквално по 3-4 слични примери:

јас)Ја испитуваме точката за континуитет

1) – функцијата е дефинирана во дадена точка.

2) Ајде да пресметаме еднострани граници:

, што значи дека постои општа граница.

За секој случај, дозволете ми да ве потсетам на еден тривијален факт: границата на константата е еднаква на самата константа. Во овој случај, границата на нула е еднаква на самата нула (ограничување на левата страна).

3) – границата на функцијата во точка е еднаква на вредноста на оваа функција во дадена точка.

Така, функцијата е континуирана во точка со дефиниција за континуитет на функција во точка.

II)Ја испитуваме точката за континуитет

1) – функцијата е дефинирана во дадена точка.

2) Најдете еднострани граници:

И тука - границата на еден е еднаква на самата единица.

– постои општа граница.

3) – границата на функцијата во точка е еднаква на вредноста на оваа функција во дадена точка.

Така, функцијата е континуирана во точка со дефиниција за континуитет на функција во точка.

Како и обично, по истражувањето го пренесуваме нашиот цртеж во финалната верзија.

Одговори: функцијата е континуирана во точките.

Ве молиме имајте предвид дека во состојбата не ни беше побарано ништо за проучување на целата функција за континуитет и се смета дека е добра математичка форма за формулирање прецизни и јасниодговорот на поставеното прашање. Патем, ако условите не бараат да изградите график, тогаш имате целосно право да не го изградите (иако подоцна наставникот може да ве принуди да го направите ова).

Мал математички „превртувач на јазици“ за сами да го решите:

Пример 7

Дадена функција . Истражете ја функцијата за континуитет во точките. Класифицирајте ги точките на прекин, доколку ги има. Извршете го цртежот.

Обидете се правилно да ги „изговорите“ сите „зборови“ =) И попрецизно нацртајте го графикот, точност, нема да биде излишно насекаде;-)

Како што се сеќавате, препорачав веднаш да го комплетирате цртежот како нацрт, но од време на време наидувате на примери каде што не можете веднаш да сфатите како изгледа графикот. Затоа, во некои случаи, поволно е прво да се најдат еднострани граници и дури потоа, врз основа на студијата, да се прикажат гранките. Во последните два примери ќе научиме и техника за пресметување на некои еднострани граници:

Пример 8

Испитајте ја функцијата за континуитет и конструирајте го нејзиниот шематски график.

Решение: лошите точки се очигледни: (го намалува именителот на експонентот на нула) и (го намалува именителот на целата дропка на нула). Не е јасно како изгледа графикот на оваа функција, што значи дека е подобро прво да се направи истражување.

Дефиниција
Функција f (x)повикани континуирано во точката x 0 соседството на оваа точка, и ако границата како x се стреми кон x 0 еднаква на вредноста на функцијата на x 0 :
.

Користејќи ги дефинициите на Коши и Хајн за границата на функцијата, можеме да дадеме проширени дефиниции за континуитет на функција во точка .

Можеме да го формулираме концептот на континуитет во во однос на зголемувањата. За да го направите ова, воведуваме нова променлива, која се нарекува зголемување на променливата x во точката. Тогаш функцијата е континуирана во точката ако
.
Ајде да воведеме нова функција:
.
Ја викаат зголемување на функцијатаво точка. Тогаш функцијата е континуирана во точката ако
.

Дефиниција за континуитет десно (лево)
Функција f (x)повикани континуирано десно (лево) во точката x 0 , ако е дефинирано на некое десно (лево) соседство на оваа точка, и ако десната (левата) граница во точката x 0 еднаква на вредноста на функцијата на x 0 :
.

Теорема за ограниченоста на континуирана функција
Нека функцијата f (x)е континуиран во точката x 0 . Потоа има населба У (x0), на кој функцијата е ограничена.

Теорема за зачувување на знакот на континуирана функција
Нека функцијата е континуирана во точката. И нека има позитивна (негативна) вредност во овој момент:
.
Потоа, постои соседство на точката каде што функцијата има позитивна (негативна) вредност:
во .

Аритметички својства на непрекинати функции
Оставете ги функциите и да бидат континуирани во точката.
Потоа функциите и се континуирани во точката.
Ако, тогаш функцијата е континуирана во точката.

Својство на континуитет лево-десно
Функцијата е континуирана во точка ако и само ако е непрекината десно и лево.

Доказите за својствата се дадени на страницата „Својства на функциите континуирани во точка“.

Континуитет на сложена функција

Теорема за континуитет за сложена функција
Нека функцијата е континуирана во точката. И нека функцијата е континуирана во точката.
Тогаш комплексната функција е континуирана во точката.

Граница на сложена функција

Теорема за граница на континуирана функција на функција
Нека постои граница на функцијата во , и таа е еднаква на:
.
Еве ја точката т 0 може да биде конечна или бесконечно далечна: .
И нека функцијата е континуирана во точката.
Тогаш постои граница на сложена функција и таа е еднаква на:
.

Теорема за граница на сложена функција
Нека функцијата има граница и мапира пробиено соседство на точка на пробиено соседство на точка. Нека функцијата е дефинирана на оваа населба и нека има ограничување на неа.
Еве ги конечните или бескрајно оддалечените точки: . Населбите и нивните соодветни граници можат да бидат или двострани или еднострани.
Тогаш постои граница на сложена функција и таа е еднаква на:
.

Точки на прекин

Одредување на точката на прекин
Нека функцијата е дефинирана на некое пробиено соседство на точката. Точката се нарекува точка на прекин на функцијата, ако е исполнет еден од двата услови:
1) не е дефинирано во ;
2) е дефинирано во , но не е во овој момент.

Определување на точката на дисконтинуитет од 1-виот вид
Точката се нарекува точка на дисконтинуитет од прв вид, ако е точка на прекин и има конечни еднострани граници лево и десно:
.

Дефиниција на функциски скок
Скок Δ функцијаво една точка е разликата помеѓу границите десно и лево
.

Одредување на точката на прекин
Точката се нарекува отстранлива точка на прекин, ако има ограничување
,
но функцијата во точката или не е дефинирана или не е еднаква на граничната вредност: .

Така, точката на отстранлив дисконтинуитет е точката на дисконтинуитет од 1-виот вид, на која скокот на функцијата е еднаков на нула.

Одредување на точката на дисконтинуитет од втор вид
Точката се нарекува точка на дисконтинуитет од втор вид, ако не е дисконтинуитетна точка од 1-виот вид. Односно, ако не постои барем една еднострана граница, или барем една еднострана граница во точка е еднаква на бесконечност.

Својства на функциите континуирани на интервал

Дефиниција на функција континуирана на интервал
Функцијата се нарекува континуирана на интервал (at) ако е континуирана во сите точки од отворениот интервал (at) и во точките a и b, соодветно.

Првата теорема на Вајерштрас за ограниченоста на функцијата континуирана на интервал
Ако функцијата е континуирана на интервал, тогаш таа е ограничена на овој интервал.

Утврдување на достижливоста на максимумот (минимумот)
Функцијата го достигнува својот максимум (минимум) во множеството доколку постои аргумент за кој
за сите .

Одредување на достапноста на горното (долното) лице
Функцијата ја достигнува својата горна (долна) граница на множеството ако има аргумент за кој
.

Втората теорема на Вајерштрас за максимумот и минимумот на континуирана функција
Непрекината функција на отсечка ги достигнува горните и долните граници на неа или, што е исто, го достигнува својот максимум и минимум на отсечката.

Теорема за средна вредност Болзано-Коши
Нека функцијата е континуирана на сегментот. И нека C е произволен број сместен помеѓу вредностите на функцијата на краевите на сегментот: и . Потоа, постои точка за која
.

Заклучок 1
Нека функцијата е континуирана на сегментот. И нека вредностите на функциите на краевите на сегментот имаат различни знаци: или . Потоа, постои точка во која вредноста на функцијата е еднаква на нула:
.

Заклучок 2
Нека функцијата е континуирана на сегментот. Пушти го . Тогаш функцијата ги зема во интервалот сите вредности од и само овие вредности:
во .

Инверзни функции

Дефиниција на инверзна функција
Нека функцијата има домен на дефиниција X и збир на вредности Y. И нека го има имотот:
за сите .
Тогаш за кој било елемент од множеството Y може да се поврзе само еден елемент од множеството X за кој . Оваа кореспонденција дефинира функција наречена инверзна функцијаДо . Инверзната функција е означена на следниов начин:
.

Од дефиницијата произлегува дека
;
за сите ;
за сите .

Лема за меѓусебната монотоност на директните и инверзните функции
Ако функцијата строго се зголемува (опаѓа), тогаш постои инверзна функција која исто така строго се зголемува (опаѓа).

Својство на симетрија на графикони на директни и инверзни функции
Графиконите на директните и инверзните функции се симетрични во однос на правата линија.

Теорема за постоење и континуитет на инверзна функција на интервал
Нека функцијата е континуирана и строго се зголемува (намалува) на сегментот. Тогаш инверзната функција е дефинирана и континуирана на отсечката, која строго се зголемува (намалува).

За зголемена функција. За намалување - .

Теорема за постоење и континуитет на инверзна функција на интервал
Нека функцијата е континуирана и строго се зголемува (намалува) на отворен конечен или бесконечен интервал. Тогаш инверзната функција е дефинирана и континуирана на интервалот, кој строго се зголемува (намалува).

За зголемена функција.
За намалување на:.

На сличен начин, можеме да ја формулираме теоремата за постоење и континуитет на инверзната функција на полуинтервал.

Својства и континуитет на елементарните функции

Елементарните функции и нивните инверзи се континуирани во нивниот домен на дефиниција. Подолу ги презентираме формулациите на соодветните теореми и обезбедуваме врски до нивните докази.

Експоненцијална функција

Експоненцијална функција f (x) = секира, со основа а > 0 е граница на низата
,
каде што е произволна низа од рационални броеви со тенденција кон x:
.

Теорема. Својства на експоненцијалната функција
Експоненцијалната функција ги има следните својства:
(стр.0)дефинирано, за, за сите;
(стр.1)за ≠ 1 има многу значења;
(стр.2)строго се зголемува во, строго се намалува во, е константна во;
(стр.3) ;
(стр.3*) ;
(стр.4) ;
(стр.5) ;
(стр.6) ;
(стр.7) ;
(стр.8)континуирано за сите;
(стр.9)во ;
во .

Логаритам

Логаритамска функција, или логаритам, y = трупна секира, со основа ае инверзна на експоненцијалната функција со основа a.

Теорема. Својства на логаритмот
Логаритамска функција со основа a, y = логирајте x, ги има следните својства:
(Л.1)дефинирани и континуирани, за и , за позитивни вредности на аргументот;
(Л.2)има многу значења;
(Л.3)строго се зголемува како , строго се намалува како ;
(Л.4)во ;
во ;
(Л.5) ;
(Л.6)во ;
(Л.7)во ;
(L.8)во ;
(L.9)во .

Експонент и природен логаритам

Во дефинициите на експоненцијалната функција и логаритамот се јавува константа која се нарекува основа на моќноста или основа на логаритамот. Во математичката анализа, во огромното мнозинство на случаи, се добиваат поедноставни пресметки ако бројот e се користи како основа:
.
Експоненцијална функција со основа e се нарекува експонент: , а логаритам со основа e се нарекува природен логаритам: .

На страниците се претставени својствата на експонентот и природниот логаритам
„Експонент, e до моќта на x“,
„Природен логаритам, ln x функција“

Функција за напојување

Функција на моќност со експонент стре функцијата f (x) = xp, чија вредност во точката x е еднаква на вредноста на експоненцијалната функција со основа x во точката p.
Покрај тоа, ѓ (0) = 0 p = 0за стр > 0 .

Овде ќе ги разгледаме својствата на функцијата моќност y = x p за ненегативни вредности на аргументот. За рационални, за непарен m, функцијата на моќност е дефинирана и за негативен x. Во овој случај, неговите својства може да се добијат со употреба на парни или непарни.
Овие случаи се детално дискутирани и илустрирани на страницата „Функција за напојување, нејзините својства и графикони“.

Теорема. Својства на функцијата моќност (x ≥ 0)
Функција на моќност, y = x p, со експонент p ги има следните својства:
(C.1)дефинирана и континуирана на сетот
во,
во ".

Тригонометриски функции

Теорема за континуитет на тригонометриските функции
Тригонометриски функции: синус ( грев х), косинус ( cos x), тангента ( tg x) и котангента ( ctg x

Теорема за континуитет на инверзни тригонометриски функции
Инверзни тригонометриски функции: лаксин ( arcsin x), лак косинус ( arccos x), арктангент ( арктан x) и лак тангента ( arcctg x), се континуирани во нивните домени на дефиниција.

Референци:
О.И. Бешов. Предавања по математичка анализа. Дел 1. Москва, 2004 година.
Л.Д. Кудрјавцев. Курс за математичка анализа. Том 1. Москва, 2003 година.
ЦМ. Николски. Курс за математичка анализа. Том 1. Москва, 1983 година.