Matemaatika. Teoreetiline mehaanika

Otsi määramatu integraal(antiderivaatide komplekt või "antiderivaadid") tähendab funktsiooni taastamist selle funktsiooni teadaolevalt tuletiselt. Taastatud antiderivaatide komplekt F(x) + KOOS funktsiooni jaoks f(x) võtab arvesse integreerimiskonstanti C. Liikumiskiiruse järgi materiaalne punkt(tuletise) selle punkti liikumisseadust (antituletist) saab taastada; vastavalt punkti liikumise kiirendusele – selle kiirusele ja liikumisseadusele. Nagu näete, on integratsioon füüsika Sherlock Holmesi tegevuse jaoks lai valdkond. Ja majandusteaduses on paljud mõisted esindatud funktsioonide ja nende tuletiste kaudu ning seetõttu on võimalik näiteks teatud ajahetkel tööviljakust kasutades taastada vastaval ajal toodetud toodete maht (tuletis).

Määramata integraali leidmiseks on vaja üsna väikest arvu põhilisi integreerimisvalemeid. Kuid selle leidmise protsess on palju keerulisem kui lihtsalt nende valemite rakendamine. Kogu keerukus ei ole seotud integreerimisega, vaid integreeritava avaldise viimisega vormile, mis võimaldab ülalmainitud põhivalemite abil leida määramatu integraali. See tähendab, et lõimumispraktika alustamiseks peate aktiveerima õpitu Keskkool väljenduse teisendamise oskus.

Õpime leidma integraale kasutades atribuudid ja määramata integraalide tabelõppetunnist selle teema põhimõistete kohta (avaneb uues aknas).

Integraali leidmiseks on mitu meetodit, millest muutuv asendusmeetod Ja integreerimine osade meetodil- kohustuslik härrasmeeste komplekt kõigile, kes on edukalt läbinud kõrgema matemaatika. Kasulikum ja mõnusam on aga hakata integreerimist valdama laiendusmeetodil, lähtudes kahest järgnevast ebamäärase integraali omaduste teoreemist, mida siinkohal mugavuse huvides kordame.

3. teoreem.Pidev kordaja integrandis võib ebamäärase integraali märgina välja võtta, s.t.

4. teoreem. Algebralise summa määramatu integraal lõplik arv funktsioonid on võrdsed algebraline summa nende funktsioonide määramata integraalid, s.o.

(2)

Lisaks võib integreerimisel olla kasulik järgmine reegel: kui integrandi avaldis sisaldab konstantset tegurit, siis antiderivaadi avaldis korrutatakse konstantse teguri pöördväärtusega, st.

(3)

Kuna see tund on integratsiooniprobleemide lahendamise sissejuhatuseks, on oluline märkida kaks asja, mis kas juba esialgne etapp, või veidi hiljem võivad nad teid üllatada. Üllatus tuleneb sellest, et integratsioon on diferentseerimise pöördoperatsioon ja määramatut integraali võib õigusega nimetada “antiderivatiiviks”.

Esimene asi, mille üle integreerimisel ei tasu imestada. Integraalide tabelis tuletistabelis valemite hulgas on valemeid, millel pole analooge . Need on järgmised valemid:

Küll aga saab veenduda, et nende valemite paremal küljel olevate avaldiste tuletised langevad kokku vastavate integrandidega.

Teine asi, mis ei tohiks integreerimisel üllatada. Kuigi mis tahes elementaarfunktsiooni tuletis on ka elementaarfunktsioon, mõne elementaarfunktsiooni määramata integraalid enam ei ole elementaarsed funktsioonid . Selliste integraalide näited võivad olla järgmised:

Integreerimistehnikate arendamiseks tulevad kasuks järgmised oskused: murdude vähendamine, murdu lugejas oleva polünoomi jagamine nimetajas oleva monoomiga (määramatute integraalide summa saamiseks), juurte teisendamine astmeteks, monoomi korrutamine polünoom, astmeni tõstmine. Neid oskusi on vaja integrandi teisendusteks, mille tulemuseks peaks olema integraalide tabelis olevate integraalide summa.

Määramatute integraalide koos leidmine

Näide 1. Leidke määramatu integraal

Lahendus. Integrandi nimetajas näeme polünoomi, milles x on ruudus. See on peaaegu kindel märk, et saate rakendada tabeliintegraali 21 (mille tulemuseks on arktangens). Nimetajast võtame välja teguri kaks (seal on selline integraali omadus - konstantse teguri saab välja võtta integraali märgist kaugemale; seda mainiti eespool kui teoreem 3). Selle kõige tulemus:

Nüüd on nimetajaks ruutude summa, mis tähendab, et saame rakendada mainitud tabeliintegraali. Lõpuks saame vastuse:

Näide 2. Leidke määramatu integraal

Lahendus. Rakendame taas teoreemi 3 - integraali omadust, mille alusel saab integraali märgist konstantse teguri välja võtta:

Rakendame integraali funktsioonile integraalide tabelist valemit 7 (muutuja astmeni):

Vähendame saadud murde ja saame lõpliku vastuse:

Näide 3. Leidke määramatu integraal

Lahendus. Rakendades omadustele kõigepealt teoreemi 4 ja seejärel teoreemi 3, leiame selle integraali kolme integraali summana:

Kõik kolm saadud integraali on tabelikujulised. Kasutame integraalide tabelist valemit (7). n = 1/2, n= 2 ja n= 1/5 ja siis

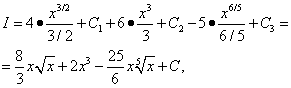
ühendab kõik kolm suvalist konstanti, mis sisestati millal leida kolm integraalid. Seetõttu tuleks sarnastes olukordades sisestada ainult üks suvaline integreerimiskonstant.

Näide 4. Leidke määramatu integraal

Lahendus. Kui integrandi nimetaja sisaldab monoomi, saame jagada lugeja nimetajaga liikme kaupa. Algne integraal muudeti kahe integraali summaks:

Tabeliintegraali rakendamiseks teisendame juured võimsusteks ja siin on lõplik vastus:

Jätkame koos määramata integraalide leidmist

Näide 7. Leidke määramatu integraal

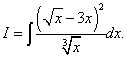
Lahendus. Kui teisendame integrandi binoom ruuduga ja jagame lugeja nimetajaga liikmega, siis saab algsest integraalist kolme integraali summa.

Kas diferentsiaalmärgi alla on võimalik liita mittelineaarne funktsioon? Jah, kui integrand on kahe teguri korrutis: üks tegur on mõne mittelineaarse funktsiooni kompleksfunktsioon ja teine tegur on selle mittelineaarse funktsiooni tuletis. Vaatame öeldut näidetega.

Leia määramata integraalid.

Näide 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) = (x²+x+2) 6 : 6 + C.

Mida see integrand esindab? Töö toitefunktsioon alates (x 2 + x + 2) ja kordajast (2x + 1), mis on võrdne astme aluse tuletisega: (x 2 + x + 2)" = 2x + 1.

See võimaldas meil diferentsiaalmärgi alla panna (2x + 1):

∫u 5 du=u 6 : 6+ C. (valem 1). )

Läbivaatus. (F (x)+ C)" =((x²+x+2) 6 : 6 + C)′=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =

=(x 2 + x + 2) 5 · (2x + 1) = (2x + 1) (x 2 + x + 2) 5 = f (x).

Näide 2.∫(3x 2 - 2x + 3) (x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 - x 2 + 3x + 1) 5 d (x 3 - x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+C

Ja kuidas see näide erineb näitest 1? Mitte midagi! Sama viies aste alusega (x 3 – x 2 + 3x + 1) korrutatakse trinoomiga (3x 2 – 2x + 3), mis on astme aluse tuletis: (x 3 – x 2 + 3x + 1)" = 3x 2 – 2x + 3. Tõime selle astme aluse diferentsiaalmärgi alla, millest alates integrandi väärtus ei muutunud, ja seejärel rakendasime sama valemit 1). Integraalid)

Näide 3.

Siin annab tuletis (2x 3 – 3x) (6x 2 – 3) ja meiega

seal on (12x 2 – 6), st avaldis in 2 korda suurem, mis tähendab, et paneme diferentsiaalmärgi alla (2x 3 – 3x) ja integraali ette teguri 2 . Rakendame valemit 2) ( leht ).

See juhtub järgmiselt.

Kontrollime, võttes arvesse järgmist:

Näited. Leia määramata integraalid.

1. ∫(6x+5) 3 dx. Kuidas me otsustame? Lehte vaadates ja me arutleme umbes nii: integrand esindab kraadi ja meil on astme integraali valem (valem 1) ), kuid selles on kraadi alus u ja ka integratsioonimuutuja u.

Ja meil on integratsioonimuutuja X, ja kraadi alus (6x+5). Teeme integratsioonimuutujas muudatuse: dx asemel kirjutame d (6x+5). Mis muutus? Kuna see, mis tuleb pärast diferentsiaalmärki d, on vaikimisi eristatud,

siis d (6x+5)=6dx, s.o. muutuja x asendamisel muutujaga (6x+5) suurenes integrandi funktsioon 6 korda, seega panime integraalimärgi ette teguri 1/6. Need argumendid saab kirjutada järgmiselt:

Niisiis lahendasime selle näite uue muutuja sisseviimisega (muutuja x asendati muutujaga 6x+5). Kuhu sa uue muutuja (6x+5) kirjutasid? Diferentsiaalmärgi all. Sellepärast, seda meetodit sageli nimetatakse uue muutuja sisseviimist meetod ( või viis ) summeerida(uus muutuja ) diferentsiaalmärgi all.

Teise näite puhul saime esmalt kraadi negatiivne näitaja, ja asetage see diferentsiaalmärgi (7x-2) alla ja kasutasite astmeintegraali valemit 1) (Integraalid ).

Vaatame näidislahendust 3.

Integraalile eelneb koefitsient 1/5. Miks? Kuna d (5x-2) = 5dx, siis asendades funktsiooni u = 5x-2 diferentsiaalmärgi all, suurendasime integrandi 5 korda, nii et väärtus antud väljend ei ole muutunud - oli vaja jagada 5-ga, st. korrutada 1/5-ga. Järgmisena kasutati valemit 2) (Integraalid) .

Kõik lihtsamad integraalvalemid näevad välja järgmised:

∫f (x) dx=F (x)+C, ja võrdsus peab olema täidetud:

(F (x) + C)" = f (x).

Integreerimisvalemeid saab saada vastavate diferentseerimisvalemite ümberpööramisel.

Tõesti,

Eksponent n võib olla murdosa. Tihti tuleb leida funktsiooni y=√x määramatu integraal. Arvutame valemi abil funktsiooni f (x)=√x integraali 1) .

Kirjutame selle näite valemina 2) .

Kuna (x+C)"=1, siis ∫dx=x+C.

3) ∫dx=x+C.

Asendades 1/x² x -2-ga, arvutame 1/x² integraali.

Kas saate selle vastuse, kui võtate ühendust kuulus valem eristamine:

Kirjutame oma mõttekäigu valemi kujul 4).

Korrutades saadud võrdsuse mõlemad pooled 2-ga, saame valemi 5).

Leiame peamiste integraalid trigonomeetrilised funktsioonid, teades nende tuletisi: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Saame integreerimisvalemid 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

Pärast demonstratiivse ja logaritmilised funktsioonid, lisame veel mõned valemid.

Põhiomadused ei ole kindel integraal.

I. Määramatu integraali tuletis on võrdne integrandiga .

(∫f (x) dx)"=f (x).

II. Määramatu integraali diferentsiaal on võrdne integrandiga.

d∫f (x) dx=f (x) dx.

III. Mõne funktsiooni diferentsiaali (tuletise) määramatu integraal võrdne summaga see funktsioon ja suvaline konstant C.

∫dF (x)=F (x)+C või ∫F"(x) dx=F (x)+C.

Pange tähele: I, II ja III omadused diferentsiaali ja integraali (integraal ja diferentsiaal) märgid “söövad” üksteist!

IV. Integraali konstantse teguri saab integraalimärgist välja võtta.

∫kf (x) dx=k ∫f (x) dx, Kus k - konstantne, ei ole võrdne nulliga.

V. Funktsioonide algebralise summa integraal on võrdne nende funktsioonide integraalide algebralise summaga.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI. Kui F (x) on f (x) antiderivaat, ja k Ja b on konstantsed väärtused ja k≠0, siis (1/k)·F (kx+b) on f (kx+b) antiderivaat. Tõepoolest, tuletise arvutamise reegli kohaselt keeruline funktsioon meil on:

Võite kirjutada:

Igaühele matemaatiline tehe on vastupidine efekt. Diferentseerimise (funktsioonide tuletiste leidmise) tegevuse jaoks on olemas ka vastupidine tegevus— integratsioon. Integreerimise teel leitakse (rekonstrueeritakse) funktsioon selle antud tuletisest või diferentsiaalist. Leitud funktsiooni kutsutakse antiderivaat.

Definitsioon. Diferentseeritav funktsioon F(x) nimetatakse funktsiooni antiderivaadiks f(x) teatud intervalliga, kui kõigi jaoks X sellest intervallist kehtib järgmine võrdsus: F'(x)=f (x).

Näited. Leia funktsioonide antiderivaadid: 1) f (x)=2x; 2) f (x) = 3 cos3x.

1) Kuna (x²)′=2x, siis definitsiooni järgi on funktsioon F (x)=x² funktsiooni f (x)=2x antituletis.

2) (sin3x)′=3cos3x. Kui tähistame f (x)=3cos3x ja F (x)=sin3x, siis antiderivaadi definitsiooni järgi saame: F'(x)=f (x) ja seetõttu on F (x)=sin3x antiderivaat f (x)=3cos3x jaoks.

Pange tähele, et (sin3x +5 )′= 3cos3x, ja (sin3x -8,2 )′= 3cos3x, ... V üldine vaade saab kirjutada: (sin3x +C)′= 3cos3x, Kus KOOS- mingi püsiv väärtus. Need näited näitavad integreerimise tegevuse mitmetähenduslikkust, erinevalt diferentseerumisest, kui igal diferentseeruval funktsioonil on üks tuletis.

Definitsioon. Kui funktsioon F(x) on funktsiooni antiderivaat f(x) teatud intervalli korral on selle funktsiooni kõigi antiderivaatide komplekt järgmine:

F(x)+C, kus C on mis tahes reaalarv.

Funktsiooni f (x) kõigi antiderivatiivide F (x) + C kogumit vaadeldaval intervallil nimetatakse määramata integraaliks ja seda tähistatakse sümboliga ∫ (integraalmärk). Kirjuta üles: ∫f (x) dx=F (x)+C.

Väljendus ∫f(x)dx loe: "integraal ef alates x kuni de x."

f(x)dx- integrandi väljend,

f(x)— integreerimisfunktsioon,

X on integratsioonimuutuja.

F(x)- funktsiooni antiderivaat f(x),

KOOS- mingi püsiv väärtus.

Nüüd saab vaadeldavad näited kirjutada järgmiselt:

1) ∫ 2xdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Mida tähis d tähendab?

d- diferentsiaalmärk - sellel on kaks eesmärki: esiteks eraldab see märk integrandi integratsioonimuutujast; teiseks kõik, mis tuleb pärast seda märki, eristatakse vaikimisi ja korrutatakse integrandiga.

Näited. Leidke integraalid: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) Pärast diferentsiaali ikooni d kulud XX, A R

∫ 2хрdx=рх²+С. Võrdle näitega 1).

Teeme kontrolli. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) Pärast diferentsiaali ikooni d kulud R. See tähendab, et integratsioonimuutuja R, ja kordaja X tuleks pidada mingiks konstantseks väärtuseks.

∫ 2хрдр=р²х+С. Võrrelge näidetega 1) Ja 3).

Teeme kontrolli. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

1. lehekülg 1-st 1

Integraalarvutus.

Antiderivatiivne funktsioon.

Definitsioon: Kutsutakse funktsioon F(x). antiderivatiivne funktsioon funktsioon f(x) segmendil, kui võrdsus on tõene selle lõigu mis tahes punktis:

Tuleb märkida, et sama funktsiooni jaoks võib olla lõpmatu arv antiderivaate. Need erinevad üksteisest mingi konstantse arvu poolest.

F 1 (x) = F 2 (x) + C.

Määramatu integraal.

Definitsioon: Määramatu integraal functionf(x) on tuletisvastaste funktsioonide kogum, mis on määratletud seosega:

Kirjuta üles:

Määramatu integraali olemasolu tingimus teatud lõigul on funktsiooni järjepidevus sellel lõigul.

Omadused:

Näide:

Määramatu integraali väärtuse leidmine on peamiselt seotud funktsiooni antituletise leidmisega. Mõne funktsiooni jaoks on see üsna keeruline ülesanne. Allpool käsitleme meetodeid määramata integraalide leidmiseks funktsioonide põhiklasside jaoks - ratsionaalne, irratsionaalne, trigonomeetriline, eksponentsiaalne jne.

Mugavuse huvides on enamiku elementaarfunktsioonide määramata integraalide väärtused kogutud spetsiaalsetesse integraalitabelitesse, mis on mõnikord üsna mahukad. Need hõlmavad mitmesuguseid sageli kasutatavaid funktsioonide kombinatsioone. Kuid enamik nendes tabelites esitatud valemeid on üksteise tagajärjed, nii et allpool esitame põhiintegraalide tabeli, mille abil saate erinevate funktsioonide määramata integraalide väärtused.

Integraalne	Tähendus	Integraalne	Tähendus

	lnsinx+ C



	ln

Integratsioonimeetodid.

Vaatleme kolme peamist integratsioonimeetodit.

Otsene integratsioon.

Otsese integratsiooni meetod põhineb eeldusel, et võimalik tähendus antiderivatiivne funktsioon koos selle väärtuse edasise kontrollimisega diferentseerimise teel. Üldiselt märgime, et diferentseerimine on võimas vahend integratsiooni tulemuste kontrollimiseks.

Vaatame selle meetodi rakendamist näite abil:

Peame leidma integraali väärtuse . Põhineb tuntud diferentseerimisvalemil
võime järeldada, et otsitav integraal on võrdne
, kus C on mingi konstantne arv. Samas teisest küljest
. Seega võime lõpuks järeldada:

Pange tähele, et erinevalt diferentseerimisest, kus tuletise leidmiseks kasutati selgeid tehnikaid ja meetodeid, tuletise leidmise reegleid ja lõpuks tuletise määratlust, ei ole sellised meetodid integreerimiseks saadaval. Kui tuletise leidmisel kasutasime nii-öelda konstruktiivseid meetodeid, mis teatud reeglitest lähtudes tulemuseni viisid, siis antiderivaadi leidmisel peame tuginema peamiselt tuletise ja antiderivaatide tabelite teadmistele.

Mis puutub otsesesse integreerimismeetodisse, siis see on rakendatav ainult mõne väga piiratud funktsiooniklassi jaoks. Väga vähe on funktsioone, mille jaoks leiaks kohe antiderivaadi. Seetõttu kasutatakse enamikul juhtudel allpool kirjeldatud meetodeid.

Asendusmeetod (muutujate asendamine).

Teoreem: Kui teil on vaja leida integraal
, kuid antiderivaati on raske leida, siis kasutades asendust x =  (t) ja dx =  (t) dt, selgub:

Tõestus : Eristagem pakutud võrdsust:

Eespool käsitletud määramatu integraali omaduse nr 2 järgi:

f(x) dx = f[  (t)]  (t) dt

mis kasutusele võetud tähistust arvesse võttes on esialgne eeldus. Teoreem on tõestatud.

Näide. Leidke määramatu integraal
.

Teeme asendus t = sinx, dt = cosxdt.

Näide.

Asendamine
Saame:

Allpool käsitleme muid näiteid asendusmeetodi kasutamisest erinevat tüüpi funktsioonide jaoks.

Integreerimine osade kaupa.

Meetod põhineb toote derivaadi üldtuntud valemil:

(uv)=uv+vu

kus uиv on mõned x-i funktsioonid.

Diferentsiaalkujul: d(uv) =udv+vdu

Integreerides saame:
, ja kooskõlas määramata integraali ülaltoodud omadustega:

või
;

Oleme saanud osade kaupa integreerimise valemi, mis võimaldab leida paljude elementaarfunktsioonide integraale.

Näide.

Nagu näete, võimaldab osade järgi integreerimise järjepidev rakendamine funktsiooni järk-järgult lihtsustada ja integraali tabeliks viia.

Näide.

On näha, et osade kaupa integreerimise korduva rakendamise tulemusena ei saanud funktsiooni lihtsustada tabelikujuliseks. Viimane saadud integraal ei erine aga algsest. Seetõttu nihutame selle võrdsuse vasakule küljele.

Seega leiti integraal ilma integraalitabeleid üldse kasutamata.

Enne erinevate funktsiooniklasside integreerimise meetodite üksikasjalikku käsitlemist toome veel mitu näidet määramata integraalide leidmiseks, taandades need tabeliteks.

Näide.

Elementaarmurdude integreerimine.

Definitsioon: Elementaarne Nimetatakse järgmisi nelja tüüpi murde:

I.
III.

II.
IV.

m,n- täisarvud(m2,n2) ja b 2 – 4ac<0.

Esimesed kaks elementaarmurdude integraalitüüpi saab üsna lihtsalt tabelitesse tuua, asendades t=ax+b.

Vaatleme III tüüpi elementaarmurdude integreerimise meetodit.

III tüüpi murdosa integraali võib esitada järgmiselt:

Siin on üldkujul näidatud III tüüpi murdosa integraali taandamine kaheks tabeliintegraaliks.

Vaatame näidete abil ülaltoodud valemi rakendamist.

Näide.

Üldiselt võib öelda, et kui kolmiktelg 2 +bx+c on avaldisega b 2 – 4ac>0, siis murd ei ole definitsiooni järgi elementaarne, kuid sellegipoolest saab seda ülaltoodud viisil integreerida.

Näide.

Vaatleme nüüd IV tüüpi lihtmurdude integreerimise meetodeid.

Esiteks vaatleme erijuhtumit, kus M = 0, N = 1.

Siis vormi integraal
saab esitada kujul, valides nimetajast täieliku ruudu
. Teeme järgmise teisenduse:

Sellesse võrdsusse kaasatud teise integraali võtame osade kaupa.

Tähistame:

Algse integraali jaoks saame:

Saadud valemit nimetatakse korduv. Kui rakendate seda n-1 korda, saate tabeli integraali
.

Tuleme nüüd tagasi üldjuhul IV tüübi elementaarmurru integraali juurde.

Saadud võrdsuses esimene integraal, mis kasutab asendust t = u 2 + s vähendatud tabeliks , ja teisele integraalile rakendatakse ülalkirjeldatud kordusvalemit.

Vaatamata IV tüüpi elementaarfraktsiooni integreerimise näilisele keerukusele, on seda praktikas üsna lihtne kasutada väikese astmega murdude puhul. n, ning lähenemisviisi universaalsus ja üldistus võimaldab selle meetodi väga lihtsat rakendamist arvutis.

Näide:

Ratsionaalsete funktsioonide integreerimine.

Ratsionaalsete murdude integreerimine.

Ratsionaalse murru integreerimiseks on vaja see lagundada elementaarmurdudeks.

Teoreem: Kui
- õige ratsionaalne murd, mille nimetaja P(x) on esitatud lineaar- ja ruuttegurite korrutisena (pange tähele, et mis tahes reaalkoefitsientidega polünoomi saab esitada sellisel kujul: P(x) = (x - a)  …(x - b)  (x 2 + px + q)  …(x 2 + rx + s)  ), siis saab selle murdosa jagada elementaarseteks vastavalt järgmisele skeemile:

kus A i ,B i ,M i ,N i ,R i,S i on mingid konstantsed suurused.

Ratsionaalsete murdude integreerimisel kasutavad nad algse murru lagundamist elementaarseteks murdudeks. Suuruste A i , B i , M i , N i , R i , S i leidmiseks kasutatakse nn. määramatute koefitsientide meetod, mille olemus seisneb selles, et selleks, et kaks polünoomi oleks identselt võrdsed, on vajalik ja piisav, et x samadel astmetel olevad koefitsiendid oleksid võrdsed.

Vaatleme selle meetodi kasutamist konkreetse näite abil.

Näide.

Vähendades ühisnimetajale ja võrdsustades vastavad lugejad, saame:

Näide.

Sest Kui murdosa on vale, peate esmalt valima selle kogu osa:

6 x 5 – 8 x 4 – 25 x 3 + 20 x 2 – 76 x – 7 3 x 3 – 4 x 2 – 17 x + 6

6 x 5 – 8 x 4 – 34 x 3 + 12 x 2 2 x 2 + 3

9x 3 + 8x 2 – 76x - 7

9x 3 - 12x 2 - 51x +18

20x 2 - 25x - 25

Faktoriseerime saadud murdosa nimetaja. On näha, et x = 3 korral muutub murdosa nimetaja nulliks. Seejärel:

3x3-4x2-17x+6x-3

3x3 – 9x2 3x2 + 5x-2

Seega 3x 3 – 4x 2 – 17x+ 6 = (x– 3) (3x 2 + 5x– 2) = (x– 3) (x+ 2) (3x– 1). Seejärel:

Vältimaks sulgude avamist, võrrandisüsteemi (mis mõnel juhul võib osutuda päris suureks) rühmitamist ja lahendamist ebakindlate kordajate leidmisel nn. meetod suvalised väärtused . Meetodi olemus seisneb selles, et ülaltoodud avaldisesse asendatakse mitu (vastavalt määramata koefitsientide arvule) suvalised x väärtused. Arvutuste lihtsustamiseks on tavaks võtta suvaliste väärtustena punkte, mille korral murdosa nimetaja on võrdne nulliga, s.o. meie puhul – 3, -2, 1/3. Saame:

Lõpuks saame:

Näide.

Leiame määramata koefitsiendid:

Seejärel antud integraali väärtus:

Mõne trigonomeetria integreerimine

funktsioonid.

Trigonomeetriliste funktsioonide integraale võib olla lõpmatu arv. Enamikku neist integraalidest ei saa üldse analüütiliselt arvutada, seega vaatleme mõnda peamised tüübid funktsioone, mida saab alati integreerida.

Vormi integraal
.

Siin R on muutujate sinx ja cosx mõne ratsionaalse funktsiooni tähistus.

Seda tüüpi integraalid arvutatakse asenduste abil
. See asendus võimaldab teil teisendada trigonomeetrilise funktsiooni ratsionaalseks.

Siis

Seega:

Ülalkirjeldatud teisendust nimetatakse universaalne trigonomeetriline asendus.

Näide.

Selle asendamise vaieldamatu eelis on see, et selle abil saate alati muuta trigonomeetrilise funktsiooni ratsionaalseks ja arvutada vastava integraali. Puudusteks on asjaolu, et teisenduse tulemuseks võib olla üsna keeruline ratsionaalne funktsioon, mille integreerimine võtab palju aega ja vaeva.

Kui aga muutuja ratsionaalsemat asendamist pole võimalik rakendada, on see meetod ainus tõhus.

Näide.

Vormi integraal
Kui

funktsiooniRcosx.

Vaatamata võimalusele arvutada selline integraal universaalse trigonomeetrilise asendusega, on ratsionaalsem kasutada asendust t = sinx.

Funktsioon
võib sisaldada cosx-i ainult paarisastmetes ja seetõttu saab selle teisendada sinxi suhtes ratsionaalseks funktsiooniks.

Näide.

Üldiselt on selle meetodi rakendamiseks vajalik ainult funktsiooni veidrus koosinuse suhtes ja funktsioonis sisalduva siinuse aste võib olla mis tahes, nii täis- kui ka murdosa.

Vormi integraal
Kui

funktsiooniRon paaritusinx.

Analoogiliselt ülaltoodud juhtumiga tehakse asendus t = cosx.

Näide.

Vormi integraal

funktsiooniRisegi suhteliseltsinxJacosx.

Funktsiooni R muutmiseks ratsionaalseks kasutage asendust

t = tgx.

Näide.

Siinuste ja koosinuste korrutise integraal

erinevaid argumente.

Sõltuvalt töö tüübist rakendatakse ühte kolmest valemist:

Näide.

Mõnikord on trigonomeetriliste funktsioonide integreerimisel mugav kasutada funktsioonide järjestuse vähendamiseks tuntud trigonomeetrilisi valemeid.

Näide.

Mõnikord kasutatakse mõnda mittestandardset tehnikat.

Näide.

Mõnede irratsionaalsete funktsioonide integreerimine.

Mitte igaüks irratsionaalne funktsioon võib olla elementaarfunktsioonidega väljendatud integraal. Irratsionaalse funktsiooni integraali leidmiseks peaksite kasutama asendust, mis võimaldab teil muuta funktsiooni ratsionaalseks, mille integraali saab alati leida, nagu alati teada.

Vaatame mõningaid tehnikaid erinevat tüüpi irratsionaalsete funktsioonide integreerimiseks.

Vormi integraal
Kusn- naturaalarv.

Asenduse kasutamine
funktsioon on ratsionaliseeritud.

Näide.

Kui irratsionaalfunktsiooni koostis sisaldab erineva astmega juuri, siis uue muutujana on ratsionaalne võtta avaldises sisalduvate juurte astmete vähima ühiskordsega võrdne astme juur.

Illustreerime seda näitega.

Näide.

Binoomdiferentsiaalide integreerimine.

Definitsioon: Binoomdiferentsiaal nimetatakse väljendiks

x m (a + bx n ) lk dx

Kus m, n, Ja lk- ratsionaalsed arvud.

Nagu tõestas akadeemik P. L. Tšebõšev. (1821-1894), saab binoomdiferentsiaali integraali väljendada elementaarfunktsioonidena ainult kolmel järgmisel juhul:

Kui R on täisarv, siis integraal ratsionaliseeritakse asendust kasutades

, kus  on ühine nimetaja m Ja n.

Funktsiooni F(x) nimetatakse funktsiooni f(x) antituletiseks intervallil (a; b), kui f(x) kõigi x (a; b) võrrandiga F (x) = f(x). 2

Teoreem 1. Kui F(x) on (a; b) f(x) antituletiv, siis F(x) + C, kus C on arv, on ka f(x) jaoks (a) olev antideriiv; b). Tõestus: (F + C) = F + C = f + 0 = f 3

Tõestame kaks abiteoreemi: Kui funktsioon g(x) on (a; b) konstantne, siis g (x) = 0. Kui g (x) = 0 kõigi x (a; b) korral, siis g( x) = C punktis (a; b). 4

Teoreem 2. Kui F(x) on f(x) antiderivaat vahemikus (a; b) ja G(x) on teine antiderivaat f(x) jaoks vahemikus (a; b), siis G = F + C, kus C on arv. 5

Funktsiooni f(x) kõigi antiderivatiivide hulka vahemikus (a; b) nimetatakse määramatuks integraaliks ja seda tähistatakse integraaliga f(x)dx. dx Määramata integraali arvutamine antud funktsioon nimetatakse integratsiooniks 6

Kui funktsioon f(x) on pidev ja funktsioonil (t) on pidev tuletis (t), siis kehtib valem: f((t)) (t) dt = f(x) dx, kus x = ( t). 8

Olgu u(x) ja v(x) diferentseeruvad funktsioonid mingil intervallil. Siis (uv) = u v + v u See tähendab (uv) dx = (u v + v u)dx = = u v dx + v u dx või uv dx = uv – u v dx. 10

See eeldab valemit, mida nimetatakse osade kaupa integreerimiseks: integreerimine osade kaupa u(x)dv(x) = u(x) v(x) – v(x)du(x) 11

Funktsiooni kindel integraal üle intervalli on piir, milleni integraalsumma selle protsessi käigus kaldub, kui piirmäär on olemas: 13

Arvu a nimetatakse integratsiooni alumiseks piiriks ja arvu b lõimimise ülemiseks piiriks Joonisel 2 kaarjas trapets varjutusega esile tõstetud. Selle trapetsi pindala S määratakse valemiga 14

Olgu funktsioon f(t) defineeritud ja pidev mingil punkti a sisaldaval intervallil. Seejärel saab selle intervalli igale arvule x omistada numbri, defineerides sellega intervalli funktsiooni I(x), mida nimetatakse muutuva ülempiiriga kindlaks integraaliks 17

Kindla integraali tuletis suhtes ülempiir punktis x on võrdne integrandi väärtusega punktis x. 18

Olgu funktsioon y = f(x) defineeritud ja pidev poollõpmatul intervallil)