Definition
Pyramid is a polyhedron composed of a polygon \(A_1A_2...A_n\) and \(n\) triangles with a common vertex \(P\) (not lying in the plane of the polygon) and sides opposite it, coinciding with the sides of the polygon.
Designation: \(PA_1A_2...A_n\) .
Example: pentagonal pyramid \(PA_1A_2A_3A_4A_5\) .
Triangles \(PA_1A_2, \PA_2A_3\), etc. are called side faces pyramids, segments \(PA_1, PA_2\), etc. – lateral ribs, polygon \(A_1A_2A_3A_4A_5\) – basis, point \(P\) – top.
Height pyramids are a perpendicular descended from the top of the pyramid to the plane of the base.
A pyramid with a triangle at its base is called tetrahedron.
The pyramid is called correct, if its base is a regular polygon and one of the following conditions is met:
\((a)\) lateral edges of the pyramid equal;
\((b)\) the height of the pyramid passes through the center of the circle circumscribed near the base;
\((c)\) the side ribs are inclined to the plane of the base at the same angle.
\((d)\) side faces inclined to the plane of the base at the same angle.
Regular tetrahedron is a triangular pyramid, all of whose faces are equal equilateral triangles.
Theorem
Conditions \((a), (b), (c), (d)\) are equivalent.
Proof
Let's find the height of the pyramid \(PH\) . Let \(\alpha\) be the plane of the base of the pyramid.

1) Let us prove that from \((a)\) it follows \((b)\) . Let \(PA_1=PA_2=PA_3=...=PA_n\) .
Because \(PH\perp \alpha\), then \(PH\) is perpendicular to any line lying in this plane, which means the triangles are right-angled. This means that these triangles are equal in common leg \(PH\) and hypotenuse \(PA_1=PA_2=PA_3=...=PA_n\) . This means \(A_1H=A_2H=...=A_nH\) . This means that the points \(A_1, A_2, ..., A_n\) are at the same distance from the point \(H\), therefore, they lie on the same circle with the radius \(A_1H\) . This circle, by definition, is circumscribed about the polygon \(A_1A_2...A_n\) .
2) Let us prove that \((b)\) implies \((c)\) .
\(PA_1H, PA_2H, PA_3H,..., PA_nH\) rectangular and equal on two legs. This means that their angles are also equal, therefore, \(\angle PA_1H=\angle PA_2H=...=\angle PA_nH\).
3) Let us prove that \((c)\) implies \((a)\) .
Similar to the first point, triangles \(PA_1H, PA_2H, PA_3H,..., PA_nH\) rectangular and along the leg and sharp corner. This means that their hypotenuses are also equal, that is, \(PA_1=PA_2=PA_3=...=PA_n\) .
4) Let us prove that \((b)\) implies \((d)\) .
Because in a regular polygon the centers of the circumscribed and inscribed circles coincide (generally speaking, this point is called the center of a regular polygon), then \(H\) is the center of the inscribed circle. Let's draw perpendiculars from the point \(H\) to the sides of the base: \(HK_1, HK_2\), etc. These are the radii of the inscribed circle (by definition). Then, according to TTP (\(PH\) is a perpendicular to the plane, \(HK_1, HK_2\), etc. are projections perpendicular to the sides) inclined \(PK_1, PK_2\), etc. perpendicular to the sides \(A_1A_2, A_2A_3\), etc. respectively. So, by definition \(\angle PK_1H, \angle PK_2H\) equal to the angles between the side faces and the base. Because triangles \(PK_1H, PK_2H, ...\) are equal (as rectangular on two sides), then the angles \(\angle PK_1H, \angle PK_2H, ...\) are equal.
5) Let us prove that \((d)\) implies \((b)\) .
Similar to the fourth point, the triangles \(PK_1H, PK_2H, ...\) are equal (as rectangular along the leg and acute angle), which means the segments \(HK_1=HK_2=...=HK_n\) are equal. This means, by definition, \(H\) is the center of a circle inscribed in the base. But because at regular polygons the centers of the inscribed and circumscribed circles coincide, then \(H\) is the center of the circumscribed circle. Chtd.
Consequence
The lateral faces of a regular pyramid are equal isosceles triangles.
Definition
The height of the lateral face of a regular pyramid drawn from its vertex is called apothem.
The apothems of all lateral faces of a regular pyramid are equal to each other and are also medians and bisectors.
Important Notes
1. Height is correct triangular pyramid falls at the point of intersection of the altitudes (or bisectors, or medians) of the base (the base is a regular triangle).
2. Height is correct quadrangular pyramid falls at the point of intersection of the diagonals of the base (the base is a square).
3. Height is correct hexagonal pyramid falls at the intersection point of the diagonals of the base (the base is a regular hexagon).
4. The height of the pyramid is perpendicular to any straight line lying at the base.
Definition
The pyramid is called rectangular, if one of its side edges is perpendicular to the plane of the base.

Important Notes
1. In a rectangular pyramid, the edge perpendicular to the base is the height of the pyramid. That is, \(SR\) is the height.
2. Because \(SR\) is perpendicular to any line from the base, then \(\triangle SRM, \triangle SRP\) – right triangles.
3. Triangles \(\triangle SRN, \triangle SRK\)- also rectangular.
That is, any triangle formed by this edge and the diagonal emerging from the vertex of this edge lying at the base will be rectangular.
\[(\Large(\text(Volume and surface area of the pyramid)))\]
Theorem
The volume of the pyramid is equal to one third of the product of the area of the base and the height of the pyramid: \
Consequences
Let \(a\) be the side of the base, \(h\) be the height of the pyramid.
1. The volume of a regular triangular pyramid is \(V_(\text(right triangle.pir.))=\dfrac(\sqrt3)(12)a^2h\),
2. The volume of a regular quadrangular pyramid is \(V_(\text(right.four.pir.))=\dfrac13a^2h\).
3. The volume of a regular hexagonal pyramid is \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).
4. Volume regular tetrahedron equals \(V_(\text(right tetr.))=\dfrac(\sqrt3)(12)a^3\).
Theorem
The area of the lateral surface of a regular pyramid is equal to the half product of the perimeter of the base and the apothem.
\[(\Large(\text(Frustum)))\]
Definition
Consider an arbitrary pyramid \(PA_1A_2A_3...A_n\) . Let us draw a plane parallel to the base of the pyramid through a certain point lying on the side edge of the pyramid. This plane will split the pyramid into two polyhedra, one of which is a pyramid (\(PB_1B_2...B_n\) ), and the other is called truncated pyramid(\(A_1A_2...A_nB_1B_2...B_n\) ).
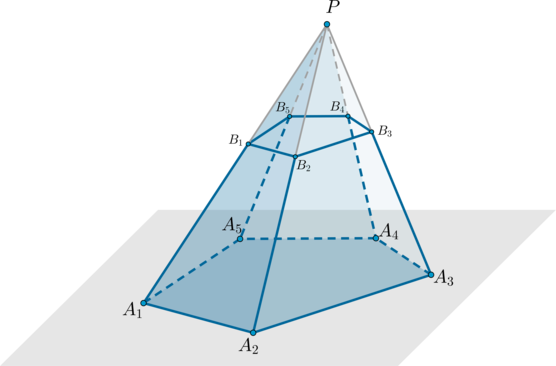
The truncated pyramid has two bases - polygons \(A_1A_2...A_n\) and \(B_1B_2...B_n\) which are similar to each other.
The height of a truncated pyramid is a perpendicular drawn from some point of the upper base to the plane of the lower base.
Important Notes
1. All lateral faces of a truncated pyramid are trapezoids.
2. The segment connecting the centers of the bases of a regular truncated pyramid (that is, a pyramid obtained by cross-section of a regular pyramid) is the height.
Let's consider what properties pyramids have, in which the side faces are perpendicular to the base.
If two adjacent lateral faces of the pyramid are perpendicular to the base, That the common lateral edge of these faces is the height of the pyramid. If the problem says that the edge of a pyramid is its height, That we're talking about specifically about this type of pyramid.
The faces of the pyramid perpendicular to the base are right triangles.
If the base of the pyramid is a triangle
The lateral surface of such a pyramid in general case we look for it as the sum of the areas of all lateral faces.
The base of the pyramid is orthogonal projection face not perpendicular to the base (in in this case, SBC). This means, according to the theorem on the area of orthogonal projection, the area of the base is equal to the product of the area of this face and the cosine of the angle between it and the plane of the base.
If the base of the pyramid is a right triangle

In this case all faces of the pyramid are right triangles.
Triangles SAB and SAC are rectangular, since SA is the height of the pyramid. Triangle ABC rectangular by condition.
The fact that the triangle SBC is right-angled follows from the theorem of three perpendiculars (AB is the projection of the inclined SB onto the plane of the base. Since AB is perpendicular to BC by condition, then SB is perpendicular to BC).
The angle between the side face of SBC and the base in this case is angle ABS.
The lateral surface area is equal to the sum of the areas of right triangles:
Since in this case
![]()
If the base of the pyramid is an isosceles triangle
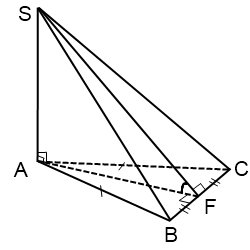
In this case, the angle between the side face plane BCS and the base plane is angle AFS, where AF is the height, median and bisector isosceles triangle ABC.
Similarly, if at the base of the pyramid lies equilateral triangle ABC.
If the base of the pyramid is a parallelogram
 In this case, the base of the pyramid is an orthogonal projection of the side faces that are not perpendicular to the base.
In this case, the base of the pyramid is an orthogonal projection of the side faces that are not perpendicular to the base.
If we divide the base into two triangles, then
where α and β are the angles between the ADS and CDS planes and the base plane, respectively.

If BF and BK are the heights of the parallelogram, then angle BFS is the angle of inclination of the side face CDS to the plane of the base, and angle BKS is the angle of inclination of the side ADS.
(the drawing was made for the case when B is an obtuse angle).
If the base of the pyramid is a rhombus ABCD, then the angles BFS and BKS are equal. Triangles ABS and CBS, as well as ADS and CDS, are also equal in this case.
If the base of the pyramid is a rectangle
 In this case, the angle between the side face plane SAD and the base plane is angle SAB,
In this case, the angle between the side face plane SAD and the base plane is angle SAB,
and the angle between the plane of the side face SCD and the plane of the base is angle SCB
(by the theorem of three perpendiculars).
Respectively,
From here lateral surface can be found as
Here all lateral faces of the pyramid are right triangles(angles SAD and SCD are right angles according to the theorem of three perpendiculars). Therefore, the lateral surface can be searched directly:
If the base of the pyramid is a square ABCD, then the problem is simplified: triangles ABS and BCS, as well as triangles ADS and CDS, are equal in this case.
15 Dec 2012
Reviews (12) on “Pyramids in which the edges are perpendicular to the base”
-
If you google “rectangular pyramid” in Russian, then your material is in the top five. I see that there is only one rectangular pyramid on this page, the last one, and the designations are not entirely correct. Google, together with Wikipedia, came up with a strange definition - a perpendicular edge and the same as at the base of a pyramid. By the way, on English language In general, a rectangular pyramid is a pyramid at the base of which there is a rectangle and it does not matter where the height is at all.
There is not a word in the text about a rectangular pyramid. Very often, in problems involving pyramids in which there are two side faces perpendicular to the base, we are talking about the angle between the plane of the side face and the plane of the base.
IN this material consider how to determine this angle depending on the polygon at the base. If the base contains a parallelogram (including a rhombus), you need to draw the heights of the parallelogram from the base of the pyramid to opposite sides(or a straight line containing these sides). If the base is a rectangle (including a square), there is no need to draw heights, since the sides of the rectangle are mutually perpendicular. In this case, the angle between the base and the side edge is determined linear angle, formed by the edges of the pyramid; the side faces are right triangles.
The right angles at the base are highlighted to highlight this difference from the case where the base is a parallelogram that is not a rectangle.Because you removed the “rectangular pyramid”, but techies who know and understand how search engines work are unlikely to be convinced by your arguments. Learn IT, not just math.
Dear Natashok! Are you accusing me of lying? I told you that I don’t use the term “rectangular pyramid” in my work.
P.S. I'm not an IT specialist, unfortunately. I agree, literacy is needed in all areas: both in mathematics and in information technology, and in spelling.
The figure illustrates the case when there is a rectangle at the base of the pyramid. In parallel design, angles are not preserved, so the rectangle is drawn as a parallelogram. The second right angle in the figure is noted in connection with the theorem of three perpendiculars.
Firstly, not a drawing, but a drawing. You draw up drawings in drawing, but in mathematics they are still drawings. Secondly, look at the last drawing. There are no theorems about three perpendiculars. I repeat, the base in the last drawing is not a rectangle. It doesn't matter how you portray it. I'm following the notations. Although I noticed that the third drawing below is not clear to me either. The parallelogram is not marked on the drawing. Just a quadrangle! Its appearance is similar to a parallelogram, but the designations leave much to be desired.
1) Yes, in geometry we make a drawing, but the illustration for the text is a drawing. In any geometry textbook they write “in Figure 1”, not “in Drawing 1”.
2) A rectangle in stereometry is depicted as a parallelogram, since angles are not preserved during parallel design. But the parallelism of the lines is preserved. The opposite sides of the quadrilateral are depicted as lying on parallel lines. It follows from this that this quadrilateral is a parallelogram.The opposite sides of the quadrilateral are depicted as lying on parallel lines. I do not see any indication that these lines are parallel and parallel design was not indicated in the text. So for me the basis is still on the last drawing arbitrary quadrilateral
Dear Natasha! Image spatial figures on the plane is carried out in accordance with the rules parallel design. This means that parallel lines in the drawing are depicted as parallel lines, and non-parallel lines are not parallel.
I do not agree with the definition of a rectangular pyramid. Rectangular pyramid is a pyramid, at one vertex of which there are three right angles. Write to me why you are spreading erroneous material at the level of an ignorant Wikipedia.
If the base of the pyramid is a rectangle, then why are two opposite corners marked in the picture to indicate it? In the last drawing, this base can be a rhomboid and another quadrilateral.
In which one of the side ribs is perpendicular to the base.
In this case, this edge will be the height of the pyramid.
Properties of the pyramid.
1. When all the side edges have the same size, then:
- near the base of the pyramid is easy to describe circle, while the top of the pyramid will be projected into the center of this circle;
- the lateral ribs form identical angles ;
- Moreover, the opposite is also true, i.e. when the lateral ribs form with the plane of the base equal angles, or when a circle can be described near the base of the pyramid and the top of the pyramid will be projected into the center of this circle, which means that all the side edges of the pyramid are the same size.
2. When the side faces have an angle of inclination to the plane of the base of the same value, then:
- it is easy to describe a circle near the base of the pyramid, and the top of the pyramid will be projected into the center of this circle;
- the heights of the side faces are equal length;
- the area of the side surface is equal to ½ the product of the perimeter of the base and the height of the side face.
3. About the pyramid can be described sphere in the event that at the base of the pyramid lies a polygon around which a circle can be described (the necessary and sufficient condition). The center of the sphere will be dot intersections of planes that pass through the middles of the edges of the pyramid perpendicular to them. From this theorem we conclude that a sphere can be described both around any triangular and around any regular pyramid;
4. A sphere can be inscribed in a pyramid if the bisector planes of the internal dihedral angles the pyramids intersect at the 1st point (a necessary and sufficient condition). This point will become the center of the sphere.
5. The cone will be inscribed in the pyramid when their vertices coincide, and the base of the cone will be inscribed in the base of the pyramid. In this case, it is possible to fit a cone into a pyramid only if the apothems of the pyramid have equal sizes (a necessary and sufficient condition);
6. Cone will be described near the pyramid if their vertices coincide, and the base of the cone will be described near the base of the pyramid. In this case, it is possible to describe a cone near the pyramid only if all the lateral edges of the pyramid have same values(necessary and sufficient condition). The heights of these cones and pyramids are the same.
7. Cylinder will be inscribed in a pyramid if one of its bases coincides with a circle that is inscribed in the section of the pyramid by a plane parallel to the base, and the second base belongs to the base of the pyramid.
8. The cylinder will be described near the pyramid when the top of the pyramid belongs to one of its bases, and the second base of the cylinder will be described near the base of the pyramid. In this case, it is possible to describe a cylinder near a pyramid only if the base of the pyramid is an inscribed polygon (a necessary and sufficient condition).
Formulas for determining the volume and area of a rectangular pyramid.
V- volume of the pyramid,
S- area of the base of the pyramid,
h- height of the pyramid,
Sb- area of the lateral surface of the pyramid,
a- apothem (not to be confused with α ) pyramids,
P- perimeter of the base of the pyramid,
n- the number of sides of the base of the pyramid,
b- length lateral rib pyramids,
α - flat angle at the top of the pyramid.
