Lesson topic: Tasks on constructing sections.
The purpose of the lesson:
Develop skills in solving problems involving constructing sections of a tetrahedron and parallelogram.
During the classes
I. Organizational moment.
II. Examination homework
Answers to questions 14, 15.
14. Is there a tetrahedron with five right angles on its faces?
(Answer: no, because there are only 4 faces, they are triangles, and a triangle with two right angles does not exist.)
15. Is there a parallelepiped that has: a) only one face - a rectangle;
b) only two adjacent rhombus faces; c) all corners of the faces are sharp; d) all angles of the faces are right; e) the number of all sharp edges is not equal to the number of all obtuse angles of the faces?
(Answer: a) no (opposite sides are equal); b) no (for the same reason); c) no (such parallelograms do not exist); d) yes ( cuboid); e) no (each face has two sharp and two obtuse angles, or all straight lines).
III. Learning new material
Theoretical part. Practical part. Theoretical part.
To solve many geometric problems associated with a tetrahedron and a parallelepiped, it is useful to be able to draw their sections in different planes in a drawing. By section we mean any plane (let's call it a cutting plane), on both sides of which there are points of a given figure (that is, a tetrahedron or parallelepiped). The cutting plane intersects the tetrahedron (parallelepiped) along segments. The polygon that will be formed by these segments is the cross section of the figure. Since a tetrahedron has four faces, its cross-section can be triangles and quadrangles. The parallelepiped has six faces. Its cross-section can be triangles, quadrangles, pentagons, hexagons.
When constructing a section of a parallelepiped, we take into account the fact that if a cutting plane intersects two opposite faces along some segments, then these segments are parallel (property 1, paragraph 11: If two parallel planes are intersected by a third, then the lines of their intersection are parallel).
To construct a section, it is enough to construct the points of intersection of the cutting plane with the edges of the tetrahedron (parallelepiped), and then draw segments connecting each two constructed points lying on the same face.
Can a tetrahedron be cut by a plane into the quadrilateral shown in the figure?
https://pandia.ru/text/78/630/images/image002_130.gif" width="626" height="287 src=">
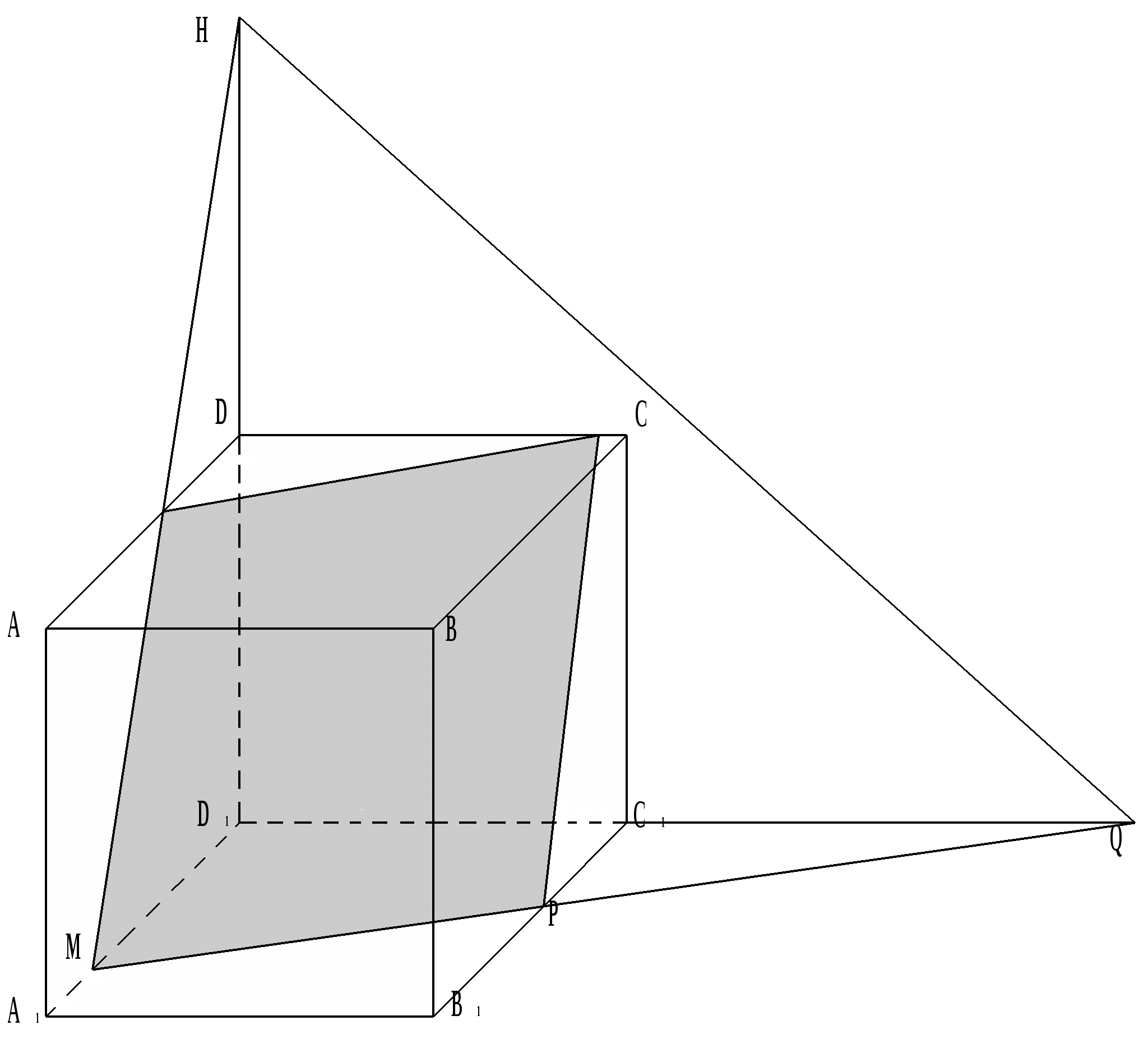
2.2. Construct a section of a cube with a plane passing through the points E, F, G, lying on the edges of the cube.
E, F, G,
let's make a direct E.F. and denote P its point of intersection with AD.
Let's denote Q point of intersection of lines PG And AB.
Let's connect the dots E And Q, F And G.
The resulting trapezoid EFGQ will be the desired section.
https://pandia.ru/text/78/630/images/image004_91.gif" width="624" height="287"> 
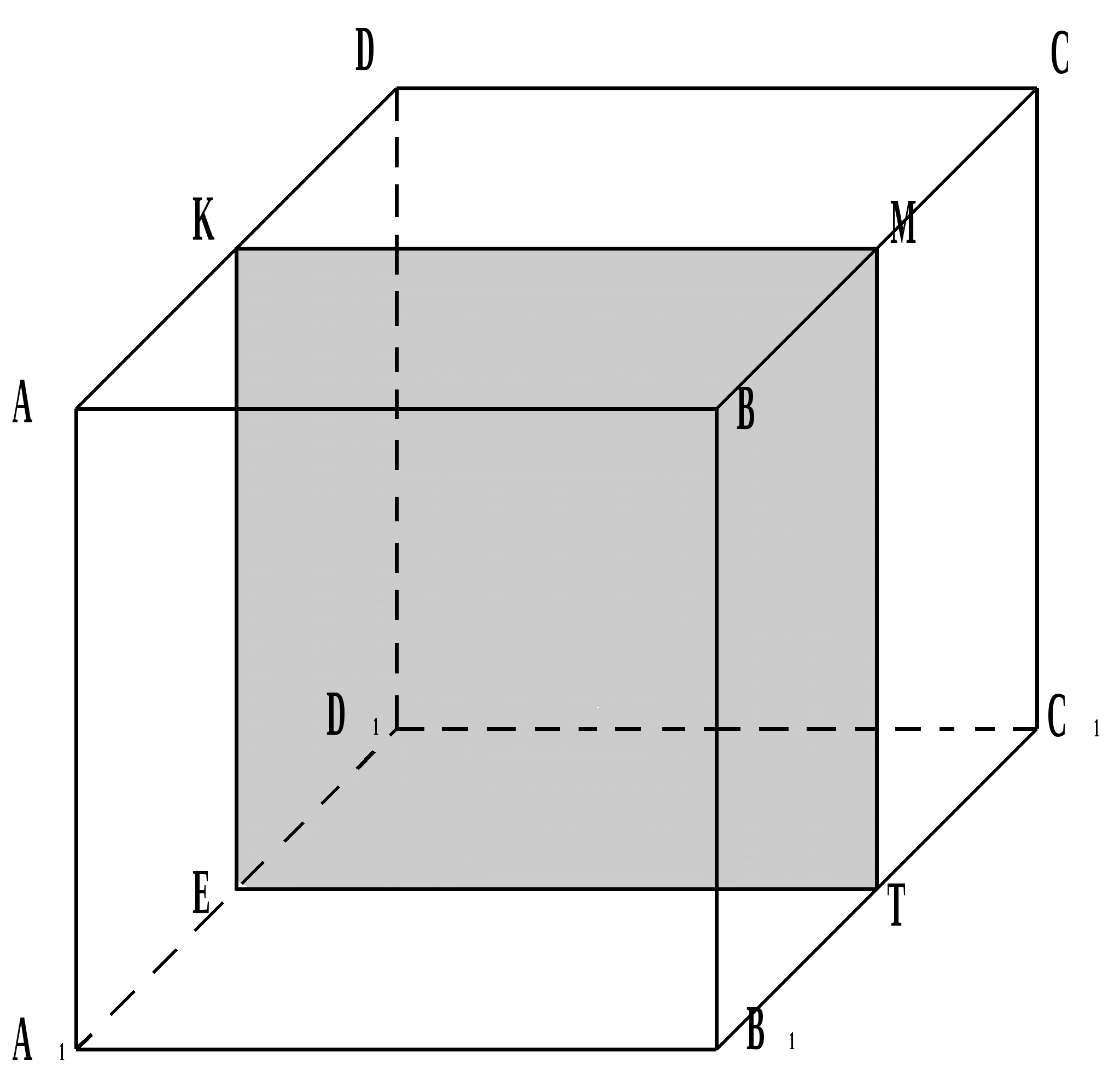
2.4. Construct a section of a cube with a plane passing through the points E, F, lying on the edges of the cube and the vertex B.
Solution. To construct a section of a cube passing through points E, F and the top B,
Let's connect the points with segments E And B, F And B.
Through dots E And F let's draw parallel lines B.F. And BE, respectively.
The resulting parallelogram BFGE will be the desired section.
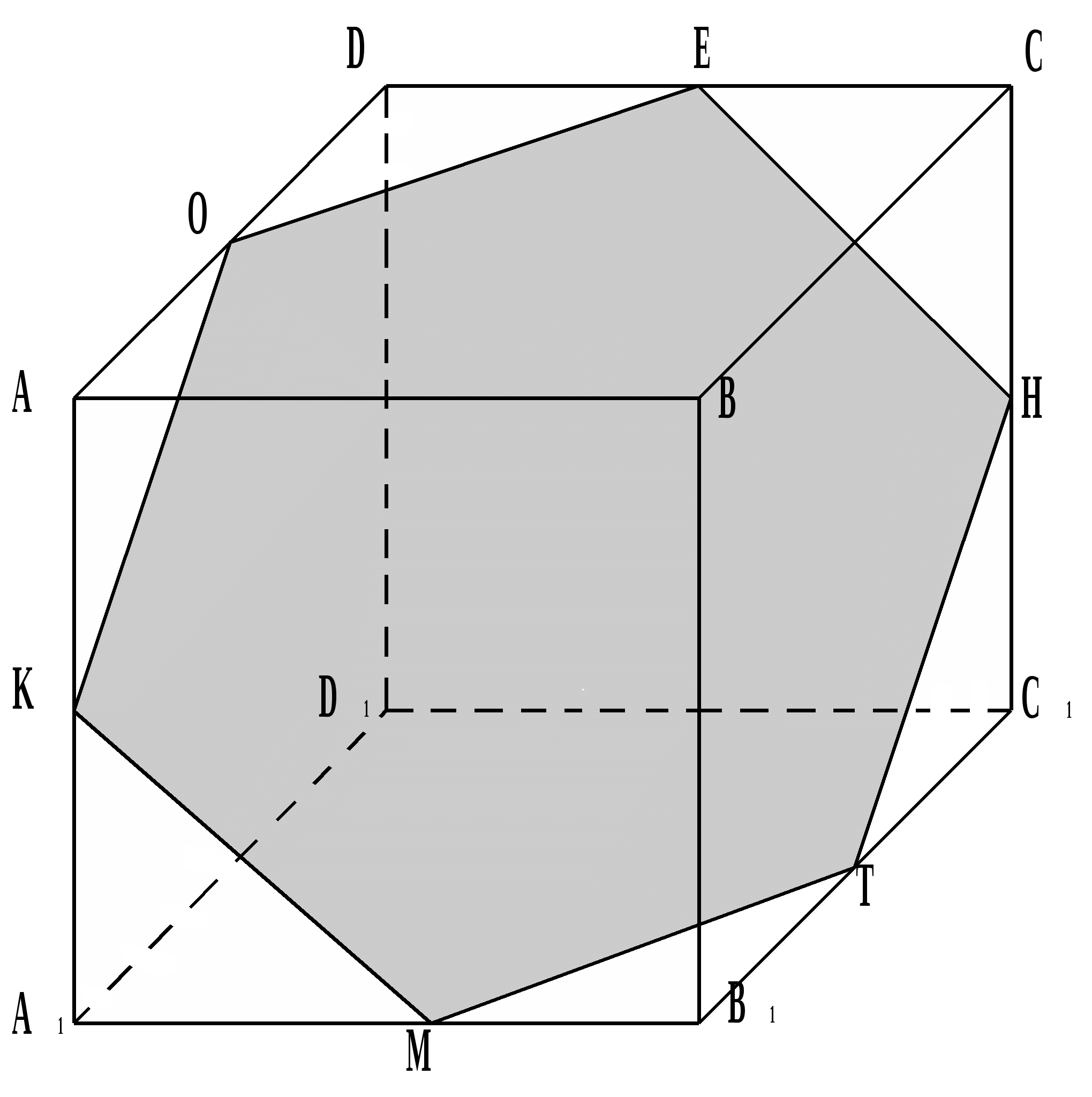
2.5. Construct a section of a cube with a plane passing through the points E, F, G, lying on the edges of the cube.
Solution. To construct a section of a cube passing through points E, F, G,
let's make a direct E.F. and denote P its point of intersection with AD.
Let's denote Q,R line intersection points PG With AB And DC.
Let's denote S intersection point FR c SS 1.
Let's connect the dots E And Q, G And S.
The resulting pentagon EFSGQ will be the desired section.
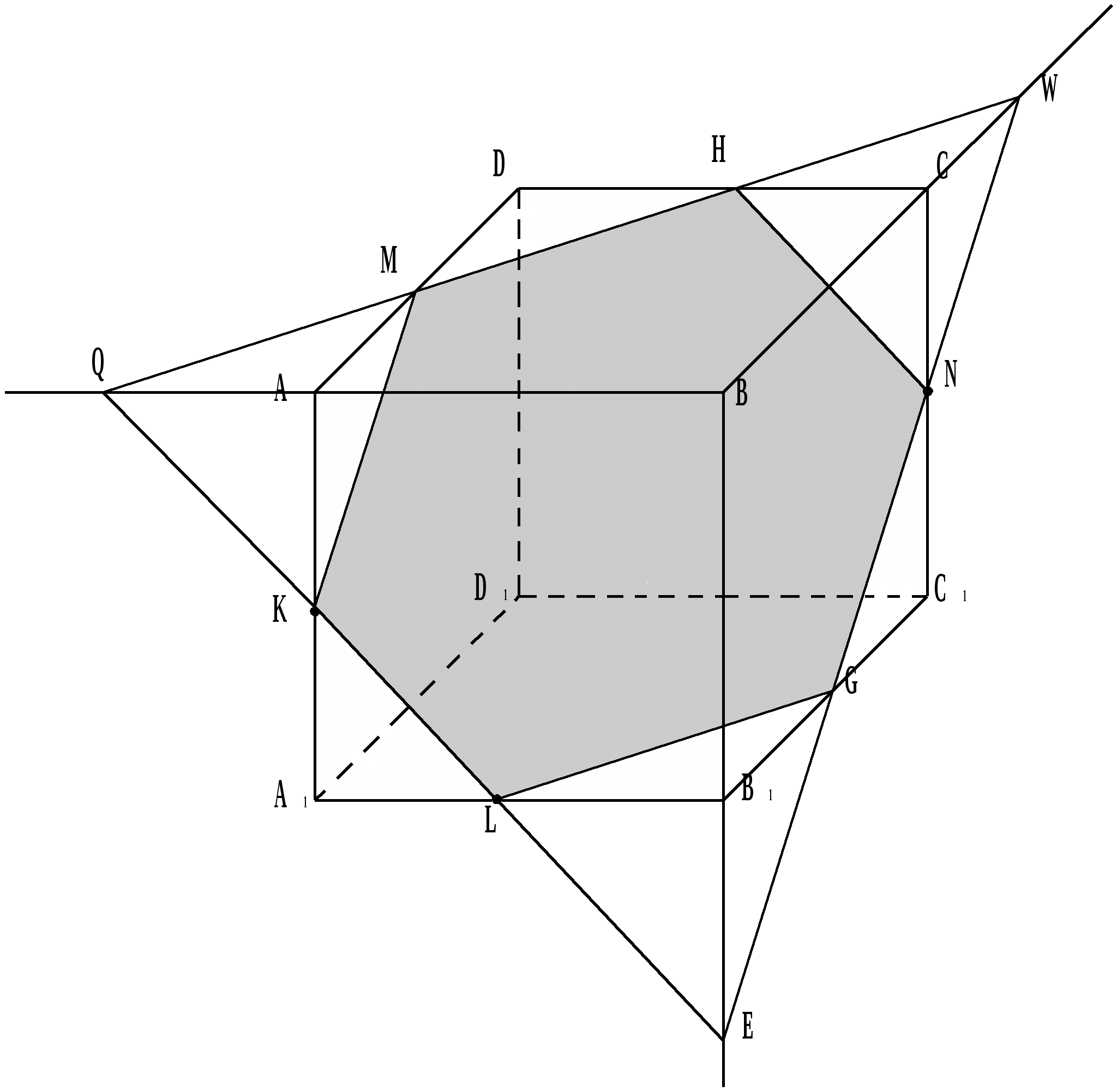
2.6. Construct a section of a cube with a plane passing through the points E, F, G, lying on the edges of the cube.
Solution. To construct a section of a cube passing through points E, F, G,
let's find a point P intersection of a straight line E.F. and face plane ABCD.
Let's denote Q, R line intersection points PG With AB And CD.
Let's make a direct RF and denote S, T its points of intersection with CC 1 and DD 1.
Let's make a direct T.E. and denote U its point of intersection with A 1D 1.
Let's connect the dots E And Q, G And S, F and U.
The resulting hexagon EUFSGQ will be the desired section.
2.7. Construct a cross section of a tetrahedron ABCD AD and passing through the points E, F.
Solution. Let's connect the dots E And F. Through the pointF let's draw a straight lineFG, parallelA.D.
Let's connect the dots G And E.
The resulting triangle EFG will be the desired section.
2.8. Construct a cross section of a tetrahedron ABCD flat, parallel to the edge CD and passing through the points E, F .
Solution. Through dots E And F let's draw straight lines E.G. And FH, parallel CD.
Let's connect the dots G And F, E And H.
The resulting triangle EFG will be the desired section.
2.9. Construct a cross section of a tetrahedron ABCD plane passing through the points E, F, G.
Solution. To construct a section of a tetrahedron passing through points E, F, G,
let's make a direct E.F. and denote P its point of intersection with BD.
Let's denote Q point of intersection of lines PG And CD.
Let's connect the dots F And Q, E And G.
The resulting quadrilateral EFQG will be the desired section.
IV. Lesson summary.
V. Homework p.14, p.27 No. 000 – option 1, 2.
Lesson Objectives
- Formation of students' skills in solving problems involving the construction of sections.
- Formation and development of spatial imagination in students.
- Development of graphic culture and mathematical speech.
- Developing the ability to work individually and in a team.
Lesson type: lesson in the formation and improvement of knowledge.
Forms of organizing educational activities: group, individual, collective.
Lesson technical support: computer, multimedia projector, screen, set of geometric bodies (cube, parallelepiped, tetrahedron).
DURING THE CLASSES
1. Organizational moment
The class is divided into 3 groups of 5-6 people. On each table there are individual and group tasks for constructing a section, a set of bodies. Introducing students to the topic and objectives of the lesson.
2. Update background knowledge
Poll theory:
– Axioms of stereometry.
– The concept of parallel lines in space.
– Theorem on parallel lines.
– Parallelism of three straight lines.
– The relative position of a straight line and a plane in space.
– A sign of parallelism between a line and a plane.
– Determination of parallelism of planes.
– Sign of parallelism of two planes.
- Properties parallel planes.
– Tetrahedron. Parallelepiped. Properties of a parallelepiped.
3. Learning new material
Teacher's word: When solving many stereometric problems, a section of a polyhedron by a plane is used. Let us call a secant plane of a polyhedron any plane on both sides of which there are points of the given polyhedron.
The cutting plane intersects the faces along segments. The polygon whose sides are these segments is called a section of the polyhedron.
Using Figures 38-39, let's find out: How many sides can a cross-section of a tetrahedron and a parallelepiped have?
Students analyze the pictures and draw conclusions. Teacher corrects students' answers, pointing out the fact that if a cutting plane intersects two opposite faces of a parallelepiped along some segments, then these segments are parallel.
Analysis solving problems 1, 2, 3 given in the textbook (oral group work).
4. Consolidation of the studied material(by groups)
1 group: explain how to construct a section of a tetrahedron with a plane passing through given points M, N, K and in problems 1-3 find the perimeter of the section if M, N, K are the midpoints of the edges and each edge of the tetrahedron is equal A.
Group 2: explain how to construct a section of a cube with a plane passing through three given points, which are either the vertices of the cube or the midpoints of its edges (the three given points are highlighted in the figures); in problems 1-4 and 6, find the perimeter of the section if the edge of the cube is equal to A. in problem 5 prove that AE = A/3
Group 3: construct a cross section of a parallelepiped ABCDA 1 B 1 C 1 D 1 plane passing through the points:
The group defends all completed tasks at the board using slides.
5. Independent work № 85, № 105.
6. Summing up the lesson
Assessing students' work in class.
7. Homework: individual cards.
Definition
Section is flat figure, which is formed when a spatial figure intersects with a plane and whose boundary lies on the surface of the spatial figure.
Comment
To construct sections of various spatial figures it is necessary to remember the basic definitions and theorems about parallelism and perpendicularity of lines and planes, as well as the properties of spatial figures. Let us recall the basic facts.
For more detailed study It is recommended to familiarize yourself with the topics “Introduction to stereometry. Parallelism" and "Perpendicularity. Angles and distances in space”.
Important Definitions
1. Two lines in space are parallel if they lie in the same plane and do not intersect.
2. Two straight lines in space intersect if a plane cannot be drawn through them.
4. Two planes are parallel if they do not have common points.
5. Two lines in space are called perpendicular if the angle between them is equal to \(90^\circ\) .
6. The straight line is called perpendicular to the plane, if it is perpendicular to any line lying in this plane.
7. Two planes are called perpendicular if the angle between them is \(90^\circ\) .
Important axioms
1. Through three points that do not lie on the same line, a plane passes through, and only one.
2. A plane, and only one, passes through a straight line and a point not lying on it.
3. A plane passes through two intersecting lines, and only one.
Important theorems
1. If a line \(a\) that does not lie in the plane \(\pi\) is parallel to some line \(p\) that lies in the plane \(\pi\) then it is parallel to this plane.
2. Let the straight line \(p\) be parallel to the plane \(\mu\) . If the plane \(\pi\) passes through the line \(p\) and intersects the plane \(\mu\) , then the line of intersection of the planes \(\pi\) and \(\mu\) is the line \(m\) - parallel to the line \(p\) .
3. If two intersecting lines from one plane are parallel to two intersecting lines from another plane, then such planes will be parallel.
4. If two parallel planes \(\alpha\) and \(\beta\) are intersected by a third plane \(\gamma\), then the lines of intersection of the planes are also parallel:
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]
5. Let the straight line \(l\) lie in the plane \(\lambda\) . If the line \(s\) intersects the plane \(\lambda\) at a point \(S\) not lying on the line \(l\), then the lines \(l\) and \(s\) intersect.
6. If a line is perpendicular to two intersecting lines lying in a given plane, then it is perpendicular to this plane.
7. Theorem about three perpendiculars.
Let \(AH\) be perpendicular to the plane \(\beta\) . Let \(AB, BH\) be the inclined plane and its projection onto the plane \(\beta\) . Then the line \(x\) in the plane \(\beta\) will be perpendicular to the inclined one if and only if it is perpendicular to the projection.
8. If a plane passes through a line perpendicular to another plane, then it is perpendicular to this plane.
Comment
Another important fact, often used to construct sections:
in order to find the point of intersection of a line and a plane, it is enough to find the point of intersection of a given line and its projection onto this plane.
For this of two arbitrary points\(A\) and \(B\) line \(a\) draw perpendiculars to the plane \(\mu\) – \(AA"\) and \(BB"\) (points \(A", B" \) are called projections of points \(A,B\) onto the plane). Then the line \(A"B"\) is the projection of the line \(a\) onto the plane \(\mu\) . The point \(M=a\cap A"B"\) is the intersection point of the straight line \(a\) and the plane \(\mu\) .
Moreover, we note that all points \(A, B, A", B", M\) lie in the same plane.
Example 1.
Given a cube \(ABCDA"B"C"D"\) . \(A"P=\dfrac 14AA", \KC=\dfrac15 CC"\). Find the intersection point of the straight line \(PK\) and the plane \(ABC\) .
Solution
1) Because the edges of the cube \(AA", CC"\) are perpendicular to \((ABC)\), then the points \(A\) and \(C\) are projections of the points \(P\) and \(K\). Then the line \(AC\) is the projection of the line \(PK\) onto the plane \(ABC\) . Let us extend the segments \(PK\) and \(AC\) beyond the points \(K\) and \(C\), respectively, and obtain the point of intersection of the lines - the point \(E\) .
2) Find the ratio \(AC:EC\) . \(\triangle PAE\sim \triangle KCE\) at two corners ( \(\angle A=\angle C=90^\circ, \angle E\)- general), means \[\dfrac(PA)(KC)=\dfrac(EA)(EC)\]
If we denote the edge of the cube as \(a\) , then \(PA=\dfrac34a, \KC=\dfrac15a, \AC=a\sqrt2\). Then:
\[\dfrac(\frac34a)(\frac15a)=\dfrac(a\sqrt2+EC)(EC) \Rightarrow EC=\dfrac(4\sqrt2)(11)a \Rightarrow AC:EC=4:11\ ]
Example 2.
Dana is correct triangular pyramid\(DABC\) with a base \(ABC\) whose height is equal to the side of the base. Let the point \(M\) divide side rib pyramid in the ratio \(1:4\), counting from the top of the pyramid, and \(N\) is the height of the pyramid in the ratio \(1:2\), counting from the top of the pyramid. Find the point of intersection of the straight line \(MN\) with the plane \(ABC\) .
Solution
1) Let \(DM:MA=1:4, \DN:NO=1:2\) (see figure). Because the pyramid is regular, then the height falls at the point \(O\) of intersection of the medians of the base. Let's find the projection of the straight line \(MN\) onto the plane \(ABC\) . Because \(DO\perp (ABC)\) , then \(NO\perp (ABC)\) . This means that \(O\) is a point belonging to this projection. Let's find the second point. Let us drop the perpendicular \(MQ\) from the point \(M\) to the plane \(ABC\) . The point \(Q\) will lie on the median \(AK\) .
Indeed, because \(MQ\) and \(NO\) are perpendicular to \((ABC)\), then they are parallel (which means they lie in the same plane). Therefore, since points \(M, N, O\) lie in the same plane \(ADK\), then the point \(Q\) will lie in this plane. But also (by construction) the point \(Q\) must lie in the plane \(ABC\), therefore, it lies on the line of intersection of these planes, and this is \(AK\) .
This means that the line \(AK\) is the projection of the line \(MN\) onto the plane \(ABC\) . \(L\) is the point of intersection of these lines.
2) Note that in order to draw the drawing correctly, it is necessary to find the exact position of the point \(L\) (for example, in our drawing the point \(L\) lies outside the segment \(OK\), although it could lie inside it; how is it correct?).
Because according to the condition, the side of the base is equal to the height of the pyramid, then we denote \(AB=DO=a\) . Then the median is \(AK=\dfrac(\sqrt3)2a\) . Means, \(OK=\dfrac13AK=\dfrac 1(2\sqrt3)a\). Let's find the length of the segment \(OL\) (then we can understand whether the point \(L\) is inside or outside the segment \(OK\): if \(OL>OK\) then it is outside, otherwise it is inside).
A) \(\triangle AMQ\sim \triangle ADO\) at two corners ( \(\angle Q=\angle O=90^\circ, \\angle A\)- general). Means,
\[\dfrac(MQ)(DO)=\dfrac(AQ)(AO)=\dfrac(MA)(DA)=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \AQ=\dfrac 45\cdot \dfrac 1(\sqrt3)a\]
Means, \(QK=\dfrac(\sqrt3)2a-\dfrac 45\cdot \dfrac 1(\sqrt3)a=\dfrac7(10\sqrt3)a\).
b) Let us denote \(KL=x\) .
\(\triangle LMQ\sim \triangle LNO\) at two corners ( \(\angle Q=\angle O=90^\circ, \\angle L\)- general). Means,
\[\dfrac(MQ)(NO)=\dfrac(QL)(OL) \Rightarrow \dfrac(\frac45 a)(\frac 23a) =\dfrac(\frac(7)(10\sqrt3)a+x )(\frac1(2\sqrt3)a+x) \Rightarrow x=\dfrac a(2\sqrt3) \Rightarrow OL=\dfrac a(\sqrt3)\]
Therefore, \(OL>OK\) means that the point \(L\) really lies outside the segment \(AK\) .
Comment
Don’t be alarmed if, when deciding similar task you will find that the length of the segment is negative. If in the conditions of the previous problem we received that \(x\) is negative, this would mean that we incorrectly chose the position of the point \(L\) (that is, that it is located inside the segment \(AK\)) .
Example 3
Dana is correct quadrangular pyramid\(SABCD\) . Find the section of the pyramid by the plane \(\alpha\) passing through the point \(C\) and the middle of the edge \(SA\) and parallel to the line \(BD\) .
Solution
1) Let us denote the middle of the edge \(SA\) by \(M\) . Because the pyramid is regular, then the height \(SH\) of the pyramid falls to the point of intersection of the diagonals of the base. Consider the plane \(SAC\) . The segments \(CM\) and \(SH\) lie in this plane, let them intersect at the point \(O\) .
In order for the plane \(\alpha\) to be parallel to the line \(BD\) , it must contain some line parallel to \(BD\) . The point \(O\) is located together with the line \(BD\) in the same plane - in the plane \(BSD\) . Let us draw in this plane through the point \(O\) the straight line \(KP\parallel BD\) (\(K\in SB, P\in SD\) ). Then, by connecting the points \(C, P, M, K\) , we obtain a section of the pyramid by the plane \(\alpha\) .
2) Let us find the relation in which the points \(K\) and \(P\) are divided by the edges \(SB\) and \(SD\) . This way we will completely define the constructed section.
Note that since \(KP\parallel BD\) , then by Thales’ theorem \(\dfrac(SB)(SK)=\dfrac(SD)(SP)\). But \(SB=SD\) means \(SK=SP\) . Thus, only \(SP:PD\) can be found.
Consider \(\triangle ASC\) . \(CM, SH\) are the medians in this triangle, therefore, the intersection point is divided in the ratio \(2:1\), counting from the vertex, that is, \(SO:OH=2:1\) .
Now according to Thales' theorem from \(\triangle BSD\) : \(\dfrac(SP)(PD)=\dfrac(SO)(OH)=\dfrac21\).
3) Note that according to the theorem of three perpendiculars, \(CO\perp BD\) is like an oblique one (\(OH\) is a perpendicular to the plane \(ABC\), \(CH\perp BD\) is a projection). So, \(CO\perp KP\) . Thus, the section is a quadrilateral \(CPMK\) whose diagonals are mutually perpendicular.
Example 4
Dana rectangular pyramid\(DABC\) with edge \(DB\) perpendicular to the plane \(ABC\) . At the base lies right triangle with \(\angle B=90^\circ\) , and \(AB=DB=CB\) . Draw a plane through the straight line \(AB\) perpendicular to the face \(DAC\) and find the section of the pyramid by this plane.
Solution
1) The plane \(\alpha\) will be perpendicular to the face \(DAC\) if it contains a line perpendicular to \(DAC\) . Let's draw a perpendicular from the point \(B\) to the plane \(DAC\) - \(BH\) , \(H\in DAC\) .
Let us draw auxiliary \(BK\) – median in \(\triangle ABC\) and \(DK\) – median in \(\triangle DAC\) .
Because \(AB=BC\) , then \(\triangle ABC\) is isosceles, which means \(BK\) is the height, that is, \(BK\perp AC\) .
Because \(AB=DB=CB\) and \(\angle ABD=\angle CBD=90^\circ\), That \(\triangle ABD=\triangle CBD\), therefore, \(AD=CD\) , therefore, \(\triangle DAC\) is also isosceles and \(DK\perp AC\) .
Let's apply the theorem about three perpendiculars: \(BH\) – perpendicular to \(DAC\) ; oblique \(BK\perp AC\) , which means projection \(HK\perp AC\) . But we have already determined that \(DK\perp AC\) . Thus, the point \(H\) lies on the segment \(DK\) .
By connecting the points \(A\) and \(H\) we obtain a segment \(AN\) along which the plane \(\alpha\) intersects the face \(DAC\) . Then \(\triangle ABN\) is the desired section of the pyramid by the plane \(\alpha\) .
2) Determine the exact position of the point \(N\) on the edge \(DC\) .
Let's denote \(AB=CB=DB=x\) . Then \(BK\) as the median dropped from the vertex right angle in \(\triangle ABC\) is equal to \(\frac12 AC\) , therefore \(BK=\frac12 \cdot \sqrt2 x\) .
Consider \(\triangle BKD\) . Let's find the ratio \(DH:HK\) .
Note that since \(BH\perp (DAC)\), then \(BH\) is perpendicular to any straight line from this plane, which means \(BH\) is the height in \(\triangle DBK\) . Then \(\triangle DBH\sim \triangle DBK\), hence
\[\dfrac(DH)(DB)=\dfrac(DB)(DK) \Rightarrow DH=\dfrac(\sqrt6)3x \Rightarrow HK=\dfrac(\sqrt6)6x \Rightarrow DH:HK=2:1 \]
Let's now consider \(\triangle ADC\) . The medians of the exact intersection triangle are divided in the ratio \(2:1\), counting from the vertex. This means that \(H\) is the intersection point of the medians in \(\triangle ADC\) (since \(DK\) is the median). That is, \(AN\) is also a median, which means \(DN=NC\) .
General education school of І-ІІІ levels No. 2
Department of Education of the Kirovskoye City Administration
“Cube section by plane
and their practical application in problems.”
Prepared by a math teacher
teacher-methodologist
Chumakova G.V.
2015
Introduction:
Problems on constructing sections of polyhedra occupy a significant place both in high school geometry courses and in exams different levels. Solving this type of problem contributes to the assimilation of the axioms of stereometry, the systematization of knowledge and skills, the development of spatial understanding and constructive skills. The difficulties that arise when solving problems involving the construction of sections are well known.
The main actions that make up the method of constructing sections are finding the point of intersection of a straight line with a plane, constructing lines of intersection of two planes, constructing a straight line parallel to a plane, and constructing a straight line perpendicular to a plane.
I will illustrate the construction of a section using one problem from school course mathematics:
№1. Construct at least two sections of the cubeABCDA 1 B 1 C 1 D 1 plane AM 1 C, if point M 1 moves along the segment BB 1 from B to B 1 . Find the boundaries of measuring the height of the section drawn from point M 1 .
Solution: Let's construct two required sections, taking point M 1
closer to point B, and point M 2
closer to B 1
. Both sections are shown in the figure. At the beginning of the movement when point M 1
just moved away from point B 1
, the section is a triangle with base AC and height M 1
O, which is slightly larger than the segment BO, i.e. 
If point M 1
will take position M 2
located very close to point B 1
, That 
AM 2
C will almost coincide with AB 1
C, and its height is M 1
O – with segment B 1
O, whose length is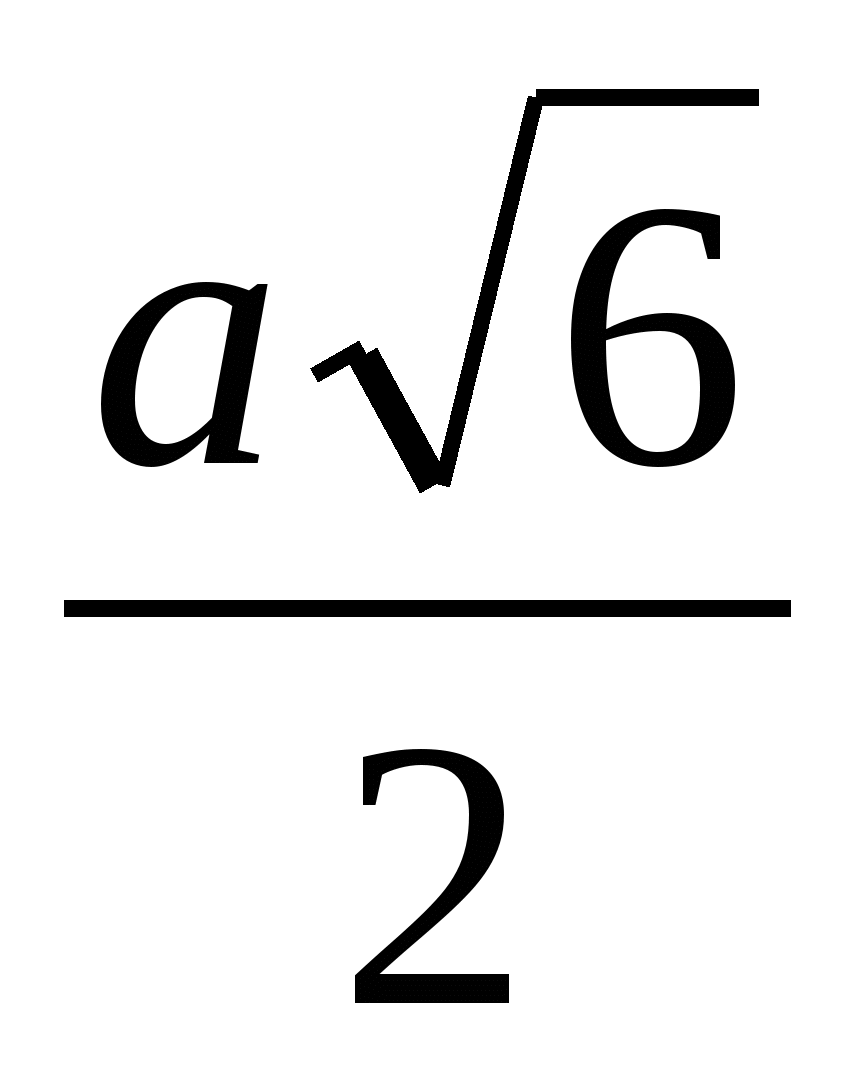 
(OB 1 = 
=
).
From here, for reasons of continuity, we conclude: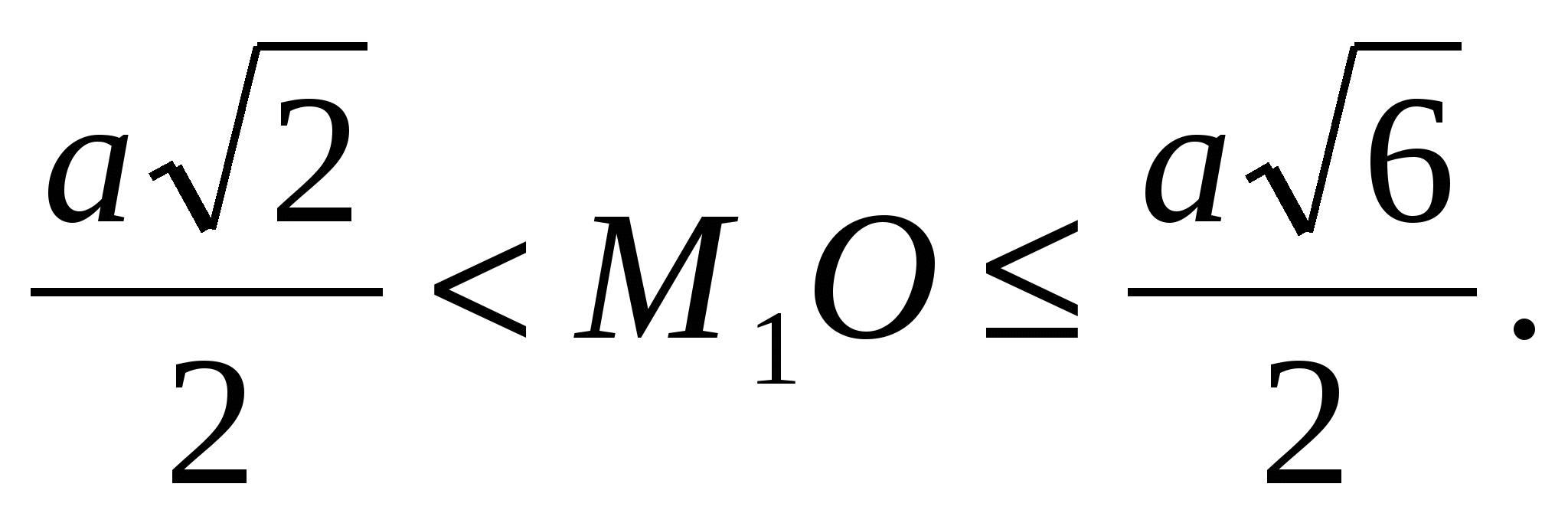 
You should especially look at what happens if point M 1 takes the position of vertex B.
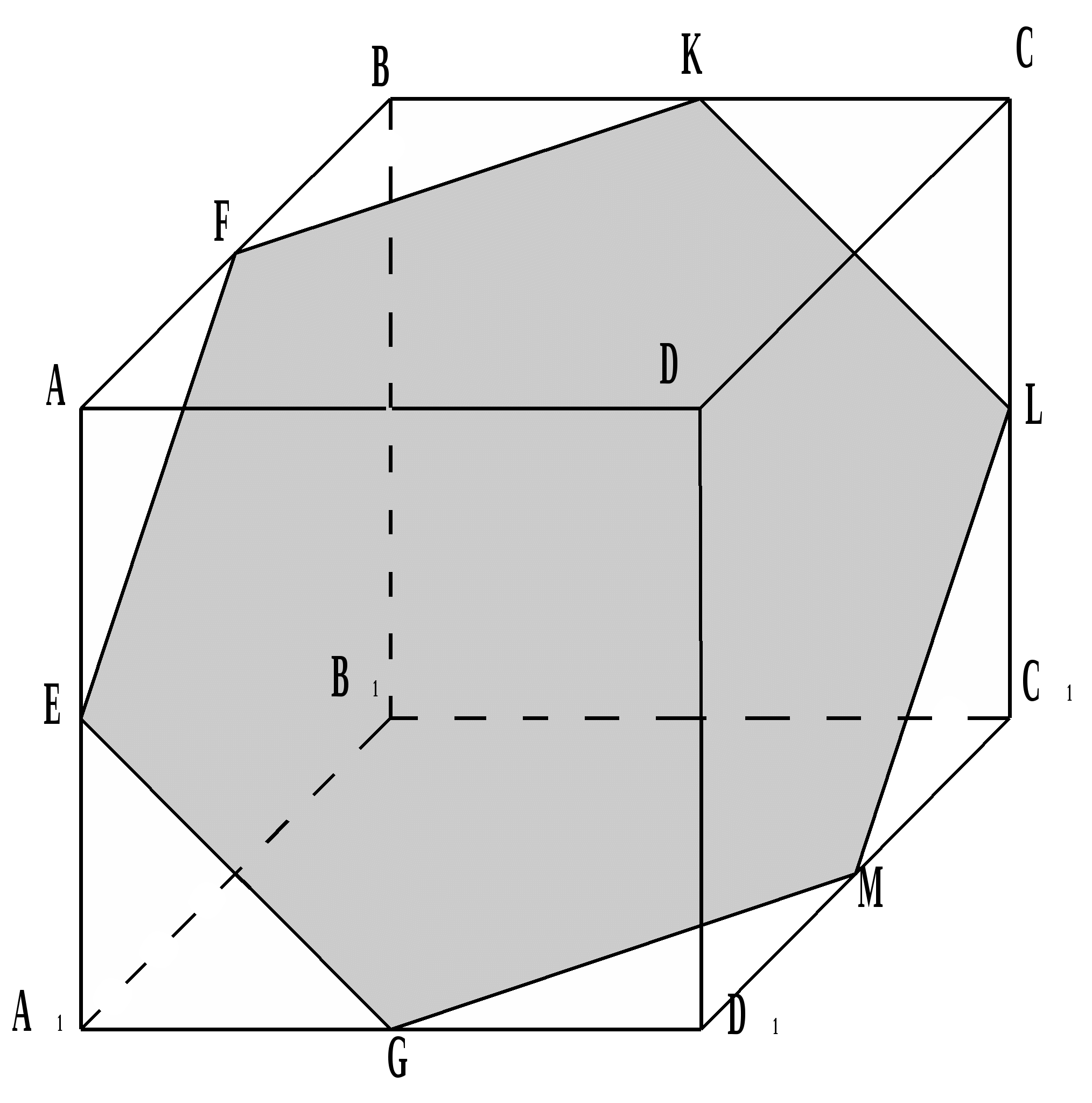
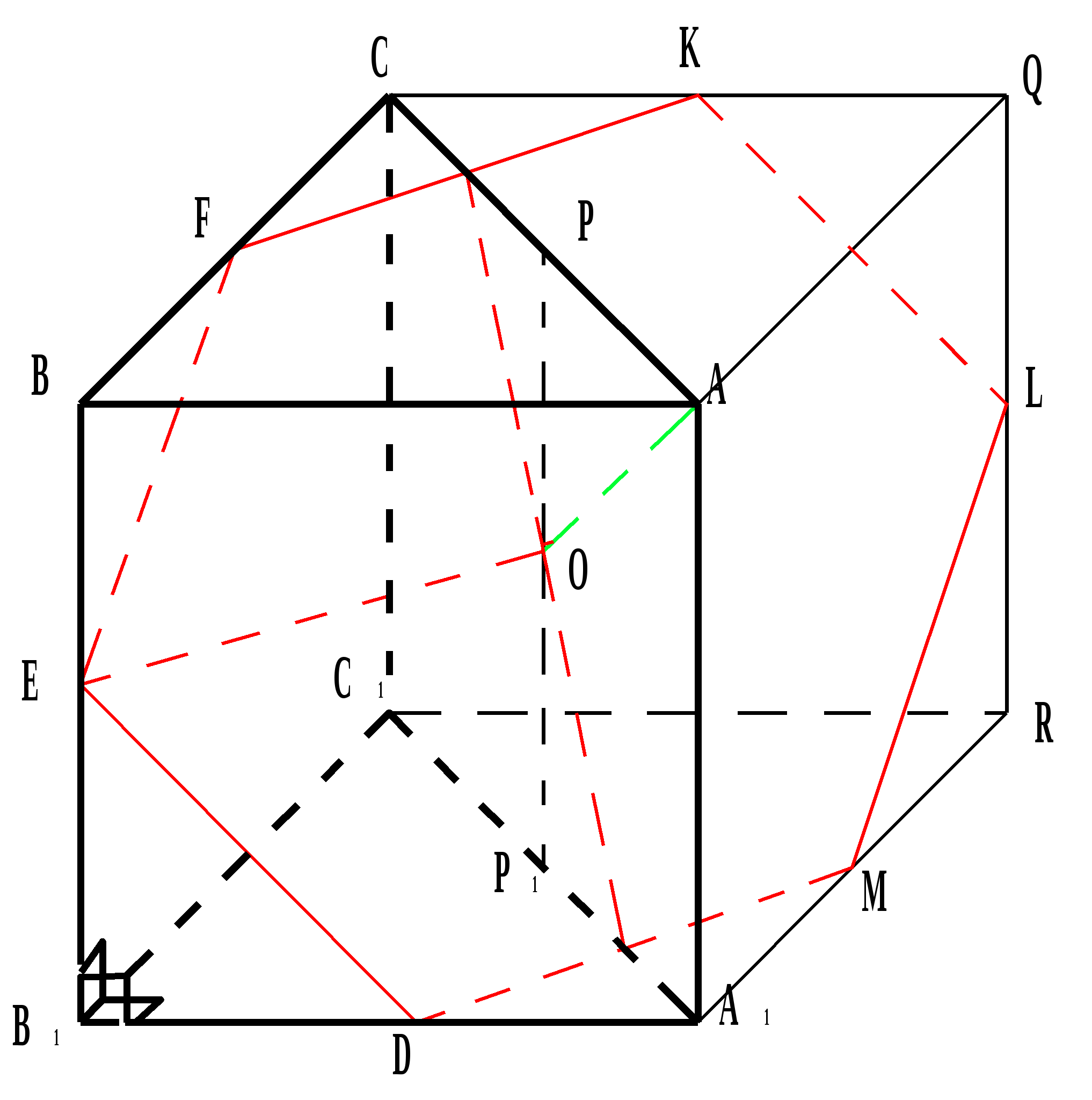
№2. Construct a section of the cube with a plane passing through three points A 1, E and L lying on the edges of the cube.
The planes of the faces A 1 ADD 1 and DD 1 C 1 C intersect along the straight line DD 1 , and the planes of the faces A 1 B 1 C 1 D 1 u DD 1 C 1 C intersect along the straight line D 1 C 1 . By connecting points A and E, we obtain a straight line of intersection of the cutting plane with the plane of the face AA 1 D 1 D, and continuing it, we find the point N, belonging to three planes: the cutting plane and the planes of the faces AA 1 D 1 D u DD 1 C 1 C.
Similarly, we find the point M common to three planes: the section plane and the planes of the faces A 1 B 1 C 1 D 1 u DD 1 C 1 C . Thus, points N u M belong to the cutting plane and the plane DD 1 C 1 C; straight line MN is the line of intersection of the section plane with the plane of the face DD 1 C 1 C, and F and K are the points of its intersection with the edges of the cube CD u CC 1. Consistently connecting points A 1 , E , F , K u L with straight lines, we obtain the pentagon A ! EFKL, which will give us the desired section.
When constructing a section of a cube using a plane X with an arbitrary arrangement of points in the section, the result is: triangle, trapezoid, rectangle, pentagon or hexagon. Naturally, the question arose of how the type of section depends on the type of location of the points defining this section
I decided to conduct a study to find out.
Construct sections of a cube by a plane when three points belonging to edges with one vertex are given.
Three points A 1 , D , C 1 are taken, which belong to the vertex D 1, and themselves are the vertices of the cube.
In cross section it turned out equilateral triangle, since A 1 C 1 , A 1 D u DC 1 are the diagonals of the faces of this cube.
Three dots: A 1 u C 1 are the vertices of the cube, and point F belongs to the edge of the cube DD 1. The points belong to the straight lines emerging from the vertex D 1 .
The cross-section results in an isosceles triangle, since F is equidistant from the points A 1 u C 1 .
Three dots: A 1 u C 1 are the vertices of the cube, and point F belongs to the straight line of the cube edge DD 1. The points belong to straight lines emerging from one vertex D 1 .
In cross section it turns out isosceles trapezoid, since F is equidistant from the points A 1 u C 1, that is, LA 1 =KC 1.
Three points belonging to edges with one vertex D 1. The points F u M belong to the continuations of the edges D 1 D u D 1 C, respectively, and the point A 1 is the vertex of the cube.
The cross-section results in a pentagon A 1 KLNG.
Three points F, M and Q are taken so that they lie on the continuation of the edges D 1 D, D 1 C 1, and D 1 A 1, respectively.
The cross-section results in a hexagon KLNGJH.
Three points lie on edges with one vertex D 1.
The cross-section results in an arbitrary triangle, but if the points are arranged so that D 1 Q =D 1 M =D 1 F , that is, if they were equidistant from the vertex D 1, then the cross-section would result in an equilateral triangle.
The cutting plane is defined by points H, Q and M. The cross-section produces a parallelogram, since KC ││ MP and MK ││ PC by the theorem on the intersection of two parallel planes with a third.
If points H, Q and M, define the cutting plane, distant from D, at a distance of 2a, where a is for the edge of the cube, then in the section it turns out regular triangle ACB 1.
Conclusion: the three points defining the section belong to three edges of the cube with a common vertex or are their continuation, then the section results in: triangle, pentagon, hexagon, trapezoid, parallelogram.
Constructing a section of a cube by a plane when three points are given, two of which lie on adjacent edges, and the third point lies on an edge not adjacent to them.
Three dots M, K u F, are taken so that M u F belong to edges with one vertex A 1, and point K lies on an edge not adjacent to them.
The cross-section results in a rectangle, since A 1 M = D 1 K and using the theorem of three perpendiculars it can be proven that MKLF is a rectangle, and if A 1 M 
D 1 K, then you can get a trapezoid or a pentagon.
Three points are taken so that K u L belong to edges emerging from one vertex A 1, and point N belongs to edge CC 1, not adjacent to them. K, L u N of the midpoints of the edges A 1 A, A 1 B 1 u CC 1 – respectively.
In cross section it turns out regular hexagon KLGNHM
Three points are taken so that K u L belong to edges emerging from one vertex A 1, and point T belongs to edge DC.
The cross-section results in a hexagon KLFRTZ.
Three points are taken so that K u L belong to the edges of the cube from one vertex A 1, and point M belongs to the edge DD 1.
The cross section results in a trapezoid LKQM.
Three dots K u L which belong to edges with one vertex A 1 and a point R which lies on edge BC.
The cross section results in a pentagon KLFRT.
Conclusion: If the cutting plane is defined by three points, two of which lie on adjacent edges, and the third on an edge not adjacent to them, then the section can result in a rectangle, pentagon, hexagon, trapezoid.
There is a parallelogram in the cross section of a cube and its special cases.
Points T, H, J defining the section are located so that T.H. 
AD, H.J. AD. The cross section results in a square HTKJ.
The section is specified by points C, F, L, with DF = FD 1, BL = LB 1. The cross-section produces a rhombus AFCL.
The section is defined by points C, G, H. B 1 H =DG. In cross section there is a parallelogram A 1 GCH.
The points defining the section are the vertices of the cube A, D, C 1. The cross section results in a rectangle
Cross section of a cube regular polygons
Triangle ABC 1 is equilateral, since its sides are the diagonals of the faces of the cube.
Triangle KMT is equilateral, since KV = MV = TV.
KMTE is a square, since the section is defined by points M, K, E and MK AD, E.K. AD.
The section has a regular hexagon KMTNEO, since the points H, E, K defining the section are the midpoints of the edges CC 1, DC, AA 1, respectively.
Cube and several problems on stereometry from the Unified State Exam.
In the manual “Unified State Exam 2005. Mathematics. Typical test problems” (Kornikova T. A. et al.) Contains 10 problems (C4) in stereometry, united by a common idea: a triangular prism ABCA is given 1
IN 1
WITH 1
the sides of the base AB and BC are mutually perpendicular and perpendicular to the edge BB 1
, AB=BC=BB 1
, vertex A is the top of the cone (or the center of one of the bases of the cylinder, or the center of the sphere), the base of the cone (the sphere or the second base of the cylinder) passes through the middle of one edge of the prism, its length is known. We need to find the volume or surface of a cone (sphere, cylinder). 
General example solutions:
Add this prism to a cube. Hexagon DEFKLM - a section of a cube by the plane of the base of a cone, the circle of which passes through the middle A 1 B 1, A is the vertex of the cone, or
DEFKLM is a section of a cube by the plane of the base of a cylinder, the circle of which passes through the middle of A 1 B 1, A is the center of the second base of the cylinder, or this is a section of a cube by a plane great circle spheres with center A, the sphere of which passes through the middle of A 1 B 1.
HexagonDEFKLM– section of a cube by a plane passing through the middle of edges A 1
IN 1
, BB 1
, VSZh when constructing points are obtainedK,
L,
M, which are the midpoints of the corresponding edges. The sides of this hexagon are the hypotenuses of the trianglesD.B. 1
E,
EBF,
FCK,
KQL,
LRM,
M.A. 1
D, the legs of which are equal to half the edge of the cube. Then the center of this hexagon is the center of the circle circumscribed around it, which intersects the edges of the cube at the pointsD,
E,
F,
K,
Land M, the radius of this circle 
, where A 1
IN 1
=
A .
A.O. E.L.
T.
To.
EAL
– isosceles:AL
=
A.E.
.
(
ABE
u
EAL– rectangular,AB=
AQ=
A,
BE
=
L.Q.
=
)
EO =OL as the midpoint of the diagonal EL of the hexagon DEFKLM, i.e. AO is the median, and according to its properties isosceles triangle and height. AO is proved in a similar way DK. Since AO is perpendicular to two intersecting straight lines of the hexagon plane, then AO is perpendicular to the entire plane.
If A is the vertex of the cone, then AO is its height, if A is the center of the second base of the cylinder, then AO is the height of the cylinder.
ABC: AC= 
,
P
– intersection points of the diagonals of the base of the cube, AP= 
, RR
1
=AA
1
=
A
. OR=RR
1
= , then from the rectangular
ROA JSC= 
. And so AO= 
.
Then, if we are talking about a cone:
=
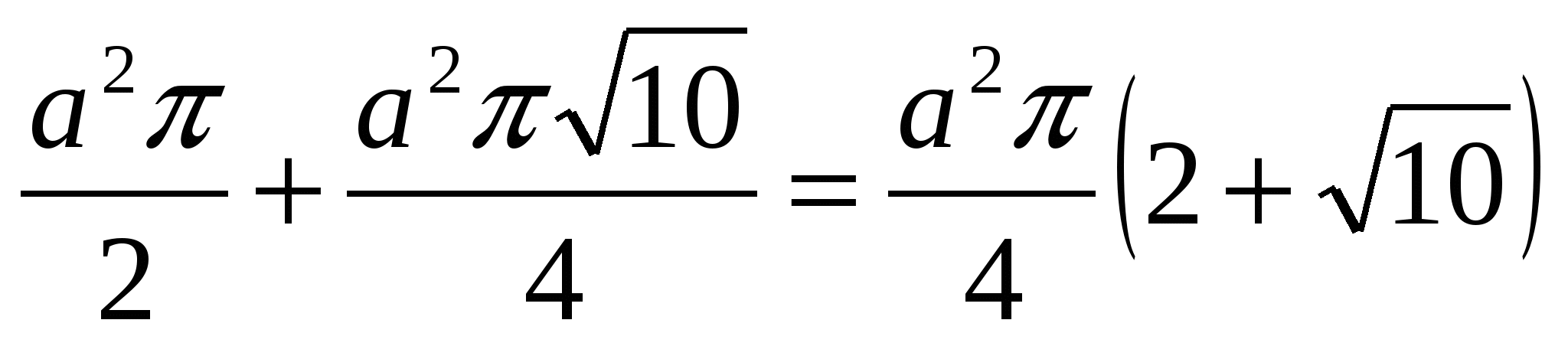
(from 
).
Answer: 
If we are talking about a cylinder:
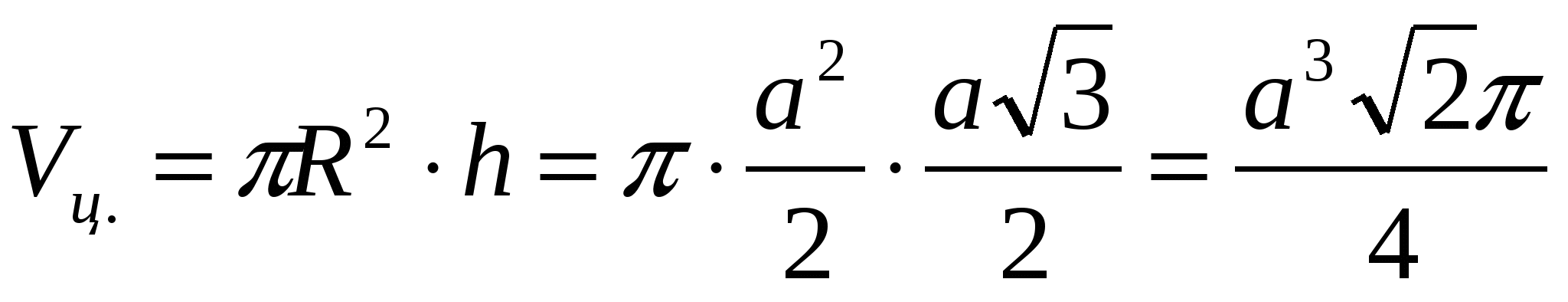
Answer: 
If we are talking about the sphere:
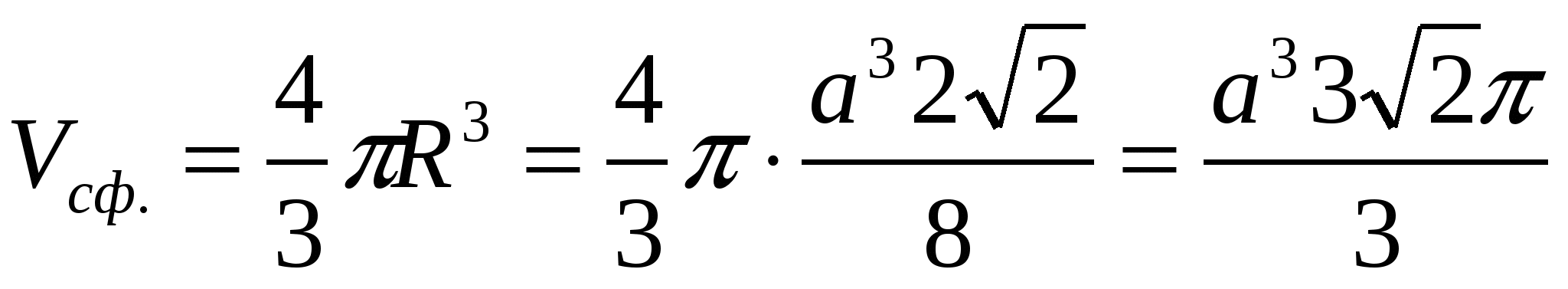
Answer: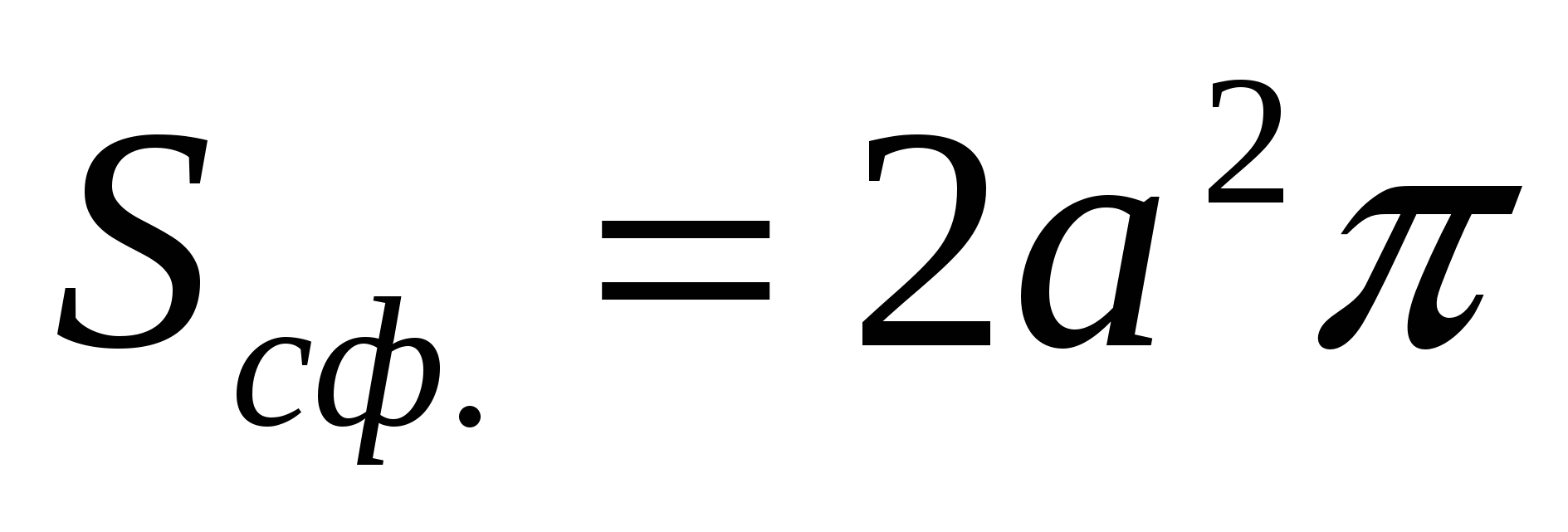 
Kornikova T. A. and other typical test tasks. Unified State Examination - 2005
Option 6.
Task. Given is a prism ABCA 1 B 1 C 1 and a cylinder. Sides AB and BC of the base of the prism are perpendicular to edge BB 1 and mutually perpendicular. The center of the base of the cylinder is point A 1; the circle of the second base passes through the middle of edge A 1 B 1.
Find the area full surface cylinder, if BB 1 =AB=BC=10. Find its volume.
Solution:
. 
.
Lesson type: Combined lesson.
Goals and objectives:
- educational – formation and development of spatial concepts in students; developing skills in solving problems involving constructing sections of the simplest polyhedra;
- educational - cultivate the will and perseverance to achieve final results when constructing sections of the simplest polyhedra; Foster a love and interest in learning mathematics.
- developing – student development logical thinking, spatial representations, development of self-control skills.
Equipment: computers with a specially developed program, handouts in the form ready-made drawings with tasks, solids of polyhedra, individual cards with homework.
Lesson structure:
- State the topic and purpose of the lesson (2 min).
- Instructions on how to complete tasks on a computer (2 min).
- Updating students' basic knowledge and skills (4 min).
- Self-test (3 min).
- Solving problems with an explanation of the solution by the teacher (15 min).
- Independent work with self-test (10 min).
- Setting homework (2 min).
- Summing up (2 min).
During the classes
1. Communicating the topic and purpose of the lesson
After checking the class’s readiness for the lesson, the teacher reports that today there is a lesson on the topic “Constructing sections of polyhedra”; problems will be considered on constructing sections of some simple polyhedra with planes passing through three points belonging to the edges of the polyhedra. The lesson will be taught using a computer presentation made in Power Point.
2. Safety instructions when working in a computer lab
Teacher. I draw your attention to the fact that you are starting to work in a computer class, and you must follow the rules of conduct and work at the computer. Secure retractable tabletops and ensure proper fit.
3. Updating the basic knowledge and skills of students
Teacher. To solve many geometric problems related to polyhedra, it is useful to be able to construct their sections in a drawing using different planes, find the point of intersection of a given line with a given plane, and find the line of intersection of two given planes. In previous lessons, we looked at sections of polyhedra by planes parallel to the edges and faces of the polyhedra. In this lesson we will look at problems involving constructing sections with a plane passing through three points located on the edges of polyhedra. To do this, consider the simplest polyhedra. What are these polyhedra? (Models of a cube, tetrahedron, regular quadrangular pyramid, straight triangular prism).
Students must determine the type of polyhedron.
Teacher. Let's see how they look on the monitor screen. We move from image to image by pressing the left mouse button.
Images of the named polyhedra appear on the screen one after another.
Teacher. Let us remember what is called a section of a polyhedron.
Student. A polygon whose sides are segments belonging to the faces of the polyhedron, with ends on the edges of the polyhedron, obtained by intersecting the polyhedron with an arbitrary cutting plane.
Teacher. What polygons can be sections of these polyhedra.
Student. Sections of a cube: three - hexagons. Sections of a tetrahedron: triangles, quadrangles. Sections of a quadrangular pyramid and a triangular prism: three - pentagons.
4. Self-testing
Teacher. In accordance with the concept of sections of polyhedra, knowledge of the axioms of stereometry and the relative position of lines and planes in space, you are asked to answer the test questions. The computer will appreciate you. Maximum score 3 points - for 3 correct answers. On each slide you must click the button with the number of the correct answer. You work in pairs, so each of you will receive the same computer-specified number of points. Click the next slide indicator. You have 3 minutes to complete the task.
I. Which figure shows a section of a cube by a plane ABC?
II. Which figure shows a cross section of a pyramid with a plane passing through the diagonal of the base? BD parallel to the edge S.A.?
III. Which figure shows a cross section of a tetrahedron passing through a point M parallel to the plane ABS?
5. Solving problems with an explanation of the solution by the teacher
Teacher. Let's move on directly to solving problems. Click the next slide indicator.
Problem 1 This task Let's look at it orally with a step-by-step demonstration of the construction on the monitor screen. The transition is carried out by clicking the mouse.
Given a cube ABCDAA 1 B 1 C 1 D 1 . On his edge BB 1 given point M. Find the point of intersection of a line C 1 M with the plane of the cube face ABCD.
Consider the image of a cube ABCDAA 1 B 1 C 1 D 1 with a dot M on the edge BB 1 Points M And WITH 1 belong to the plane BB 1 WITH 1 What can be said about the straight line C 1 M ?
Student. Straight C 1 M belongs to the plane BB 1 WITH 1
Teacher. Searched point X belongs to the line C 1 M, and therefore planes BB 1 WITH 1 . What's it like mutual arrangement planes BB 1 WITH 1 and ABC?
Student. These planes intersect in a straight line B.C..
Teacher. That means everything common points planes BB 1 WITH 1 and ABC belong to the line B.C.. Searched point X must simultaneously belong to the planes of two faces: ABCD And BB 1 C 1 C; from this it follows that point X must lie on the line of their intersection, i.e. on the straight line Sun. This means that point X must lie on two straight lines simultaneously: WITH 1 M And Sun and, therefore, is their point of intersection. Construction the desired point look at it on the monitor screen. You will see the construction sequence by pressing the left mouse button: continue WITH 1 M And Sun to the intersection at the point X, which is the desired intersection point of the line WITH 1 M with face plane ABCD.
Teacher. To move to the next task, use the next slide indicator. Let's consider this problem with a brief description of the construction.
A) Construct a section of a cube with a plane passing through the points A 1 , MD 1 C 1 and NDD 1 and b) Find the line of intersection of the cutting plane with the plane of the lower base of the cube.
Solution. I. The cutting plane has a face A 1 B 1 C 1 D 1 two common points A 1 and M and, therefore, intersects with it along a straight line passing through these points. Connecting the dots A 1 and M straight line segment, we find the line of intersection of the plane of the future section and the plane top edge. We will record this fact in the following way: A 1 M. Press the left mouse button, pressing again will construct this straight line.
Similarly, we find the lines of intersection of the cutting plane with the faces AA 1 D 1 D And DD 1 WITH 1 WITH. By clicking the mouse button, you will see a brief recording and construction progress.
Thus, A 1 NM? the desired section.
Let's move on to the second part of the problem. Let's find the line of intersection of the cutting plane with the plane of the lower base of the cube.
II. The cutting plane intersects with the plane of the base of the cube in a straight line. To depict this line, it is enough to find two points belonging to this line, i.e. common points of the cutting plane and the face plane ABCD. Relying on previous task such points will be: point X=. Press the key, you will see a short recording and construction. And period Y, what do you guys think, how to get it?
Student. Y =
Teacher. Let's look at its construction on the screen. Click the mouse button. Connecting the dots X And Y(Record X-Y), we obtain the desired straight line - the line of intersection of the cutting plane with the plane of the lower base of the cube. Press the left mouse button - short recording and construction.
Problem 3 Construct a section of the cube with a plane passing through the points:
Also, by pressing the mouse button, you will see the construction progress and a short recording on the monitor screen. Based on the concept of a section, it is enough for us to find two points in the plane of each face to construct the line of intersection of the cutting plane and the plane of each face of the cube. Points M And N belong to the plane A 1 IN 1 WITH 1 . By connecting them, we get the line of intersection of the cutting plane and the plane of the upper face of the cube (press the mouse button). Let's continue the straight lines MN And D 1 C 1
before the intersection. Let's get a point X, belonging to both the plane A 1 IN 1 WITH 1 and plane DD 1 C 1 (mouse click). Points N And TO belong to the plane BB 1 WITH 1 . By connecting them, we get the line of intersection of the cutting plane and the face BB 1 WITH 1 WITH. (Mouse click). Connecting the dots X And TO,
and continue straight HC to the intersection with the line DC. Let's get a point R and segment KR – line of intersection of the cutting plane and the face DD 1 C 1 C. (Mouse click). Continuing straight KR And DD 1 before intersection, we get a point Y, belonging to the plane AA 1 D 1 . (Mouse click). In the plane of this face we need one more point, which we obtain as a result of the intersection of lines MN And A 1 D 1 . This is the point 
. (Mouse click). Connecting the dots Y And Z, we get
And . (Mouse click). Connecting Q And R, R And M, will we get it? the desired section.
Brief description of the construction:
2) 
;
6) 
;
7) 
;
13) ? the desired section.