Определение
Пирамидае полиедър, съставен от многоъгълник \(A_1A_2...A_n\) и \(n\) триъгълници с общ връх \(P\) (не лежащ в равнината на многоъгълника) и страни срещу него, съвпадащи с страни на многоъгълника.
Обозначение: \(PA_1A_2...A_n\) .
Пример: петоъгълна пирамида \(PA_1A_2A_3A_4A_5\) .
Триъгълници \(PA_1A_2, \PA_2A_3\) и др. се наричат странични лицапирамиди, сегменти \(PA_1, PA_2\) и др. – странични ребра, многоъгълник \(A_1A_2A_3A_4A_5\) – база, точка \(P\) – отгоре.
Височинапирамидите са перпендикуляр, спуснат от върха на пирамидата към равнината на основата.
Нарича се пирамида с триъгълник в основата тетраедър.
Пирамидата се нарича правилно, ако основата му е правилен многоъгълник и е изпълнено едно от следните условия:
\((a)\) страничен ръбове на пирамидатаравен;
\((b)\) височината на пирамидата минава през центъра на окръжността, описана близо до основата;
\((c)\) страничните ребра са наклонени към равнината на основата под същия ъгъл.
\((d)\) странични лицанаклонени към равнината на основата под същия ъгъл.
Правилен тетраедъре триъгълна пирамида, чиито лица са равни равностранни триъгълници.
Теорема
Условия \((a), (b), (c), (d)\) са еквивалентни.
Доказателство
Нека намерим височината на пирамидата \(PH\) . Нека \(\alpha\) е равнината на основата на пирамидата.

1) Нека докажем, че от \((a)\) следва \((b)\) . Нека \(PA_1=PA_2=PA_3=...=PA_n\) .
защото \(PH\perp \alpha\), тогава \(PH\) е перпендикулярен на всяка права, лежаща в тази равнина, което означава, че триъгълниците са правоъгълни. Това означава, че тези триъгълници са равни по общ катет \(PH\) и хипотенуза \(PA_1=PA_2=PA_3=...=PA_n\) . Това означава \(A_1H=A_2H=...=A_nH\) . Това означава, че точките \(A_1, A_2, ..., A_n\) са на едно и също разстояние от точката \(H\), следователно, те лежат на една и съща окръжност с радиус \(A_1H\) . Тази окръжност, по дефиниция, е описана около многоъгълника \(A_1A_2...A_n\) .
2) Нека докажем, че \((b)\) предполага \((c)\) .
\(PA_1H, PA_2H, PA_3H,..., PA_nH\)правоъгълна и равна на два крака. Това означава, че техните ъгли също са равни, следователно, \(\ъгъл PA_1H=\ъгъл PA_2H=...=\ъгъл PA_nH\).
3) Нека докажем, че \((c)\) предполага \((a)\) .
Подобно на първата точка, триъгълници \(PA_1H, PA_2H, PA_3H,..., PA_nH\)правоъгълна и по крака и остър ъгъл. Това означава, че техните хипотенузи също са равни, тоест \(PA_1=PA_2=PA_3=...=PA_n\) .
4) Нека докажем, че \((b)\) предполага \((d)\) .
защото в правилен многоъгълник центровете на описаната и вписаната окръжност съвпадат (най-общо казано, тази точка се нарича център на правилен многоъгълник), тогава \(H\) е центърът на вписаната окръжност. Нека начертаем перпендикуляри от точката \(H\) към страните на основата: \(HK_1, HK_2\) и т.н. Това са радиусите на вписаната окръжност (по дефиниция). Тогава според TTP (\(PH\) е перпендикулярен на равнината, \(HK_1, HK_2\) и т.н. са проекции, перпендикулярни на страните) наклонен \(PK_1, PK_2\) и т.н. перпендикулярно на страните \(A_1A_2, A_2A_3\) и т.н. съответно. И така, по дефиниция \(\ъгъл PK_1H, \ъгъл PK_2H\)равни на ъглите между страничните стени и основата. защото триъгълници \(PK_1H, PK_2H, ...\) са равни (като правоъгълни от двете страни), тогава ъглите \(\ъгъл PK_1H, \ъгъл PK_2H, ...\)са равни.
5) Нека докажем, че \((d)\) предполага \((b)\) .
Подобно на четвъртата точка, триъгълниците \(PK_1H, PK_2H, ...\) са равни (като правоъгълни по крака и остър ъгъл), което означава, че сегментите \(HK_1=HK_2=...=HK_n\) са равен. Това означава, че по дефиниция \(H\) е центърът на окръжност, вписана в основата. Но защото при правилни многоъгълницицентровете на описаната и вписаната окръжност съвпадат, тогава \(H\) е центърът на описаната окръжност. Chtd
Последица
Страничните стени на правилната пирамида са равни равнобедрени триъгълници.
Определение
Височината на страничната страна на правилна пирамида, изтеглена от нейния връх, се нарича апотема.
Апотемите на всички странични стени на правилната пирамида са равни една на друга и също са медиани и ъглополовящи.
Важни бележки
1. Височината е правилна триъгълна пирамидапопада в точката на пресичане на височините (или ъглополовящите, или медианите) на основата (основата е правилен триъгълник).
2. Височината е правилна четириъгълна пирамидапопада в точката на пресичане на диагоналите на основата (основата е квадрат).
3. Височината е правилна шестоъгълна пирамидапопада в пресечната точка на диагоналите на основата (основата е правилен шестоъгълник).
4. Височината на пирамидата е перпендикулярна на всяка права линия, лежаща в основата.
Определение
Пирамидата се нарича правоъгълен, ако един от страничните му ръбове е перпендикулярен на равнината на основата.

Важни бележки
1. В правоъгълна пирамида ръбът, перпендикулярен на основата, е височината на пирамидата. Тоест \(SR\) е височината.
2. Защото Тогава \(SR\) е перпендикулярна на която и да е права от основата \(\триъгълник SRM, \триъгълник SRP\) – правоъгълни триъгълници.
3. Триъгълници \(\триъгълник SRN, \триъгълник SRK\)- също правоъгълни.
Тоест всеки триъгълник, образуван от този ръб и диагоналът, излизащ от върха на този ръб, лежащ в основата, ще бъде правоъгълен.
\[(\Large(\text(Обем и повърхност на пирамидата)))\]
Теорема
Обемът на пирамидата е равен на една трета от произведението на площта на основата и височината на пирамидата: \
Последици
Нека \(a\) е страната на основата, \(h\) е височината на пирамидата.
1. Обемът на правилна триъгълна пирамида е \(V_(\текст(десен триъгълник.pir.))=\dfrac(\sqrt3)(12)a^2h\),
2. Обемът на правилна четириъгълна пирамида е \(V_(\text(right.four.pir.))=\dfrac13a^2h\).
3. Обемът на правилна шестоъгълна пирамида е \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).
4. Обем правилен тетраедърравни \(V_(\текст(дясно тетр.))=\dfrac(\sqrt3)(12)a^3\).
Теорема
Площта на страничната повърхност на правилната пирамида е равна на полупродукта на периметъра на основата и апотемата.
\[(\Large(\text(Frustum)))\]
Определение
Да разгледаме произволна пирамида \(PA_1A_2A_3...A_n\) . Нека начертаем равнина, успоредна на основата на пирамидата през определена точка, разположена на страничния ръб на пирамидата. Този самолетще раздели пирамидата на два полиедъра, единият от които е пирамида (\(PB_1B_2...B_n\)), а другият се нарича пресечена пирамида(\(A_1A_2...A_nB_1B_2...B_n\) ).
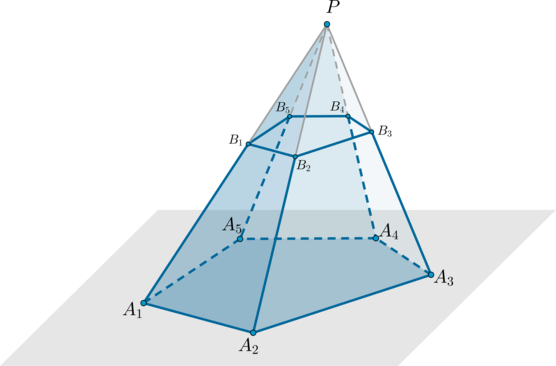
Пресечената пирамида има две основи - многоъгълници \(A_1A_2...A_n\) и \(B_1B_2...B_n\), които са подобни един на друг.
Височината на пресечена пирамида е перпендикуляр, прекаран от някаква точка на горната основа към равнината на долната основа.
Важни бележки
1. Всички странични лица на пресечена пирамида са трапецовидни.
2. Сегментът, свързващ центровете на основите на правилна пресечена пирамида (т.е. пирамида, получена чрез напречно сечение на правилна пирамида), е височината.
Нека да разгледаме какви свойства имат пирамидите, в които страничните стени са перпендикулярни на основата.
Ако две съседни странични стени на пирамидата са перпендикулярни на основата, Това общият страничен ръб на тези лица е височината на пирамидата. Ако проблемът казва това ръбът на пирамидата е нейната височина, Това ние говорим законкретно за този тип пирамида.
Лицата на пирамидата, перпендикулярни на основата, са правоъгълни триъгълници.
Ако основата на пирамидата е триъгълник
Страничната повърхност на такава пирамида в общ случайние го търсим като сбор от площите на всички странични лица.
Основата на пирамидата е ортогонална проекциялицето не е перпендикулярно на основата (в в този случай, SBC). Това означава, че според теоремата за площта на ортогоналната проекция площта на основата е равна на произведението на площта на това лице и косинуса на ъгъла между него и равнината на основата .
Ако основата на пирамидата е правоъгълен триъгълник

В този случай всички лица на пирамидата са правоъгълни триъгълници.
Триъгълниците SAB и SAC са правоъгълни, тъй като SA е височината на пирамидата. Триъгълник ABCправоъгълен по условие.
Фактът, че триъгълникът SBC е правоъгълен, следва от теоремата за трите перпендикуляра (AB е проекцията на наклонената SB върху равнината на основата. Тъй като AB е перпендикулярен на BC по условие, тогава SB е перпендикулярен на BC).
Ъгълът между страничната повърхност на SBC и основата в този случай е ъгъл ABS.
Площта на страничната повърхност е равна на сумата от площите на правоъгълни триъгълници:
Тъй като в този случай
![]()
Ако основата на пирамидата е равнобедрен триъгълник
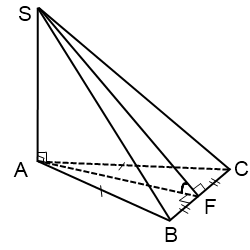
В този случай ъгълът между равнината на страничната повърхност BCS и основната равнина е ъгъл AFS, където AF е височината, медианата и ъглополовящата равнобедрен триъгълник ABC.
По същия начин, ако в основата на пирамидата лежи равностранен триъгълник ABC.
Ако основата на пирамидата е успоредник
 В този случай основата на пирамидата е ортогонална проекция на страничните лица, които не са перпендикулярни на основата.
В този случай основата на пирамидата е ортогонална проекция на страничните лица, които не са перпендикулярни на основата.
Ако разделим основата на два триъгълника, тогава
където α и β са съответно ъглите между равнините ADS и CDS и основната равнина.

Ако BF и BK са височините на успоредника, тогава ъгъл BFS е ъгълът на наклона на страничната страна CDS към равнината на основата, а ъгъл BKS е ъгълът на наклона на страната ADS.
(чертежът е направен за случая, когато B е тъп ъгъл).
Ако основата на пирамидата е ромб ABCD, то ъглите BFS и BKS са равни. Триъгълниците ABS и CBS, както и ADS и CDS, също са равни в този случай.
Ако основата на пирамидата е правоъгълник
 В този случай ъгълът между страничната лицева равнина SAD и основната равнина е ъгъл SAB,
В този случай ъгълът между страничната лицева равнина SAD и основната равнина е ъгъл SAB,
и ъгълът между равнината на страничната повърхност SCD и равнината на основата е ъгъл SCB
(по теоремата за трите перпендикуляра).
съответно
Оттук странична повърхностможе да се намери като
тук всички странични стени на пирамидата са правоъгълни триъгълници(ъглите SAD и SCD са прави ъгли според теоремата за трите перпендикуляра). Следователно страничната повърхност може да се търси директно:
Ако основата на пирамидата е квадрат ABCD, тогава проблемът е опростен: триъгълниците ABS и BCS, както и триъгълниците ADS и CDS са равни в този случай.
15 декември 2012 г
Отзиви (12) за “Пирамиди, в които ръбовете са перпендикулярни на основата”
-
Ако търсите в Google „правоъгълна пирамида“ на руски, тогава вашият материал е в първите пет. Виждам, че на тази страница има само една правоъгълна пирамида, последната, и обозначенията не са съвсем правилни. Google, съвместно с Wikipedia, излязоха със странна дефиниция - перпендикулярен ръб и същият като в основата на пирамида. Между другото, на английскиПо принцип правоъгълна пирамида е пирамида, в основата на която има правоъгълник и изобщо няма значение къде е височината.
В текста няма нито дума за правоъгълна пирамида. Много често при задачи, свързани с пирамиди, в които има две странични стени, перпендикулярни на основата, говорим за ъгъл между равнината на страничната стена и равнината на основата.
IN този материалпомислете как да определите този ъгъл в зависимост от многоъгълника в основата. Ако основата съдържа успоредник (включително ромб), трябва да начертаете височините на успоредника от основата на пирамидата до противоположни страни(или права линия, съдържаща тези страни). Ако основата е правоъгълник (включително квадрат), няма нужда да чертаете височини, тъй като страните на правоъгълника са взаимно перпендикулярни. В този случай се определя ъгълът между основата и страничния ръб линеен ъгъл, образувана от ръбовете на пирамидата; страничните лица са правоъгълни триъгълници.
Правите ъгли в основата са подчертани, за да се подчертае тази разлика от случая, когато основата е успоредник, който не е правоъгълник.Защото премахнахте „правоъгълната пирамида“, но техничарите, които знаят и разбират как работят търсачките, едва ли ще бъдат убедени от вашите аргументи. Научете IT, не само математика.
Скъпа Наташок! В лъжа ли ме обвинявате? Казах ви, че не използвам термина "правоъгълна пирамида" в работата си.
P.S. Не съм IT специалист, за съжаление. Съгласен съм, грамотността е необходима във всички области: както в математиката, така и в информационни технологии, и в правописа.
Фигурата илюстрира случая, когато в основата на пирамидата има правоъгълник. При паралелен дизайн ъглите не се запазват, така че правоъгълникът се изчертава като успоредник. Вторият прав ъгъл на фигурата е отбелязан във връзка с теоремата за три перпендикуляра.
Първо, не рисунка, а рисунка. В чертежа рисувате чертежи, но в математиката те все още са рисунки. Второ, погледнете последната рисунка. Няма теореми за три перпендикуляра. Повтарям, основата на последния чертеж не е правоъгълник. Няма значение как го представяте. Следвам обозначенията. Въпреки че забелязах, че и третият чертеж отдолу не ми е ясен. Успоредникът не е отбелязан на чертежа. Просто четириъгълник! Външният му вид е подобен на успоредник, но обозначенията оставят много да се желае.
1) Да, в геометрията правим чертеж, но илюстрацията към текста е чертеж. Във всеки учебник по геометрия пишат „на фигура 1“, а не „на чертеж 1“.
2) Правоъгълник в стереометрията се изобразява като успоредник, тъй като ъглите не се запазват при паралелно проектиране. Но успоредността на линиите е запазена. Противоположните страни на четириъгълника са изобразени като лежащи на успоредни прави. От това следва, че този четириъгълник е успоредник.Противоположните страни на четириъгълника са изобразени като лежащи на успоредни прави. Не виждам никаква индикация, че тези линии са успоредни и текстът не показва паралелен дизайн. Така че за мен основата е все още на последния чертеж произволен четириъгълник
Скъпа Наташа! Изображение пространствени фигурив самолета се извършва в съответствие с правилата паралелен дизайн. Това означава, че успоредните прави на чертежа са изобразени като успоредни прави, а неуспоредните прави не са успоредни.
Не съм съгласен с определението за правоъгълна пирамида. Правоъгълна пирамидае пирамида, в един от върховете на която има три прави ъгъла. Напишете ми защо разпространявате грешни материали на ниво невежа Уикипедия.
Ако основата на пирамидата е правоъгълник, тогава защо на снимката са отбелязани два срещуположни ъгъла, които го обозначават? В последния чертеж тази основа може да бъде ромбоид и друг четириъгълник.
При което едно от страничните ребра е перпендикулярно на основата.
В този случай този ръб ще бъде височината на пирамидата.
Свойства на пирамидата.
1. Когато всички странични ръбове са с еднакъв размер, тогава:
- близо до основата на пирамидата е лесно да се опише кръг, докато върхът на пирамидата ще бъде проектиран в центъра на този кръг;
- страничните ребра са идентични ъгли ;
- Освен това е вярно и обратното, т.е. когато страничните ребра се образуват с равнината на основата равни ъгли, или когато кръг може да бъде описан близо до основата на пирамидата и върхът на пирамидата ще бъде проектиран в центъра на този кръг, което означава, че всички странични ръбове на пирамидата са с еднакъв размер.
2. Когато страничните повърхности имат ъгъл на наклон към равнината на основата със същата стойност, тогава:
- лесно е да се опише кръг близо до основата на пирамидата и върхът на пирамидата ще бъде проектиран в центъра на този кръг;
- височините на страничните лица са еднаква дължина;
- площта на страничната повърхност е равна на ½ произведението на периметъра на основата и височината на страничната повърхност.
3. За пирамидата може да се опише сферав случай, че в основата на пирамидата лежи многоъгълник, около който може да се опише кръг (необходимите и достатъчно условие). Центърът на сферата ще бъде точкапресечни точки на равнини, които минават през средата на ръбовете на пирамидата перпендикулярно на тях. От тази теорема заключаваме, че една сфера може да бъде описана както около всяка триъгълна, така и около всяка правилна пирамида;
4. Сфера може да бъде вписана в пирамида, ако ъглополовящите равнини на вътрешните двустенни ъглипирамидите се пресичат в 1-ва точка (необходимо и достатъчно условие). Тази точка ще стане център на сферата.
5. Конусът ще бъде вписан в пирамидата, когато върховете им съвпадат, а основата на конуса ще бъде вписана в основата на пирамидата. В този случай е възможно да се постави конус в пирамида само ако апотемите на пирамидата имат равни размери (необходимо и достатъчно условие);
6. Конусще бъдат описани близо до пирамидата, ако върховете им съвпадат, а основата на конуса ще бъде описана близо до основата на пирамидата. В този случай е възможно да се опише конус близо до пирамидата само ако всички странични ръбове на пирамидата имат същите стойности(необходимо и достатъчно условие). Височините на тези конуси и пирамиди са еднакви.
7. Цилиндърще бъде вписана в пирамида, ако една от нейните основи съвпада с окръжност, която е вписана в сечението на пирамидата от равнина, успоредна на основата, а втората основа принадлежи на основата на пирамидата.
8. Цилиндърът ще бъде описан близо до пирамидата, когато върхът на пирамидата принадлежи към една от нейните основи, а втората основа на цилиндъра ще бъде описана близо до основата на пирамидата. В този случай е възможно да се опише цилиндър близо до пирамида само ако основата на пирамидата е вписан многоъгълник (необходимо и достатъчно условие).
Формули за определяне на обема и площта на правоъгълна пирамида.
V- обем на пирамидата,
С- площта на основата на пирамидата,
ч- височина на пирамидата,
сб- площ на страничната повърхност на пирамидата,
а- апотема (да не се бърка с α ) пирамиди,
П- периметър на основата на пирамидата,
п- броят на страните на основата на пирамидата,
b- дължина странично ребропирамиди,
α - плосък ъгъл на върха на пирамидата.
