ГЛАВА ТРЕТЬЯ

МНОГОГРАННИКИ

II ОБЪЕМ ПРИЗМЫ И ПИРАМИДЫ

82. Основные допущения в объёмах. Величина части пространства, занимаемого геометрическим телом, называется объёмом этого тела.

Мы ставим, задачу - найти для этой величины выражение в виде некоторого числа, измеряющего эту величину. При этом мы будем руководствоваться следующими исходными положениями:

1) Равные тела имеют равные объёмы .

2) Объём какого-нибудь тела (например, каждого параллелепипеда, изображённого на черт. 87), состоящего из частей (Р и Q), равен сумме объёмов этих частей .

Два тела, имеющие одинаковые объемы, называются равновеликими.

83. Единица объёма. За единицу объёмов при измерении их берут объём такого куба, у которого каждое ребро равно линейной единице. Так, употребительны кубические метры (м 3), кубические сантиметры (см 3) и т. д.

Объём параллелепипеда

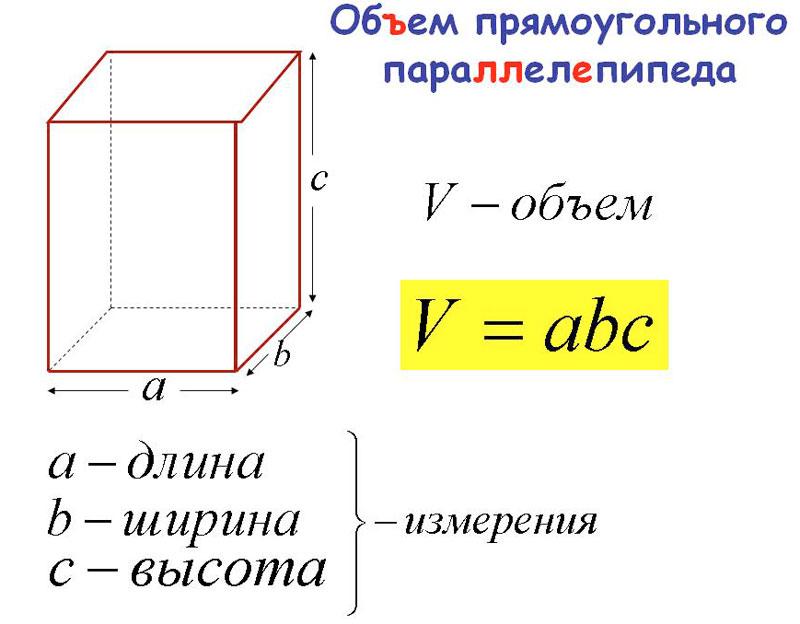
84. Теорема. Объём прямоугольного параллелепипедa равен произведению трёх его измерений.

В таком кратком выражения теорему эту надо понимать так: число, выражающее объём прямоугольного параллелепипеда в кубической единице, равно произведению чисел, выражающих три его измерения в соответствующей линейной единице, т. е. в единице, являющейся ребром куба, объём которого принят за кубическую единицу. Так, если х есть число, выражающее объём прямоугольного параллелепипеда в кубических сантиметрах, и а, b и с -числа, выражающие три его измерения в линейных сантиметрах, то теорема утверждает, что x = abc .

При доказательстве рассмотрим особо следующие три случая:

1) Измерения выражаются целыми числами .

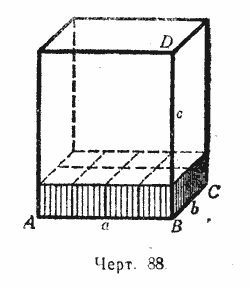
Пусть, например, измерения будут (черт. 88): АВ = а , ВС = b и BD = c ,
где а, b и с - какие-нибудь целые числа (например, как изображено у нас на чертеже: а = 4, b = 2 и с = 5). Тогда основание параллелепипеда содержит ab таких квадратов, из которых каждый представляет собой соответствующую квадратную единицу. На каждом из этих квадратов, очевидно, можно поместить по одной кубической единице. Тогда получится слой (изображённый на чертеже), состоящий из ab кубических единиц. Так как высота этого слоя равна одной линейной единице, а высота всего параллелепипеда содержит с таких единиц, то внутри параллелепипеда можно поместить с таких слоев. Следовательно, объём этого параллелепипеда равен abc кубических единиц.

2) Измерения выражаются дробными числами . Пусть измерения параллелепипеда будут:

m / n , p / q , r / s

. (некоторые из этих дробей могут равняться целому числу). Приведя дроби к одинаковому знаменателю, будем иметь:

mqs / nqs , pns / nqs , rnq / nqs

Примем 1 / nqs долю линейной единицы за новую (вспомогательную) единицу длины. Тогда в этой новой единице измерения данного параллелепипеда выразятся целыми числами, а именно: mqs, pns и rnq , и потому по доказанному (в случае 1) объём параллелепипеда равен произведению (mqs ) (pns ) (rnq ), если измерять этот объём новой кубической единицей, соответствующей новой линейной единице. Таких кубических единиц в одной кубической единице, соответствующей прежней линейной единице, содержится (nqs ) 3 ; значит, новая кубическая единица составляет 1 /(nqs ) 3 прежней. Поэтому объём параллелепипеда, выраженный в прежних единицах, равен:

3) Измерения выражаются иррациональными числами . Пусть у данного параллелепипеда (черт. 89), который для краткости мы, обозначим одной буквой Q, измерения будут:

АВ = α ; AС = β; AD = γ,

где все числа α , β и γ или только некоторые из них иррациональные.

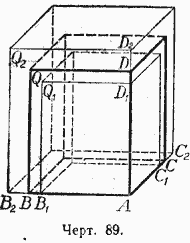
Каждое из чисел α , β и γ может быть представлено в виде бесконечной десятичной дроби. Возьмём приближённые значения этих дробей с п десятичными знаками сначала с недостатком, а затем с избытком. Значения с недостатком обозначим α n , β n , γ n , значения с избытком α" n , β" n , γ" n . Отложим на ребре АВ, начиная от точки А, два отрезка AB 1 = α n и АВ 2 = α" n .
На ребре АС от той же точки А отложим отрезки АС 1 = β n и AС 2 = β" n и на ребре AD от той же точки-отрезки АD 1 = γ n и AD 2 = γ" n .

При этом мы будем иметь:

AB 1 < АВ < АВ 2 ; АС 1 < АС < АС 2 ; AD 1 < AD < AD 2 .

Построим теперь два вспомогательных параллелепипеда; один (обозначим его Q 1) с измерениями АВ 1 , АС 1 и AD 1 и другой (обозначим его Q 2) с измерениями АВ 2 , АС 2 и AD 2 . Параллелепипед Q 1 будет весь помещаться внутри параллелепипеда Q, а параллелепипед Q 2 будет содержать внутри себя параллелепипед Q.

По доказанному (в случае 2) будем иметь:

объём Q 1 = α n β n γ n (1)

объём Q 2 = α" n β" n γ" n (2)

Оричём объём Q 1 < объёма Q 2 .

Начнём теперь увеличивать число п . Это значит, что мы берём приближённые значения чисел α , β , γ всё с большей и большей степенью точности.

Посмотрим, как при этом изменяются объемы параллелепипедов Q 1 и Q 2 .

При неограниченном возрастании п объём Q 1 , очевидно, увеличивается и в силу равенства (1) при беспредельном увеличении n имеет споим пределом предел произведения (α n β n γ n ). Объём Q 2 , очевидно, уменьшается и в силу равенства (2) имеет пределом предел произведения (α" n β" n γ" n ). Но из алгебры известно, что оба произведения
α n β n γ n и α" n β" n γ" n при неограниченном увеличении п имеют общий предел, который является произведением иррациональных чисел αβγ.

Этот предел мы и принимаем за меру объёма параллелепипеда Q: объём Q = αβγ.

Можно доказать, что определённый таким образом объём удовлетворяет тем условиям, которые установлены для объёма (§ 82). В самом деле, при таком определении объёма равные параллелепипеды, очевидно, имеют равные объёмы. Следовательно, первое условие (§ 82) выполняется. Разобьём теперь данный параллелепипед Q плоскостью, параллельной его основанию, надвое: Q 1 и Q 2 (черт. 90).

Тогда будем иметь:

объём Q = АВ АС АD,
объём Q 1 = АВ АА 1 АD,
объём Q 2 = А 1 В 1 А 1 С А 1 D 1 .

Складывая почленно два последних равенства и замечая, что А 1 В 1 = АВ и А 1 D 1 =АD, получим:

объём Q 1 +объём Q 2 = АВ АА 1 АD+АВ А 1 С АD = АВ АD (АА 1 + А 1 С) = АВ АD АC, отсюда получаем:

объём Q 1 +объём Q 2 = объёму Q.

Следовательно, и второе условие § 82 тоже выполняется, если параллелепипед складывать из двух частей, полученных разрезанием его плоскостью, параллельной одной из граней.

85. Следствие. Пусть измерения прямоугольного параллелепипеда, служащие сторонами его основания, выражаются числами а и b , а третье измерение (высота)-числом с . Тогда, обозначая объём его в соответствующих кубических единицах буквой V, можем написать:

V = аbс .

Так как произведение аb выражает площадь основания, то можнo сказать, что объём прямоугольного параллелепипеда равен произведению площади основания на высоту .

Замечание. Отношение двух кубических единиц разных названий равно третьей степени отношения тех линейных единиц, которые служат рёбрами для этих кубических единиц. Так, отношение кубического метра к кубическому дециметру равно 10 3 , т. е. 1000. Поэтому, например, если мы имеем куб с ребром длиной а линейных единиц и другой куб с ребром длиной 3а линейных единиц, то отношение их объёмов будет равно 3 3 , т. е. 27, что ясно видно из чертежа 91.

86. Лемма. Наклонная призма равновелика такой прямой призме, основание которой равно перпендикулярному сечению наклонной призмы, а высота - её боковому ребру.

Пусть дана наклонная призма ABCDEA 1 B 1 C 1 D 1 E 1 (черт. 92).

Продолжим все её боковые рёбра и боковые грани в одном направлении.

Возьмём на продолжении одного какого-нибудь ребра произвольную точку а и проведём через неё перпендикулярное сечение abcde . Затем, отложив аа 1 = АА 1 , проведём через а 1 перпендикулярное сечение a 1 b 1 c 1 d 1 e 1 . Так как плоскости обоих сечений параллельны, то bb 1 = сс 1 = dd 1 = ее 1 = аа 1 = АА 1 (§17). Вследствие этого многогранник a 1 d , у которого за основания приняты проведённые нами сечения, есть прямая призма, о которой говорится в теореме.

Докажем, что данная наклонная призма равновелика этой прямой. Для этого предварительно убедимся, что многогранники a D и a 1 D 1 равны. Основания их abcde и a 1 b 1 c 1 d 1 e 1 равны как основания призмы a 1 d ; с другой стороны, прибавив к обеим частям равенства А 1 А = а 1 а по одному и тому же отрезку прямой А 1 а , получим: а А = а 1 А 1 ; подобно этому b В = b 1 В 1 , с С = с 1 С 1 и т. д. Вообразим теперь, что многогранник a D вложен в многогранник a 1 D 1 так, что основания их совпали; тогда боковые рёбра, будучи перпендикулярны к основаниям и соответственно равны, также совпадут; поэтому многогранник a D совместится с многогранником a 1 D 1 ; значит, эти тела равны. Теперь заметим, что если к прямой призме a 1 d добавим многогранник a D, а к наклонной призме A 1 D добавим многогранник a 1 D 1 , равный a D, то получим один и тот же многогранник a 1 D. Из этого следует, что две призмы A 1 D и a 1 d равновелики.

87. Теорема. Объём параллелепипеда равен произведению площади основания на высоту.

Ранее мы доказали эту теорему для параллелепипеда п р я м о у г о л ь н о г о, теперь докажем её для параллелепипеда п р я м о г о, а потом и н а к л о н н о г о.

1). Пусть (черт. 93) АС 1 - прямой параллелепипед, т. е. такой, у которого основание ABCD - какой-нибудь параллелограмм, а все боковые грани - прямоугольники.

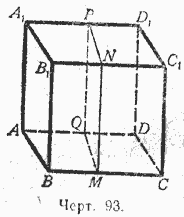
Возьмём в нём за основание боковую грань АА 1 В 1 В; тогда параллелепипед будет
н а к л о н н ы й. Рассматривая его как частный случай наклонной п р и з м ы, мы на основании леммы предыдущего параграфа можем утверждать, что этот параллелепипед равновелик такому прямому параллелепипеду, у которого основание есть перпендикулярное сечение MNPQ, а высота ВС. Четырёхугольник MNPQ- прямоугольник, потому что его углы служат линейными углами прямых двугранных углов; поэтому прямой параллелепипед, имеющий основанием прямоугольник MNPQ, должен быть прямоугольным и, следовательно, его объём равен произведению трёх его измерений, за которые можно принять отрезки МN, МQ и ВС. Таким образом,

объём AС 1 = МN МQ ВС = МN (МQ ВС).

Но произведение МQ ВС выражает площадь параллелограмма АВСD, поэтому

объём АСХ = (площади АВСD) МN = (площади АВСD) ВВ 1 .

2) Пусть (черт. 94) АС 1 - наклонный параллелепипед.

Он равновелик такому прямому, у которого основанием служит перпендикулярное сечение МNРQ (т. е. перпендикулярное к рёбрам АD, ВС, . . .), а высотой - ребро ВС. Но, по доказанному, объём прямого параллелепипеда равен произведению площади основания на высоту; значит,

объём АС 1 = (площади МNРQ) ВС.

Если RS есть высота сечения МNРQ, то площадь МNРQ = МQ RS, поэтому

объём АС 1 = МQ RS ВС = (ВС MQ) RS.

Произведение ВС MQ выражает площадь параллелограмма АВСD; следовательно, объём АС 1 = (площади АВСОD) RS.

Остаётся теперь доказать, что отрезок RS представляет собой высоту параллелепипеда. Действительно, сечение МNРQ, будучи перпендикулярно к рёбрам ВС, В 1 С 1 , .. . , должно быть перпендикулярно к граням АВСD, ВВ 1 С 1 С, .... проходящим через эти рёбра (§ 43). Поэтому если мы из точки S восставим перпендикуляр к плоскости АВСD, то он должен лежать весь в плоскости МNРQ (§ 44) и, следовательно, должен слиться с прямой RS, лежащей в этой плоскости и перпендикулярной к МQ. Значит, отрезок SR есть высота параллелепипеда. Таким образом, объем и наклонного параллелепипеда равен произведению площади основания на высоту.

Следствие. Если V, В и H суть числа, выражающие в соответствующих единицах объём, площадь основания и высоту параллелепипеда, то можно написать.

Формулы объема

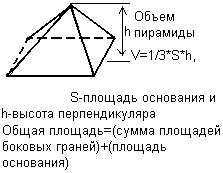
Объемы простых тел. Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед.

Объемы и площади поверхностей правильных тел.

Общая информация об объемах и площадях поверхностей правильных тел приведена в таблице.

Название фигуры	Площадь и объем фигуры S	Название фигуры	Площадь и объем фигуры S
Прямоугольный параллелепипед		Цилиндр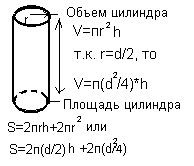
Сфера		Параллелепипед

Пример 1.Расчет объема прямоугольного бака.

Бак для воды имеет форму прямоугольного параллелепипеда длиной 1 м, шириной 65 см и высотой 30 см. Определить объем бака в м 3 , см 3 , литрах

Объем прямоугольного параллелепипеда равен l*b*h

а)V бака =1*0.65*03=0.195 м 3

б) 1 м 315000 мм 2 =315000/100=3150 см 2

1 м 3 =10 6 см 3 , значит, 0.195 м 3 =0.195*10 6 =195000 см 3

в) 1 литр=1000 см 3 , значит 195000 см 3 =195 л

Пример 2. Расчет объема и площади поверхности трапецеидальной призмы.

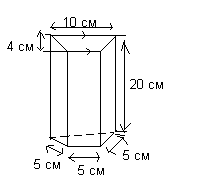
Вычислить объем и общую площадь поверхности призмы, показанной на рис.

Тело, показанное на рис. - это трапецеидальная призма.

Так как объем = площадь поперечного сечения * высота, то

V=1/2*(10+5)*4*20=30*20=600 cм 3

Так как площадь поверхности вычисляется сложением суммы площадей двух трапеций и суммы площадей четырех прямоугольников, то

S=(2*30)+3(5*20)+(10*20)=560 см 2

Пример 3. Расчет объема и общей площади поверхности правильной пирамиды.

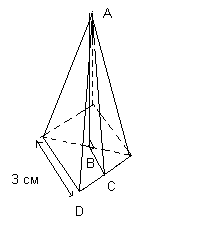
Определить объем и общую площадь поверхности правильной пирамиды с квадратным основанием, показанной на рис., если ее высота равна 15 см.

Так как объем пирамиды =1/3(площадь основания)*высота, то

V=1/3*(5*5)*15=125 см 3

Общая площадь поверхности включает площадь квадратного основания и площади четырех равных треугольников.

Площадь треугольника ADE=1/2*основание*(высота грани).

Высоту грани АС можно найти по теореме Пифагора из треугольника АВС, где АВ=15 см, ВС=1/2*3=1.5 см, и АС 2 =AB 2 +BC 2 =225+2.25=227.25

Следовательно, площадь треугольника ADE

S ADE =1/2*3*15.07=22.605 см 2

Общая площадь пирамиды S=(3*3)+4*22.605=99.42 cм 2 .

Пример 4. Расчет объема и общей площади поверхности конуса.

Определить объем и общую площадь поверхности конуса радиусом 4 см и высотой 10 см.

Объем конуса V=1/3πr 2 h =1/3*π4 2 *10=167.5см 3

Общая площадь поверхности равна сумме площади конической поверхности и площади основания, т.е. S=πrl+πr 2

Из рисунка видно, что длину образующей l можно найти по теореме Пифагора.

l 2 =10 2 +4 2 =116 см

Следовательно, общая площадь поверхности равна

S=π*4*10.8)+(π*4 2 =185.89 cм 2

Пример 5. Расчет объема и общей площади поверхности призмы.

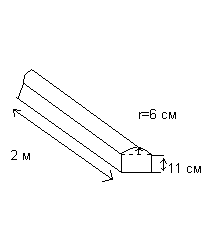
На рис. показан деревянный профиль. Найдем: а) его объем в м 3

б) общую площадь его поверхности

Профиль представляет собой призму, поперечное сечение которой состоит из прямоугольника и полукруга. Поскольку радиус полукруга равен 6 см, диаметр равен 12 см.

Тогда размеры прямоугольника 12*11 см

Площадь поперечного сечения S . =(11*12)+1/2* π 6 2 =188,52 см 2

Поскольку объем деревянной детали равен произведению площади поперечного сечения на длину, то

a) V=188,52*200=37704 см 3 =37704 см 3 /10 6 = 0,037704 м 3

б) Общая площадь включает два торца (площадь каждого 188,52 см 2), три прямоугольника и криволинейную поверхность (которая представляет собой полуцилиндр). Следовательно, общая площадь поверхности

S=(2*188,52)+2*(11*200)+(12*200)+1/2*(2π*6*200)=377,04+4400+2400+3768=10945,04 см 2 =1,094504 м 2 .

Пример 6. Расчет объема и общей площади поверхности сложного бойлера.

Бойлер состоит из цилиндрической секции длиной 9 м и диаметром 5 м, к одному концу которой присоединена полусферическая секция диаметром 5 м, а к другому концу - коническая секция высотой 3 м и диаметром основания 5 м. Вычислить объем бойлера и общую площадь его поверхности.

V полусферы P =2/3*πr 3 =2/3*π*2,5 3 =10,42 π м 3

V цилиндра Q = π r 2 h=π*2,5 2 *9=56,25 π м 3

V конуса R =1/3 π r 2 =1/3*π*2,5 2 *3=6,25π м 3

Общий объем бойлера V= 10,42 π м 3 +56,25 π м 3 +6,25π м 3 =72,92π=228,97 м 3

S полусферы P. =2*(πr 2)=2*π*2,5 2 =12,5π м 2

S бок. поверхности цилиндра Q. =2πrh=2*π*2,5*9=45π м 2 (т.к. этот цилиндр представляет собой трубу без оснований)

Длина образующей конуса l рассчитывается по теореме Пифагора из треугольника ABC;

l=(3 2 +2,5 2) 1/2 =3,9 м.

S конуса R. =πrl=π*2,5*3,9=9,75 π м 2

Общая площадь поверхности бойлера

S= 12,5π+45π+9,75 π=67,25π=211,2 м 2

Всем доброго дня! Зовут меня Иван, и я папа школьника, который не слишком силен в математике. Недавно сыну задали задание – найти объем параллелепипеда и немного покорпев над ним и так и не сумев решить задачку, он обратился ко мне. Школьных знаний в моей памяти осталось немного, а потому пришлось браться за учебники, перечитывать их и потом объяснять изученный материал сыну. Наверняка мой опыт окажется полезным и для других родителей и потому я и написал эту статью, в которой подробно рассказана информация по решению задач на объем этой геометрической фигуры.

Немного теории

Прежде чем я расскажу, как собственно найти объем и площадь параллелепипеда, и по какой формуле, давайте вместе вспомним, что же это за такое. У этой геометрической фигуры имеется три равнозначных трактовки:

1. Параллелепипедом считается многогранник с 6-ью гранями, особенность которых заключается в том, что любая – это параллелограмм.
2. Под термин попадает и шестигранник с 3-мя парами граней, которые будут параллельны друг дружке.
3. Параллелепипедом называется и призма, в основе которой будет параллелограмм.

Чаще всего исчислить объем требуется у параллелепипедов нескольких разных видов. Для каждого случая есть своя формула и свое решение и ниже я подробно объясню, как решать типовые задачи по исчислению объемов разных видов этой геометрической фигуры.

Переходим к практике

Как решить задачу на нахождение объема прямоугольного параллелепипеда? Особенностью этого типа фигуры является то, что каждая ее грань – это прямоугольник. Если хотите понять, как выглядит прямоугольный параллелепипед – посмотрите на самую обычную коробку из-под обуви.

Чтобы решить задачку, сначала ищем значения двух сторон основания фигуры. Стороны имеют перпендикулярное расположение друг к другу и находятся по формуле: П-АхБ, где А – это длина, а Б – это ширина. Далее выясняем еще один ключевой параметр, а именно находим высоту. И затем переходим к вычислению объема, в котором рабочей будет такая формула: V=ПхН, то есть для получения объема нужно площадь основания умножить на высоту. Как найти высоту – тут стоит заглянуть в учебник по геометрии и выписать формулу по нахождению ребра фигуры.

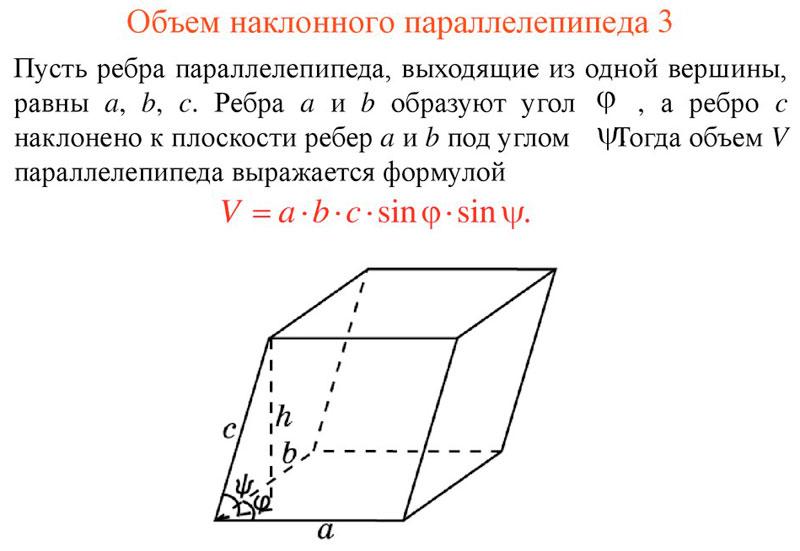Чтобы найти объем прямого параллелепипеда прямого, разберемся с тем, как выглядит эта конкретная фигура. Ее боковые грани – прямоугольники, перпендикулярные основанию, а потому объем будет вычисляться идентично задаче выше, но только следует учесть, что высотой будет выступать не ребро фигуры, а отрезок, соединяющий грани противоположные друг другу и перпендикулярный основе. Основание здесь параллелограмм и потому формула будет чуть сложней: П=АхБхsin(а). А, Б – это длина и ширина основания, а «а» — это угол, который они будут образовывать, пересекаясь.

Объём параллелепипеда

Разберемся с объемом наклонного типа фигуры. Грани этого типа фигуры не перпендикулярны ее основанию, а потому расчеты следует начать с нахождения высоты. Высоту умножаем на площадь основания и получаем объем, то есть формула у нас выглядит следующим образом: V=ПхН.

Остается узнать, как исчислить объем фигуры, грани которой квадратные. Такую фигуру чаще называют кубом, но в тоже время она является параллелепипедом, каждая грань которого – квадрат. А потому все ее ребра будут равны между собой. Формула вычисления объема будет максимально простой: нужно измерить ребра и результат исчислений возвести в 3-ю степень.

Вот так находится объем такой интересной геометрической фигуры как параллелепипед. Надеюсь, написанная мною короткая шпаргалка станет хорошим подспорьем для школьников и родителей в решении задач по геометрии и ни одну контрольную ваш ученик не напишет на плохую отметку!