Тип задания: 14
Условие
На рёбрах AD и BD правильного тетраэдра DABC взяты точки M и K соответственно так, что MD:AM=BK:KD=2.
а) Пусть L — точка пересечения прямой KM с плоскостью ABC . Докажите, что AB:AL=3.
б) Найдите угол между прямой KM и плоскостью ABC .
Показать решениеРешение
а) План решения.
1. Выполним схематический чертёж.
2. Сделаем предположение, что MK \perp BD, и докажем это утверждение (например, методом «от противного»).
3. Обозначим ребро тетраэдра какой-нибудь буквой (например, a ) и через неё выразим другие величины.
4. Рассмотрим треугольник AML , найдём его углы. Из равенства \angle AML=\angle ALM сделаем вывод о том, что треугольник равнобедренный: AL=AM.
5. Найдём отношение AB:AL.
Решение.
1. Так как MK и AB лежат в плоскости ABD , то они пересекутся, L — точка их пересечения.
2. В \triangle MDK,\, \angle MDK=60^{\circ}, MD=2DK, значит, MK \perp BD. Действительно, допустим, что это не так. Тогда опустим перпендикуляр MK", MK" \perp BD. В прямоугольном треугольнике MK"D по определению косинуса \frac{K"D}{MD}=\cos \angle MDK", K"D=MD \cos 60^{\circ}=\frac12MD. Но тогда точки K и K" совпадают. Получили противоречие. Значит, MK \perp BD.
3. Обозначим AB=AD=a, тогда MD =\frac23a, DK =\frac13a, AM=\frac13a.
4. \angle DMK=30^{\circ}. Следовательно, \angle AML=30^{\circ} (по свойству вертикальных углов). Так как \angle MLA= 180^{\circ}-\angle MAL-\angle AML= 180^{\circ}-120^{\circ}-30^{\circ}= 30^{\circ}, то \triangle AML — равнобедренный и AL=AM=\frac13a.
5. Тогда AB:AL=a:\frac13a=3.
Замечание. Вместо рассуждений, проведённых в пункте 4 , можно было рассмотреть прямоугольный треугольник LBK и воспользоваться свойством катета, лежащего против угла в 30^{\circ}.
б) План решения.
1. Угол между прямой и плоскостью — это угол между прямой и её проекцией на плоскость. Построим проекцию отрезка KL на плоскость ABC . Для этого опустим перпендикуляр KH, KH \perp ABC, точка H лежит в плоскости ABC . HL — проекция KL .
2. Найдём \sin \angle KLH (из треугольника KHL ) и по синусу угла определим угол. Для этого выполним следующие действия.
2.1. Пусть O — центр основания ABC тетраэдра. Из подобия треугольников KHB и DOB найдём KH (для этого найдём DO ).
2.2. Из треугольника BKL найдём KL .
2.3. Из треугольника KHL найдём \sin \angle KLH и \angle KLH.
Решение.
1. Искомый угол равен углу KLH .
2. Найдём \sin \angle KLH =\frac{KH}{KL}
2.1. \triangle KHB \sim \triangle DOB. Следовательно,
KH= \frac23DO= \frac23\sqrt {BD^2-BO^2}= \frac23\sqrt{BD^2-\left(\frac23BF\right)^2}= \frac23\sqrt {a^2-\left(\frac23\cdot \left(\frac{a\sqrt 3}2\right) \right) ^2}= \frac{2\sqrt 2}{3\sqrt 3}\cdot a.
2.2. В прямоугольном треугольнике BKL,\, BL =\frac43a, BK=\frac23a найдём KL=\sqrt {BL^2-BK^2} =\frac{2\sqrt 3}3a.
2.3. \sin \angle KLH =\frac{KH}{KL}=\frac{\sqrt 2}{3}, \angle KLH=arcsin \frac{\sqrt 2}3.
Ответ
arcsin \frac{\sqrt 2}3.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 14
Тема:
Угол между прямой и плоскостью
Условие
Основанием четырехугольной пирамиды SABCD является прямоугольник со сторонами AB=12,BC=5 . Боковые ребра SA= 3\sqrt{3},SB= \sqrt{171}, SD = 2\sqrt{13}.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между SC и BD .
Показать решениеРешение

а) Заметим, что треугольник SAB является прямоугольным, так как в нем SB^2=171=27+144=SA^2+AB^2. Аналогично треугольник SAD тоже является прямоугольным, поскольку SD^2=52=27+25=SA^2+AD^2. Получаем, что прямая SA перпендикулярна прямым AB и AD , а значит, перпендикулярна плоскости основания ABCD .
б) Отложим на прямой AD за точку D отрезок DE , равный отрезку AD . Тогда в четырехугольнике BCED стороны BC и DE равны и параллельны. Следовательно, BCED является параллелограммом, поэтому BD\parallel CE , и угол между SC и BD будет равен углу между SC и CE .
По теореме Пифагора BD^2=AB^2+AD^2=144+25=169,
SC^2= SA^2+AC^2= SA^2+BD^2= 27+169= 196 ,
SE^2=SA^2+AE^2=27+100=127.
Значит, BD=CE=13, SC=14, SE=\sqrt{127}.
Пусть \angle SCE=\alpha. По теореме косинусов для треугольника SCE имеем: SE^2=SC^2+CE^2-2SC\cdot CE\cdot \cos \alpha,
\cos \alpha= \frac{SC^2+CE^2-SE^2}{2SC\cdot CE}= \frac{196+169-127}{2\cdot 13\cdot 14}= \frac{119}{182} .
Откуда \alpha=\arccos\frac{119}{182}.
В правильной четырехугольной пирамиде SABCD точка S — вершина. Точка M — середина ребра SA, точка К — середина ребра SC. Найдите угол между плоскостями BMK и ABC, если AB = 8, SC=10.
Решение задачи
Данный урок показывает решение геометрической задачи, которое можно использовать с целью успешной подготовки к ЕГЭ по математике, в частности, при решении задач типа С1.
Условие задачи для наглядности изображается схематически на рисунке. Решение основывается на определении тангенса угла прямоугольного треугольника, согласно которому он равен отношению противолежащего катета к прилежащему. Отмечается, что отрезок — является высотой данной пирамиды и, следовательно, треугольник , содержащий искомый угол , — прямоугольный. Таким образом, верно равенство . Противолежащий катет равен половине высоты пирамиды по свойству средней линии треугольника . Так как в основании правильной четырехугольной пирамиды лежит квадрат, точка делит диагональ пополам, то есть прилежащий катет равен половине диагонали . Учитывая это, приведенное равенство преобразуется: . Применяя теорему Пифагора, вычисляются неизвестные значения. После подстановки их в формулу, искомый угол определяется как угол обратной тригонометрической функции арктангенс.
Метод объёмов можно использовать, вычисляя:
расстояние от точки до плоскости;
угол между прямой и плоскостью;
угол между плоскостями;
расстояние между скрещивающимися прямыми.
С идейной точки зрения метод объёмов весьма прост. Всё, что здесь нужно, это найти подходящую треугольную пирамиду и аккуратно провести вычисления. Правда, вычислений обычно получается несколько больше, чем в методах, рассмотренных выше. Но тут уж ничего не поделаешь за простоту метода приходится платить.
13.1 Расстояние от точки до плоскости
Замечательный факт состоит в том, что при вычислении объёма треугольной пирамиды можно в качестве основания выбрать любую её грань. Это используется при нахождении расстояния от точки до плоскости; нужно лишь представить искомое расстояние как высоту подходящей пирамиды.
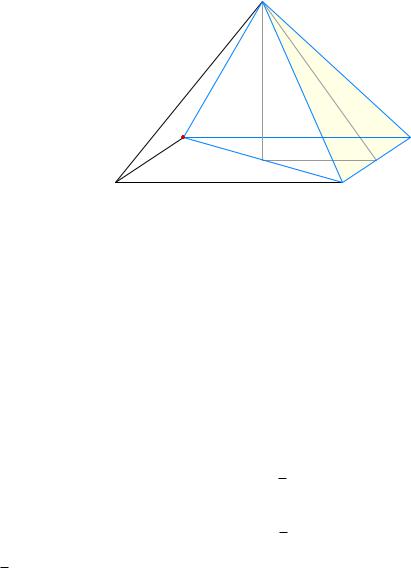
А именно, предположим, что нам нужно найти расстояние от некоторой точки C до некоторой плоскости ABD. Рассмотрим треугольную пирамиду ABCD (рис. 73 ). Тогда искомое расстояние это высота d данной пирамиды, проведённая из вершины C.
Рис. 73. S0 h = Sd
Пусть S0 площадь грани ABC, h высота, опущенная на эту грань, S площадь грани
ABD. С одной стороны, объём пирамиды ABCD может быть найден по формуле: | ||||||
S0 h: | ||||||
С другой стороны, за основание можно принять грань ABD, и тогда | ||||||
Приравнивая правые части формул (1 ) и (2 ), получим:
S0 h = Sd: |
Из соотношения (3 ) можно найти искомую величину d.
Давайте посмотрим, как всё это работает в конкретной задаче. Разберём задачу, которую мы уже решали выше в разделе ¾Расстояние от точки до плоскости¿.
Задача 1. В правильной четырёхугольной пирамиде P ABCD (с вершиной P) сторона основания равна 2 и высота равна 1. Найдите расстояние от точки D до плоскости BCP .
Решение. Рассмотрим треугольную пирамиду BCDP (рис. 74 ). Искомое расстояние d есть высота этой пирамиды, проведённая из вершины D.
По условию P O = 1. Легко находим SBCD = 2. Остаётся вычислить площадь треугольника |
|||||||
BCP . Его высоту P M найдём из треугольника P OM: P M = p | |||||||
S BCP= | |||||||
Подставляем найденные величины в (4 ):
откуда p d = 2:
Метод объёмов легко справляется с задачами, решить которые прежними методами было бы затруднительно.

Задача 2. В прямоугольном параллелепипеде ABCDA B C D известны рёбра: AB = 1,
p p 1 1 1 1
AD = 3, AA1 = 6. Найдите расстояние от точки B до плоскости AB1 C.
Решение. Ситуация изображена на рис. 75 . Подходящую треугольную пирамиду здесь увидеть легко это пирамида ABCB1 . Надо найти её высоту d, опущенную из точки B.
Рис. 75. К задаче 2 | |||||||||||||||||||||||||||||||||||
Снова имеем согласно (3 ): | |||||||||||||||||||||||||||||||||||
S ABCBB 1= S AB1 Cd: |
|||||||||||||||||||||||||||||||||||
Очевидно, что | |||||||||||||||||||||||||||||||||||
S ABC= | |||||||||||||||||||||||||||||||||||
Теперь нужно найти площадь треугольника AB1 C. По теореме Пифагора вычисляем его |
|||||||||||||||||||||||||||||||||||
AC = 2; AB1 =p | ; B1 C = 3; | ||||||||||||||||||||||||||||||||||
и по формуле Герона легко получаем: | |||||||||||||||||||||||||||||||||||
S AB1 C= s | |||||||||||||||||||||||||||||||||||
5 + p 7 | 1 + p 7 | 5 p 7 | |||||||||||||||||||||||||||||||||
Подставляем найденные величины в (5 ): | |||||||||||||||||||||||||||||||||||
Ответ: 3 6 .
Почему при решении этой задачи прежними методами мы столкнулись бы с проблемами? Дело в том, что в пирамиде ABCB1 отсутствует симметрия все рёбра пирамиды имеют различную длину. Соответственно, к проекции точки B на плоскость AB1 C не так-то просто ¾подобраться¿. Но методу объёмов, как видите, данная трудность нипочём мы нашли искомую высоту d, даже не выясняя, куда именно проектируется точка B.
Освоив столь мощный метод нахождения расстояния от точки до плоскости, мы в качестве ¾дополнительной опции¿ немедленно получаем метод вычисления угла между прямой и плоскостью.

13.2 Угол между прямой и плоскостью
Идея вычисления угла между прямой и плоскостью очень проста и основана на предварительном вычислении расстояния от точки до плоскости. Давайте посмотрим на рис. 76 .
Рис. 76. Угол между прямой и плоскостью
Предположим, нам нужно найти угол " между прямой BC и плоскостью ABD. Вычисляем сначала высоту CN, после чего находим:
sin " = CN BC :
В качестве иллюстрации рассмотрим задачу с теми же исходными данными, что и предыдущая.
Задача 3. В прямоугольном параллелепипеде ABCDA B C D известны рёбра: AB = 1,
p p 1 1 1 1
AD = 3, AA1 = 6. Найдите угол между прямой BB1 и плоскостью AB1 C.
Решение. Ситуация показана на рис. 77 .
Рис. 77. К задаче 3 |
||
Расстояние от точки B до плоскости AB1 C мы уже нашли в предыдущей задаче:
BN = 3 6 .
