Пирамида. Правильная пирамида
Многогранники
Данный видеоурок поможет пользователям получить представление о теме Пирамида. Правильная пирамида. На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение. Рассмотрим, что такое правильная пирамида и какими свойствами она обладает. Затем докажем теорему о боковой поверхности правильной пирамиды.
На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение.
Рассмотрим многоугольник А 1 А 2 ...А n , который лежит в плоскости α, и точку P , которая не лежит в плоскости α (рис. 1). Соединим точку P с вершинами А 1 , А 2 , А 3 , … А n . Получим n треугольников: А 1 А 2 Р , А 2 А 3 Р и так далее.
Определение . Многогранник РА 1 А 2 …А n , составленный из n -угольника А 1 А 2 ...А n и n треугольников РА 1 А 2 , РА 2 А 3 …РА n А n -1 , называется n -угольной пирамидой. Рис. 1.
Рис. 1
Рассмотрим четырехугольную пирамиду PABCD (рис. 2).
Р - вершина пирамиды.
ABCD - основание пирамиды.
РА - боковое ребро.
АВ - ребро основания.
Из точки Р опустим перпендикуляр РН на плоскость основания АВСD . Проведенный перпендикуляр является высотой пирамиды.
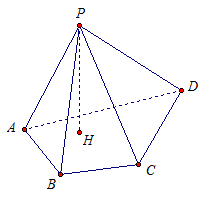
Рис. 2
Полная поверхность пирамиды состоит из поверхности боковой, то есть площади всех боковых граней, и площади основания:
S полн = S бок + S осн
Пирамида называется правильной, если:
- ее основание - правильный многоугольник;
- отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Пояснение на примере правильной четырехугольной пирамиды
Рассмотрим правильную четырехугольную пирамиду PABCD (рис. 3).
Р - вершина пирамиды. Основание пирамиды АВСD - правильный четырехугольник, то есть квадрат. Точка О , точка пересечения диагоналей, является центром квадрата. Значит, РО - это высота пирамиды.
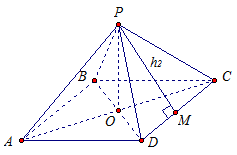
Рис. 3
Пояснение : в правильном n -угольнике центр вписанной и центр описанной окружности совпадает. Этот центр и называется центром многоугольника. Иногда говорят, что вершина проектируется в центр.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой и обозначается h а .
1. все боковые ребра правильной пирамиды равны;
2. боковые грани являются равными равнобедренными треугольниками.
Доказательство этих свойств приведем на примере правильной четырехугольной пирамиды.
Дано : РАВСD - правильная четырехугольная пирамида,
АВСD - квадрат,
РО - высота пирамиды.
Доказать :
1. РА = РВ = РС = РD
2. ∆АВР = ∆ВCР =∆СDР =∆DAP См. Рис. 4.
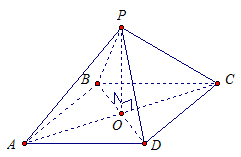
Рис. 4
Доказательство .
РО - высота пирамиды. То есть, прямая РО перпендикулярна плоскости АВС , а значит, и прямым АО, ВО, СО и DО , лежащим в ней. Значит, треугольники РОА, РОВ, РОС, РОD - прямоугольные.
Рассмотрим квадрат АВСD . Из свойств квадрата следует, что АО = ВО = СО = DО.
Тогда у прямоугольных треугольников РОА, РОВ, РОС, РОD катет РО - общий и катеты АО, ВО, СО и DО равны, значит, эти треугольники равны по двум катетам. Из равенства треугольников вытекает равенство отрезков, РА = РВ = РС = РD. Пункт 1 доказан.
Отрезки АВ и ВС равны, так как являются сторонами одного квадрата, РА = РВ = РС . Значит, треугольники АВР и ВCР - равнобедренные и равны по трем сторонам.
Аналогичным образом получаем, что треугольники АВР, ВCР, СDР, DAP равнобедренны и равны, что и требовалось доказать в пункте 2.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:
![]()
Для доказательства выберем правильную треугольную пирамиду.
Дано : РАВС - правильная треугольная пирамида.
АВ = ВС = АС.
РО - высота.
Доказать
: ![]() . См. Рис. 5.
. См. Рис. 5.
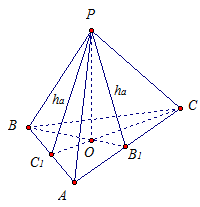
Рис. 5
Доказательство.
РАВС
- правильная треугольная пирамида. То есть АВ
= АС = ВС
. Пусть О
- центр треугольника АВС
, тогда РО
- это высота пирамиды. В основании пирамиды лежит равносторонний треугольник АВС
. Заметим, что ![]() .
.
Треугольники РАВ, РВC, РСА - равные равнобедренные треугольники (по свойству). У треугольной пирамиды три боковые грани: РАВ, РВC, РСА . Значит, площадь боковой поверхности пирамиды равна:
S бок = 3S РАВ
Теорема доказана.
Радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м, высота пирамиды равна 4 м. Найдите площадь боковой поверхности пирамиды.
Дано : правильная четырехугольная пирамида АВСD ,
АВСD - квадрат,
r = 3 м,
РО - высота пирамиды,
РО = 4 м.
Найти : S бок. См. Рис. 6.
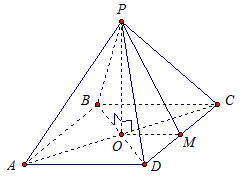
Рис. 6
Решение .
По доказанной теореме, ![]() .
.
Найдем сначала сторону основания АВ . Нам известно, что радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м.
Тогда, м.
Найдем периметр квадрата АВСD со стороной 6 м:
Рассмотрим треугольник BCD
. Пусть М
- середина стороны DC
. Так как О
- середина BD
, то ![]() (м).
(м).
Треугольник DPC - равнобедренный. М - середина DC . То есть, РМ - медиана, а значит, и высота в треугольнике DPC . Тогда РМ - апофема пирамиды.
РО - высота пирамиды. Тогда, прямая РО перпендикулярна плоскости АВС , а значит, и прямой ОМ , лежащей в ней. Найдем апофему РМ из прямоугольного треугольника РОМ .
Теперь можем найти боковую поверхность пирамиды:
Ответ : 60 м 2 .
Радиус окружности, описанной около основания правильной треугольной пирамиды, равен м. Площадь боковой поверхности равна 18 м 2 . Найдите длину апофемы.
Дано : АВСP - правильная треугольная пирамиды,
АВ = ВС = СА,
R = м,
S бок = 18 м 2 .
Найти : . См. Рис. 7.
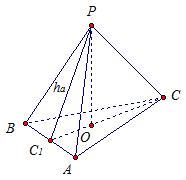
Рис. 7
Решение .
В правильном треугольнике АВС дан радиус описанной окружности. Найдем сторону АВ этого треугольника с помощью теоремы синусов.
![]()
Зная сторону правильного треугольника ( м), найдем его периметр.
По теореме о площади боковой поверхности правильной пирамиды ![]() , где h а
- апофема пирамиды. Тогда:
, где h а
- апофема пирамиды. Тогда:
![]()
Ответ : 4 м.
Итак, мы рассмотрели, что такое пирамида, что такое правильная пирамида, доказали теорему о боковой поверхности правильной пирамиды. На следующем уроке мы познакомимся с усечённой пирамидой.
Список литературы
- Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. - 5-е изд., испр. и доп. - М.: Мнемозина, 2008. - 288 с.: ил.
- Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. - М.: Дрофа, 1999. - 208 с.: ил.
- Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. - 6-е изд., стереотип. - М.: Дрофа, 008. - 233 с.: ил.
- Интернет портал «Якласс» ()
- Интернет портал «Фестиваль педагогических идей «Первое сентября» ()
- Интернет портал «Slideshare.net» ()
Домашнее задание
- Может ли правильный многоугольник быть основанием неправильной пирамиды?
- Докажите, что непересекающиеся ребра правильной пирамиды перпендикулярны.
- Найдите величину двугранного угла при стороне основания правильной четырехугольной пирамиды, если апофема пирамиды равна стороне ее основания.
- РАВС - правильная треугольная пирамида. Постройте линейный угол двугранного угла при основании пирамиды.
Чудаева Е.В., МОУ «Инсарская СОШ №1», г. Инсар, Республика Мордовия
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
(по материалам ЕГЭ)
Задача №1
Задача №2
Задача №3
Задача №4
. Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна 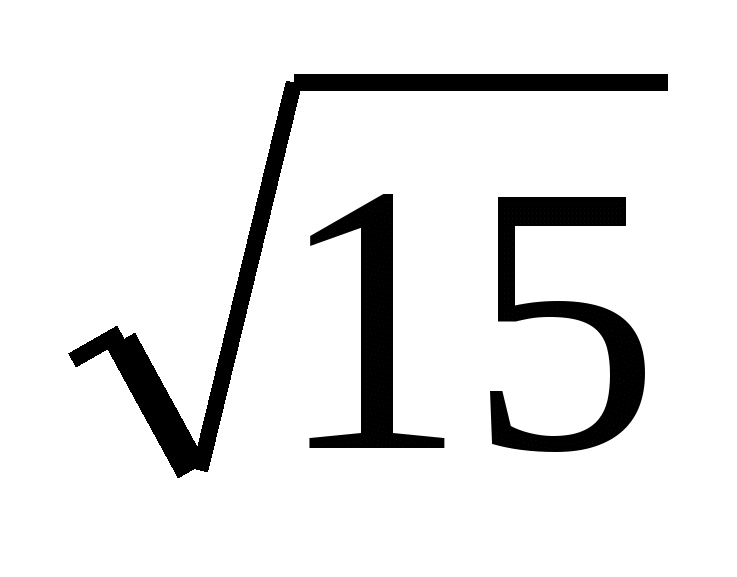 .
.
Задача №5
. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 2, а высота правильной пирамиды равна 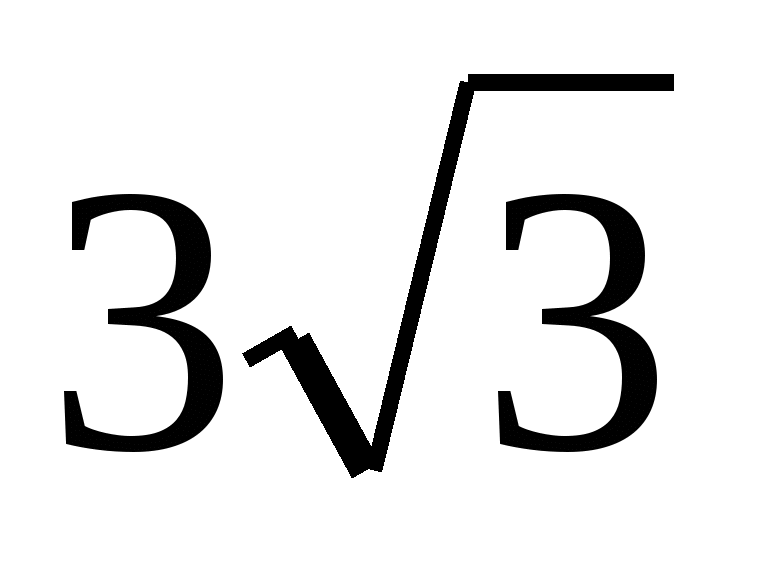 .
.
Задача №6
. Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3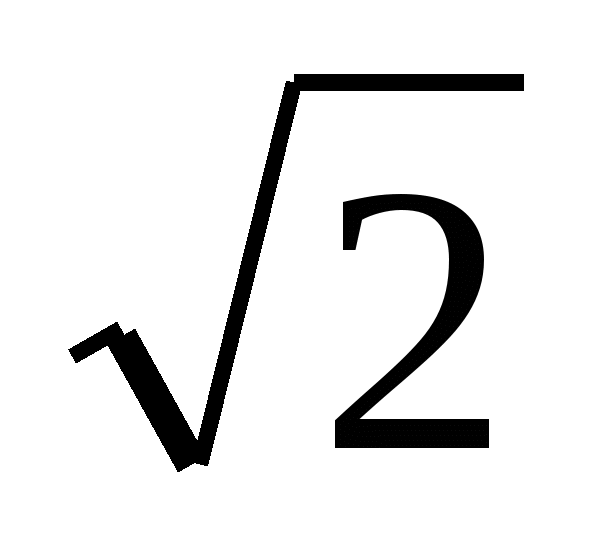 .
.
Задача №7
Задача №8
Задача №9
. В правильной шестиугольной пирамиде сторона основания равна 2, а боковое ребро равно 2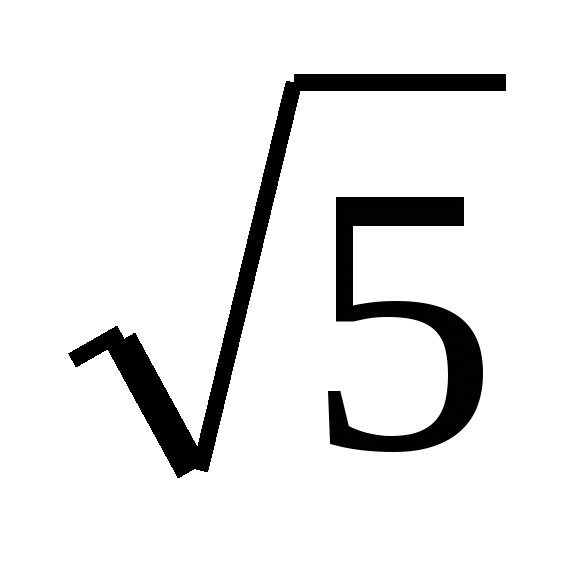 . Найдите объём пирамиды.
. Найдите объём пирамиды.
Задача № 10 R удовлетворяет уравнению R 2 + R – 6 = 0. Найдите объём призмы.
Задача №11
. Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно 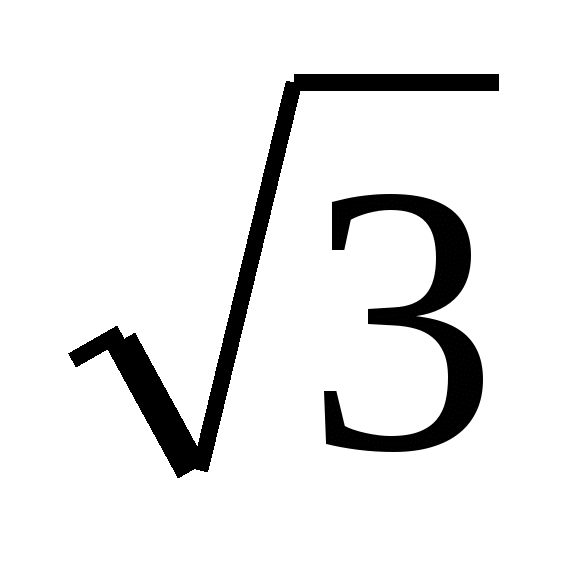 . Высота цилиндра равна трем его радиусам. Найдите объём призмы.
. Высота цилиндра равна трем его радиусам. Найдите объём призмы.
Задача №12
Задача №13
Задача №14
. В правильную четырехугольную призму вписан цилиндр. Объем цилиндра равен 16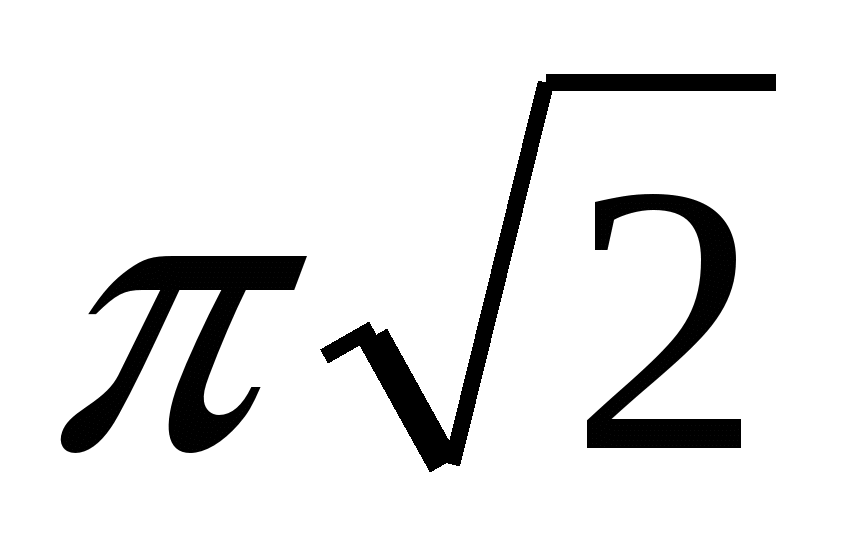 , а радиус окружности, описанной вокруг основания призмы, равен
, а радиус окружности, описанной вокруг основания призмы, равен 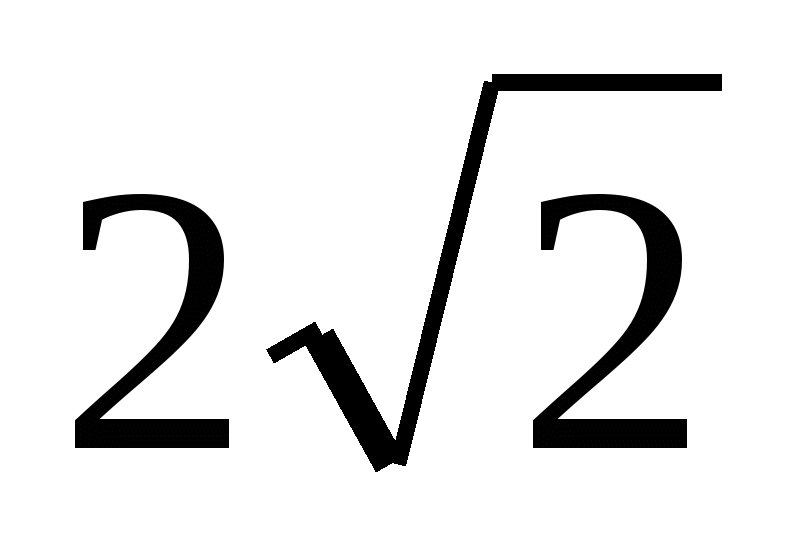 . Найдите диагональ призмы.
. Найдите диагональ призмы.
Задача №15 . В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если её площадь равна 54 , а радиус цилиндра равен 3.
Задача № 16
. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 16
, высота цилиндра равна 4. Найдите объём призмы.
Задача №17 . Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 10 . Найдите объём цилиндра, вписанного в эту же призму.
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
(по материалам ЕГЭ)
Задача №1 . Вычислите объём правильной треугольной пирамиды, если радиус описанной вокруг основания окружности равен , а высота пирамиды равна 4.
Р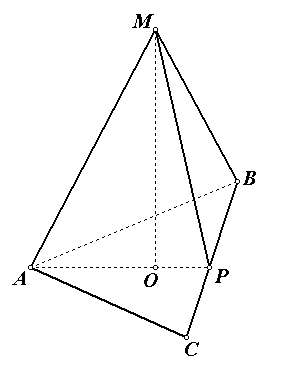 ешение.
ешение.
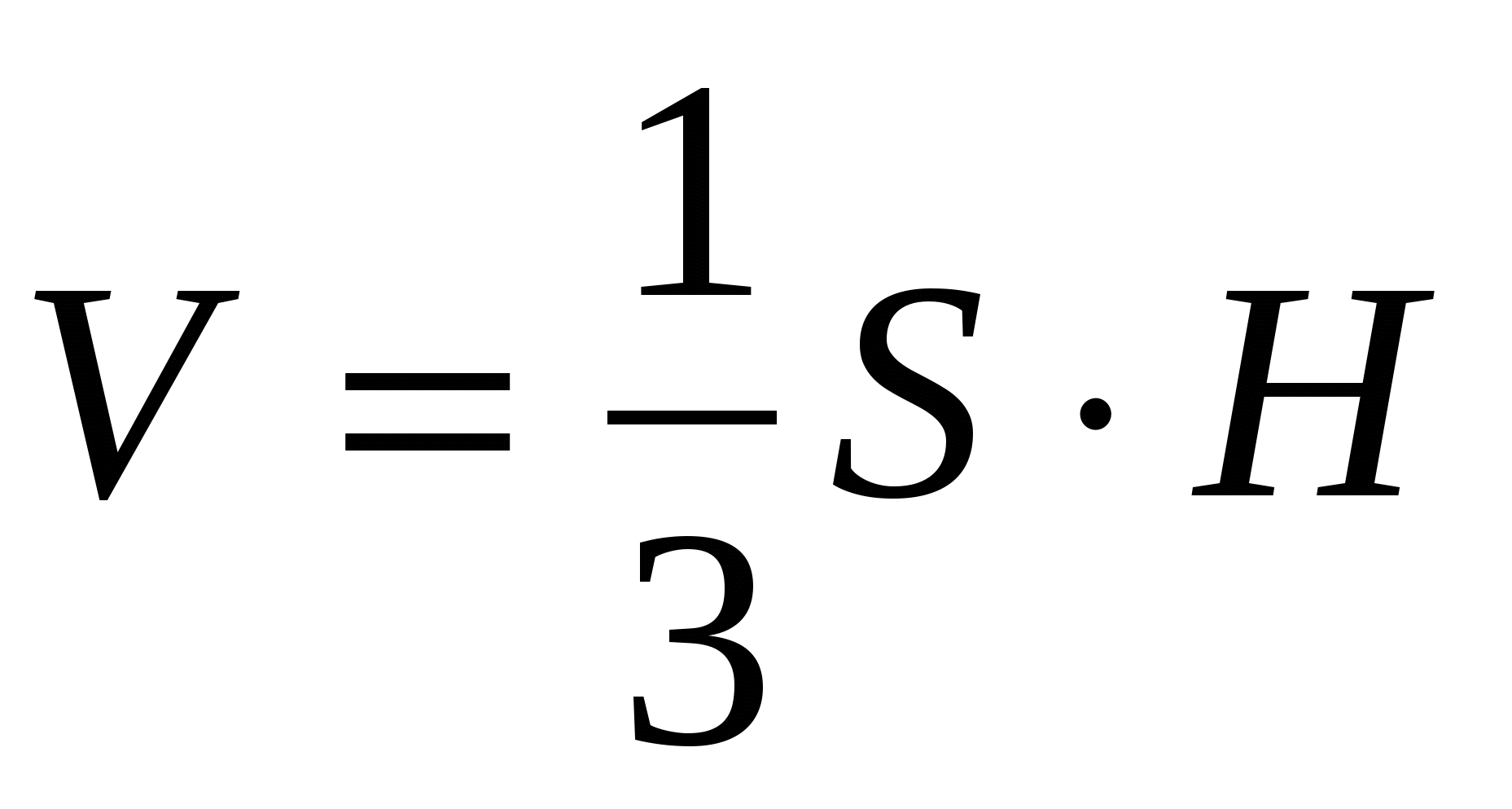 .
.
1) найдем сторону основания правильной пирамиды по формуле 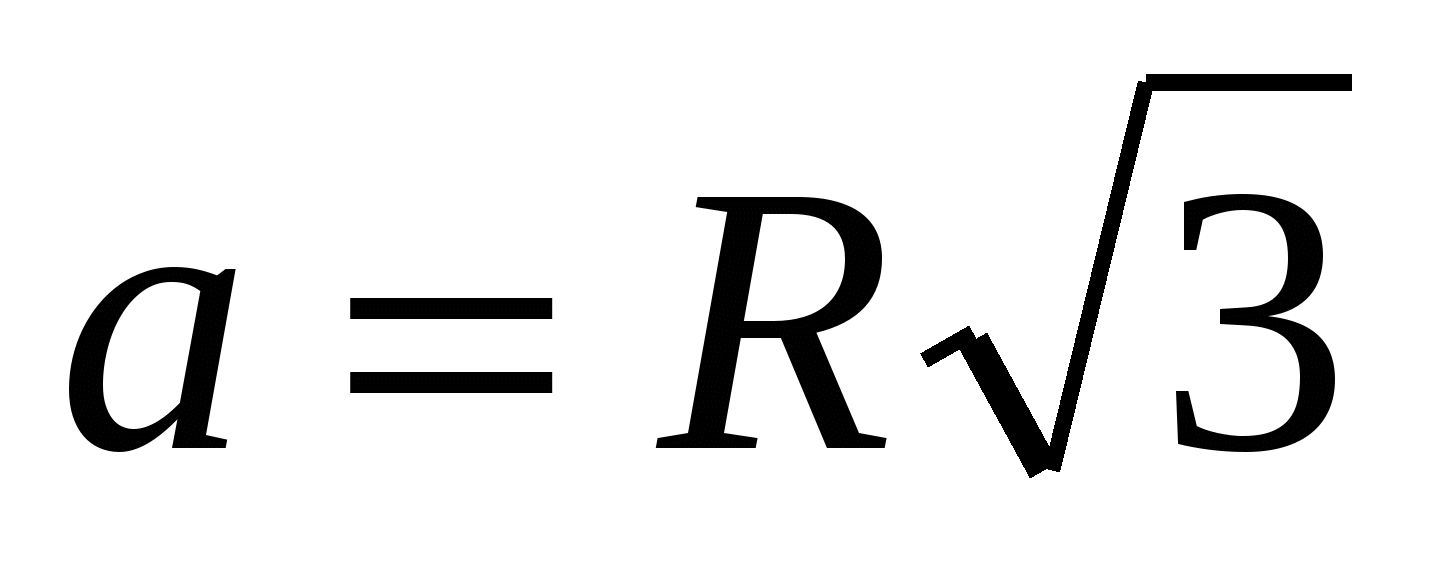 ,
, 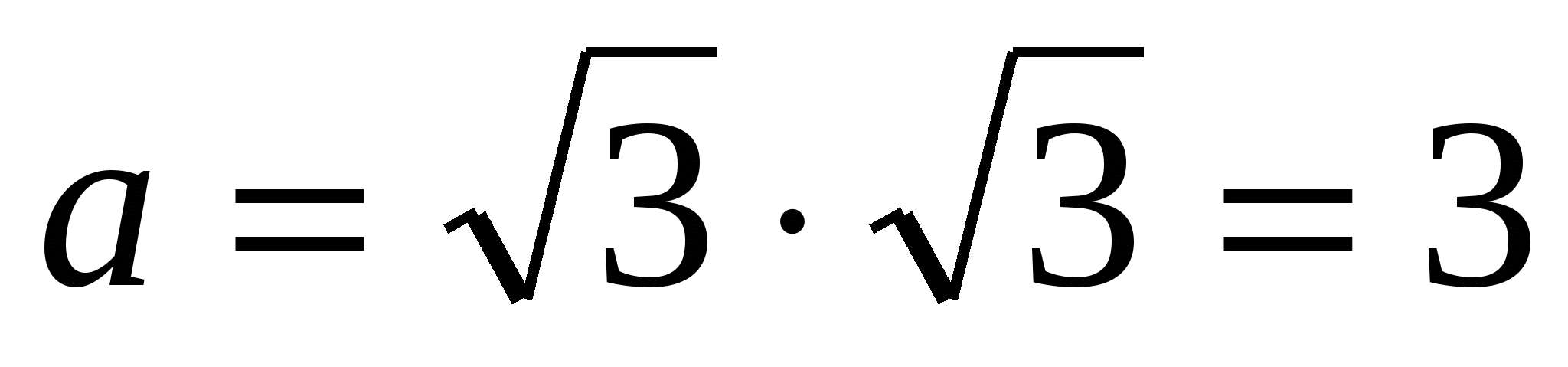 .
.
2) найдем площадь основания, как площадь правильного треугольника 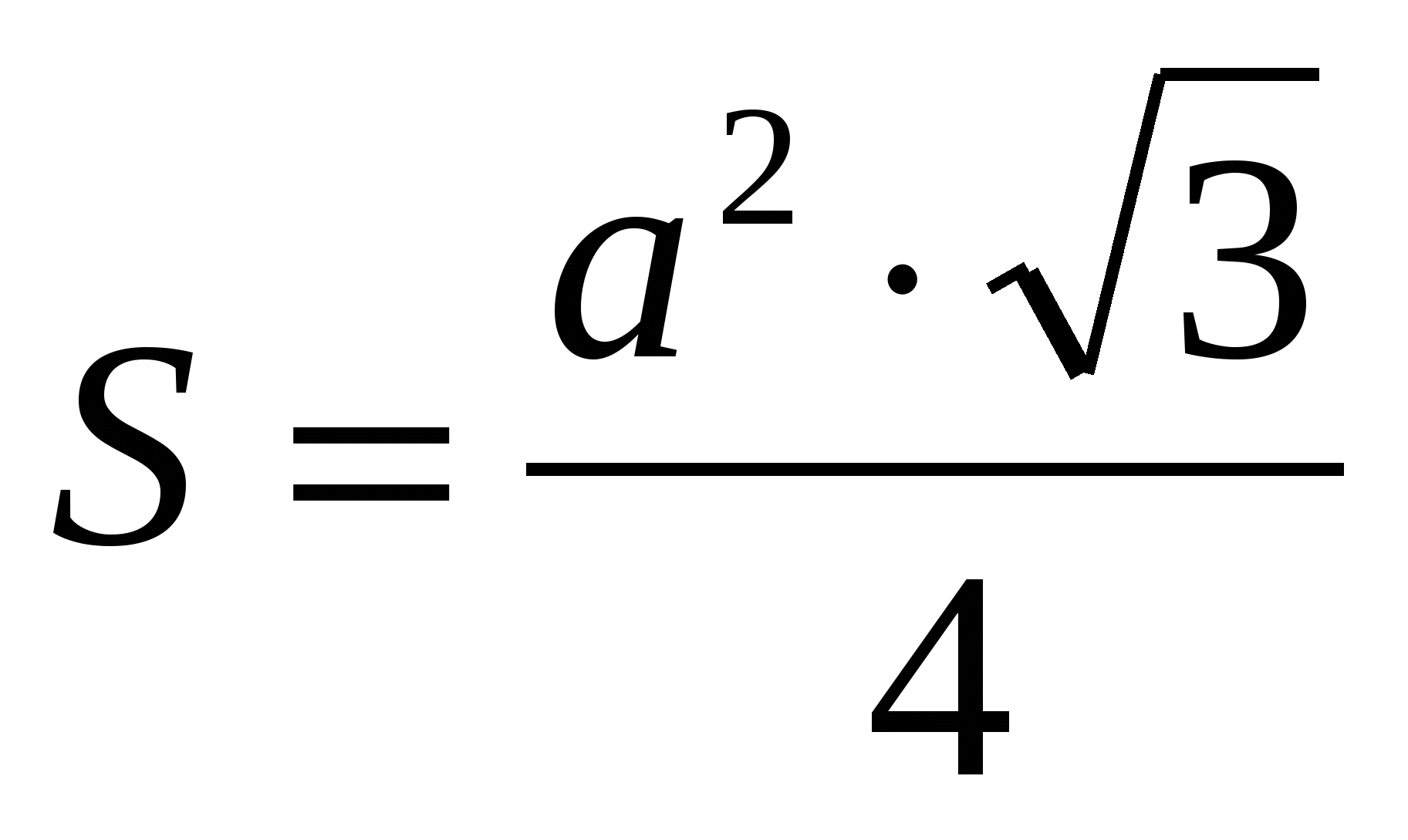 ,
, 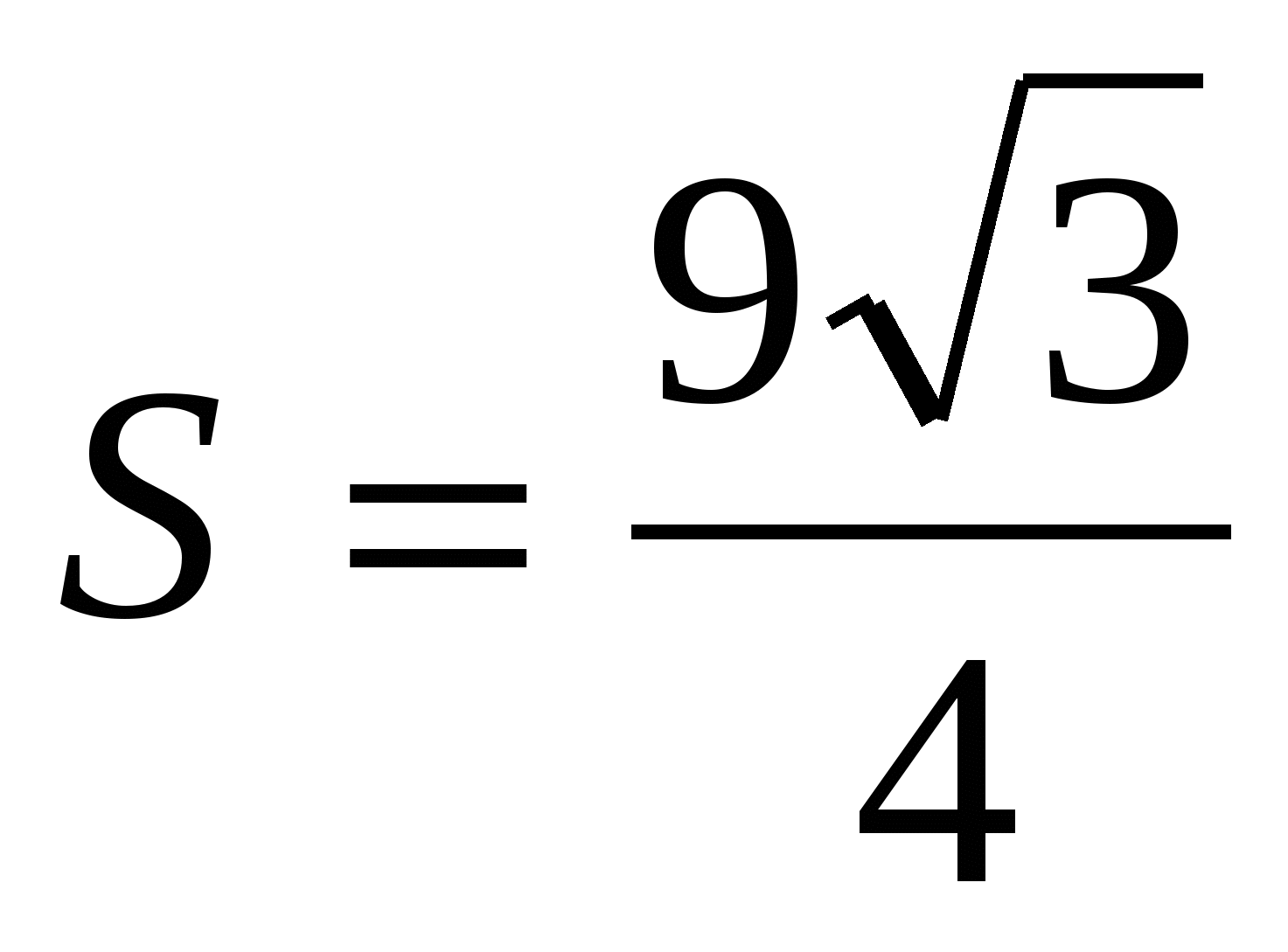 .
.
3) вычислим объём пирамиды
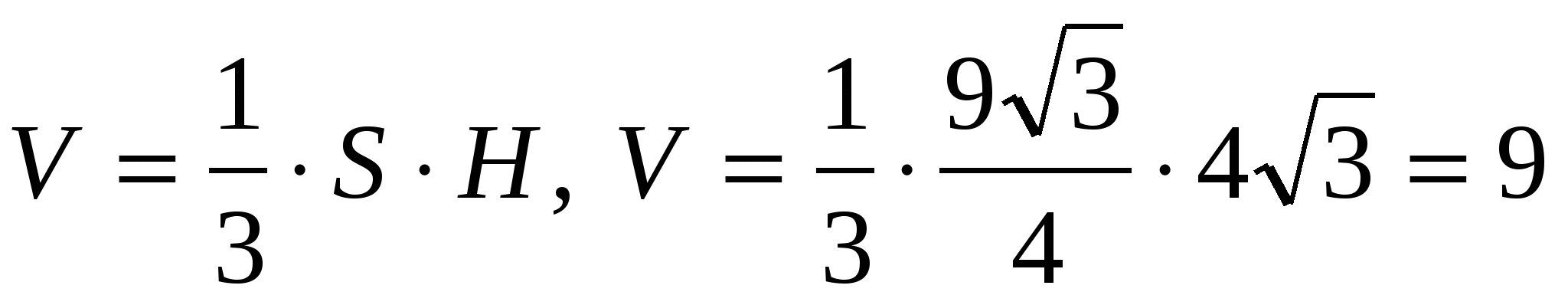 .
.
Ответ. 9
Задача №2 . Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен , а боковые ребра пирамиды равны 6.
Решение.
1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. 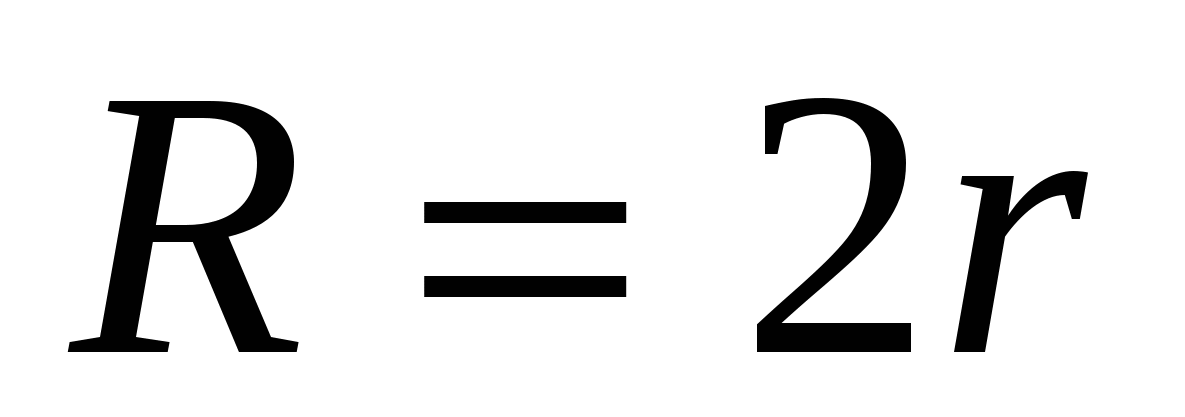 , тогда
, тогда 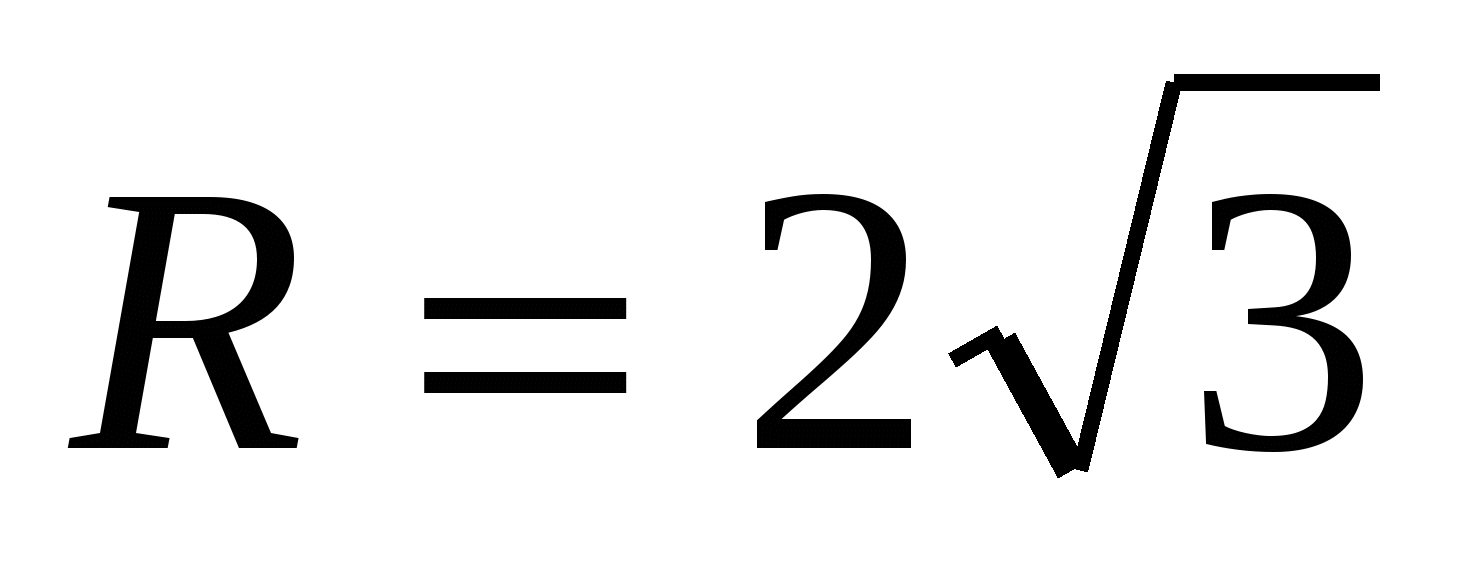 .
.
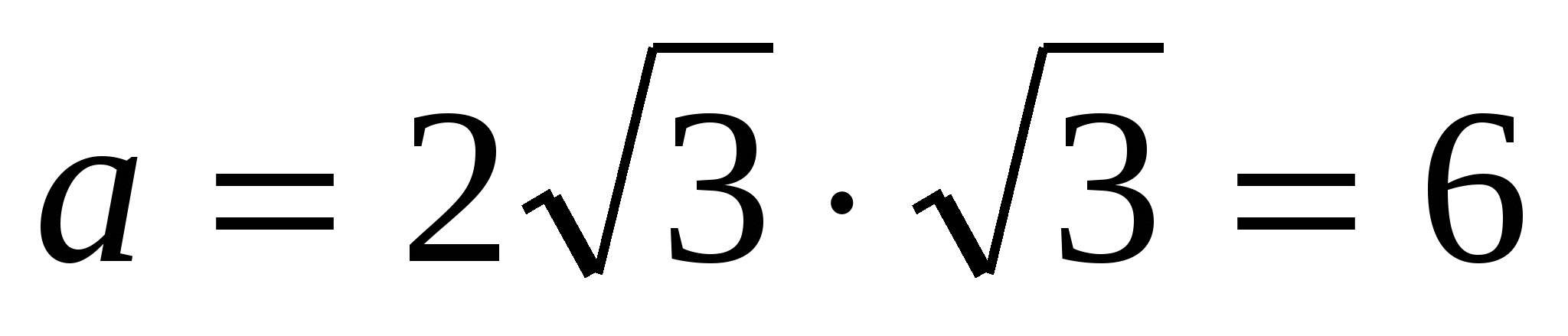 .
.
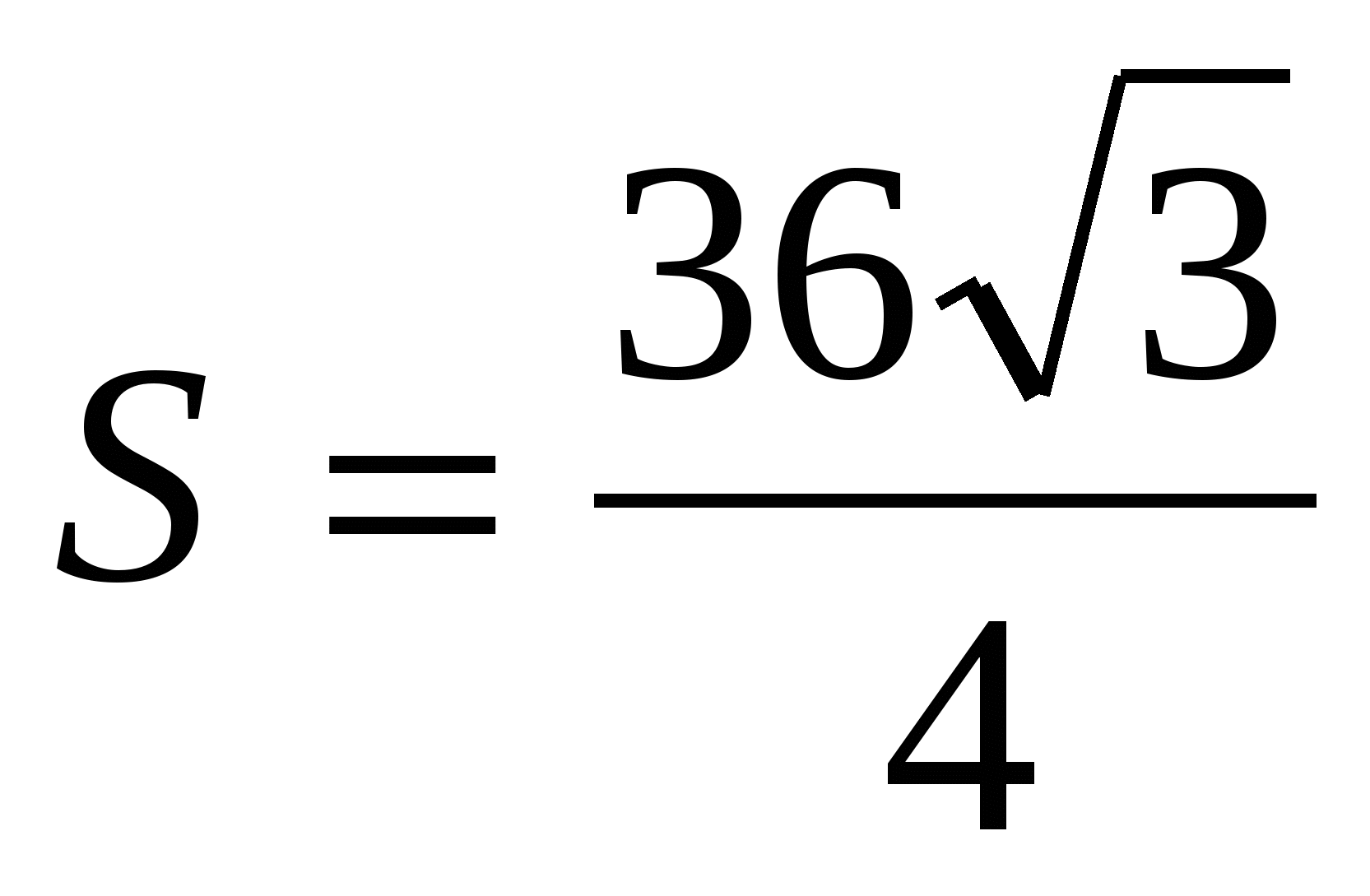 .
.
4) из прямоугольного треугольника 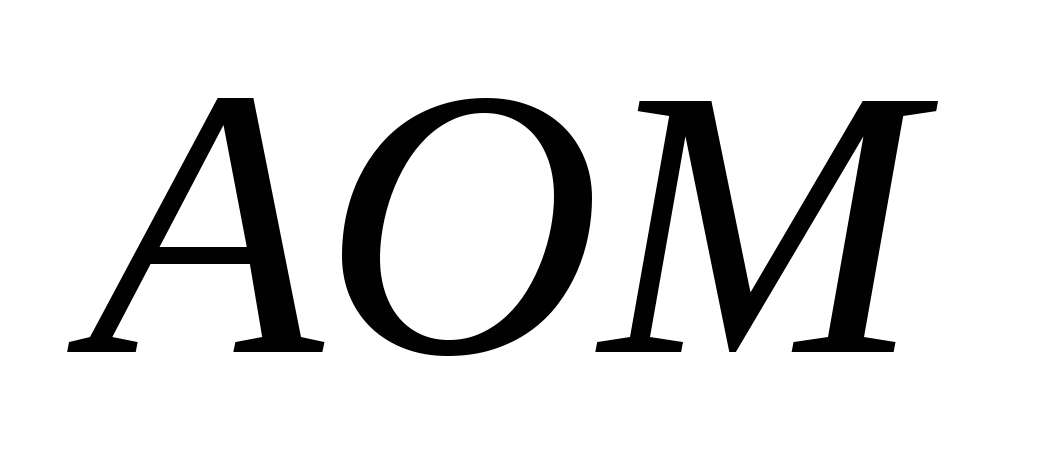 по теореме Пифагора находим высоту пирамиды:
по теореме Пифагора находим высоту пирамиды: 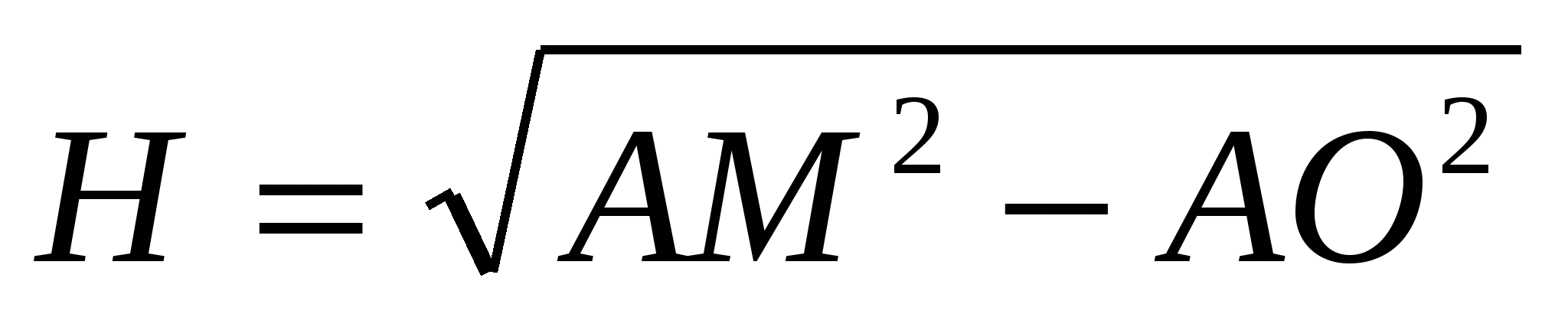 , .
, .
5) вычислим объём пирамиды
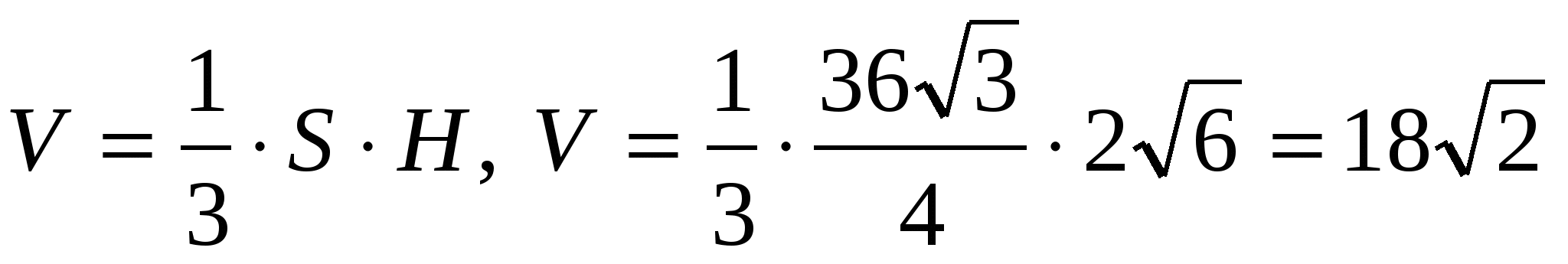 .
.
Ответ. 18.
Задача №3 . Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен , а высота пирамиды равны 1.
Р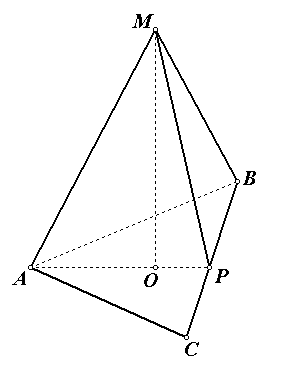 ешение.
ешение.
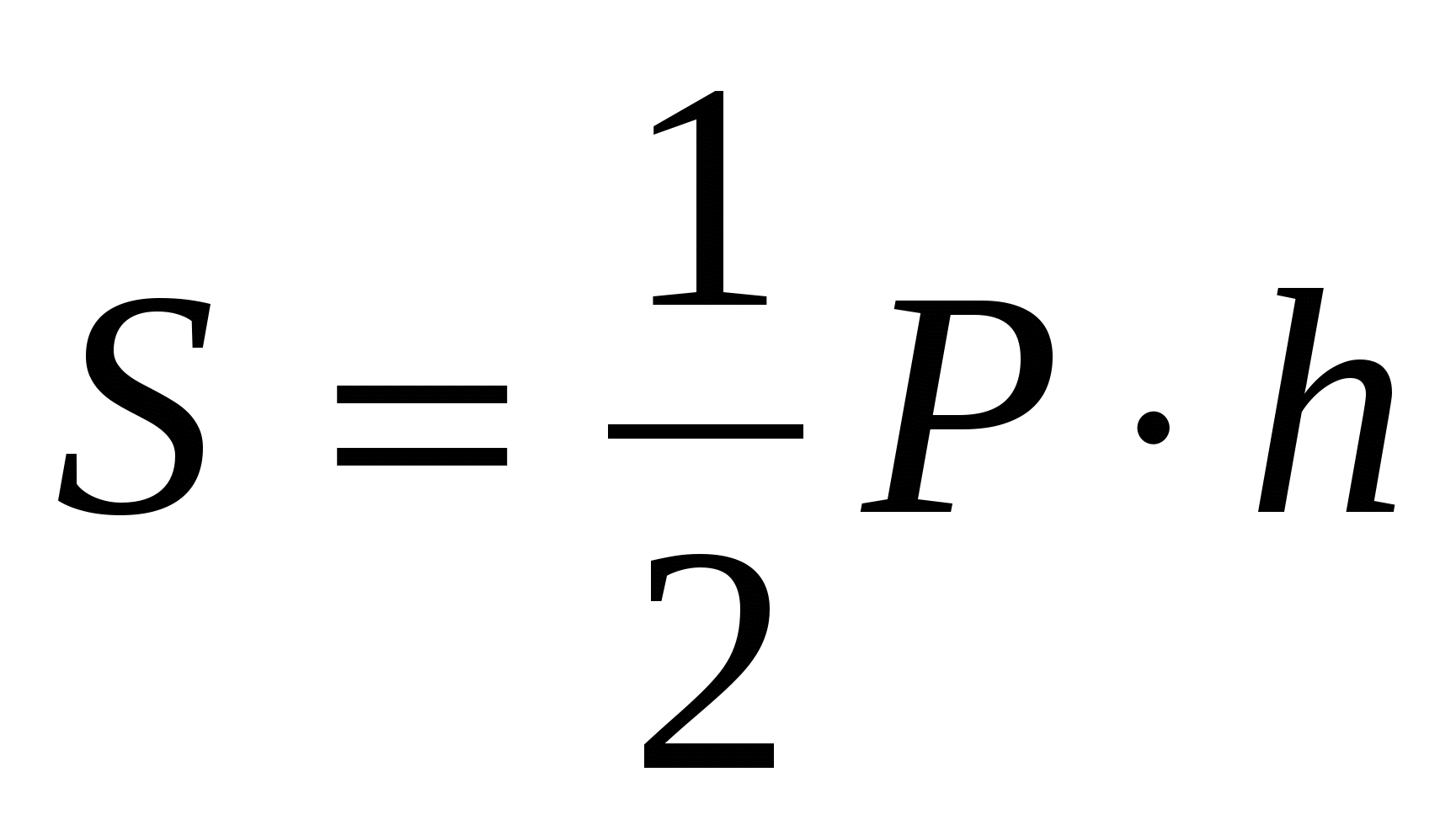
1) найдем сторону основания правильной пирамиды по формуле , .
2) найдем периметр основания Р = 3· а ,
Р = 9.
3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда 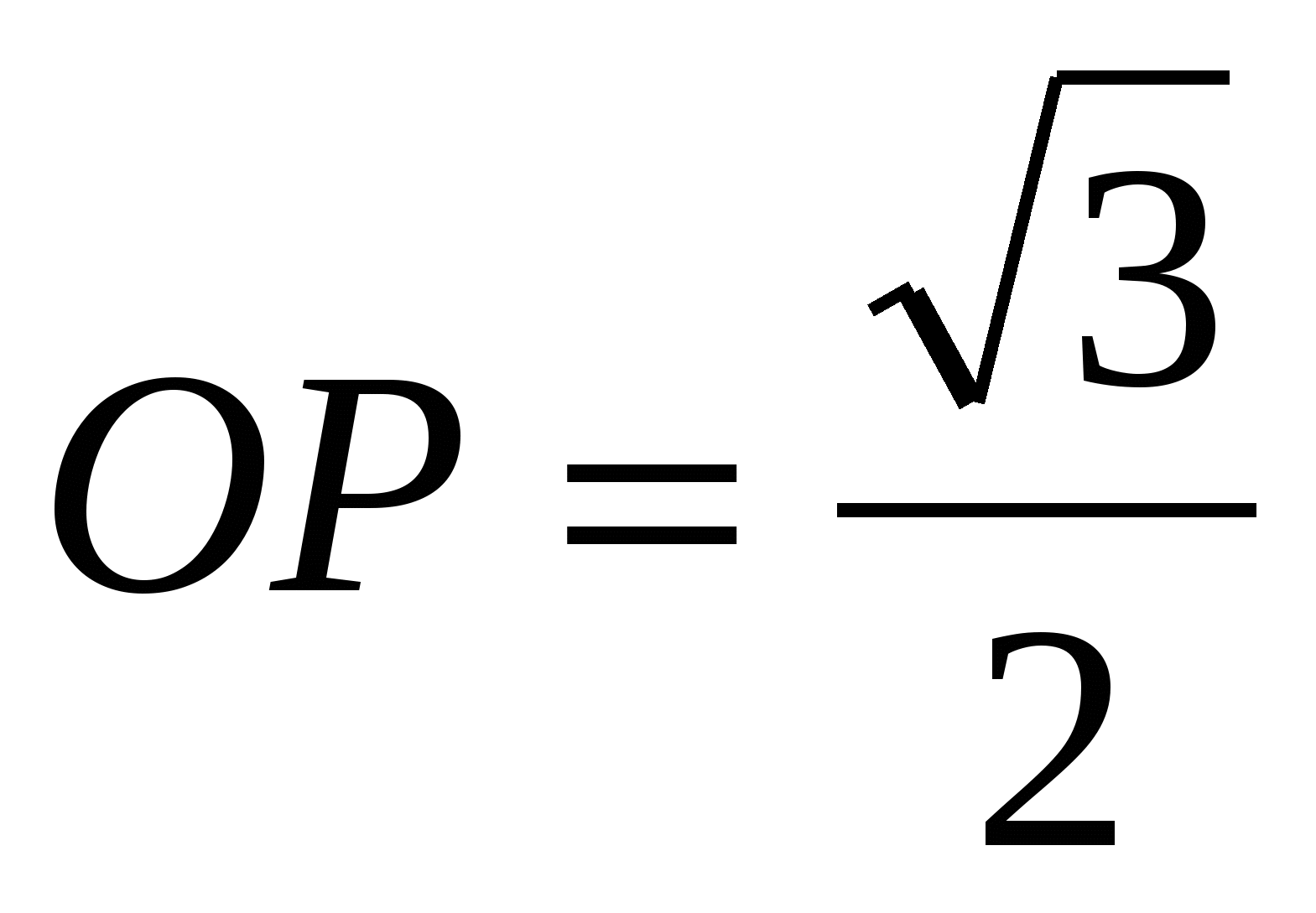 .
.
4) из прямоугольного треугольника
МОР
МР
: ![]() ,
,
МР
= 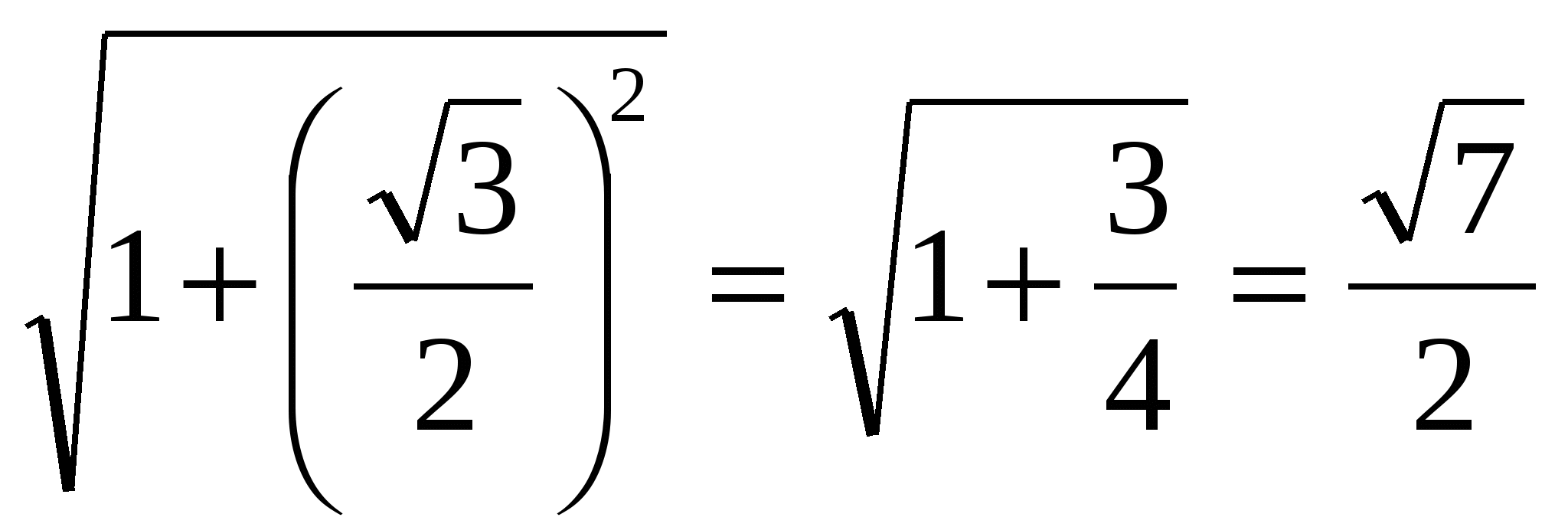
5) вычислим площадь боковой поверхности правильной пирамиды:
,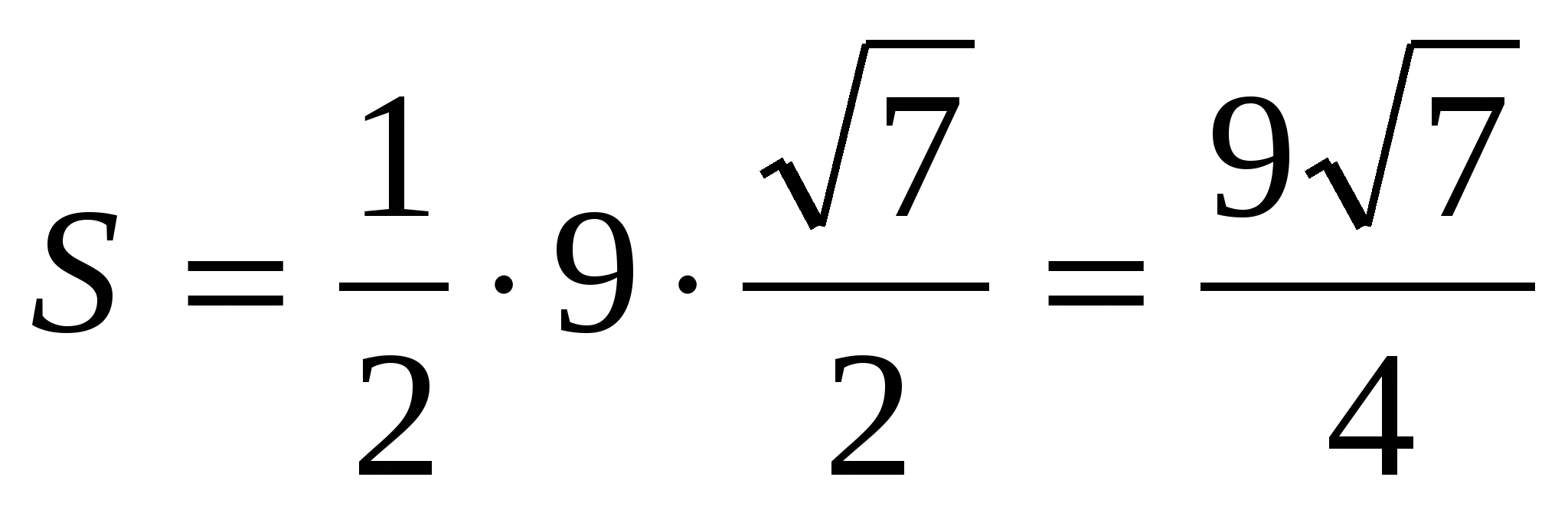 .
.
Ответ. 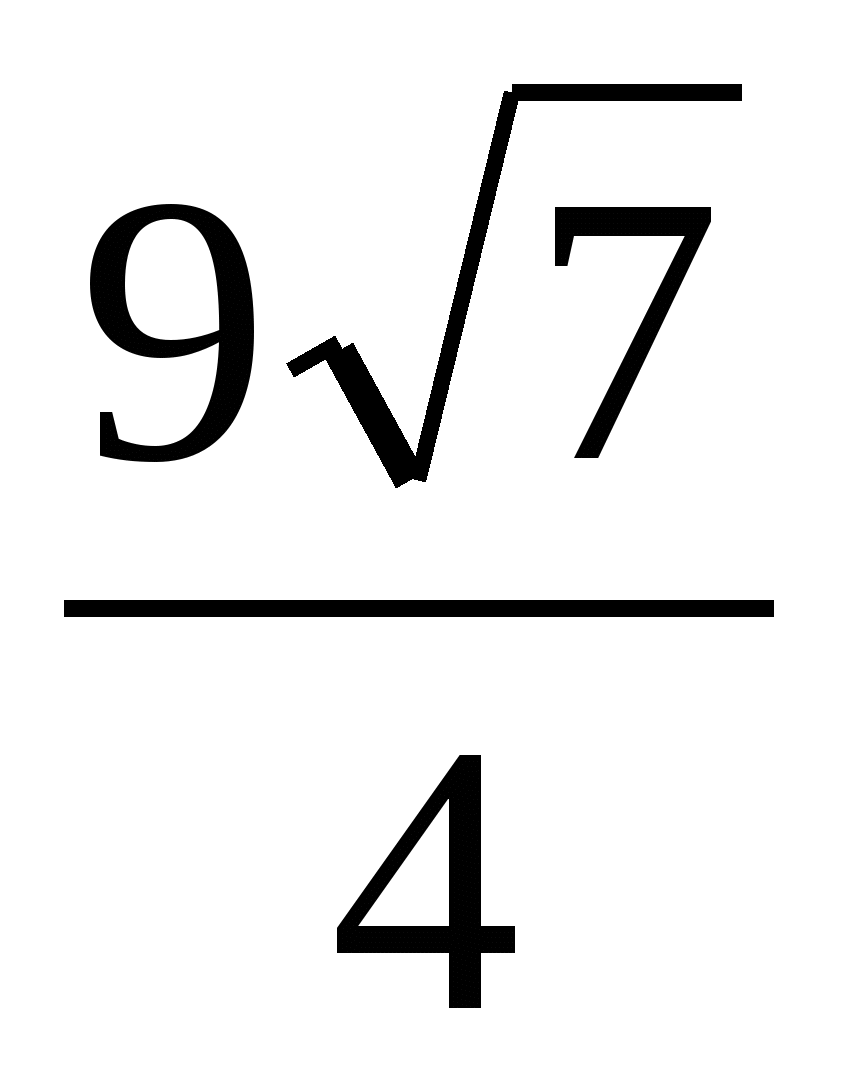 .
.
Задача №4 . Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна .
Решение. ,
1) найдем радиус описанной около основания и вписанной в основание окружностей: , 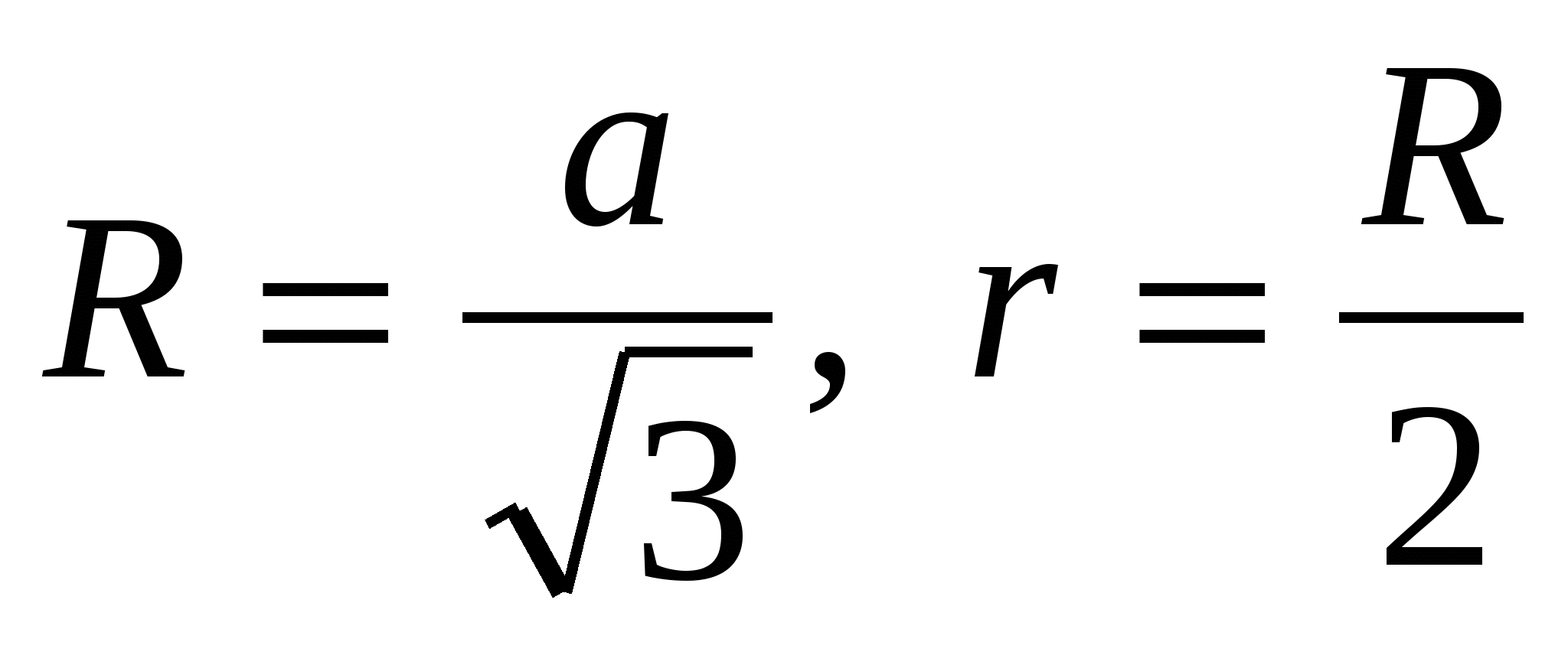 то есть
то есть 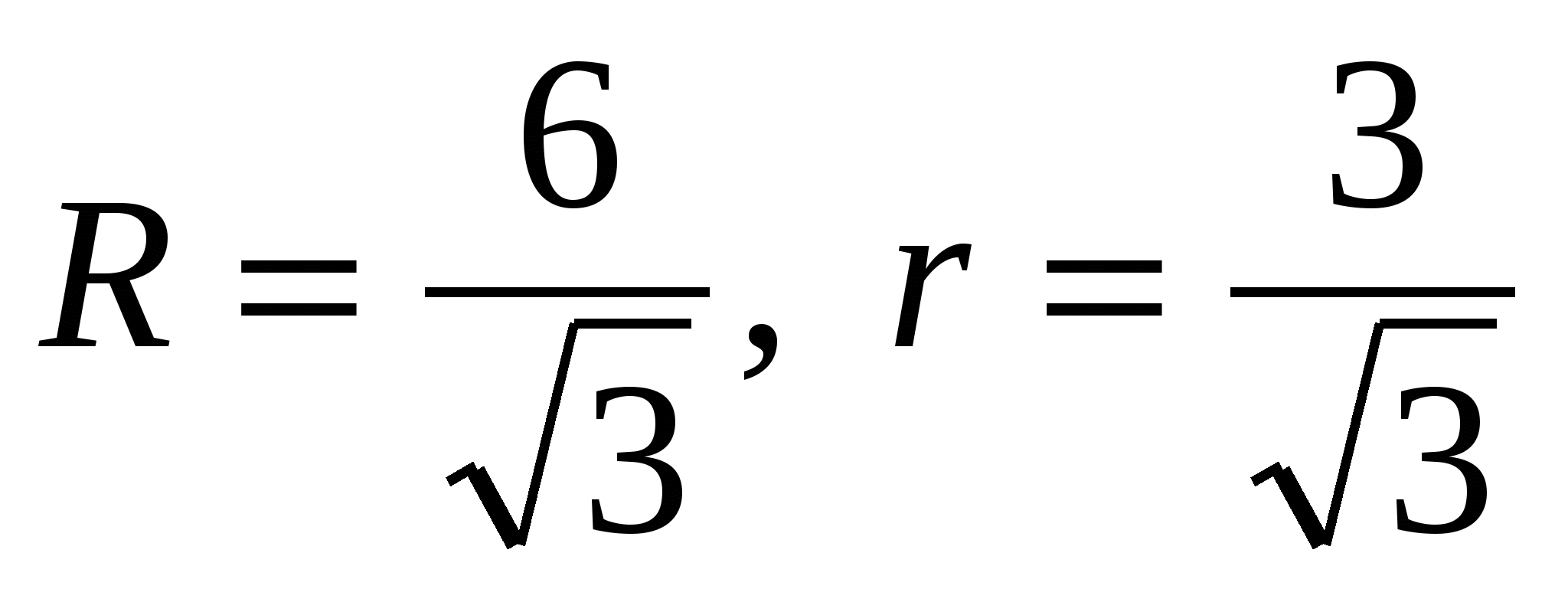 .
.
2) найдем площадь основания, как площадь правильного треугольника , 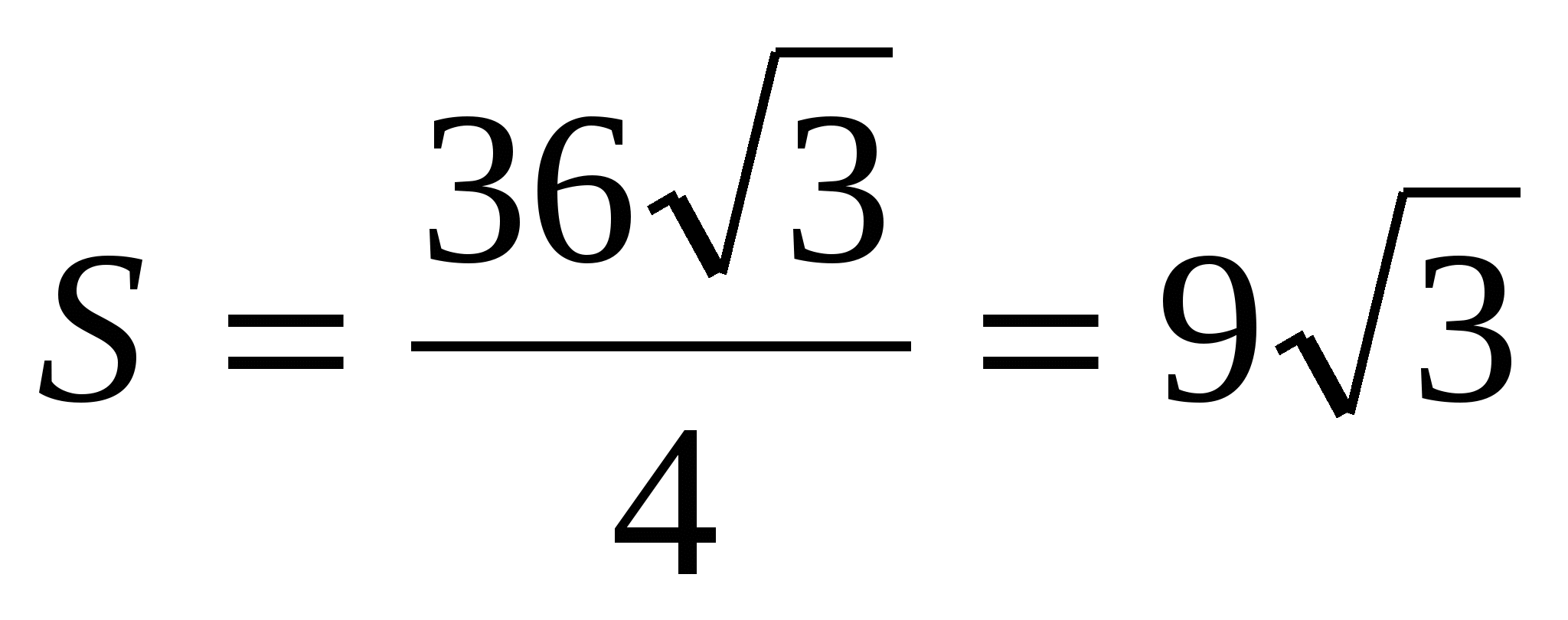 .
.
МОР
по теореме Пифагора находим высоту:  , МО =
, МО = 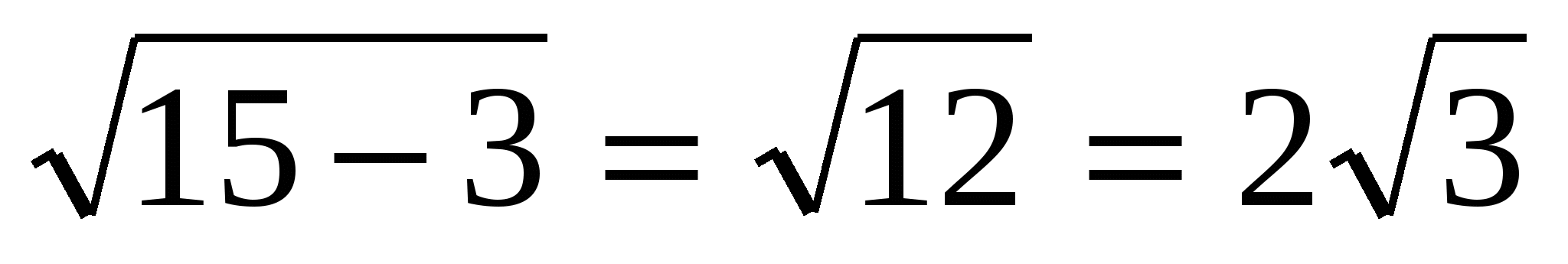 .
.
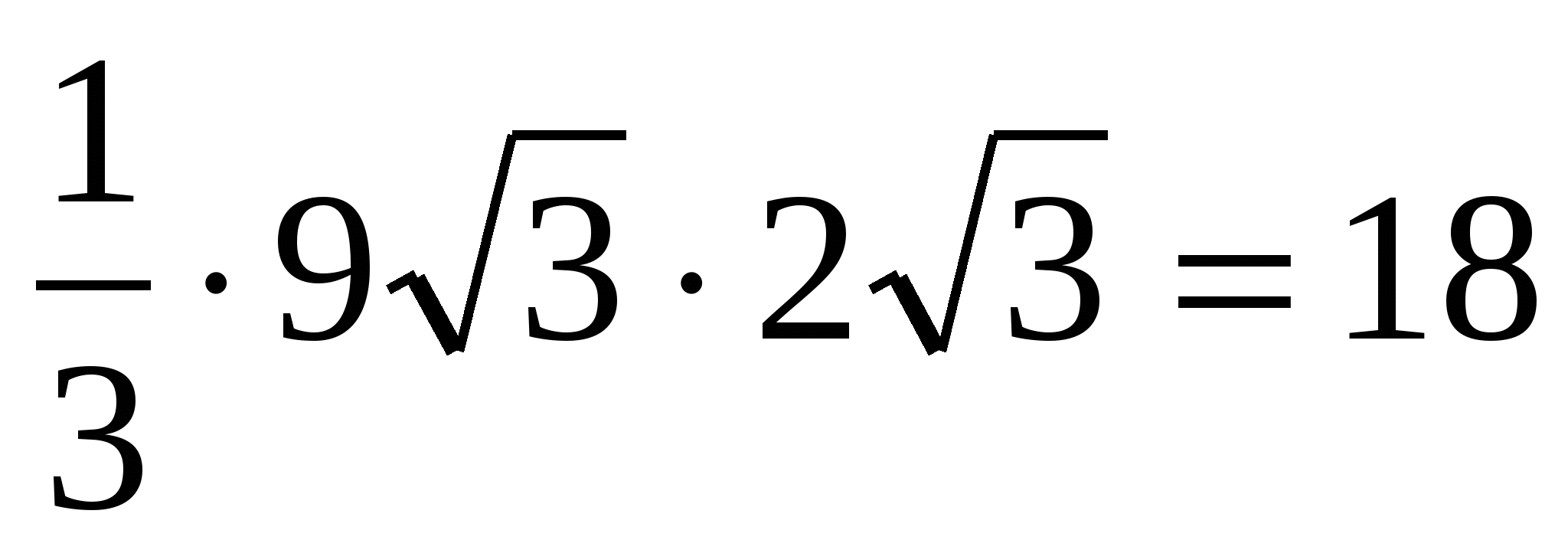 .
.
Ответ. 18.
Задача №5 . Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 2, а высота правильной пирамиды равна .
Решение.
1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда 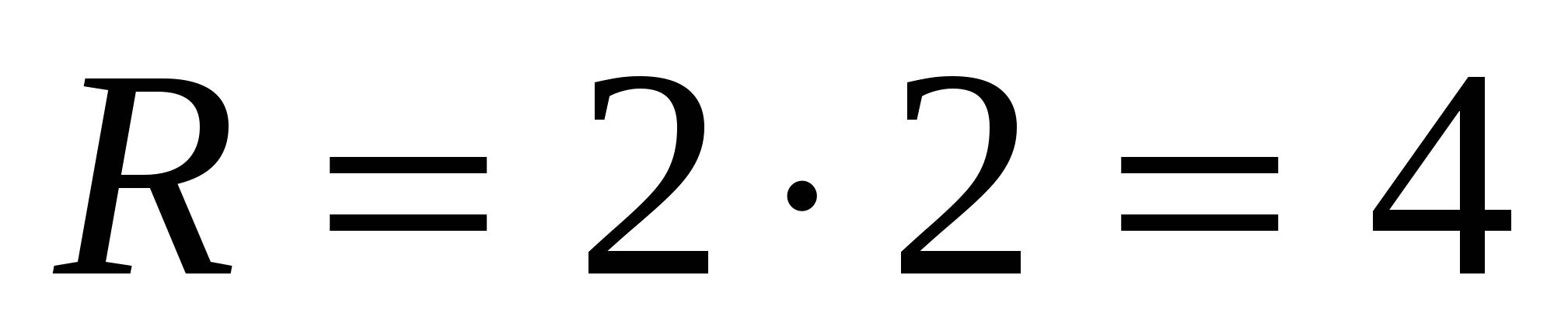 .
.
2) найдем сторону основания правильной пирамиды по формуле , 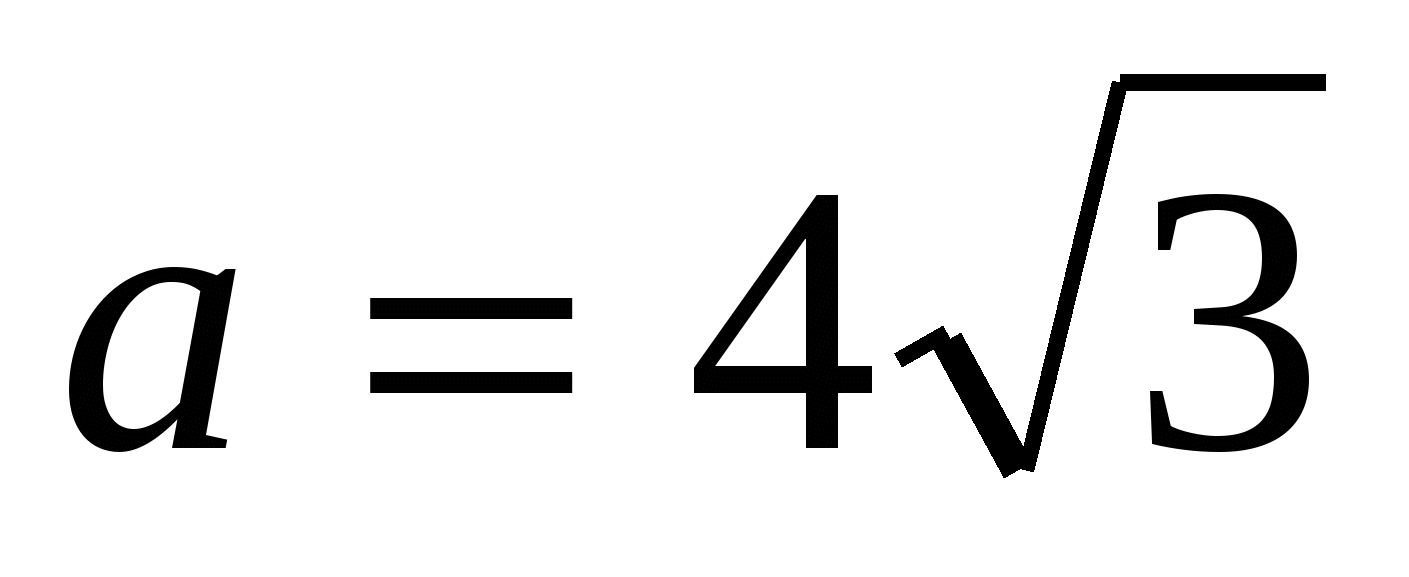 .
.
3) найдем площадь основания, как площадь правильного треугольника , 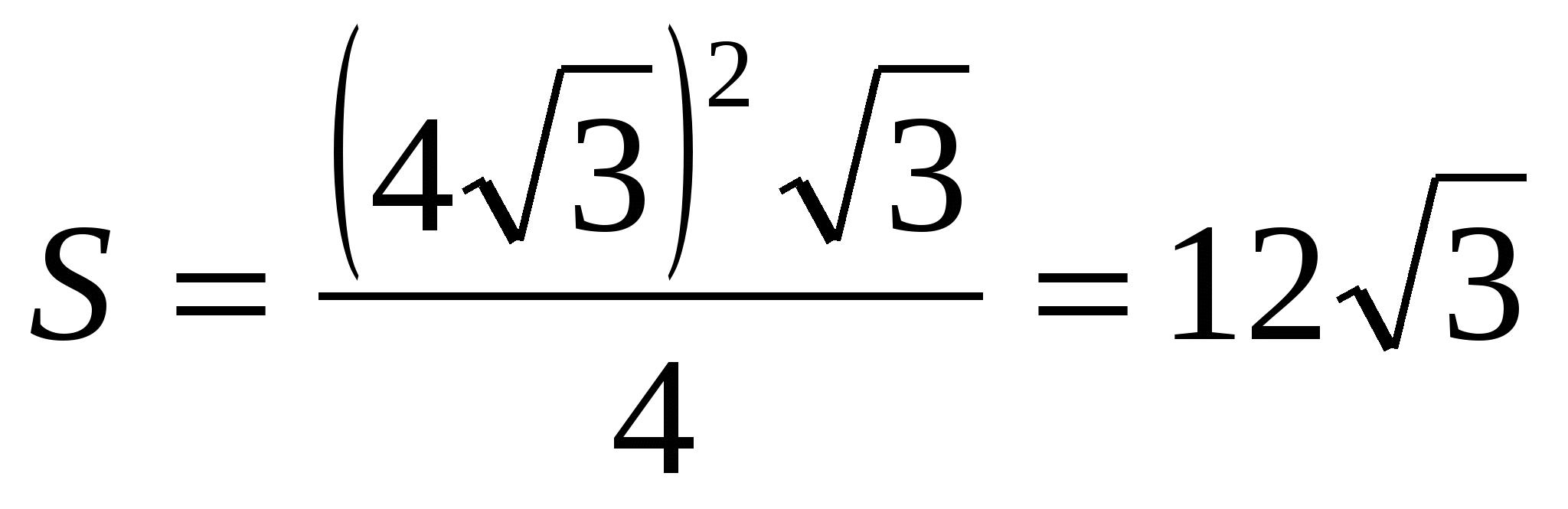 .
.
4) вычислим объём правильной пирамиды: = 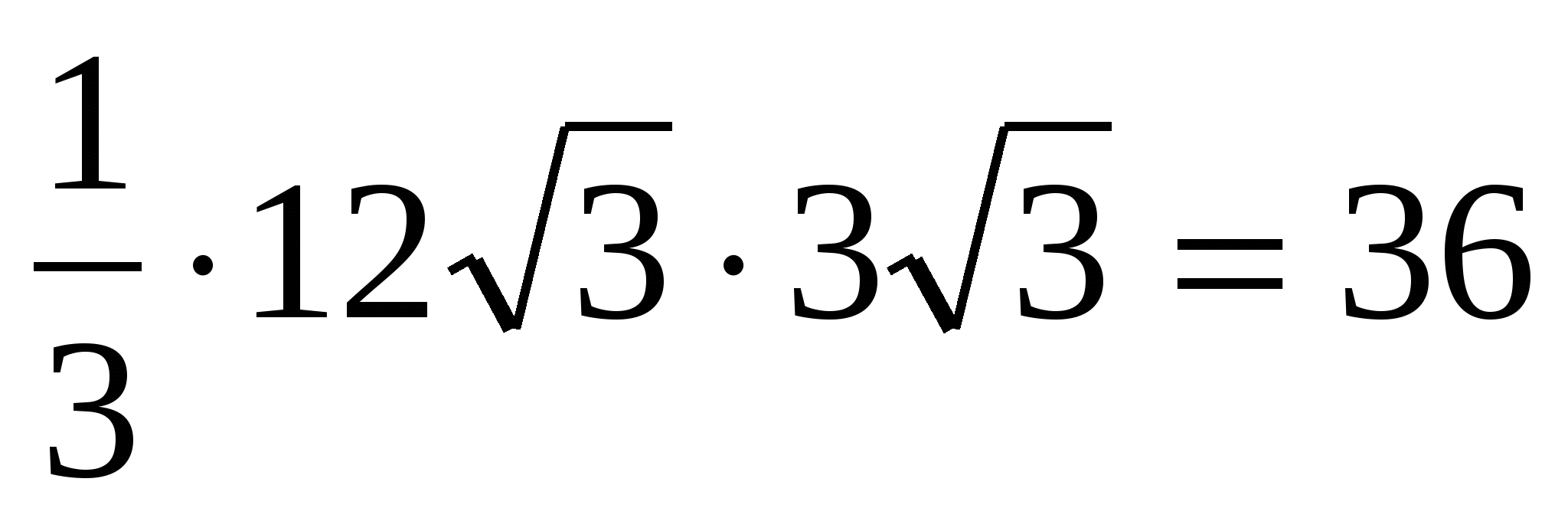 .
.
Ответ. 36.
Задача №6 . Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3.
Р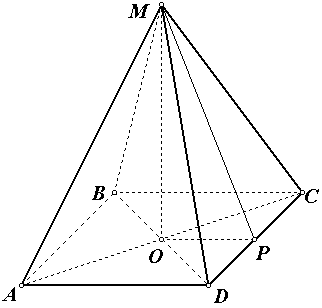 ешение
.
ешение
.
1) найдем сторону основания по формуле 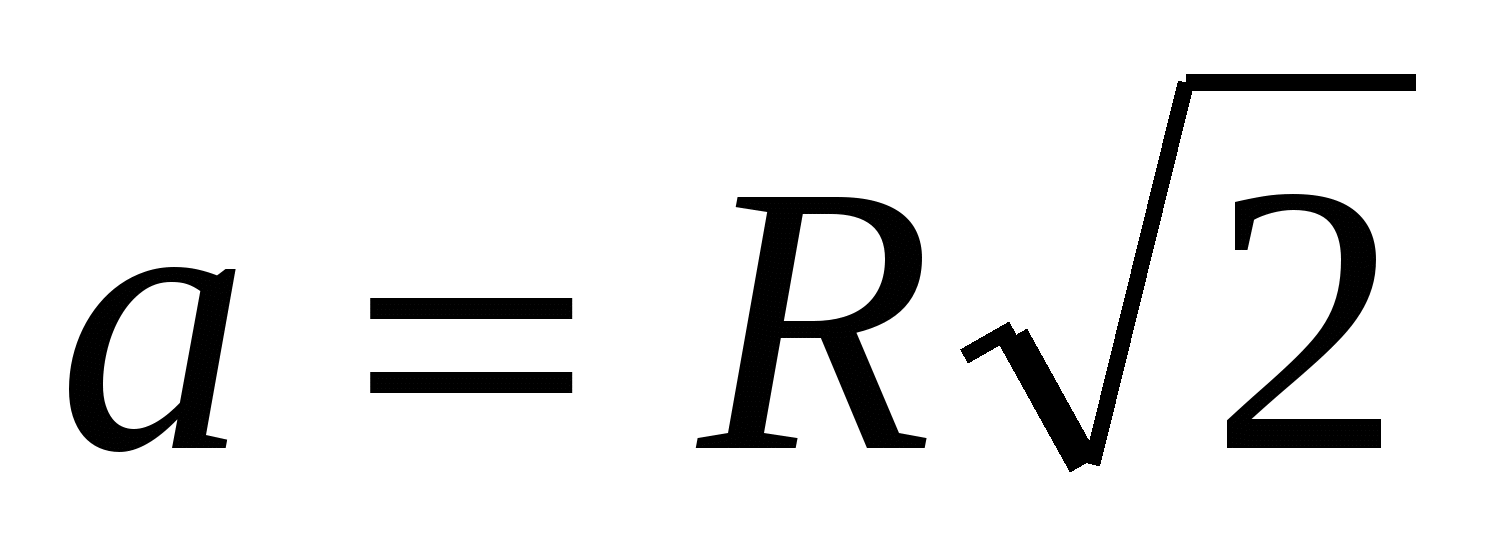 , т.е.
, т.е. 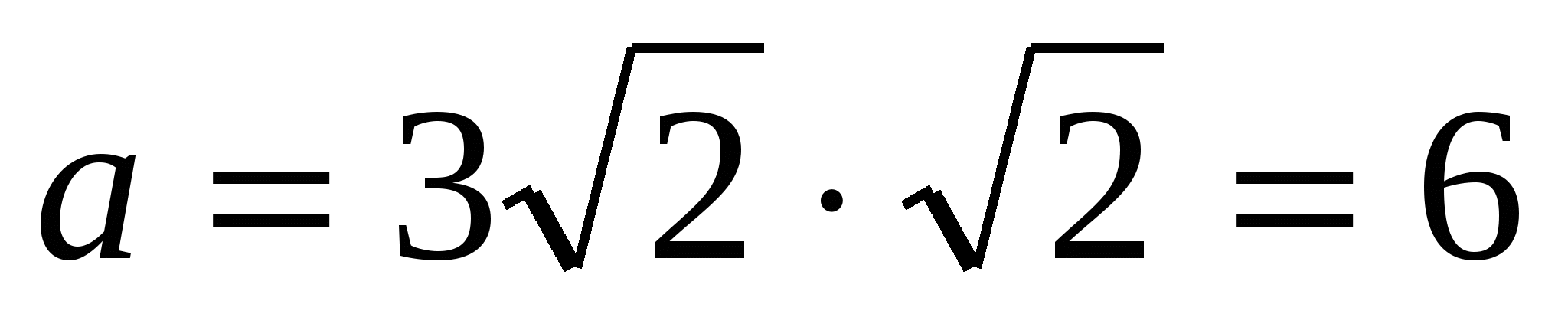 .
.
2) найдем периметр основания: Р = 4а ,
Р = 24.
3) из прямоугольного треугольника
М
D
Р
по теореме Пифагора находим апофему
МР
: 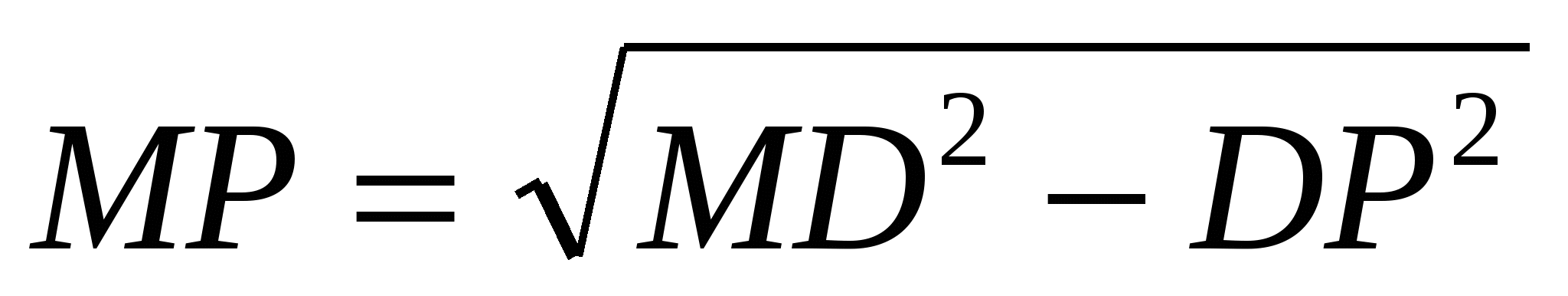 ,
DP
=
,
DP
=
тогда:
МР
= 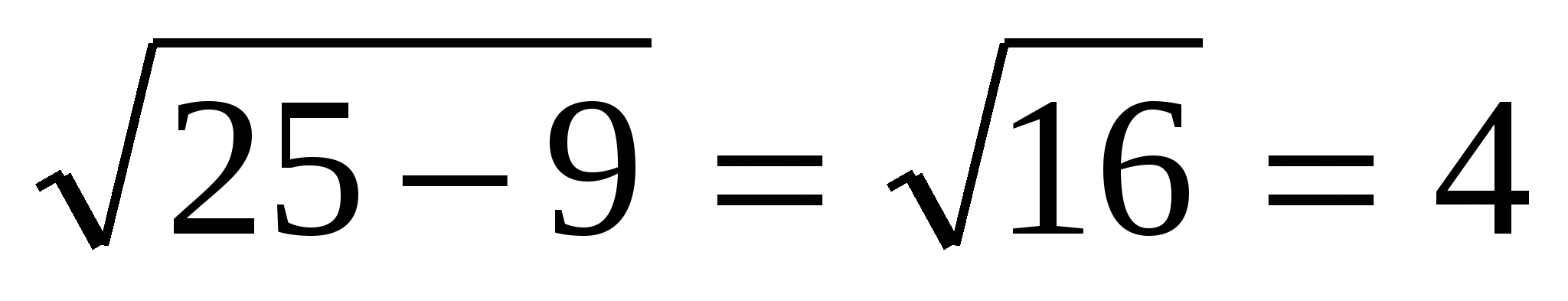 .
.
4) вычислим площадь боковой поверхности пирамиды: = 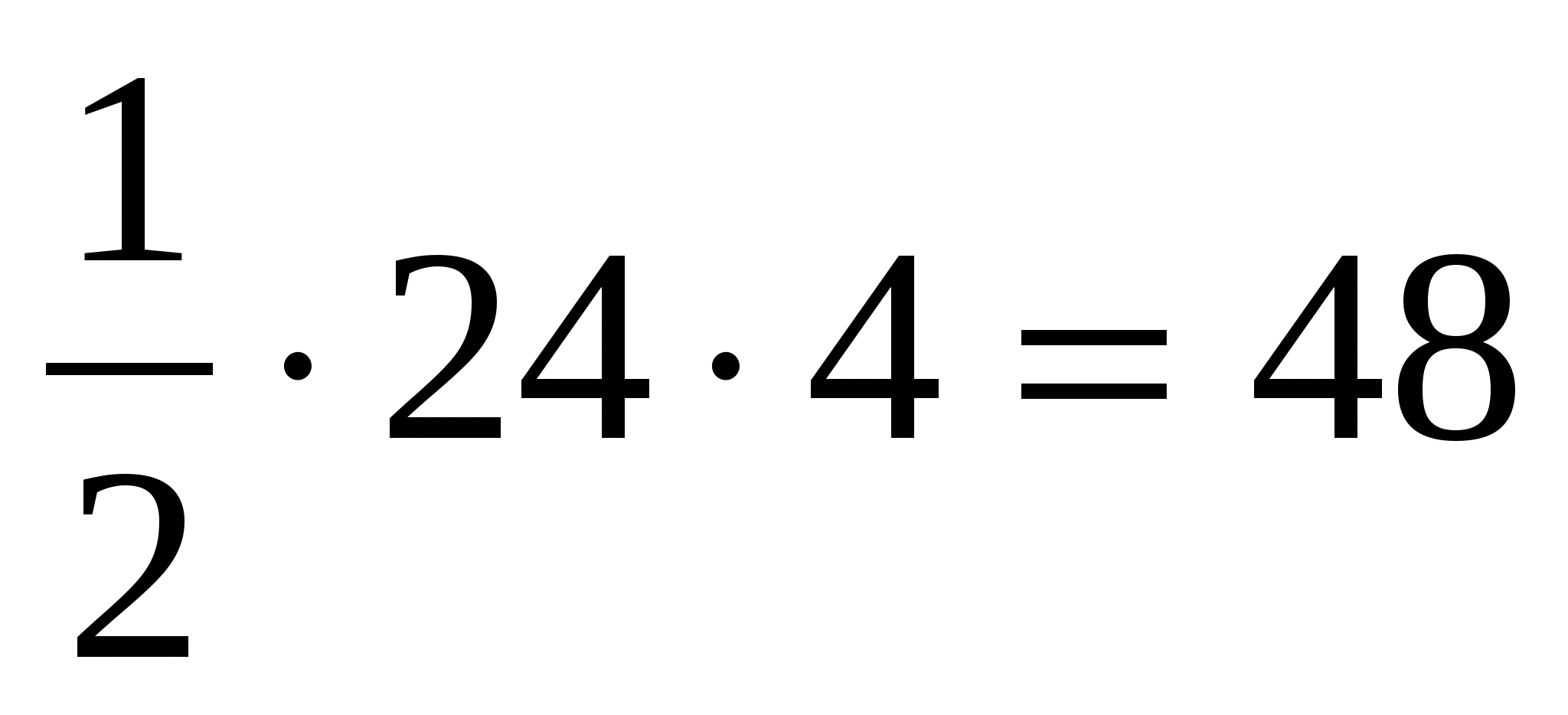 .
.
Ответ. 48.
Задача №7 . В правильной четырехугольной пирамиде площадь боковой поверхности равна 16, а площадь основания 4. Найдите высоту пирамиды.
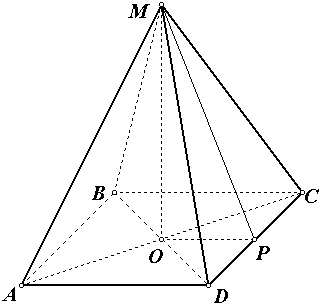
Решение .
1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2, а его периметр 8.
2) по условию = 16 т.е.
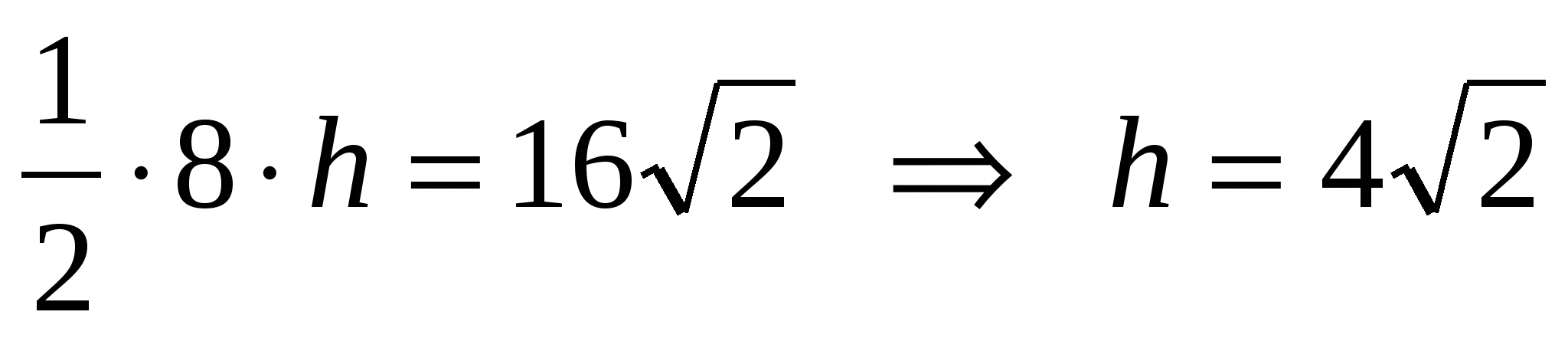 .
.
3) из прямоугольного треугольника
МОР
по теореме Пифагора находим высоту: , учитывая, что ОР = 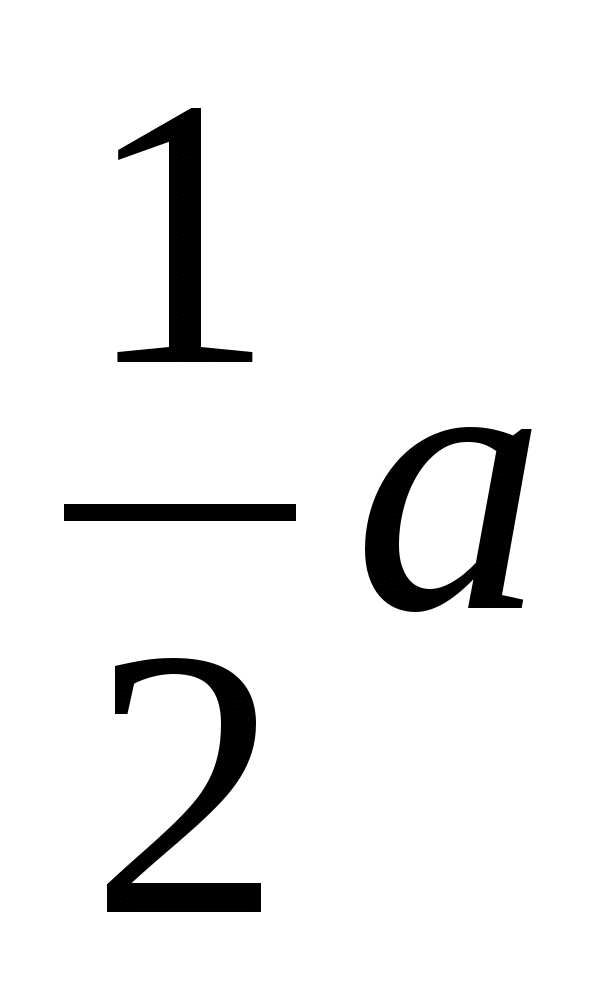 = 1, получаем: МО =
= 1, получаем: МО = 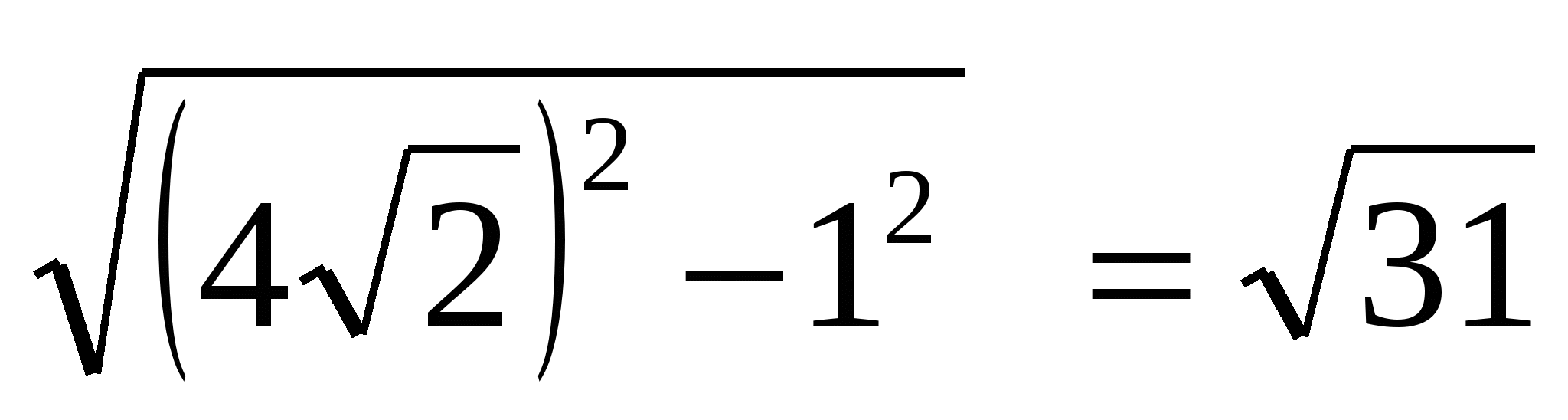 .
.
Ответ. 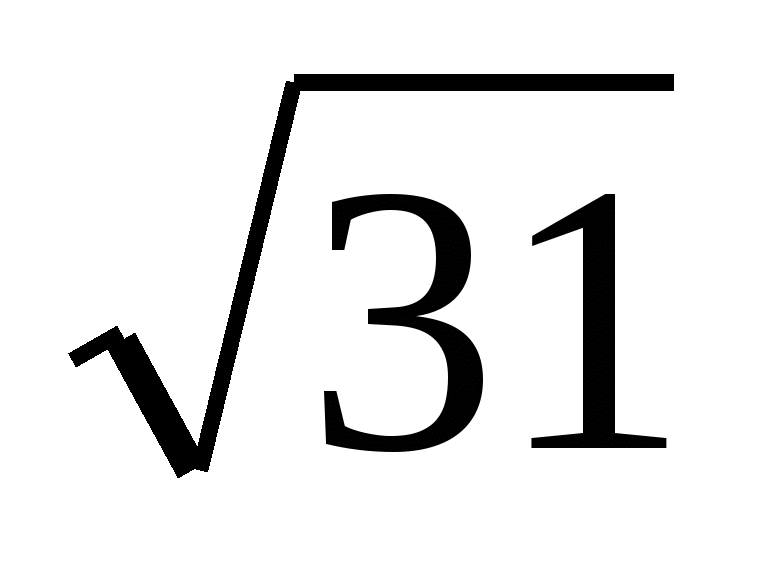 .
.

Задача №8
. Вычислите объём правильной шестиугольной пирамиды, если сторона основания равна 4, а боковые ребра пирамиды равны 5.
Решение.
1) сторона основания правильного шестиугольника равна радиусу описанной около него окружности т.е. 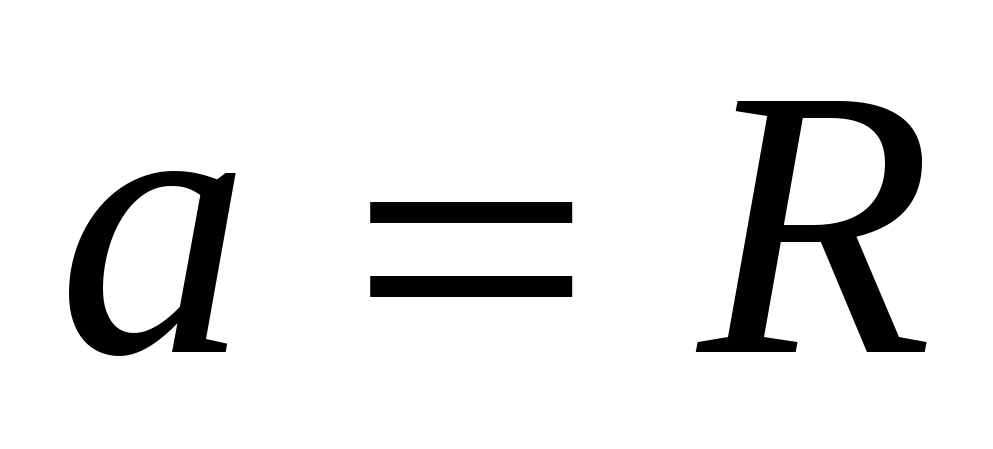 ,
, 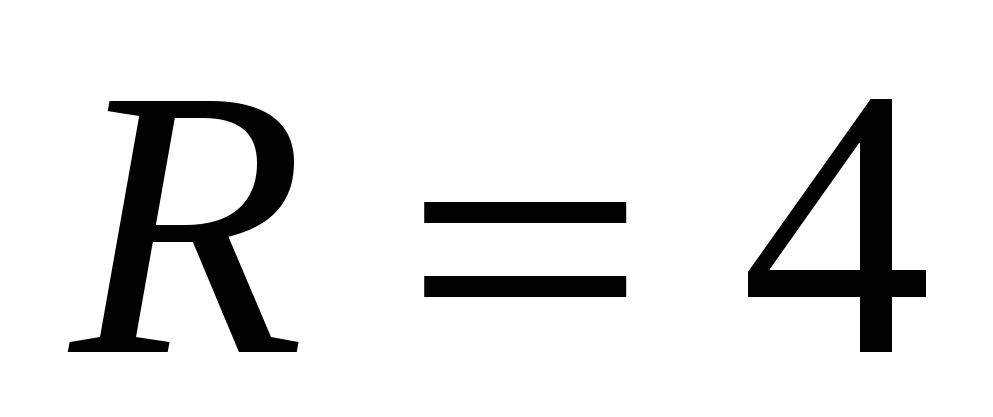
2) площадь правильного шестиугольника найдем по формуле 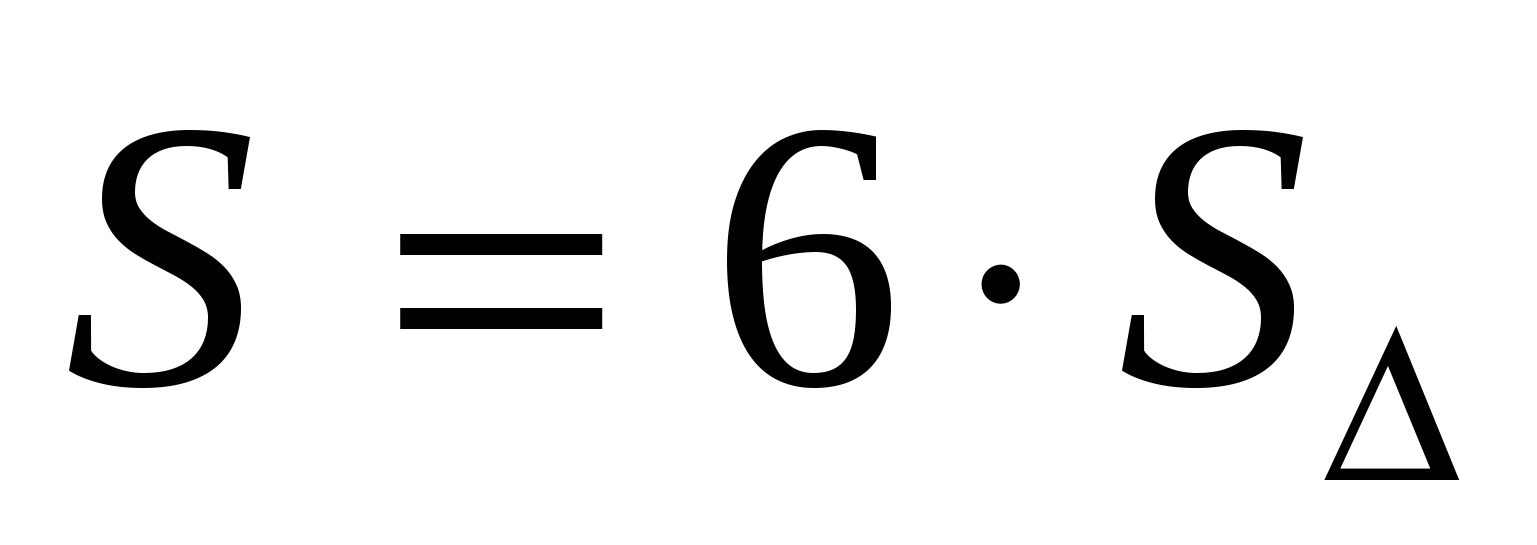 или
или 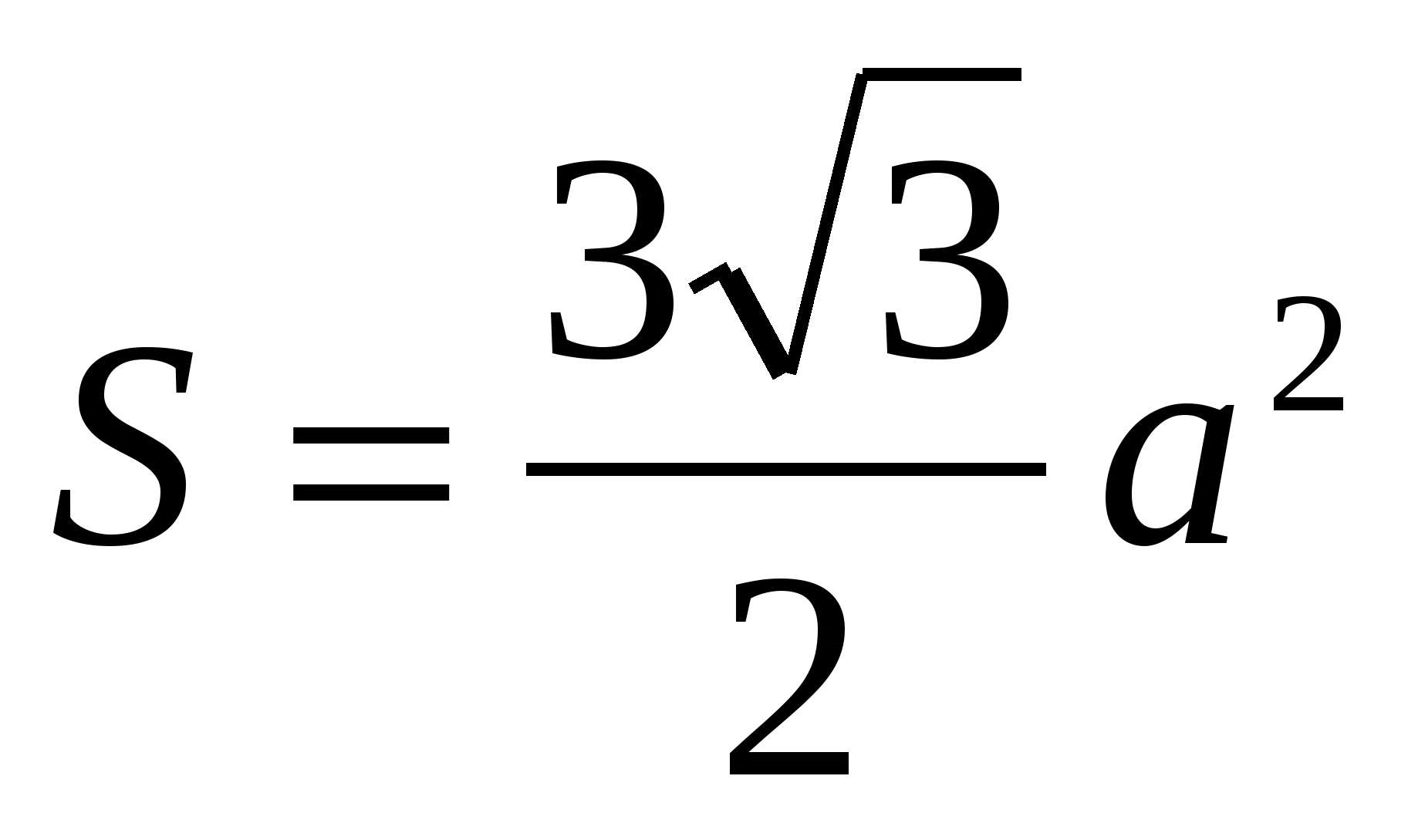 = 24.
= 24.
3) из прямоугольного треугольника МОВ найдем высоту МО : .
4) вычисляем объём пирамиды: =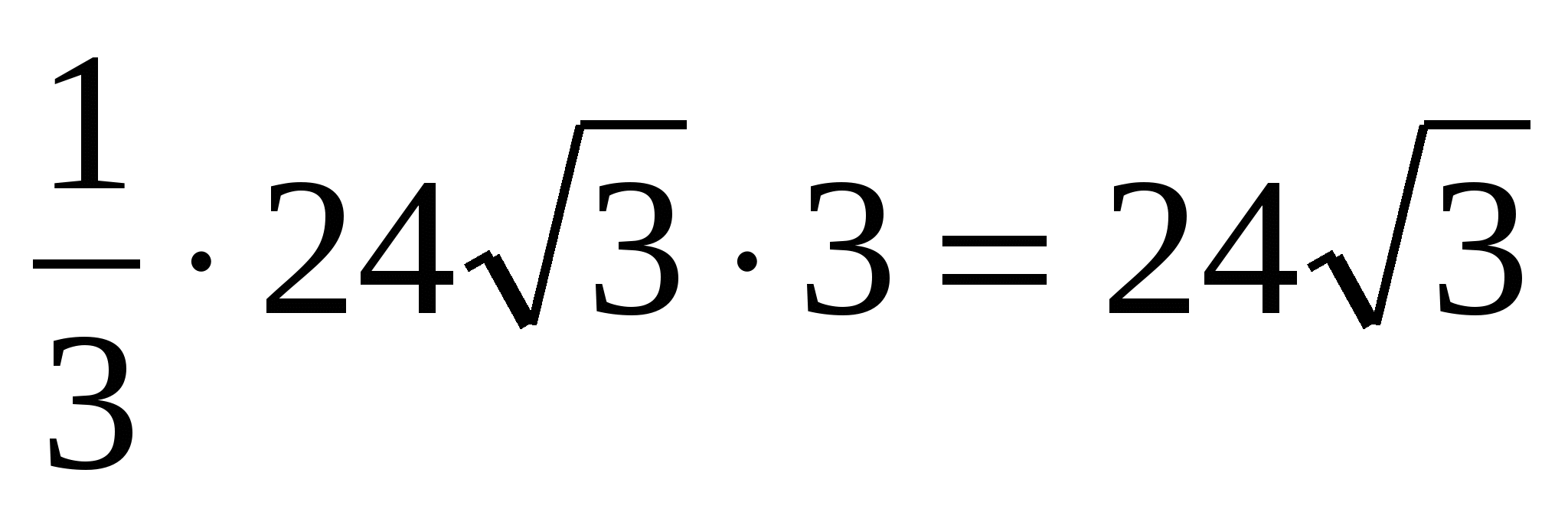 .
.
Ответ. 24.
Задача №9 . В правильной шестиугольной пирамиде сторона основания равна 2, а боковое ребро равно 2. Найдите объём пирамиды.
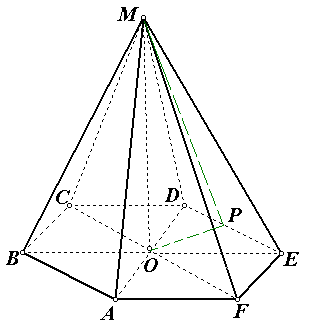
Решение.
1) найдем площадь правильного шестиугольника по формуле или = 12.
2) из прямоугольного треугольника МОВ найдем высоту МО, учитывая, что в правильном шестиугольнике : .
3) вычисляем объём пирамиды: =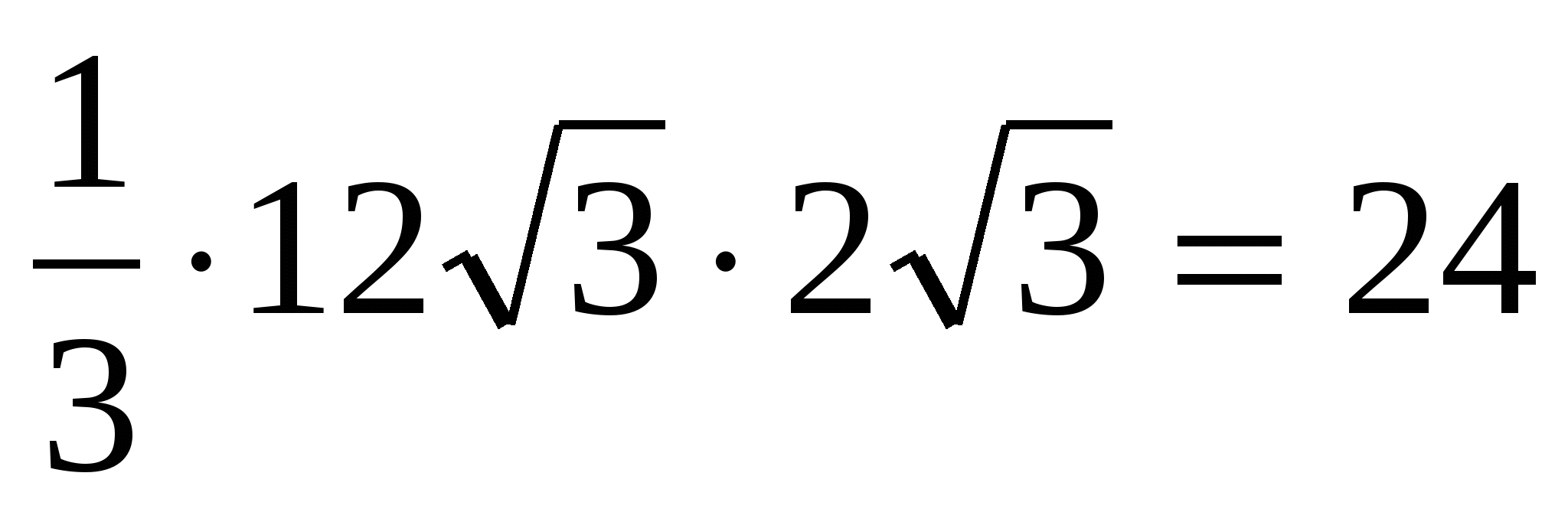 .
.
Ответ: 24.
Задача № 10 . Около правильной треугольной призмы описан цилиндр. Высота цилиндра равна 5, а радиус его основания R удовлетворяет уравнению R 2 + R – 6 = 0. Найдите объём призмы.
Р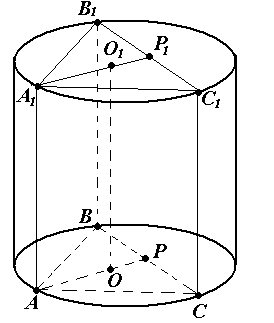 ешение.
V
= S
·
H
ешение.
V
= S
·
H
1) так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, Н = 5.
2) по условию R удовлетворяет уравнению R 2 + R – 6 = 0, решая которое находим
R 1 = - 3, R 2 = 2, так как радиус величина положительная то -3 не удовлетворяет условию задачи.
3) найдем сторону вписанного правильного треугольника по формуле 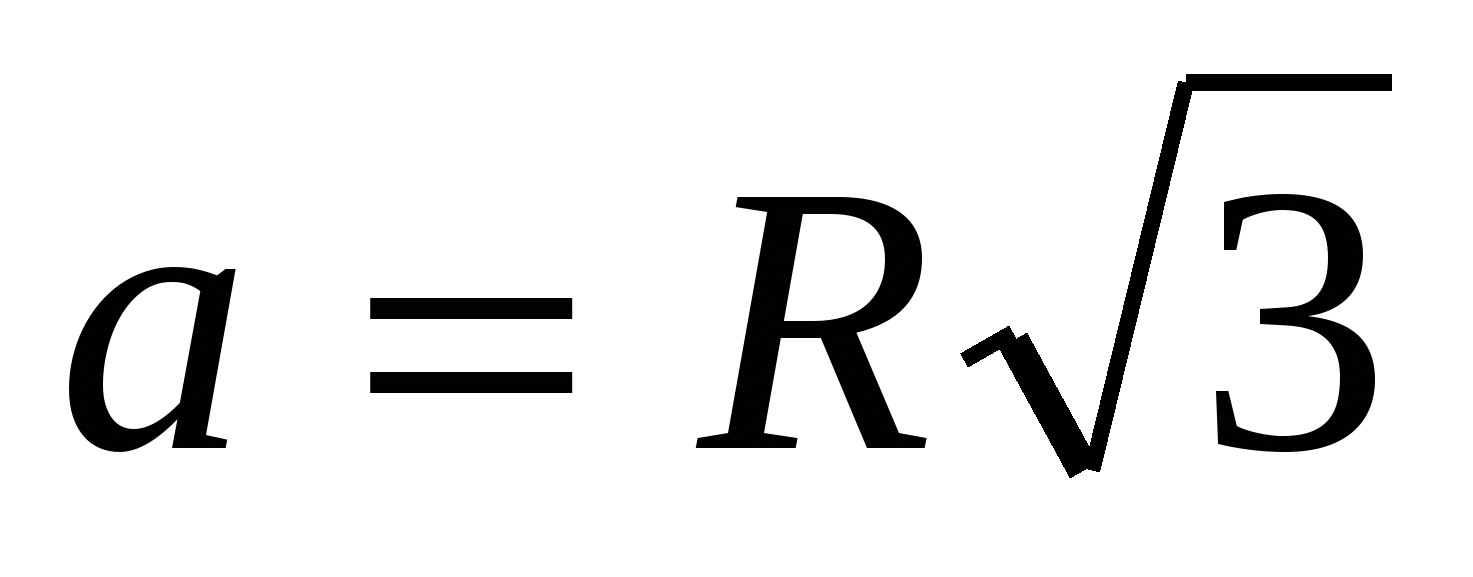 ,
, 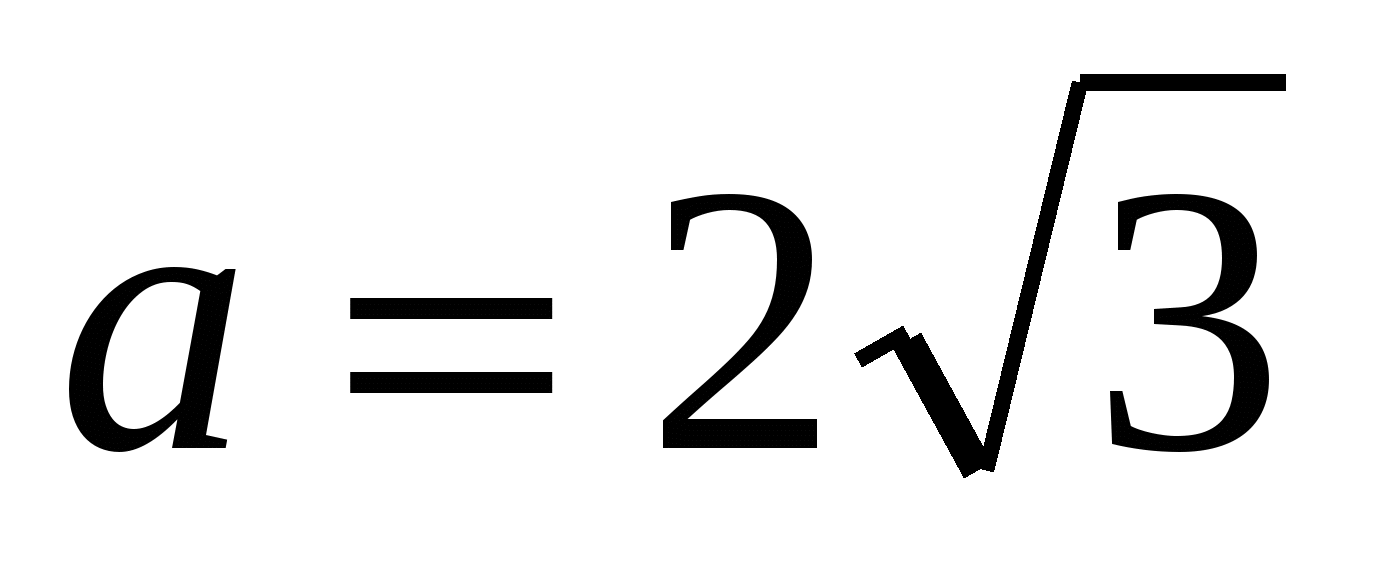 .
.
4) найдем площадь основания правильной призмы, как площадь правильного треугольника: 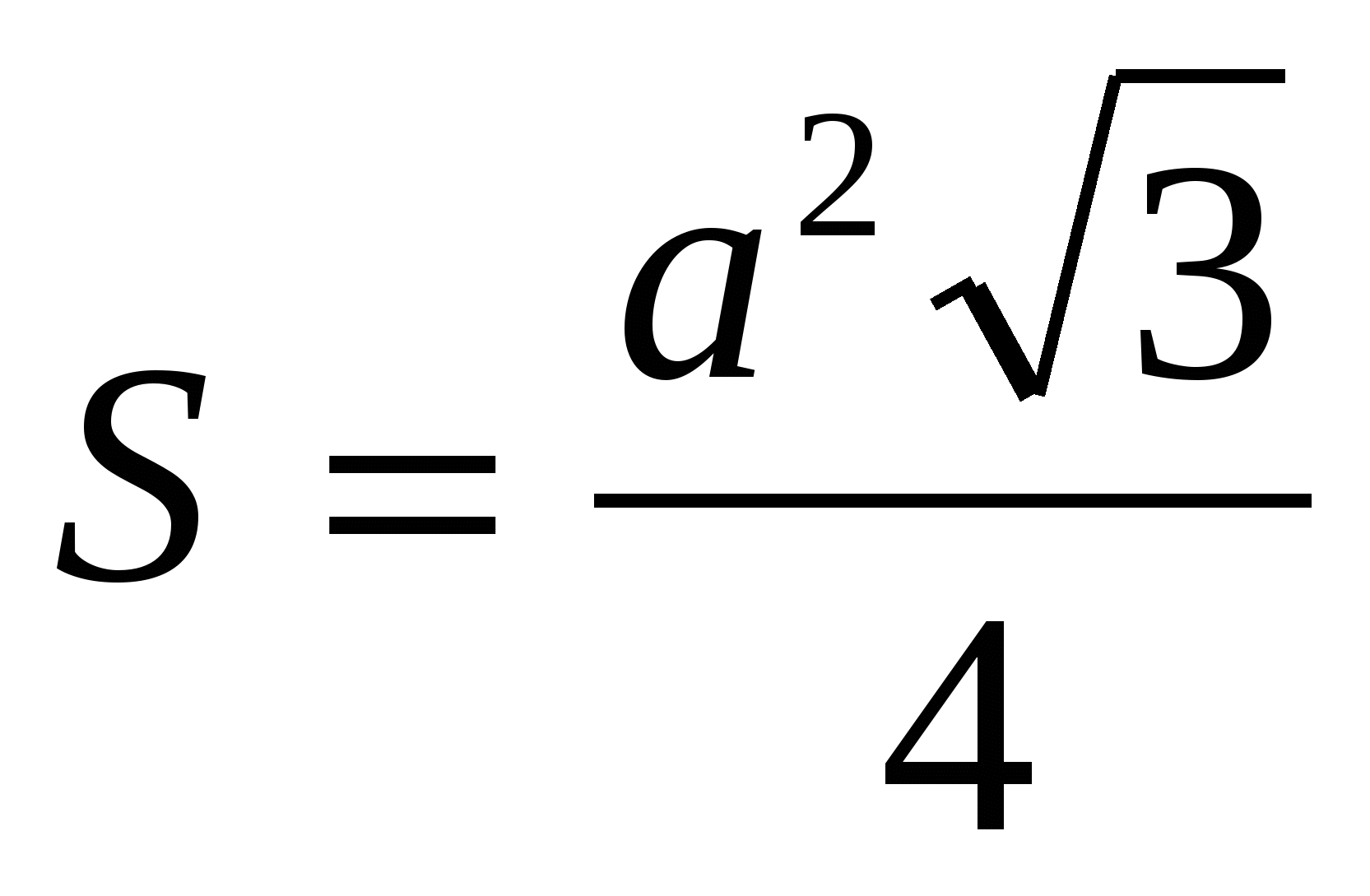 =
= 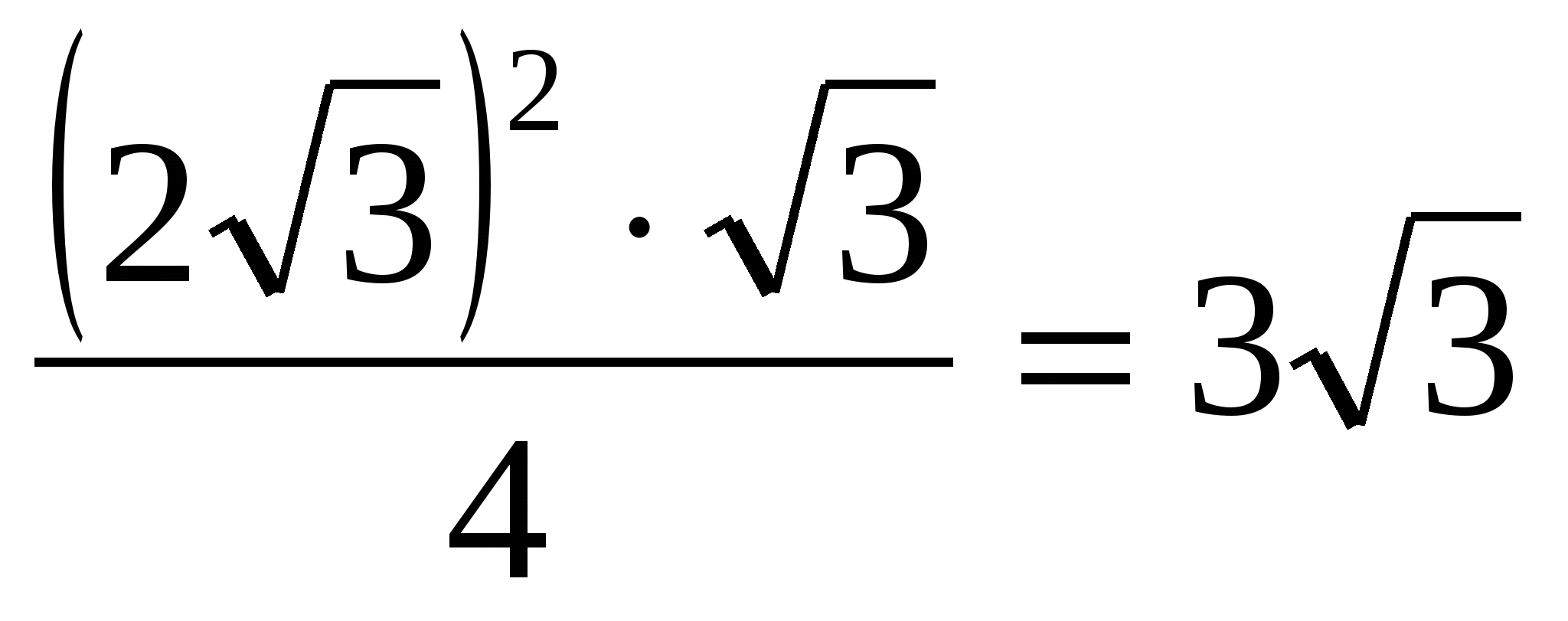
5) вычислим объём призмы:
V
=
S
·
H
=
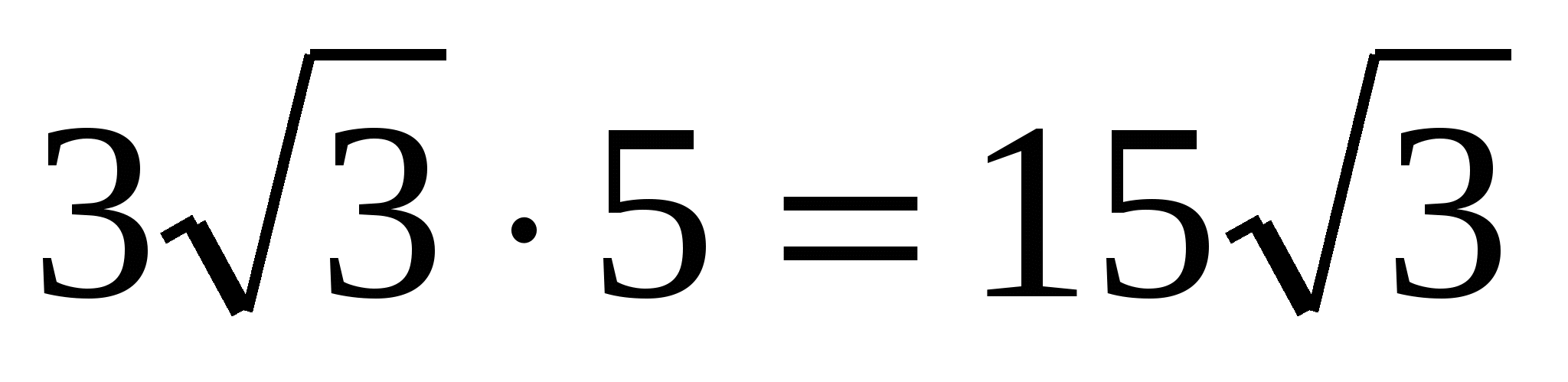 .
.
Ответ. 15.
Задача №11 . Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно . Высота цилиндра равна трем его радиусам. Найдите объём призмы.
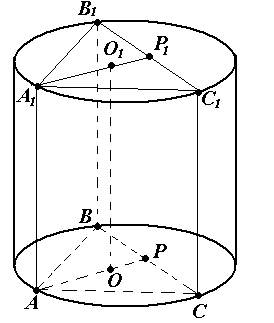
Решение. V = S · H
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, по условию Н = 3 R ..
2) Расстояние между осью цилиндра и стороной основания призмы равно радиусу вписанной в треугольник
АВС
окружности, т.е. 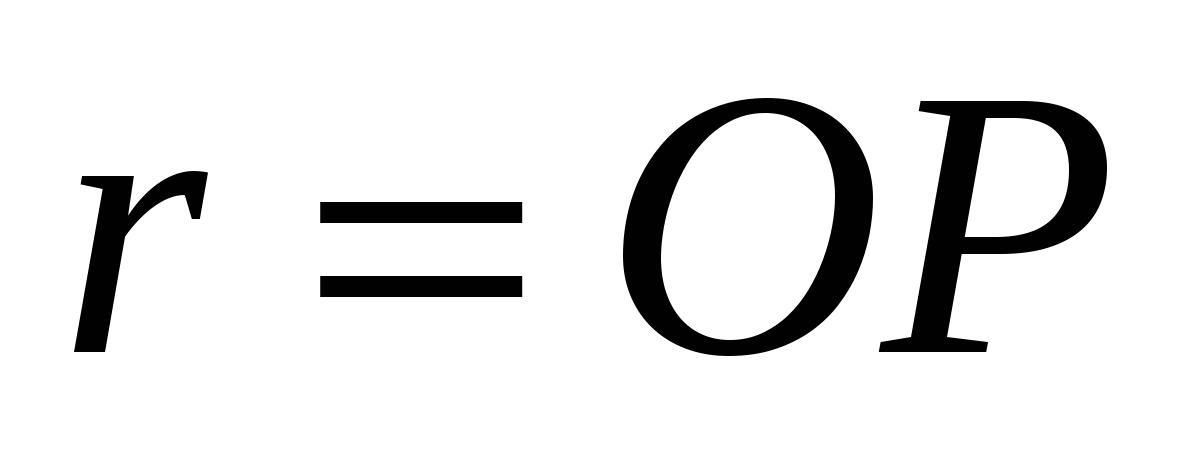 , и по условию равно .
, и по условию равно .
3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .
4) найдем сторону вписанного правильного треугольника по формуле , 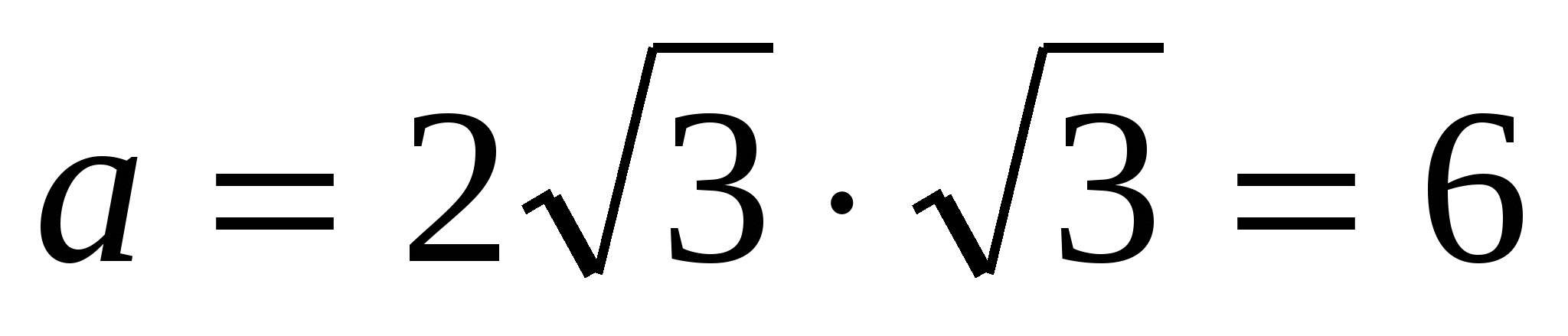 .
.
5) найдем площадь основания правильной призмы, как площадь правильного треугольника: = 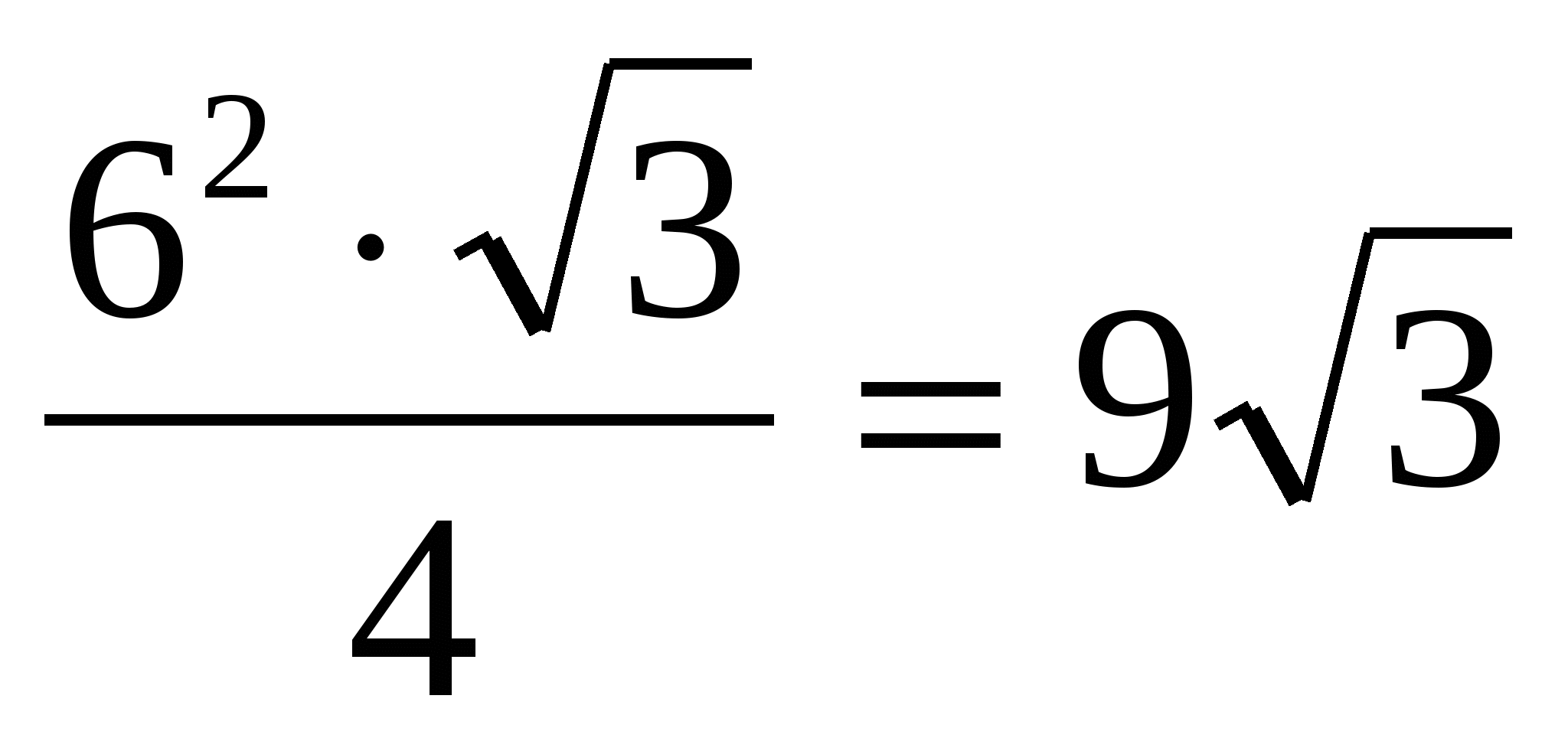
6) вычислим объём призмы:
V
=
S
·
H
=
S
·
3
·
R
=
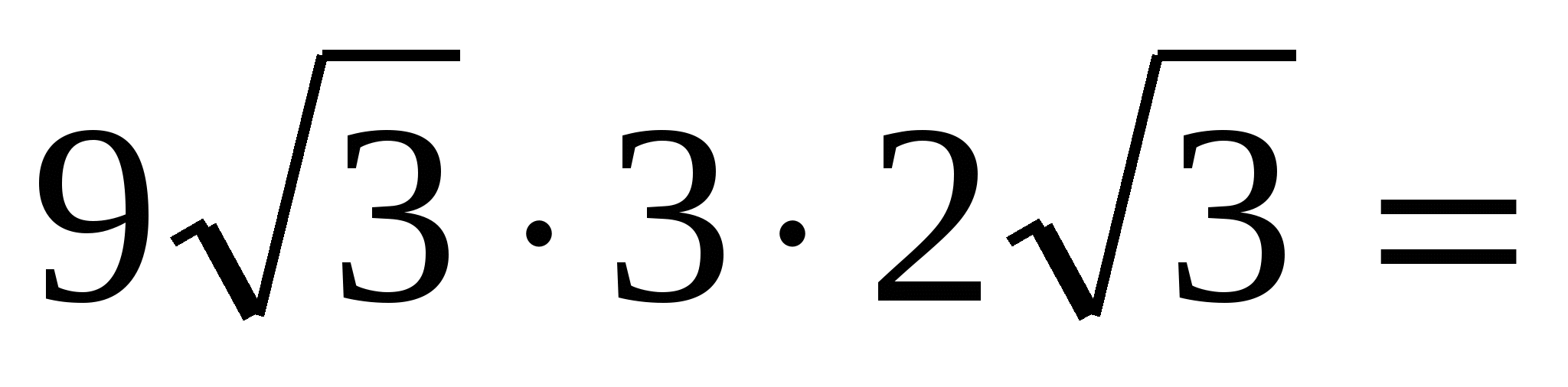 162.
162.
Ответ. 162.
Задача №12 . Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16 . Найдите объём призмы, если сторона её основания равна 5.
Решение . V = S · H
2) Найдем площадь основания правильной призмы, как площадь правильного треугольника: =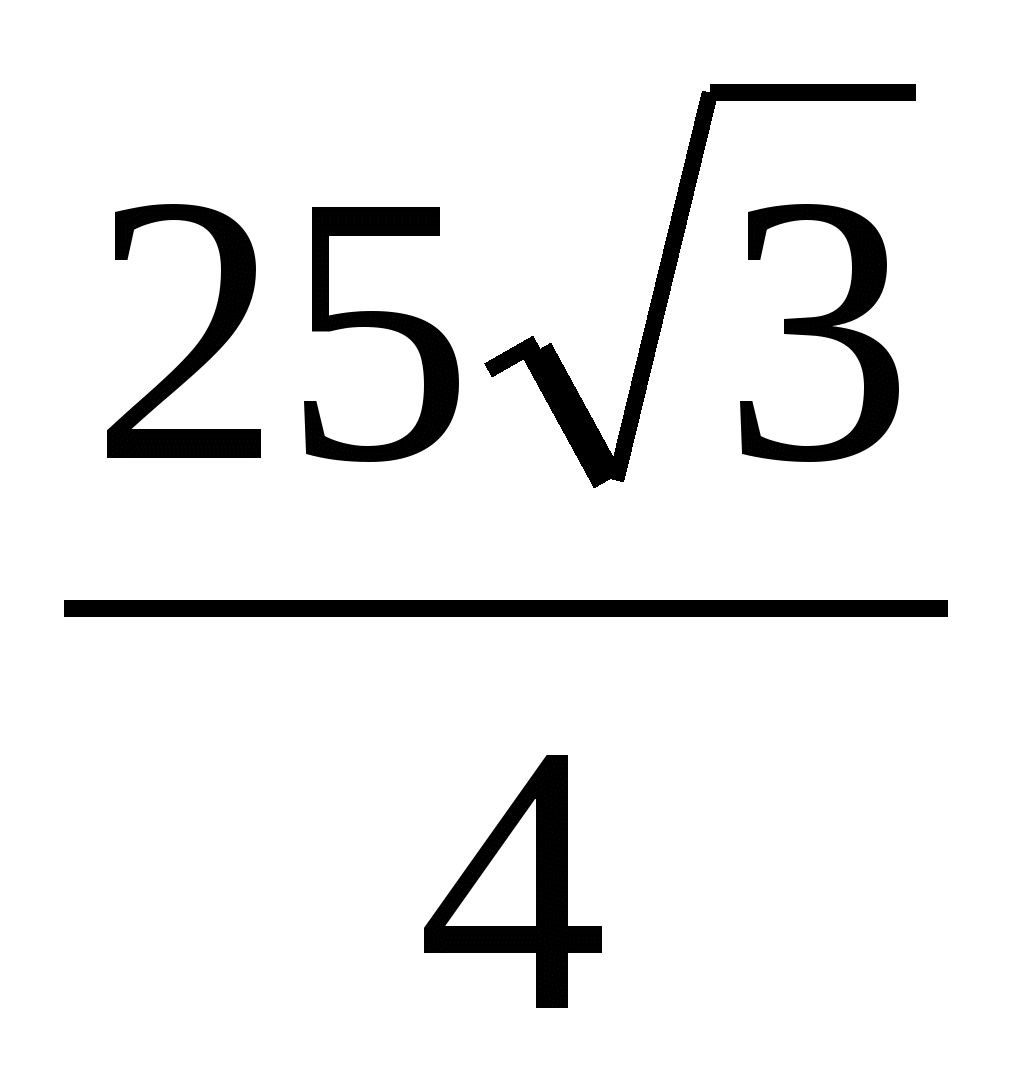 .
.
3) Сторона вписанного правильного треугольника находится по формуле , тогда 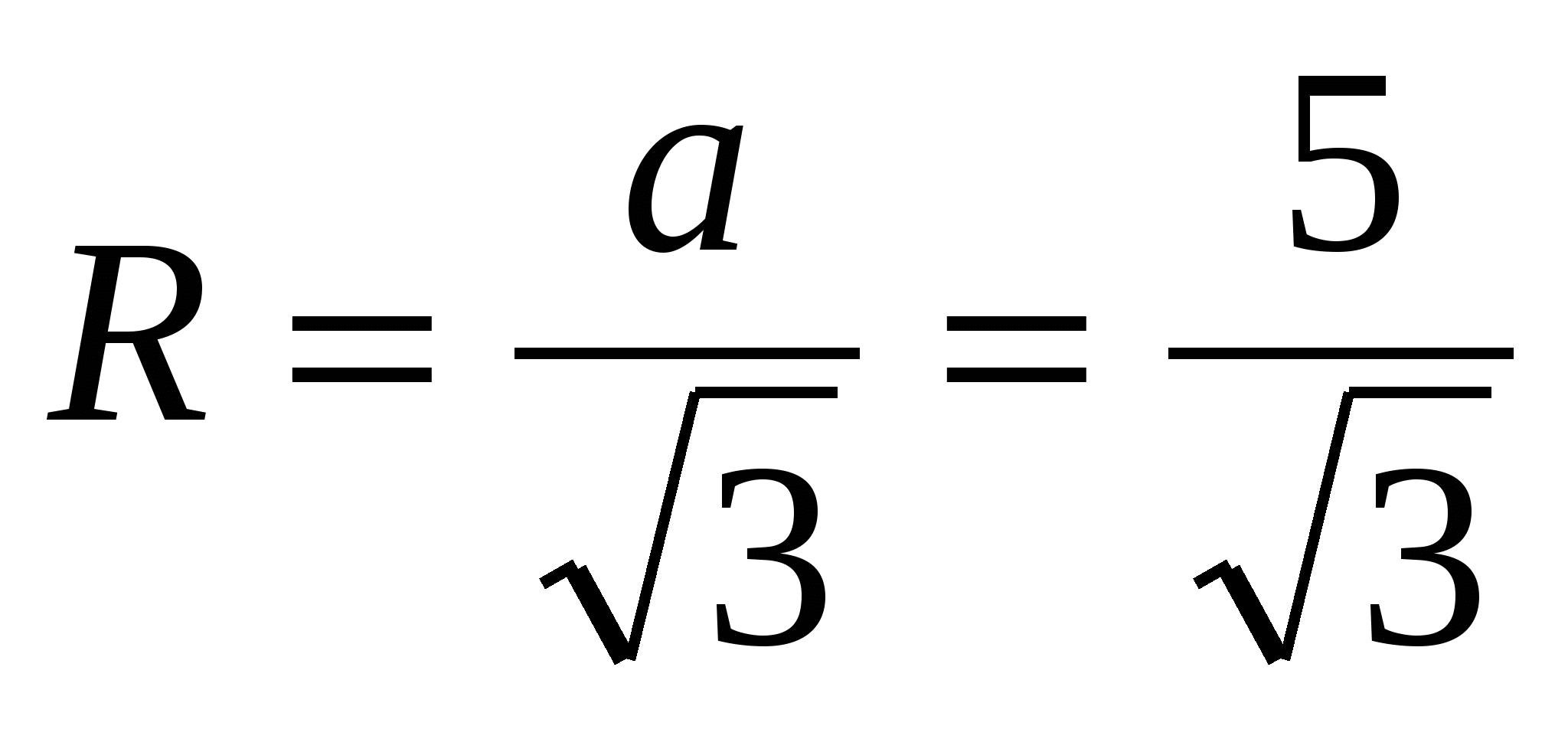 .
.
4) По условию площадь боковой поверхности цилиндра равна 16
·
т.е.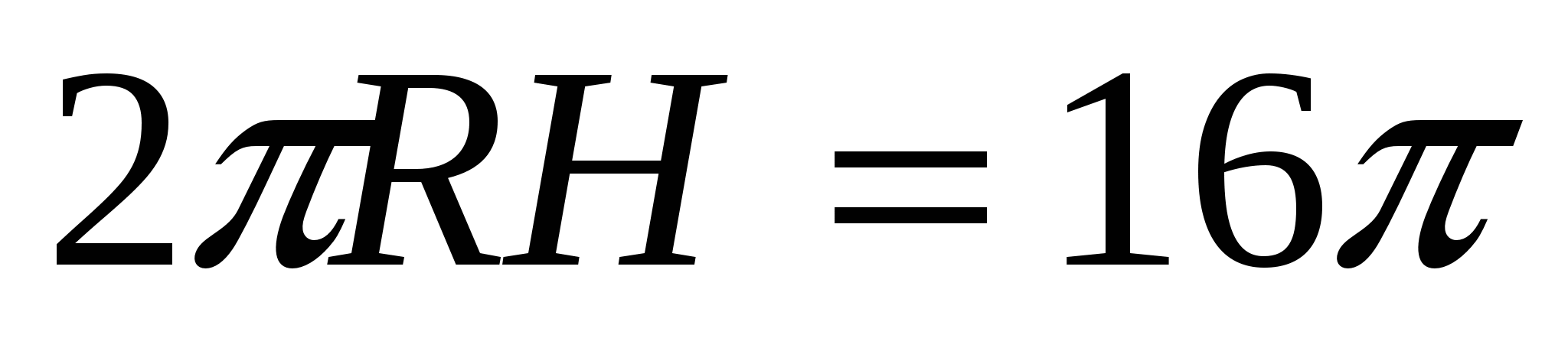 , откуда
Н
=
, откуда
Н
= 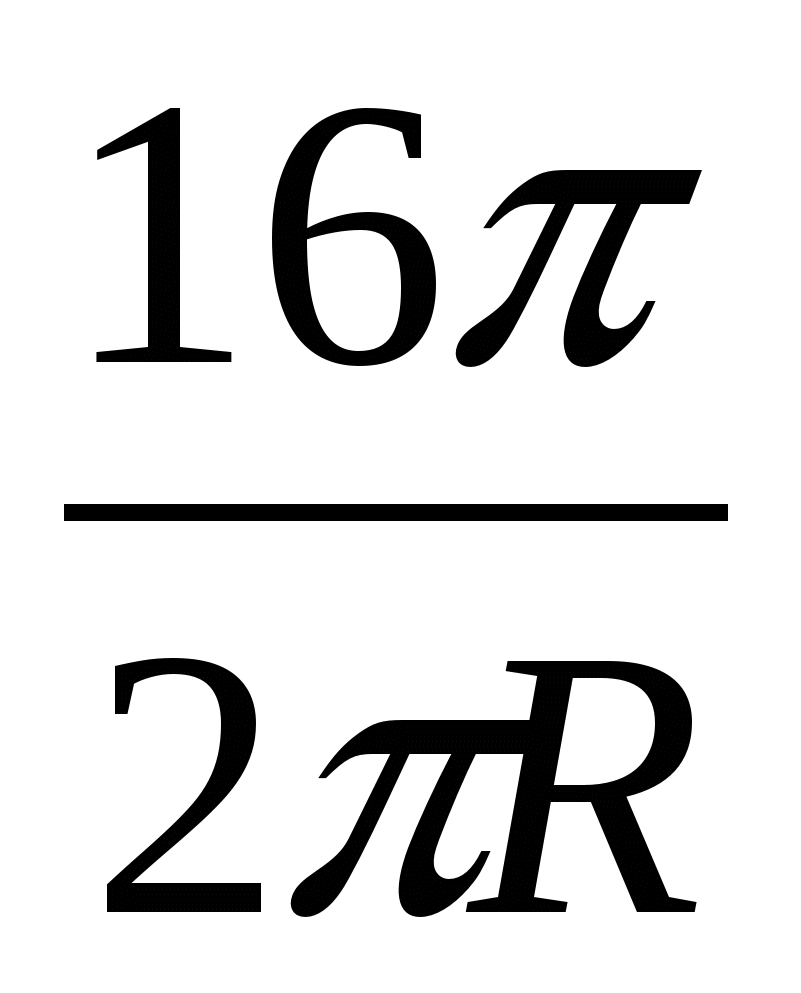 =
= 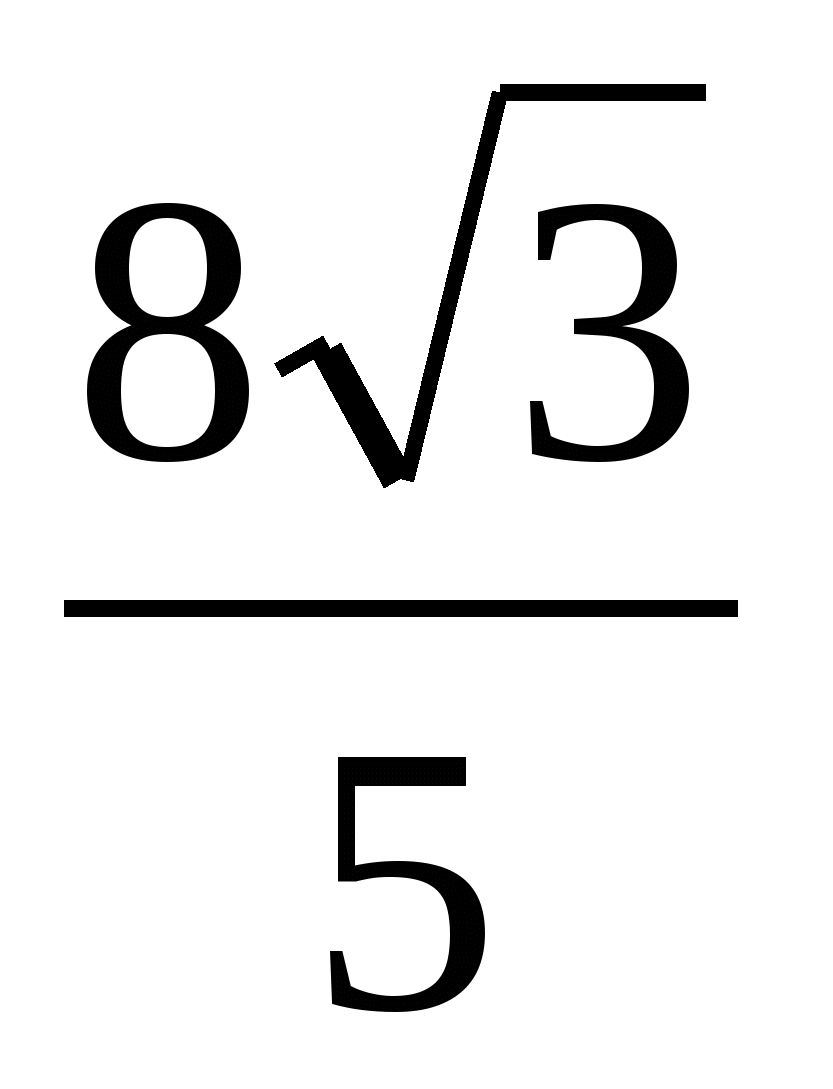 .
.
5) Вычислим объём призмы: V = S · H = · = 30.
Ответ. 30.
Задача №13 . Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20 . Найдите площадь боковой поверхности призмы.
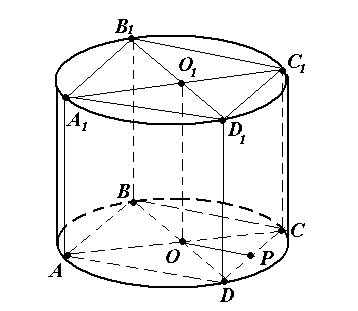 Решение.
Решение. 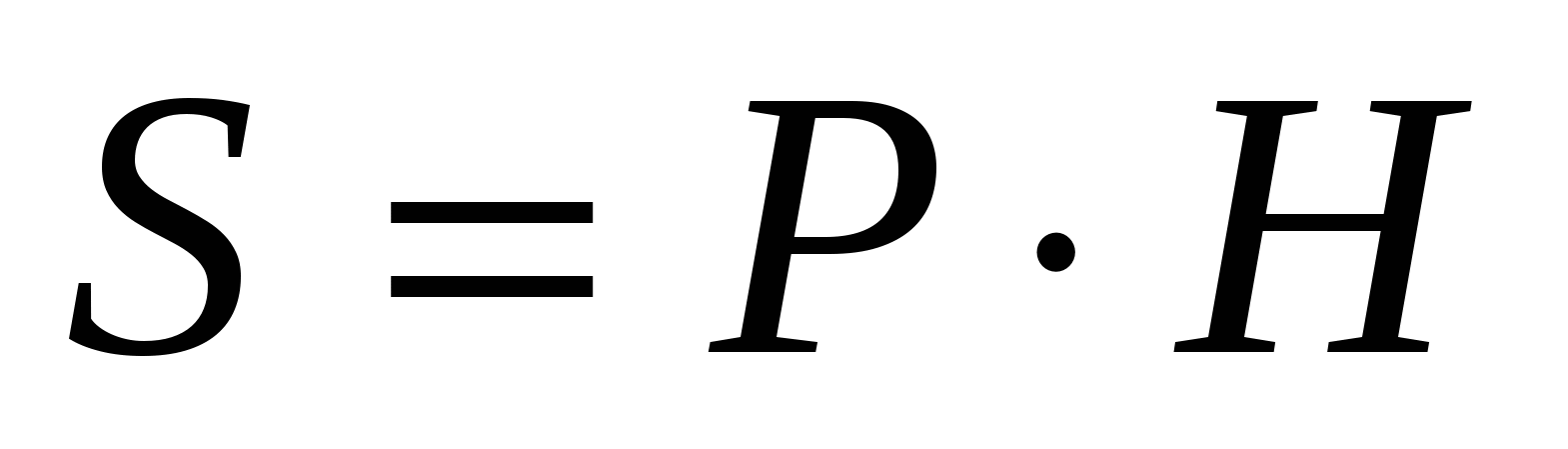
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра.
2) По условию площадь боковой поверхности цилиндра равна 20
, т.е. 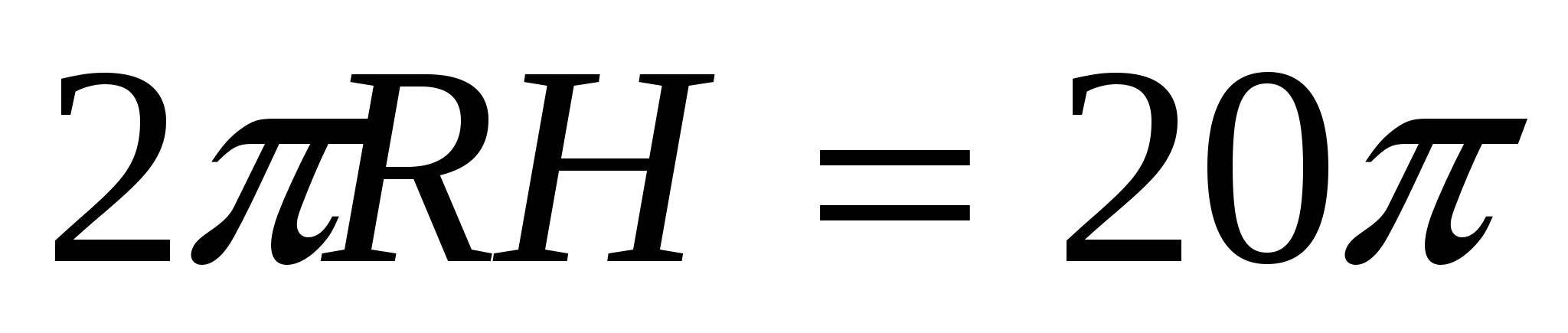 ,
, 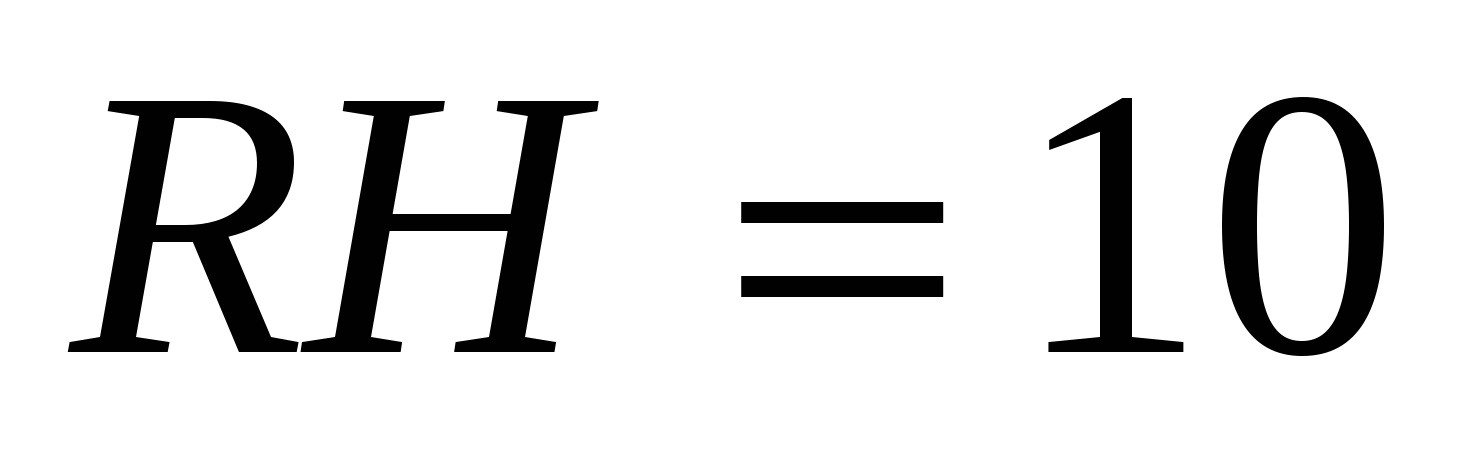 .
.
3) так как призма правильная, то в её основании лежит квадрат, со стороной 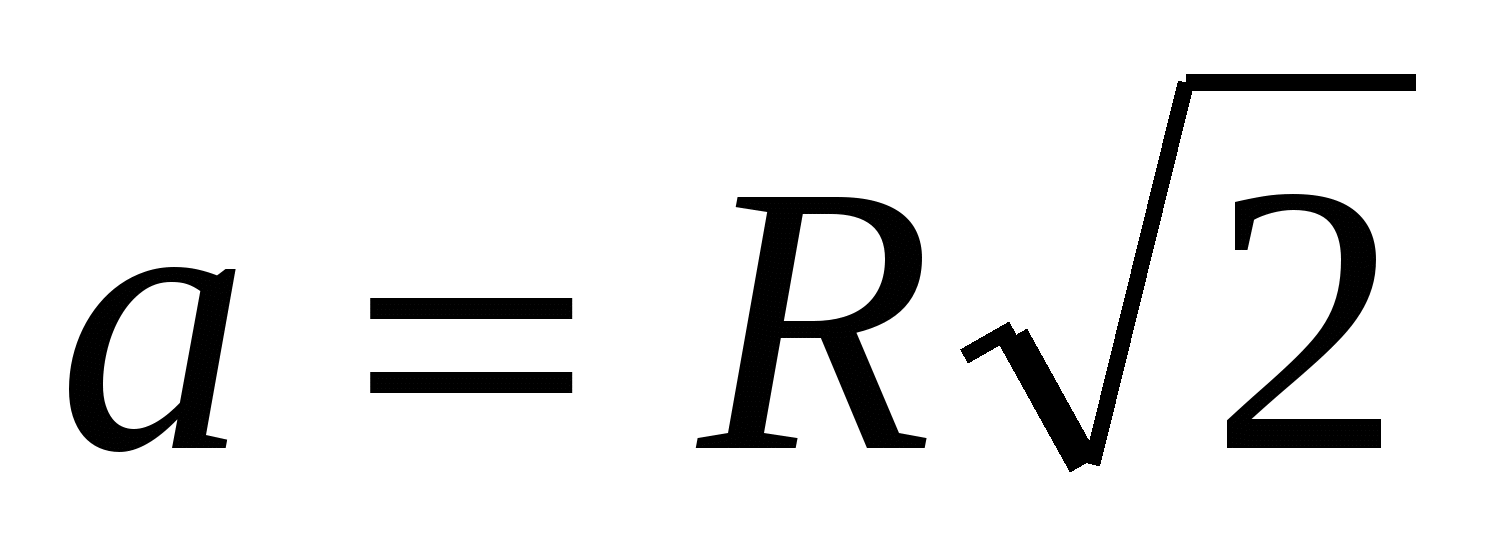 , тогда периметр основания равен
, тогда периметр основания равен 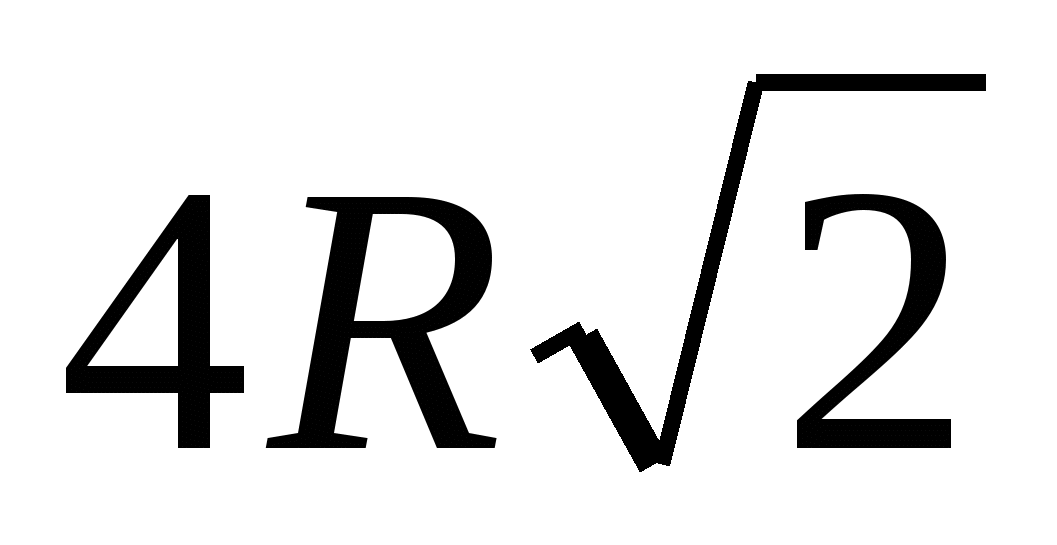 .
.
4) вычислим площадь боковой поверхности призмы = .
, т.е.
– 36 а
·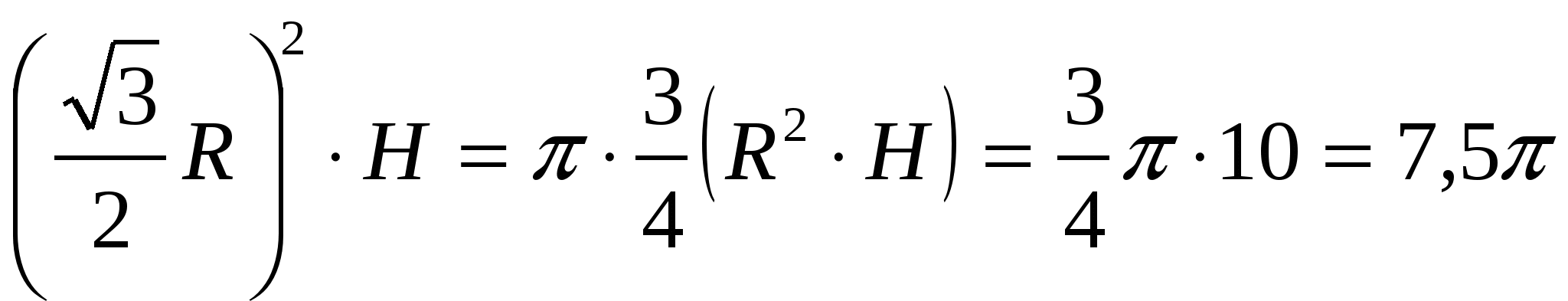 .
.
Ответ. 7,5 .
Чудаева Е.В., МОУ «Инсарская СОШ №1», г. Инсар, Республика Мордовия
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
(по материалам ЕГЭ)
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача № 10 R удовлетворяет уравнению R 2 + R – 6 = 0. Найдите объём призмы.
Задача №11
Задача №12
Задача №13
Задача №14 . В правильную четырехугольную призму вписан цилиндр. Объем цилиндра равен 16 , а радиус окружности, описанной вокруг основания призмы, равен . Найдите диагональ призмы.
Задача №15 . В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если её площадь равна 54 , а радиус цилиндра равен 3.
Задача № 16
. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 16
, высота цилиндра равна 4. Найдите объём призмы.
Задача №17 . Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 10 . Найдите объём цилиндра, вписанного в эту же призму.
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
(по материалам ЕГЭ)
Задача №1 . Вычислите объём правильной треугольной пирамиды, если радиус описанной вокруг основания окружности равен , а высота пирамиды равна 4.
Решение.
3) вычислим объём пирамиды
Ответ. 9
Задача №2 . Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен , а боковые ребра пирамиды равны 6.
Решение.
4) из прямоугольного треугольника по теореме Пифагора находим высоту пирамиды: , .
5) вычислим объём пирамиды
Ответ. 18.
Задача №3 . Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен , а высота пирамиды равны 1.
Решение.
1) найдем сторону основания правильной пирамиды по формуле , .
2) найдем периметр основания Р = 3· а ,
Р = 9.
4) из прямоугольного треугольника МОР МР : ,
МР =
5) вычислим площадь боковой поверхности правильной пирамиды:
Ответ. .
Задача №4 . Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна .
Решение. ,
1) найдем радиус описанной около основания и вписанной в основание окружностей: , то есть .
2) найдем площадь основания, как площадь правильного треугольника , .
МОР по теореме Пифагора находим высоту: , МО = .
Ответ. 18.
Задача №5 . Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 2, а высота правильной пирамиды равна .
Решение.
1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .
2) найдем сторону основания правильной пирамиды по формуле , .
3) найдем площадь основания, как площадь правильного треугольника , .
4) вычислим объём правильной пирамиды: = .
Ответ. 36.
Задача №6 . Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3.
Решение .
1) найдем сторону основания по формуле , т.е. .
2) найдем периметр основания: Р = 4а ,
Р = 24.
3) из прямоугольного треугольника М D Р по теореме Пифагора находим апофему МР : , DP =
тогда: МР = .
4) вычислим площадь боковой поверхности пирамиды: = .
Ответ. 48.
Задача №7 . В правильной четырехугольной пирамиде площадь боковой поверхности равна 16, а площадь основания 4. Найдите высоту пирамиды.
Решение .
1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2, а его периметр 8.
2) по условию = 16 т.е.
3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: , учитывая, что ОР = = 1, получаем: МО = .
Ответ. .
Задача №8
. Вычислите объём правильной шестиугольной пирамиды, если сторона основания равна 4, а боковые ребра пирамиды равны 5.
Решение.
1) сторона основания правильного шестиугольника равна радиусу описанной около него окружности т.е. ,
2) площадь правильного шестиугольника найдем по формуле или = 24.
3) из прямоугольного треугольника МОВ найдем высоту МО : .
4) вычисляем объём пирамиды: =.
Ответ. 24.
Задача №9 . В правильной шестиугольной пирамиде сторона основания равна 2, а боковое ребро равно 2. Найдите объём пирамиды.
Решение.
1) найдем площадь правильного шестиугольника по формуле или = 12.
2) из прямоугольного треугольника МОВ найдем высоту МО, учитывая, что в правильном шестиугольнике : .
3) вычисляем объём пирамиды: =.
Ответ: 24.
Задача № 10 . Около правильной треугольной призмы описан цилиндр. Высота цилиндра равна 5, а радиус его основания R удовлетворяет уравнению R 2 + R – 6 = 0. Найдите объём призмы.
Решение. V = S · H
1) так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, Н = 5.
2) по условию R удовлетворяет уравнению R 2 + R – 6 = 0, решая которое находим
R 1 = - 3, R 2 = 2, так как радиус величина положительная то -3 не удовлетворяет условию задачи.
3) найдем сторону вписанного правильного треугольника по формуле , .
4) найдем площадь основания правильной призмы, как площадь правильного треугольника: =
5) вычислим объём призмы:
V
=
S
·
H
=
.
Ответ. 15.
Задача №11 . Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно . Высота цилиндра равна трем его радиусам. Найдите объём призмы.
Решение. V = S · H
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, по условию Н = 3 R ..
2) Расстояние между осью цилиндра и стороной основания призмы равно радиусу вписанной в треугольник АВС окружности, т.е. , и по условию равно .
3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .
4) найдем сторону вписанного правильного треугольника по формуле , .
5) найдем площадь основания правильной призмы, как площадь правильного треугольника: =
6) вычислим объём призмы: V = S · H = S · 3 · R = 162.
Ответ. 162.
Задача №12 . Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16 . Найдите объём призмы, если сторона её основания равна 5.
Решение . V = S · H
2) Найдем площадь основания правильной призмы, как площадь правильного треугольника: =.
3) Сторона вписанного правильного треугольника находится по формуле , тогда .
4) По условию площадь боковой поверхности цилиндра равна 16 · т.е., откуда Н = = .
5) Вычислим объём призмы: V = S · H = · = 30.
Ответ. 30.
Задача №13 . Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20 . Найдите площадь боковой поверхности призмы.
Решение.
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра.
2) По условию площадь боковой поверхности цилиндра равна 20 , т.е. , .
3) так как призма правильная, то в её основании лежит квадрат, со стороной , тогда периметр основания равен .
4) вычислим площадь боковой поверхности призмы = . , а радиус цилиндра равен 3. , высота цилиндра равна 4. Найдите объём призмы. .
5) запишем формулу вычисления объёма вписанного в призму цилиндра: V = S · H , т.е.:
V = = ·.
Ответ. 7,5 .
