Продовжуємо розглядати завдання, що входять до ЄДІ з математики. Ми вже досліджували завдання, де в умові дано і потрібно визначити відстань між двома даними точками чи кут.
У цій статті ми з вами розглянемо завдання на вирішення правильної піраміди. Це піраміди в основі яких лежить правильний багатокутник(у поданих задачах рівносторонній трикутникчи квадрат).
Потрібно знайти якийсь елемент, площу бічної поверхні, об'єм, висоту. Зрозуміло, необхідно знати теорему Піфагора, формулу площі бічної поверхні піраміди, формулу знаходження обсягу піраміди.
у статті « » представлені всі формули, які потрібні для вирішення. Отже, завдання:
SABCDкрапка O- центр основи,Sвершина, SO = 51, AC= 136. Знайдіть бічне реброSC.
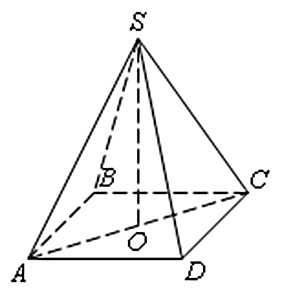
У даному випадкув основі лежить квадрат. Це означає, що діагоналі AC і BD рівні, вони перетинаються і точкою перетину діляться навпіл. Зазначимо, що в правильної пірамідівисота опущена з її вершини проходить через центр основи піраміди. Таким чином, SO є висотою, а трикутникSOCпрямокутний. Тоді за теоремою Піфагора:
Як видобувати корінь з великої кількості.
Відповідь: 85
Вирішіть самостійно:
У правильній чотирикутній піраміді SABCDкрапка O- центр основи, Sвершина, SO = 4, AC= 6. Знайдіть бічне ребро SC.
У правильній чотирикутній піраміді SABCDкрапка O- центр основи, Sвершина, SC = 5, AC= 6. Знайдіть довжину відрізка SO.
У правильній чотирикутній піраміді SABCDкрапка O- центр основи, Sвершина, SO = 4, SC= 5. Знайдіть довжину відрізка AC.
SABC R- середина ребра BC, S- Вершина. Відомо що AB= 7, а SR= 16. Знайдіть площу бічної поверхні.
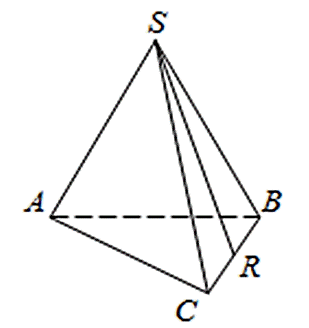
Площа бічної поверхні правильної трикутної піраміди дорівнює половині добутку периметра основи апофему (апофема це висота бічної грані правильної піраміди, проведена з її вершини):
Або можна сказати так: площа бічної поверхні піраміди дорівнює сумі площ трьохбічних граней. Боковими гранями у правильній трикутній піраміді є рівні за площею трикутники. В даному випадку:
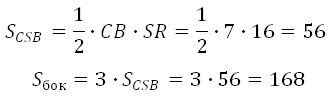
Відповідь: 168
Вирішіть самостійно:
У правильній трикутній піраміді SABC R- середина ребра BC, S- Вершина. Відомо що AB= 1, а SR= 2. Знайдіть площу бічної поверхні.
У правильній трикутній піраміді SABC R- середина ребра BC, S- Вершина. Відомо що AB= 1, а площа бічної поверхні дорівнює 3. Знайдіть довжину відрізка SR.
У правильній трикутній піраміді SABC L- середина ребра BC, S- Вершина. Відомо що SL= 2, а площа бічної поверхні дорівнює 3. Знайдіть довжину відрізка AB.
Завдання 14.У правильній чотирикутній піраміді SABCDз вершиною S сторона основи дорівнює 6. Точка L – середина ребра SC. Тангенс кута між прямими BL та SA дорівнює 2.
а) Нехай O – центр основи піраміди. Доведіть, що прямі AS та OL паралельні.
б) Знайдіть площу поверхні піраміди.
Рішення.
а)У основі правильної піраміди лежить квадрат, тобто ABCD – квадрат. Діагоналі у квадраті перетинаються у точці O і діляться цією точкою навпіл. Крапка L – середина SC за умовою завдання. Звідси випливає, що OL – середня лінія трикутника SAC і, отже, і .
б)Спочатку знайдемо довжину бічного ребра AS. Враховуючи пункт а) можна зробити висновок, що в задачі дано значення 
(Див. малюнок). Розглянемо рівнобедрений трикутник DLB (оскільки DL=LB), у якому точка O лежить у середині BD, отже, LO – медіана і висота трикутника DLB, тобто і трикутник LOB – прямокутний. Тоді можна записати, що
.
У свою чергу OB дорівнює половині BD і прямокутного трикутника BDC за теоремою Піфагора, маємо:
.
У пункті а) було показано, що , тобто
9 березня 2012
Вирішуючи завдання C2 методом координат, багато учнів стикаються з однією проблемою. Вони не можуть розрахувати координати точок, що входять до формули скалярного твору. Найбільші труднощі викликають піраміди. І якщо точки основи вважаються більш-менш нормально, то вершини – справжнє пекло.
Сьогодні ми займемося правильною чотирикутною пірамідою. Є ще трикутна піраміда (вона ж - тетраедр). Це більше складна конструкціятому їй буде присвячений окремий урок.
Для початку згадаємо визначення:
Правильна піраміда - це така піраміда, у якої:
- В основі лежить правильний багатокутник: трикутник, квадрат тощо;
- Висота, проведена до основи, проходить через його центр.
Зокрема, основою чотирикутної піраміди є квадрат. Прямо як у Хеопса, тільки трохи менше.
Нижче наведені розрахунки для піраміди, у якої всі ребра дорівнюють 1. Якщо у вашому завданні це не так, викладки не змінюються - просто числа будуть іншими.
Вершини чотирикутної піраміди
Отже, нехай дана правильна чотирикутна піраміда SABCD, де S – вершина, основа ABCD – квадрат. Усі ребра дорівнюють 1. Потрібно ввести систему координат і знайти координати всіх точок. Маємо:
Вводимо систему координат з початком у точці A:
- Вісь OX спрямована паралельно ребру AB;
- Ось OY - паралельно AD. Оскільки ABCD - квадрат, AB ⊥ AD;
- Нарешті, вісь OZ направимо вгору, перпендикулярно площині ABCD.
Тепер рахуємо координати. Додаткова побудова: SH – висота, проведена до основи. Для зручності винесемо основу піраміди на окремий малюнок. Оскільки точки A, B, C і D лежать у площині OXY, їх координата z = 0. Маємо:
- A = (0; 0; 0) - збігається з початком координат;
- B = (1; 0; 0) - крок на 1 по осі OX від початку координат;
- C = (1; 1; 0) - крок на 1 по осі OX і на 1 по осі OY;
- D = (0; 1; 0) - крок тільки по осі OY.
- H = (0,5; 0,5; 0) – центр квадрата, середина відрізка AC .
Залишилося знайти координати точки S. Зауважимо, що координати x і y точок S і H збігаються, оскільки вони лежать на прямій, паралельної осі OZ. Залишилося знайти координату z для точки S.
Розглянемо трикутники ASH і ABH:
- AS = AB = 1 за умовою;
- Кут AHS = AHB = 90°, оскільки SH – висота, а AH ⊥ HB як діагоналі квадрата;
- Сторона AH – загальна.
Отже, прямокутні трикутники ASH та ABH рівніпо одному катету та гіпотенузі. Значить, SH = BH = 0,5 · BD. Але BD – діагональ квадрата зі стороною 1. Тому маємо:
Разом координати точки S:
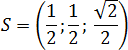
На закінчення випишемо координати всіх вершин правильної прямокутної піраміди:
Що робити, коли ребра різні
А якщо бічні ребра піраміди не рівні ребрам основи? У цьому випадку розглянемо трикутник AHS:
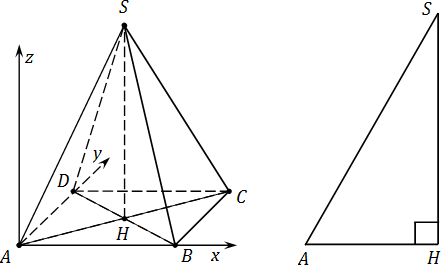
Трикутник AHS - прямокутний, Причому гіпотенуза AS - це одночасно і бічне ребро вихідної піраміди SABCD. Катет AH легко вважається: AH = 0,5 · AC. катет SH, що залишився, знайдемо за теоремою Піфагора. Це буде координата z для точки S .
Завдання. Дано правильну чотирикутну піраміду SABCD , в основі якої лежить квадрат зі стороною 1. Бокове ребро BS = 3. Знайдіть координати точки S .
Координати x та y цієї точки ми вже знаємо: x = y = 0,5. Це випливає із двох фактів:
- Проекція точки S на площину OXY - це точка H;
- Одночасно точка H - центр квадрата ABCD, всі сторони якого 1.
Залишилося знайти координату точки S. Розглянемо трикутник AHS. Він прямокутний, причому гіпотенуза AS = BS = 3, катет AH – половина діагоналі. Для подальших обчислень нам знадобиться його довжина:
Теорема Піфагора для трикутника AHS: AH2 + SH2 = AS2. Маємо:
Отже, координати точки S :
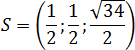
У правильній чотирикутній піраміді SABCD точка О - центр основи, SD = 26, AC = 20. Знайдіть довжину відрізка SO.
Рішення завдання
У відео уроці представлено обчислювальне завдання з ЄДІ (В13) на знаходження бічного ребра чотирикутної піраміди. При розв'язанні задачі згадується, що висотою у правильній чотирикутній піраміді є відрізок, який з'єднує вершину цієї піраміди з центром основи. Використовується поняття правильної чотирикутної піраміди. Це піраміда, у якої основою є квадрат, а бічні ребрарівні. Робиться висновок, що точка в центрі квадрата поділяє діагональ на дві рівні частини. Розглядається прямокутний трикутник. Для знаходження катета в прямокутному трикутникувикористовується теорема Піфагора: квадрат гіпотенузи дорівнює суміквадратів катетів. Виражається потрібна величина.
Розв'язання цього завдання призначений для учнів 10 класу щодо теми: «Правильна піраміда» (Поняття правильної піраміди. Розв'язання задач). Навчальний відео урок буде корисним учням 11 класу під час підготовки до ЄДІ.