Mekaniske transformasjoner av grafen til en funksjon. Konvertering av grafer

Konvertering av funksjonsgrafer

I denne artikkelen vil jeg introdusere deg til lineære transformasjoner av funksjonsgrafer og vise deg hvordan du bruker disse transformasjonene for å få en funksjonsgraf fra en funksjonsgraf

En lineær transformasjon av en funksjon er en transformasjon av funksjonen i seg selv og/eller dens argument til formen , samt en transformasjon som inneholder en argument- og/eller funksjonsmodul.

De største vanskelighetene ved å konstruere grafer ved hjelp av lineære transformasjoner er forårsaket av følgende handlinger:

Isolering grunnleggende funksjon, faktisk grafen som vi transformerer.
Definisjoner av rekkefølgen av transformasjoner.

OG Det er på disse punktene vi vil dvele mer detaljert.

La oss se nærmere på funksjonen

Den er basert på funksjonen. La oss ringe henne grunnleggende funksjon.

Når du plotter en funksjon vi utfører transformasjoner på grafen til grunnfunksjonen.

Hvis vi skulle utføre funksjonstransformasjoner i samme rekkefølge som verdien ble funnet når en viss verdi argument, altså

La oss vurdere hvilke typer lineære transformasjoner av argument og funksjon som finnes, og hvordan de skal utføres.

Argumenttransformasjoner.

1. f(x) f(x+b)

1. Bygg en graf over funksjonen

2. Flytt grafen til funksjonen langs OX-aksen med |b| enheter

venstre hvis b>0
rett hvis b<0

La oss plotte funksjonen

1. Bygg en graf over funksjonen

2. Flytt den 2 enheter til høyre:

2. f(x) f(kx)

1. Bygg en graf over funksjonen

2. Del abscissen til grafpunktene med k, og la ordinatene til punktene være uendret.

La oss bygge en graf av funksjonen.

1. Bygg en graf over funksjonen

2. Del alle abscisser av grafpunktene med 2, og la ordinatene være uendret:

3. f(x) f(-x)

1. Bygg en graf over funksjonen

2. Vis den symmetrisk i forhold til OY-aksen.

La oss bygge en graf av funksjonen.

1. Bygg en graf over funksjonen

2. Vis den symmetrisk i forhold til OY-aksen:

4. f(x) f(|x|)

1. Bygg en graf over funksjonen

2. Den delen av grafen som er plassert til venstre for OY-aksen, slettes, delen av grafen til høyre for OY-aksen fullføres symmetrisk i forhold til OY-aksen:

Funksjonsgrafen ser slik ut:

La oss plotte funksjonen

1. Vi bygger en graf av funksjonen (dette er en graf av funksjonen, forskjøvet langs OX-aksen med 2 enheter til venstre):

2. En del av grafen plassert til venstre for OY (x)-aksen<0) стираем:

3. Vi fullfører den delen av grafen som ligger til høyre for OY-aksen (x>0) symmetrisk i forhold til OY-aksen:

Viktig! To hovedregler for å transformere et argument.

1. Alle argumenttransformasjoner utføres langs OX-aksen

2. Alle transformasjoner av argumentet utføres "omvendt" og "i omvendt rekkefølge".

For eksempel, i en funksjon er sekvensen av argumenttransformasjoner som følger:

1. Ta modulen til x.

2. Legg til tallet 2 til modulo x.

Men vi konstruerte grafen i omvendt rekkefølge:

Først ble transformasjon 2 utført - grafen ble forskjøvet med 2 enheter til venstre (det vil si at abscissen til punktene ble redusert med 2, som om "i revers")

Deretter utførte vi transformasjonen f(x) f(|x|).

Kort fortalt er sekvensen av transformasjoner skrevet som følger:

La oss nå snakke om funksjonstransformasjon . Forvandlinger finner sted

1. Langs OY-aksen.

2. I samme rekkefølge som handlingene utføres.

Dette er transformasjonene:

1. f(x)f(x)+D

2. Flytt den langs OY-aksen med |D| enheter

opp hvis D>0
ned hvis D<0

La oss plotte funksjonen

1. Bygg en graf over funksjonen

2. Flytt den langs OY-aksen 2 enheter opp:

2. f(x)Af(x)

1. Bygg en graf av funksjonen y=f(x)

2. Vi multipliserer ordinatene til alle punktene i grafen med A, og lar abscissene være uendret.

La oss plotte funksjonen

1. La oss bygge en graf av funksjonen

2. Multipliser ordinatene til alle punktene på grafen med 2:

3.f(x)-f(x)

1. Bygg en graf av funksjonen y=f(x)

La oss bygge en graf av funksjonen.

1. Bygg en graf over funksjonen.

2. Vi viser den symmetrisk i forhold til OX-aksen.

4. f(x)|f(x)|

1. Bygg en graf av funksjonen y=f(x)

2. Den delen av grafen som ligger over OX-aksen forblir uendret, delen av grafen som ligger under OX-aksen vises symmetrisk i forhold til denne aksen.

La oss plotte funksjonen

1. Bygg en graf over funksjonen. Den oppnås ved å flytte funksjonsgrafen langs OY-aksen med 2 enheter ned:

2. Nå vil vi vise den delen av grafen som ligger under OX-aksen symmetrisk i forhold til denne aksen:

Og den siste transformasjonen, som strengt tatt ikke kan kalles en funksjonstransformasjon, siden resultatet av denne transformasjonen ikke lenger er en funksjon:

|y|=f(x)

1. Bygg en graf av funksjonen y=f(x)

2. Vi sletter den delen av grafen som ligger under OX-aksen, og fullfører deretter den delen av grafen som ligger over OX-aksen symmetrisk i forhold til denne aksen.

La oss plotte ligningen

1. Vi bygger en graf av funksjonen:

2. Slett den delen av grafen som ligger under OX-aksen:

3. Vi fullfører den delen av grafen som ligger over OX-aksen symmetrisk i forhold til denne aksen.

Og til slutt foreslår jeg at du ser en VIDEO TUTORIAL der jeg viser en trinn-for-trinn-algoritme for å konstruere en graf av en funksjon

Grafen til denne funksjonen ser slik ut:

Avhengig av betingelsene for fysiske prosesser, får noen størrelser konstante verdier og kalles konstanter, andre endres under visse forhold og kalles variabler.

En nøye studie av miljøet viser at fysiske mengder er avhengige av hverandre, det vil si at en endring i noen mengder innebærer en endring i andre.

Matematisk analyse omhandler studiet av kvantitative sammenhenger mellom gjensidig varierende størrelser, abstrahert fra den spesifikke fysiske betydningen. Et av de grunnleggende begrepene i matematisk analyse er funksjonsbegrepet.

Vurder elementene i settet og elementene i settet
(Fig. 3.1).

Hvis det etableres en viss samsvar mellom elementene i settene
Og i form av en regel , så merker de at funksjonen er definert
.

Definisjon 3.1. Korrespondanse , som assosieres med hvert element ikke tomt sett
et godt definert element ikke tomt sett ,kalt en funksjon eller tilordning
V .

Symbolsk visning
V er registrert på følgende måte:

Samtidig mange
kalles funksjonens definisjonsdomene og betegnes
.

Til gjengjeld mange kalles funksjonens verdiområde og betegnes
.

I tillegg bør det bemerkes at elementene i settet
kalles uavhengige variabler, elementene i settet kalles avhengige variabler.

Metoder for å spesifisere en funksjon

Funksjonen kan spesifiseres på følgende hovedmåter: tabellform, grafisk, analytisk.

Hvis det, basert på eksperimentelle data, kompileres tabeller som inneholder verdiene til funksjonen og de tilsvarende argumentverdiene, kalles denne metoden for å spesifisere funksjonen tabell.

På samme tid, hvis noen studier av det eksperimentelle resultatet vises på en opptaker (oscilloskop, opptaker, etc.), bemerkes det at funksjonen er spesifisert grafisk.

Det vanligste er den analytiske måten å spesifisere en funksjon på, dvs. en metode der en uavhengig og avhengig variabel kobles sammen ved hjelp av en formel. I dette tilfellet spiller definisjonsdomenet til funksjonen en betydelig rolle:

forskjellige, selv om de er gitt av de samme analytiske relasjonene.

Hvis du bare spesifiserer funksjonsformelen
, så anser vi at definisjonsdomenet til denne funksjonen sammenfaller med settet med disse verdiene til variabelen , som uttrykket for
har betydningen. I denne forbindelse spiller problemet med å finne definisjonsdomenet til en funksjon en spesiell rolle.

Oppgave 3.1. Finn domenet til en funksjon

Løsning

Det første begrepet tar reelle verdier når
, og den andre kl. Altså å finne definisjonsdomenet for denne funksjonen det er nødvendig å løse systemet med ulikheter:

Som et resultat er løsningen på et slikt system . Derfor er definisjonsdomenet til funksjonen segmentet
.

De enkleste transformasjonene av funksjonsgrafer

Konstruksjonen av funksjonsgrafer kan forenkles betydelig hvis du bruker de velkjente grafene til grunnleggende elementære funksjoner. Hoved elementære funksjoner Følgende funksjoner kalles:

1) strømfunksjon
Hvor
;

2)eksponentiell funksjon
Hvor
Og
;

3) logaritmisk funksjon
, Hvor - ethvert positivt tall annet enn ett:
Og
;

4) trigonometriske funksjoner

;
.

5) inverse trigonometriske funksjoner
;
;
;
.

Elementære funksjoner er funksjoner som er hentet fra grunnleggende elementære funksjoner ved å bruke fire aritmetiske operasjoner og superposisjoner brukt et begrenset antall ganger.

Enkel geometriske transformasjoner lar deg også forenkle prosessen med å konstruere en graf over funksjoner. Disse transformasjonene er basert på følgende utsagn:

Grafen til funksjonen y=f(x+a) er grafen y=f(x), forskjøvet (for en >0 til venstre, for en< 0 вправо) на |a| единиц параллельно осиOx.

Grafen til funksjonen y=f(x) +b er grafen til y=f(x), forskjøvet (ved b>0 opp, ved b< 0 вниз) на |b| единиц параллельно осиOy.

Grafen til funksjonen y = mf(x) (m0) er grafen til y = f(x), strukket (ved m>1) m ganger eller komprimert (ved 0

Grafen til funksjonen y = f(kx) er grafen til y = f(x), komprimert (for k >1) k ganger eller strukket (for 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.

Grunnleggende elementære funksjoner i ren form uten transformasjon er sjeldne, så oftest må du jobbe med elementære funksjoner som ble hentet fra de viktigste ved å legge til konstanter og koeffisienter. Slike grafer er konstruert ved hjelp av geometriske transformasjoner av gitte elementære funksjoner.

La oss se på et eksempel kvadratisk funksjon av formen y = - 1 3 x + 2 3 2 + 2, hvis graf er parabelen y = x 2, som er komprimert tre ganger i forhold til O y og symmetrisk i forhold til O x, og forskjøvet med 2 3 langs O x til høyre, med 2 enheter langs O u opp. På en koordinatlinje ser det slik ut:

Yandex.RTB R-A-339285-1

Geometriske transformasjoner av grafen til en funksjon

Ved å bruke geometriske transformasjoner av en gitt graf, får vi at grafen er avbildet med en funksjon av formen ± k 1 · f (± k 2 · (x + a)) + b, når k 1 > 0, k 2 > 0 er kompresjonskoeffisienter ved 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 langs O y og O x. Tegnet foran koeffisientene k 1 og k 2 indikerer en symmetrisk visning av grafen i forhold til aksene, a og b forskyver den langs O x og langs O y.

Definisjon 1

Det er 3 typer geometriske transformasjoner av grafen:

Skalering langs O x og O y. Dette påvirkes av koeffisientene k 1 og k 2 forutsatt at de ikke er lik 1 når 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, så strekkes grafen langs O y og komprimeres langs O x.
Symmetrisk visning i forhold til koordinatakser. Hvis det er et "-"-tegn foran k 1, er symmetrien i forhold til O x, og foran k 2 er den i forhold til O y. Hvis "-" mangler, hoppes elementet over ved løsning;
Parallell overføring (skift) langs O x og O y. Transformasjonen utføres hvis det er koeffisienter a og b ulik 0. Hvis a er positiv, forskyves grafen til venstre med | en | enheter, hvis a er negativ, så til høyre i samme avstand. b-verdien bestemmer bevegelsen langs O y-aksen, som betyr at når b er positiv, beveger funksjonen seg opp, og når b er negativ, beveger den seg ned.

La oss se på løsninger ved å bruke eksempler, og begynne med strømfunksjon.

Eksempel 1

Transformer y = x 2 3 og plott funksjonen y = - 1 2 · 8 x - 4 2 3 + 3 .

Løsning

La oss representere funksjonene på denne måten:

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Der k 1 = 2, er det verdt å være oppmerksom på tilstedeværelsen av "-", a = - 1 2, b = 3. Herfra får vi at geometriske transformasjoner utføres ved å strekke seg langs O y to ganger, vist symmetrisk i forhold til O x, forskjøvet til høyre med 1 2 og oppover med 3 enheter.

Hvis vi skildrer den opprinnelige kraftfunksjonen, får vi det

når strukket to ganger langs O y har vi det

Kartleggingen, symmetrisk med hensyn til O x, har formen

og flytt til høyre med 12

en bevegelse på 3 enheter opp ser ut som

La oss se på transformasjoner av eksponentielle funksjoner ved å bruke eksempler.

Eksempel 2

Konstruer en graf av eksponentialfunksjonen y = - 1 2 1 2 (2 - x) + 8.

Løsning.

La oss transformere funksjonen basert på egenskapene til en potensfunksjon. Da får vi det

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

Fra dette kan vi se at vi får en kjede av transformasjoner y = 1 2 x:

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

Vi finner at den opprinnelige eksponentialfunksjonen har formen

Klem to ganger langs O y gir

Strekker seg langs O x

Symmetrisk kartlegging med hensyn til O x

Kartleggingen er symmetrisk med hensyn til O y

Flytt opp 8 enheter

La oss se på løsningen ved å bruke et eksempel logaritmisk funksjon y = log(x) .

Eksempel 3

Konstruer funksjonen y = ln e 2 · - 1 2 x 3 ved å bruke transformasjonen y = ln (x) .

Løsning

For å løse det er det nødvendig å bruke egenskapene til logaritmen, da får vi:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Transformasjonene av en logaritmisk funksjon ser slik ut:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

La oss plotte den opprinnelige logaritmiske funksjonen

Vi komprimerer systemet i henhold til O y

Vi strekker oss langs O x

Vi utfører en kartlegging med hensyn til O y

Vi skifter opp med 2 enheter, får vi

For å konvertere grafer trigonometrisk funksjon det er nødvendig å tilpasse et løsningsskjema på formen ± k 1 · f (± k 2 · (x + a)) + b. Det er nødvendig at k 2 er lik T k 2 . Herfra får vi den 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

La oss se på eksempler på å løse problemer med transformasjoner y = sin x.

Eksempel 4

Konstruer en graf av y = - 3 sin 1 2 x - 3 2 - 2 ved å bruke transformasjoner av funksjonen y=sinx.

Løsning

Det er nødvendig å redusere funksjonen til formen ± k 1 · f ± k 2 · x + a + b. For dette:

y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2

Det kan sees at k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Siden det er en "-" før k 1, men ikke før k 2, får vi en kjede av transformasjoner av formen:

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2

Detaljert sinusbølgetransformasjon. Når vi plotter den opprinnelige sinusformen y = sin (x), finner vi at den minste positive perioden anses å være T = 2 π. Finne maksimum ved punktene π 2 + 2 π · k; 1, og minimum - - π 2 + 2 π · k; - 1, k ∈ Z.

O y strekkes tre ganger, noe som betyr at økningen i amplituden til svingninger vil øke med 3 ganger. T = 2 π er den minste positiv periode. Maksima går til π 2 + 2 π · k; 3, k ∈ Z, minimum - - π 2 + 2 π · k; - 3, k ∈ Z.

Når vi strekker langs O x med det halve, finner vi at den minste positive perioden øker med 2 ganger og er lik T = 2 π k 2 = 4 π. Maksima går til π + 4 π · k; 3, k ∈ Z, minimumsverdier – i - π + 4 π · k; - 3, k ∈ Z.

Bildet produseres symmetrisk i forhold til O x. Den minste positive perioden i i dette tilfellet endres ikke og er lik T = 2 π k 2 = 4 π . Den maksimale overgangen ser ut som - π + 4 π · k; 3, k ∈ Z, og minimum er π + 4 π · k; - 3, k ∈ Z.

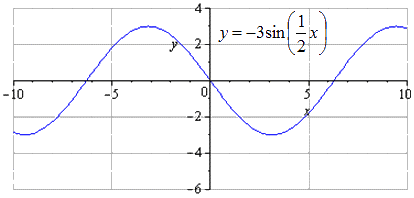
Grafen er forskjøvet ned med 2 enheter. Minste fellesperiode endres ikke. Finne maksima med overgang til punkter - π + 3 + 4 π · k; 1, k ∈ Z, minimum - π + 3 + 4 π · k; - 5 , k ∈ Z .

På sånn som det er nå grafen til en trigonometrisk funksjon anses som transformert.

La oss vurdere detaljert konvertering funksjoner y = cos x.

Eksempel 5

Konstruer en graf for funksjonen y = 3 2 cos 2 - 2 x + 1 ved å bruke en funksjonstransformasjon av formen y = cos x.

Løsning

I følge algoritmen er det nødvendig gitt funksjon reduser til formen ± k 1 · f ± k 2 · x + a + b. Da får vi det

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Fra betingelsen er det klart at k 1 = 3 2, k 2 = 2, a = - 1, b = 1, hvor k 2 har “-”, men før k 1 er den fraværende.

Fra dette ser vi at vi får en graf av en trigonometrisk funksjon av formen:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1

Trinn-for-steg-kosinustransformasjon med grafisk illustrasjon.

På gitt tidsplan y = cos (x) det er klart at den minste generell periode er lik T = 2 π. Finne maksima i 2 π · k ; 1, k ∈ Z, og det er π + 2 π · k minima; - 1, k ∈ Z.

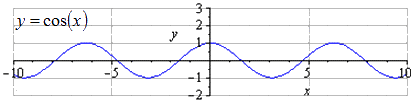
Når strekk langs Oy med 3 2 ganger, øker amplituden av oscillasjoner med 3 2 ganger. T = 2 π er den minste positive perioden. Finne maksima i 2 π · k ; 3 2, k ∈ Z, minimum i π + 2 π · k; - 3 2 , k ∈ Z .

Når komprimert langs O x med halvparten, finner vi at den minste positive perioden er tallet T = 2 π k 2 = π. Overgangen av maksima til π · k skjer; 3 2 , k ∈ Z , minimum - π 2 + π · k ; - 3 2 , k ∈ Z .

Symmetrisk kartlegging med hensyn til Oy. Siden grafen er merkelig, vil den ikke endre seg.

Når grafen er forskjøvet med 1 . Det er ingen endringer i den minste positive perioden T = π. Finne maksima i π · k + 1 ; 3 2, k ∈ Z, minimum - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Når den forskyves med 1, er den minste positive perioden lik T = π og endres ikke. Finne maksima i π · k + 1 ; 5 2, k ∈ Z, minimum i π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Kosinusfunksjonstransformasjonen er fullført.

La oss vurdere transformasjoner ved å bruke eksemplet y = t g x.

Eksempel 6

Konstruer en graf av funksjonen y = - 1 2 t g π 3 - 2 3 x + π 3 ved å bruke transformasjoner av funksjonen y = t g (x) .

Løsning

Til å begynne med er det nødvendig å redusere den gitte funksjonen til formen ± k 1 · f ± k 2 · x + a + b, hvoretter vi får det

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Det er godt synlig at k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, og foran koeffisientene k 1 og k 2 er det en “-”. Dette betyr at etter transformasjon av tangentsoidene får vi

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Trinn-for-trinn transformasjon av tangenter med grafisk representasjon.

Vi har at den opprinnelige grafen er y = t g (x) . Endringen i positiv periode er lik T = π. Definisjonsdomenet anses å være - π 2 + π · k ; π 2 + π · k, k ∈ Z.

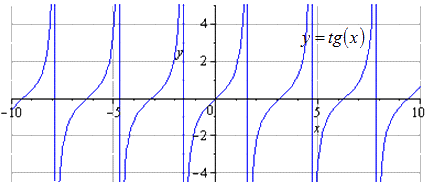
Vi komprimerer den 2 ganger langs Oy. T = π regnes som den minste positive perioden, der definisjonsdomenet har formen - π 2 + π · k; π 2 + π · k, k ∈ Z.

Strekk langs O x 3 2 ganger. La oss beregne den minste positive perioden, og den var lik T = π k 2 = 3 2 π . Og definisjonsdomenet til funksjonen med koordinater er 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, bare definisjonsdomenet endres.

Symmetri går på O x-siden. Perioden vil ikke endres på dette tidspunktet.

Det er nødvendig å vise koordinatakser symmetrisk. Definisjonsdomenet i dette tilfellet er uendret. Tidsplanen er sammenfallende med den forrige. Dette antyder at tangentfunksjonen er oddetall. Hvis til merkelig funksjon angi en symmetrisk kartlegging av O x og O y, og transformer deretter til den opprinnelige funksjonen.

Tilbake fremover

Merk følgende! Lysbildeforhåndsvisninger er kun til informasjonsformål og representerer kanskje ikke alle funksjonene i presentasjonen. Hvis du er interessert denne jobben, last ned fullversjonen.

Hensikten med leksjonen: Bestem mønstrene for transformasjon av funksjonsgrafer.

Oppgaver:

Pedagogisk:

Lær elevene å konstruere grafer av funksjoner ved å transformere grafen til en gitt funksjon ved å bruke parallell overføring, kompresjon (spenning), forskjellige typer symmetri.

Pedagogisk:

Bringe opp personlige kvaliteter elever (evne til å lytte), velvilje overfor andre, oppmerksomhet, nøyaktighet, disiplin, evne til å jobbe i gruppe.
Dyrk interesse for faget og behovet for å tilegne seg kunnskap.

Utviklingsmessig:

Utvikle romlig fantasi Og logisk tenkning studenter, evnen til raskt å navigere i miljøet; utvikle intelligens, oppfinnsomhet og trene hukommelse.

Utstyr:

Multimediainstallasjon: datamaskin, projektor.

Litteratur:

Bashmakov, M. I. Matematikk [tekst]: lærebok for institusjoner som begynner. og onsdag prof. utdanning / M.I. Bashmakov - 5. utgave, revidert. – M.: Publiseringssenter“Akademiet”, 2012. – 256 s.
Bashmakov, M. I. Matematikk. Problembok [Tekst]: lærebok. stipend for utdanning institusjoner tidlig og onsdag prof. utdanning / M. I. Bashmakov – M.: Publishing Center “Academy”, 2012. – 416 s.

Timeplan:

Organisatorisk øyeblikk (3 min).
Oppdatering av kunnskap (7 min).
Forklaring av nytt materiale (20 min).
Konsolidering av nytt materiale (10 min).
Leksjonssammendrag (3 min).
Hjemmelekser(2 minutter).

I løpet av timene

1. Org. øyeblikk (3 min).

Sjekker de tilstedeværende.

Fortell hensikten med leksjonen.

De grunnleggende egenskapene til funksjoner som avhengigheter mellom variable størrelser bør ikke endres vesentlig når man endrer metoden for å måle disse størrelsene, dvs. når måleskalaen og referansepunktet endres. Men på grunn av mer rasjonelt valg målemetode variabler Det er vanligvis mulig å forenkle registreringen av avhengigheten mellom dem og bringe dette opptaket til en eller annen standardform. På geometrisk språk betyr endring av måten verdier måles på noen enkle transformasjoner av grafer, som vi skal studere i dag.

2. Oppdatering av kunnskap (7 min).

Før vi snakker om graftransformasjoner, la oss gå gjennom materialet vi dekket.

Muntlig arbeid. (lysbilde 2).

Funksjoner gitt:

3. Beskriv grafene for funksjoner: , , , .

3. Forklaring av nytt stoff (20 min).

De enkleste transformasjonene av grafer er deres parallelle overføring, kompresjon (strekk) og noen typer symmetri. Noen transformasjoner er presentert i tabellen (vedlegg 1), (lysbilde 3).

Arbeid i grupper.

Hver gruppe konstruerer grafer over gitte funksjoner og presenterer resultatet for diskusjon.

Funksjon	Transformere grafen til en funksjon	Funksjonseksempler	Lysbilde
	OU på EN enheter opp hvis EN>0, og på \|A\| enheter ned hvis EN<0.	,	(lysbilde 4)
	Parallell overføring langs aksen Åh på EN enheter til høyre hvis EN>0, og på - EN enheter til venstre hvis EN<0.	,	(lysbilde 5)