Cari terbitan bagi fungsi trigonometri. Pelajaran algebra dan permulaan analisis "terbitan fungsi trigonometri"

Untuk mencari terbitan bagi fungsi trigonometri perlu guna jadual derivatif, iaitu terbitan 6-13.

Apabila anda menjumpai terbitan perdana fungsi trigonometri Untuk mengelakkan kesilapan biasa, anda harus memberi perhatian kepada perkara berikut:

• dalam ungkapan fungsi, salah satu istilah selalunya sinus, kosinus atau fungsi trigonometri lain bukan dari hujah fungsi, tetapi dari nombor (malar), oleh itu terbitan istilah ini adalah sama dengan sifar;
• hampir selalu anda perlu memudahkan ungkapan yang diperoleh hasil daripada pembezaan, dan untuk ini anda perlu yakin menggunakan pengetahuan operasi dengan pecahan;
• untuk memudahkan ungkapan yang anda hampir selalu perlu tahu identiti trigonometri, sebagai contoh, formula sudut berganda dan formula unit sebagai hasil tambah kuasa dua sinus dan kosinus.

Contoh 1. Cari terbitan bagi suatu fungsi

Penyelesaian. Katakan dengan terbitan kosinus semuanya jelas, ramai yang mula mengkaji derivatif akan berkata. Bagaimana pula terbitan sinus dua belas dibahagikan dengan pi? Jawapan: kira sama dengan sifar! Di sini sinus (suatu fungsi selepas semua!) ialah perangkap, kerana hujahnya bukanlah pembolehubah X atau mana-mana pembolehubah lain, tetapi hanya nombor. Iaitu, sinus nombor ini juga adalah nombor. Dan terbitan nombor (malar), seperti yang kita ketahui daripada jadual terbitan, adalah sama dengan sifar. Jadi, kami hanya meninggalkan sinus tolak X dan mencari terbitannya, tidak melupakan tanda:

.

Contoh 2. Cari terbitan bagi suatu fungsi

.

Penyelesaian. Penggal kedua adalah kes yang sama seperti penggal pertama dalam contoh sebelumnya. Iaitu, ia adalah nombor, dan terbitan nombor itu ialah sifar. Kami mendapati terbitan sebutan kedua sebagai terbitan hasil bagi:

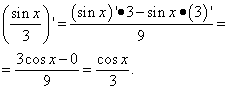
Contoh 3. Cari terbitan bagi suatu fungsi

Penyelesaian. Ini adalah masalah lain: di sini dalam istilah pertama tidak ada arcsine atau fungsi trigonometik lain, tetapi terdapat x, yang bermaksud ia adalah fungsi x. Oleh itu, kami membezakannya sebagai istilah dalam jumlah fungsi:

Di sini kemahiran dalam operasi dengan pecahan diperlukan, iaitu, dalam menghapuskan struktur tiga tingkat pecahan.

Contoh 4. Cari terbitan bagi suatu fungsi

.

Penyelesaian. Di sini huruf "phi" memainkan peranan yang sama seperti "x" dalam kes sebelumnya (dan dalam kebanyakan kes lain, tetapi bukan semua) - pembolehubah bebas. Oleh itu, apabila kita mencari terbitan hasil darab fungsi, kita tidak akan tergesa-gesa untuk mengisytiharkan terbitan punca “phi” bersamaan dengan sifar. Jadi:

Tetapi penyelesaiannya tidak berakhir di sana. Memandangkan istilah yang serupa dikumpul dalam dua kurungan, kami masih dikehendaki mengubah (memudahkan) ungkapan tersebut. Oleh itu, kami mendarabkan kurungan dengan faktor di belakangnya, dan kemudian kami membawa istilah kepada penyebut biasa dan melakukan transformasi asas lain:

Contoh 5. Cari terbitan bagi suatu fungsi

Penyelesaian. Dalam contoh ini, kita perlu mengetahui hakikat bahawa terdapat fungsi trigonometri - sekan - dan formulanya melalui kosinus. Mari bezakan:

Contoh 6. Cari terbitan bagi suatu fungsi

.

Penyelesaian. Dalam contoh ini, kita akan dikehendaki mengingati formula sudut berganda dari sekolah. Tetapi pertama-tama mari kita bezakan:

,

(ini ialah formula sudut berganda)

Dari kursus geometri dan matematik, pelajar sekolah terbiasa dengan fakta bahawa konsep derivatif disampaikan kepada mereka melalui kawasan angka, pembezaan, had fungsi, serta had. Mari cuba lihat konsep terbitan dari sudut yang berbeza, dan tentukan bagaimana fungsi derivatif dan trigonometri boleh dikaitkan.

Jadi, mari kita pertimbangkan beberapa lengkung arbitrari yang diterangkan oleh fungsi abstrak y = f(x).

Bayangkan jadual itu adalah peta laluan pelancong. Kenaikan ∆x (delta x) dalam rajah ialah jarak tertentu laluan, dan ∆y ialah perubahan ketinggian laluan di atas paras laut.
Kemudian ternyata nisbah ∆x/∆y akan mencirikan kerumitan laluan pada setiap segmen laluan. Setelah mempelajari nilai ini, anda dengan yakin boleh mengatakan sama ada pendakian/penurunan itu curam, sama ada anda memerlukan peralatan mendaki dan sama ada pelancong memerlukan latihan fizikal. Tetapi penunjuk ini hanya sah untuk satu jurang kecil∆x.

Jika penganjur perjalanan mengambil nilai untuk permulaan dan titik akhir laluan, iaitu, ∆x – akan sama panjang laluan, ia tidak akan dapat memperoleh data objektif tentang tahap kesukaran perjalanan. Oleh itu, adalah perlu untuk membina graf lain yang akan mencirikan kelajuan dan "kualiti" perubahan dalam laluan, dengan kata lain, tentukan nisbah ∆x/∆y untuk setiap "meter" laluan.

Graf ini akan menjadi derivatif visual untuk laluan tertentu dan secara objektif akan menerangkan perubahannya pada setiap selang minat. Sangat mudah untuk mengesahkan ini; nilai ∆x/∆y tidak lebih daripada pembezaan yang diambil makna khusus x dan y. Marilah kita menggunakan pembezaan bukan pada koordinat tertentu, tetapi pada fungsi secara keseluruhan:

Fungsi terbitan dan trigonometri

Fungsi trigonometri berkait rapat dengan derivatif. Ini dapat difahami daripada lukisan berikut. Pada imej paksi koordinat fungsi Y = f (x) ditunjukkan - lengkung biru.

K (x0; f (x0)) – titik sewenang-wenangnya, x0 + ∆x ialah kenaikan di sepanjang paksi OX, dan f (x0 + ∆x) ialah kenaikan di sepanjang paksi OY pada titik L tertentu.

Mari kita lukis garis lurus melalui titik K dan L dan bina segi tiga tepat KLN. Jika anda secara mental menggerakkan segmen LN sepanjang graf Y = f (x), maka titik L dan N akan cenderung kepada nilai K (x0; f (x0)). Mari kita panggil titik ini sebagai permulaan bersyarat bagi graf - had jika fungsi itu tidak terhingga, sekurang-kurangnya pada salah satu selang, kecenderungan ini juga akan menjadi tidak terhingga, dan nilai hadnya hampir kepada 0.

Sifat kecenderungan ini boleh digambarkan dengan tangen kepada titik y = kx + b yang dipilih atau dengan graf terbitan bagi fungsi asal dy - garis lurus hijau.

Tetapi di mana trigonometri di sini?! Semuanya sangat mudah, pertimbangkan segi tiga tepat KLN. Nilai pembezaan untuk titik K tertentu ialah tangen bagi sudut α atau ∠K:

Dengan cara ini, kita boleh menghuraikan makna geometri bagi terbitan dan hubungannya dengan fungsi trigonometri.

Formula terbitan untuk fungsi trigonometri

Penjelmaan sinus, kosinus, tangen dan kotangen semasa menentukan terbitan mesti dihafal.

Dua formula terakhir bukanlah ralat, maksudnya ialah terdapat perbezaan antara mentakrifkan derivatif hujah mudah dan fungsi dalam kapasiti yang sama.

Mari kita pertimbangkan jadual perbandingan dengan formula untuk terbitan sinus, kosinus, tangen dan kotangen:

Formula juga telah diperolehi untuk terbitan arcsine, arccosine, arctangent dan arccotangent, walaupun ia jarang digunakan:

Perlu diingat bahawa formula di atas jelas tidak mencukupi untuk penyelesaian yang berjaya tugas biasa Peperiksaan Negeri Bersepadu, apa yang akan ditunjukkan semasa menyelesaikan contoh konkrit mencari terbitan bagi ungkapan trigonometri.

Senaman: Ia adalah perlu untuk mencari terbitan fungsi dan mencari nilainya untuk π/4:

Penyelesaian: Untuk mencari y’ perlu mengingat semula formula asas untuk menukar fungsi asal kepada terbitan, iaitu.

Subjek:"Terbitan fungsi trigonometri".
Jenis pelajaran– pengajaran dalam memantapkan ilmu.
Borang pelajaran– pelajaran bersepadu.
Tempat pelajaran dalam sistem pelajaran untuk bahagian ini- pelajaran umum.
Matlamat ditetapkan secara menyeluruh:

• pendidikan: mengetahui peraturan pembezaan, boleh menggunakan peraturan untuk mengira terbitan semasa menyelesaikan persamaan dan ketaksamaan; meningkatkan subjek, termasuk pengiraan, kemahiran dan kebolehan; Kemahiran komputer;
• membangun: pembangunan kemahiran intelek dan logik serta minat kognitif;
• pendidikan: memupuk kebolehsuaian kepada keadaan moden latihan.

Kaedah:

• pembiakan dan produktif;
• praktikal dan lisan;
• kerja bebas;
• pembelajaran berprogram, T.S.O.;
• gabungan hadapan, kumpulan dan kerja individu;
• pembelajaran yang dibezakan;
• induktif-deduktif.

Bentuk kawalan:

• tinjauan lisan,
• kawalan terprogram,
• kerja bebas,
• tugasan individu pada komputer,
• semakan rakan sebaya menggunakan kad diagnostik pelajar.

SEMASA KELAS

saya. mengatur masa

II. Pengemaskinian ilmu rujukan

a) Mengkomunikasikan matlamat dan objektif:

• mengetahui peraturan pembezaan, dapat menggunakan peraturan untuk mengira terbitan semasa menyelesaikan masalah, persamaan dan ketaksamaan;
• meningkatkan subjek, termasuk pengiraan, kemahiran dan kebolehan; Kemahiran komputer;
• membangunkan kemahiran intelek dan logik dan minat kognitif;
• memupuk kebolehsuaian kepada keadaan pembelajaran moden.

b) Pengulangan bahan pendidikan

Peraturan untuk mengira derivatif (pengulangan formula pada komputer dengan bunyi). doc.7.

1. Apakah terbitan sinus?
2. Apakah terbitan kosinus?
3. Apakah terbitan tangen?
4. Apakah terbitan bagi kotangen?

III. Kerja lisan

Cari terbitan.
Pilihan 1.		Pilihan 2.
di = 2X + 5.		di = 2X – 5.
di= 4kos X.		di= 3 dosa X.
di= tg X+ctg X.		di= tg X-ctg X.
di= dosa 3 X.		di= cos 4 X.
Pilihan jawapan.
	– 4 dosa X		– 3 cos X
1/kos 2 X+ 1/dosa 2 X	1/kos 2 X–1/dosa 2 X	1/dosa 2 X–1/kos 2 X
	– 4sin4 X		– 3cos3 X

Bertukar buku nota. Dalam kad diagnostik, tandakan tugasan yang telah disiapkan dengan betul dengan tanda +, dan tugas yang salah disiapkan dengan tanda –.

IV. Menyelesaikan persamaan menggunakan derivatif

– Bagaimana untuk mencari titik di mana terbitan adalah sifar?

Untuk mencari titik di mana terbitan fungsi ini sama dengan sifar, anda perlukan:

- menentukan sifat fungsi,
– cari kawasan definisi fungsi,
– cari terbitan bagi fungsi ini,
– selesaikan persamaan f "(x) = 0,
- pilih jawapan yang betul.

Tugasan 1.

Diberi: di = X–dosa x.
Cari: titik di mana terbitan adalah sifar.
Penyelesaian. Fungsi ditakrifkan dan boleh dibezakan pada set semua nombor nyata, kerana fungsi ditakrifkan dan boleh dibezakan pada set semua nombor nyata g(x) = x Dan t(x) = – dosa x.
Menggunakan peraturan pembezaan, kita dapat f "(x) = (x–dosa x)" = (x)" – (dosa x)" = 1 – cos x.
Jika f "(x) = 0, kemudian 1 – cos x = 0.
cos x= 1/; mari kita hapuskan ketidakrasionalan dalam penyebut, kita mendapat kos x = /2.
Mengikut formula t= ± arccos a+ 2n, n Z, kita dapat: X= ± arccos /2 + 2n, n Z.
Jawapan: x = ± /4 + 2n, n Z.

V. Menyelesaikan persamaan menggunakan algoritma

Cari pada titik mana terbitan itu hilang.

f(x) = dosa x+kos x

f(x) = dosa 2 x – x

f(x) = 2x+cos(4 x – )

Pelajar boleh memilih mana-mana daripada tiga contoh. Contoh pertama diberi nilai " 3 ", kedua -" 4 ", ketiga - " 5 " Penyelesaian dalam buku nota diikuti dengan pemeriksaan bersama. Seorang pelajar membuat keputusan di dewan. Jika penyelesaian ternyata tidak betul, maka pelajar perlu kembali kepada algoritma dan cuba menyelesaikannya semula.

Kawalan terprogram.

Pilihan 1		Pilihan 2
y = 2X 3		y = 3X 2
y = 1/4 X 4 + 2X 2 – 7		y = 1/2 X 4 + 4X + 5
y = X 3 + 4X 2 – 3X. Selesaikan persamaan y " = 0		y = 2X 3 – 9X 2 + 12X + 7. Selesaikan persamaan y " = 0.
y= dosa 2 X– cos 3 X.		y= cos 2 X- dosa 3 X.
y= tg X–ctg( X + /4).		y=ctg X+ tg( X – /4).
y= dosa 2 X.		y= cos 2 X.
Pilihan jawapan.
Apabila memperoleh formula pertama jadual, kita akan meneruskan dari definisi fungsi terbitan pada satu titik. Jom bawa ke mana x– mana-mana nombor sebenar, itu dia, x– sebarang nombor daripada domain takrifan fungsi. Mari kita tuliskan had nisbah pertambahan fungsi kepada pertambahan hujah di : Perlu diingatkan bahawa di bawah tanda had ungkapan diperoleh, yang bukan ketidakpastian sifar dibahagikan dengan sifar, kerana pengangka tidak mengandungi nilai yang sangat kecil, tetapi tepatnya sifar. Dalam erti kata lain, kenaikan fungsi malar sentiasa sifar. Oleh itu, terbitan bagi fungsi malaradalah sama dengan sifar di seluruh domain definisi. Terbitan fungsi kuasa. Formula terbitan fungsi kuasa kelihatan seperti , di mana eksponen hlm– sebarang nombor nyata. Mari kita buktikan dahulu formula untuk eksponen semula jadi, iaitu, untuk p = 1, 2, 3, … Kami akan menggunakan definisi derivatif. Mari kita tuliskan had nisbah pertambahan fungsi kuasa kepada pertambahan hujah: Untuk memudahkan ungkapan dalam pengangka, kita beralih kepada formula binomial Newton: Oleh itu, Ini membuktikan formula untuk terbitan fungsi kuasa untuk eksponen semula jadi. Terbitan bagi fungsi eksponen. Kami membentangkan terbitan formula terbitan berdasarkan definisi: Kita telah tiba pada ketidakpastian. Untuk mengembangkannya, kami memperkenalkan pembolehubah baharu, dan pada . lepas tu . Dalam peralihan terakhir, kami menggunakan formula untuk beralih kepada asas logaritma baharu. Mari kita gantikan ke dalam had asal: Jika kita mengingati had kedua yang luar biasa, kita sampai pada formula untuk terbitan fungsi eksponen: Terbitan bagi fungsi logaritma. Mari kita buktikan formula untuk terbitan fungsi logaritma untuk semua x dari domain definisi dan semua nilai asas yang sah a logaritma Dengan definisi derivatif kita mempunyai: Seperti yang anda perhatikan, semasa pembuktian, transformasi telah dijalankan menggunakan sifat-sifat logaritma. Kesaksamaan adalah benar kerana had kedua yang luar biasa. Terbitan fungsi trigonometri. Untuk mendapatkan formula bagi derivatif fungsi trigonometri, kita perlu mengingati beberapa formula trigonometri, serta had pertama yang luar biasa. Dengan takrif terbitan untuk fungsi sinus yang kita ada . Mari kita gunakan formula perbezaan sinus: Ia kekal untuk beralih kepada had pertama yang luar biasa: Oleh itu, terbitan fungsi dosa x Terdapat kerana x. Formula untuk terbitan kosinus dibuktikan dengan cara yang sama. Oleh itu, terbitan bagi fungsi kerana x Terdapat –dosa x. Kami akan memperoleh formula untuk jadual terbitan bagi tangen dan kotangen menggunakan kaedah-kaedah pembezaan yang terbukti (terbitan pecahan). Terbitan fungsi hiperbolik. Peraturan pembezaan dan formula untuk terbitan fungsi eksponen daripada jadual terbitan membolehkan kita memperoleh formula untuk terbitan sinus hiperbolik, kosinus, tangen dan kotangen. Terbitan bagi fungsi songsang. Untuk mengelakkan kekeliruan semasa pembentangan, mari kita nyatakan dalam subskrip hujah fungsi yang mana pembezaan dilakukan, iaitu, ia adalah terbitan fungsi f(x) Oleh x. Sekarang mari kita rumuskan peraturan untuk mencari terbitan fungsi songsang. Biarkan fungsi y = f(x) Dan x = g(y) saling songsang, ditakrifkan pada selang dan masing-masing. Jika pada satu titik terdapat terbitan bukan sifar terhingga bagi fungsi itu f(x), maka pada titik itu terdapat terbitan terhingga bagi fungsi songsang g(y), dan . Dalam jawatan lain . Peraturan ini boleh dirumus semula untuk mana-mana x daripada selang , maka kita dapat . Mari kita semak kesahihan formula ini. Mari kita cari fungsi songsang untuk logaritma asli (Di sini y ialah fungsi, dan x- hujah). Setelah menyelesaikan persamaan ini untuk x, kita dapat (di sini x ialah fungsi, dan y– hujahnya). Itu dia, dan fungsi saling songsang. Daripada jadual derivatif kita melihat bahawa Dan . Mari kita pastikan bahawa formula untuk mencari derivatif bagi fungsi songsang membawa kita kepada keputusan yang sama: Terbitan bagi fungsi trigonometri songsang dan terbitan formulanya dibentangkan. Ungkapan untuk derivatif tertib tinggi juga diberikan. Pautan ke halaman dengan lebih banyak lagi pernyataan terperinci formula keluaran. Pertama, kami memperoleh formula untuk terbitan arcsine. biarlah y= arcsin x. Oleh kerana arcsine ialah fungsi songsang sinus, maka . Di sini y ialah fungsi bagi x. Bezakan berkenaan dengan pembolehubah x: . Kami memohon: . Jadi kami mendapati: . Kerana, kemudian. Kemudian . Dan formula sebelumnya mengambil bentuk: . Dari sini . Dengan cara ini, anda boleh mendapatkan formula untuk terbitan kosinus arka. Walau bagaimanapun, lebih mudah untuk menggunakan formula yang berkaitan dengan fungsi trigonometri songsang: . Kemudian . Penerangan yang lebih terperinci dibentangkan pada halaman "Derivatif terbitan arcsine dan arccosine". Ada diberi terbitan derivatif dalam dua cara- dibincangkan di atas dan mengikut formula terbitan bagi fungsi songsang. Terbitan terbitan arctangent dan arccotangent Dengan cara yang sama kita akan mencari terbitan arctangent dan arccotangent. biarlah y= arctan x. Artangen ialah fungsi songsang tangen: . Bezakan berkenaan dengan pembolehubah x: . Kami menggunakan formula untuk terbitan fungsi kompleks: . Jadi kami mendapati: . Terbitan arka cotangen: . Derivatif Arcsine biarlah . Kami telah menemui terbitan tertib pertama arcsine: . Dengan membezakan, kita dapati derivatif tertib kedua: ; . Ia juga boleh ditulis dalam bentuk berikut: . Dari sini kita dapat persamaan pembezaan, yang dipenuhi oleh derivatif arcsine bagi urutan pertama dan kedua: . Dengan membezakan persamaan ini, kita boleh mencari derivatif tertib tinggi. Terbitan arcsine of nth order Terbitan lengkok susunan n mempunyai pandangan seterusnya: , di manakah polinomial darjah . Ia ditentukan oleh formula: ; . Di sini. Polinomial memenuhi persamaan pembezaan: . Terbitan arccosine of nth order Terbitan arccosine diperoleh daripada derivatif arcsine menggunakan formula trigonometri: . Oleh itu, derivatif fungsi ini berbeza hanya dalam tanda: . Terbitan arctangent biarlah . . Kami mendapati terbitan cotangen arka tertib pertama: . Mari pecahkan pecahan ke dalam bentuk termudah: Berikut ialah unit khayalan, . . Kami membezakan sekali dan membawa pecahan kepada penyebut biasa: . Menggantikan , kita mendapat: Terbitan arctangent bagi urutan ke-n ; . Oleh itu, terbitan arctangen tertib ke-n boleh diwakili dalam beberapa cara: Terbitan arka cotangen . Biarkan sekarang. Mari gunakan formula yang menghubungkan fungsi trigonometri songsang: . Kemudian terbitan tertib ke-n bagi tangen arka hanya berbeza dalam tanda daripada terbitan tangen arka: . Menggantikan , kita dapati: Rujukan: N.M. Gunter, R.O. Kuzmin, Koleksi masalah pada matematik yang lebih tinggi