Second order determinant

and is calculated according to the rule

Numbers are called elements of the determinant (the first index indicates the line number, and the second
number of the column at the intersection of which this element stands); diagonal formed by elements
,
, called main , elements
,

side .

The concept of a third-order determinant is introduced similarly.

Third order determinant is the number that is represented by the symbol

and is calculated according to the rule

Diagonal formed by elements
,
,
, called main , elements
,
,

side .

To remember which products on the right side of equality (1) are taken with the sign “
", and some with the sign "
", it is useful to use the following "rule of triangles":

You can introduce the concept of a determinant of the 4th, 5th, etc. orders.

Minor
of a certain element of a determinant is a determinant formed from a given element by deleting the row and column at the intersection of which this element is located.

Algebraic complement of some element of the determinant is the minor of this element multiplied by
, Where
line number,
number of the column at the intersection of which this element is located:

.

Properties of determinants.

The value of the determinant will not change if its rows and columns are swapped.

The operation in question is called transposition. Property 1

establishes equality of rows and columns of the determinant.

Task 1. Calculate determinants:

1) 2)3)4).

Task 2. Calculate the determinants by decomposing them into the elements of the first column:

1)
2)

Task 3. Find from the equations:

1)
2)

1.2. Solving systems of linear equations using determinants. Cramer's formulas

I) System of two linear homogeneous equations with two unknowns

Let's denote

main determinant of the system;

,
auxiliary qualifiers.

a) If the determinant of the system

,
. (1)

b) If the determinant of the system
, then the following cases are possible:

1)
(the equations are proportional), then the system contains only one equation, for example,
and has infinitely many solutions (uncertain system). To solve it, it is necessary to express one variable in terms of another, the value of which is chosen arbitrarily;

2) if at least one of the determinants
is different from zero, then the system has no solutions (inconsistent system).

II) System of two linear homogeneous equations with three variables

(2)

The linear equation is called homogeneous , if the free term of this equation equal to zero.

and if
, then system (2) is reduced to one equation (for example, the first), from which one unknown is expressed through two others, the values ​​of which are chosen arbitrarily.

b) If the condition
is not satisfied, then to solve system (2) we move one variable to the right and solve the system of two linear inhomogeneous equations using Cramer’s formulas (1).

III) A system of three linear inhomogeneous equations with three unknowns:

Let's compose and calculate the main determinant and auxiliary qualifiers ,.

and if
, then the system has only decision, which is found using Cramer’s formulas:

,
,
(3)

b) If
, then the following cases are possible:

1)
, then the system will have infinitely many solutions, it will be reduced to either a system consisting of one or two equations (we move one unknown to the right and solve a system of two equations with two unknowns);

2) at least one of the determinants
is different from zero, the system has no solution.

IV) A system of three linear homogeneous equations with three unknowns:

This system is always compatible, since it has zero solution.

a) If the determinant of the system
, then it has a unique zero solution.

b) If
, then the system reduces either to two equations (the third is their consequence), or to one equation (the other two are its consequences) and has infinitely many solutions (see Section II).

Task 4. Solve system of equations

Solution. Let's calculate the determinant of the system

Because
, then the system has a unique solution. Let's use Cramer's formulas (3). To do this, we calculate auxiliary determinants:

,
,

,
,

Task 5. Solve system of equations

Solution. Let us calculate the determinant of the system:

Consequently, a system of homogeneous equations has infinitely many non-zero solutions. We solve the system of the first two equations (the third equation is their consequence):

Let's move the variable to the right side of the equality:

From here, using formulas (1) we obtain

,
.

Problems to solve independently

Task 6. Solve using determinants of the system of equations:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)	12)

1.1. Systems of two linear equations and second order determinants

Consider a system of two linear equations with two unknowns:

Odds with unknowns And have two indices: the first indicates the equation number, the second – the variable number.

Cramer's rule: The solution to the system is found by dividing the auxiliary determinants by main determinant systems

,

Note 1. Using Cramer's rule is possible if the determinant of the system not equal to zero.

Note 2. Cramer's formulas are generalized to systems of higher order.

Example 1. Solve the system:
.

Solution.

;
;

;

Examination:

Conclusion: The system is solved correctly:
.

1.2. Systems of three linear equations and third-order determinants

Consider a system of three linear equations with three unknowns:

A determinant made up of coefficients for unknowns is called system determinant or main determinant:

.

If
then the system has a unique solution, which is determined by Cramer’s formulas:

where are the determinants
– are called auxiliary and are obtained from the determinant by replacing its first, second or third column with a column of free members of the system.

Example 2. Solve the system
.

Let's form the main and auxiliary determinants:

It remains to consider the rules for calculating third-order determinants. There are three of them: the rule of adding columns, the Sarrus rule, the rule of decomposition.

a) The rule for adding the first two columns to the main determinant:

The calculation is carried out in the following way: the products of the elements of the main diagonal and along parallels to it go with their sign, with the opposite sign they take the products of the elements of the secondary diagonal and along parallels to it.

b) Sarrus' rule:

With their sign, take the products of the elements of the main diagonal and along parallels to it, and the missing third element is taken from opposite corner. With the opposite sign, take the products of the elements of the secondary diagonal and along the parallels to it, the third element is taken from the opposite corner.

c) Rule of decomposition by elements of a row or column:

If
, Then .

Algebraic complement is a lower order determinant obtained by crossing out the corresponding row and column and taking into account the sign
, Where – line number, – column number.

For example,

,
,
etc.

Using this rule, we calculate the auxiliary determinants And , expanding them according to the elements of the first row.

Having calculated all the determinants, we find the variables using Cramer’s rule:

Examination:

Conclusion: the system is solved correctly: .

Basic properties of determinants

It must be remembered that the determinant is number, found according to some rules. Its calculation can be simplified if we use basic properties that are valid for determinants of any order.

Property 1. The value of the determinant will not change if all its rows are replaced by columns corresponding in number and vice versa.

The operation of replacing rows with columns is called transposition. From this property it follows that any statement that is true for the rows of the determinant will also be true for its columns.

Property 2. If two rows (columns) in the determinant are swapped, the sign of the determinant will change to the opposite.

Property 3. If all elements of any row of a determinant are equal to 0, then the determinant is equal to 0.

Property 4. If the elements of the determinant string are multiplied (divided) by some number , then the value of the determinant will increase (decrease) in once.

If the elements of a row have a common factor, then it can be taken out of the determinant sign.

Property 5. If a determinant has two identical or proportional rows, then such a determinant is equal to 0.

Property 6. If the elements of any row of a determinant are the sum of two terms, then the determinant is equal to the sum of the two determinants.

Property 7. The value of the determinant will not change if the elements of a row are added to the elements of another row, multiplied by the same number.

In this determinant, first the third row was added to the second row, multiplied by 2, then the second was subtracted from the third column, after which the second row was added to the first and third, as a result we got a lot of zeros and simplified the calculation.

Elementary transformations the determinant is called its simplification through the use of the specified properties.

Example 1. Compute determinant

Direct calculation according to one of the rules discussed above leads to cumbersome calculations. Therefore, it is advisable to use the properties:

a) from line 1, subtract the second, multiplied by 2;

b) from line II subtract the third, multiplied by 3.

As a result we get:

Let us expand this determinant into the elements of the first column, which contains only one non-zero element.

.

Systems and determinants of higher orders

system linear equations with unknowns can be written as follows:

For this case, it is also possible to compose the main and auxiliary determinants, and determine the unknowns using Cramer’s rule. The problem is that higher order determinants can only be calculated by lowering the order and reducing them to third order determinants. This can be done by direct decomposition into elements of rows or columns, as well as using preliminary elementary transformations and further decomposition.

Example 4. Calculate fourth order determinant

Solution we can find it in two ways:

a) by direct expansion into the elements of the first row:

b) through preliminary transformations and further decomposition

	a) from line I subtract III
	b) add line II to IV

Example 5. Compute the fifth-order determinant, obtaining zeros in the third row using the fourth column

from the first line we subtract the second, from the third we subtract the second, from the fourth we subtract the second multiplied by 2.

subtract the third from the second column:

subtract the third from the second line:

Example 6. Solve the system:

Solution. Let's compose a determinant of the system and, using the properties of determinants, calculate it:

(from the first row we subtract the third, and then in the resulting third-order determinant from the third column we subtract the first, multiplied by 2). Determinant
, therefore, Cramer's formulas are applicable.

Let's calculate the remaining determinants:

The fourth column was multiplied by 2 and subtracted from the rest

The fourth column was subtracted from the first, and then, multiplied by 2, subtracted from the second and third columns.

.

Here we performed the same transformations as for
.

.

When you find the first column was multiplied by 2 and subtracted from the rest.

According to Cramer's rule we have:

After substituting the found values ​​into the equations, we are convinced that the solution to the system is correct.

2. MATRICES AND THEIR USE

IN SOLVING SYSTEMS OF LINEAR EQUATIONS

• Systems m linear equations with n unknown.
  Solving a system of linear equations- this is such a set of numbers ( x 1 , x 2 , …, x n), when substituted into each of the equations of the system, the correct equality is obtained.
  Where a ij , i = 1, …, m; j = 1, …, n— system coefficients;
  b i , i = 1, …, m- free members;
  x j , j = 1, …, n- unknown.
  The above system can be written in matrix form: A X = B,
  
  
  
  
  Where ( A|B) is the main matrix of the system;
  A— extended system matrix;
  X— column of unknowns;
  B— column of free members.
  If matrix B is not a null matrix ∅, then this system linear equations is called inhomogeneous.
  If matrix B= ∅, then this system of linear equations is called homogeneous. A homogeneous system always has a zero (trivial) solution: x 1 = x 2 = …, x n = 0.
  Joint system of linear equations is a system of linear equations that has a solution.
  Inconsistent system of linear equations is an unsolvable system of linear equations.
  A certain system of linear equations is a system of linear equations that has a unique solution.
  Indefinite system of linear equations- is having infinite set solutions to a system of linear equations.
• Systems of n linear equations with n unknowns
  If the number of unknowns is equal to the number of equations, then the matrix is ​​square. The determinant of a matrix is ​​called the main determinant of a system of linear equations and is denoted by the symbol Δ.
  Cramer method for solving systems n linear equations with n unknown.
  Cramer's rule.
  If the main determinant of a system of linear equations is not equal to zero, then the system is consistent and defined, and the only solution is calculated using the Cramer formulas:
  where Δ i are determinants obtained from the main determinant of the system Δ by replacing i th column to the column of free members. .
• Systems of m linear equations with n unknowns
  Kronecker–Capelli theorem.
  
  
  In order for a given system of linear equations to be consistent, it is necessary and sufficient that the rank of the system matrix be equal to the rank of the extended matrix of the system, rang(Α) = rang(Α|B).
  If rang(Α) ≠ rang(Α|B), then the system obviously has no solutions.
  If rang(Α) = rang(Α|B), then two cases are possible:
  1) rank(Α) = n(number of unknowns) - the solution is unique and can be obtained using Cramer’s formulas;
  2) rank(Α)< n - there are infinitely many solutions.
• Gauss method for solving systems of linear equations
  
  
  Let's create an extended matrix ( A|B) of a given system from the coefficients of the unknowns and the right-hand sides.
  The Gaussian method or the method of eliminating unknowns consists of reducing the extended matrix ( A|B) using elementary transformations over its rows to a diagonal form (to the upper triangular view). Returning to the system of equations, all unknowns are determined.
  TO elementary transformations above the lines are the following:
  1) swap two lines;
  2) multiplying a string by a number other than 0;
  3) adding another string to a string, multiplied by an arbitrary number;
  4) throwing out a zero line.
  The extended matrix reduced to diagonal form corresponds to linear system, equivalent to this one, the solution of which does not cause difficulties. .
• System of homogeneous linear equations.
  A homogeneous system has the form:
  
  corresponds to it matrix equation A X = 0.
  1) A homogeneous system is always consistent, since r(A) = r(A|B), there is always a zero solution (0, 0, …, 0).
  2) In order to homogeneous system had a non-zero solution, it is necessary and sufficient that r = r(A)< n , which is equivalent to Δ = 0.
  3) If r< n , then obviously Δ = 0, then free unknowns arise c 1 , c 2 , …, c n-r, the system has non-trivial solutions, and there are infinitely many of them.
  4) General solution X at r< n can be written in matrix form as follows:
  X = c 1 X 1 + c 2 X 2 + … + c n-r X n-r,
  where are the solutions X 1, X 2, …, X n-r form a fundamental system of solutions.
  5) The fundamental system of solutions can be obtained from general solution homogeneous system:
  
  ,
  if we sequentially set the parameter values ​​equal to (1, 0, …, 0), (0, 1, …, 0), …, (0, 0, …, 1).
  Expansion of the general solution in fundamental system solutions is a record of a general solution in the form of a linear combination of solutions belonging to the fundamental system.
  Theorem. In order for a system of linear homogeneous equations to have a non-zero solution, it is necessary and sufficient that Δ ≠ 0.
  So, if the determinant Δ ≠ 0, then the system has a unique solution.
  If Δ ≠ 0, then the system of linear homogeneous equations has an infinite number of solutions.
  Theorem. In order for a homogeneous system to have a nonzero solution, it is necessary and sufficient that r(A)< n .
  Proof:
  1) r there can't be more n(the rank of the matrix does not exceed the number of columns or rows);
  2) r< n , because If r = n, then the main determinant of the system Δ ≠ 0, and, according to Cramer’s formulas, there is a unique trivial solution x 1 = x 2 = … = x n = 0, which contradicts the condition. Means, r(A)< n .
  Consequence. In order for a homogeneous system n linear equations with n unknowns had a non-zero solution, it is necessary and sufficient that Δ = 0.

Cramer's method is based on the use of determinants in solving systems of linear equations. This significantly speeds up the solution process.

Cramer's method can be used to solve a system of as many linear equations as there are unknowns in each equation. If the determinant of the system is not equal to zero, then Cramer’s method can be used in the solution, but if it is equal to zero, then it cannot. In addition, Cramer's method can be used to solve systems of linear equations that have a unique solution.

Definition. A determinant made up of coefficients for unknowns is called a determinant of the system and is denoted (delta).

Determinants

are obtained by replacing the coefficients of the corresponding unknowns with free terms:

;

.

Cramer's theorem. If the determinant of the system is nonzero, then the system of linear equations has one unique solution, and the unknown is equal to the ratio of the determinants. The denominator contains the determinant of the system, and the numerator contains the determinant obtained from the determinant of the system by replacing the coefficients of this unknown with free terms. This theorem holds for a system of linear equations of any order.

Example 1. Solve a system of linear equations:

According to Cramer's theorem we have:

So, the solution to system (2):

online calculator, decisive method Kramer.

Three cases when solving systems of linear equations

As is clear from Cramer's theorem, when solving a system of linear equations, three cases can occur:

First case: a system of linear equations has a unique solution

(the system is consistent and definite)

Second case: a system of linear equations has an infinite number of solutions

(the system is consistent and uncertain)

** ,

those. the coefficients of the unknowns and the free terms are proportional.

Third case: the system of linear equations has no solutions

(the system is inconsistent)

So the system m linear equations with n called variables non-joint, if she does not have a single solution, and joint, if it has at least one solution. A simultaneous system of equations that has only one solution is called certain, and more than one – uncertain.

Examples of solving systems of linear equations using the Cramer method

Let the system be given

.

Based on Cramer's theorem

………….
,

Where
-

system determinant. We obtain the remaining determinants by replacing the column with the coefficients of the corresponding variable (unknown) with free terms:

Example 2.

.

Therefore, the system is definite. To find its solution, we calculate the determinants

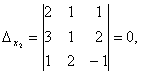
Using Cramer's formulas we find:

So, (1; 0; -1) is the only solution to the system.

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

If in a system of linear equations there are no variables in one or more equations, then in the determinant the corresponding elements are equal to zero! This is the next example.

Example 3. Solve a system of linear equations using the Cramer method:

.

Solution. We find the determinant of the system:

Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore the system is definite. To find its solution, we calculate the determinants for the unknowns

Using Cramer's formulas we find:

So, the solution to the system is (2; -1; 1).

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

Top of page

We continue to solve systems using Cramer's method together

As already mentioned, if the determinant of the system is equal to zero, and the determinants of the unknowns are not equal to zero, the system is inconsistent, that is, it has no solutions. Let us illustrate with the following example.

Example 6. Solve a system of linear equations using the Cramer method:

Solution. We find the determinant of the system:

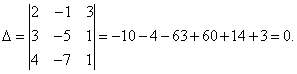
The determinant of the system is equal to zero, therefore, the system of linear equations is either inconsistent and definite, or inconsistent, that is, has no solutions. To clarify, we calculate determinants for unknowns

The determinants of the unknowns are not equal to zero, therefore, the system is inconsistent, that is, it has no solutions.

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

In problems involving systems of linear equations, there are also those where, in addition to letters denoting variables, there are also other letters. These letters represent a number, most often real. In practice, search problems lead to such equations and systems of equations general properties any phenomena or objects. That is, have you invented any new material or a device, and to describe its properties, which are common regardless of the size or number of an instance, you need to solve a system of linear equations, where instead of some coefficients for variables there are letters. You don't have to look far for examples.

The following example is for a similar problem, only the number of equations, variables, and letters denoting a certain real number increases.

Example 8. Solve a system of linear equations using the Cramer method:

Solution. We find the determinant of the system:

Finding determinants for unknowns

Matrix - rectangular table, made up of numbers.

Let it be given square matrix 2 orders:

The determinant (or determinant) of order 2 corresponding to a given matrix is ​​the number

A 3rd order determinant (or determinant) corresponding to a matrix is ​​a number

Example 1: Find determinants of matrices and

System of linear algebraic equations

Let a system of 3 linear equations with 3 unknowns be given

System (1) can be written in matrix-vector form

where A is the coefficient matrix

B - extended matrix

X is the required component vector;

Solving systems of equations using Cramer's method

Let a system of linear equations with two unknowns be given:

Let's consider solving systems of linear equations with two and three unknowns using Cramer's formulas. Theorem 1. If the main determinant of the system is different from zero, then the system has a solution, and a unique one. The solution of the system is determined by the formulas:

where x1, x2 are the roots of the system of equations,

The main determinant of the system, x1, x2 are auxiliary determinants.

Auxiliary qualifiers:

Solving systems of linear equations with three unknowns using Cramer's method.

Let a system of linear equations with three unknowns be given:

Theorem 2. If the main determinant of the system is different from zero, then the system has a solution, and a unique one. The solution of the system is determined by the formulas:

where x1, x2, x3 are the roots of the system of equations,

The main determinant of the system,

x1, x2, x3 are auxiliary determinants.

The main determinant of the system is determined by:

Auxiliary qualifiers:

• 1. Make a table (matrix) of coefficients for unknowns and calculate the main determinant.
• 2. Find - an additional determinant of x obtained by replacing the first column with a column of free terms.
• 3. Find - an additional determinant of y obtained by replacing the second column with a column of free terms.
• 4. Find - an additional determinant of z, obtained by replacing the third column with a column of free terms. If the main determinant of the system is not equal to zero, then step 5 is performed.
• 5. Find the value of the variable x using the formula x / .
• 6. Find the value of the variable y using the formula y /.
• 7. Find the value of the variable z using the formula z / .
• 8. Write down the answer: x=...; y=…, z=… .