Instructions. To solve online, you need to select the type of equation and set the dimension of the corresponding matrices.
where A, B, C are the specified matrices, X is the desired matrix. Matrix equations of the form (1), (2) and (3) are solved through the inverse matrix A -1. If the expression A·X - B = C is given, then it is necessary to first add the matrices C + B and find a solution for the expression A·X = D, where D = C + B (). If the expression A*X = B 2 is given, then the matrix B must first be squared. It is also recommended to familiarize yourself with the basic operations on matrices.Example No. 1. Exercise. Find the solution to the matrix equation
Solution. Let's denote:
Then the matrix equation will be written in the form: A·X·B = C.
The determinant of matrix A is equal to detA=-1
Since A is a non-singular matrix, there is an inverse matrix A -1 . Multiply both sides of the equation on the left by A -1: Multiply both sides of this equation on the left by A -1 and on the right by B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Since A A -1 = B B -1 = E and E X = X E = X, then X = A -1 C B -1
Inverse matrix A -1: ![]()
Let's find the inverse matrix B -1.
Transposed matrix B T:
Inverse matrix B -1: ![]()
We look for matrix X using the formula: X = A -1 ·C·B -1 ![]()
Answer:
Example No. 2. Exercise. Solve matrix equation ![]()
Solution. Let's denote:
Then the matrix equation will be written in the form: A·X = B.
The determinant of matrix A is detA=0
Since A is a singular matrix (the determinant is 0), therefore the equation has no solution.
Example No. 3. Exercise. Find the solution to the matrix equation
Solution. Let's denote:
Then the matrix equation will be written in the form: X A = B.
The determinant of matrix A is detA=-60
Since A is a non-singular matrix, there is an inverse matrix A -1 . Let's multiply both sides of the equation on the right by A -1: X A A -1 = B A -1, from where we find that X = B A -1
Let's find the inverse matrix A -1 .
Transposed matrix A T: 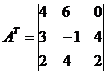
Inverse matrix A -1: 
We look for matrix X using the formula: X = B A -1 
Answer: > 
Using the online matrix calculator you can fold, subtract, multiply, transpose matrices, calculate reverse matrix, pseudoinverse matrix, rank matrices, determinant matrix, m-norm and l-norm of the matrix, raise matrix to power, multiply matrix by number, do skeletal decomposition matrices, remove linearly dependent rows from a matrix or linearly dependent columns, conduct Gaussian exclusion, solve matrix equation AX=B, do LU decomposition of a matrix,calculate the kernel (null space) of a matrix, do Gram-Schmidt orthogonalization and Gram-Schmidt orthonormalization.
The online matrix calculator works not only with decimal numbers, but also with fractions. To enter fractions, you need to enter the original matrices and enter numbers in the form a or a/b, Where a And b integers or decimals ( b positive number). For example 12/67, -67.78/7.54, 327.6, -565.
The button in the upper left corner of the matrix opens a menu (Fig. 1) for transforming the original matrix (creating an identity matrix, a zero matrix, or clearing the contents of cells).

During calculations, an empty cell is treated as zero.
For single matrix operations (i.e. transpose, inverse, pseudo-inverse, skeletal decomposition, etc.), first select a specific matrix using the radio button.
The Fn1, Fn2 and Fn3 buttons switch different groups of functions.
By clicking on the calculated matrices, a menu opens (Fig. 2), which allows you to write this matrix into the original matrices and , as well as convert the elements of the matrix in place into a common fraction, a mixed fraction or a decimal number.
Calculate the sum, difference, product of matrices online
sum, difference or product of matrices. To calculate the sum or difference of matrices, it is necessary that they be of the same dimension, and to calculate the product of matrices, the number of columns of the first matrix must be equal to the number of rows of the second matrix.
To calculate the sum, difference or product of matrices:
Online matrix inverse calculation
An online matrix calculator can be used to calculate the inverse matrix. For an inverse matrix to exist, the original matrix must be a non-singular square matrix.
To calculate the inverse matrix:
For detailed inverse matrix calculation step by step, use this matrix inverse calculator. See the theory of calculating the inverse matrix.
Calculate the determinant of a matrix online
An online matrix calculator can be used to calculate the determinant of a matrix. In order for a matrix determinant to exist, the original matrix must be a non-singular square matrix.
To calculate the determinant of a matrix:
For a detailed calculation of the determinant of a matrix step by step, use this calculator to calculate the determinant of a matrix. See the theory of calculating the determinant of a matrix.
Calculate matrix rank online
An online matrix calculator can be used to calculate the rank of a matrix.
To calculate the rank of a matrix:
To calculate the matrix rank step by step in detail, use this matrix rank calculator. See the theory of calculating the rank of a matrix.
Online pseudoinverse matrix calculation
An online matrix calculator can be used to calculate the pseudoinverse matrix. A pseudo-inverse to a given matrix always exists.
To calculate the pseudoinverse matrix:
Removing linearly dependent matrix rows or columns online
The online matrix calculator allows you to remove linearly dependent rows or columns from a matrix, i.e. create a full rank matrix.
To remove linearly dependent matrix rows or columns:
Skeletal matrix decomposition online
To perform skeletal matrix decomposition online
Solving a matrix equation or system of linear equations AX=B online
Using an online matrix calculator, you can solve the matrix equation AX=B with respect to the matrix X. In the special case, if the matrix B is a column vector, then X will be a solution to the system of linear equations AX=B.
To solve the matrix equation:
Please note that matrices and must have an equal number of rows.
Gaussian elimination or reducing a matrix to triangular (step) form online
The online matrix calculator performs Gaussian elimination for both square matrices and rectangular matrices of any rank. First, the usual Gaussian method is performed. If at some stage the leading element is equal to zero, then another option of Gaussian elimination is chosen by selecting the largest leading element in the column.
To eliminate Gaussian or reduce the matrix to triangular form
LU decomposition or LUP decomposition of a matrix online
This matrix calculator allows you to perform LU decomposition of a matrix (A=LU) or LUP decomposition of a matrix (PA=LU), where L is a lower triangular matrix, U is an upper triangular (trapezoidal) matrix, P is a permutation matrix. First, the program performs LU decomposition, i.e. such a decomposition in which P=E, where E is the identity matrix (i.e. PA=EA=A). If this is not possible, then LUP decomposition is performed. Matrix A can be either a square or a rectangular matrix of any rank.
For LU(LUP) decomposition:
Constructing the kernel (null space) of a matrix online
Using a matrix calculator, you can construct the null space (kernel) of a matrix.
To construct the null space (kernel) of the matrix.
>Hello everyone!!! Is there a formula by which you can remove scaling from a matrix without knowing the scaling factors???
We immediately remembered polar decomposition. Well, the matrix M is represented as O * P. Where O is orthogonal, and P is positive definite, symmetrical - that is, a compression or expansion matrix. Here we will take the matrix O.
The question arises. And if we expand M on the other side, we get P’ * O’. Decomposition in a different order, with different a priori matrices. Why not take O'? I struggled with the question for about five minutes until I remembered how I had given students a failure on this matter. Matrix O’ actually coincides with matrix O. If you have recently graduated from university or are still studying, you can even try to prove this fact.
So, polar expansion:
To find the positive square root of a matrix, positive science suggests calculating the eigenvalues. For each eigenvalue, find its own subspace, then carefully make the actual square root of the operator.
As I imagined what would happen for a matrix close to the identity matrix, I shuddered. Everything will die due to the inaccuracies of the float, the ranks of the matrices will go down - a complete collapse promises to happen.
Why don't noble dons try iterations that are known to be divine?
Here, the root of a number is found using Newton's method. Sequence a_(i+1) = 0.5 * (a_i + x / a_i); proudly converges to the square root of x. As a test, I took someone’s library about mat3x3 and riveted a matrix analogue.
A direct analogue of Newton’s method quickly converges in 3-4 iterations, tests pass like a breeze. The result is a polar decomposition for matrices; the efficiency of the algorithm is obvious from the elementary spectral theory of operators. Obvious after half an hour of squeaking my brain.
So, we have found the polar decomposition. The question is - why? And here I am forced to move on to the main point of my report. Teaching is evil. The time you spent remembering spectral operator theory has been successfully wasted.
The Scale Shear Rotate decomposition is searched for once. We apply the process of orthogonalization and orthonormalization to the matrix. By columns. We get an excellent matrix. And why will the result be worse? Nothing!
I saw a post with code in Pascal that calculates this same Scale Shear Rotate decomposition, and suddenly I realized that I have no arguments for polar decomposition. Which requires who knows what kind of computer technology.
Of course, there are minor objections, almost quibbles. For example, tangent space is easier to consider as orthonormal. Computationally simpler. Usually we consider dPosition/du, the normal, and the third vector is taken perpendicular to this pair. It is clear that the method is asymmetrical with respect to texture coordinates; which of them is first and which is second is completely unclear. It seems to be correct to apply the polar decomposition to the local transformation matrix.
You may notice the difference between the “correct” polar decomposition and the “incorrect” column orthogonalization process. You probably won't notice. And the picture certainly won’t get any better.
P.S. It’s also very cool to store animations in Scale Shear Rotate. Three vectors, one quaternion. Shear is almost always 0, Scale is almost always 1, constant tracks can be thrown out. And where there are non-constant tracks, there’s a way to squeeze it out by specializing the template. Or something else.
1)
Let us first consider real matrices. Suppose that the root is extracted from the matrix $%A$%, i.e. there is a matrix $%B$% such that $%B \cdot B=A$%. Let us also assume that the matrix $%B$% can be reduced to diagonal form, i.e. there is a matrix $%S$% such that $%S^(-1)BS=B"$%, where $%B"$% is a diagonal matrix. From the equalities $%B"B"=S^(-1)BSS^(-1)BS=S^(-1)BBS=S^(-1)AS$% it follows that $%A"=S^ (-1)AS$% is also a diagonal matrix, i.e. the matrices $%A$% and $%B$% are reduced to diagonal form by the same transformation, since the elements of primed matrices are the eigenvalues of unprimed ones , then the following conclusions follow from the above considerations.
1.1)If the matrix $%A$% is a symmetric positive definite matrix, then the root is extracted from it in the form of a real matrix.
1.2) The algorithm for calculating the root of such a matrix is as follows: solve the eigenvalue problem, extract the roots from the eigenvalues, compose a diagonal matrix from them, apply to it a transformation inverse to the transformation that converts the matrix $%A$% to a diagonal form.
1.3) The number of different matrices $%B$% is equal to $%2^n$%, because For each eigenvalue there are 2 root values - positive and negative.
2) For a complex matrix, the reasoning will remain valid if we replace symmetry with unitarity. The requirement of positive definiteness will naturally be removed.
3)
Solution for the general case. Let us assume that the transformation $%S$% brings the matrix $%B$% not to diagonal, but to upper triangular form, i.e. the matrix $%B"$% is upper triangular. Such a transformation exists for any square matrix. It is easy to verify that the matrix $%A"$% will also turn out to be upper triangular, and the diagonal elements of the matrix $%A"$% will be squares corresponding diagonal elements of the matrix $%B"$%. This allows you to find all the diagonal elements of the matrix $%B"$% by taking the root of the diagonal elements of the matrix $%A"$%, and then, along the chain, find all the other elements of the matrix $%B"$%. From here the following conclusions are obtained.
3.1) A root is extracted from any complex matrix; in the general case, such roots are $%2^n$%, but there may be coinciding (multiple) ones among them.
3.2) The algorithm for calculating the roots is as follows: transform the matrix $%A$% to upper triangular form, find the matrix $%B"$% using the formulated algorithm and do the inverse transformation.
3.3) A necessary and sufficient condition for the reality of the roots of a real matrix is that the diagonal elements are not negative after transforming the matrix to a triangular form. The non-negativity of the determinant is a necessary but not sufficient condition.
Addendum 1 (reply to comment). You meant "to a triangular view". In general, in paragraphs. 1, 2, everything is absolutely clear, but point 3, apparently, needs some more thought. The point is that the Gaussian method may not be reduced to the transformation $%S^(-1)AS$%, and the proof is based on this. Those. the proof is applicable only to those matrices that can be reduced to triangular form by the transformation $%S^(-1)AS$%.
Addendum 2. It seems that in paragraph 3, in general, everything is correct, you just need to use the transformation of the matrix $%A$% to the Jordan form - for this transformation there is always a matrix obtained from solving the eigenvalue problem. The problem is that the square of a Jordan matrix is not a Jordan matrix (although it is triangular and even bidiagonal). A rigorous justification of the algorithm requires proof of the following theorem: “If $%A"=B"^2$% and $%A"$% is a Jordan matrix, then $%B"$% is a triangular matrix." The statement seems true, but I don’t know how to prove it yet.
