Complex numbers and
coordinate
plane

The geometric model of the set R of real numbers is the number line. Any real number corresponds to a single point

on
number line and any point on the line
only one matches
real number!

By adding one more dimension to the number line corresponding to the set of all real numbers - the line containing the set of pure numbers

By adding to the number line corresponding to the set
of all real numbers one more dimension -
a straight line containing a set of purely imaginary numbers –
we obtain a coordinate plane in which each
the complex number a+bi can be associated
point (a; b) coordinate plane.
i=0+1i corresponds to point (0;1)
2+3i corresponds to point (2;3)
-i-4 corresponds to point (-4;-1)
5=5+1i corresponds to melancholy (5;0)

Geometric meaning of the conjugation operation

! The mating operation is axial
symmetry about the abscissa axis.
!! Conjugated to each other
complex numbers are equidistant from
origin.
!!! Vectors depicting
conjugate numbers, inclined to the axis
abscissa under same angle, But
located according to different sides from
this axis.

Image of real numbers

Picture of complex numbers

Algebraic
way
Images:
Complex number
a+bi is depicted
plane point
with coordinates
(a;b)

Examples of depicting complex numbers on the coordinate plane

(We are interested
complex numbers
z=x+yi , for which
x=-4. This is the equation
straight,
parallel axis
ordinate)
at
X= - 4
Valid
part is -4
0
X

Draw on the coordinate plane the set of all complex numbers for which:

Imaginary part
is even
unambiguous
natural
number
(We are interested
complex numbers
z=x+yi, for which
y=2,4,6,8.
Geometric image
consists of four
straight, parallel
x-axis)
at
8
6
4
2
0
X

Complex numbers

Imaginary And complex numbers. Abscissa and ordinate

complex number. Conjugate complex numbers.

Operations with complex numbers. Geometric

performance complex numbers. Complex plane.

Modulus and argument of a complex number. Trigonometric

complex number form. Operations with complex

numbers in trigonometric form. Moivre's formula.

Initial information O imaginary And complex numbers are given in the section “Imaginary and complex numbers”. The need for these numbers of a new type arose when solving quadratic equations for the caseD< 0 (здесь D– discriminant quadratic equation). For a long time these numbers were not found physical application, which is why they were called “imaginary” numbers. However, now they are very widely used in various fields of physics.

and technology: electrical engineering, hydro- and aerodynamics, elasticity theory, etc.

Complex numbers are written in the form:a+bi. Here a And b – real numbers , A i – imaginary unit, i.e. e. i 2 = –1. Number a called abscissa, a b – ordinatecomplex numbera + bi.Two complex numbersa+bi And a–bi are called conjugate complex numbers.

Main agreements:

1. Real numberAcan also be written in the formcomplex number:a+ 0 i or a – 0 i. For example, records 5 + 0i and 5 – 0 imean the same number 5 .

2. Complex number 0 + bicalled purely imaginary number. Recordbimeans the same as 0 + bi.

3. Two complex numbersa+bi Andc + diare considered equal ifa = c And b = d. Otherwise complex numbers are not equal.

Addition. Sum of complex numbersa+bi And c + diis called a complex number (a+c ) + (b+d ) i.Thus, when adding complex numbers, their abscissas and ordinates are added separately.

This definition corresponds to the rules for operations with ordinary polynomials.

Subtraction. The difference of two complex numbersa+bi(diminished) and c + di(subtrahend) is called a complex number (a–c ) + (b–d ) i.

Thus, When subtracting two complex numbers, their abscissas and ordinates are subtracted separately.

Multiplication. Product of complex numbersa+bi And c + di is called a complex number:

(ac–bd ) + (ad+bc ) i.This definition follows from two requirements:

1) numbers a+bi And c + dimust be multiplied like algebraic binomials,

2) number ihas the main property:i 2 = – 1.

EXAMPLE ( a+ bi )(a–bi) =a 2 + b 2 . Hence, work

two conjugate complex numbers is equal to the real

a positive number.

Division. Divide a complex numbera+bi (divisible) by anotherc + di(divider) - means to find the third numbere + f i(chat), which when multiplied by a divisorc + di, results in the dividenda + bi.

If the divisor is not equal to zero, division is always possible.

EXAMPLE Find (8 +i ) : (2 – 3 i) .

Solution. Let's rewrite this ratio as a fraction:

Multiplying its numerator and denominator by 2 + 3i

AND Having performed all the transformations, we get:

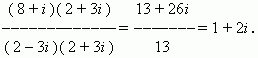
Geometric representation of complex numbers. Real numbers are represented by points on the number line:

Here is the point Ameans the number –3, dotB– number 2, and O- zero. In contrast, complex numbers are represented by points on the coordinate plane. For this purpose, we choose rectangular (Cartesian) coordinates with the same scales on both axes. Then the complex numbera+bi will be represented by a dot P with abscissa a and ordinate b (see picture). This coordinate system is called complex plane .

Module complex number is the length of the vectorOP, representing a complex number on the coordinate ( comprehensive) plane. Modulus of a complex numbera+bi denoted | a+bi| or letter r

Specifying a complex number is equivalent to specifying two real numbers a, b - the real and imaginary parts of a given complex number. But an ordered pair of numbers is depicted in Cartesian rectangular system coordinates by a point with coordinates. Thus, this point can serve as an image for the complex number z: a one-to-one correspondence is established between complex numbers and points of the coordinate plane. When using the coordinate plane to depict complex numbers, the Ox axis is usually called the real axis (since the real part of the number is taken as the abscissa of the point), and the Oy axis is the imaginary axis (since the imaginary part of the number is taken as the ordinate of the point). The complex number z represented by the point (a, b) is called the affix of this point. In this case, real numbers are represented by points lying on the real axis, and all purely imaginary numbers (for a = 0) are represented by points lying on the imaginary axis. The number zero is represented by the point O.

In Fig. 8 images of numbers are constructed.

Two complex conjugate numbers are represented by points symmetrical about the Ox axis (points in Fig. 8).

Often associated with a complex number is not only the point M, representing this number, but also the vector OM (see paragraph 93), leading from O to M; The representation of a number as a vector is convenient from the point of view of the geometric interpretation of the action of addition and subtraction of complex numbers.

In Fig. 9, a it is shown that the vector representing the sum of complex numbers is obtained as the diagonal of a parallelogram constructed on vectors representing the terms.

This rule for adding vectors is known as the parallelogram rule (for example, for adding forces or velocities in a physics course). Subtraction can be reduced to addition with opposite vector(Fig. 9, b).

As is known (item 8), the position of a point on the plane can also be specified by its polar coordinates. Thus, the complex number - the affix of the point will also be determined by the task From Fig. 10 it is clear that at the same time the modulus of a complex number is: the polar radius of the point representing the number, equal to modulus this number.

The polar angle of a point M is called the argument of the number represented by this point. The argument of a complex number (like the polar angle of a point) is not defined ambiguously; if is one of its values, then all its values ​​are expressed by the formula

All values ​​of the argument are collectively denoted by the symbol.

So, every complex number can be associated with a pair of real numbers: modulus and argument given number, and the argument is defined ambiguously. On the contrary, it corresponds to the given module and argument singular, having the given module and argument. Special properties has the number zero: its modulus is zero, and no specific value is assigned to the argument.

To achieve unambiguity in the definition of the argument of a complex number, one can agree to call one of the values ​​of the argument the main one. It is designated by the symbol. Typically, the main value of the argument is chosen to be a value that satisfies the inequalities

(in other cases inequalities).

Let us also pay attention to the values ​​of the argument of real and purely imaginary numbers:

Real and imaginary parts of a complex number (as Cartesian coordinates points) are expressed through its modulus and argument ( polar coordinates points) according to formulas (8.3):

and a complex number can be written in the following trigonometric form.

Complex numbers

Basic Concepts

The initial data on the number dates back to the Stone Age - Paleomelitic. These are “one”, “few” and “many”. They were recorded in the form of notches, knots, etc. The development of labor processes and the emergence of property forced man to invent numbers and their names. The first to appear integers N, obtained by counting items. Then, along with the need to count, people had a need to measure lengths, areas, volumes, time and other quantities, where they had to take into account parts of the measure used. This is how fractions came into being. Formal justification of the concepts of fractional and negative number was carried out in the 19th century. Set of integers Z– these are natural numbers, natural numbers with a minus sign and zero. Whole and fractional numbers formed a set rational numbers Q, but it also turned out to be insufficient for studying continuously changing variables. Genesis again showed the imperfection of mathematics: the impossibility of solving an equation of the form X 2 = 3, which is why irrational numbers appeared I. Union of the set of rational numbers Q And irrational numbers I– set of real (or real) numbers R. As a result, the number line was filled: each real number corresponded to a point on it. But on many R there is no way to solve an equation of the form X 2 = – A 2. Consequently, the need arose again to expand the concept of number. This is how complex numbers appeared in 1545. Their creator J. Cardano called them “purely negative.” The name “imaginary” was introduced in 1637 by the Frenchman R. Descartes, in 1777 Euler proposed using the first letter French number i to denote the imaginary unit. This symbol came into general use thanks to K. Gauss.

During the 17th and 18th centuries, the discussion of the arithmetic nature of imaginaries and their geometric interpretation continued. The Dane G. Wessel, the Frenchman J. Argan and the German K. Gauss independently proposed to represent a complex number as a point on the coordinate plane. Later it turned out that it is even more convenient to represent a number not by the point itself, but by a vector going to this point from the origin.

Only towards the end of the 18th and beginning of the 19th centuries did complex numbers take their rightful place in mathematical analysis. Their first use is in theory differential equations and in the theory of hydrodynamics.

Definition 1.Complex number is called an expression of the form , where x And y are real numbers, and i– imaginary unit, .

Two complex numbers and equal if and only if , .

If , then the number is called purely imaginary; if , then the number is a real number, this means that the set R WITH, Where WITH– a set of complex numbers.

Conjugate to a complex number is called a complex number.

Geometric image complex numbers.

Any complex number can be represented by a point M(x, y) plane Oxy. A pair of real numbers also denotes the coordinates of the radius vector , i.e. between the set of vectors on the plane and the set of complex numbers, one can establish a one-to-one correspondence: .

Definition 2.Real part X.

Designation: x= Re z(from Latin Realis).

Definition 3.Imaginary part complex number is a real number y.

Designation: y= Im z(from Latin Imaginarius).

Re z is deposited on the axis ( Oh), Im z is deposited on the axis ( Oh), then the vector corresponding to the complex number is the radius vector of the point M(x, y), (or M(Re z, Im z)) (Fig. 1).

Definition 4. A plane whose points are associated with a set of complex numbers is called complex plane. The abscissa axis is called real axis, since it contains real numbers. The ordinate axis is called imaginary axis, it contains purely imaginary complex numbers. The set of complex numbers is denoted WITH.

Definition 5.Module complex number z = (x, y) is called the length of the vector: , i.e. .

Definition 6.Argument complex number is the angle between the positive direction of the axis ( Oh) and vector: .

The following forms of complex numbers exist: algebraic(x+iy), trigonometric(r(cos+isin )), indicative(re i ).

Any complex number z=x+iy can be represented on XOU plane in the form of a point A(x,y).

The plane on which complex numbers are depicted is called the plane of the complex variable z (we put the symbol z on the plane).

The OX axis is the real axis, i.e. it contains real numbers. OU is an imaginary axis with imaginary numbers.

x+iy- algebraic form of writing a complex number.

Let us derive the trigonometric form of writing a complex number.

We substitute the obtained values ​​into the initial form: , i.e.

r(cos+isin) - trigonometric form of writing a complex number.

The exponential form of writing a complex number follows from Euler’s formula:
,Then

z= re i - exponential form of writing a complex number.

Operations on complex numbers.

1. addition. z 1 +z 2 =(x1+iy1)+ (x2+iy2)=(x1+x2)+i(y1+y2);

2 . subtraction. z 1 -z 2 =(x1+iy1)- (x2+iy2)=(x1-x2)+i(y1-y2);

3. multiplication. z 1 z 2 =(x1+iy1)*(x2+iy2)=x1x2+i(x1y2+x2y1+iy1y2)=(x1x2-y1y2)+i(x1y2+x2y1);

4 . division. z 1 /z 2 =(x1+iy1)/(x2+iy2)=[(x1+iy1)*(x2-iy2)]/[ (x2+iy2)*(x2-iy2)]=

Two complex numbers that differ only in the sign of the imaginary unit, i.e. z=x+iy (z=x-iy) are called conjugate.

Work.

z1=r(cos +isin ); z2=r(cos +isin ).

That product z1*z2 of complex numbers is found: , i.e. the modulus of the product is equal to the product of the moduli, and the argument of the product is equal to the sum of the arguments of the factors.

;
;

Private.

If complex numbers are given in trigonometric form.

If complex numbers are given in exponential form.

Exponentiation.

1. Complex number given in algebraic form.

z=x+iy, then z n is found by Newton's binomial formula:

- the number of combinations of n elements of m (the number of ways in which n elements from m can be taken).

; n!=1*2*…*n; 0!=1;
.

Apply for complex numbers.

In the resulting expression, you need to replace the powers i with their values:

i 0 =1 From here, to general case we get: i 4k =1

i 1 =i i 4k+1 =i

i 2 =-1 i 4k+2 =-1

i 3 =-i i 4k+3 =-i

Example.

i 31 = i 28 i 3 =-i

i 1063 = i 1062 i=i

2. trigonometric form.

z=r(cos +isin ), That

- Moivre's formula.

Here n can be either “+” or “-” (integer).

3. If a complex number is given in indicative form:

Root extraction.

Consider the equation:
.

Its solution will be the nth root of the complex number z:
.

The nth root of a complex number z has exactly n solutions (values). Root of current date nth degree has only one solution. In complex ones there are n solutions.

If a complex number is given in trigonometric form:

z=r(cos +isin ), then the nth root of z is found by the formula:

, where k=0.1…n-1.

Rows. Number series.

Let the variable a take sequentially the values ​​a 1, a 2, a 3,…, a n. Such a renumbered set of numbers is called a sequence. It is endless.

A number series is the expression a 1 + a 2 + a 3 +…+a n +…= . The numbers a 1, a 2, a 3,..., and n are members of the series.

For example.

and 1 is the first term of the series.

and n is the nth or common term of the series.

A series is considered given if the nth (common term of the series) is known.

The number series has infinite number members.

Numerators – arithmetic progression (1,3,5,7…).

The nth term is found by the formula a n =a 1 +d(n-1); d=a n -a n-1 .

Denominator – geometric progression. b n =b 1 q n-1 ;
.

Consider the sum of the first n terms of the series and denote it Sn.

Sn=a1+a2+…+a n.

Sn – nth partial amount row.

Consider the limit:

S is the sum of the series.

Row convergent , if this limit is finite (a finite limit S exists).

Row divergent , if this limit is infinite.

In the future, our task is to establish which row.

One of the simplest but most common series is the geometric progression.

, C=const.

Geometric progression isconvergent near, If
, and divergent if
.

Also found harmonic series(row
). This row divergent .