Общие сведения о прямой призме
Боковой поверхностью призмы (точнее, площадью боковой поверхности) называется сумма
площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 19.1. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра.
Доказательство. Боковые грани прямой призмы - прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Отсюда следует, что боковая поверхность призмы равна
S = a 1 l + a 2 l + ... + a n l = pl,
где a 1 ,а n - длины ребер основания, р - периметр основания призмы, а I - длина боковых ребер. Теорема доказана.
Практическое задание
Задача (22) . В наклонной призме проведено сечение , перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны l.
Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 411). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl.
Обобщение пройденной темы
А теперь давайте попробуем с вами подвести итоги пройденной темы о призме и вспомним, какими свойствами обладает призма.

Свойства призмы
Во-первых, у призмы все ее основания являются равными многоугольниками;
Во-вторых, у призмы все ее боковые грани являются параллелограммами;
В-третьих, у такой многогранной фигуры, как призма, все боковые ребра равны;
Также, следует вспомнить, что такие многогранники, как призмы могут быть прямыми и наклонными.
Какая призма называется прямой?
Если же у призмы боковое ребро расположено перпендикулярно плоскости ее основания, то такая призма носит название прямой.
Не будет лишним напомнить, что боковые грани прямой призмы являются прямоугольниками.
Какую призму называют наклонной?
А вот если же у призмы боковое ребро не расположено перпендикулярно плоскости ее основания, то можно смело утверждать, что это наклонная призма.
Какую призму называют правильной?

Если у основания прямой призмы лежит правильный многоугольник, то такая призма является правильной.
Теперь вспомним свойства, которыми обладает правильная призма.
Свойства правильной призмы
Во-первых, всегда основаниями правильной призмы служат правильные многоугольники;
Во-вторых, если рассматривать у правильной призмы боковые грани, то они всегда бывают равными прямоугольниками;
В-третьих, если сравнивать размеры боковых ребер, то в правильной призме они всегда равны.
В-четвертых, правильная призма всегда прямая;
В-пятых, если же в правильной призмы боковые грани имеют форму квадратов, то такую фигуру, как правило, называют полуправильным многоугольником.
Сечение призмы
А теперь давайте рассмотрим сечение призмы:

Домашнее задание
А теперь давайте попробуем закрепить изученную тему с помощью решения задач.
Давайте нарисуем наклонную треугольную призму, у которой расстояние между ее ребрами будет равно: 3 см, 4 см и 5 см, а боковая поверхность этой призмы будет равна 60 см2. Имея такие параметры, найдите боковое ребро данной призмы.
А вы знаете, что геометрические фигуры постоянно окружают нас не только на уроках геометрии, но и в повседневной жизни встречаются предметы, которые напоминают ту или иную геометрическую фигуру.

У каждого дома, в школе или на работе имеется компьютер, системный блок которого имеет форму прямой призмы.
Если вы возьмете в руки простой карандаш, то вы увидите, что основной частью карандаша, является призма.
Идя по центральной улице города, мы видим, что у нас под ногами лежит плитка, которая имеет форму шестиугольной призмы.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Ответ на этот вопрос "что такое призма?", как в случае с любым геометрическим термином, становится понятен, если изучить свойства данного объекта. Конечно, можно заучить сложный научный термин, согласно которому призма - один из видов многогранников, основания которого параллельны, а боковые грани являются параллелограммами, однако проще запомнить свойства объекта и тогда можно будет даже самостоятельно сформулировать понятие призмы.
Элементы призмы
Довольно простые свойства призмы сложно понять, не изучив предварительно ряд терминов, которые применяются для обозначения тех или иных элементов данного геометрического тела. Выделяют следующие элементы призмы:
- Каждая призма имеет два основания, они являются многоугольниками и расположены в параллельных плоскостях.
- Боковые грани - все грани призмы (за исключением оснований).
- Боковая поверхность - совокупность боковых граней.
- Полная поверхность - совокупность боковых граней и оснований.
- Боковые ребра - общие для боковых граней стороны.
- Высота - отрезок, проведенный от одного основания к другому перпендикулярно плоскостям, в которых они расположены.
- Диагональ - отрезок, проведенный из одной вершины призмы к другой.
- Диагональная плоскость - плоскость, которая проходит через одно из боковых ребер призмы и диагональ одного из оснований.
- Диагональное сечение - сечение, образуемое пересечением призмы и диагональной плоскости.
- Ортогональное сечение - сечение, образуемое пересечением призмы и плоскости, которая перпендикулярна боковому ребру.
- Развертка призмы - представление всех граней призмы на одной плоскости без искажения размеров граней.
Свойства призмы
Теперь, когда вы знакомы с элементами призмы, можно рассмотреть ее основные свойства, а также формулы, позволяющие находить объем и площадь фигуры:
- Основания призмы представляют собой равные многоугольники.
- Боковые грани призмы - параллелограммы.
- Все боковые ребра призмы равны между собой и параллельны.
- Ортогональное сечение перпендикулярно всем боковым ребрам.
Формулы для вычисления площади и объема
Для нахождения объема призмы существует очень простая формула: V = S*h, где S - площадь призмы, h - высота.
Чтобы найти площадь полной поверхности призмы, необходимо найти площадь ее боковой поверхности и умножить полученную величину на удвоенную площадь основания. В свою очередь, для нахождения площади боковой поверхности можно использовать формулу: S = P*l, где P - периметр перпендикулярного сечения, l - длина бокового ребра.
Особые виды призмы
Некоторые призмы имеют особые отличительные свойства, и для них придуманы специальные названия:
- параллелепипед (признак - параллелограммы в основании);
- прямая призма (признак - боковые ребра перпендикулярны основаниям);
- правильная призма (признак - многоугольник с равными сторонами и углами в основании, прямоугольники в основаниях);
- полуправильная призма (признак - квадраты в основаниях).
Призма в оптике
В оптике призмой называют объект в форме геометрического тела (призмы), выполненный из прозрачного материала. Свойства призм широко используются в оптике, в частности, в биноклях. В призматических биноклях применяются двойная призма Порро и призма Аббе, названные так в честь своих изобретателей. Эти призмы за счет особой структуры и расположения создают тот или иной оптический эффект.
Призма Порро - это призма, в основании которой лежит равнобедренный треугольник. Двойная призма Порро создается благодаря особому расположению в пространстве двух призм Порро. Двойная призма Порро позволяет переворачивать изображение, увеличивать оптическое расстояние между объективом и окуляром, сохраняя внешние габариты.
Призма Аббе - это призма, в основании которой лежит треугольник с углами - 30 о, 60 о, 90 о. призма Аббе используется, когда необходимо перевернуть изображение без отклонения линии взгляда на объект.
В основании призмы может лежать любые многоугольник – треугольник, четырехугольник, пятиугольник и т.д. Оба основания абсолютно одинаковы, а соответственно, ребра , которыми углы параллельных граней соединяются между собой, всегда параллельны. В основании правильной призмы лежит правильный многоугольник, то есть такой, у которого все стороны равны. У прямой призмы ребра между боковыми гранями перпендикулярны основанию. При этом в основании прямой призмы может лежать многоугольник с любым количеством углов. Призма, основанием которой является параллелограмм, называется параллелепипедом. Прямоугольник – частный случай параллелограмма. Если в основании лежит именно эта фигура, а боковые грани расположены к основанию под прямым углом, параллелепипед называется прямоугольным. Второе название этого геометрического тела – прямоугольная призма .Как она выглядит
Прямоугольных призм в окружении современного человека довольно много. Это, например, обычная картонная коробка из-под обуви, компьютерных комплектующих и т.п. Оглядитесь по сторонам. Даже в комнате вы наверняка увидите множество прямоугольных призм. Это и компьютерный корпус, и книжная полка , и холодильник, и шкаф, и множество других предметов. Форма чрезвычайно популярна главным образом потому, что позволяет использовать место максимально эффективно, вне зависимости от того, оформляете вы интерьер или укладываете вещи в картонные коробки перед переездом.Свойства прямоугольной призмы
Прямоугольная призма обладает рядом специфических свойств. Любая пара граней может служить ее основаниями , поскольку все соседние грани расположены друг к другу под одним и тем же углом, и угол этот составляет 90°. Объем и площадь поверхности прямоугольной призмы вычислить проще, чем у любой другой. Возьмите любой предмет, имеющий форму прямоугольной призмы. Измерьте его длину, ширину и высоту. Чтобы найти объем прямоугольного параллелепипеда , достаточно перемножить эти мерки. То есть формула выглядит так: V=a*b*h, где V – объем, a и b – стороны основания, h - высота, которая у этого геометрического тела совпадает с боковым ребром. Площадь основания вычисляется по формуле S1=a*b. Чтобы найти площадь боковой поверхности, нужно сначала вычислить периметр основания по формуле P=2(a+b), а затем умножить его на высоту. Получается формула S2=P*h=2(a+b)*h. Для вычисления полной поверхности прямоугольной призмы сложите удвоенную площадь основания и площадь боковой поверхности. Получится формула S=2S1+S2=2*a*b+2*(a+b)*h=2Сечения призмы
Определение 1. Сечением тела некоторой плоскостью α называют фигуру, состоящую из всех точек этого тела, лежащих в плоскости α .
В качестве примера рассмотрим сечение куба ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точку D и середины ребер A 1 B 1 и B 1 C 1 . Рассмотрим процесс построения сечения подробно.
Обозначим буквами E и F середины ребер A 1 B 1 и B 1 C 1 (рис. 1).
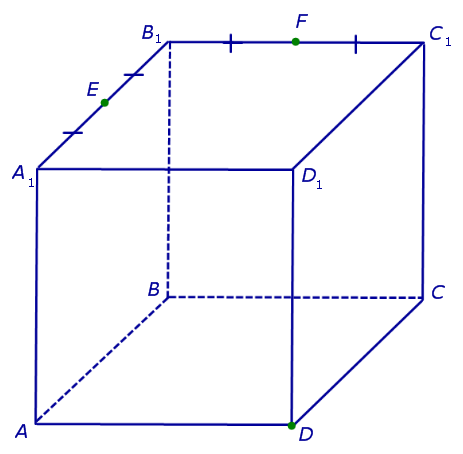
Поскольку точки E и F лежат на ребрах одной грани куба A 1 B 1 C 1 D 1 , то проведем прямую EF до пересечения с продолжениями двух других ребер этой грани . Обозначим буквой G точку пересечения прямой EF с продолжением отрезка D 1 C 1 за точку C 1 , а буквой Н - точку пересечения прямой EF с продолжением отрезка D 1 A 1 за точку A 1 . Эти точки пересечения существуют, поскольку все указанные прямые лежат в одной плоскости A 1 B 1 C 1 D 1 и не параллельны попарно (рис. 2).

Точки G и D принадлежат плоскости сечения, а, значит, и вся прямая DG лежит в плоскости сечения. С другой стороны, эти точки лежат на ребрах (или их продолжениях) одной грани куба DD 1 C 1 C . Значит, точка пересечения DG с ребром куба C 1 C (точка N ) будет принадлежать сечению. Таким образом, мы получаем еще два отрезка сечения: FN и DN (рис. 3).

Теперь, действуя аналогичным образом, проводим прямую HD, обозначаем точку перечения этой прямой с ребром AA 1 буквой M и проводим линии сечения ME и MD в плоскостях граней AA 1 B 1 B и AA 1 D 1 D (рис. 4).

В результате, как и показано на рисунке 4, получаем, что искомое сечение - пятиугольник DMEFN. наклонной треугольной призмы - треугольник KLM. Хотим обратить Ваше внимание на то, что призма на рисунке 5 изображена лежащей на одной из своих боковых граней . Такой способ представления призмы на чертеже часто очень удобен при решении задач.

Замечание 1. Все перпендикулярные сечения призмы равны между собой.
Замечание 2. С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».
Замечание 3. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы» .
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра "Резольвента" учебными материалами для подготовки к ЕГЭ по математике .
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике, физике или русскому языку на высокий балл, учебный центр "Резольвента" проводит
