Найти неопределённый интеграл (множество первообразных или "антипроизводных") означает восстановить функцию по известной производной этой функции. Восстановленное множество первообразных F (x ) + С для функции f (x ) учитывает константу интегрирования C . По скорости перемещения материальной точки (производной) может быть восстановлен закон движения этой точки (первообразная); по ускорению движения точки - её скорость и закон движения. Как видно, интегрирование - широкое поле для деятельности Шерлоков Холмсов от физики. Да и в экономике многие понятия представляются через функции и их производные и поэтому, например, можно по производительности труда в определённый момент времени (производной) восстановить объём продукции, выпущенный в соответствующее время.
Чтобы найти неопределённый интеграл, требуется довольно небольшое количество основных формул интегрирования. Но процесс его нахождения значительно труднее, чем одно лишь применение этих формул. Вся сложность относится не к интегрированию, а к приведению интегрируемого выражения к такому виду, который даёт возможность найти неопределённый интеграл по упомянутым выше основным формулам. Это означает, что для начала практики интегрирования нужно активизировать полученные в средней школе навыки преобразования выражений.
Учиться находить интегралы будем, пользуясь свойствами и таблицей неопределённых интегралов из урока об основных понятиях этой темы (откроется в новом окне).
Существует несколько методов нахождения интеграла, из которых метод замены переменной и метод интегрирования по частям - обязательный джентльменский набор каждого, кто успешно сдал высшую математику. Однако начинать осваивать интегрирование полезнее и приятнее с применением метода разложения, основанном на следующих двух теоремах о свойствах неопределённого интеграла, которые для удобства повторим здесь.
Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
 (2)
(2)
Кроме того, в интегрировании может пригодиться следующее правило: если выражение подынтегральной функции содержит постоянный множитель, то выражение первообразной домножается на число, обратное постоянному множителю, то есть
![]() (3)
(3)
Поскольку этот урок - вводный в решение задач интегрирования, важно отметить две вещи, которые либо уже на самом начальном этапе, либо несколько позже могут вас удивить. Удивление связано с тем фактом, что интегрирование - операция обратная дифференцированию и неопределённый интеграл можно справедливо называть "антипроизводной".
Первая вещь, которой не следует удивляться при интегрировании. В таблице интегралов существуют формулы, которые не имеют аналогов среди формул таблицы производной . Это следующие формулы:
![]()
![]()
Однако можно убедиться в том, что производные выражений, стоящих в правых частях этих формул, совпадают с соответствующими подынтегральными функциями.
Вторая вещь, которой не следует удивляться при интегрировании . Хотя производная любой элементарной функции представляет собой также элементарную функцию, неопределённые интегралы от некоторых элементарных функций уже не являются элементарными функциями . Примерами таких интегралов могут быть следующие:
![]()
![]()
![]()
Для выработки техники интегрирования пригодятся следующие навыки: сокращение дробей, деление многочлена в числителе дроби на одночлен в знаменателе (для получения суммы неопределённых интегралов), преобразование корней в степени, умножение одночлена на многочлен, возведение в степень. Эти навыки нужны для преобразований подынтегрального выражения, в результате которых должна получиться сумма интегралов, присутствующих в таблице интегралов.
Находим неопределённые интегралы вместе
Пример 1. Найти неопределённый интеграл
![]() .
.
Решение. Видим в знаменателе подынтегрального выражения многочлен, в котором икс в квадрате. Это почти верный признак того, что можно применить табличный интеграл 21 (с арктангенсом в результате). Выносим из знаменателя множитель-двойку (есть такое свойство интеграла - постоянный множитель можно выносить за знак интеграла, выше оно было упомянуто как теорема 3). Результат всего этого:
Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:
![]() .
.
Пример 2. Найти неопределённый интеграл
Решение. Вновь применяем теорему 3 - свойство интеграла, на основании которого постоянный множитель можно выносить за знак интеграла:
Применяем формулу 7 из таблицы интегралов (переменная в степени) к подынтегральной функции:
![]() .
.
Сокращаем получившиеся дроби и перед нами конечный ответ:
Пример 3. Найти неопределённый интеграл
![]()
Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:
Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда

![]()
объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования.
Пример 4. Найти неопределённый интеграл
Решение. Когда в знаменателе подынтегральной дроби - одночлен, можем почленно разделить числитель на знаменатель. Исходный интеграл превратился в сумму двух интегралов:
![]() .
.
Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:

Продолжаем находить неопределённые интегралы вместе
Пример 7. Найти неопределённый интеграл
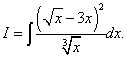
Решение. Если мы преобразуем подынтегральную функцию, возведя двучлен в квадрат и разделив почленно числитель на знаменатель, то исходный интеграл станет суммой трёх интегралов.
Первообразная функция и неопределённый интеграл
Факт 1. Интегрирование - действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F (x ) называется первообразной для функции f (x ).
Определение 1. Функция F (x f (x ) на некотором промежутке X , если для всех значений x из этого промежутка выполняется равенство F "(x )=f (x ), то есть данная функция f (x ) является производной от первообразной функции F (x ). .
Например, функция F (x ) = sin x является первообразной для функции f (x ) = cos x на всей числовой прямой, так как при любом значении икса (sin x )" = (cos x ) .
Определение 2. Неопределённым интегралом функции f (x ) называется совокупность всех её первообразных . При этом употребляется запись
∫
f (x )dx
,где знак ∫ называется знаком интеграла, функция f (x ) – подынтегральной функцией, а f (x )dx – подынтегральным выражением.
Таким образом, если F (x ) – какая-нибудь первообразная для f (x ) , то
∫
f (x )dx = F (x ) +C
где C - произвольная постоянная (константа).
Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция - "быть дверью". А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции "быть дверью", то есть её неопределённым интегралом, является функция "быть деревом + С", где С - константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции "сделана" из первообразной функции при помощи формулы, которую мы узнали, изучая производную .
Тогда таблица функций распространённых предметов и соответствующих им первообразных ("быть дверью" - "быть деревом", "быть ложкой" - "быть металлом" и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых "сделаны" эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.
Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C , а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C , например, так: 5x ³+С . Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x ³+4 или 5x ³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.
Поставим задачу интегрирования: для данной функции f (x ) найти такую функцию F (x ), производная которой равна f (x ).
Пример 1. Найти множество первообразных функции
Решение. Для данной функции первообразной является функция
Функция F (x ) называется первообразной для функции f (x ), если производная F (x ) равна f (x ), или, что одно и то же, дифференциал F (x ) равен f (x ) dx , т.е.
![]() (2)
(2)
Следовательно, функция - первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции
где С – произвольная постоянная. В этом можно убедиться дифференцированием.
Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.
Теорема (формальное изложение факта 2). Если F (x ) – первообразная для функции f (x ) на некотором промежутке Х , то любая другая первообразная для f (x ) на том же промежутке может быть представлена в виде F (x ) + C , где С – произвольная постоянная.
В следующем примере уже обращаемся к таблице интегралов, которая будет дана в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.
Пример 2. Найти множества первообразных функций:
Решение. Находим множества первообразных функций, из которых "сделаны" данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.
1) Применяя формулу (7) из таблицы интегралов при n = 3, получим
![]()
2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем
3) Так как
то по формуле (7) при n = -1/4 найдём
![]()
Под знаком интеграла пишут не саму функцию f , а её произведение на дифференциал dx . Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,
![]() ,
,
![]() ;
;
здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x , а во втором - как функция от z .
Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.
Геометрический смысл неопределённого интеграла
Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.
Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F"(x) . Значит, нужно найти такую функцию F(x) , для которой F"(x)=f(x) . Требуемая в задаче функция F(x) является первообразной от f(x) . Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) - одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy .
Назовём график первообразной функции от f(x) интегральной кривой. Если F"(x)=f(x) , то график функции y=F(x) есть интегральная кривая.
Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых , как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C .

Свойства неопределённого интеграла
Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f (x ) равен функции f (x ) с точностью до постоянного слагаемого , т.е.
![]() (3)
(3)
Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.
Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла , т.е.
Решение тригонометрических неравенств с помощью единичной окружности
При решении тригонометрических неравенств вида, где --- одна из тригонометрических функций, удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и записать ответ. Основным методом решения тригонометрических неравенств является сведение их к простейшим неравенствам типа. Разберём на примере, как решать такие неравенства.
Пример Решите неравенство.
Решение. Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит.


Для решением данного неравенства будут. Ясно также, что если некоторое число будет отличаться от какого-нибудь числа из указанного интервала на, то также будет не меньше. Следовательно, к концам найденного отрезка решения нужно просто добавить. Окончательно, получаем, что решениями исходного неравенства будут все.


Для решения неравенств с тангенсом и котангенсом полезно понятие о линии тангенсов и котангенсов. Таковыми являются прямые и соответственно (на рисунке (1) и (2)), касающиеся тригонометрической окружности.

Легко заметить, что если построить луч с началом в начале координат, составляющий угол с положительным направлением оси абсцисс, то длина отрезка от точки до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.
Пример Решите неравенство.




Решение. Обозначим, тогда неравенство примет вид простейшего: . Рассмотрим интервал длиной, равной наименьшему положительному периоду (НПП) тангенса. На этом отрезке с помощью линии тангенсов устанавливаем, что. Вспоминаем теперь, что необходимо добавить, поскольку НПП функции. Итак, . Возвращаясь к переменной, получаем, что

Неравенства с обратными тригонометрическими функциями удобно решать с использованием графиков обратных тригонометрических функций. Покажем, как это делается на примере.
Решение тригонометрических неравенств графическим методом
Заметим, что если --- периодическая функция, то для решения неравенства необходимо найти его решения на отрезке, длина которого равна периоду функции. Все решения исходного неравенства будут состоять из найденных значений, а также всех, отличающихся от найденных на любое целое число периодов функции
Рассмотрим решение неравенства ().
Поскольку, то при неравенство решений не имеет. Если, то множество решений неравенства --- множество всех действительных чисел.
Пусть. Функция синус имеет наименьший положительный период, поэтому неравенство можно решить сначала на отрезке длиной, например, на отрезке. Строим графики функций и ().

На отрезке функция синус возрастает, и уравнение, где, имеет один корень. На отрезке функция синус убывает, и уравнение имеет корень. На числовом промежутке график функции расположен выше графика функции. Поэтому для всех из промежутка) неравенство выполняется, если. В силу периодичности функции синус все решения неравенства задаются неравенствами вида: .
Решать неравенства с тангенсом мы будем с помощью единичной окружности.
Алгоритм решения неравенств с тангенсом:
- перерисовываем клише, изображённое на вышестоящем рисунке;
- на линии тангенса отмечаем $a$ и проводим до этой точки из начала координат прямую;
- точка пересечения этой прямой с полуокружностью будет закрашенной, если неравенство нестрогое и не закрашенное, если строгое;
- область будет находится снизу от прямой и до окружности, если неравенство содержит знак “$>$”, и снизу прямой и до окружности, если неравенство содержит знак “$<$”;
- для нахождения точки пересечения, достаточно найти арктангенс $a$, т.е. $x_{1}={\rm arctg} a$;
- в ответ выписывается полученный промежуток, добавляя к концам $+ \pi n$.
Примеры решения неравенств с помощью алгоритма.
Пример 1: Решить неравенство:
${\rm tg}{x} \leq 1.$
Таким образом, решение примет вид:
$x \in \left(-\frac{\pi}{2} + \pi n; \frac{\pi}{4} + \pi n\right], \ n \in Z.$
Важно! Точки $-\frac{\pi}{2}$ и $\frac{\pi}{2}$ у тангенса всегда (независимо от знака неравенства) выколоты!
Пример 2: Решить неравенство:
${\rm tg}{x} > – \sqrt{3}.$
Отмечаем на линии тангенса точку $- \sqrt{3}$ и проводим прямую из начала координат до неё. Точка пересечения этой прямой с полуокружностью будет не закрашенной, так как неравенство строгое. Область будет находится выше прямой и до окружности, так как знак неравенства $>$. найдём точку пересечения:
$x_{1} = {\rm arctg}{\left(-\sqrt{3}\right)} = -\frac{\pi}{3}.$
$t \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right).$
Возвращаемся к исходной переменной:
$\left(2x-\frac{\pi}{3}\right) \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right).$
Последнее равносильно системе неравенств
$\left\{\begin{array}{c} 2x-\frac{\pi}{3} > -\frac{\pi}{3} + \pi n, \\ 2x-\frac{\pi}{3} < \frac{\pi}{2}+\pi n, \end{array} \right.$
решив которую мы получим ответ. Действительно,
$\left\{\begin{array}{c} 2x > \pi n, \\ 2x < \frac{5 \pi}{6} + \pi n, \end{array} \right.$
$\left\{\begin{array}{c} x > \frac{\pi n}{2}, \\ x < \frac{5\pi}{12}+\frac{\pi n}{2}. \end{array} \right. $
И окончательно получаем:
$x \in \left(\frac{\pi n}{2}; \frac{5\pi}{12} + \frac{\pi n}{2}\right), \ n \in Z.$
Неравенства – это соотношения вида a › b, где a и b – есть выражения, содержащие как минимум одну переменную. Неравенства могут быть строгими — ‹, › и нестрогими — ≥, ≤.
Тригонометрические неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими функциями.
Примером простейшего тригонометрического неравенства является: sin x ‹ 1/2. Решать подобные задачи принято графически, для этого разработаны два способа.
Способ 1 — Решение неравенств с помощью построения графика функции
Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:
- На координатной оси построить синусоиду y = sin x.
- На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
- Отметить точки пересечения двух графиков.
- Заштриховать отрезок являющийся, решением примера.
Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:
![]()
Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки — . Ответ задачи можно также записать в виде очередного неравенства: ![]()
Способ 2 — Решение тригонометрических неравенств с помощью единичной окружности
Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:
- Сначала стоит начертить единичную окружность.
- Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
- Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
- После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
- Записать ответ в требуемой форме.
Разберем этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки α и β – значения
![]()
Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.

Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.

Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.

Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.
Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти. Углы
Являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.

Сложные тригонометрические неравенства
Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:

Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:

В результате должна получиться красивая кривая.
Для простоты поиска решения заменим сложный аргумент функции

