ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из которых выбрано направление и единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называются осями координат и обозначаются так: Ох, Оy, Оz, имеют свои названия: ось абсцисс, ось ординат и ось аппликат соответственно, а их общая точка - началом координат. Обычно она обозначается буквой О.
Вся система координат обозначается Охуz.
Если через оси координат Ох и Оу, Оу и Оz, Оz и Ох провести плоскости, то такие плоскости будут называться координатными плоскостями и обозначаться: Оху, Оуz, Оzх соответственно.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч — отрицательной полуосью.
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости.
Посмотрим, как это делается.
Проведем через точку М три плоскости, перпендикулярные осям координат, и обозначим через М₁, М₂ и М₃ точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат.
Первая координата точки М (она называется абсциссой и обозначается обычно буквой х) определяется так: х = ОМ₁, если М₁ - точка положительной полуоси;
х= - ОМ₁, если М₁ - точка отрицательной полуоси; х =0, если М₁ совпадает с точкой О.
Аналогично с помощью точки М₂ определяется вторая координата (ордината) у точки М,
а с помощью точки М₃ — третья координата (аппликата) z точки М.
Координаты точки М записываются в скобках после обозначения точки М (х; у; z).
Запомните, что первой указывают абсциссу, второй - ординату, третьей — аппликату.
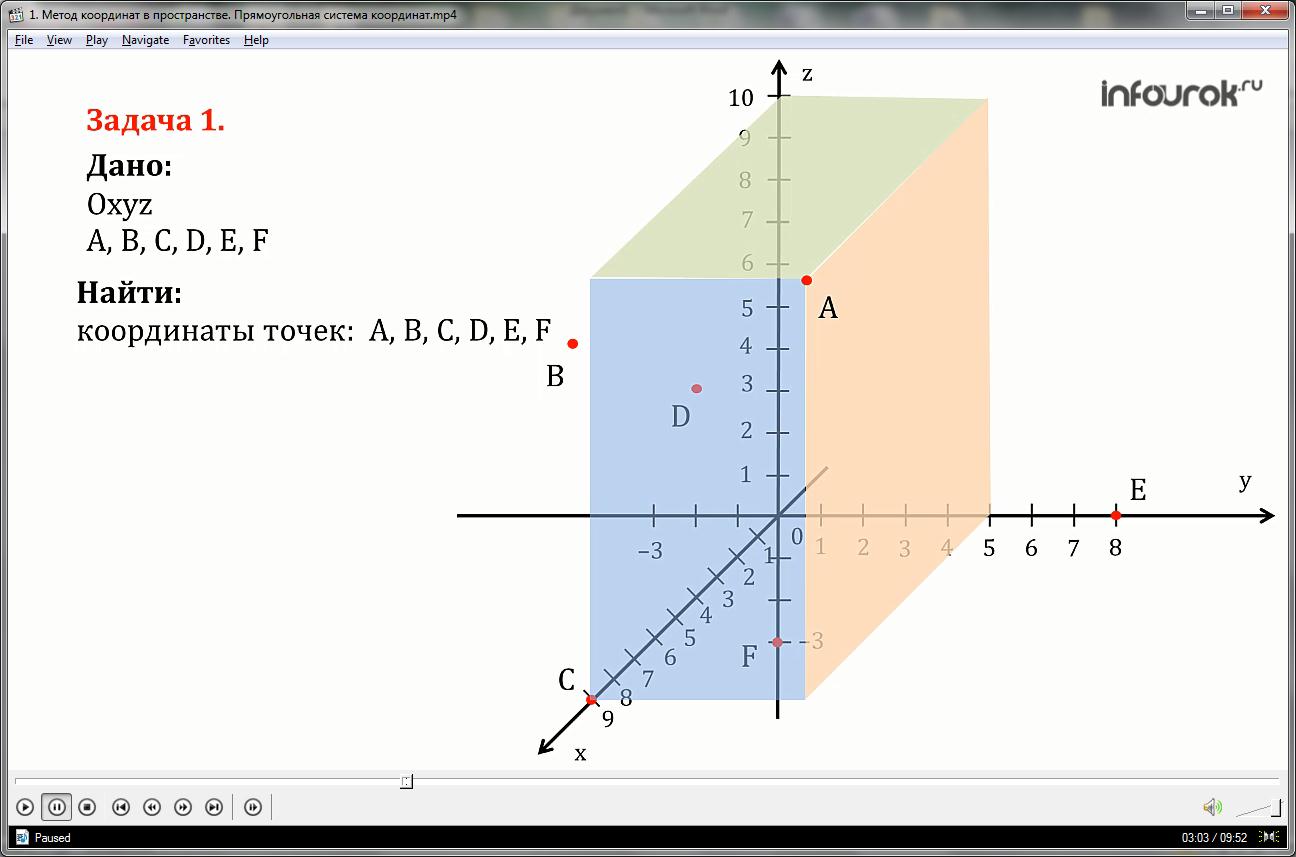
Найдем координаты точек А, В, С, D, E, F, представленные на рисунке.
Проведем через точку А три плоскости, перпендикулярные к осям координат, тогда точки пересечения этих плоскостей соответственно с осями абсцисс, ординат и аппликат будут координатами точки А. Точка А имеет координаты: абсцисса = 9, ордината = 5, аппликата = 10 и записывается это так: А (9; 5;10).
Аналогично записываются координаты следующих точек:
Точка В имеет координаты: абсцисса = 4, ордината = -3, аппликата = 6
Точка С имеет координаты: абсцисса = 9, ордината = 0, аппликата = 0
Точка имеет D координаты: абсцисса = 4, ордината = 0, аппликата = 5
Точка Е имеет координаты: абсцисса = 0, ордината = 8, аппликата = 0
Точка F имеет координаты: абсцисса = 0, ордината = 0, аппликата = -3
Если точка М (х; у; z) лежит на координатной плоскости на оси координат, то некоторые ее координаты равны нулю.
Если МЄОху (точка М принадлежит плоскости Оху), то аппликата точки М равна нулю: z=0.
Аналогично, если МЄОхz (точка М принадлежит плоскости Оxz), то у = 0, а если МЄОуz (точка М принадлежит плоскости Oyz), то х = 0.
Если МЄОх (точка М лежит на оси абсцисс) ордината и аппликата точки М равны нулю: у=о и z=0. В нашем примере это точка С.
Если МЄОу (точка М лежит на оси ординат), то х=0 и z=0. В нашем примере это точка Е.
Если МЄОz (точка М лежит на оси аппликат), то х = 0 и у = 0. В нашем примере это точка F.
Если все три координаты точки М равны нулю, то это значит, что М=О (0; 0; 0) - начало координат.
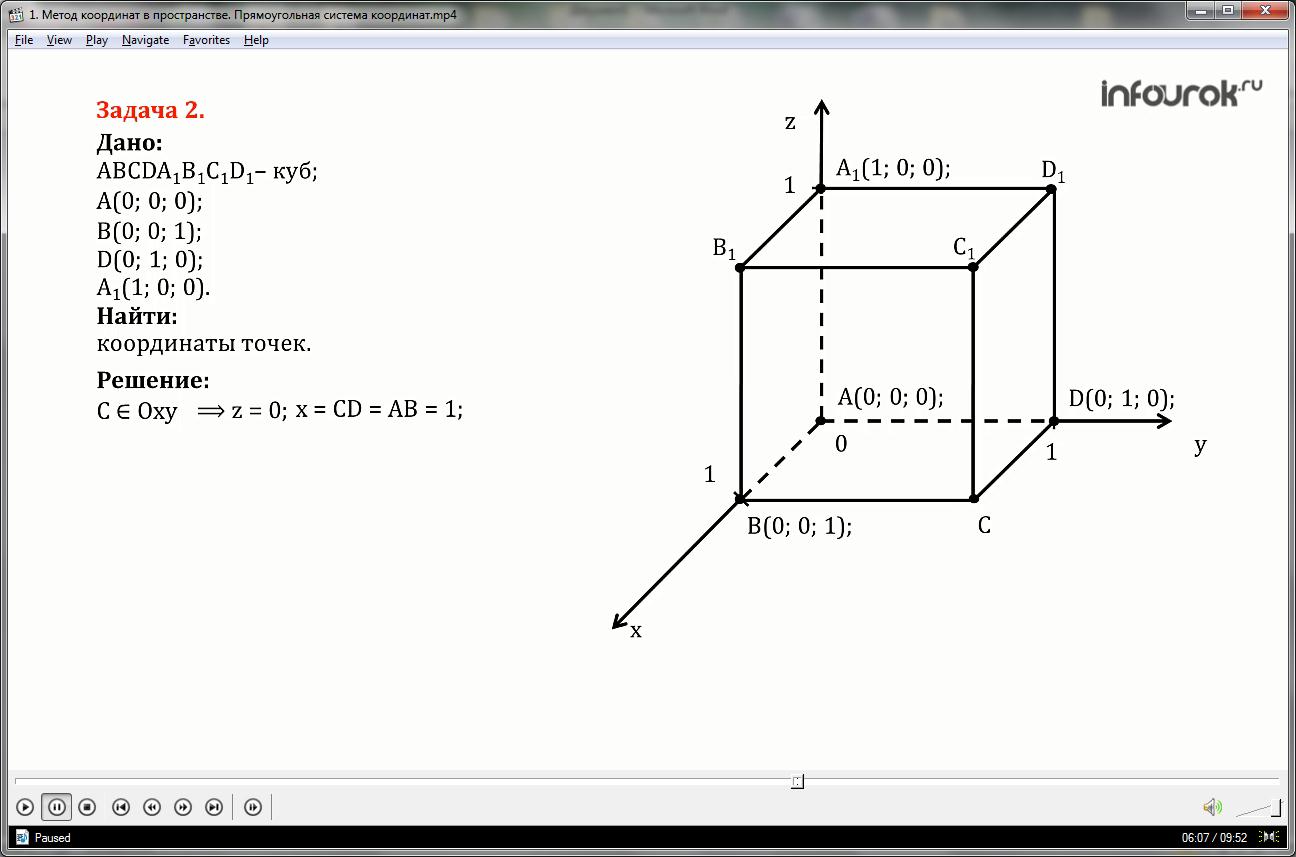
Даны координаты четырех вершин куба ABCDA 1 B 1 C 1 D 1: A(0; 0; 0); B(0; 0; 1); D(0; 1; 0); A 1 (1; 0; 0). Найдите координаты остальных вершин куба.
Так как фигура — куб, то все стороны равны единице, все грани являются квадратами.
Точка С принадлежит плоскости Оху, то есть ее координата z равна нулю, координата х равна стороне СД и равна АВ, значит равна единице, координата игрек равна стороне куба СВ, значит равна АД и равна единице.
Аналогично, Точка В 1 принадлежи плоскости Охz, то еcть ее координата y равна нулю, координата х равна стороне координата х равна стороне А1B1 и равна АВ значит равна единице, координата зет равна стороне куба В В1значит равна АА1 и равна единице.
Точка Д 1 принадлежи плоскости Оуz, то еcть ее координата х равна нулю, координата у равна стороне А 1 Д 1 и равна АД, значит равна единице, координата зет равна стороне куба А 1 В 1 , значит равна АВ и равна единице.
Точка С 1 не принадлежит никакой плоскости, то еcть все координаты отличны от нуля, координата х равна стороне C 1 D 1 и равна АB, значит равна единице, координата игрек равна стороне куба В 1 С 1 , значит равна АД и равна единице, и координата зет равна стороне CC 1 , то есть AA 1 и также равна единице.
Найдите координаты проекций точки C(; ;) на координатные плоскости Oxy, Oxz, Oyz и координатные оси Ox, Oy, Oz.
1) опустим перпендикуляры на плоскость Oxy— это CN, на плоскость Oxz - CL, и на плоскость Oyz прямая CR.
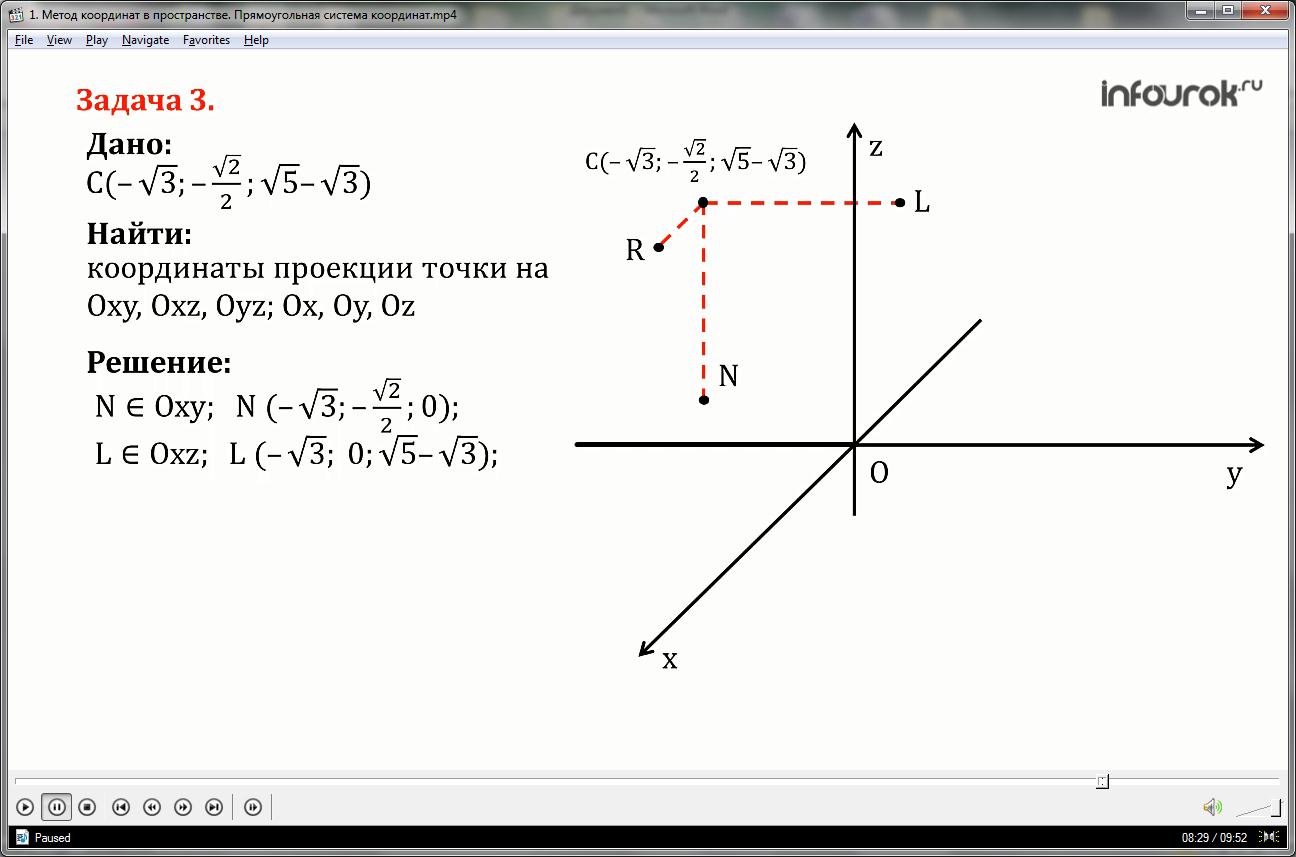
Таким образом, проекция точки С на плоскость Oxy это точка N и она имеет координаты икс равный минус корень из трех, игрек равен минус корень из двух на два, зет равнен нулю.
Проекция точки С на плоскость Oxz - это точка L и она имеет координаты икс равен минус корень из трех, игрек равен нулю, зет равен корень из пяти минус корень из трех.
Проекция точки С на плоскость Oyz- это точка R и она имеет координаты икс равен нулю, игрек равен минус корень из двух на два, зет равен корень из пяти минус корень из трех.
2)Из точки N проводим перпендикуляры на ось Ох - прямая NK, а на Оу - прямая NG, и на ось Оz проводим перпендикуляр из точки R- это прямая RP.
Проекция точки С на ось Ох - точка К имеет координаты икс равный минус корень из трех, а игрек и зет равны нулю.
Проекция точки С на ось Оy- точка G имеет координаты икс и зет равны нулю, игрек равен минус корень из двух на два.
Проекция точки С на ось Оz- точка P имеет координаты икс и игрек равны нулю, зет равный корень из пяти минус корень из трех.
Министерство Образования Российской Федерации
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школы №18»
РЕФЕРАТ
ПО ГЕОМЕТРИИ
ТЕМА: МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Выполнил ученик 11 класса «C»
Мельник Роман
Руководитель
учитель математики Бакшеева И.К.
Бийск - 2008г
Содержание
Введение ……………………………………………………………..… 3.
Глава 1.
Метод координат: история развития………………………….............4
Координаты точки в пространстве……………………………….…...5
Задание фигур в пространстве………………………………….……...8
Глава 2.
Разложение вектора по координатным векторам. Координаты
вектора………………………………………………………………..……..10
Линейные операции над векторами в координатах…………..………12
Условие коллинеарности двух векторов в координатах……………..13
Простейшие задачи в координатах………………………………….....14
Скалярное произведение векторов и вычисление угла между векторами через их координатами……………………………………….…………15
Вычисление углов между прямыми и плоскостями…………………..16
4. Глава 3.
4.1. Применение координатного метода к решению стереометрических
задач………………………………………………………..…………….. 19
Заключение. ……………………………………………………………. .26
Список литературы……………………………………………………... 27
Введение
Тема моей работы «Метод координат в пространстве». Данная тема актуальна на сегодняшний момент для любого выпускника средней школы так как:
Цель работы: систематизировать знания по данной теме и рассмотреть применение данного метода при решении различных стереометрических задач.
Для достижения цели были поставлены следующие задачи:
позволяет многие экзаменационные геометрические задачи решать аналитически, что требует меньшего объема знаний по геометрии и значительно сокращает время выполнения;
данный метод лежит в основе аналитической геометрии, которая изучается в курсе высшей математики.
изучить теоретический материал по теме;
систематизировать и обобщить изученный материал;
выявить особенности применения метода;
рассмотреть применение метода координат к решению стереометрических задач;
сравнить применение метода координат с другими методами к решению стереометрических задач.
Применяемые методы :
метод анализа и синтеза,
метод сравнения.
Глава 1
1. Метод координат: история развития.
Метод координат – это способ определять положение точки или тела с помощью чисел или других символов.
Числа, с помощью которых определяется положение точки, называют координатами точки.
Хорошо известные нам географические координаты определяют положение точки на поверхности Земли – каждая точка на земной поверхности имеет две координаты: широту и долготу.
Чтобы определить положение точки в пространстве, нужны три числа. Например, чтобы определить положение спутника, можно указать высоту его над поверхностью Земли, а также широту и долготу точки, над которой он находится.
С помощью метода координат можно изложить почти весь курс школьной геометрии без единого чертежа, используя только числа и алгебраические операции. Например, окружность можно определить как совокупность точек, удовлетворяющих уравнению, а прямую линию как совокупность точек удовлетворяющих уравнению . Таким образом, с помощью данного метода удалось связать между собой, казалось бы, совершенно разные науки алгебру и геометрию. Данное установление связи было, по существу, революцией в математике. Оно восстановило математику как единую науку.
. Таким образом, с помощью данного метода удалось связать между собой, казалось бы, совершенно разные науки алгебру и геометрию. Данное установление связи было, по существу, революцией в математике. Оно восстановило математику как единую науку.
Создателем метода координат считают французского философа и математика Рене Декарта (1596-1650), который в последней части большого философского трактата Декарта, вышедшего в 1637 году, дал описание метода координат и его применение к решению геометрических задач.
Развитие идей Декарта привело к возникновению особой ветви математики, которую теперь называют аналитической геометрией.
Само это название выражает основную идею теории. Аналитическая геометрия – это та часть математики, которая решает геометрические задачи аналитически (т.е. алгебраическими) средствами.
Наряду с Декартом основоположником аналитической геометрии является замечательный французский математик П.Ферма. С помощью метода координат Ферма изучил прямые линии и кривые второго порядка. Изучение аналитической геометрии в пространстве трех измерений существенно продвинул в XVIII веке А.Клеро. Явно и последовательно аналитическую геометрию на плоскости и в трехмерном пространстве изложил Л.Эйлер в 1748 г. в учебнике «Введение в анализ бесконечных».
В
XIX
веке был сделан еще один шаг в развитии геометрии – изучены многомерные пространства. Основной идеей для творцов теории была аналогия с «Геометрией» Декарта. У него точка на плоскости - это пара чисел 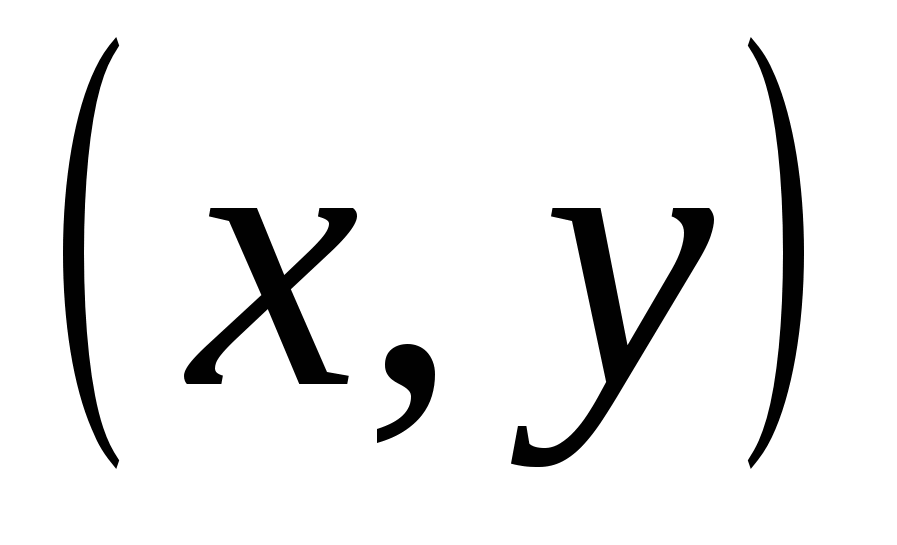 , точка в трехмерном пространстве – тройка чисел
, точка в трехмерном пространстве – тройка чисел 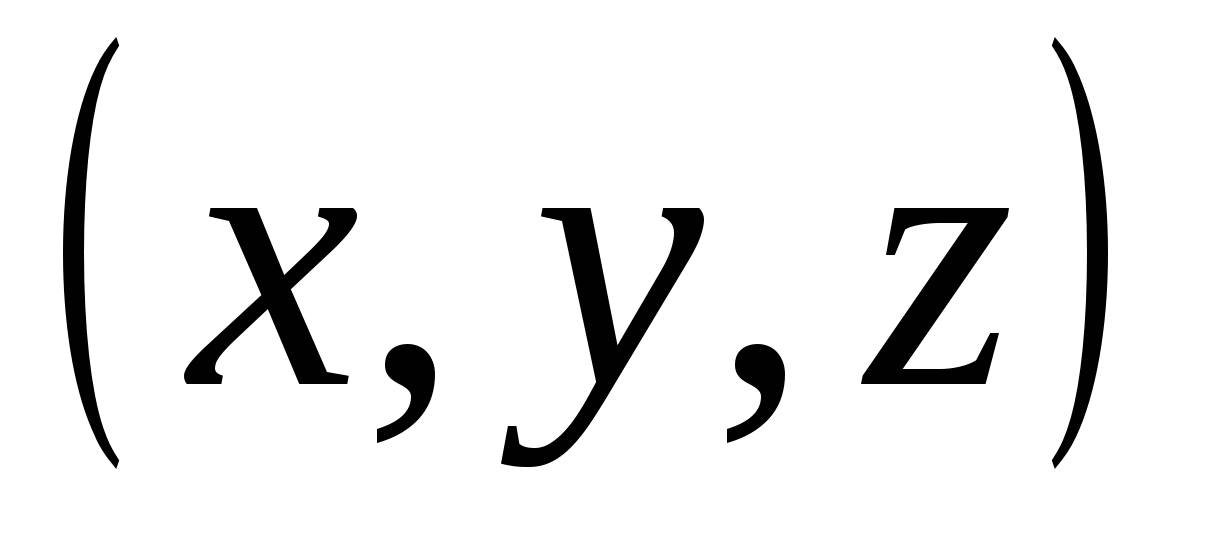 ; в новой теории точка четырехмерного пространства – это четверка чисел
; в новой теории точка четырехмерного пространства – это четверка чисел 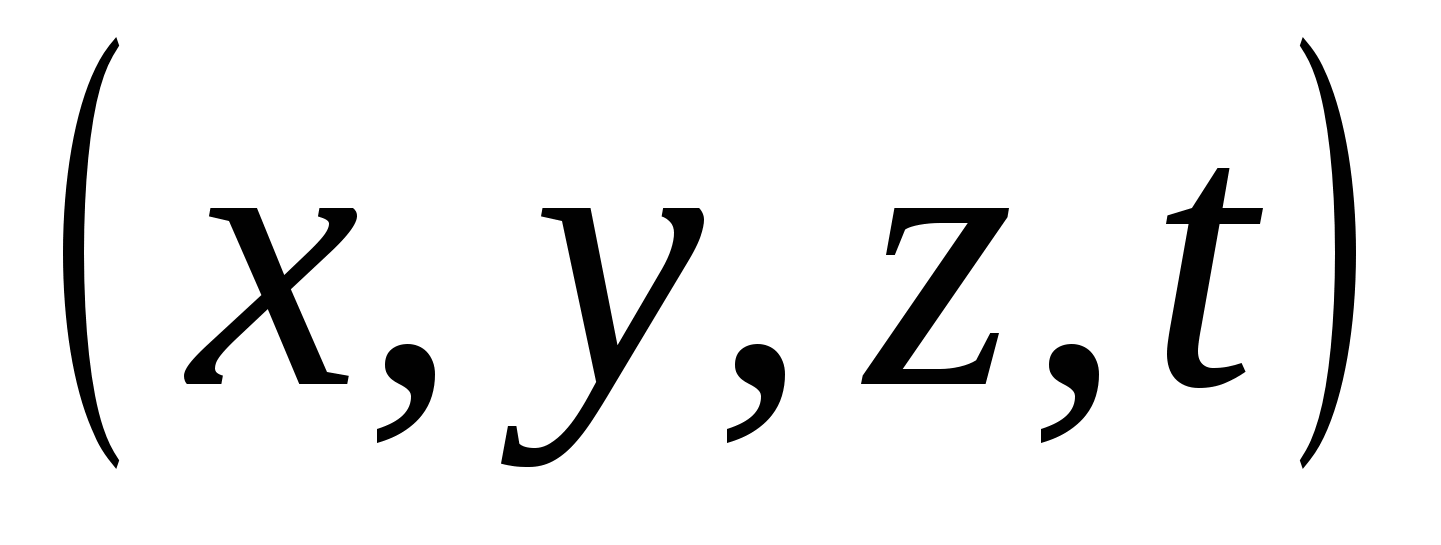 . У Декарта
. У Декарта 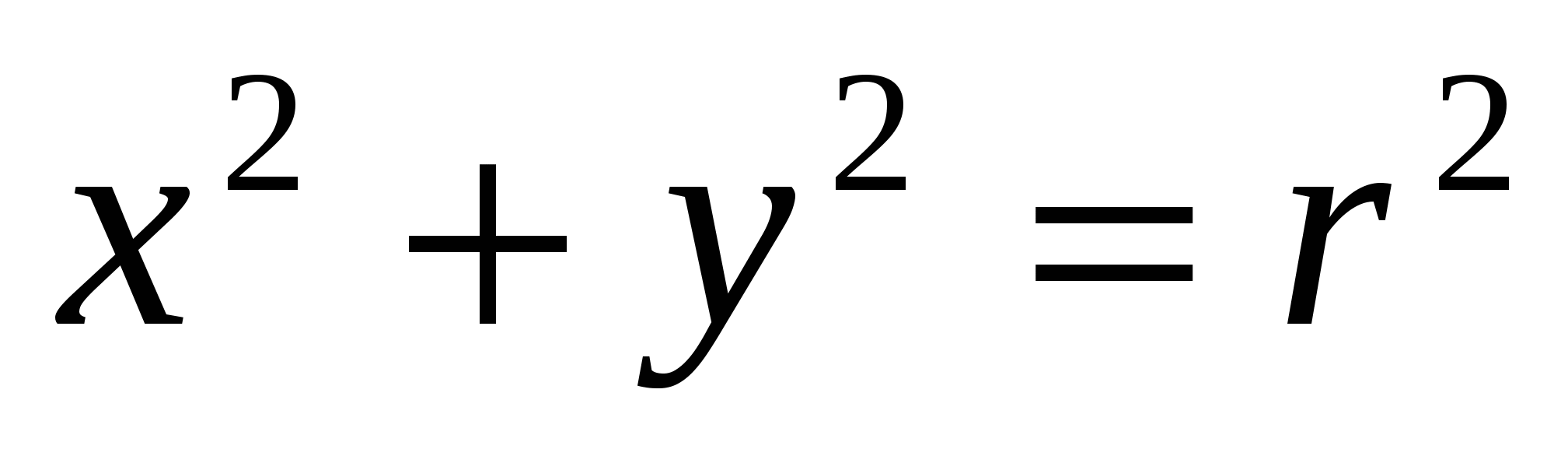 - уравнение окружности на плоскости,
- уравнение окружности на плоскости,  - уравнение поверхности шара в трехмерном пространстве; в новой теории
- уравнение поверхности шара в трехмерном пространстве; в новой теории 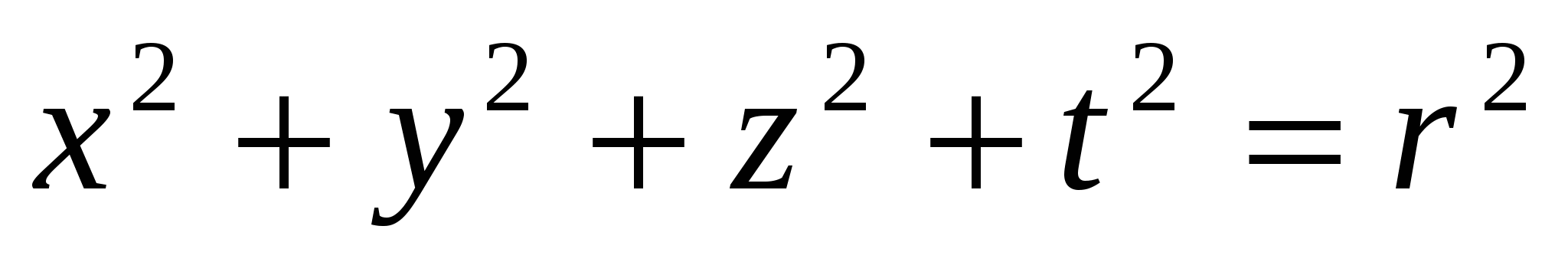 поверхность сферы в четырехмерном пространстве. Аналогичным образом в
n
-
мерной геометрии рассматриваются плоскости, прямые, расстояния между точками, углы между прямыми и т.д.
поверхность сферы в четырехмерном пространстве. Аналогичным образом в
n
-
мерной геометрии рассматриваются плоскости, прямые, расстояния между точками, углы между прямыми и т.д.
Идеи многомерной геометрии прочно вошли в математику в конце XIX века, а в самом начале XX века, они нашли применение в специальной теории относительности, где к трем пространственным координатам добавляется четвертая – время. Таким образом, идеи геометрии Декарта, развитые учеными последующих поколений, лежат в основе современной науки.
2. Координаты точки в пространстве .
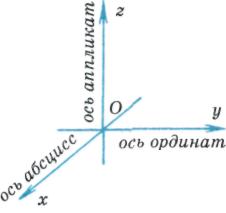 Говорят, что задана прямоугольная (декартовая) система координат, если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков. Плоскости, проходящие соответственно через оси координат
Говорят, что задана прямоугольная (декартовая) система координат, если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков. Плоскости, проходящие соответственно через оси координат 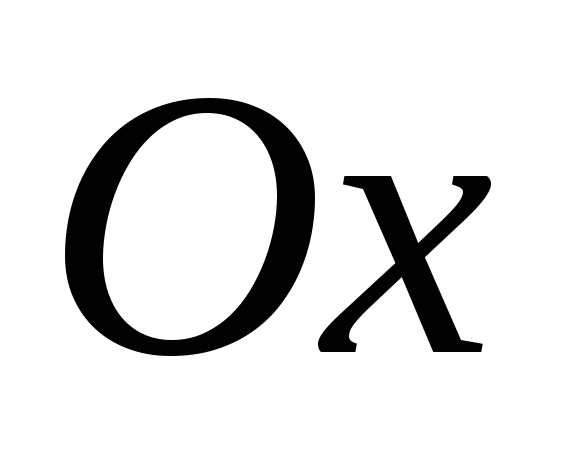 и
и 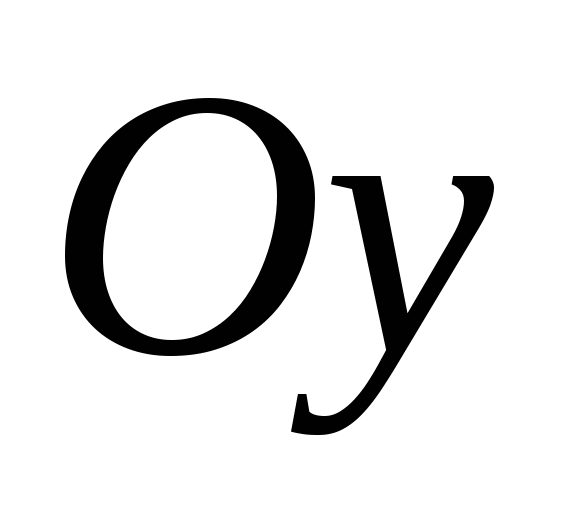 ,
, 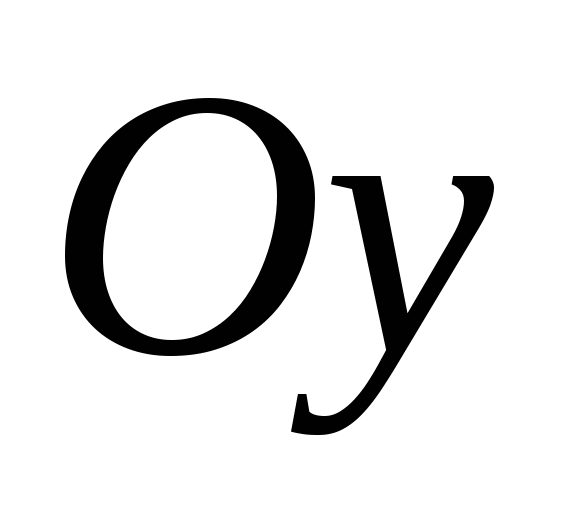 и
и  ,
,  и
и 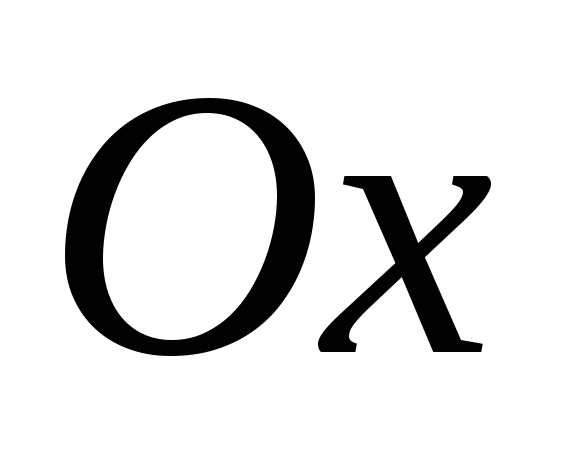 , называются
координатными плоскостями
и обозначаются
, называются
координатными плоскостями
и обозначаются 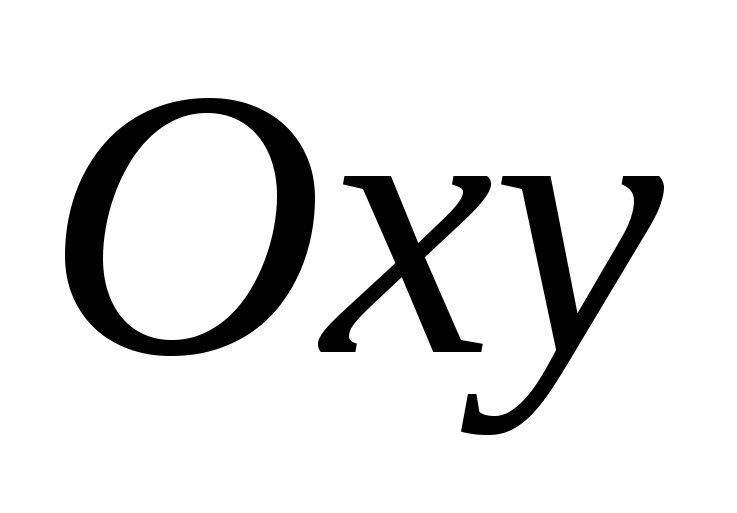 ,
, 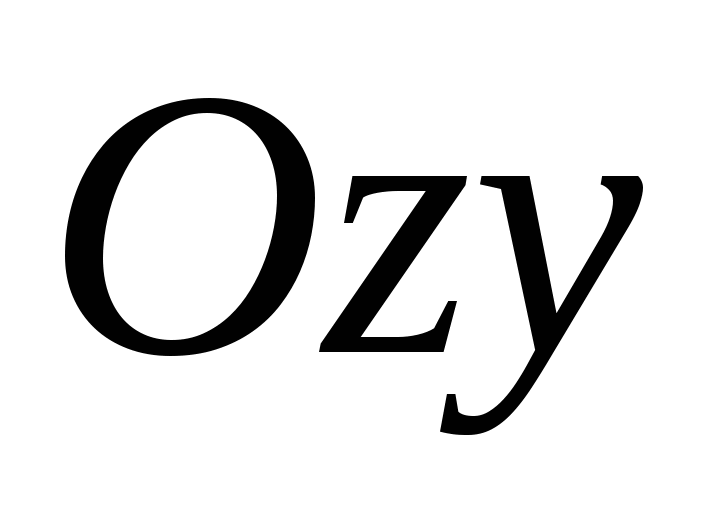 ,
,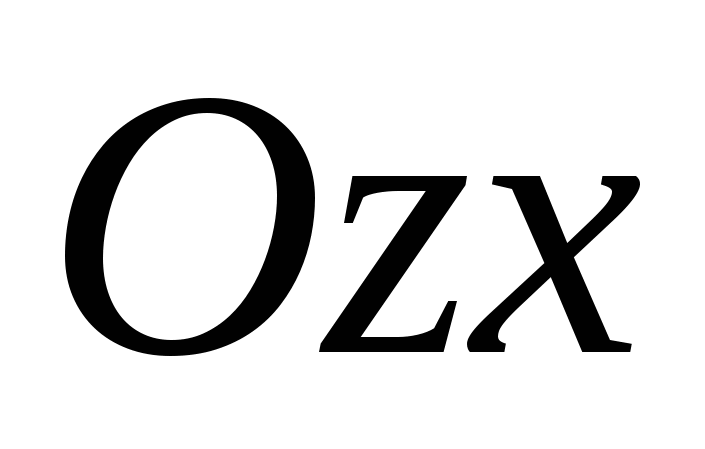 .
.
К оординатами точки в пространстве называются координаты проекций этой точки на координатные оси.
оординатами точки в пространстве называются координаты проекций этой точки на координатные оси.
Координаты точек: 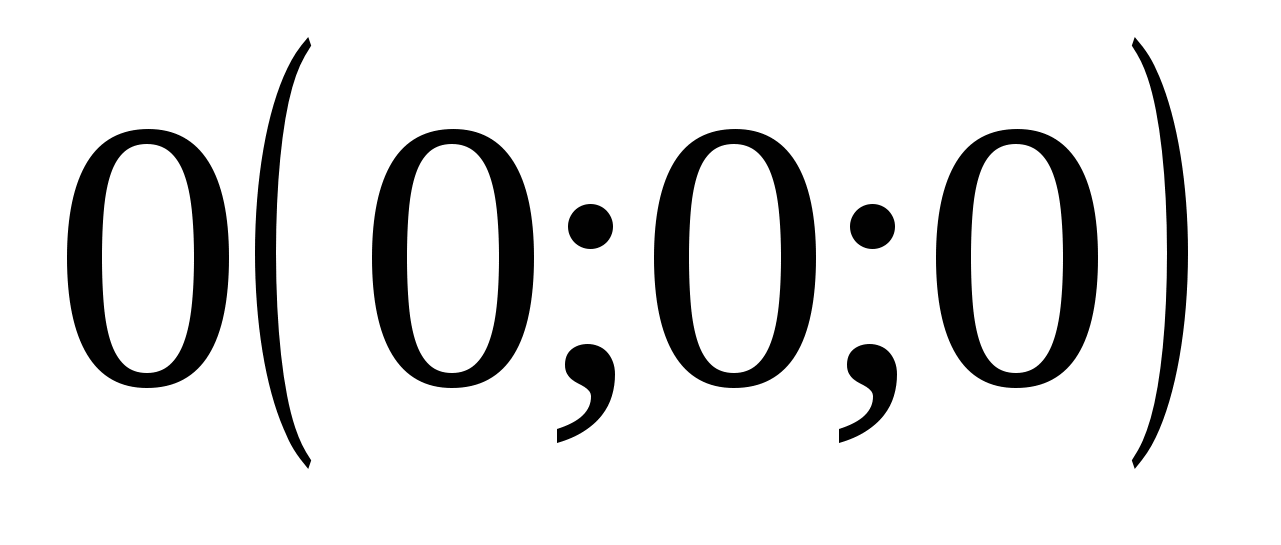 ,
, 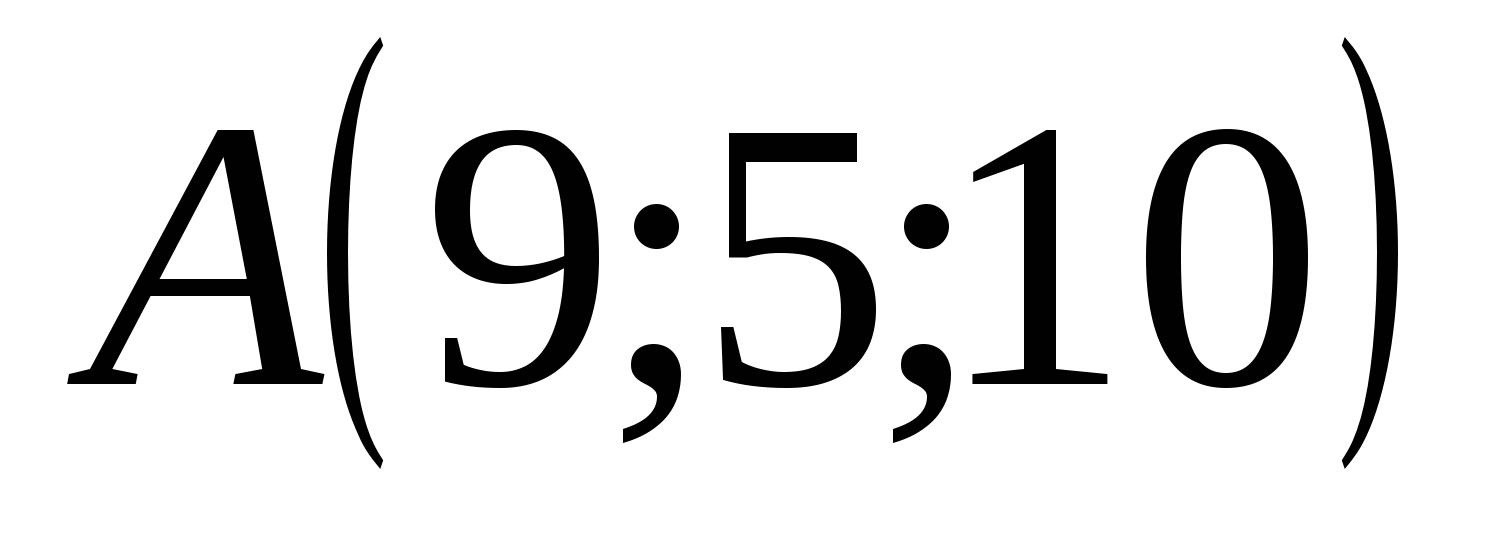 ,
, 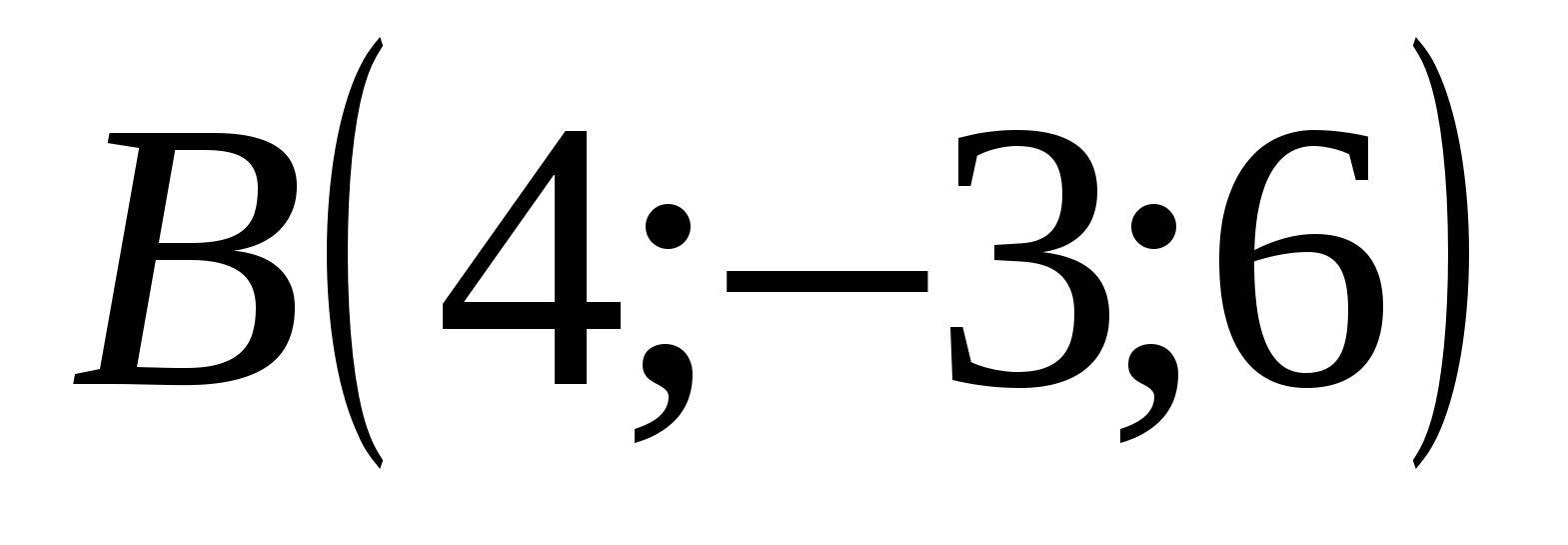 ,
, 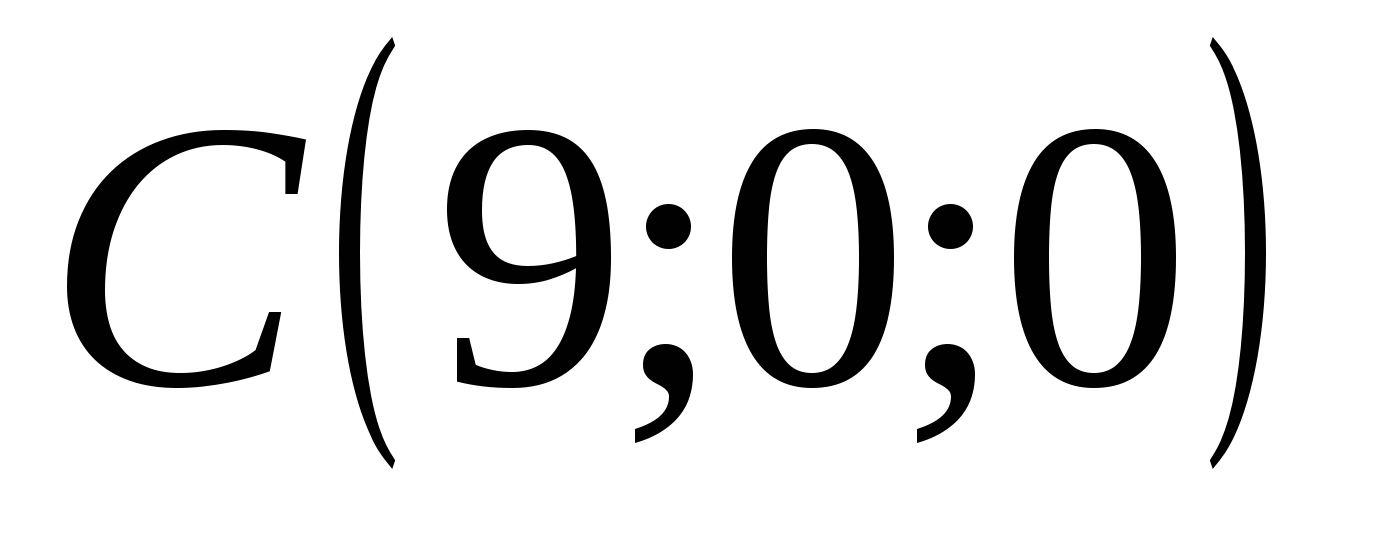 ,
, 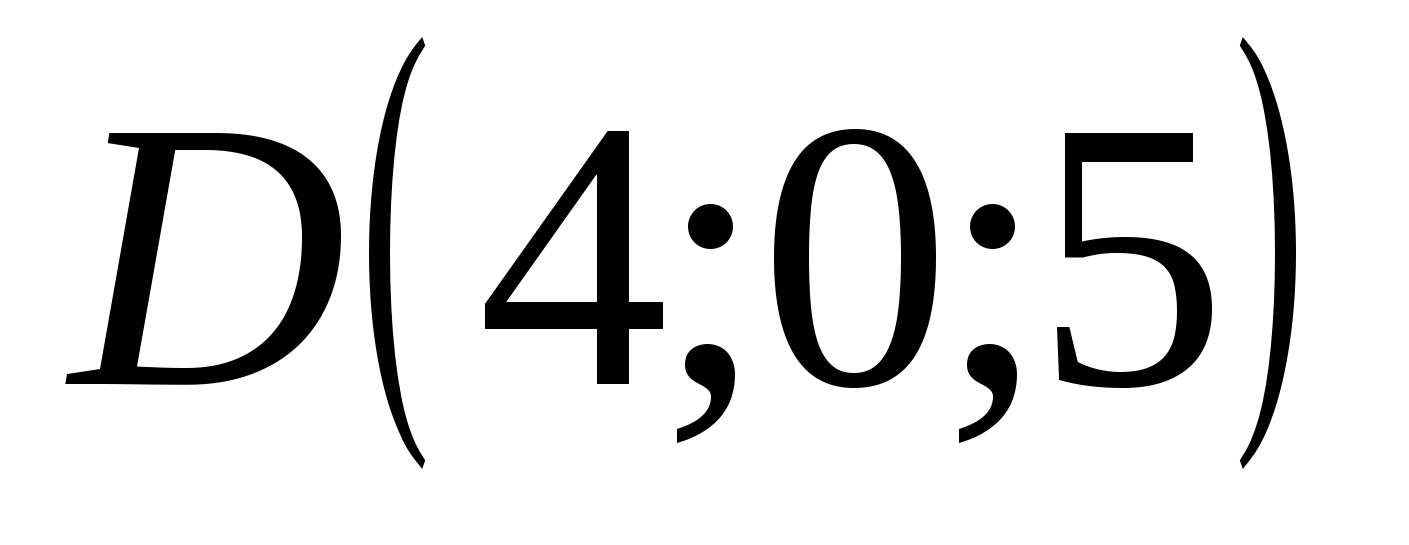 ,
, 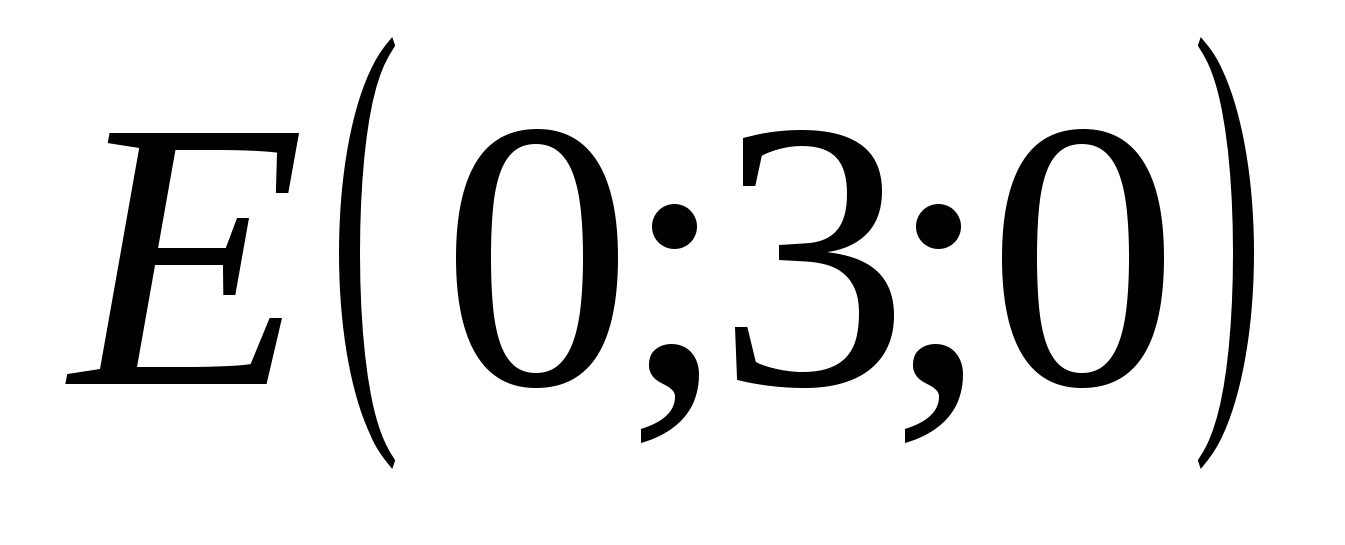 ,
, 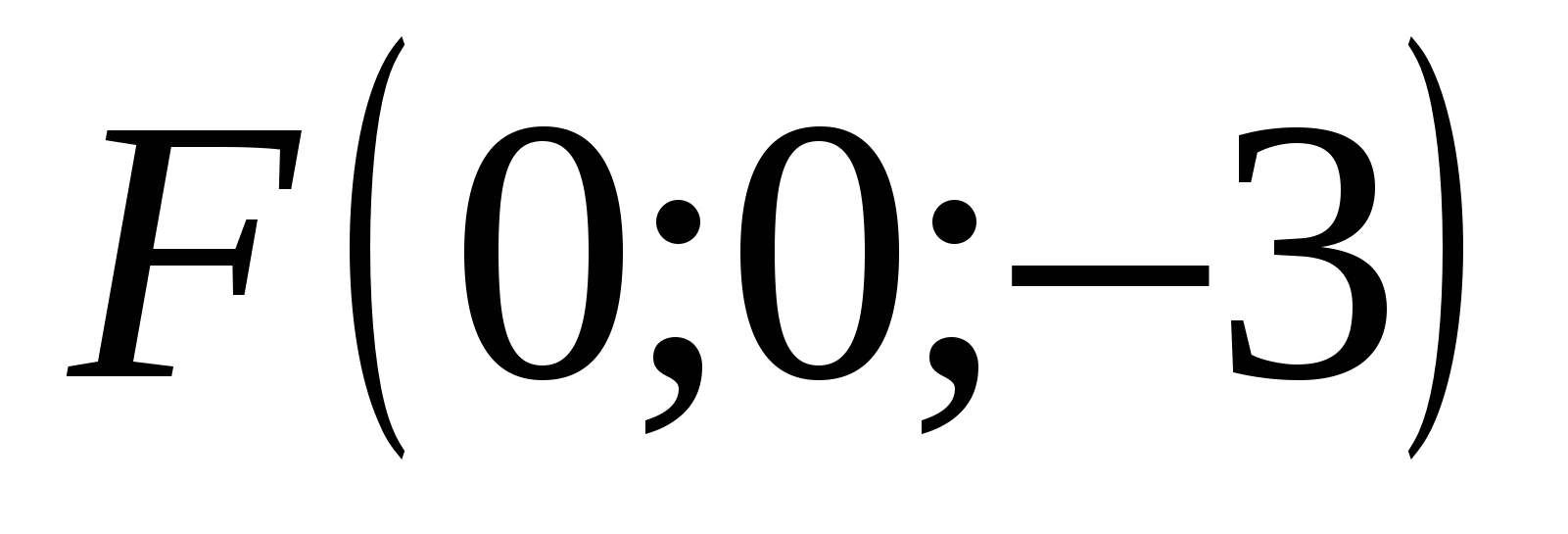 .
.
В пространстве, кроме координатных осей, удобно рассматривать еще координатные плоскости, т.е. плоскости, проходящие через две какие-либо оси. Таких плоскостей три:
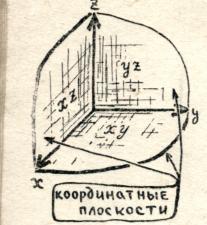
Плоскость ![]() (проходящая через оси
(проходящая через оси  и
и 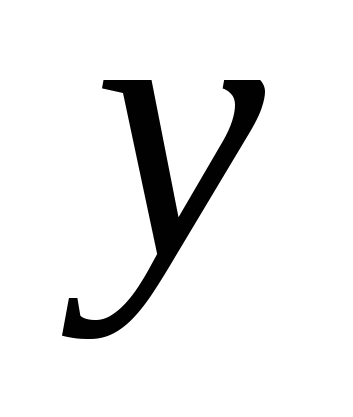 )- множество точек вида
)- множество точек вида , где
, где  и
и 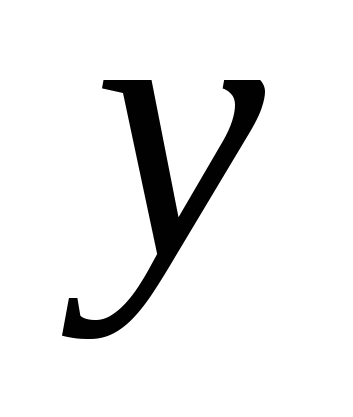 - любые числа;
- любые числа;
Плоскость 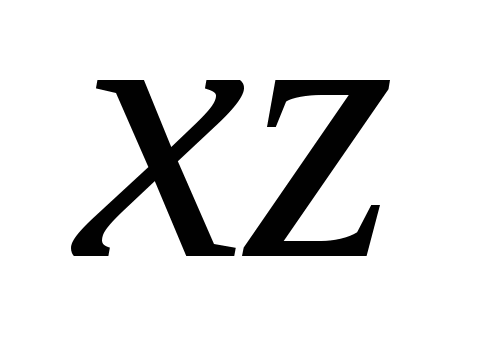 (проходящая через оси
(проходящая через оси  и
и  )- множество точек вида
)- множество точек вида 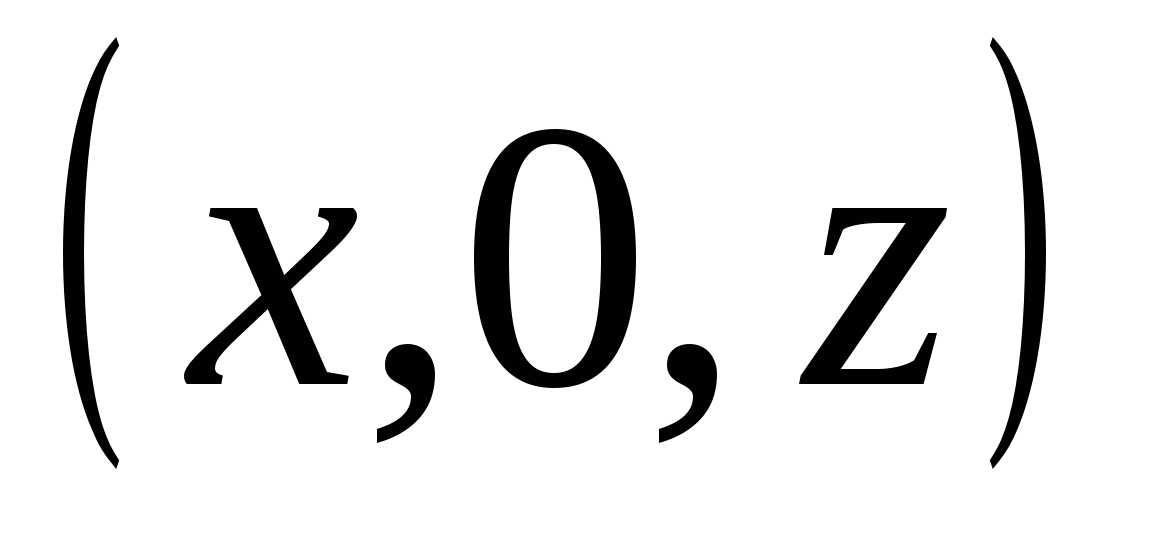 , где
, где  и
и  - любые числа;
- любые числа;
Плоскость  (проходящая через оси
(проходящая через оси 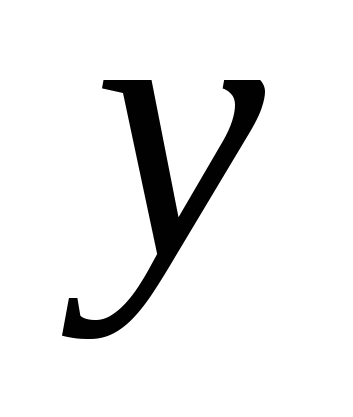 и
и  )- множество точек вида
)- множество точек вида 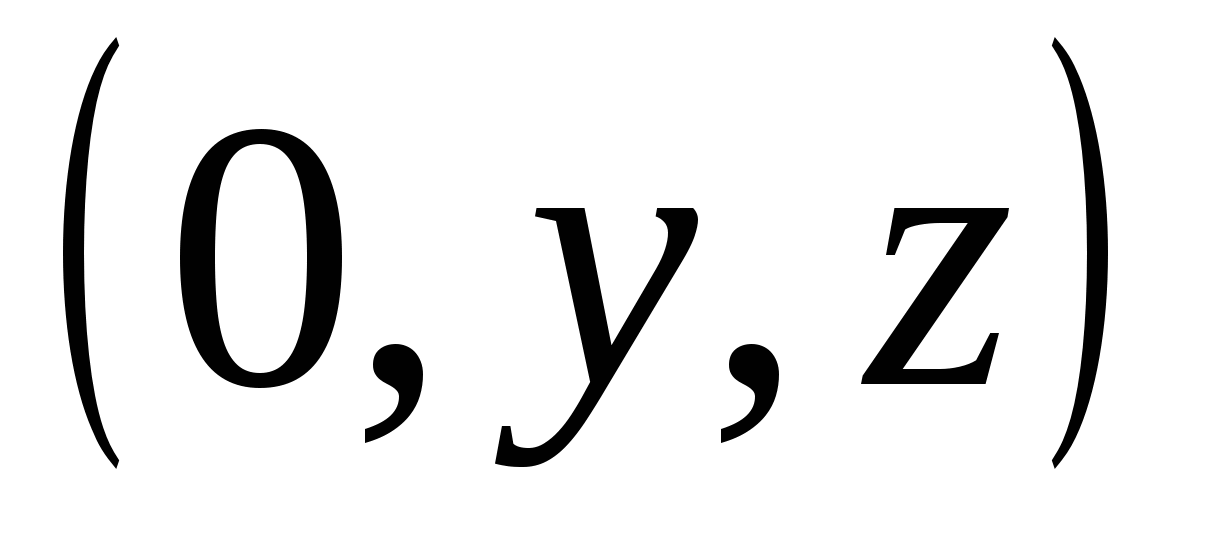 , где
, где 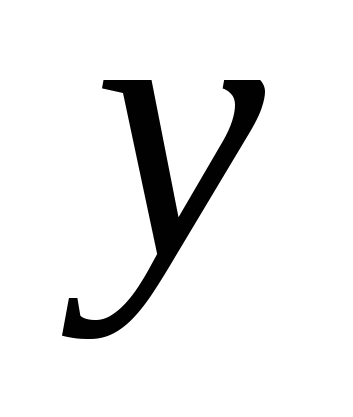 и
и  - любые числа.
- любые числа.
Для любой точки М пространства можно найти три числа 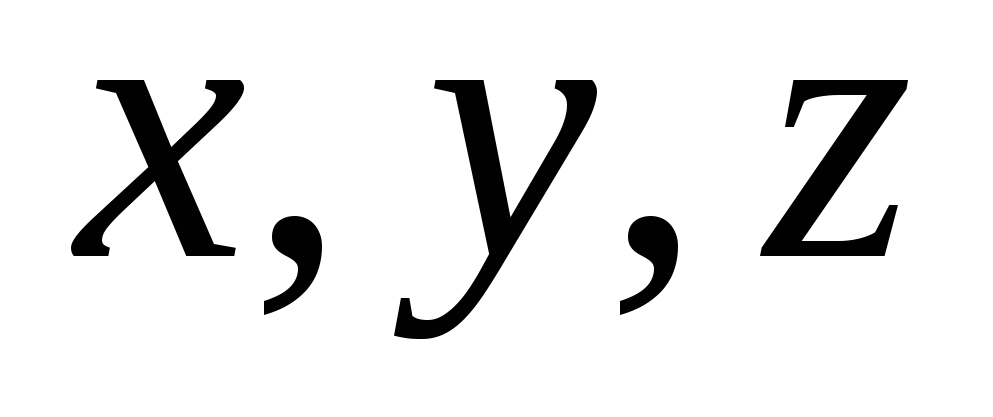 , которые будут служить ее координатами.
, которые будут служить ее координатами.
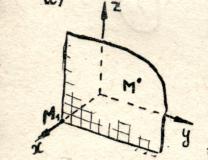 Чтобы найти первое число
Чтобы найти первое число  , проведем через точку М плоскость, параллельную координатной плоскость
, проведем через точку М плоскость, параллельную координатной плоскость  (перпендикулярную к оси
x
).Точка пересечения этой плоскости с осью
(перпендикулярную к оси
x
).Точка пересечения этой плоскости с осью  (точка М
1
) имеет на этой оси координату
(точка М
1
) имеет на этой оси координату  .Это число
.Это число  - координата точки М
1
на оси
- координата точки М
1
на оси  - называется
абсциссой
точки М.
- называется
абсциссой
точки М.
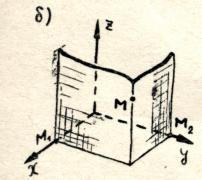 Чтобы найти вторую координату, через точку М проводят плоскость параллельную плоскости
Чтобы найти вторую координату, через точку М проводят плоскость параллельную плоскости 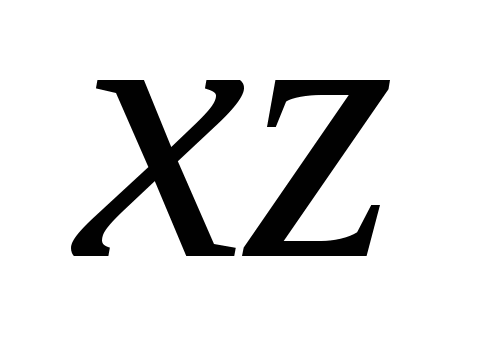 (перпендикулярную к оси
y
), находят на оси
y
точку М
2
. Число
y
– координата точки М
2
на оси
y
– называется
ординатой
точки М.
(перпендикулярную к оси
y
), находят на оси
y
точку М
2
. Число
y
– координата точки М
2
на оси
y
– называется
ординатой
точки М.
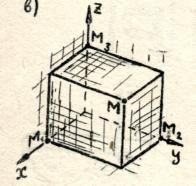 Третью координату точки М найдем, проведя аналогичные построения, но перпендикулярно оси z
. Полученное число z
назовем аппликатой
точки М.
Третью координату точки М найдем, проведя аналогичные построения, но перпендикулярно оси z
. Полученное число z
назовем аппликатой
точки М.
3. Задание фигур в пространстве.
Также как на плоскости, координаты в пространстве дают возможность задавать с помощью чисел и числовых соотношений не только точки, но и линии, поверхности и другие множества точек. Посмотрим, например, какое множество точек получится, если задать только две координаты, а третью считать произвольной.
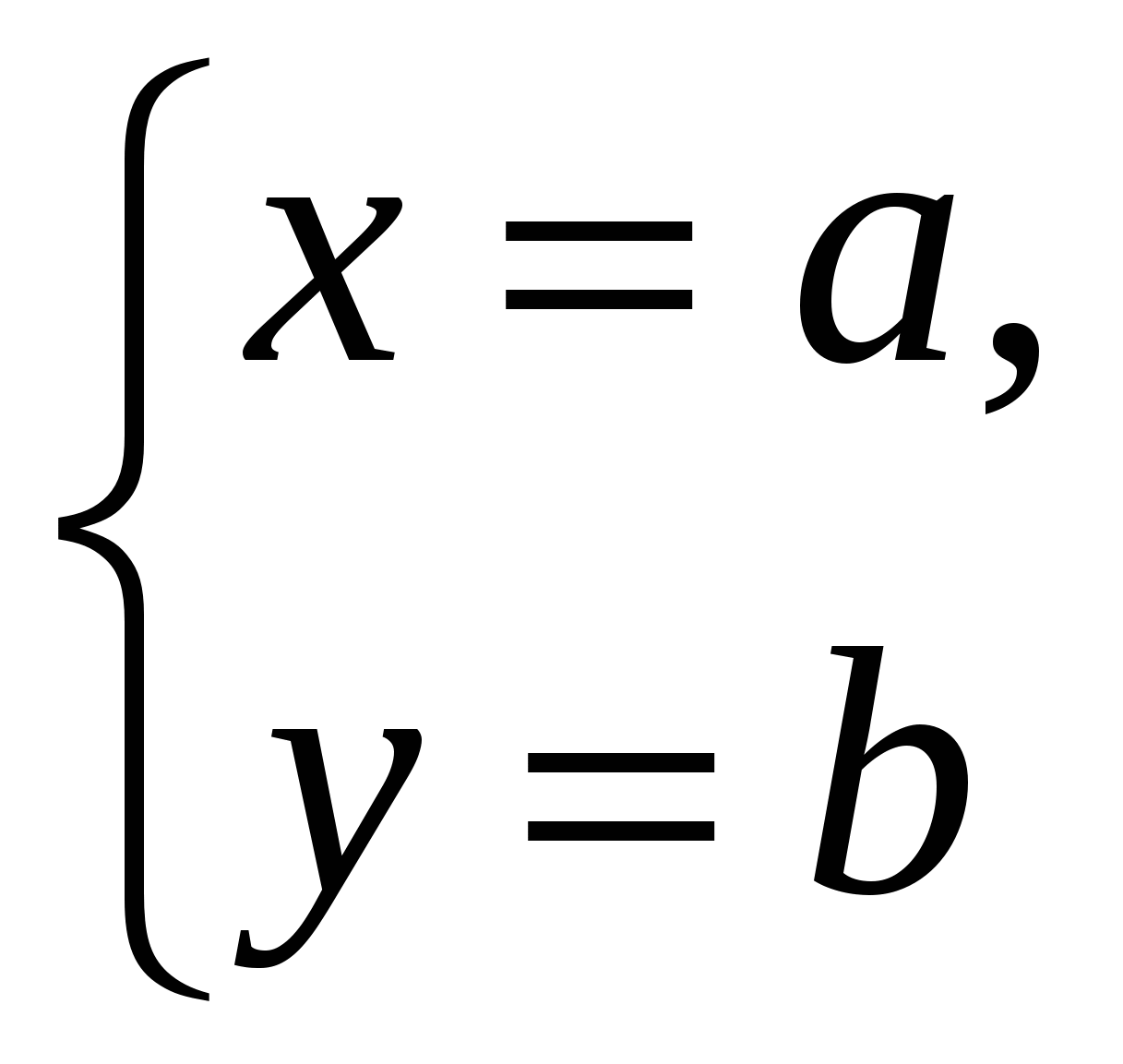
(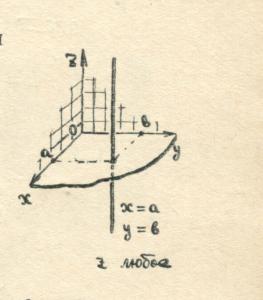 например,
например, 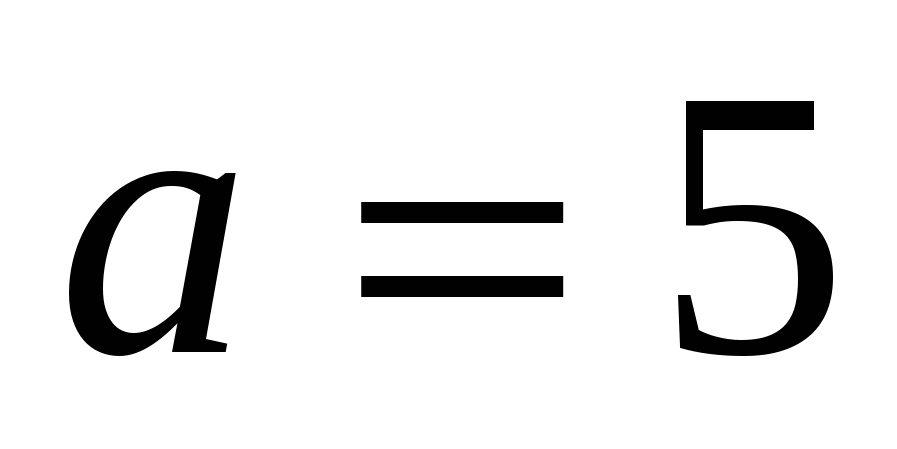
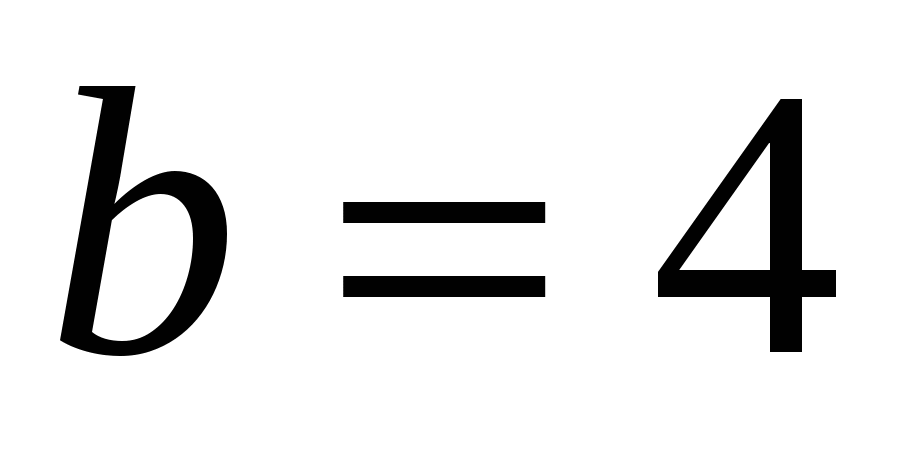 ), задают в пространстве прямую, параллельную оси
), задают в пространстве прямую, параллельную оси  .
.
Все точки такой прямой имеют одну и ту же абсциссу и одну ординату. Координата  может принимать любые значения.
может принимать любые значения.
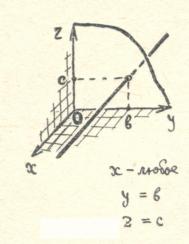


Рассмотрим еще несколько примеров, показывающих как можно задать в
пространстве различные множества с помощью уравнений и других соотношений между координатами.
1). Рассмотрим уравнение .
Поскольку расстояние точки 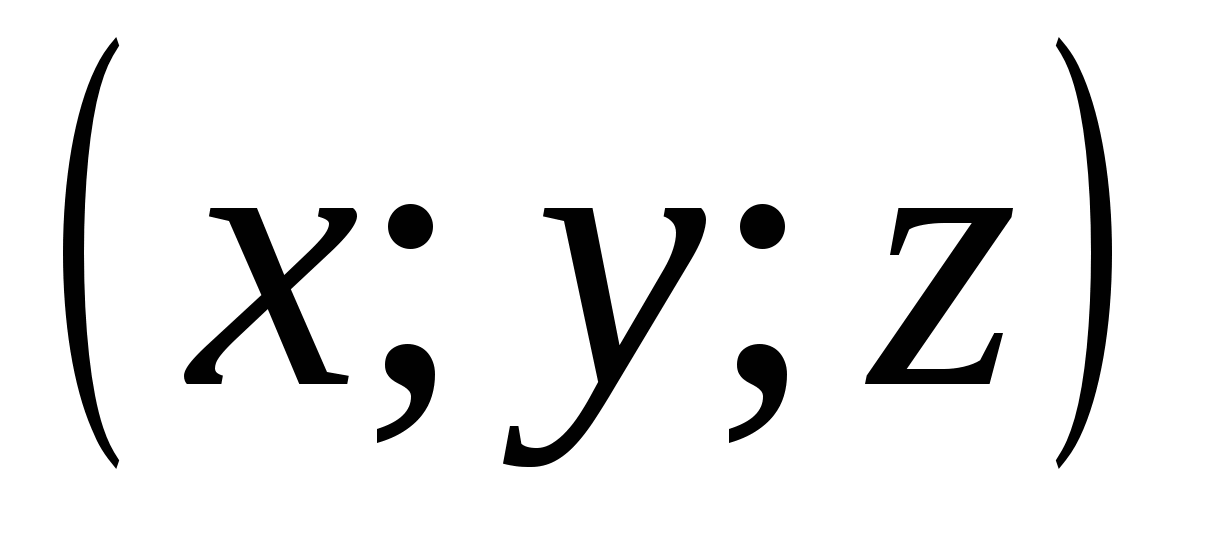 от начала координат задается выражением
от начала координат задается выражением 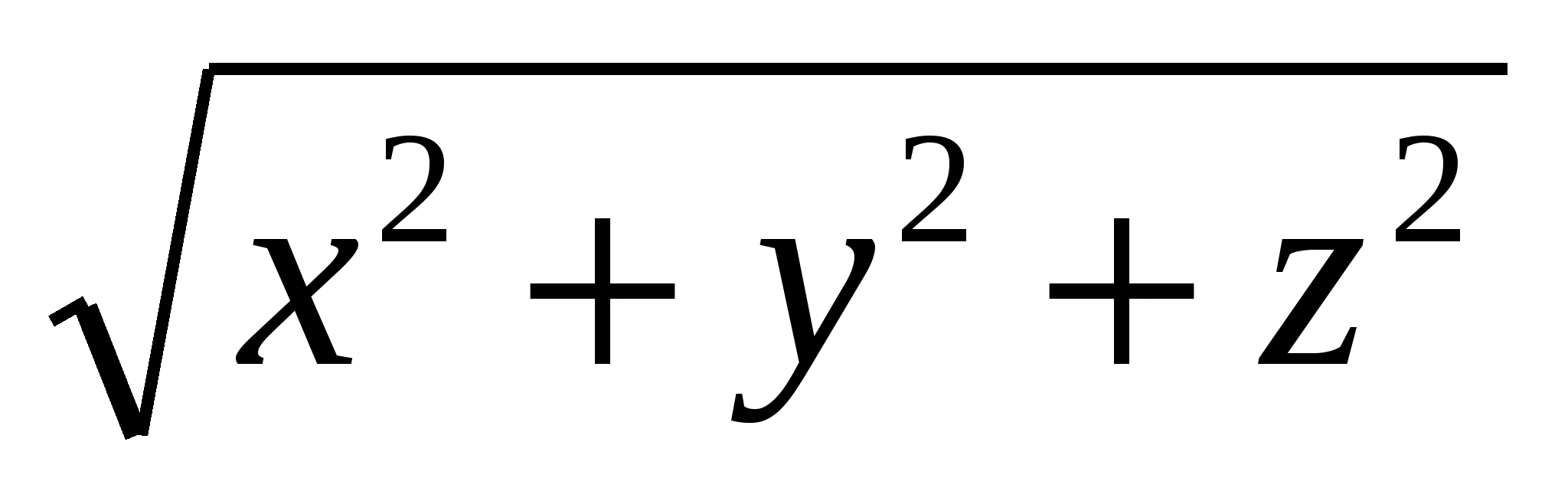 , то ясно, что в переводе на геометрический язык соотношение
, то ясно, что в переводе на геометрический язык соотношение 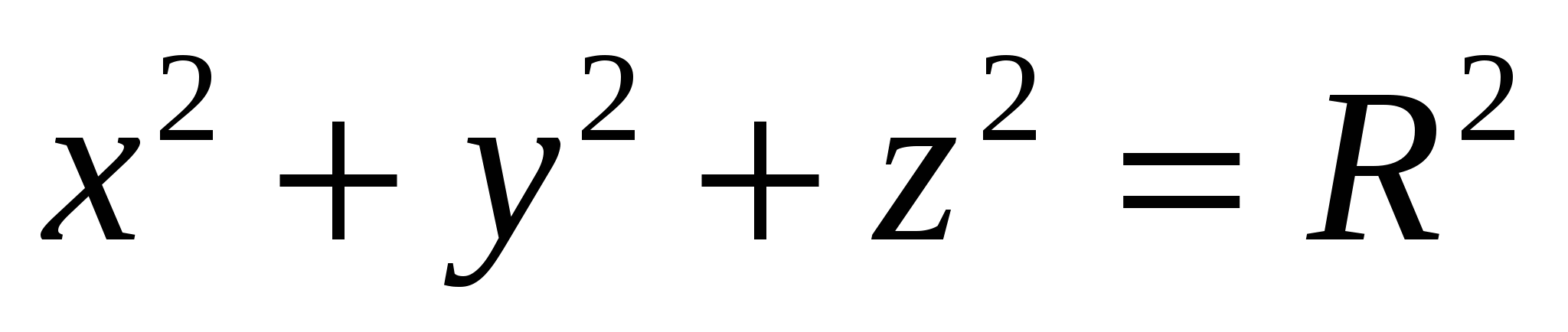 означает, что точка с координатами
означает, что точка с координатами 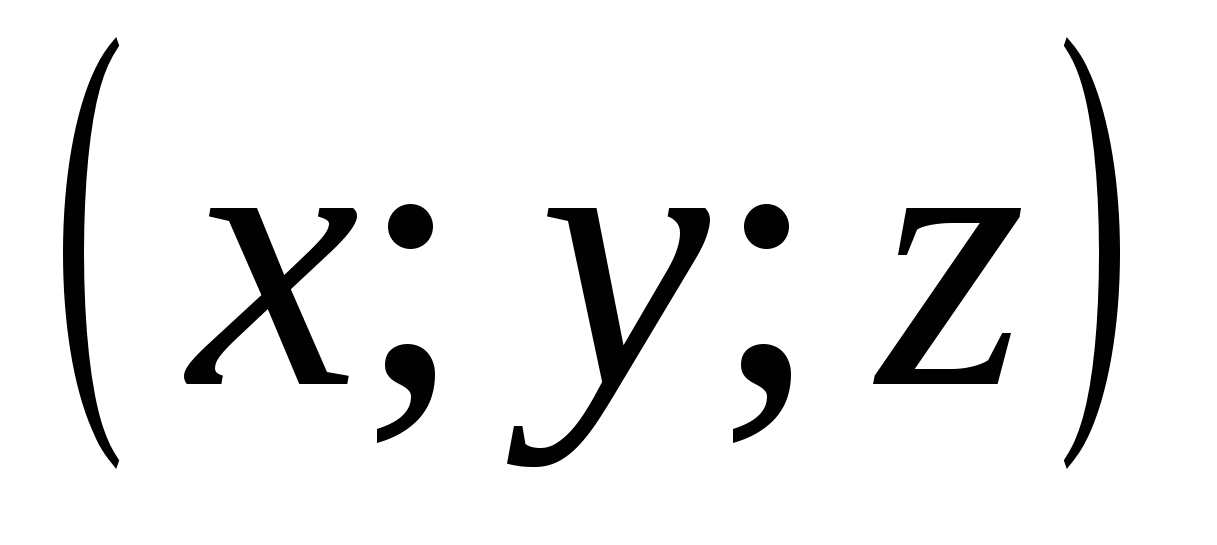 , находится на расстоянии
R
от начала координат. Значит, множеством всех точек, для которых выполняется соотношение
, находится на расстоянии
R
от начала координат. Значит, множеством всех точек, для которых выполняется соотношение 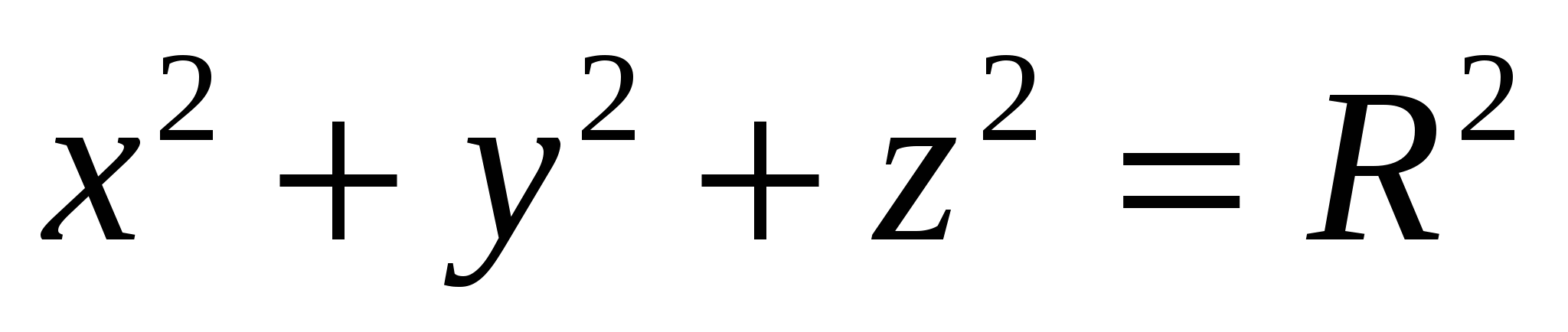 , является поверхность шара - сфера с центром в начале координат и радиусом
R
.
, является поверхность шара - сфера с центром в начале координат и радиусом
R
.
2). Рассмотрим, где расположены точки, координаты которых удовлетворяют соотношению  .
.
Так как это соотношение означает, что расстояние точки 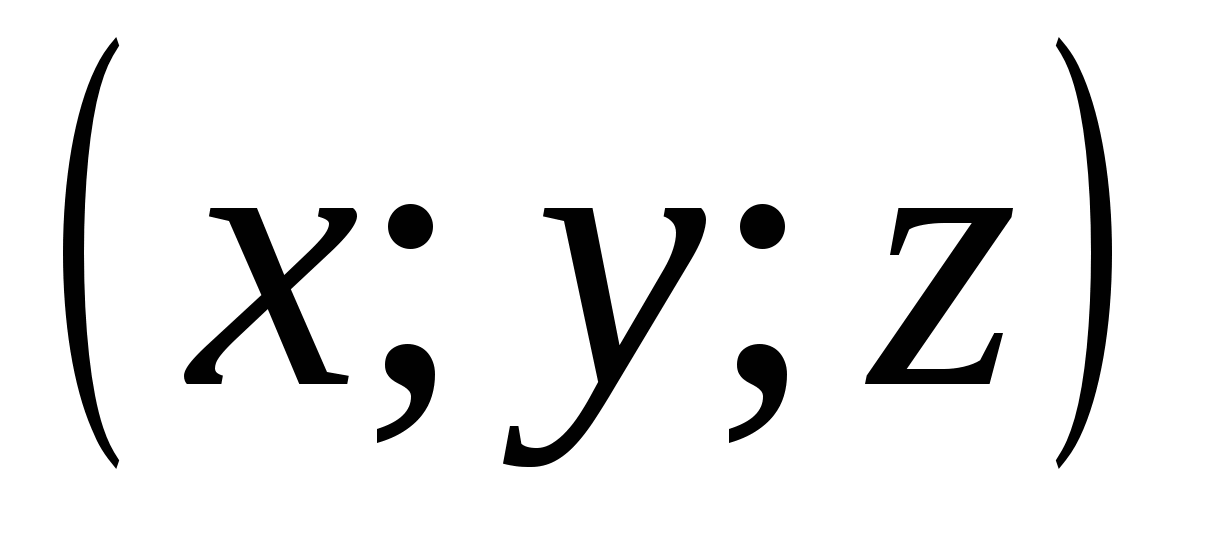 от начала координат меньше единицы, то искомое множество - это множество точек, лежащих внутри шара с центром в начале координат и радиусом, равным единице.
от начала координат меньше единицы, то искомое множество - это множество точек, лежащих внутри шара с центром в начале координат и радиусом, равным единице.
Глава 2
1.Разложение вектора по координатным векторам. Координаты вектора.
Базисом пространства называется любая упорядоченная тройка некомпланарных векторов 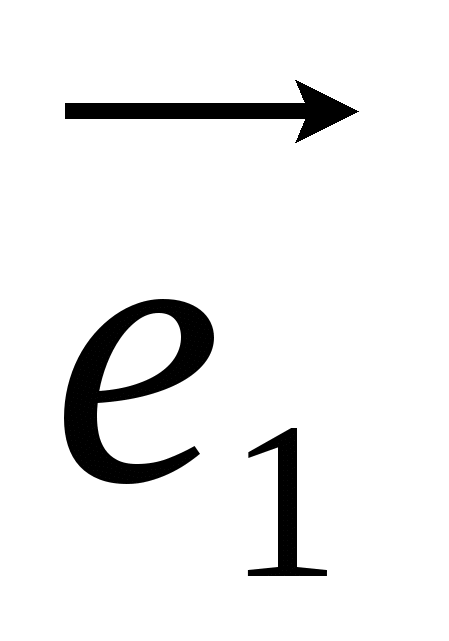 ,
, 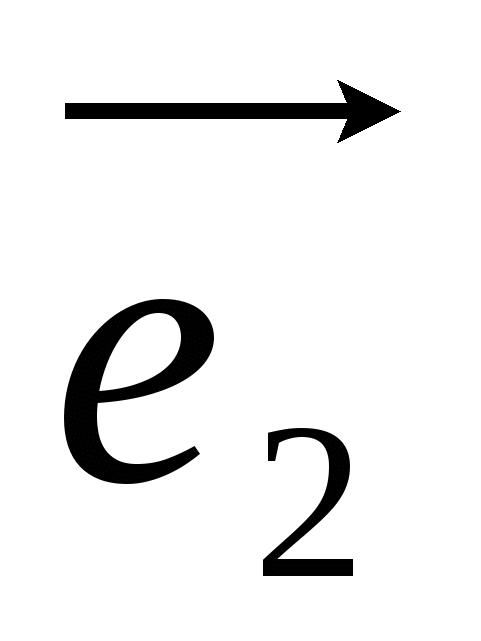 ,
, 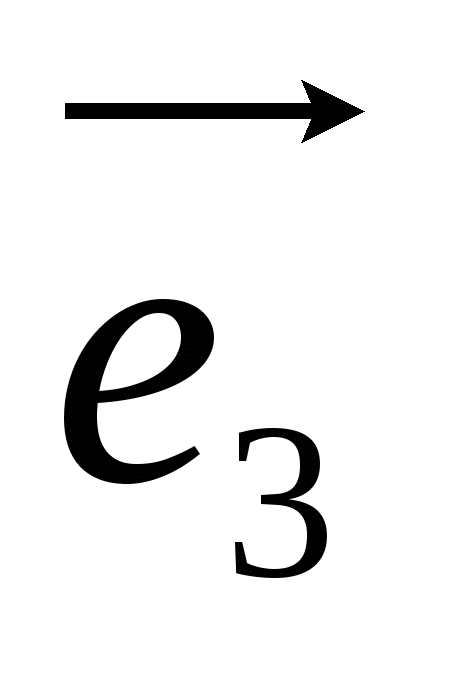 , обозначаемая символом
, обозначаемая символом
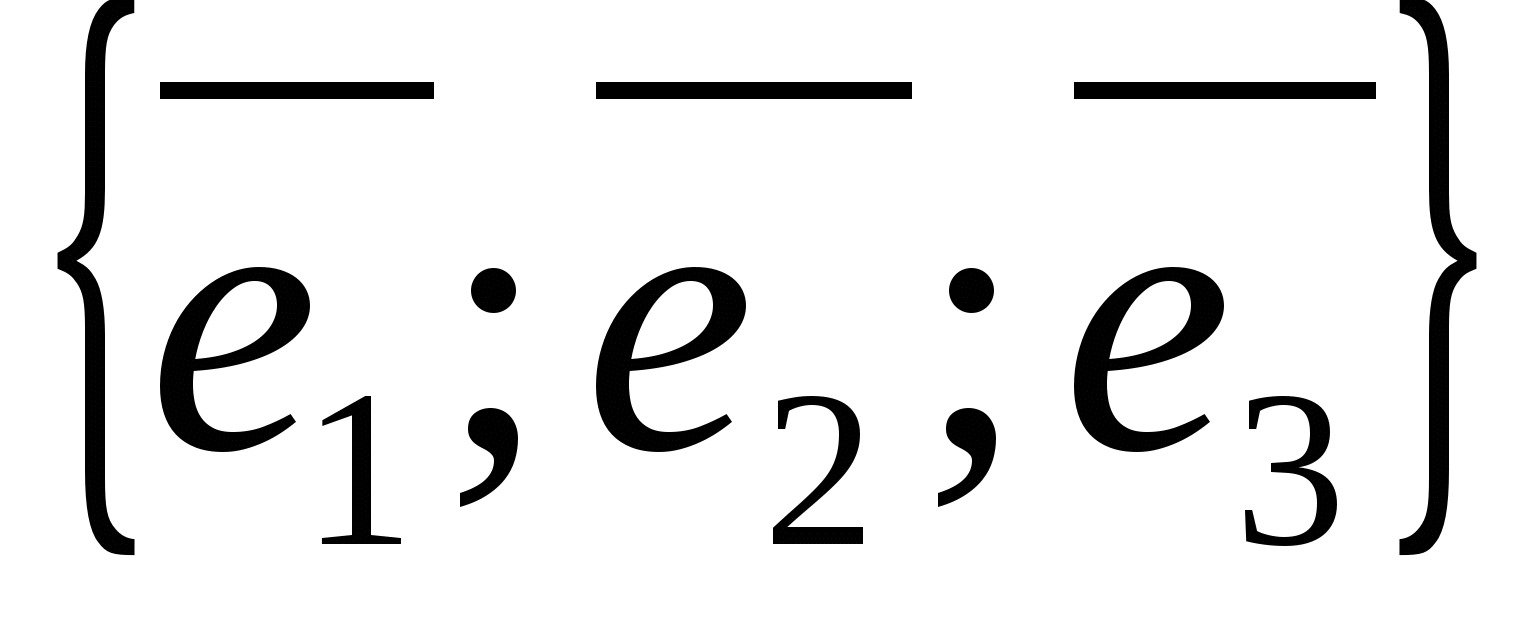 .
.
Частным случаем является прямоугольный ортонормированный базис 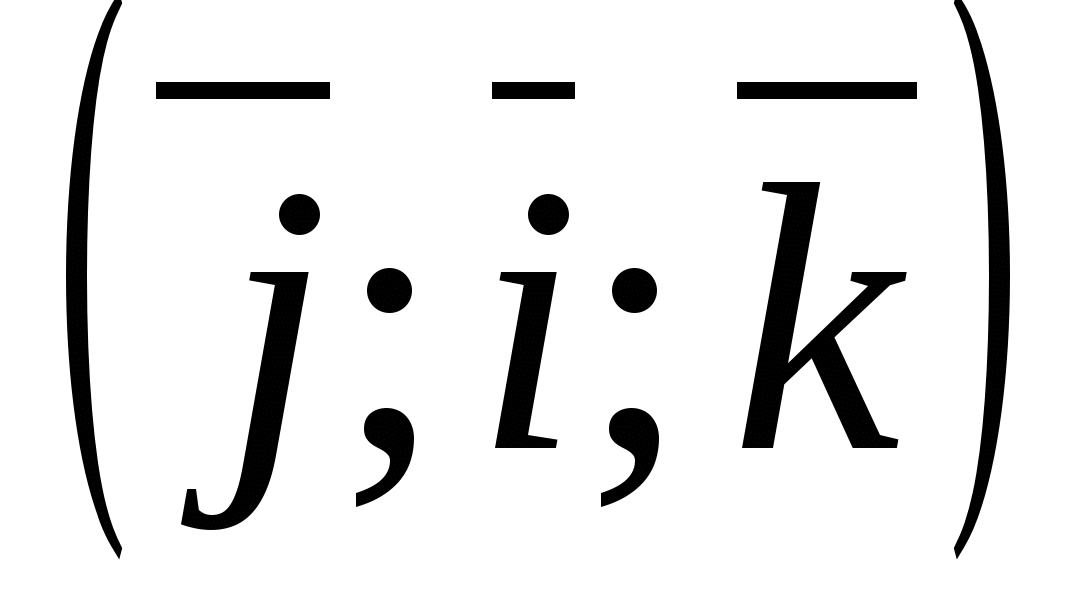 , где
, где 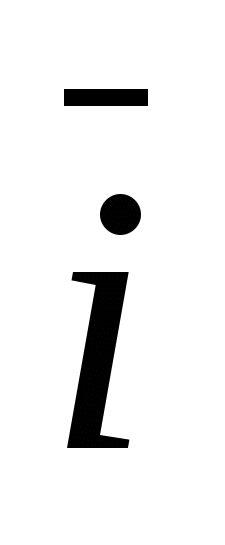 - единичный вектор оси абсцисс, через -
- единичный вектор оси абсцисс, через -  единичный вектор оси ординат и через
единичный вектор оси ординат и через 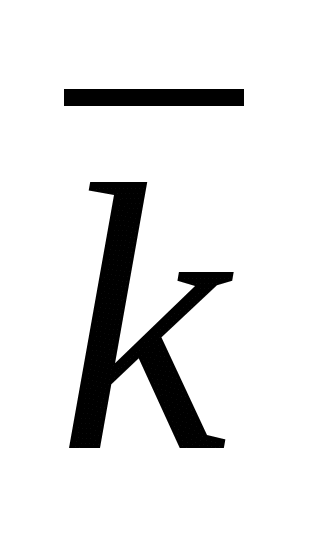 -единичный вектор оси аппликат, т.е.
-единичный вектор оси аппликат, т.е. 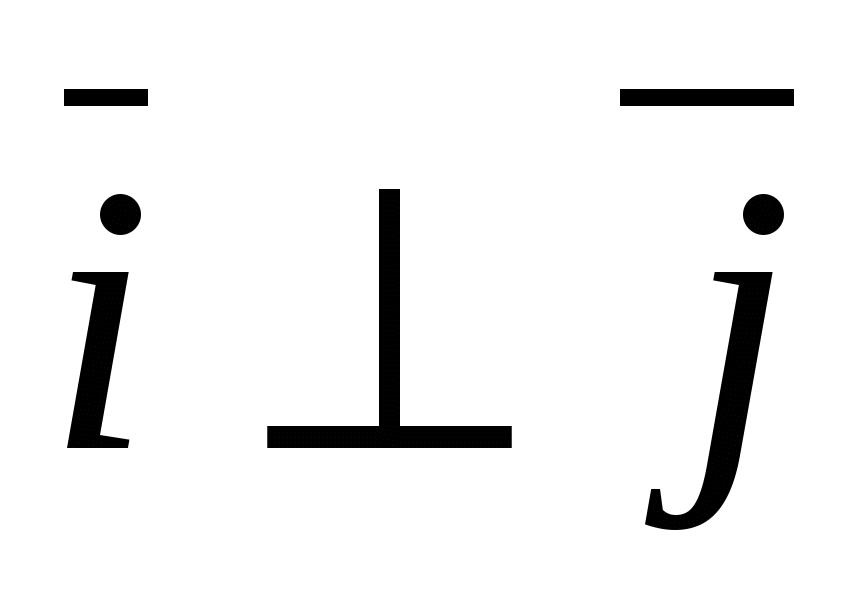 ,
, 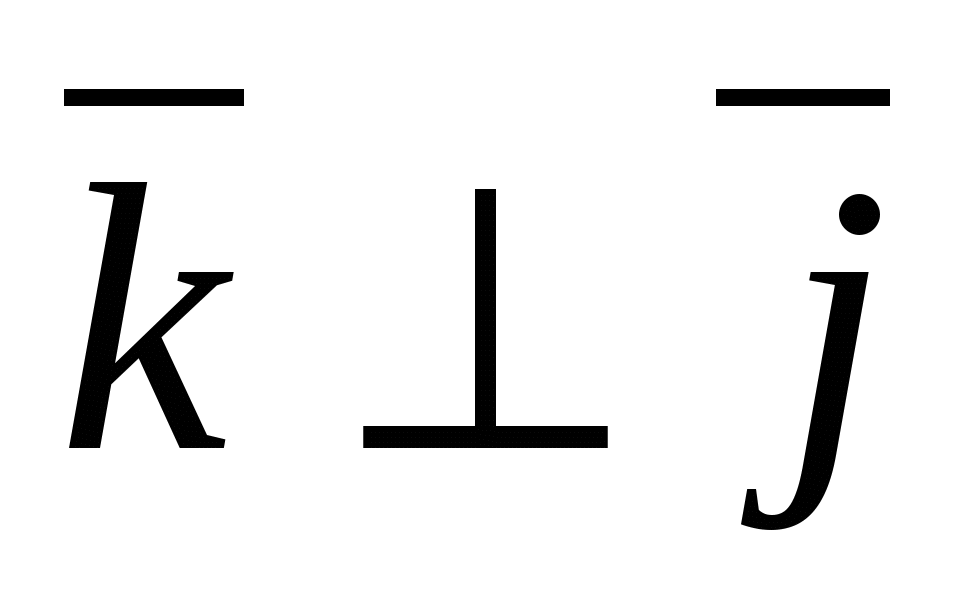 ,
, 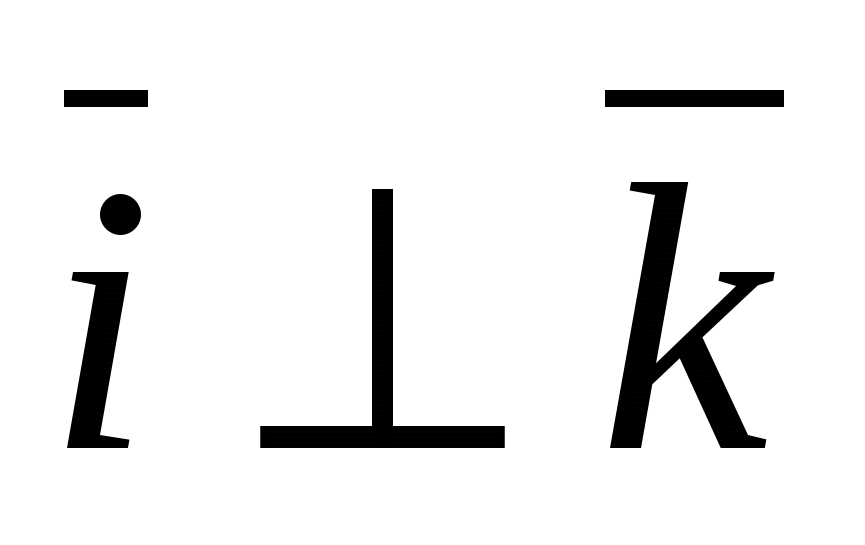 ,
,  .
.
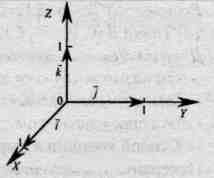
Этот базис 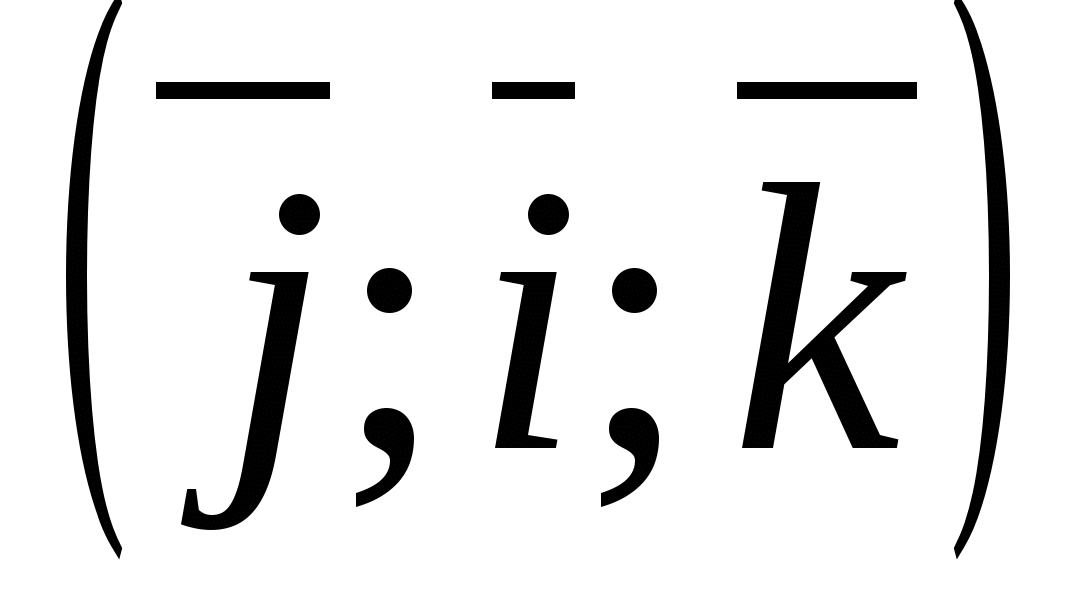 и начало отсчета
О
определяют прямоугольную декартову систему координат
и начало отсчета
О
определяют прямоугольную декартову систему координат  в пространстве.
в пространстве.
Теорема 1
Любой вектор пространства
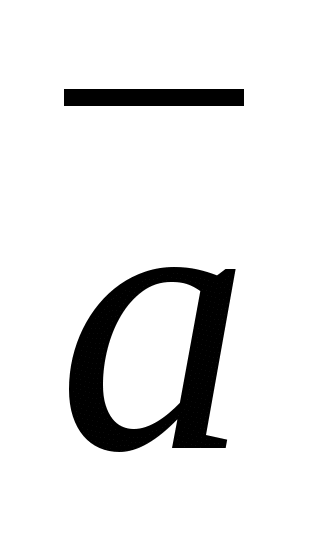 можно разложить по координатным векторам, т.е. представить в виде -
можно разложить по координатным векторам, т.е. представить в виде -
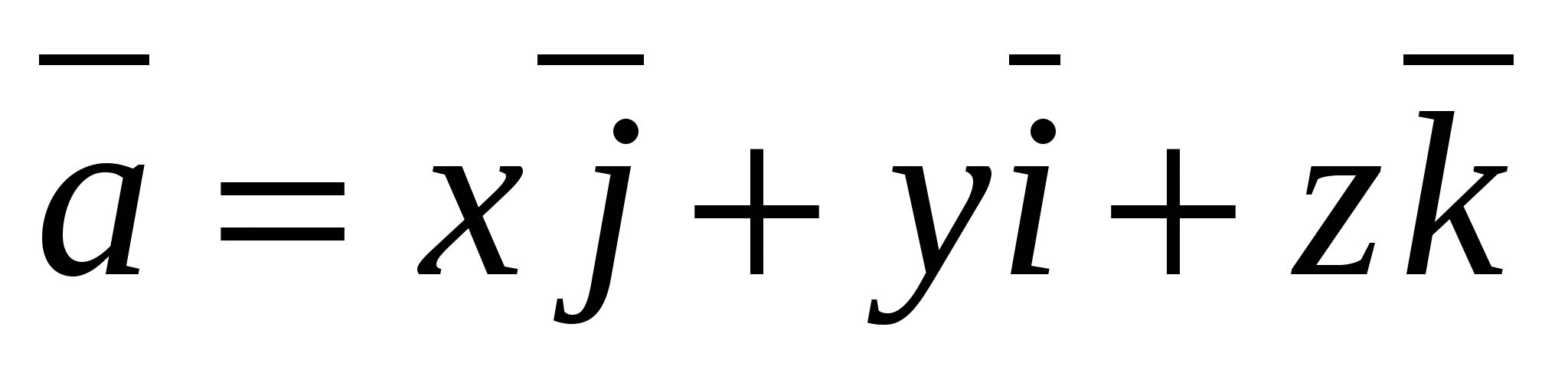 ,
,
причем коэффициенты разложения 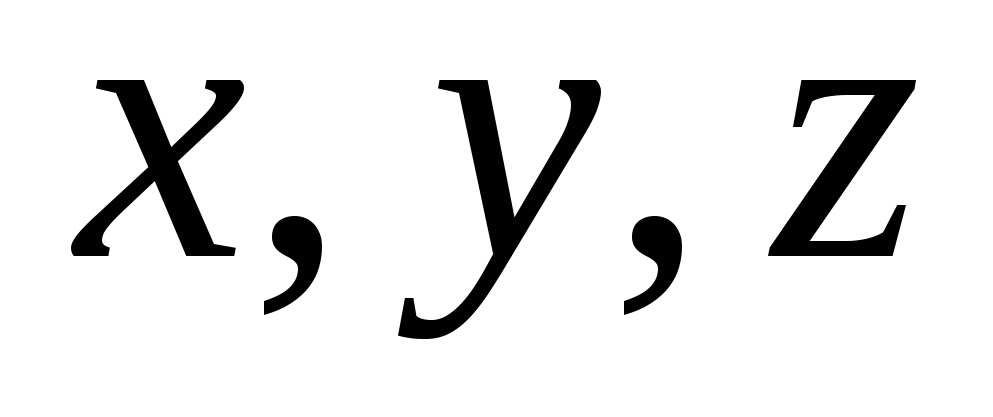 определяются единственным образом.
определяются единственным образом.
Ч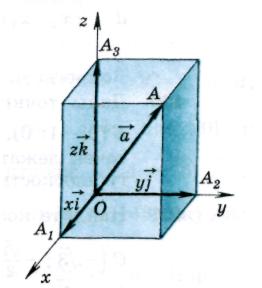 исла
исла
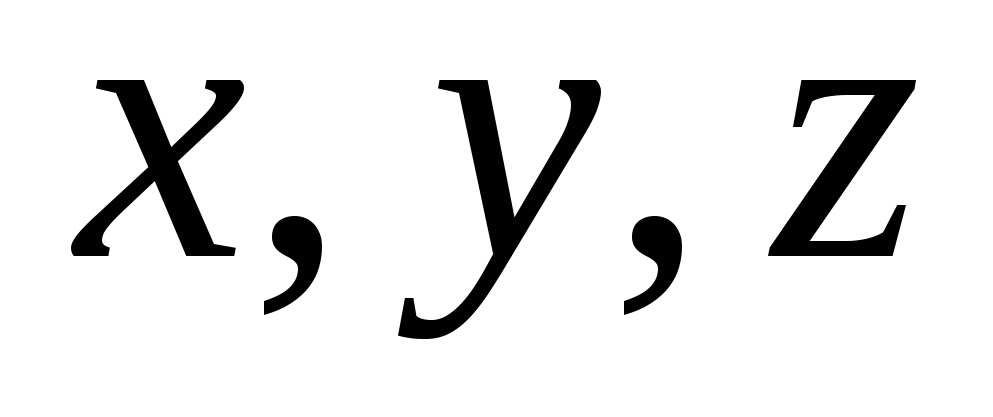 называются координатами вектора
называются координатами вектора 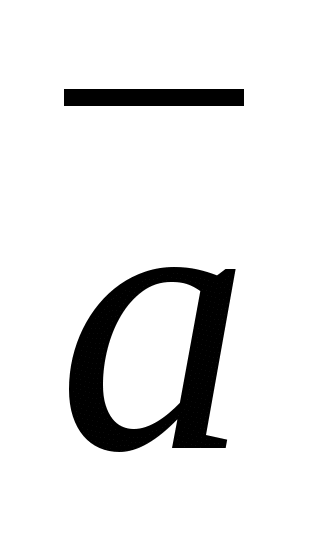 , т.е.
, т.е.
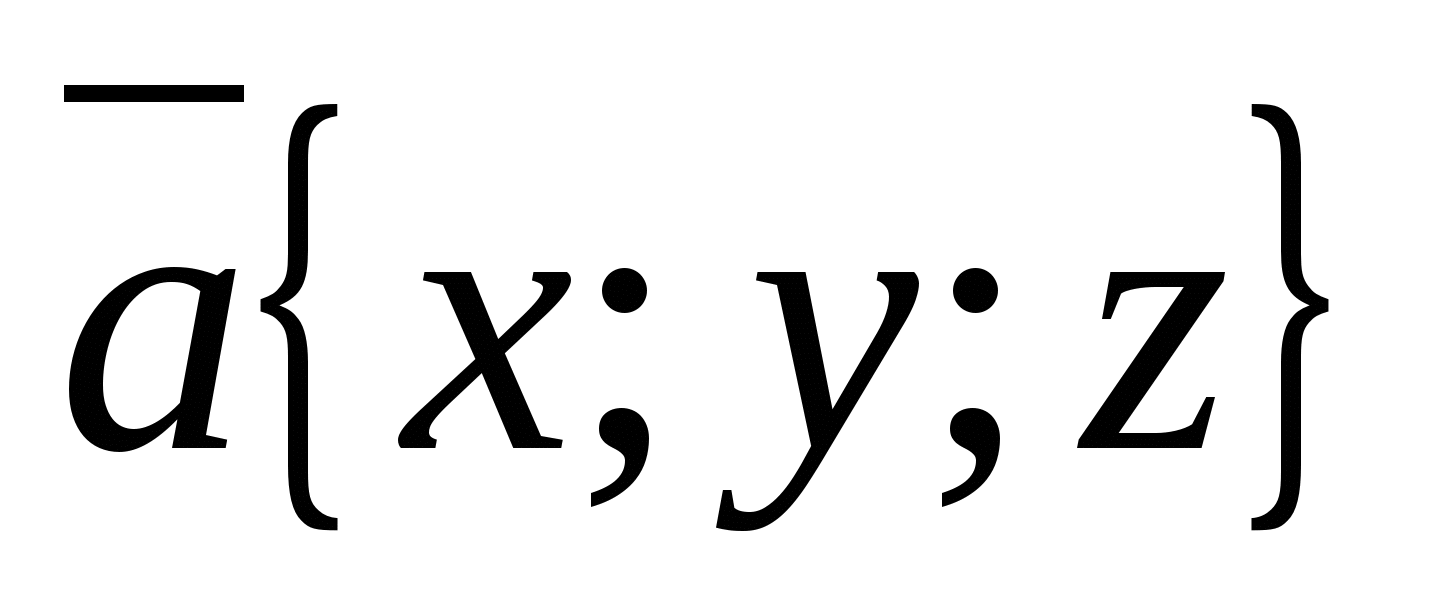 . Так как нулевой вектор можно представить в виде
. Так как нулевой вектор можно представить в виде 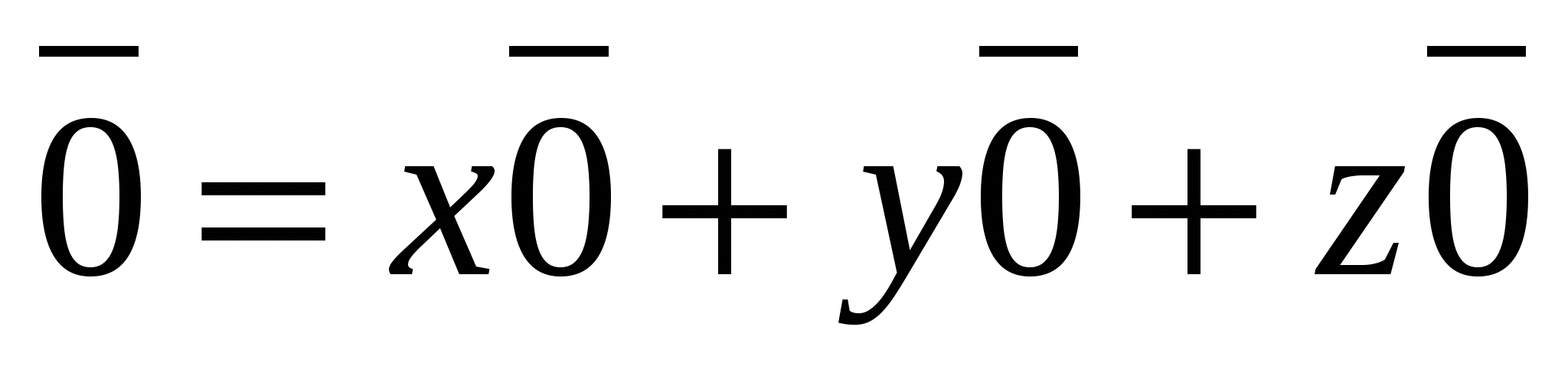 , то все координаты нулевого вектора равны нулю,
, то все координаты нулевого вектора равны нулю,
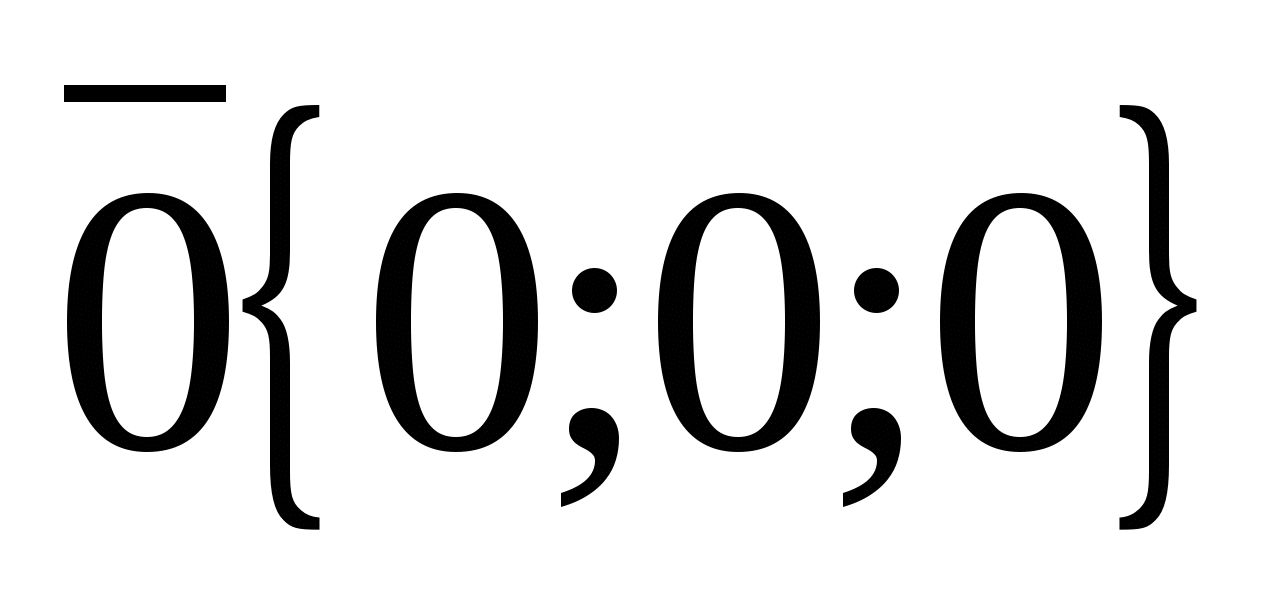 .
.
2. Линейные операции над векторами в координатах.
Правило 1.
Координаты равных
векторов соответственно равны,
т.е. если векторы
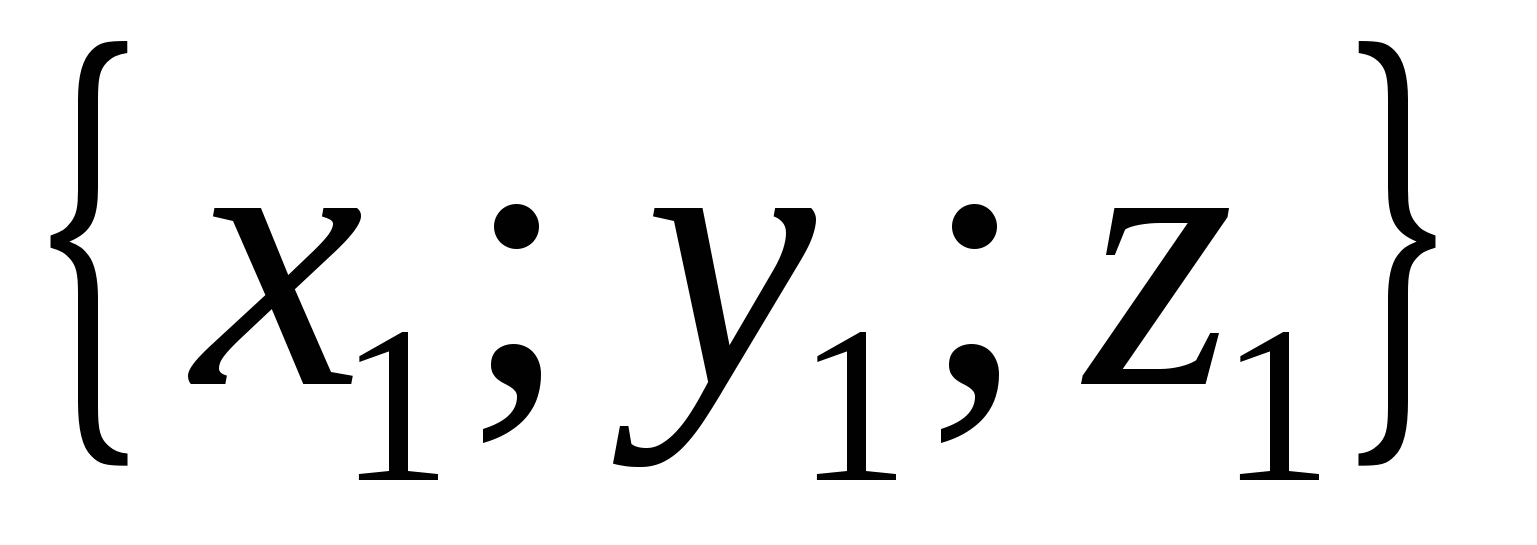 и
и 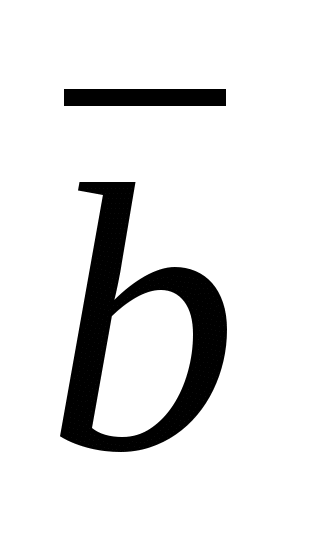
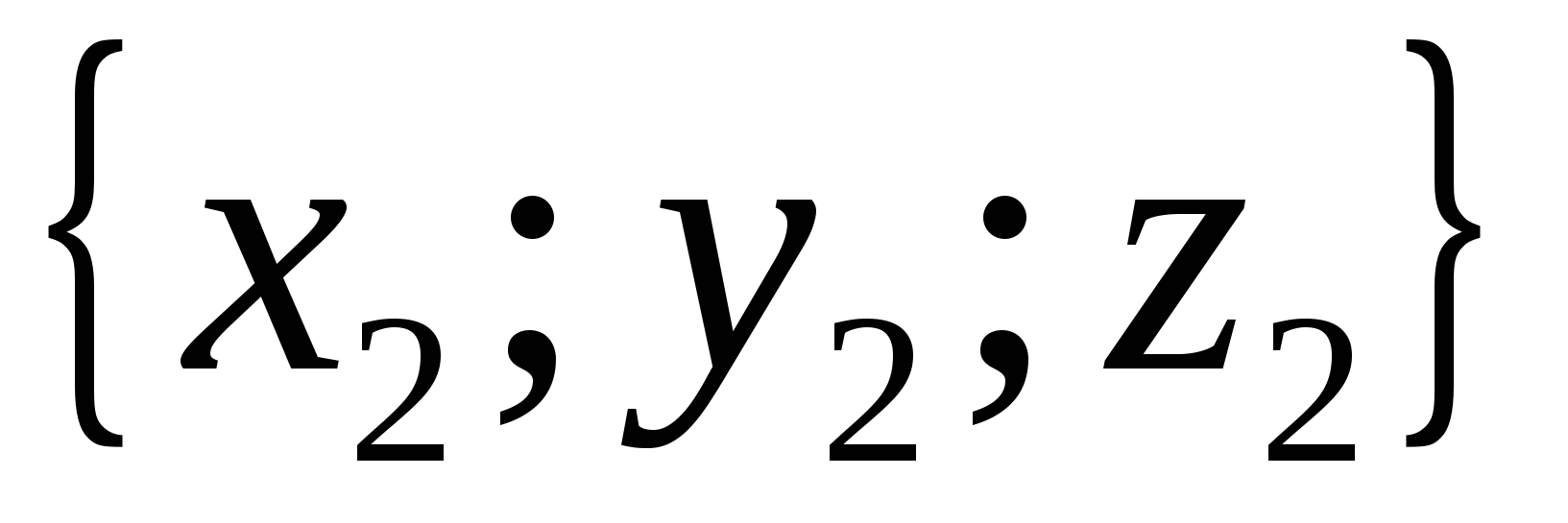 равны, то
равны, то 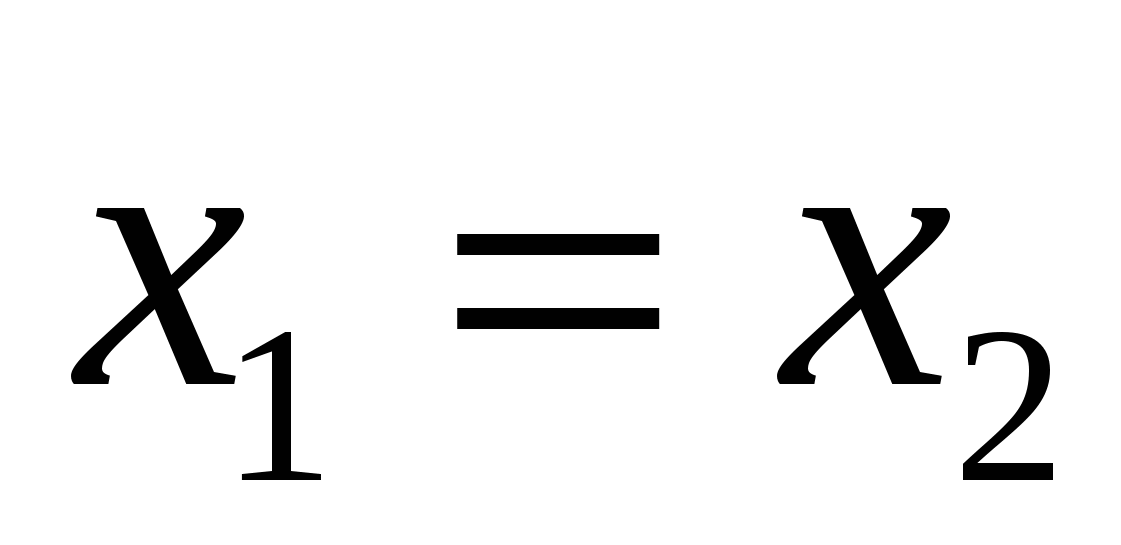 ,
,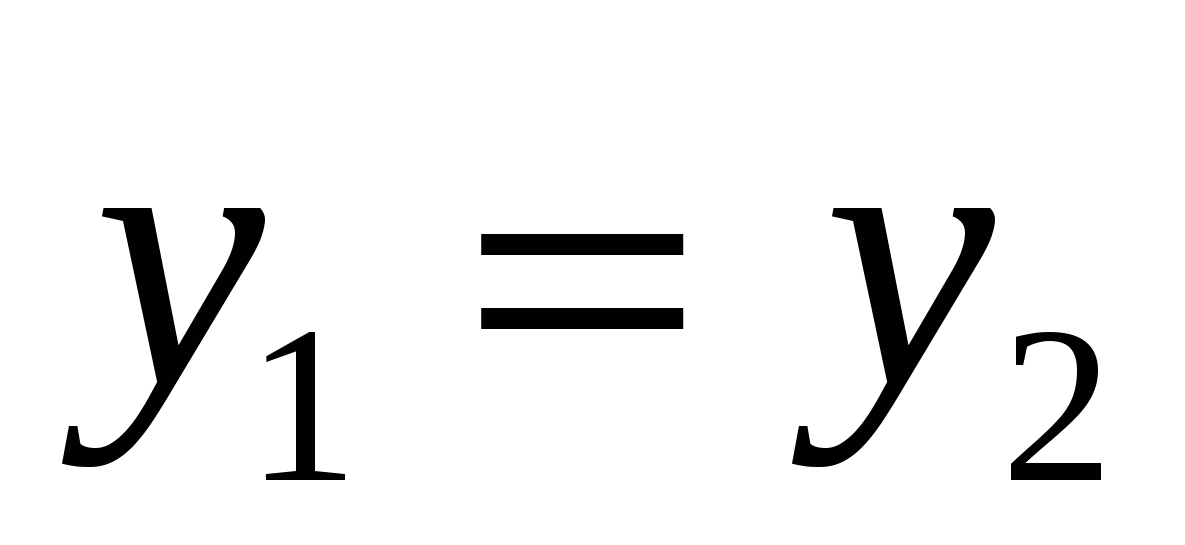 и
и 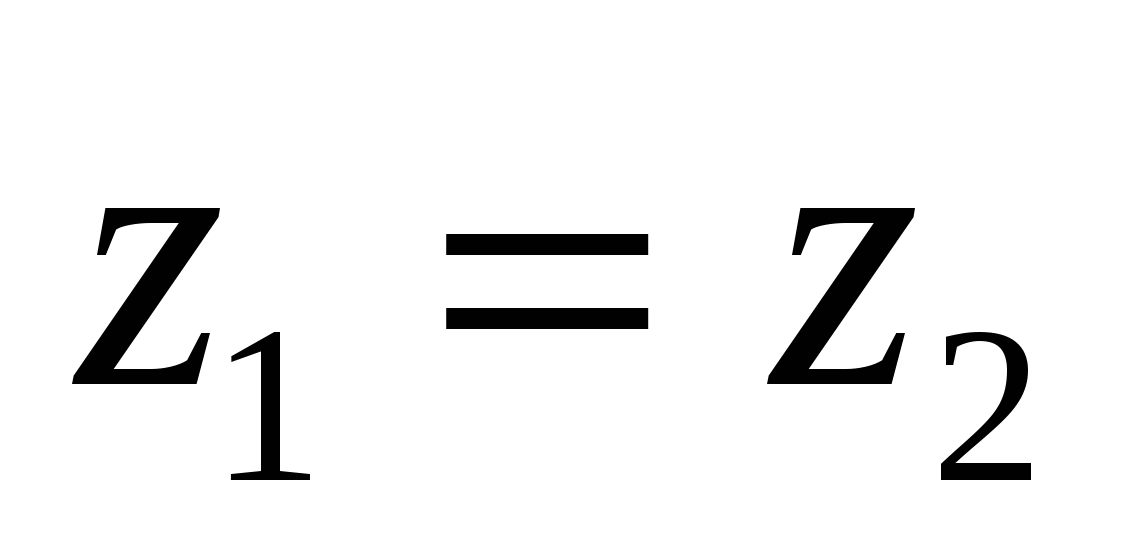 .
.
Правило 2.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Другими словами, если
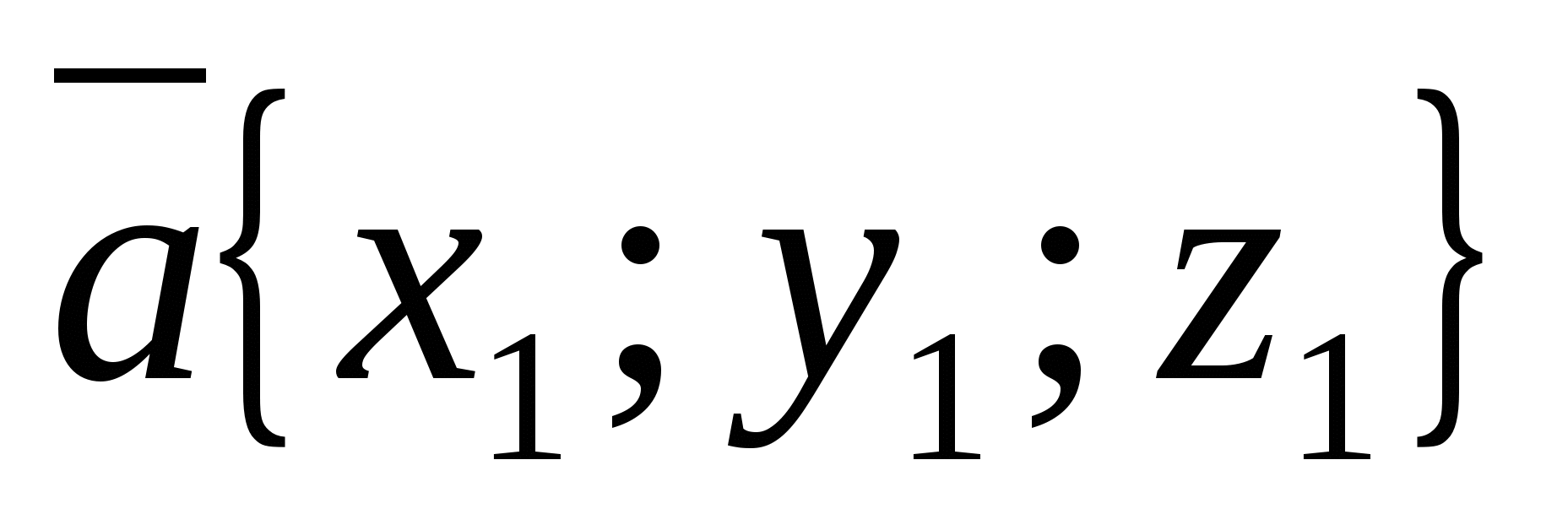 и
и
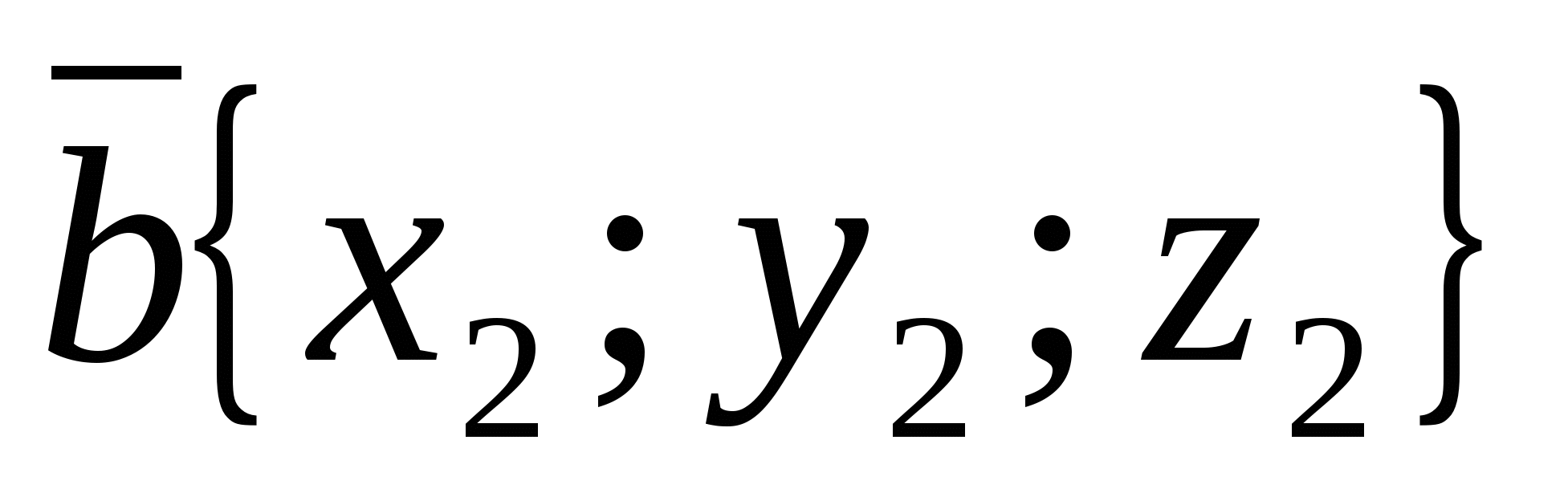 -данные векторы, то вектор
-данные векторы, то вектор 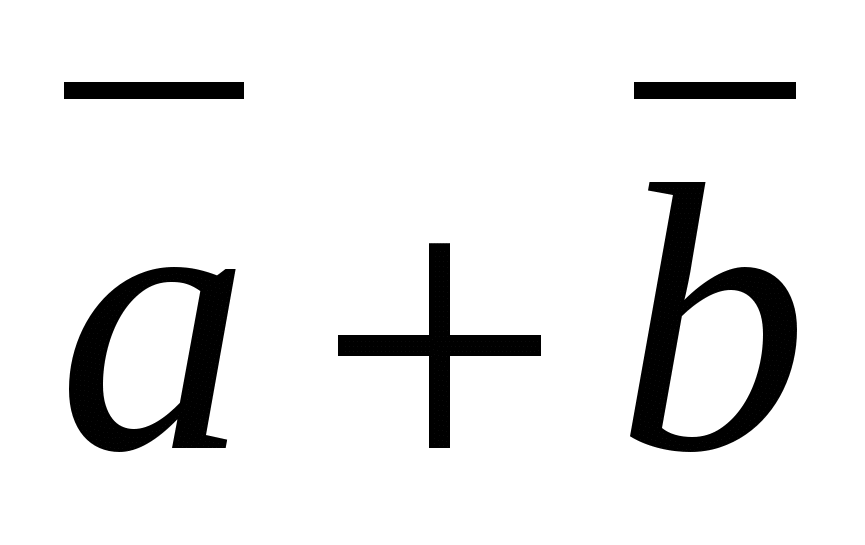 имеет координаты .
имеет координаты .
Правило 3.
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов .
Другими словами, если
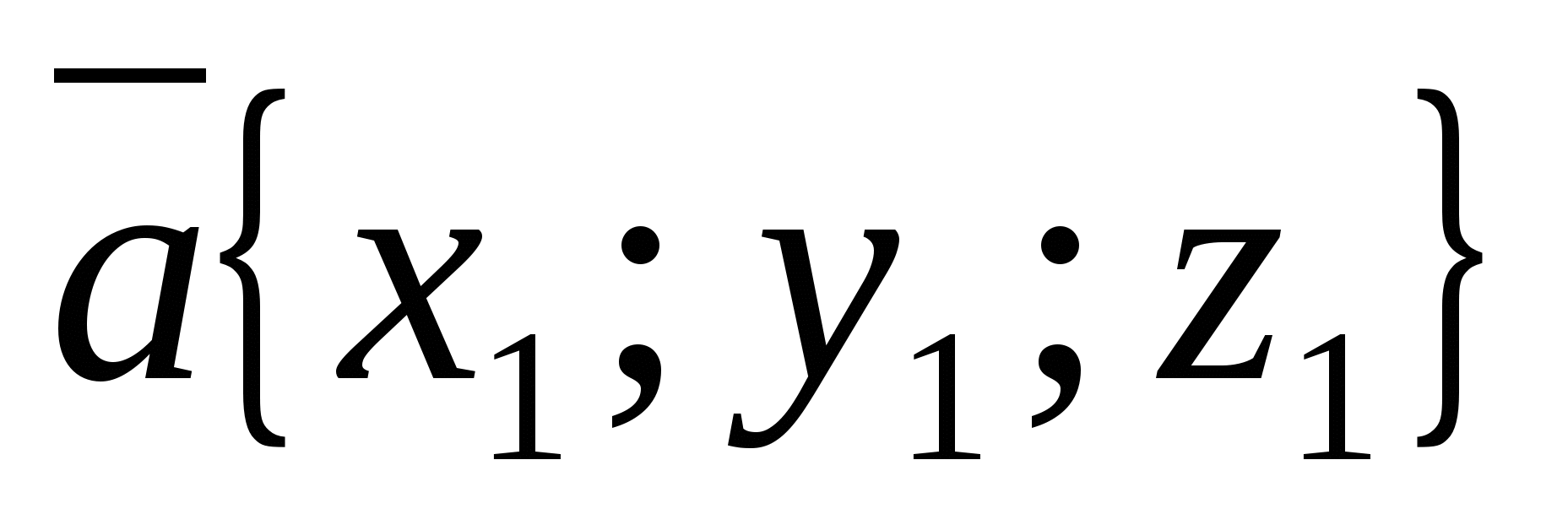 и
и
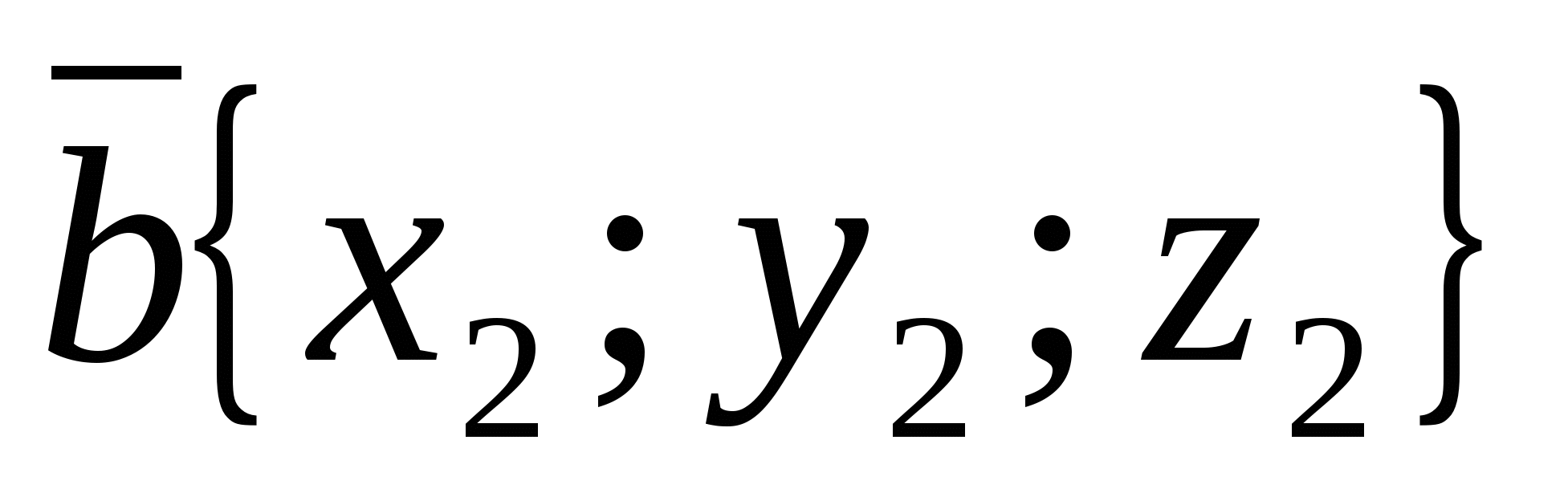 -данные векторы, то вектор
-данные векторы, то вектор 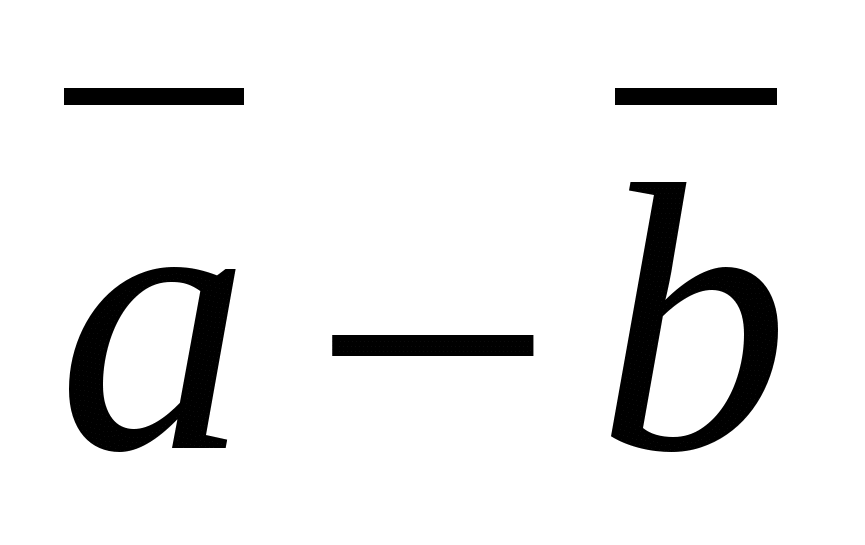 имеет координаты
имеет координаты
Правило 4.
Каждая координата произведения вектора на число равна произведению соответствующих координат вектора на это число.
Другими словами, если
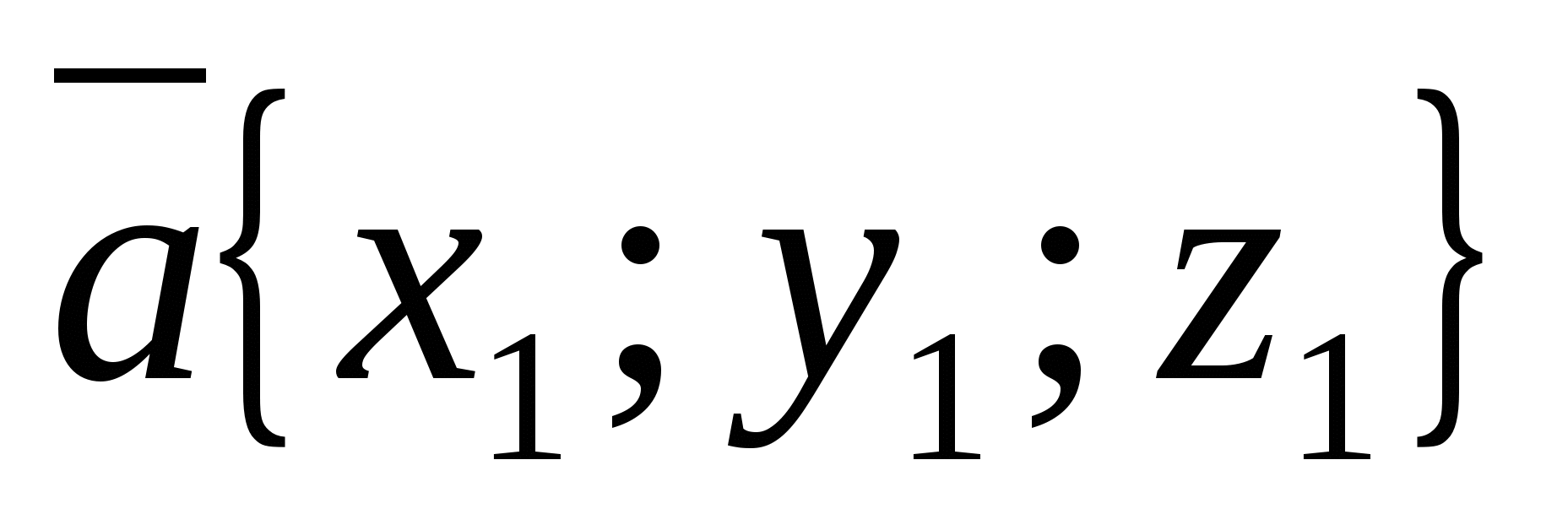 -данный вектор,
-данный вектор, ![]() -данное число, то вектор
-данное число, то вектор 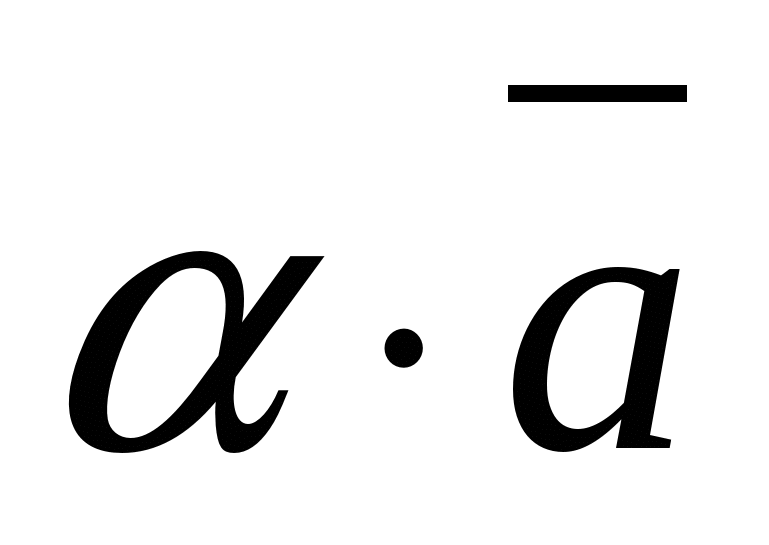 имеет координаты.
имеет координаты.
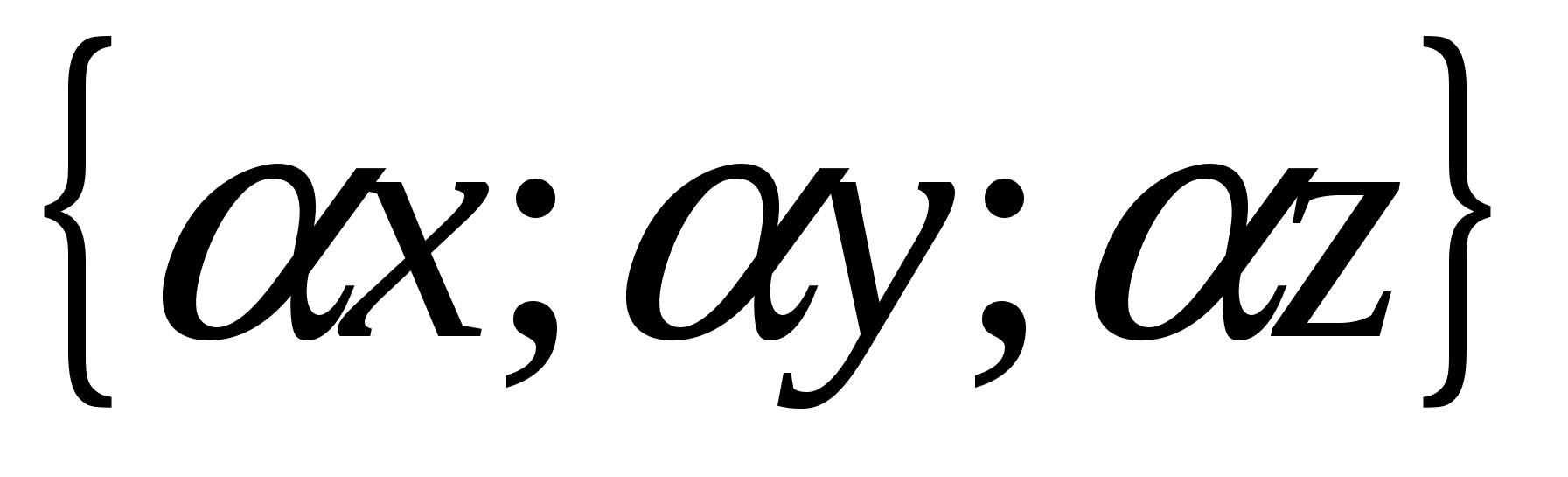 .
.
Пример .
Найти координаты вектора 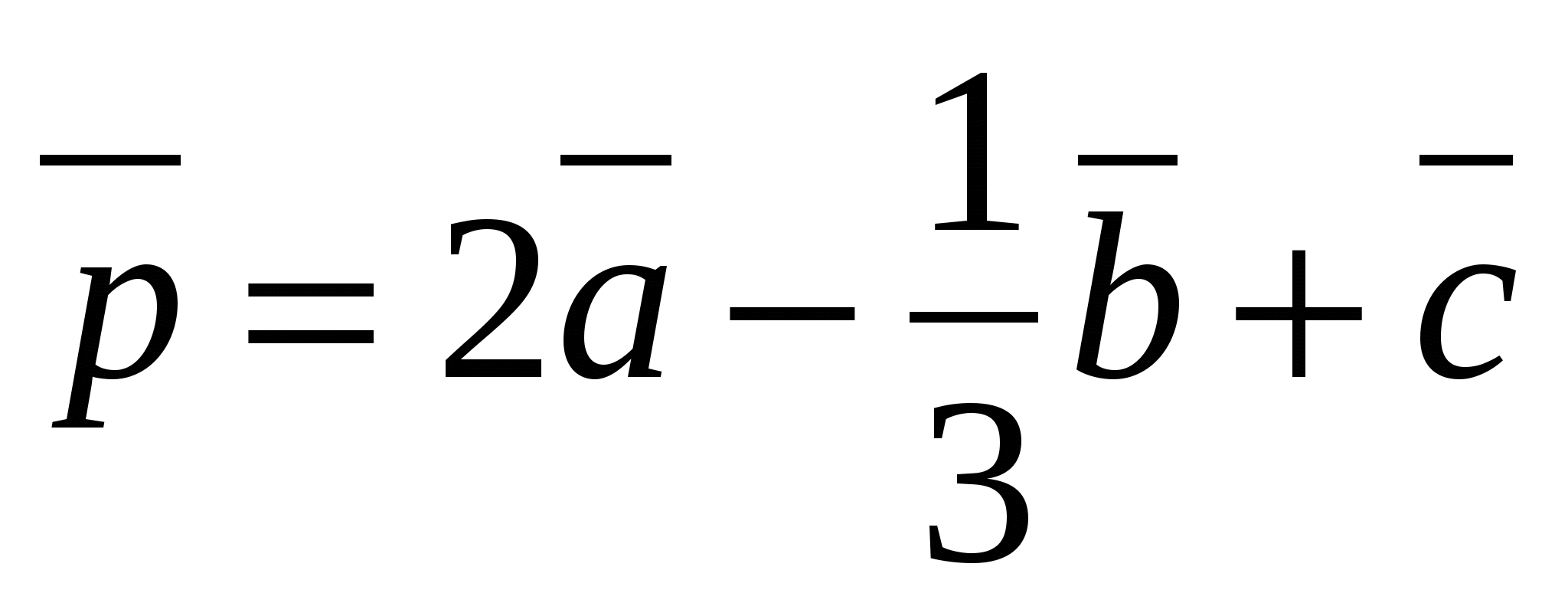 , если
, если 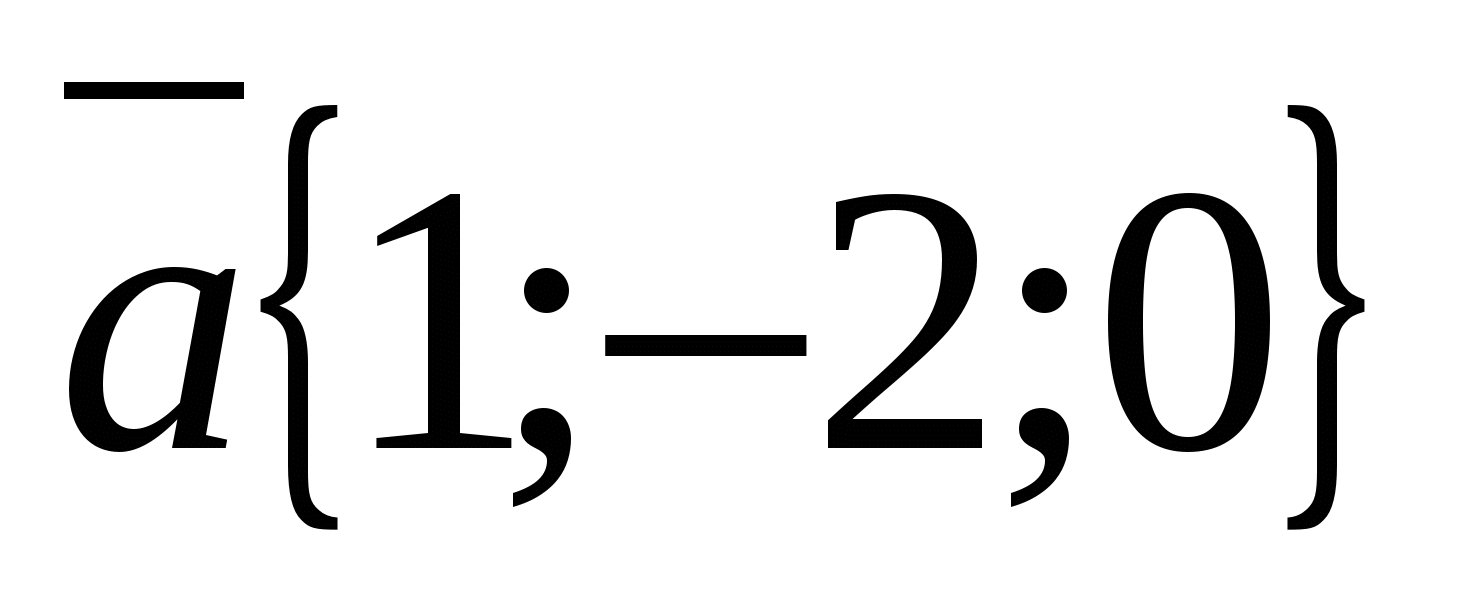 ,
, 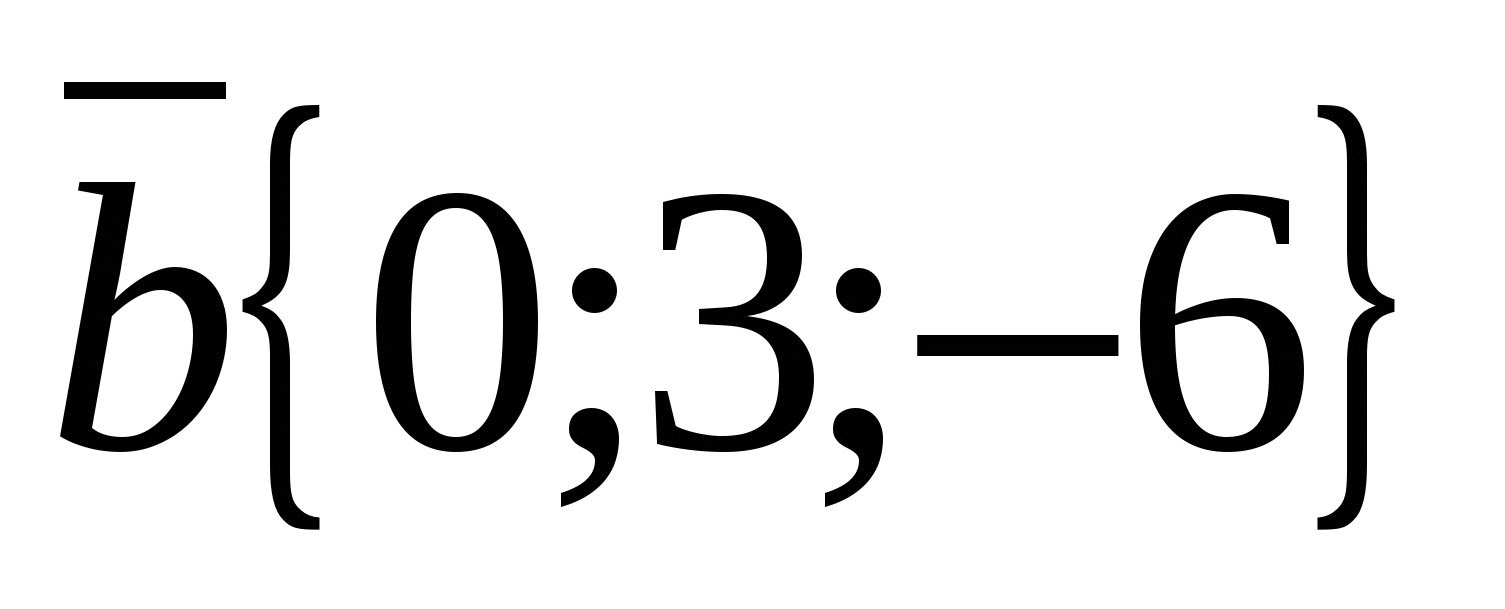 ,
, 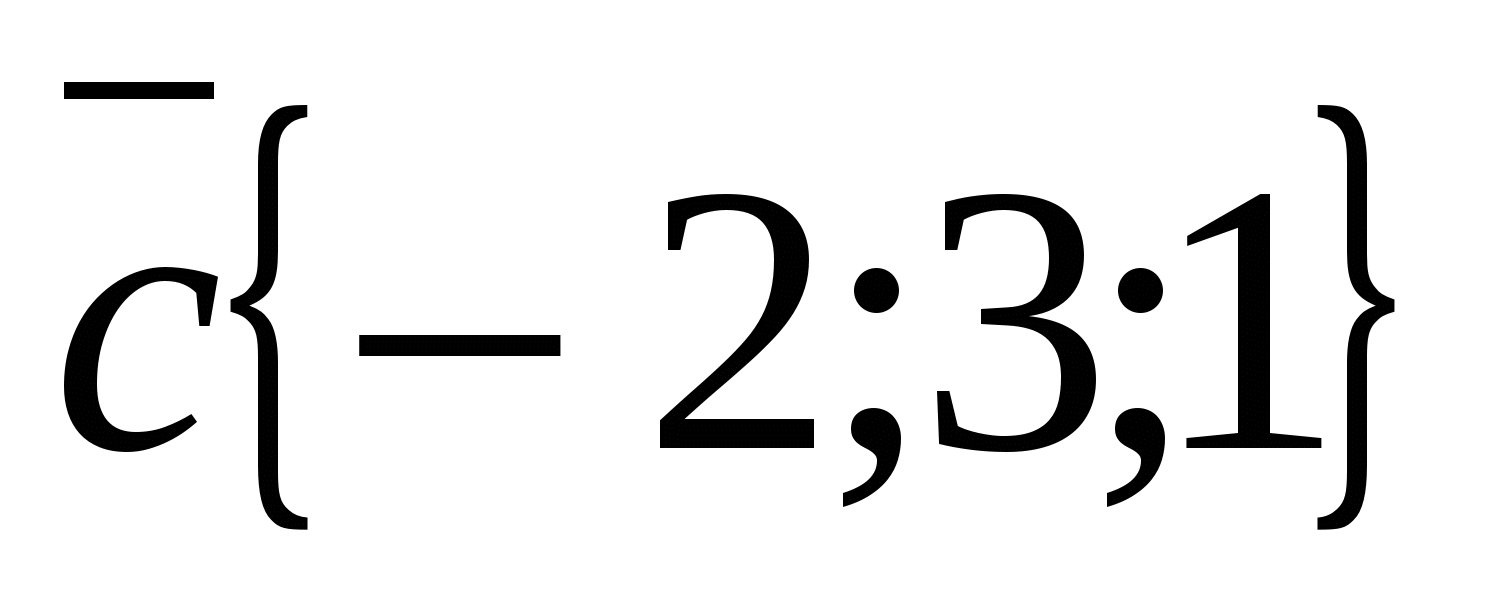 .
.
Решение.
Вектор 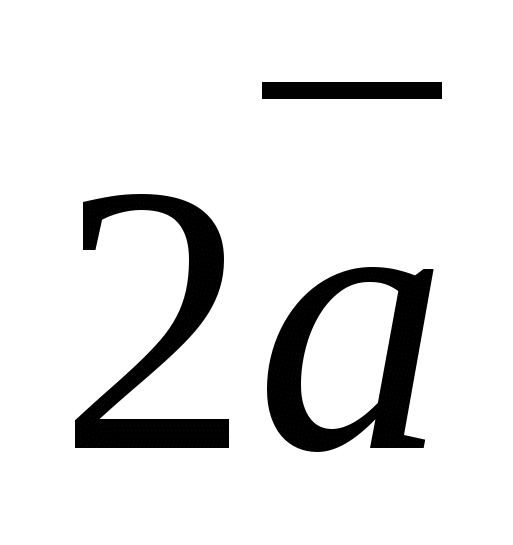 имеет координаты
имеет координаты 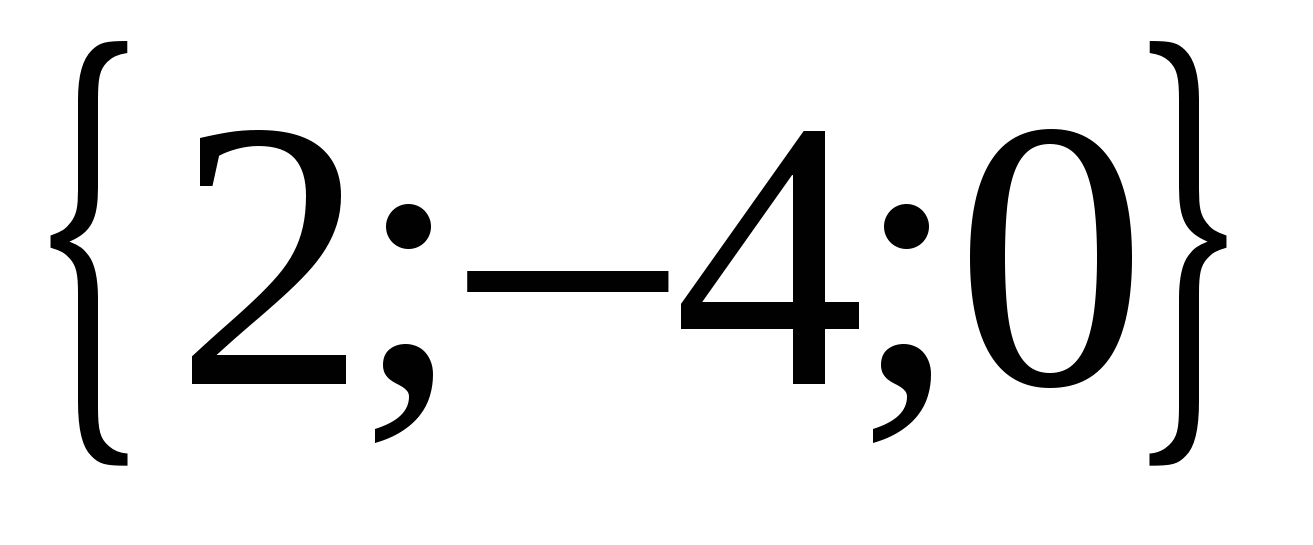 , а вектор
, а вектор  - координаты
- координаты 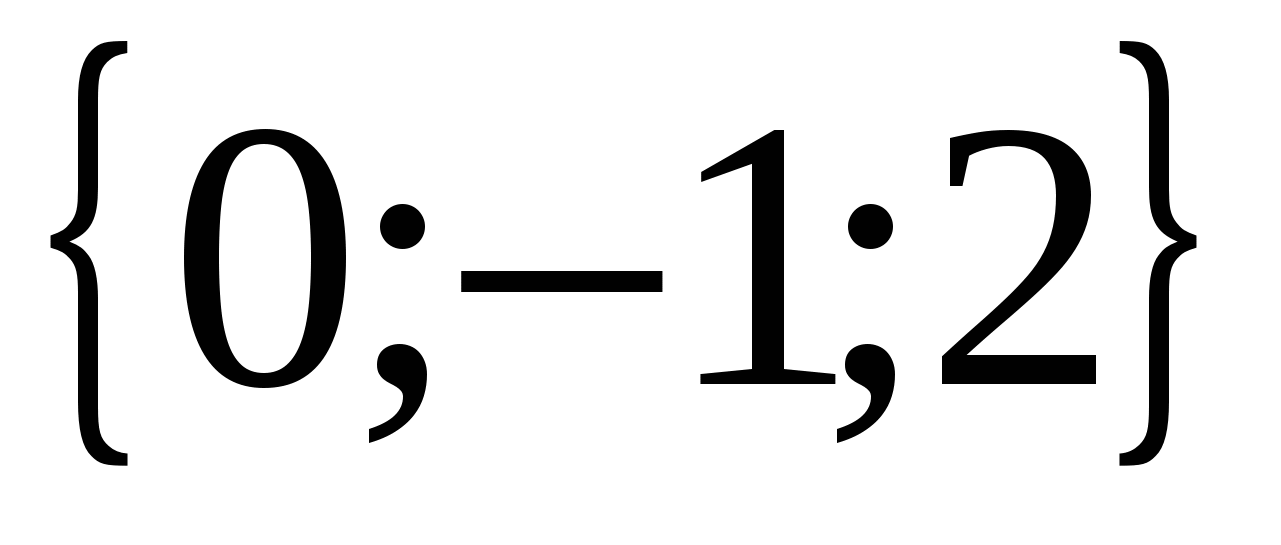 .
.
Так как 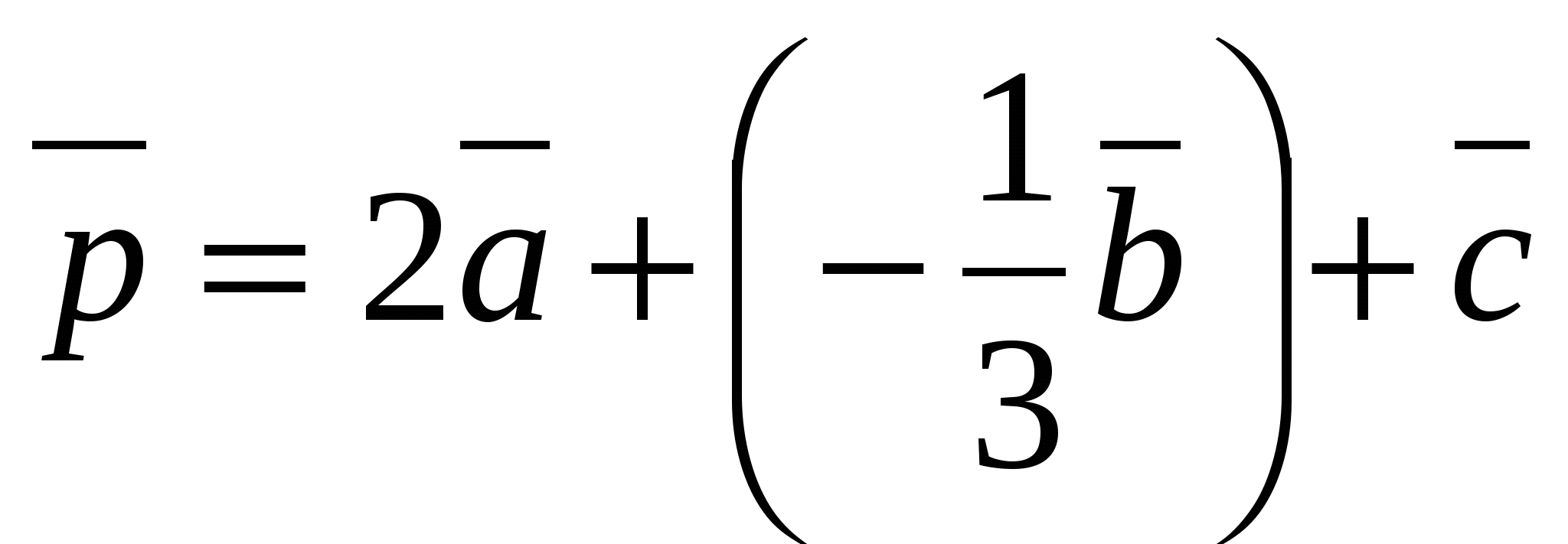 , то его координаты
, то его координаты  можно вычислить как:
можно вычислить как:  ,
, 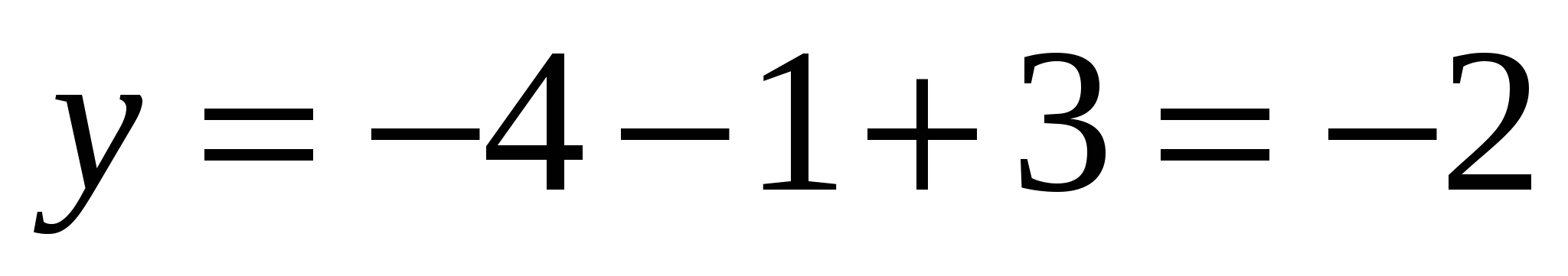 ,
, 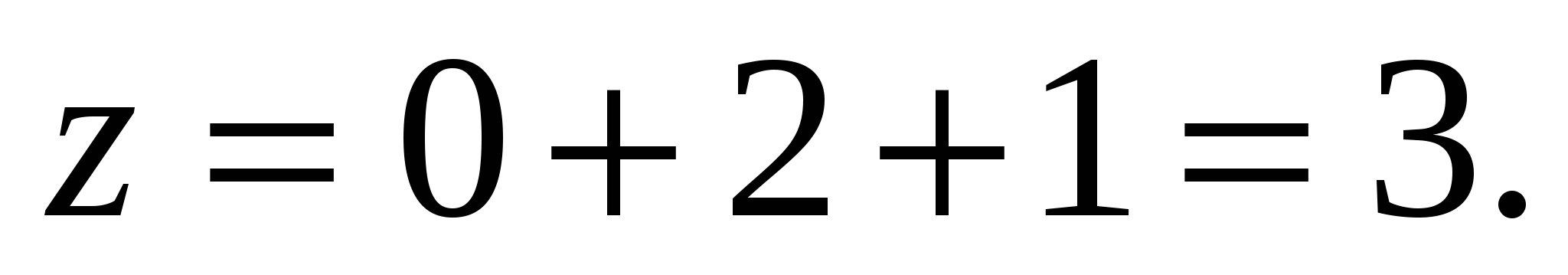 Значит вектор
Значит вектор 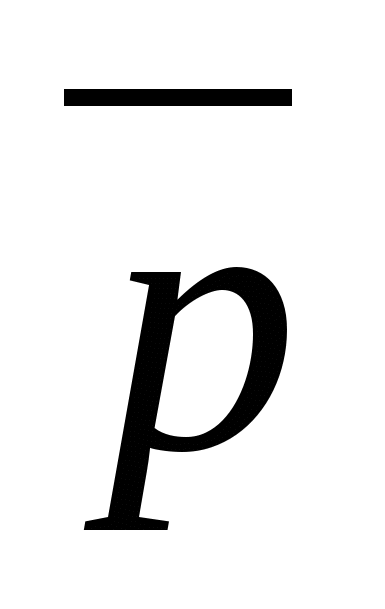 имеет координаты
имеет координаты 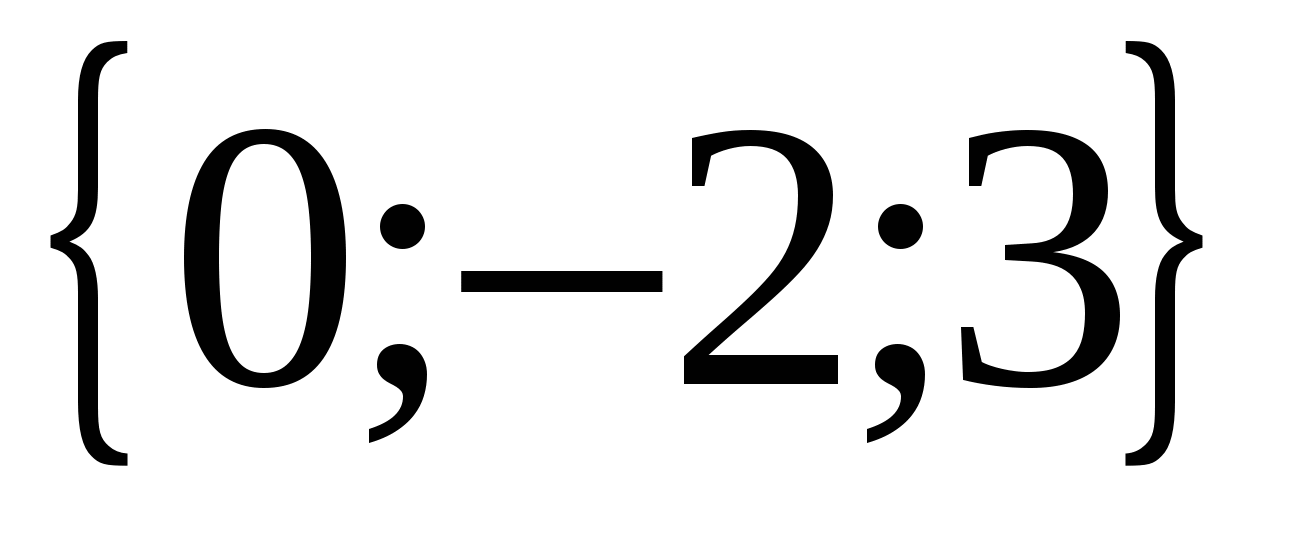 .
.
3.Связь между координатами векторов и координатами точек.
Определение.
Вектор, конец которого совпадает с данной точкой, а начало - с началом координат, называется радиус-вектором данной точки.
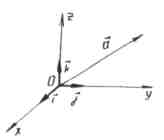
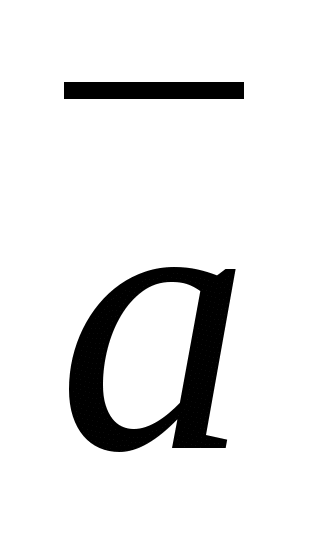
 - радиус вектор
- радиус вектор
 ,
,
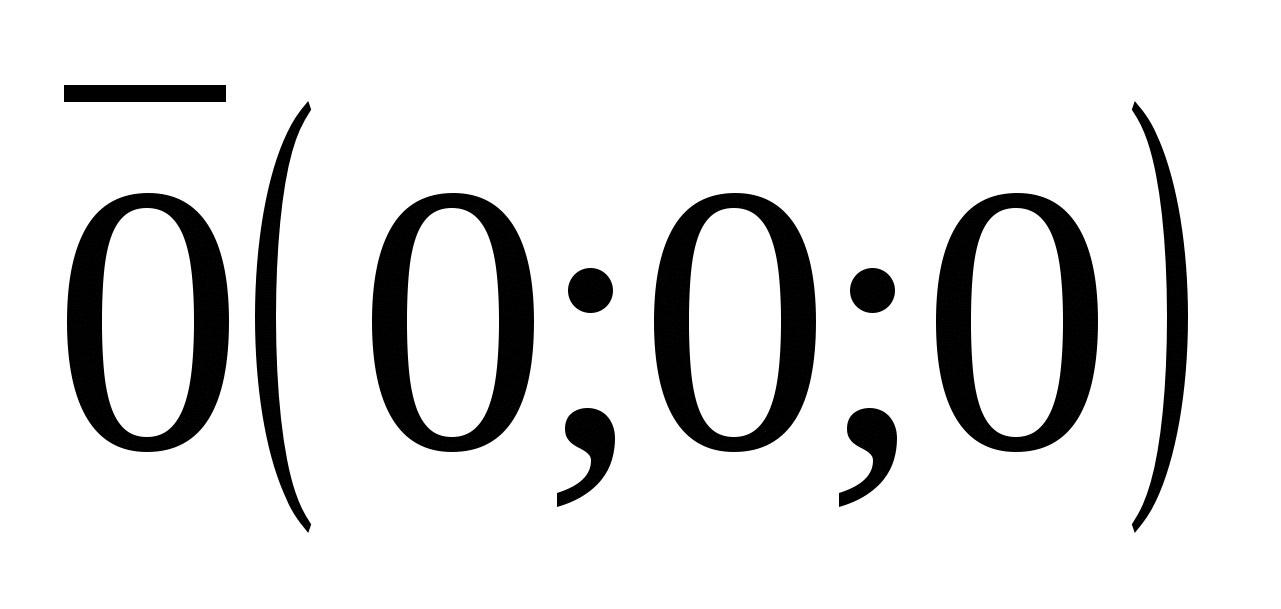 ;
;
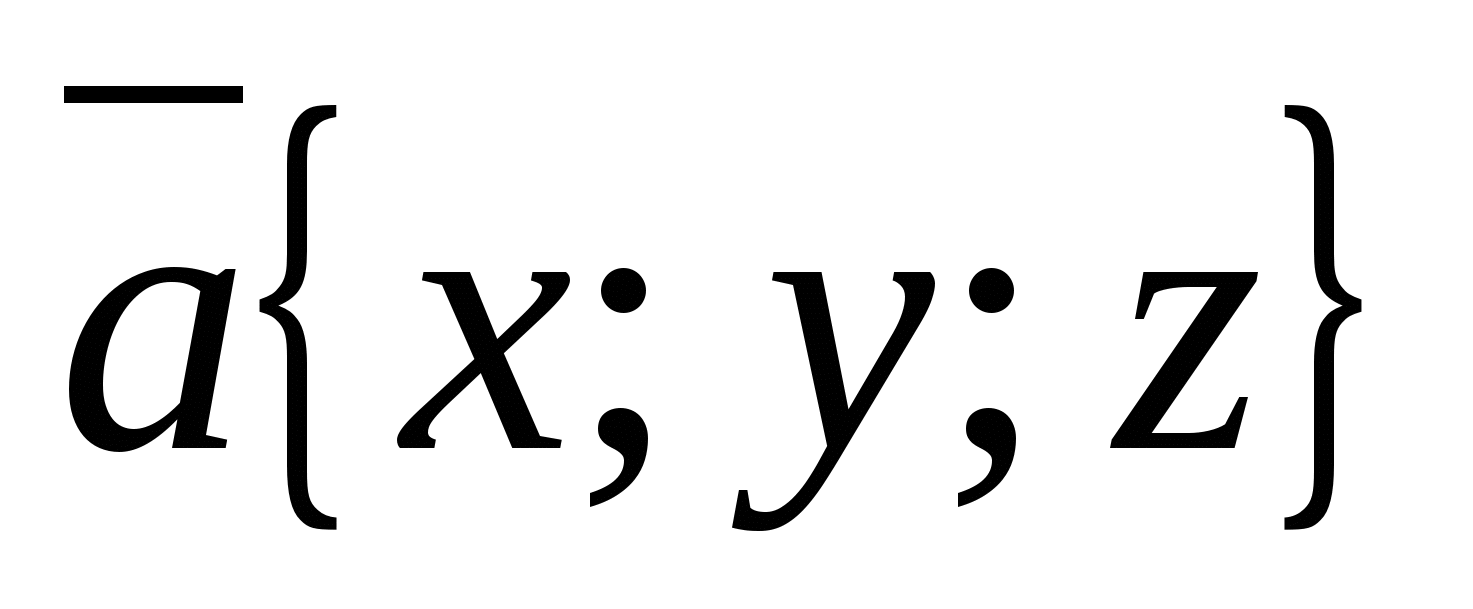
Правило 5.
Координаты любой точки равны соответствующим координатам ее радиус - вектора. ,.

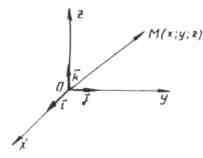
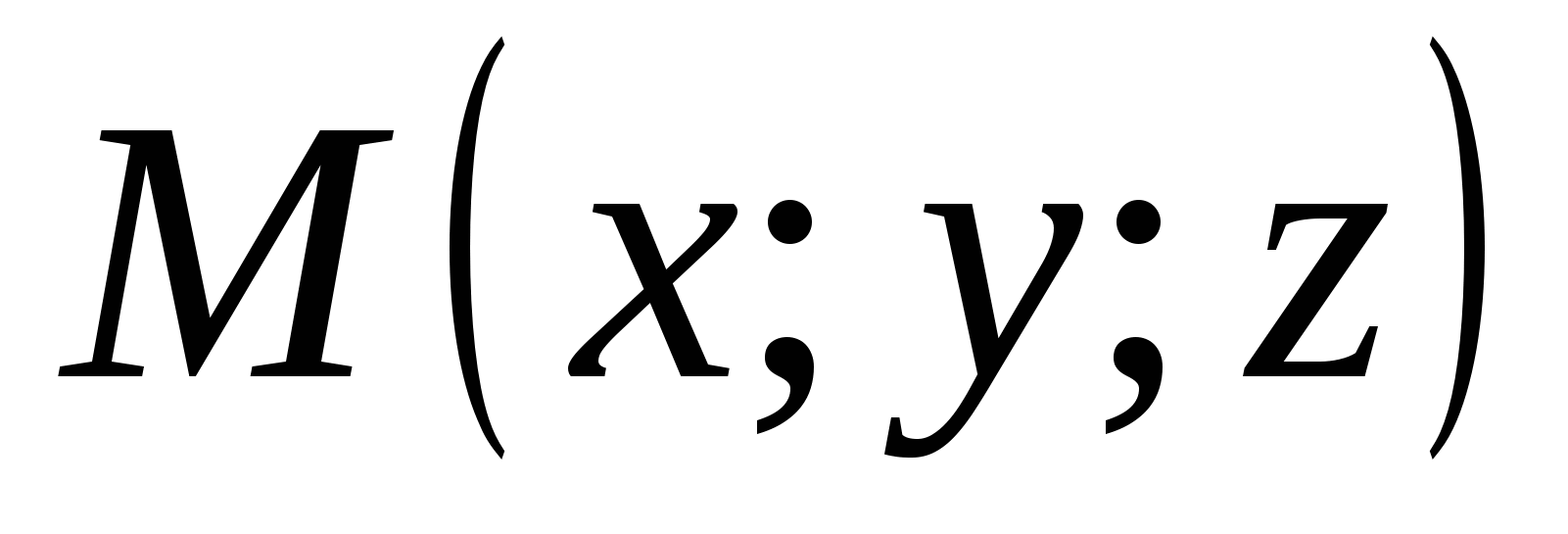
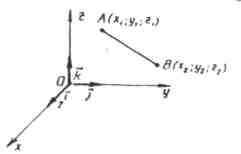
Правило 6.
Каждая координата вектора равна разности соответствующих координат его конца и начала.
 .
.
4.Условие коллинеарности двух векторов в координатах.
Пусть в системе координат  заданы два вектора своими координатами
заданы два вектора своими координатами  и
и 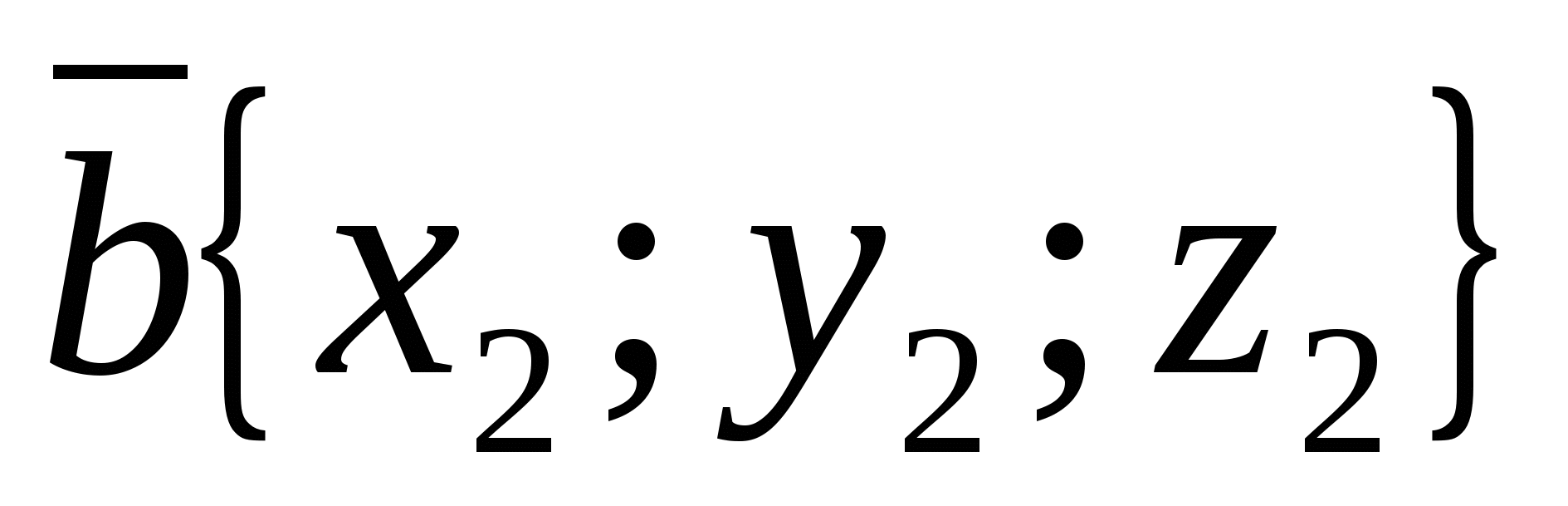 .
.
Правило 7.
Векторы
 и
и 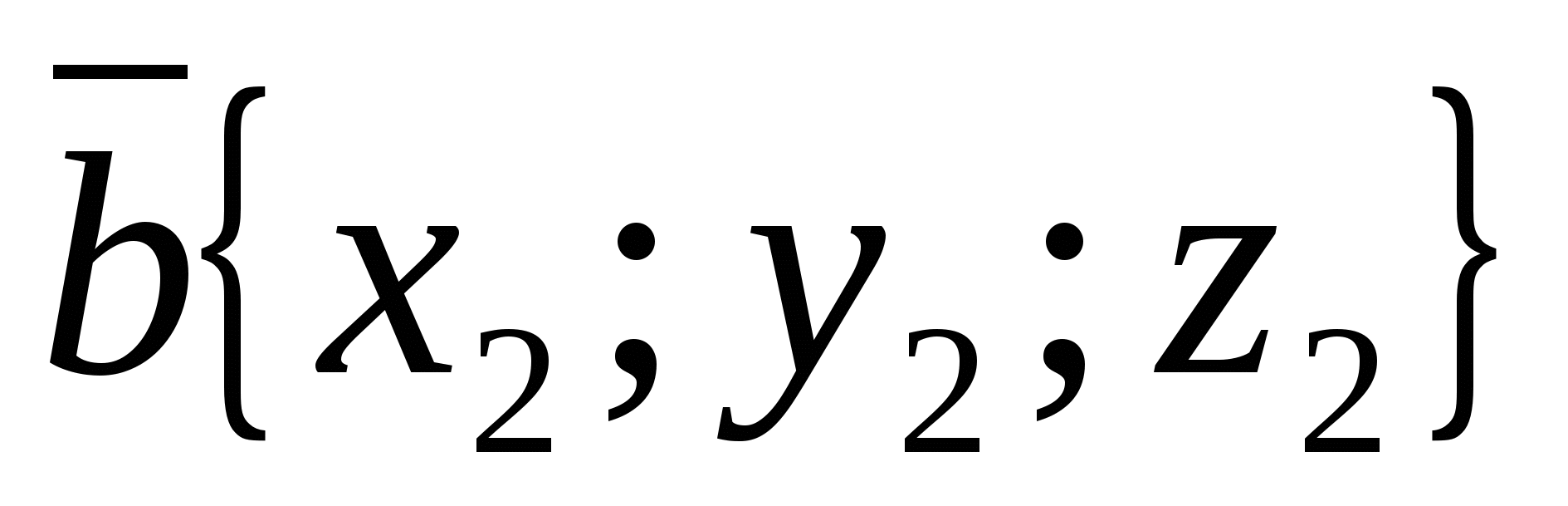 коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны,
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, 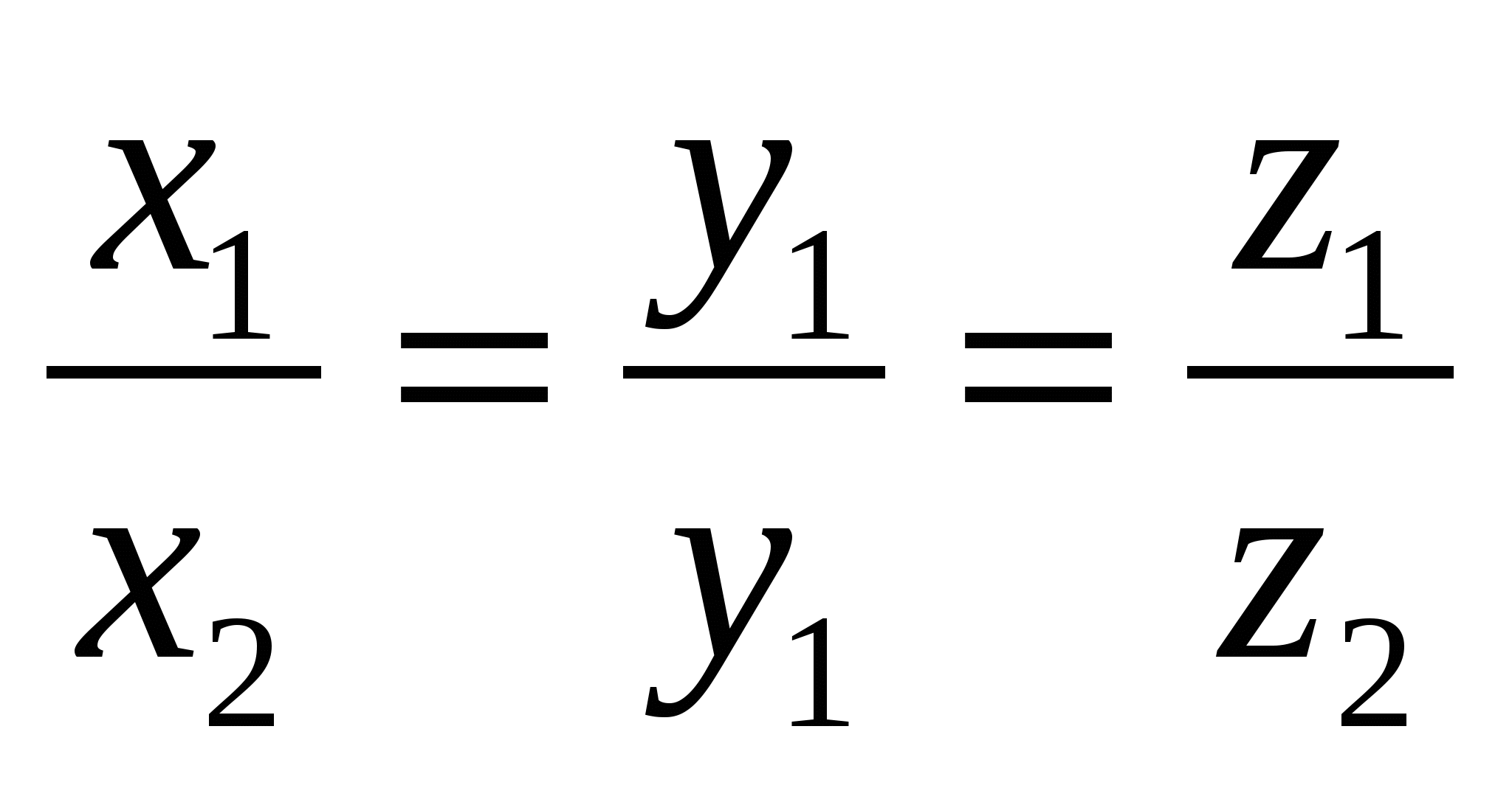 .
.
Пример.
а) Рассмотрим векторы 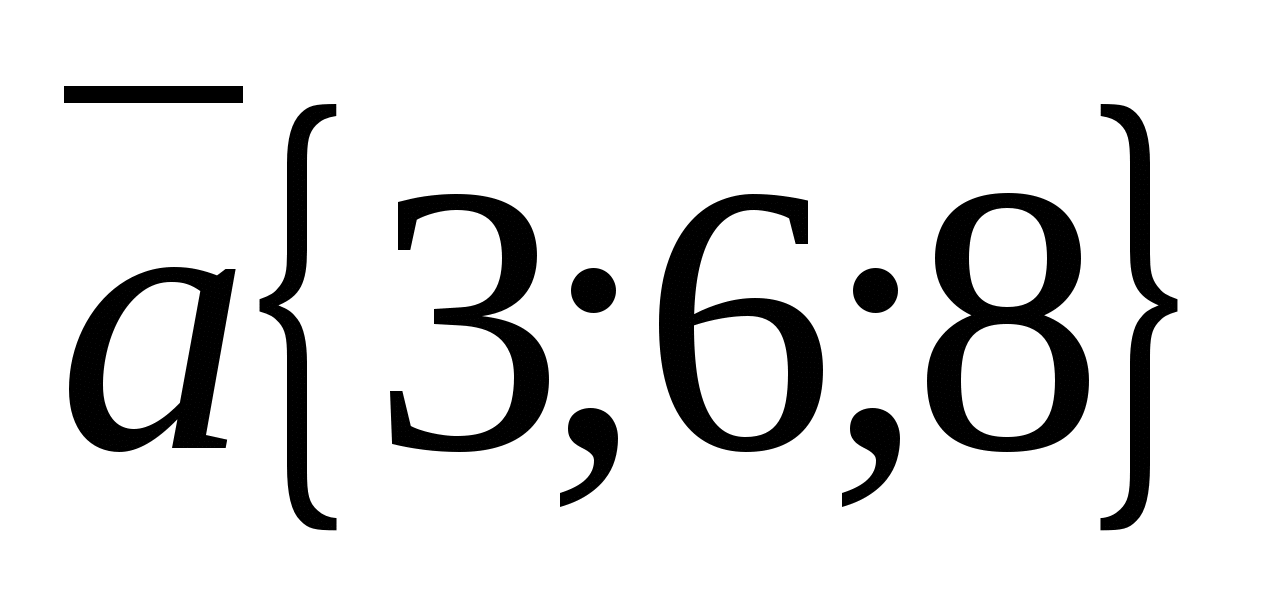 и
и 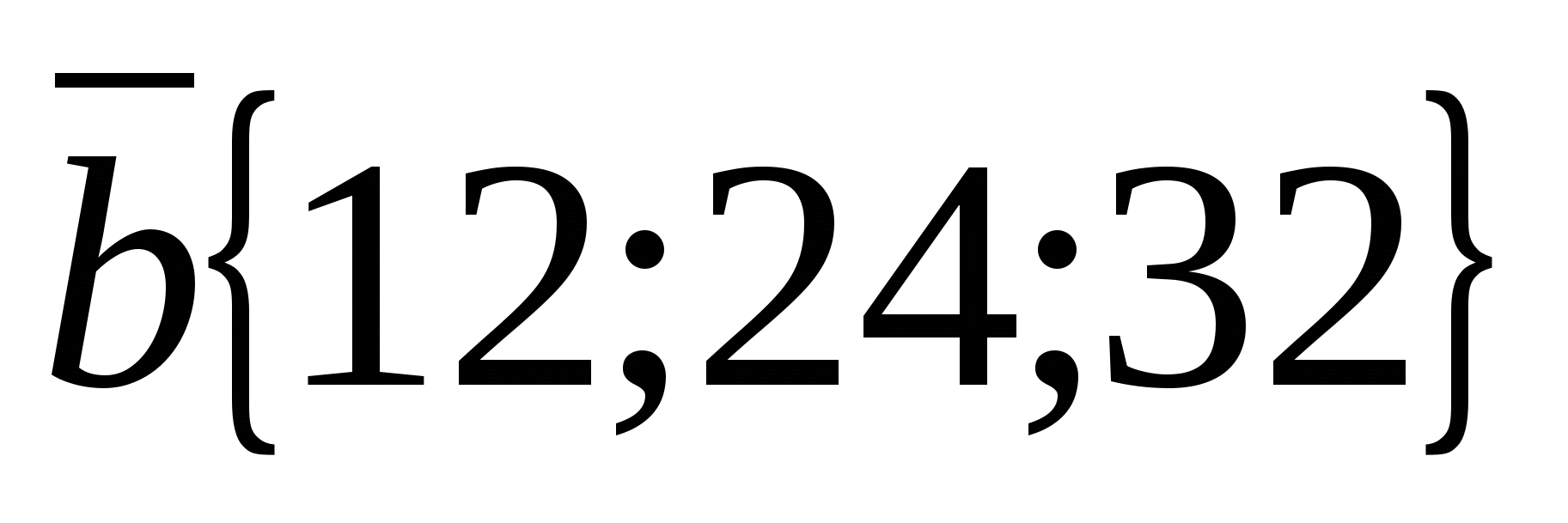 .
.
Координаты вектора 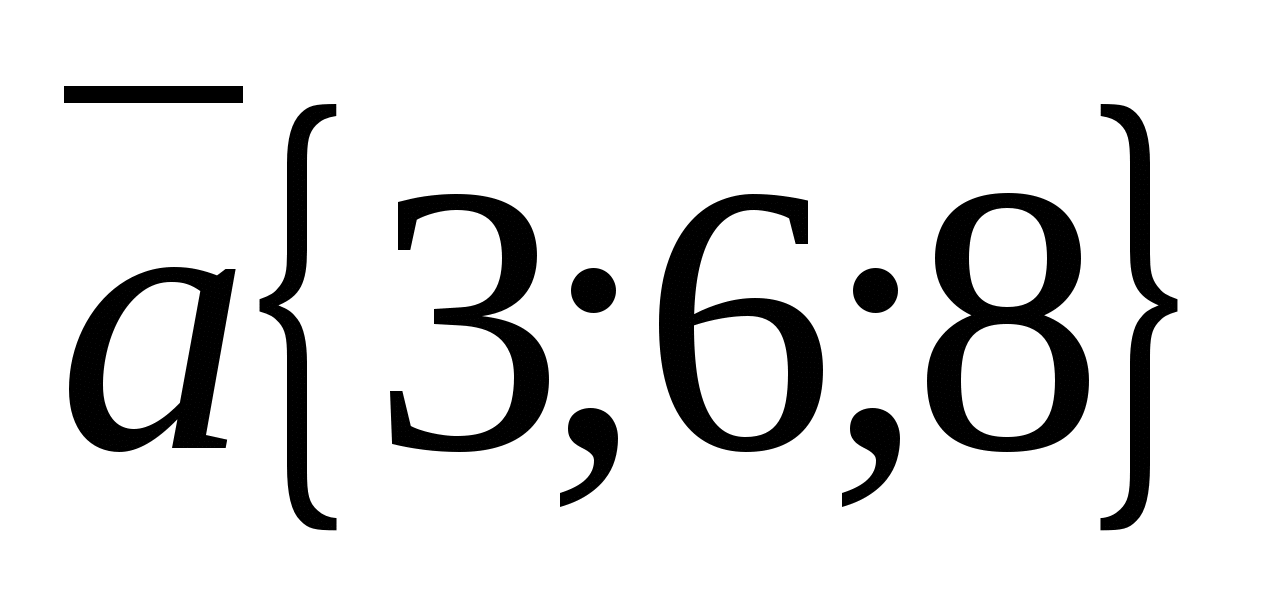 пропорциональны соответствующим координатам вектора
пропорциональны соответствующим координатам вектора 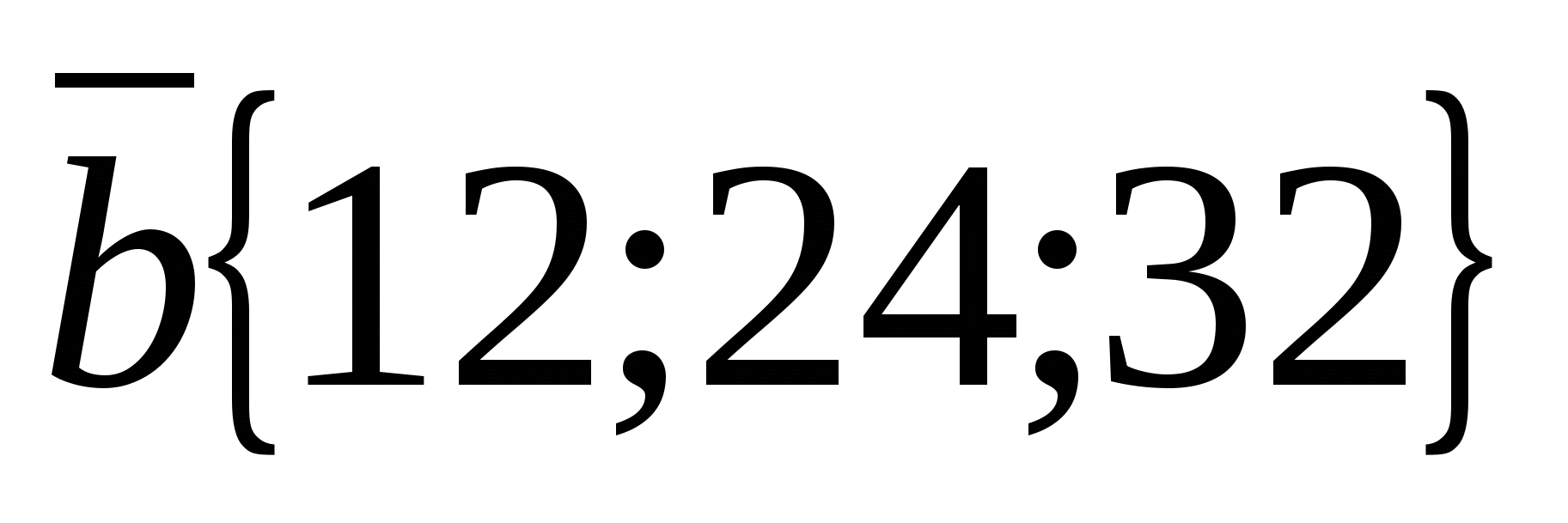 :
: 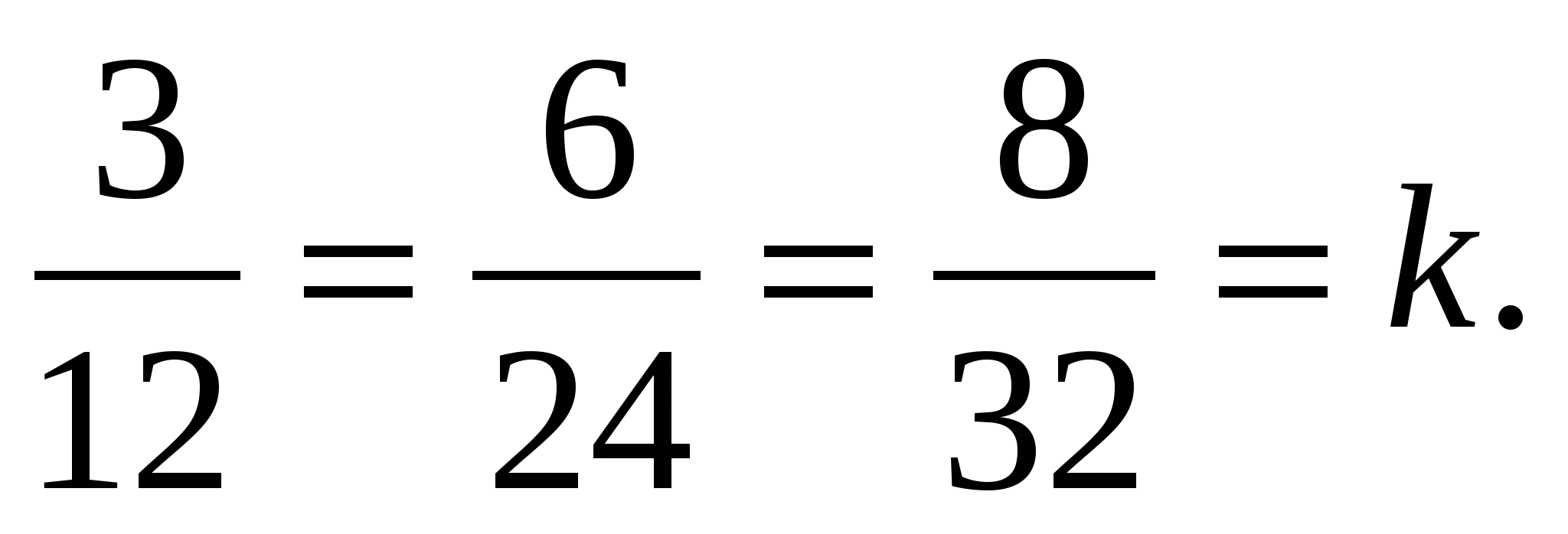 Поэтому
Поэтому 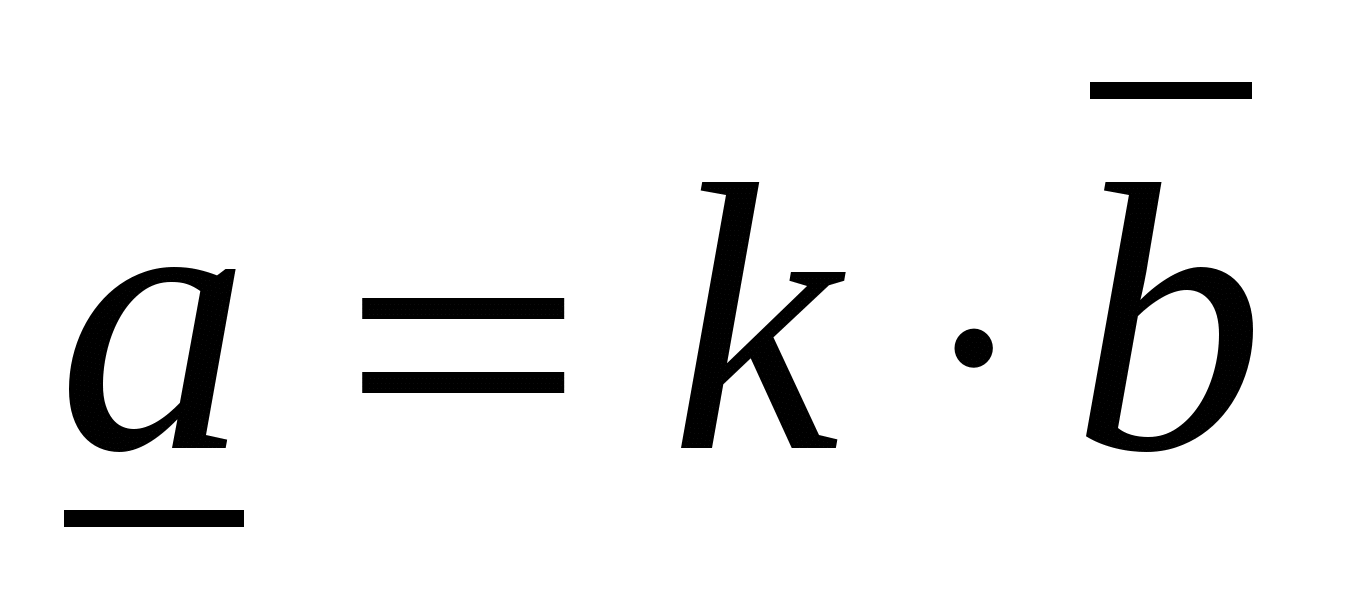 , и, следовательно векторы коллинеарны.
, и, следовательно векторы коллинеарны.
б) Рассмотрим векторы 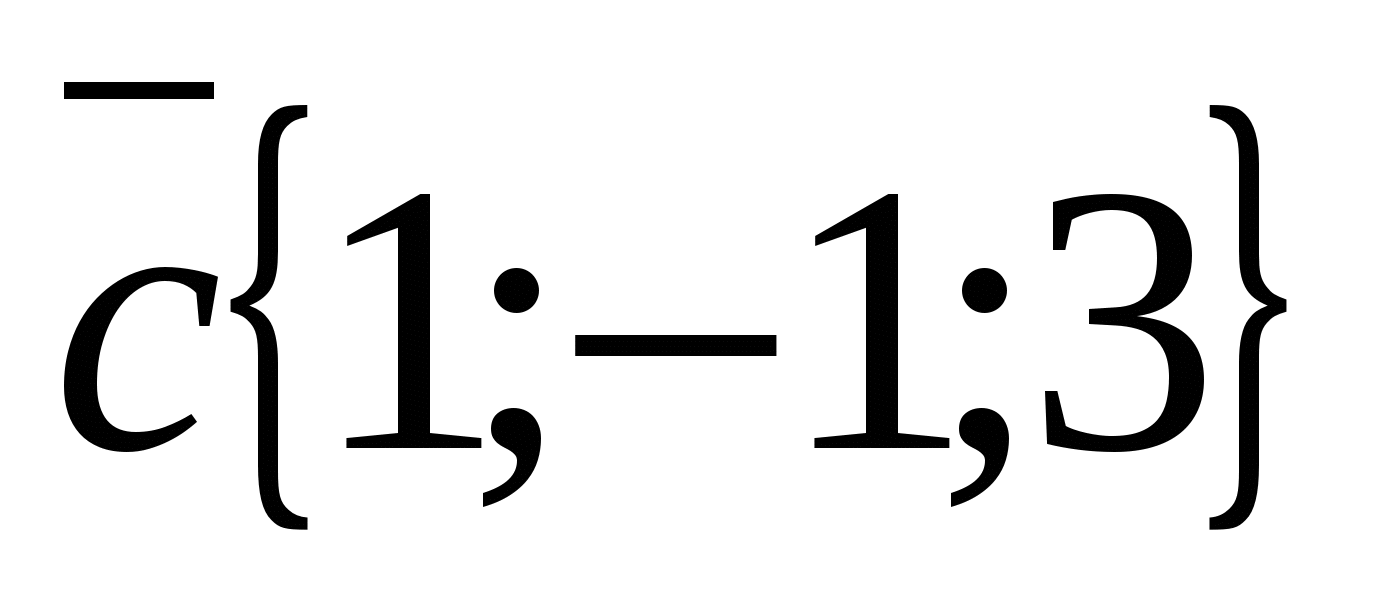 и
и 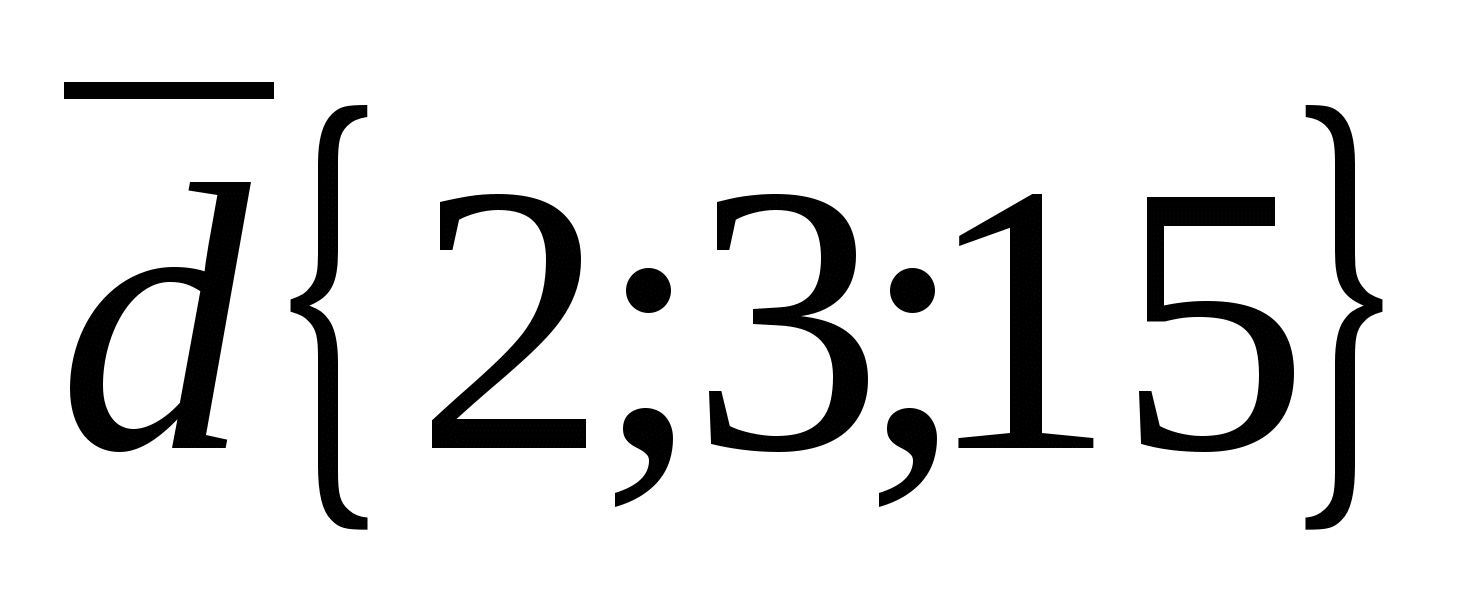 .
.
Координаты вектора 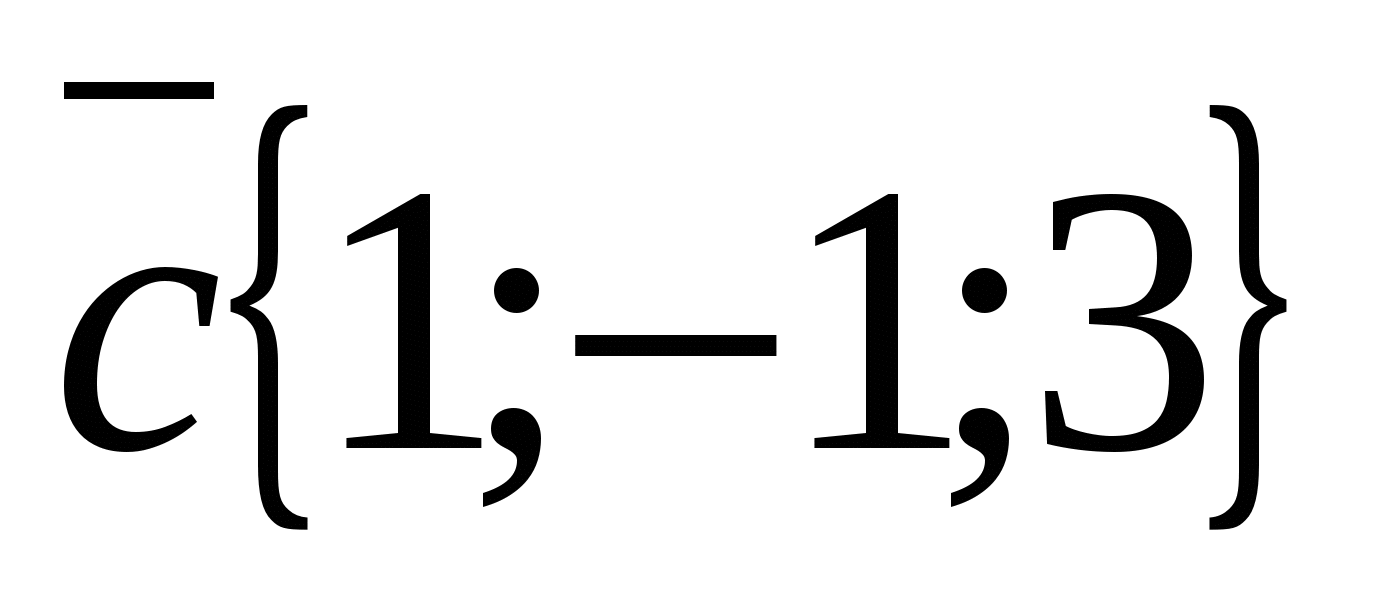 не пропорциональны соответствующим координатам вектора
не пропорциональны соответствующим координатам вектора 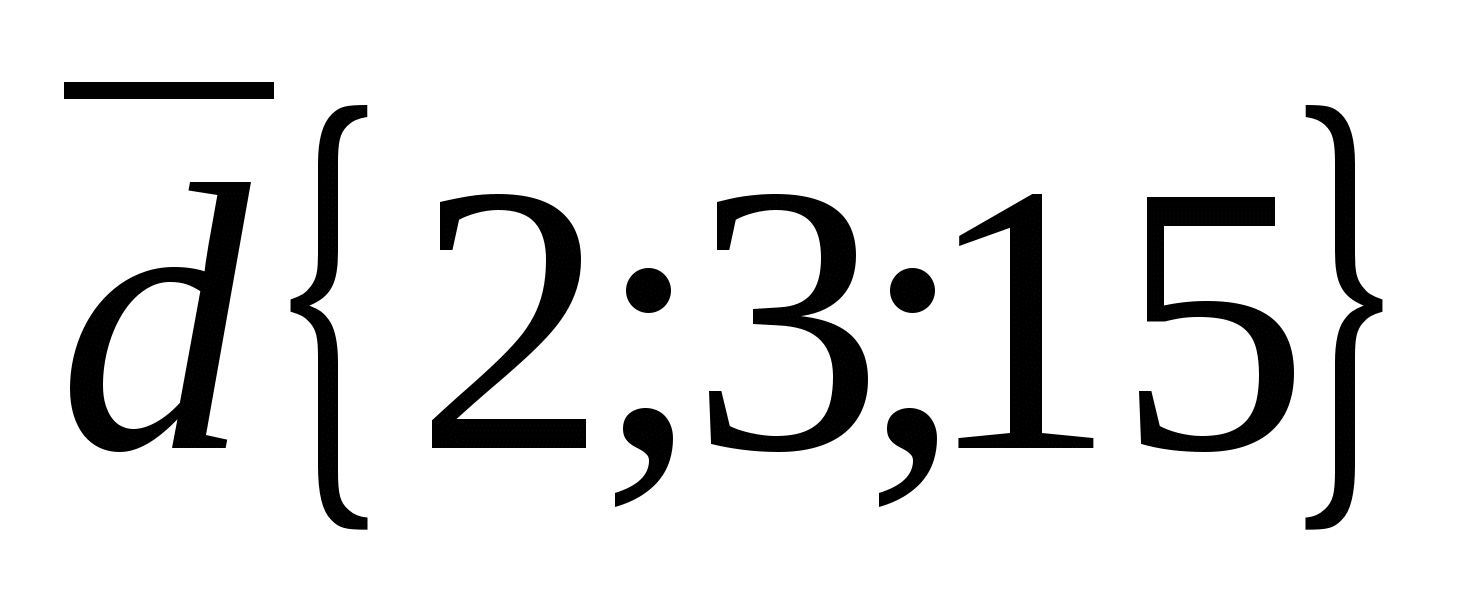 , например
, например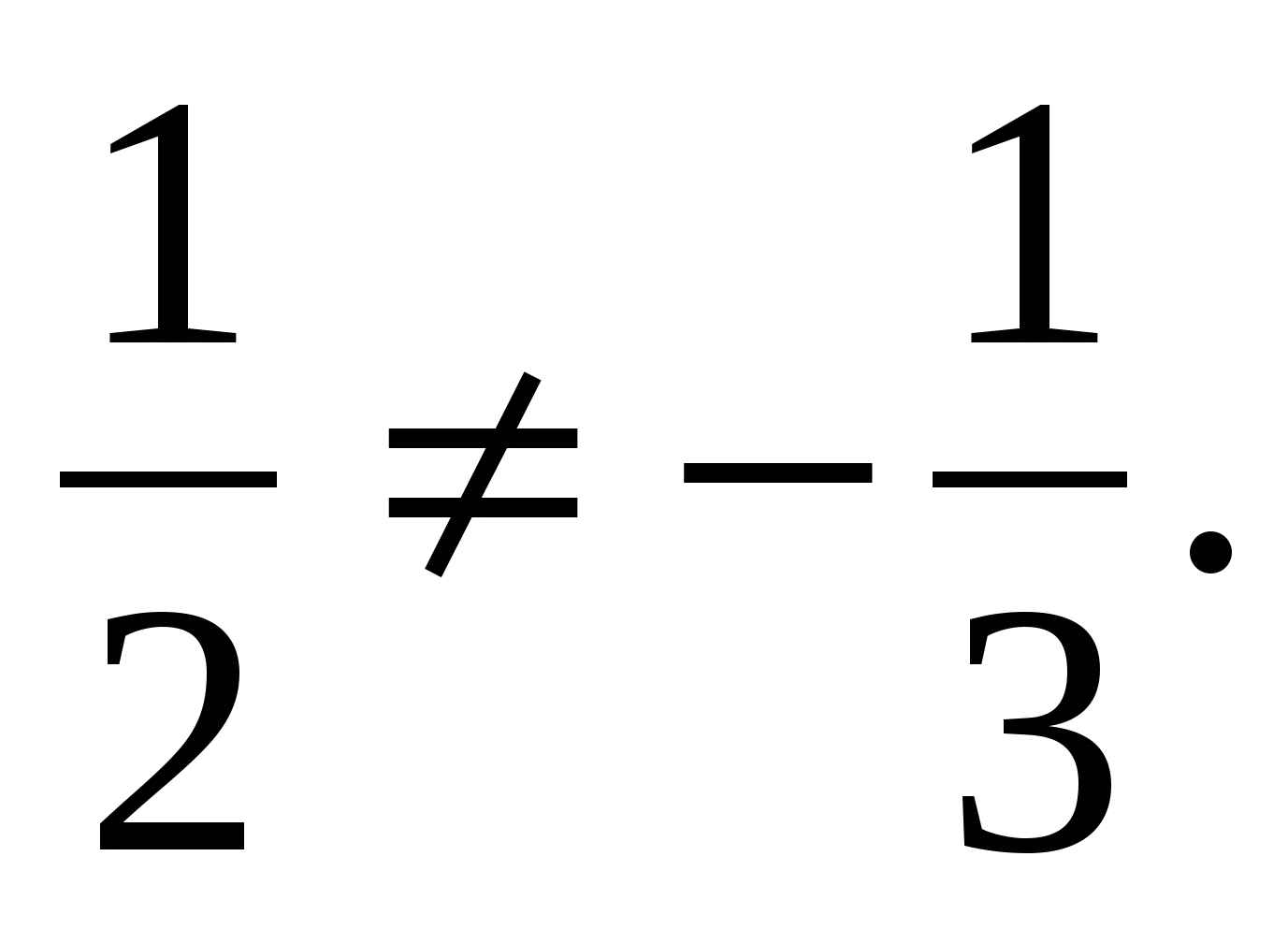 Значит векторы не являются коллинеарными.
Значит векторы не являются коллинеарными.
5.Простейшие задачи в координатах .
Задача 1.
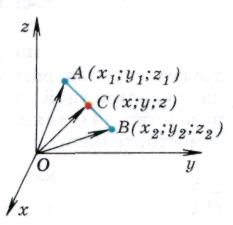 Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
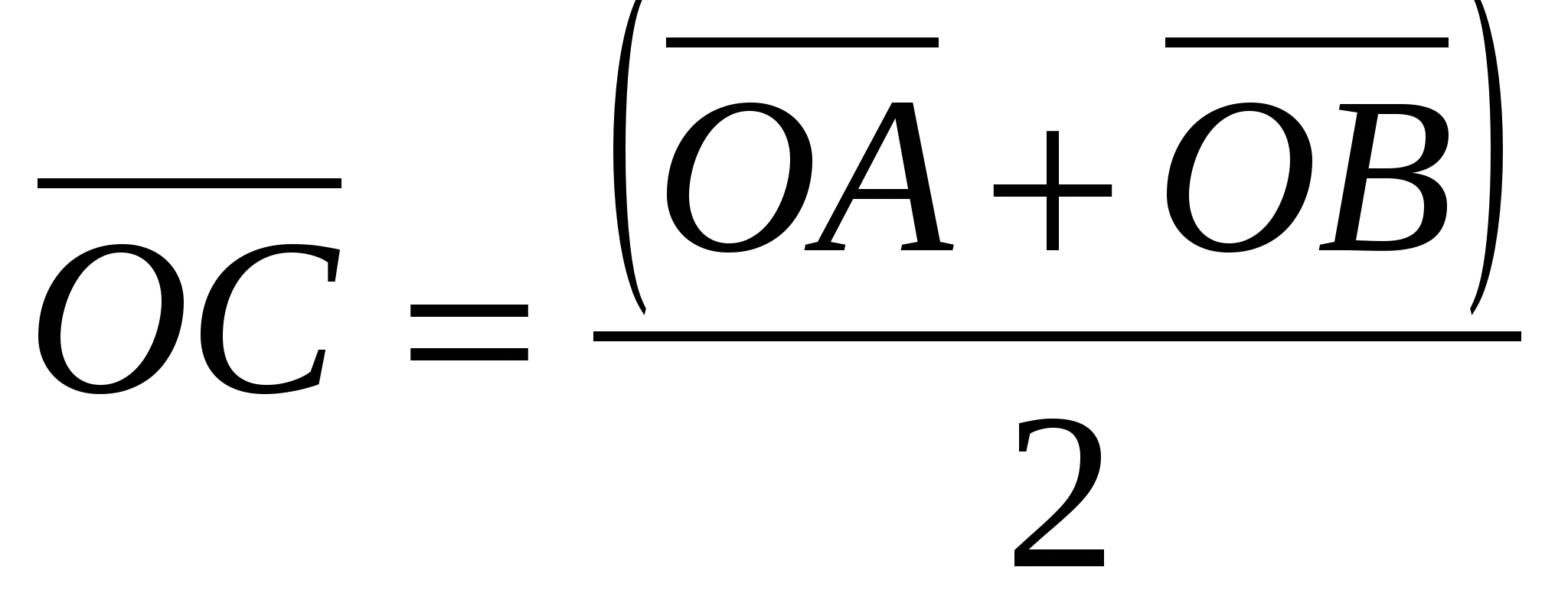 , где
, где 
 ,
, 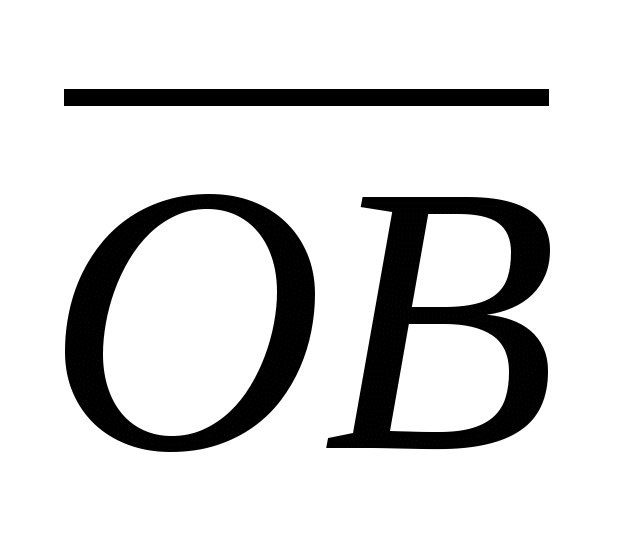
 и
и 
 .
.
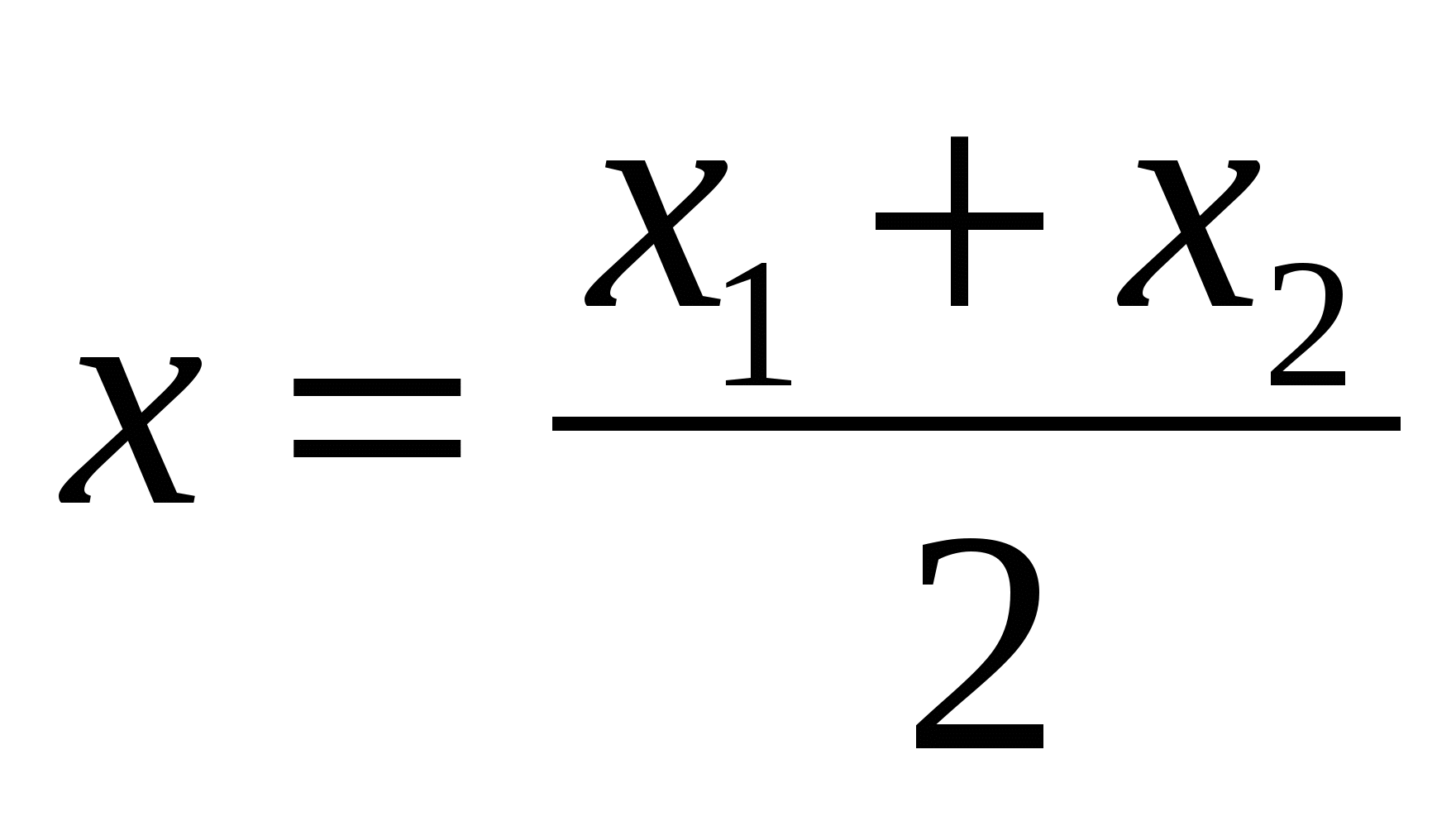 ,
,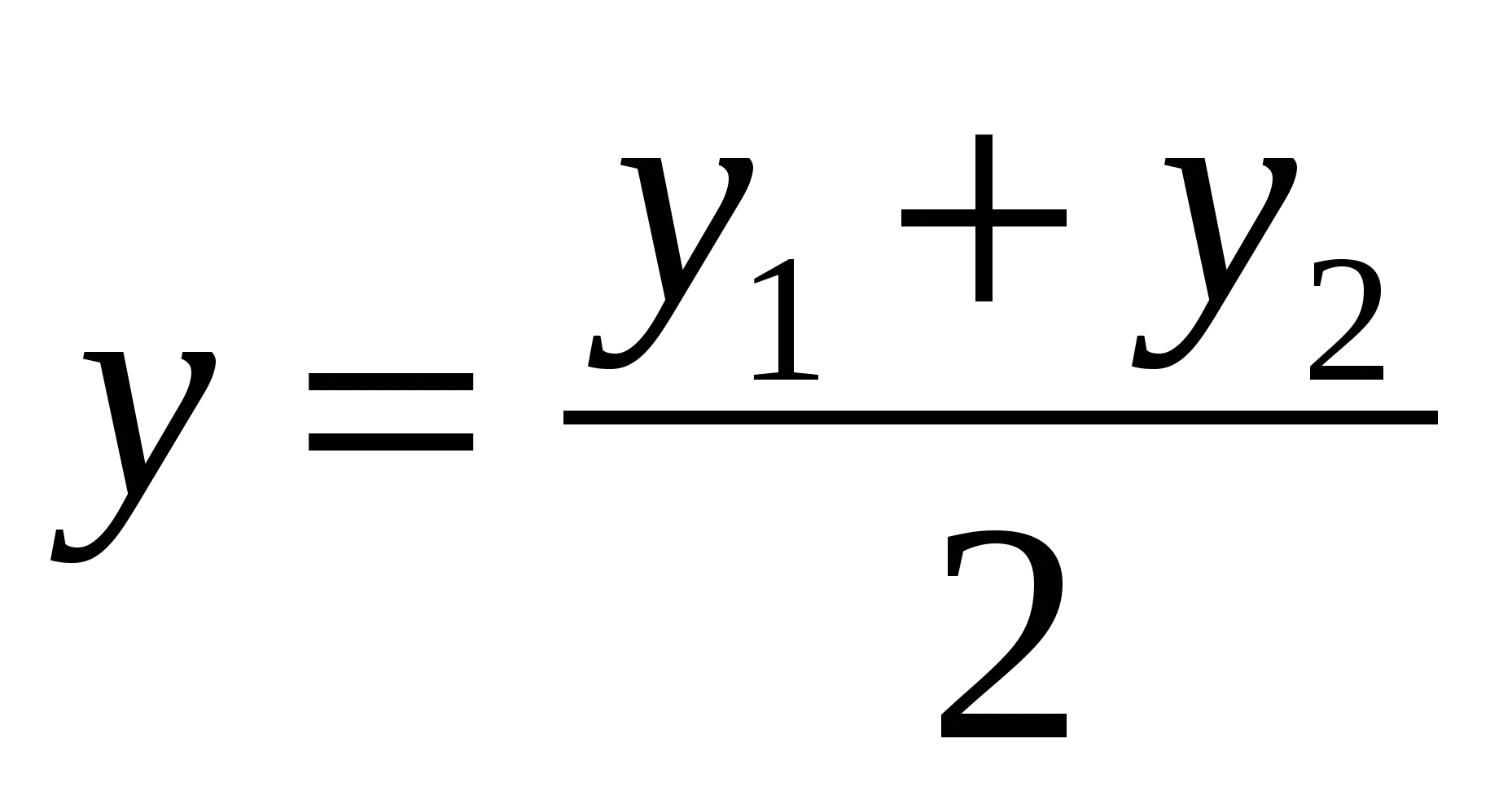 ,
, 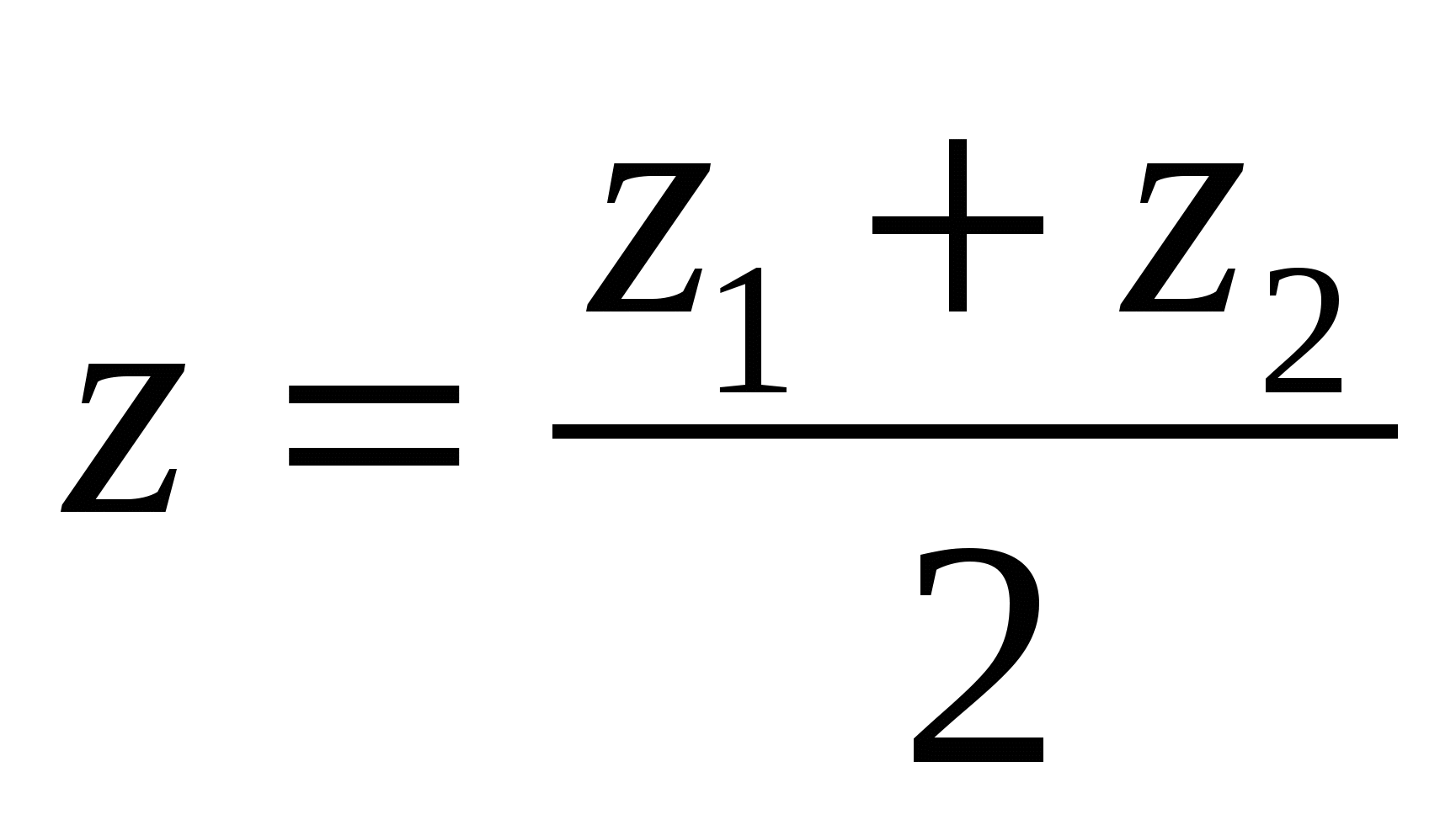 ,
,
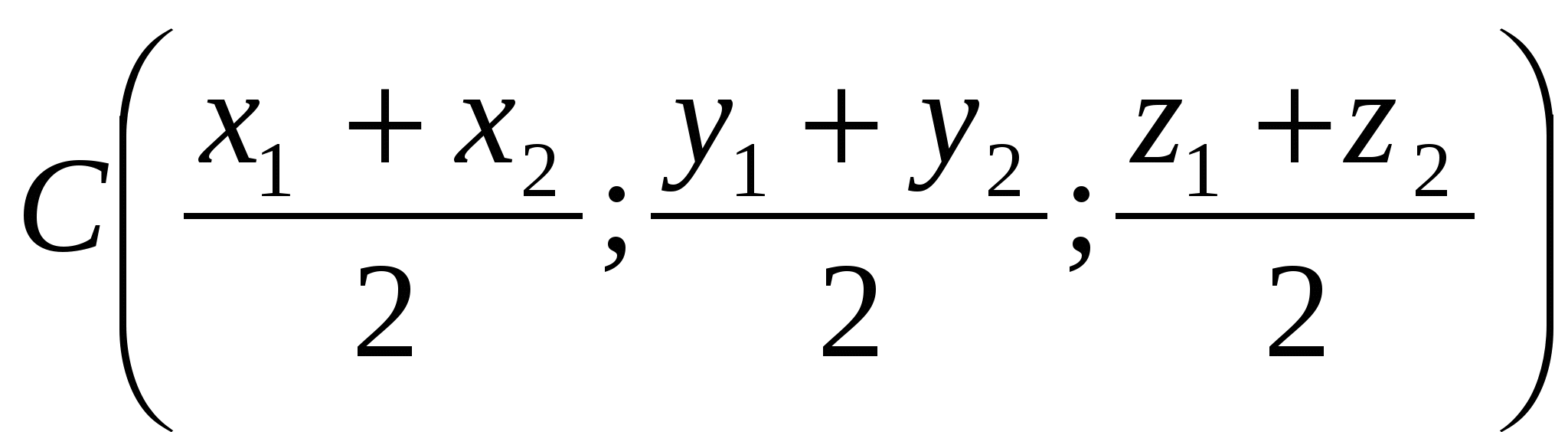
б) Вычисление длины вектора по его координатам.
Рассмотрим вектор
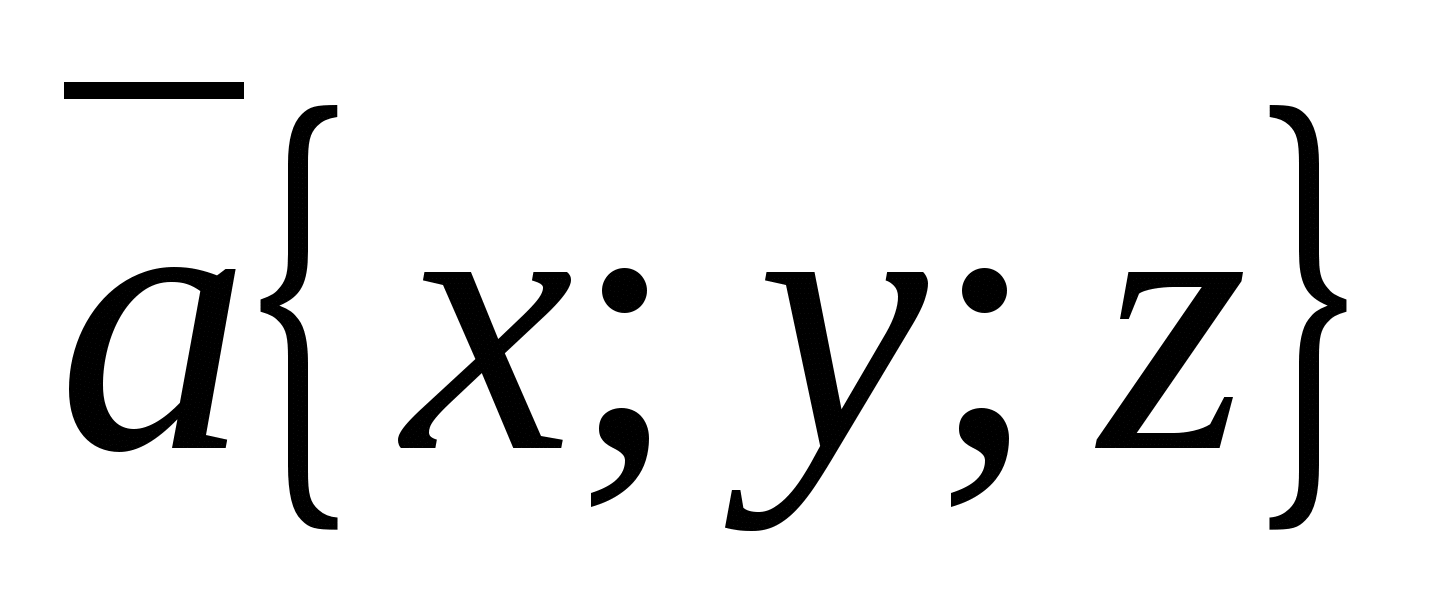 ,
,
длина вектора вычисляется по формуле
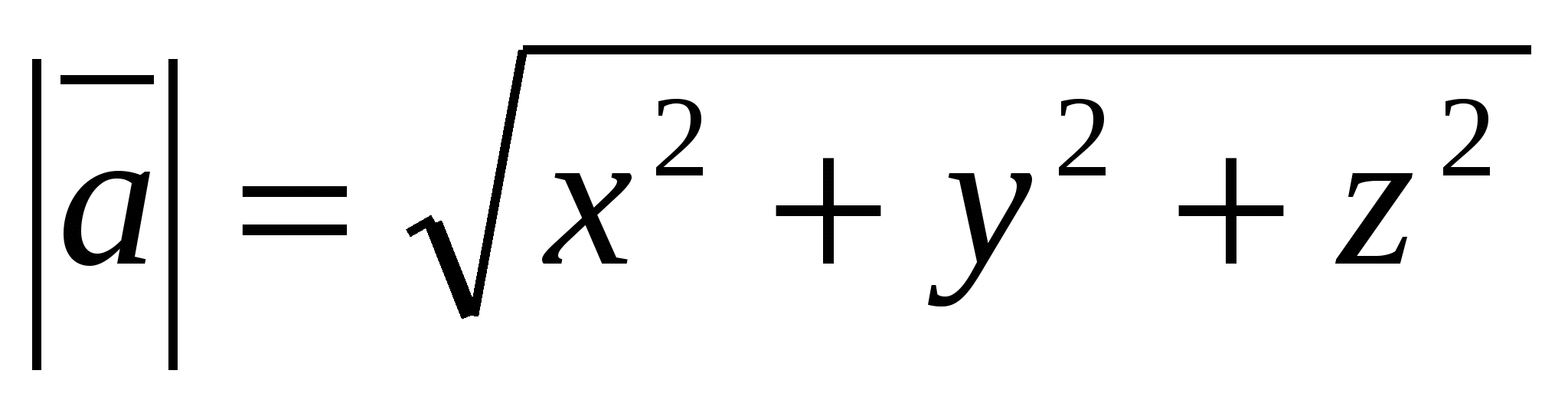 .
.
Так как
 =
=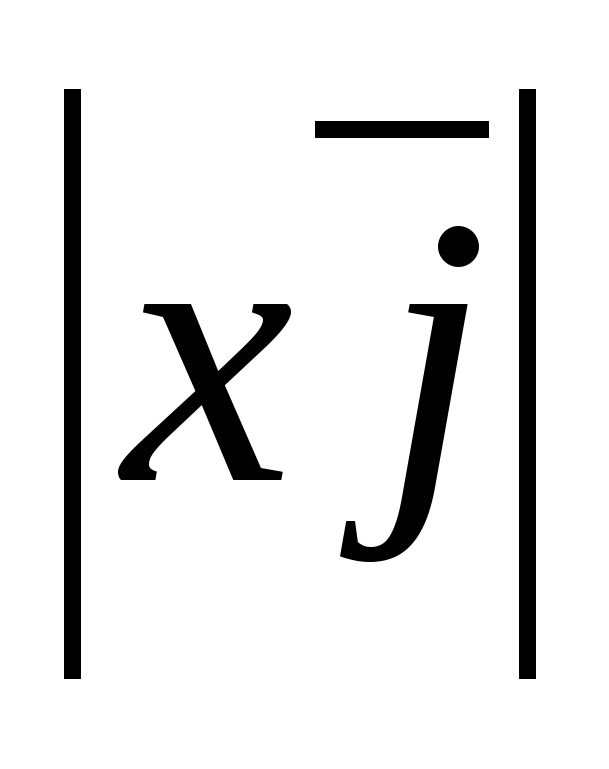 =
=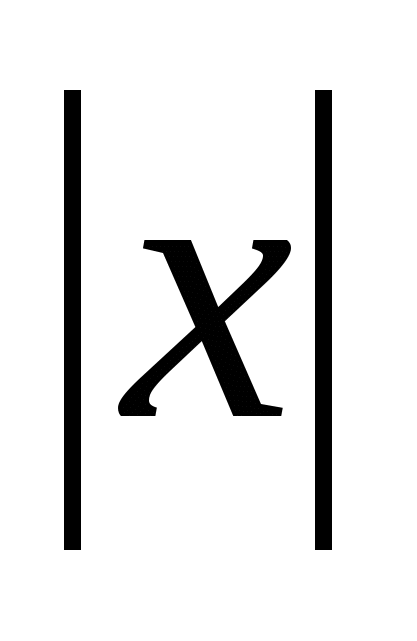 ,
,
 =
= =
=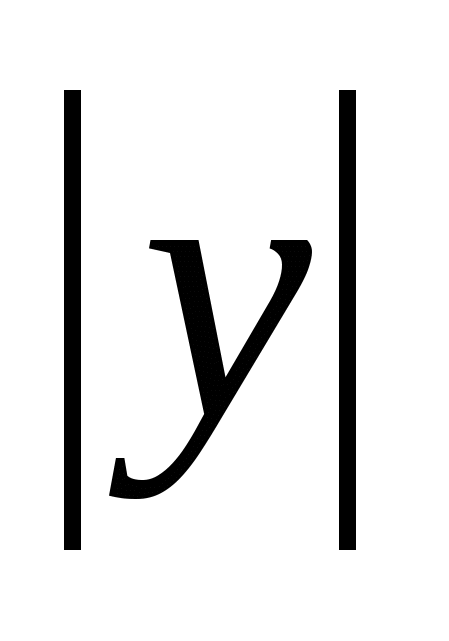 ,
,
 =
= =
= , и
, и 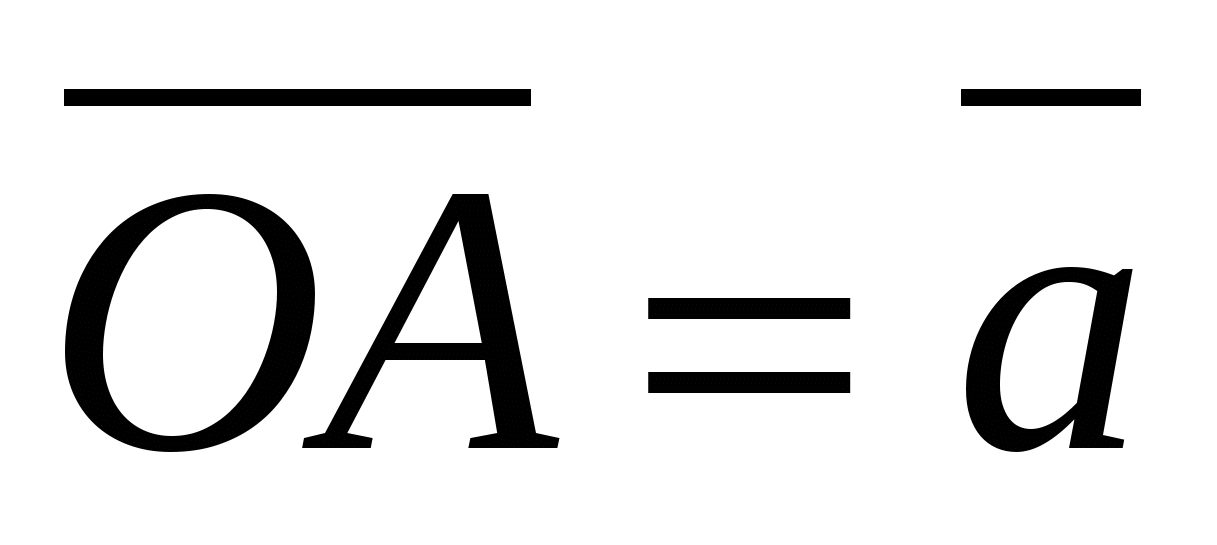 , то из равенства
, то из равенства 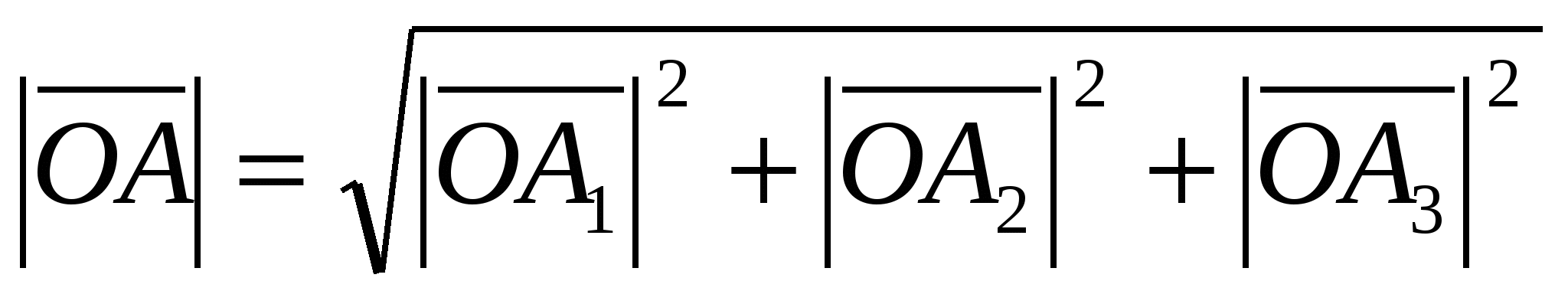 получаем формулу: .
получаем формулу: .
в) Расстояние между двумя точками.
 Рассмотрим две произвольные точки: точку
Рассмотрим две произвольные точки: точку  и точку
и точку
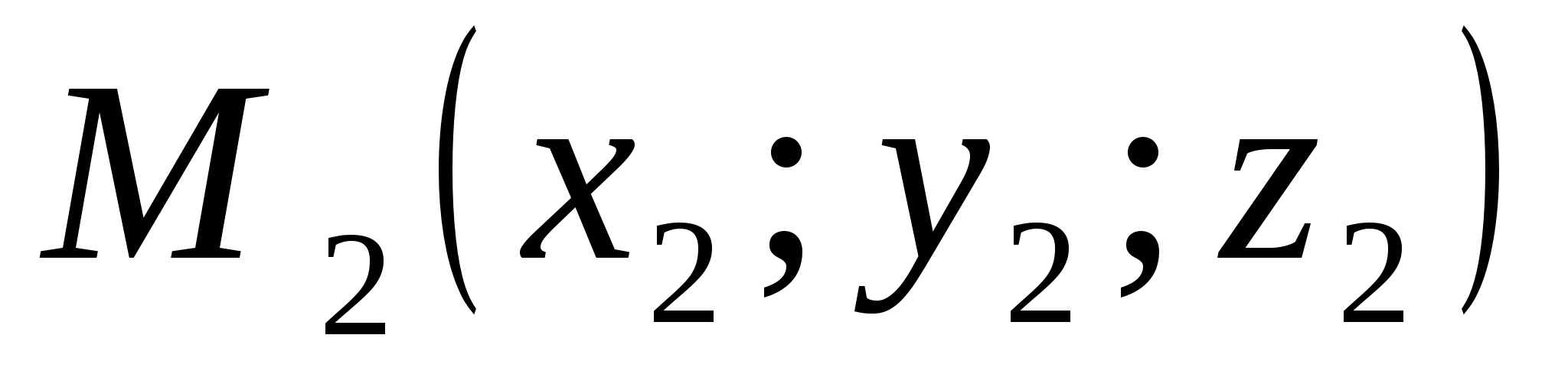 . Выразим расстояние
d
между точками
. Выразим расстояние
d
между точками 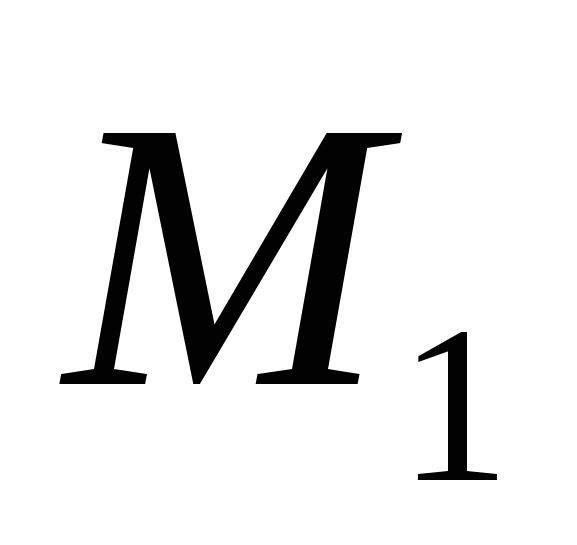 и
и 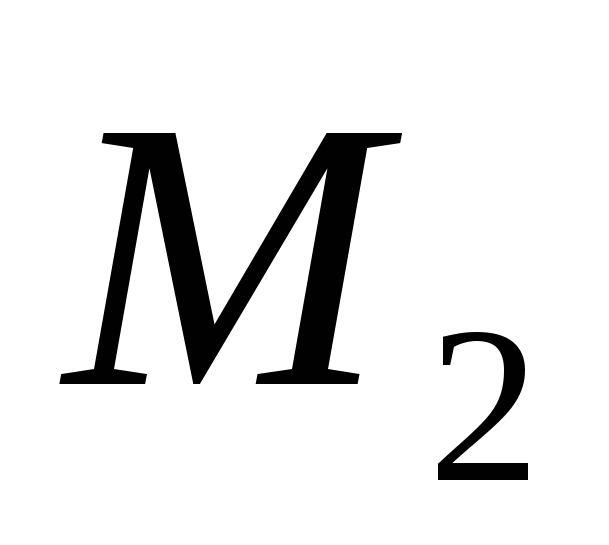 через их координаты.
через их координаты.
Рассмотрим вектор , где .
Но 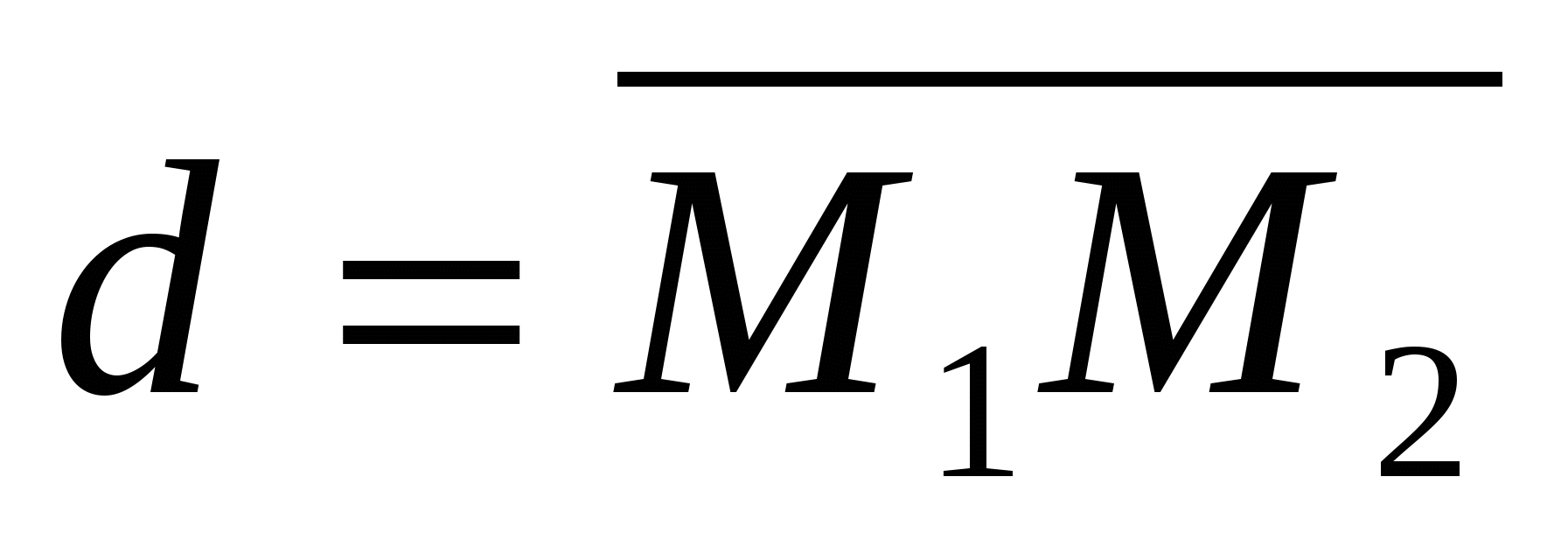 . Таким образом,
расстояние между точками
. Таким образом,
расстояние между точками 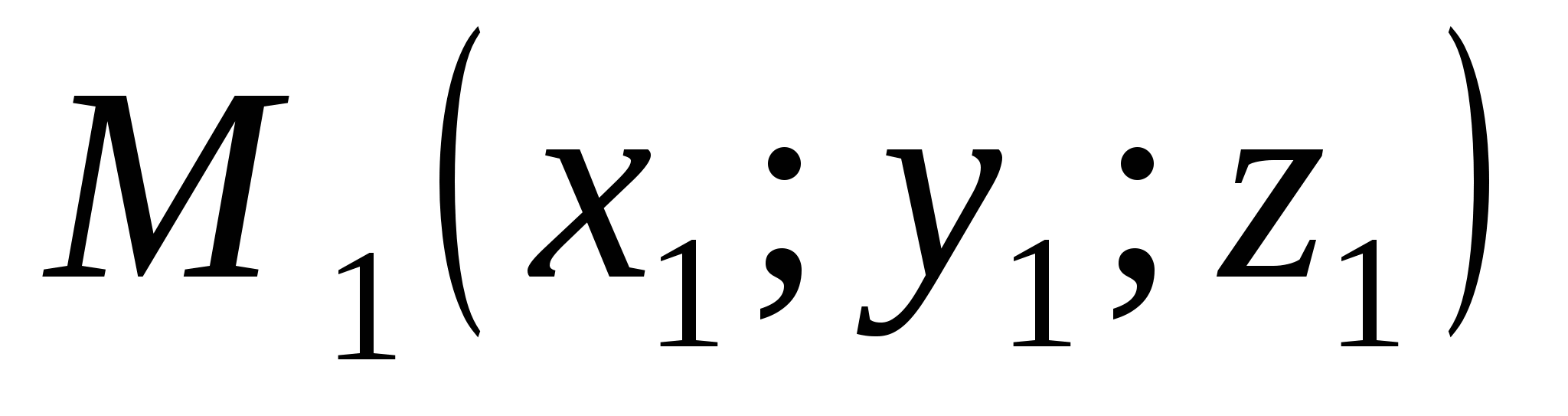 и
и 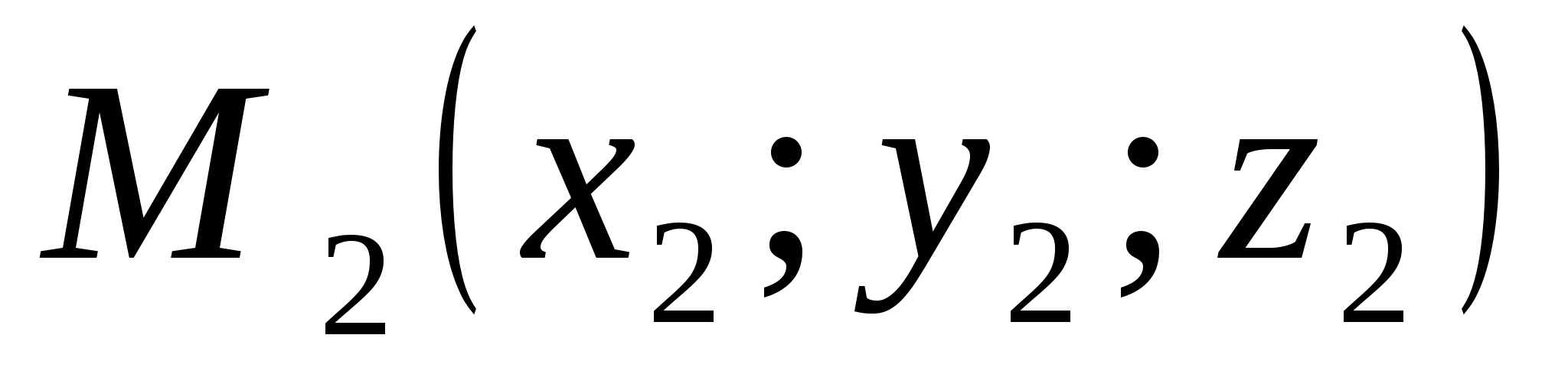
вычисляется по формуле .
6.Скалярное произведение векторов и вычисление угла между векторами через их координаты.
1) Скалярное произведение векторов
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
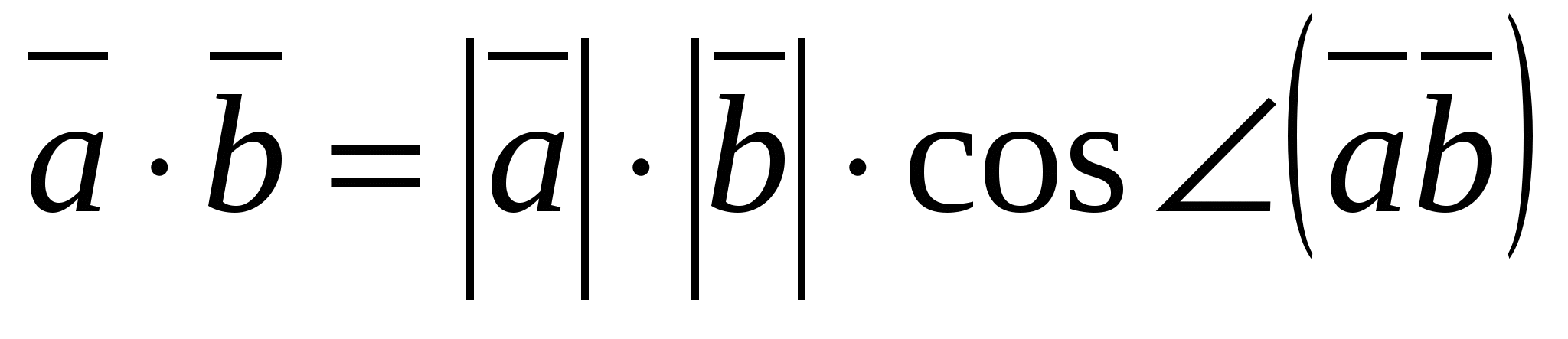
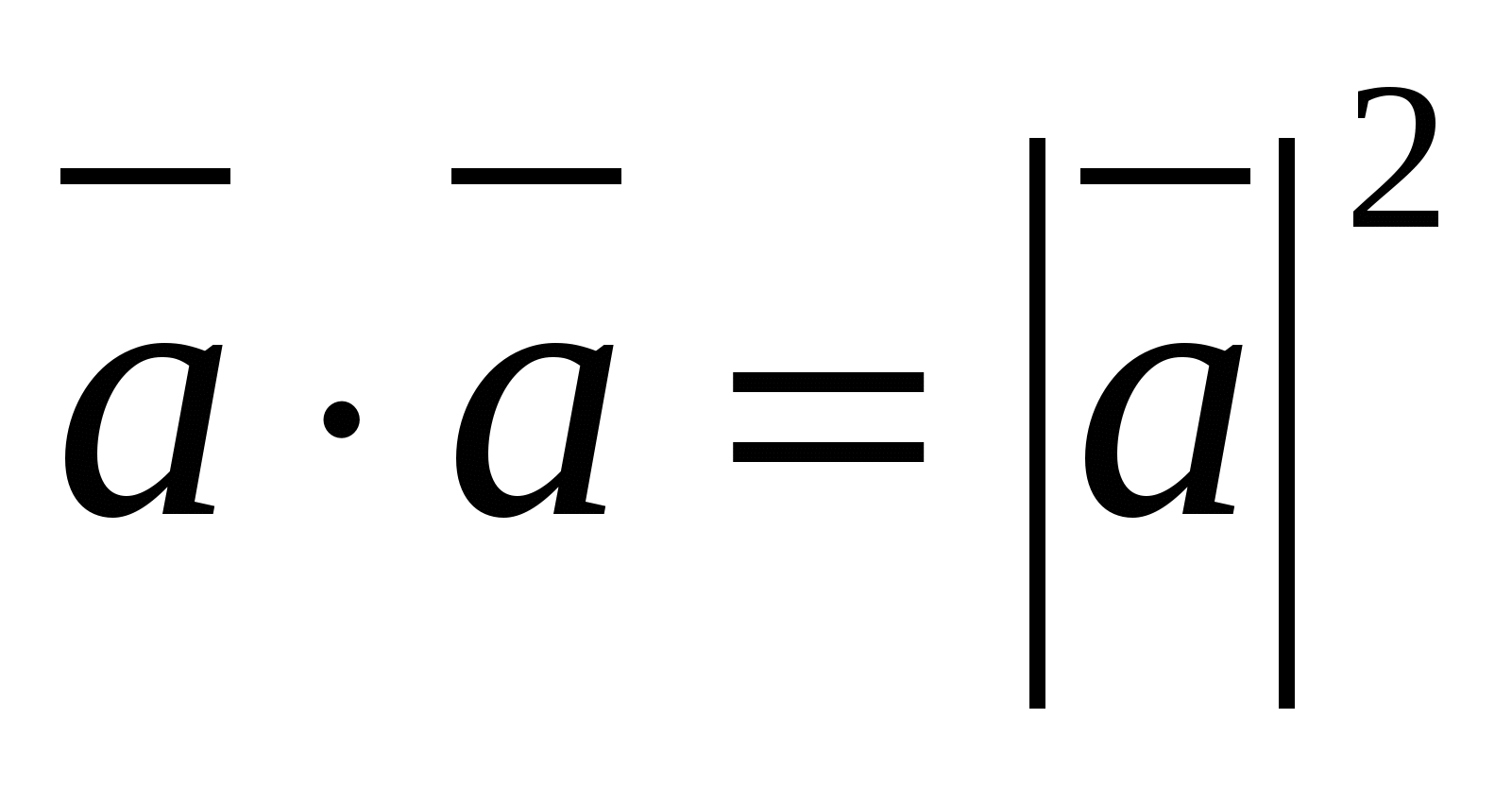
т.е.
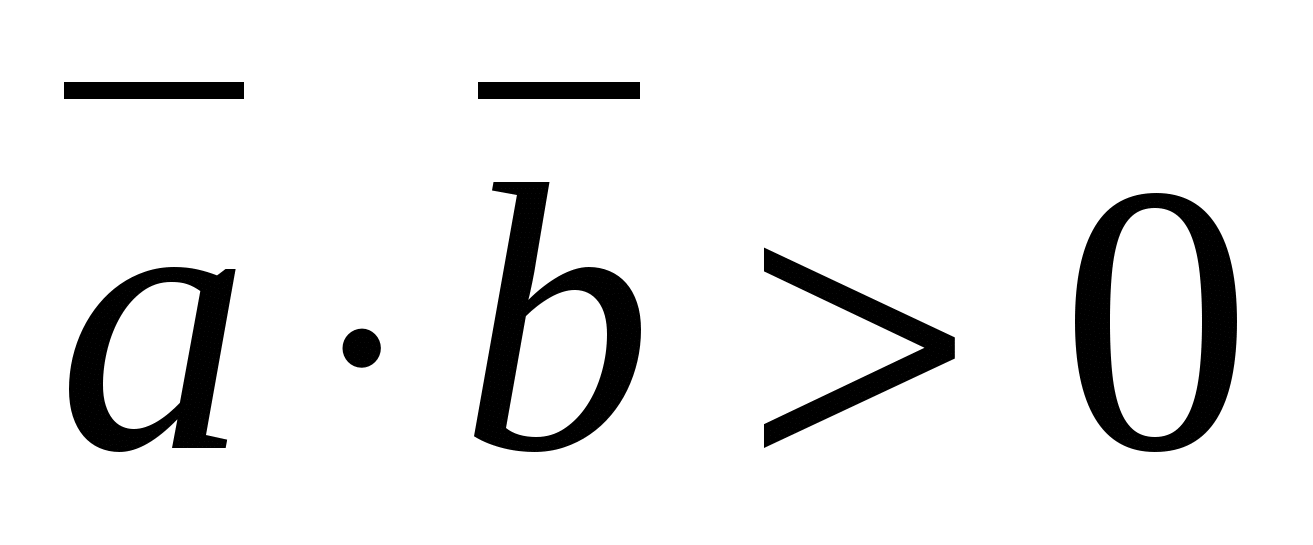

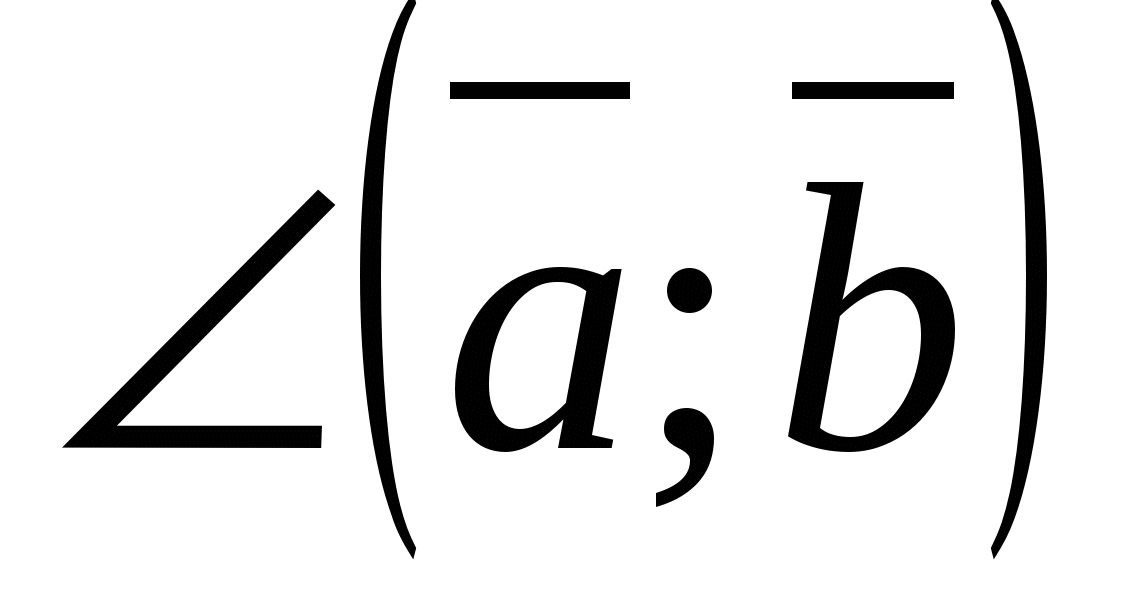 - острый.
- острый.
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами - тупой,
т.е.
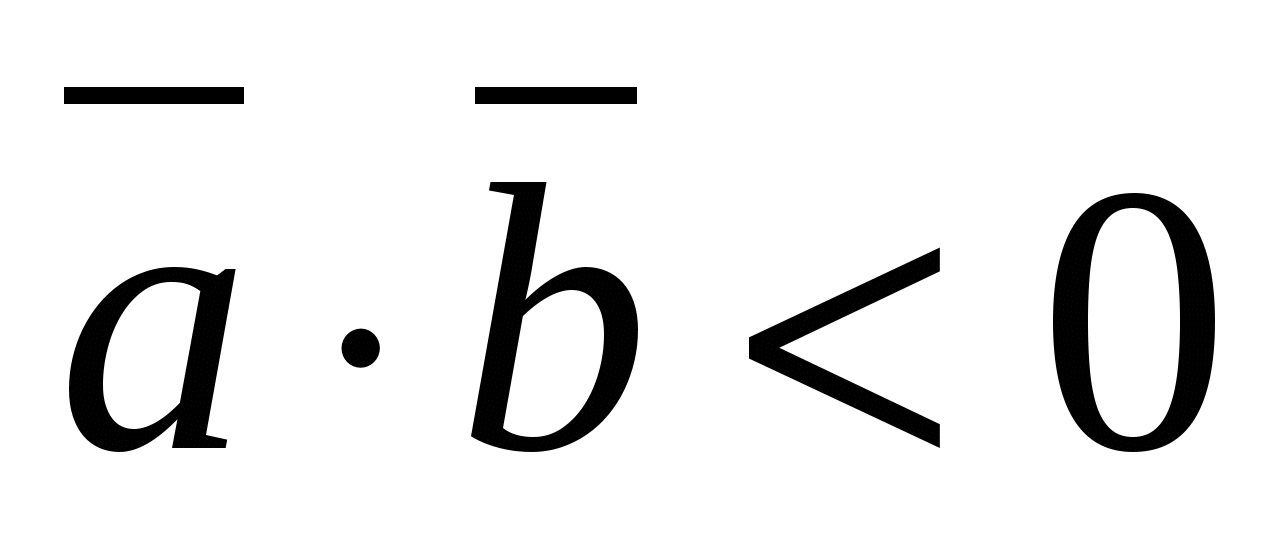

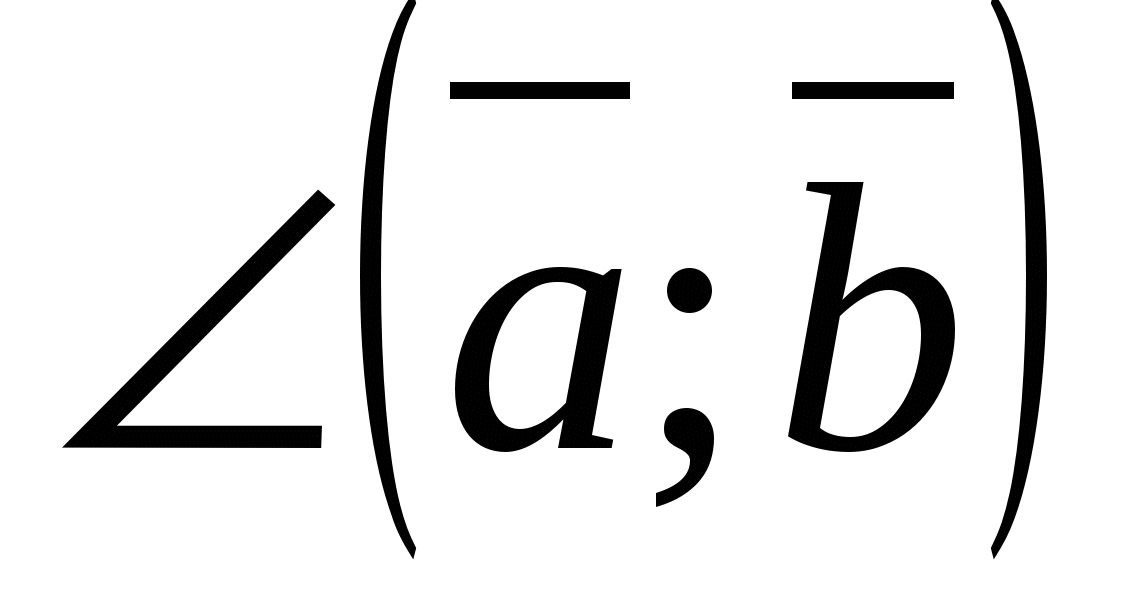 - тупой.
- тупой.
Для любых векторов , 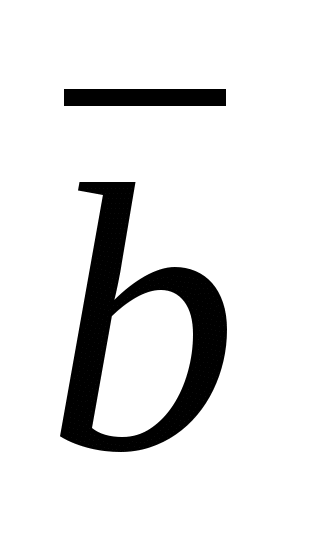 ,
, 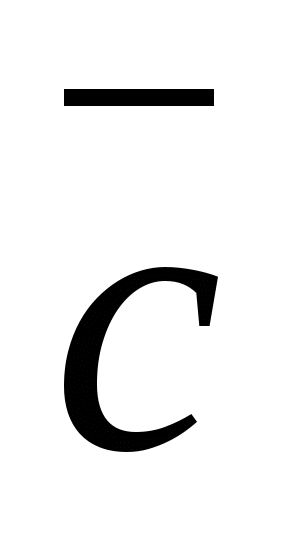 , и любого числа
k
справедливы равенства:
, и любого числа
k
справедливы равенства:
1. 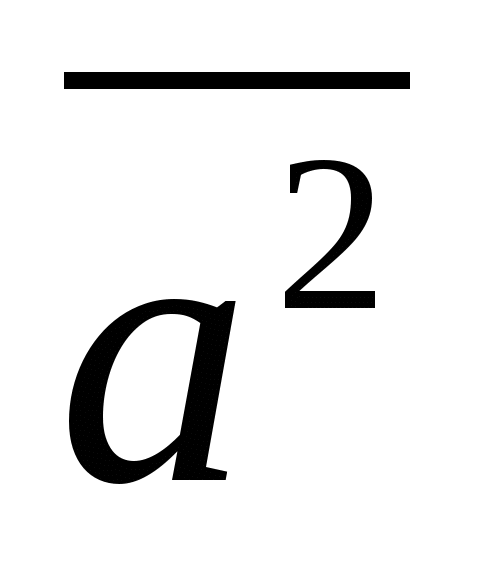
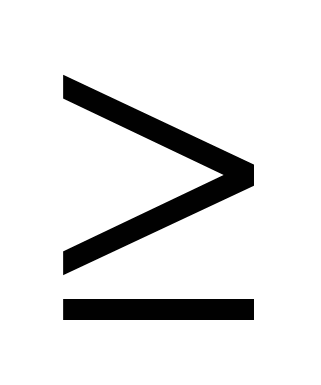 0, причем
0, причем 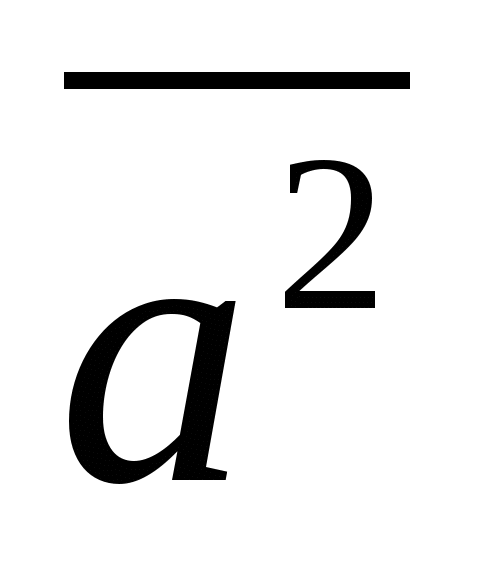 >0 при
>0 при 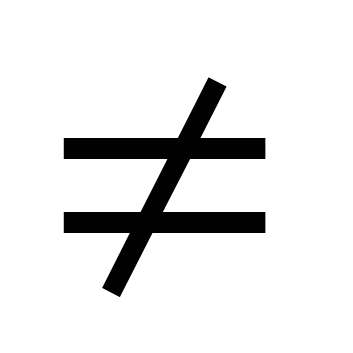 0.
0.
2. 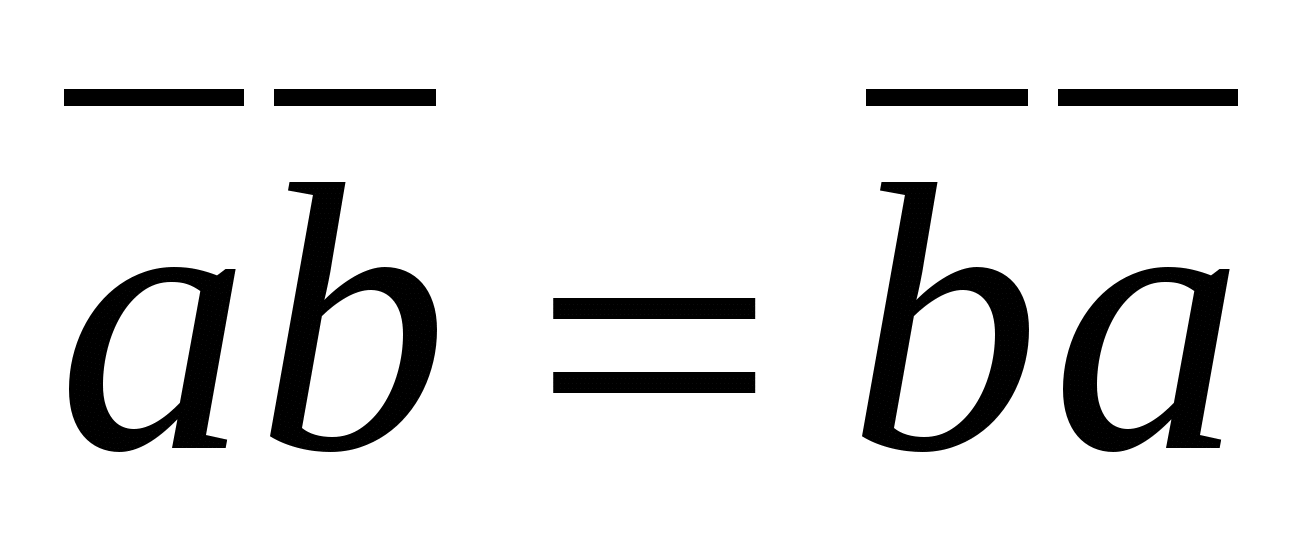 (переместительный закон).
(переместительный закон).
3.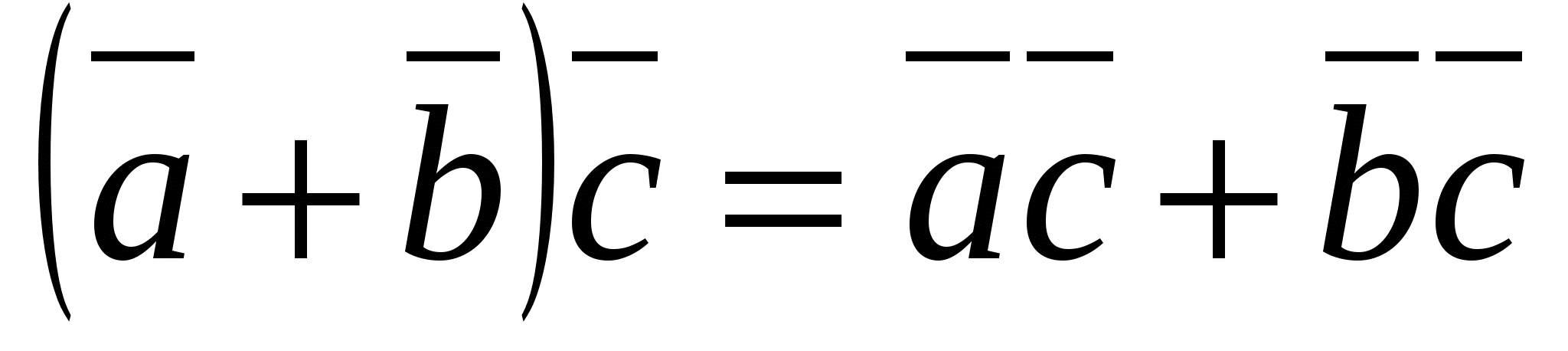 (распределительный закон).
(распределительный закон).
4. 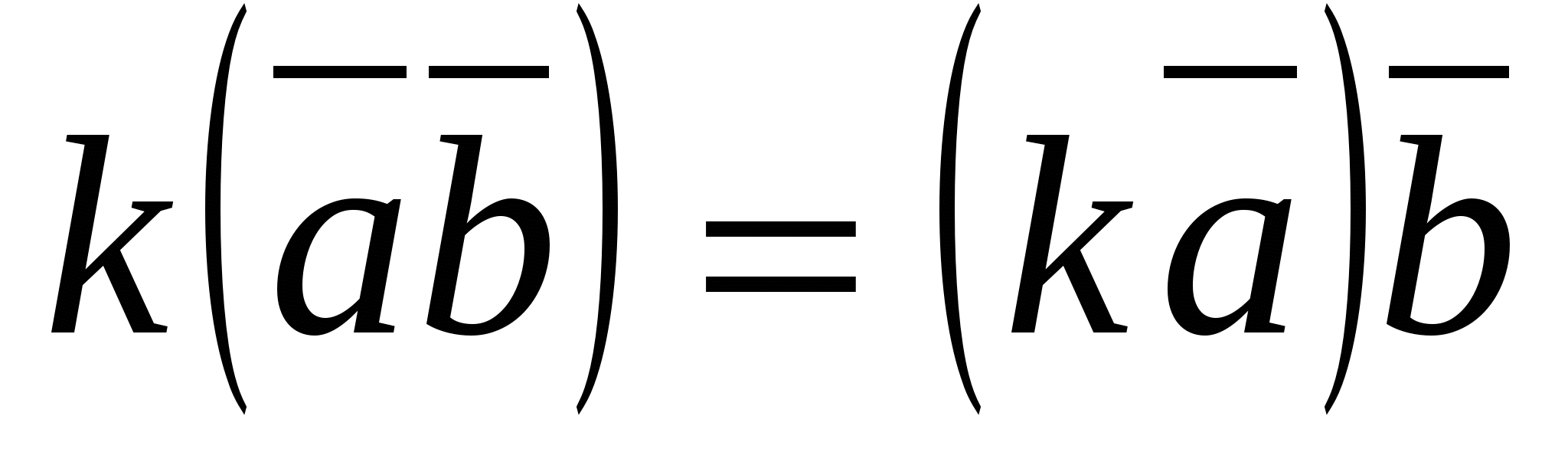 (сочетательный закон).
(сочетательный закон).
2) Вычисление угла между векторами через их координаты.
Косинус угла  между ненулевыми векторами
между ненулевыми векторами
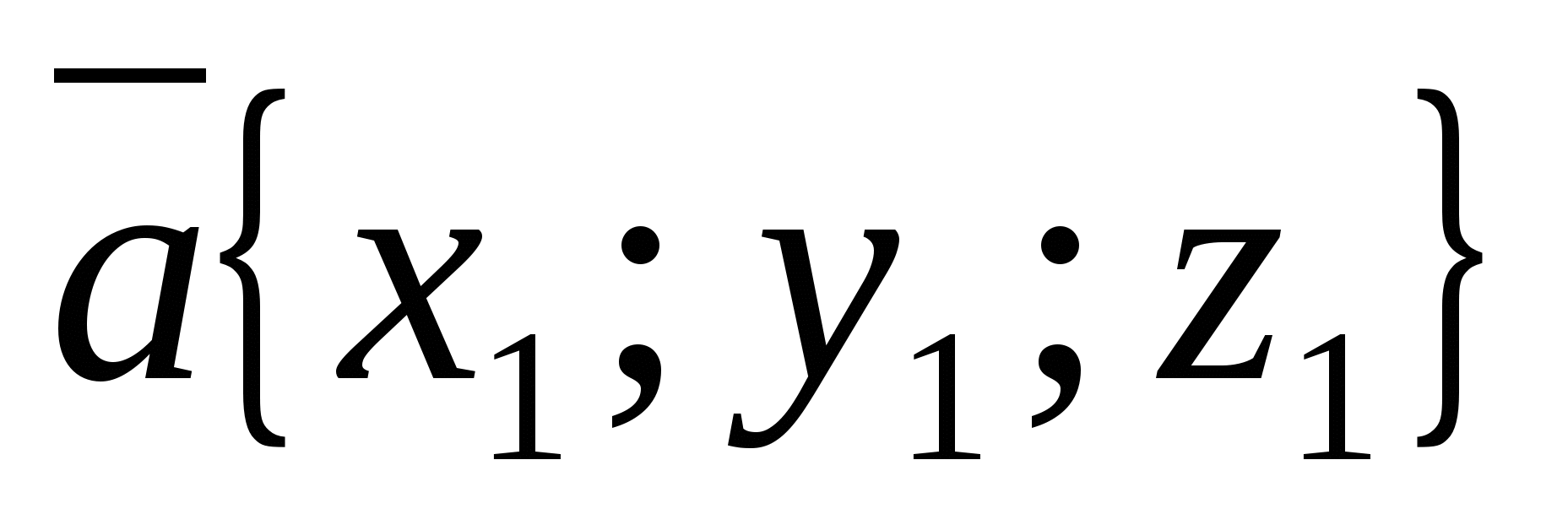 и
и 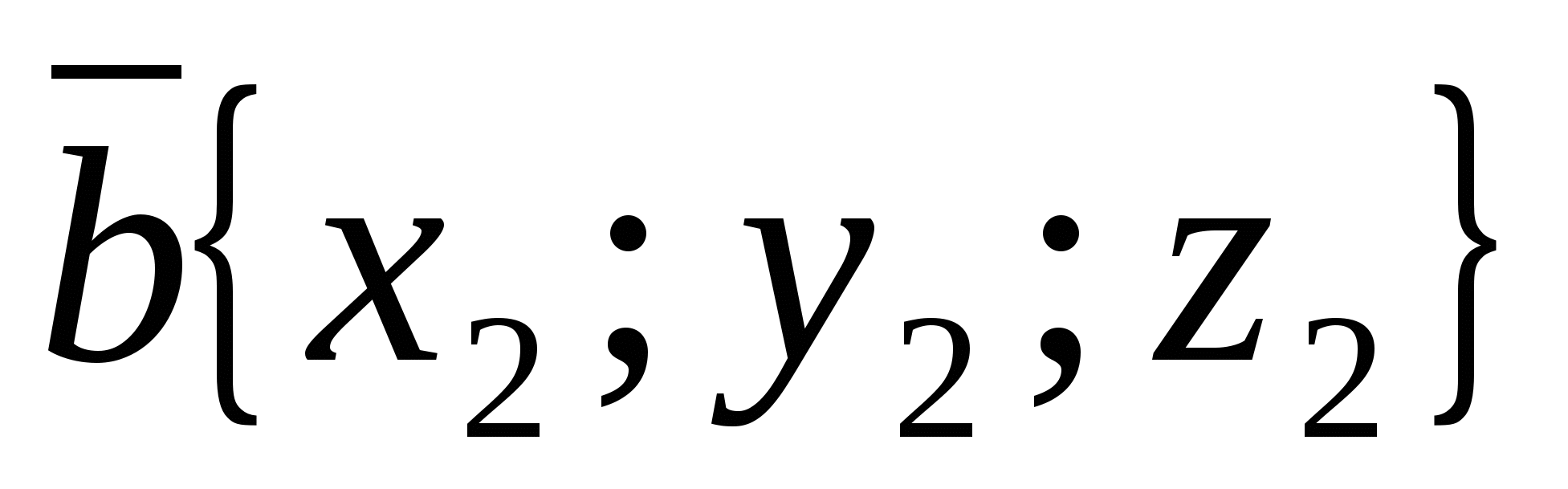 вычисляется по формуле
вычисляется по формуле
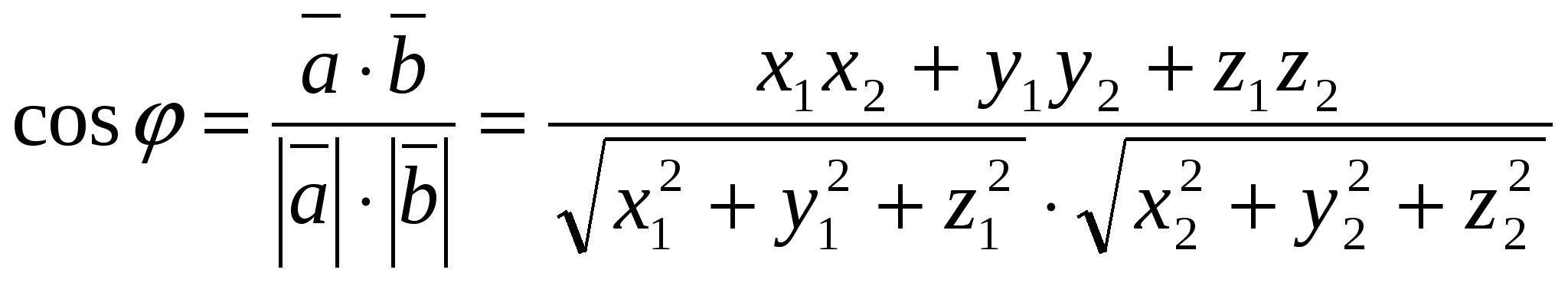 ,
,
где 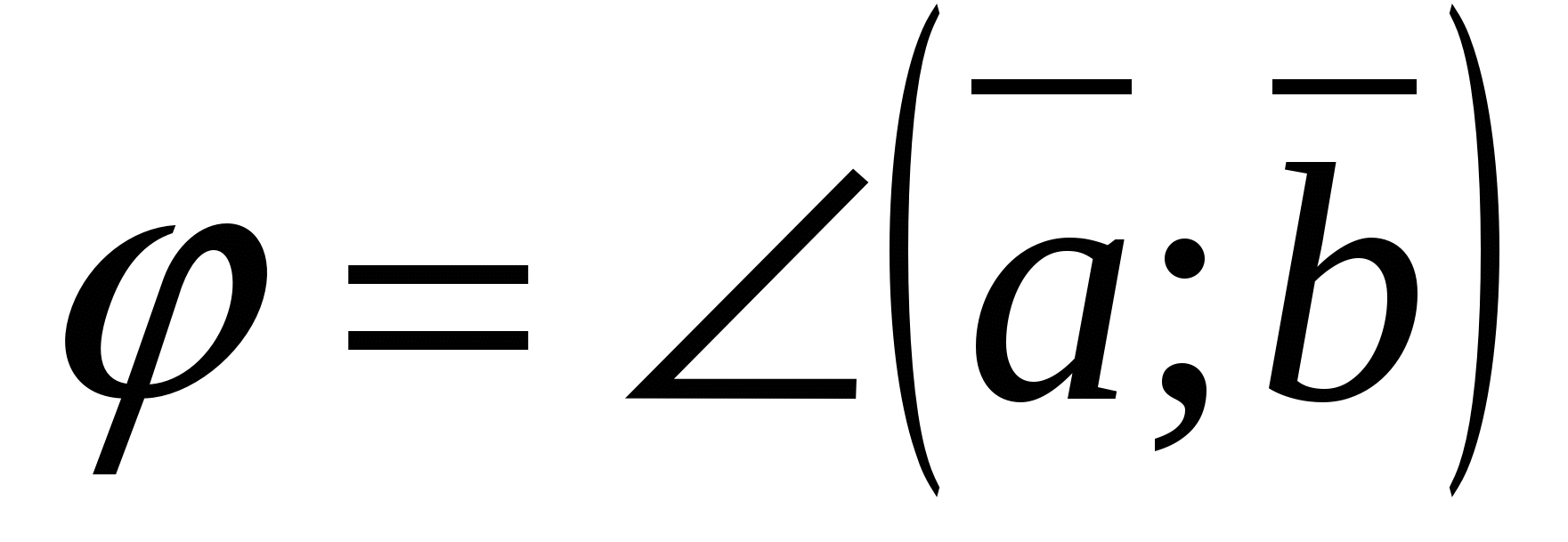
7. Вычисление углов между прямыми и плоскостями.
1) Угол между прямыми .
Для решения данной задачи введем понятие направляющего вектора прямой.
Определение.
Ненулевой вектор называется направляющим вектором прямой a , если он лежит, либо на прямой a , либо на прямой, параллельной a .
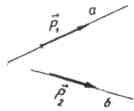 Пример
Пример
Векторы 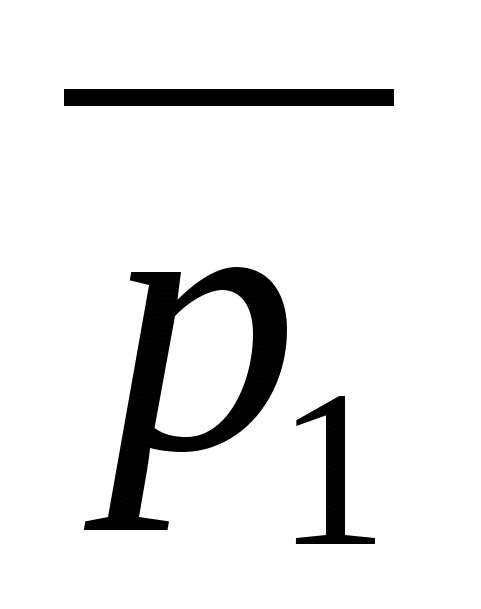 и
и  направляющие прямых
a
и
b
, соответственно.
направляющие прямых
a
и
b
, соответственно.
Определение.
Углом между прямыми называется угол между направляющими векторами данных прямых.
Угол между прямыми
a
и
b
равен углу между направляющими векторами данных прямых, 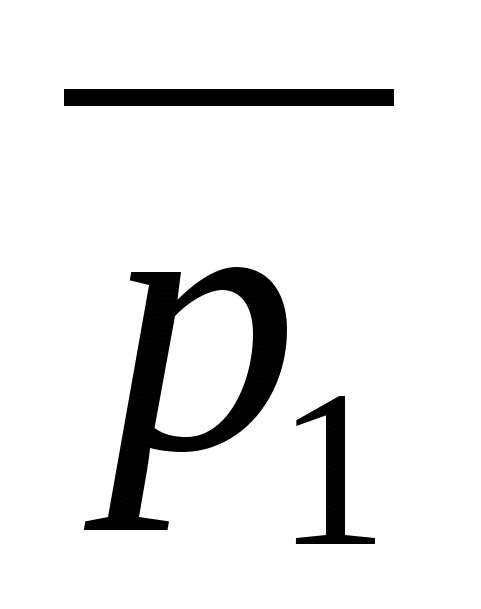 и
и 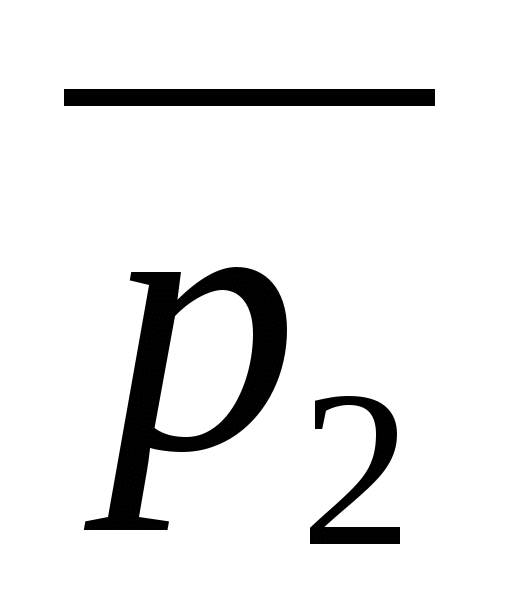 .
.
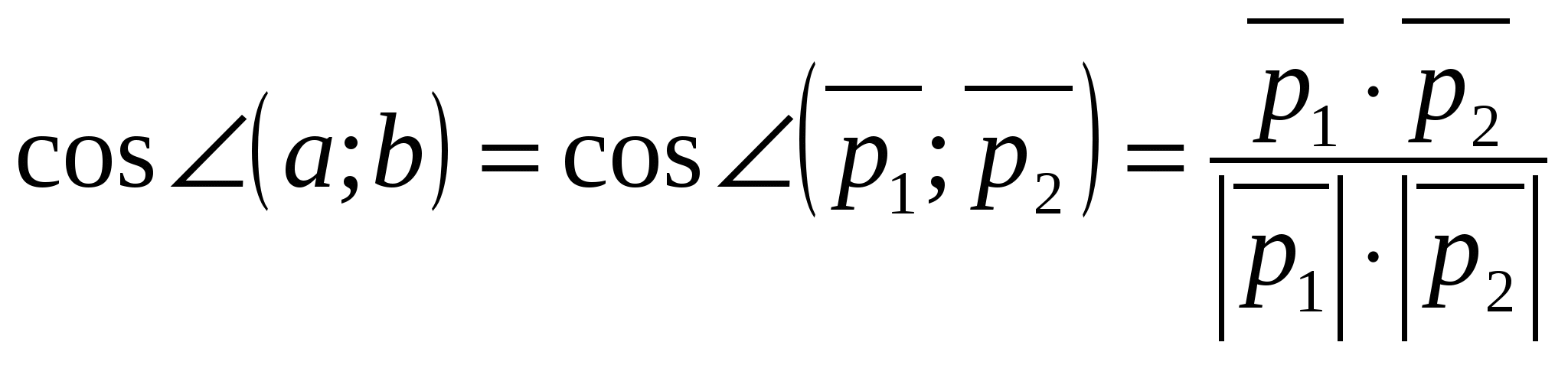 .
.
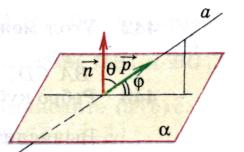
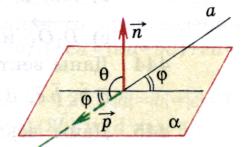
2).Угол между прямой и плоскостью .
Определение.
Углом между прямой и плоскостью называется угол между направляющим вектором данной прямой и ненулевым вектором перпендикулярным плоскости (нормаль).
Пусть
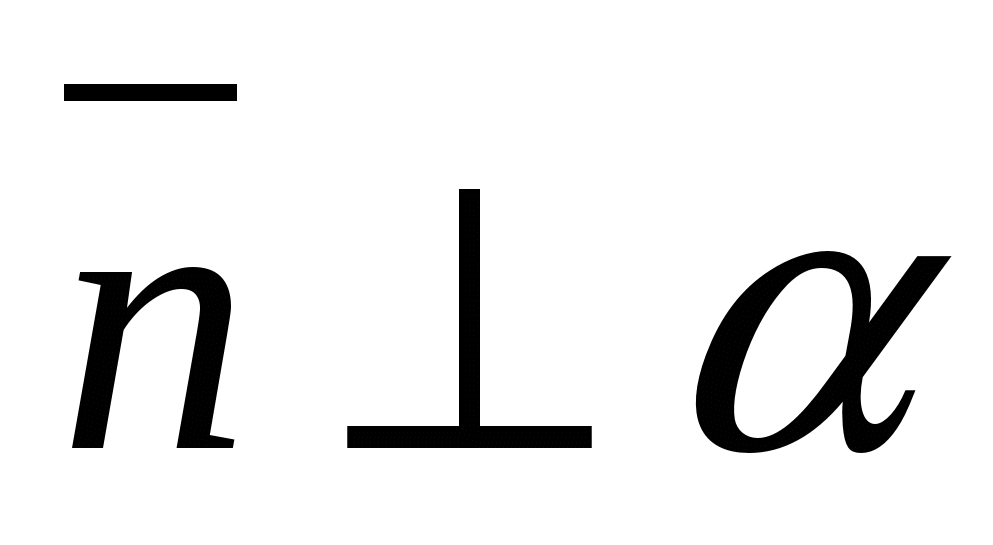 , (
, (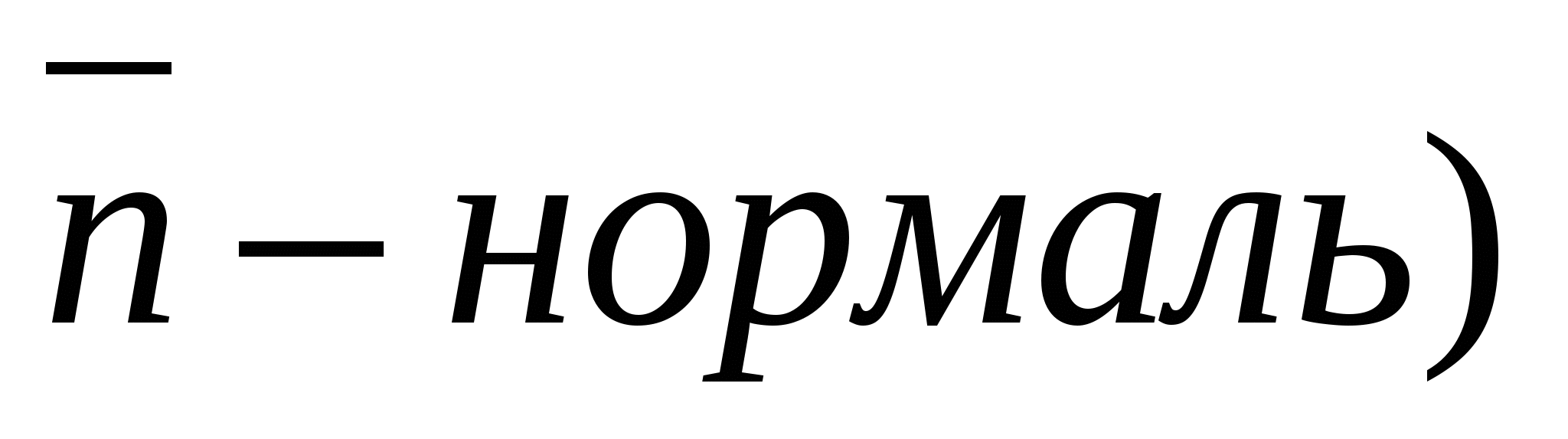
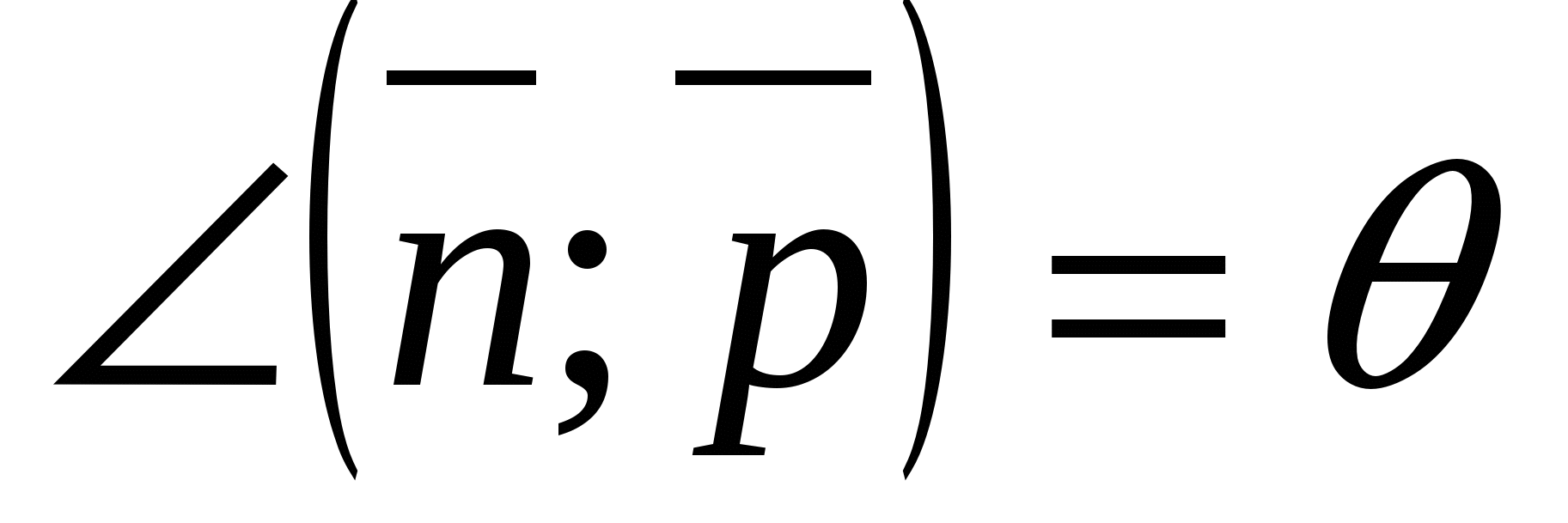 , а
, а 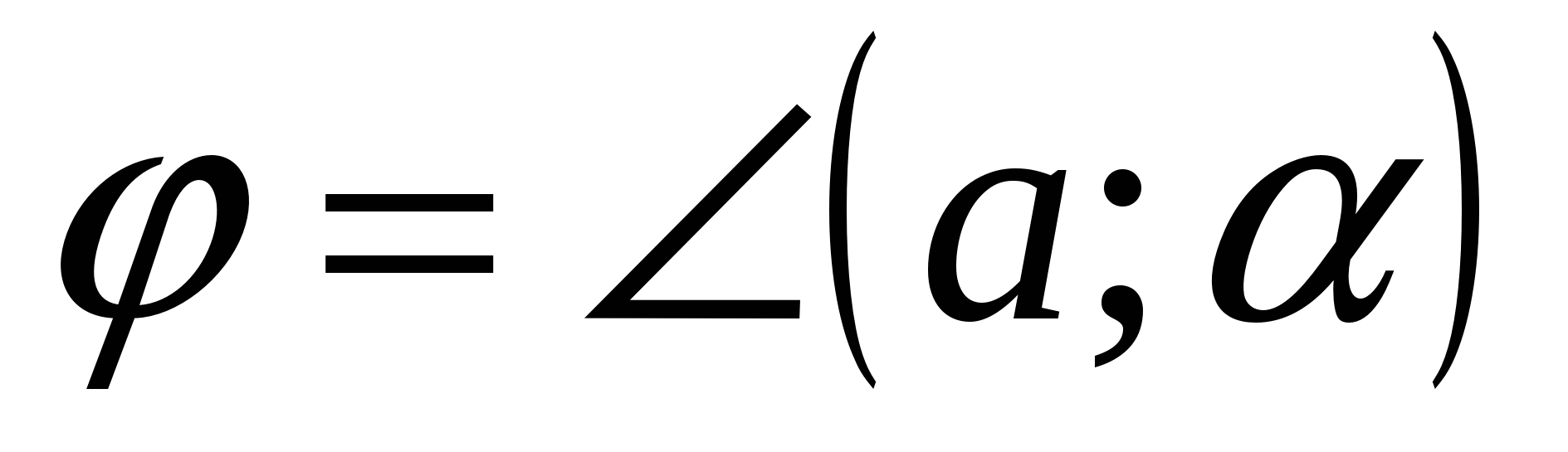 - искомый угол (
- искомый угол (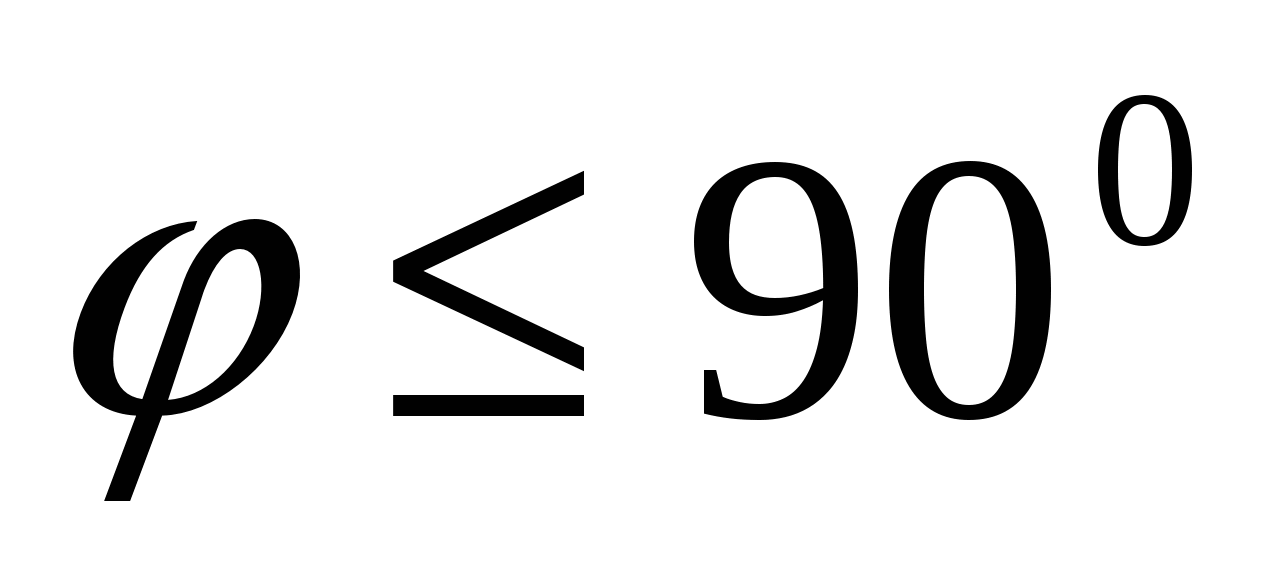 ).
).
Тогда

Значит  .
.
Глава 3.
Применение координатного метода к решению стереометрических задач.
Задача.1
В основании пирамиды МАВС лежит прямоугольный треугольник АВС. 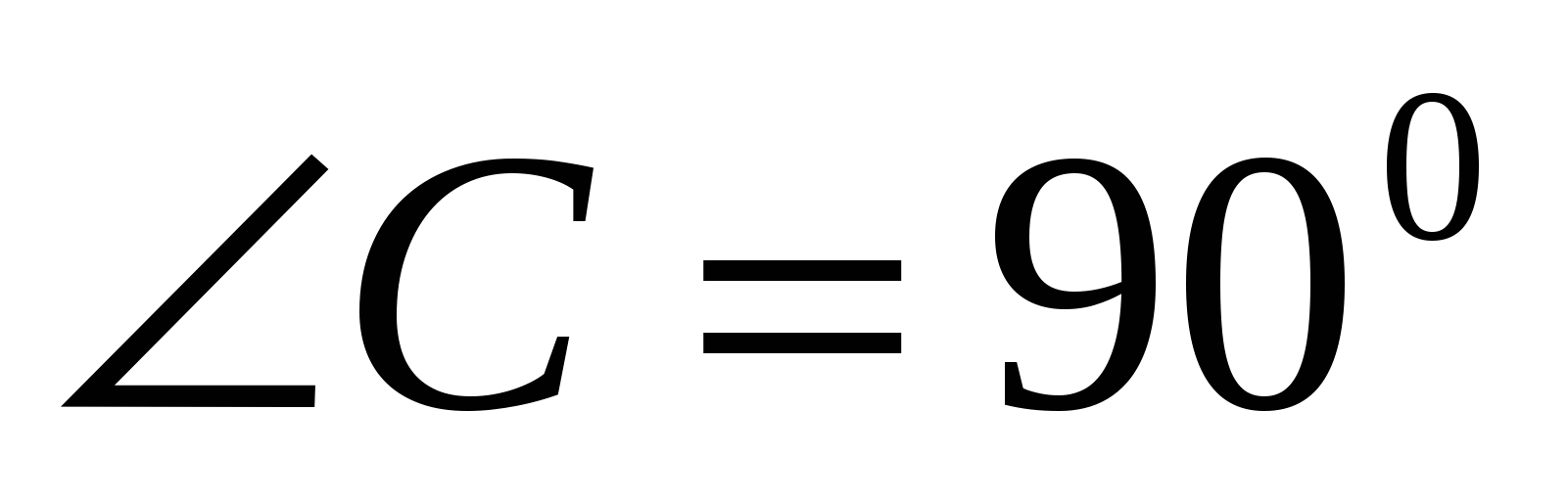 ,
AC
=3,
BC
=5. Ребро АМ перпендикулярно АС, АМ=4,
,
AC
=3,
BC
=5. Ребро АМ перпендикулярно АС, АМ=4, 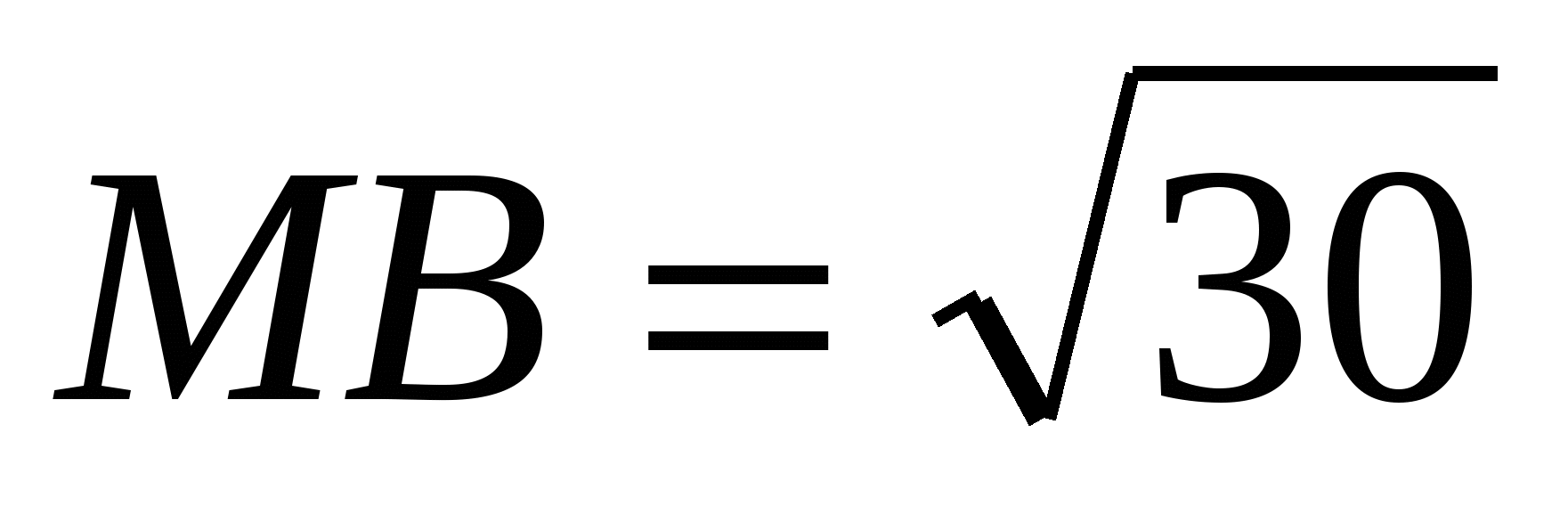 . Найти объем пирамиды.
. Найти объем пирамиды.
Р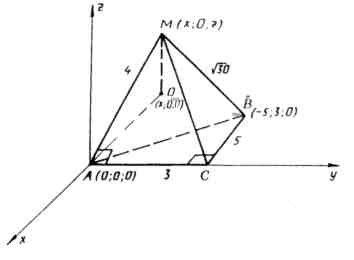 ешение.
ешение.
1) Введем прямоугольную систему координат с началом в точке  . Ось
. Ось 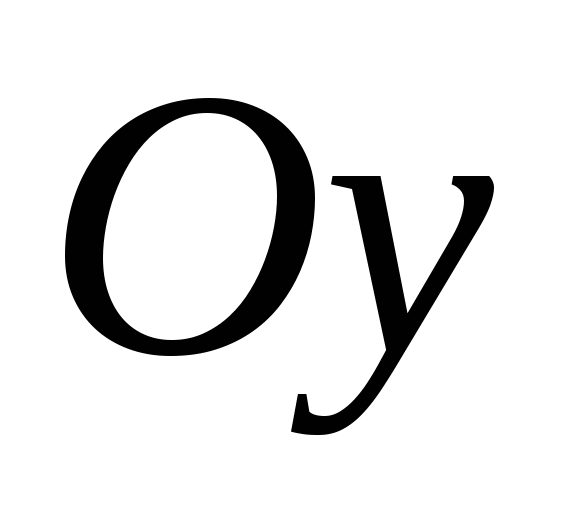 направим вдоль ребра
АС
, а плоскость
Ох
y
вдоль основания пирамиды
АВС.
направим вдоль ребра
АС
, а плоскость
Ох
y
вдоль основания пирамиды
АВС.
В этой системе координат: 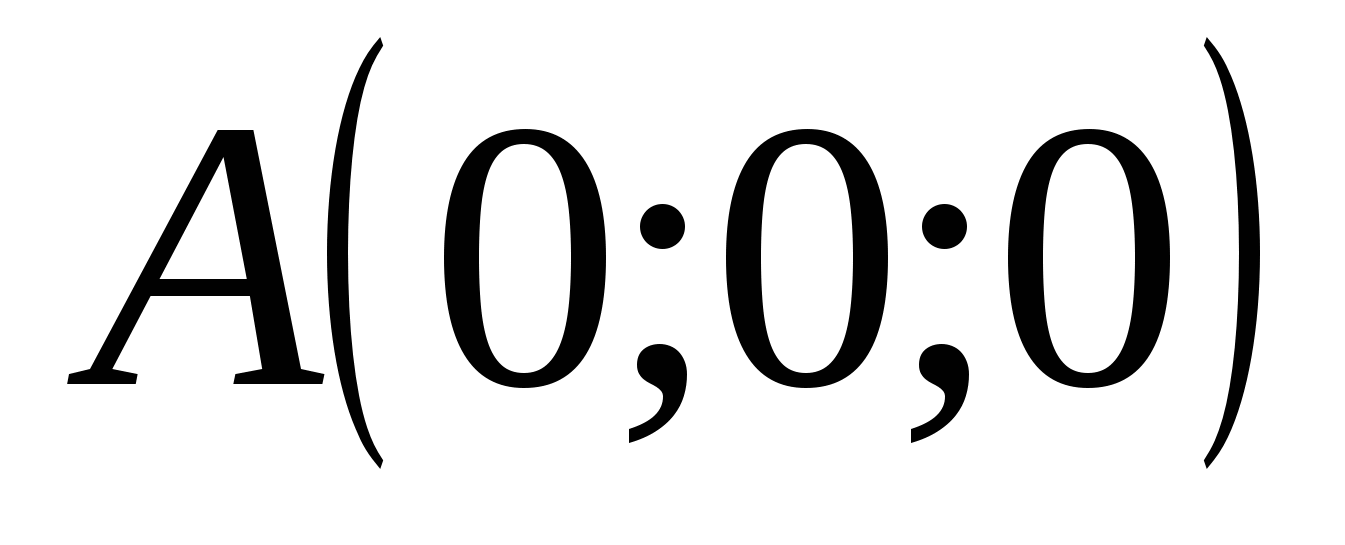 ,
, 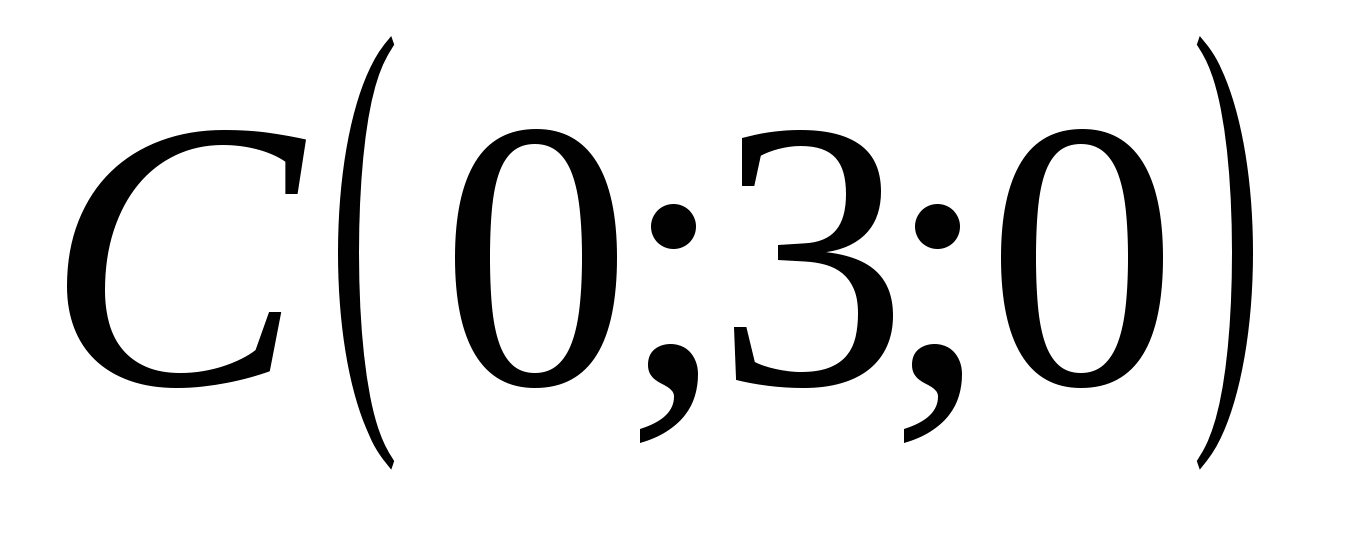 ,
, 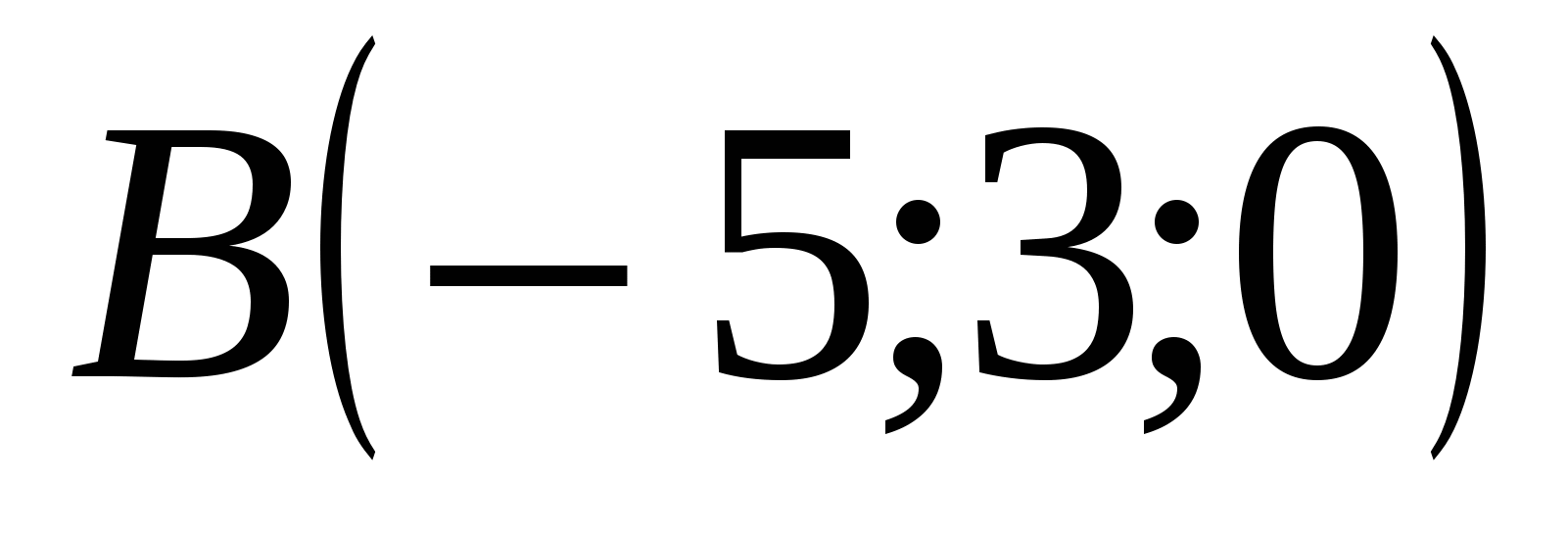 . Так как по условию
. Так как по условию
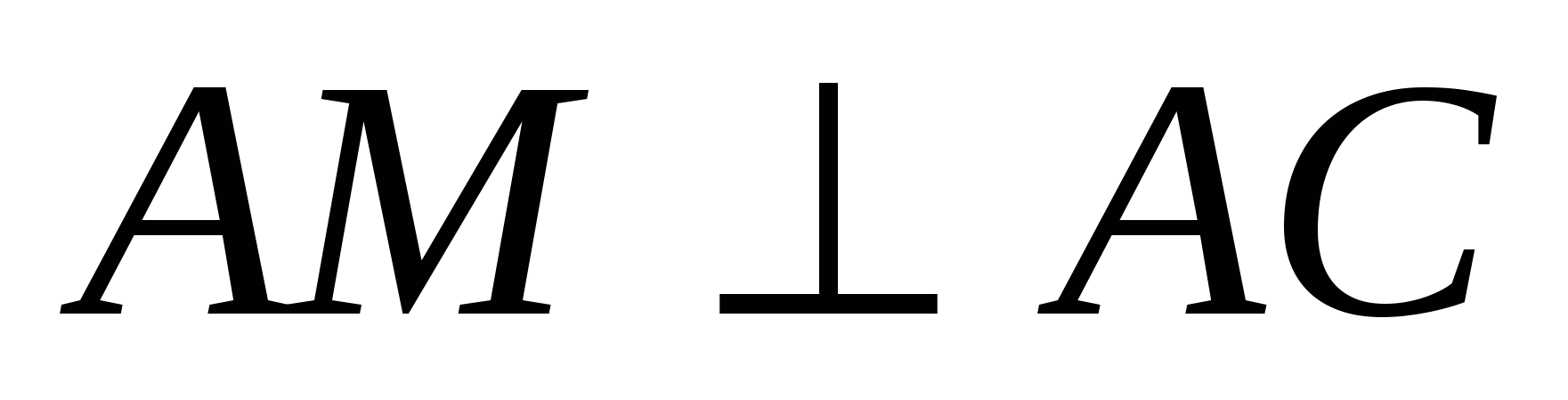 , то точка М лежит в плоскости
xz
и имеет координаты
, то точка М лежит в плоскости
xz
и имеет координаты
 .
.
2) 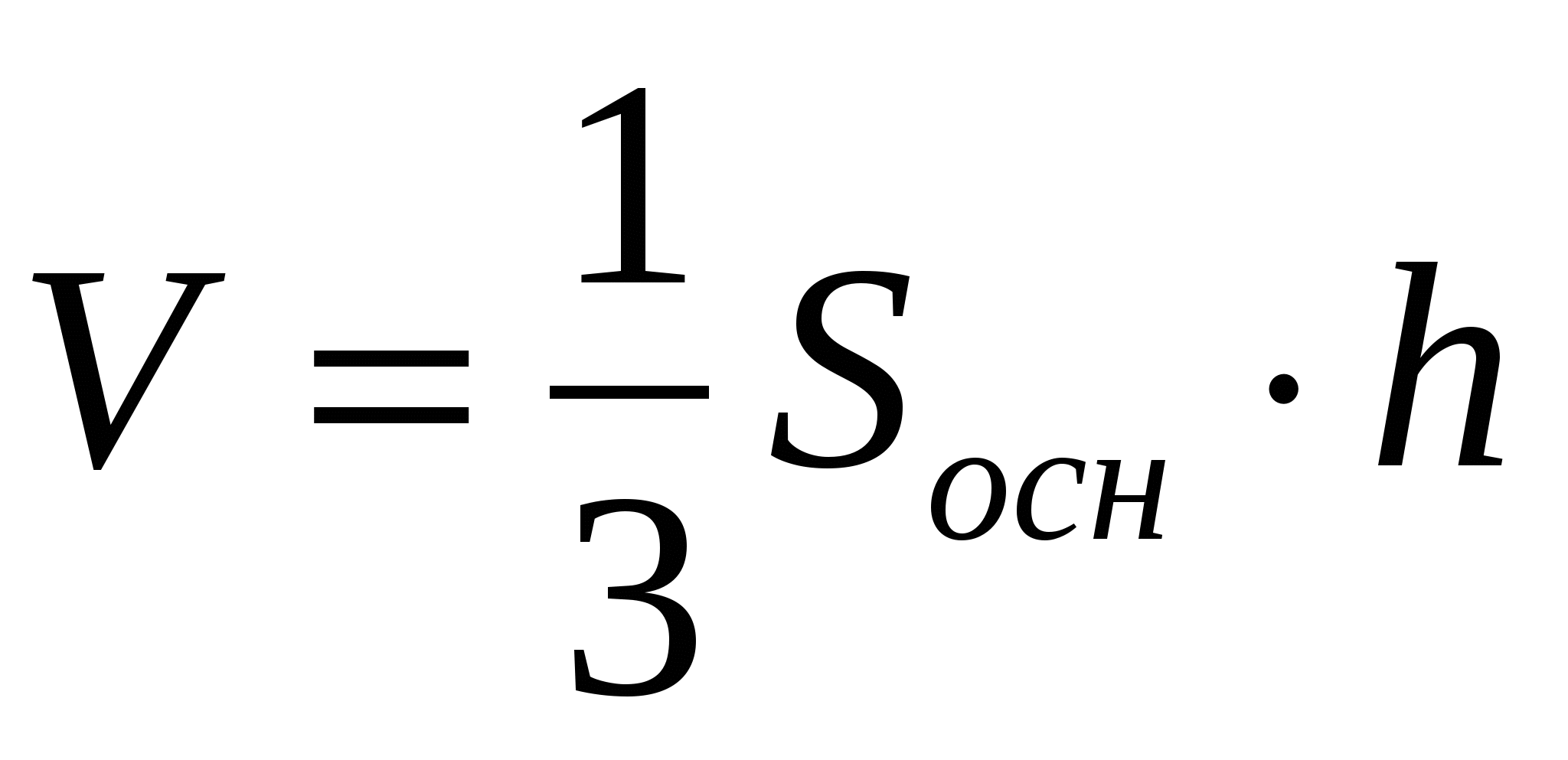 ,
, 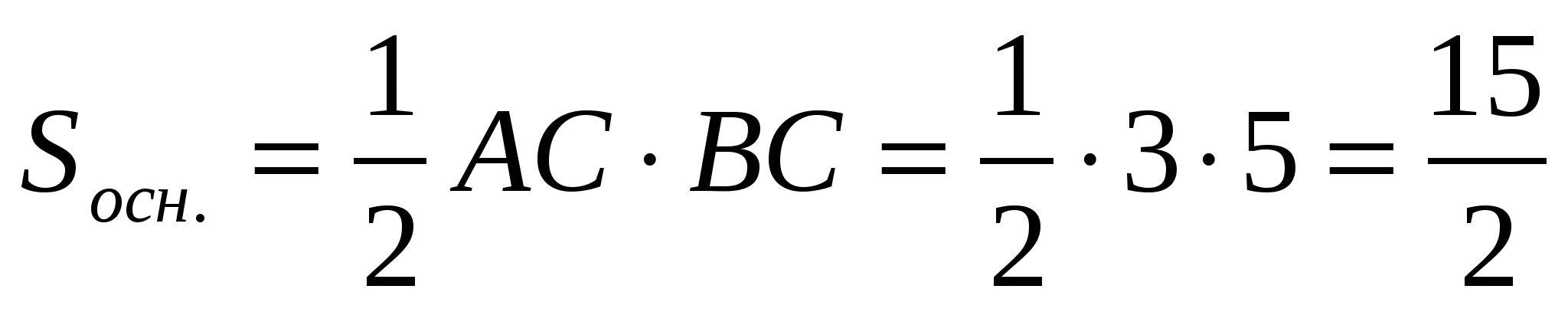 .
.
Найдем высоту пирамиды. Опустим из точки
М
перпендикуляр
М
D
на плоскость
(АВС),
тогда  , т.к.
, т.к. 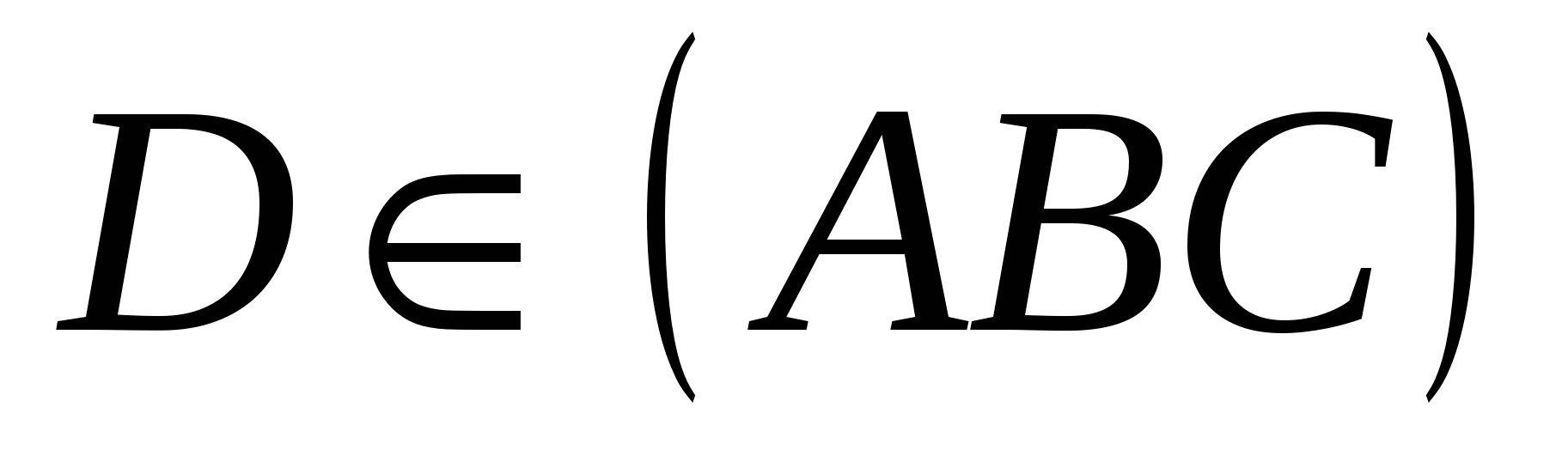 . Следовательно,
. Следовательно,  и расстояние между точками
М
и
D
равно , т.к.
и расстояние между точками
М
и
D
равно , т.к. 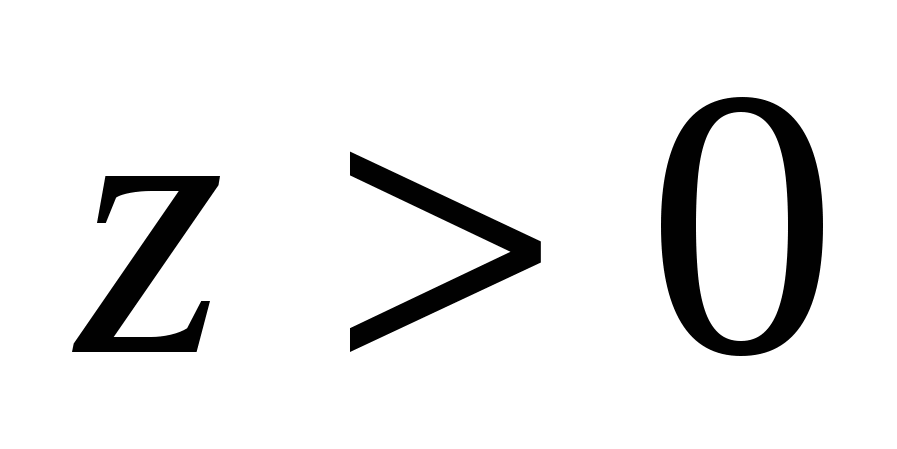 .
.
Найдем значение координаты
z
используя расстояния между точками, содержащими данную координату: 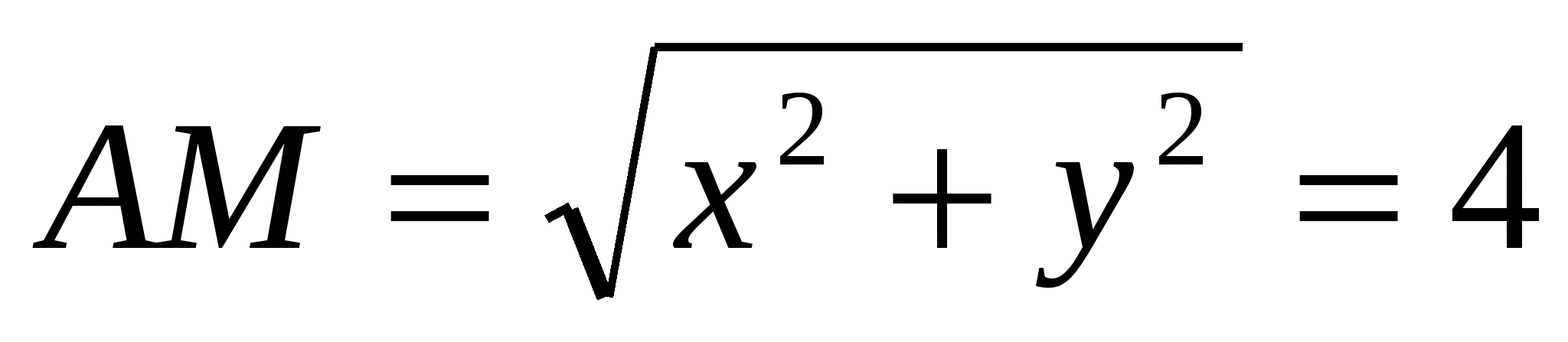 ,
,  . , т.е.
. , т.е. 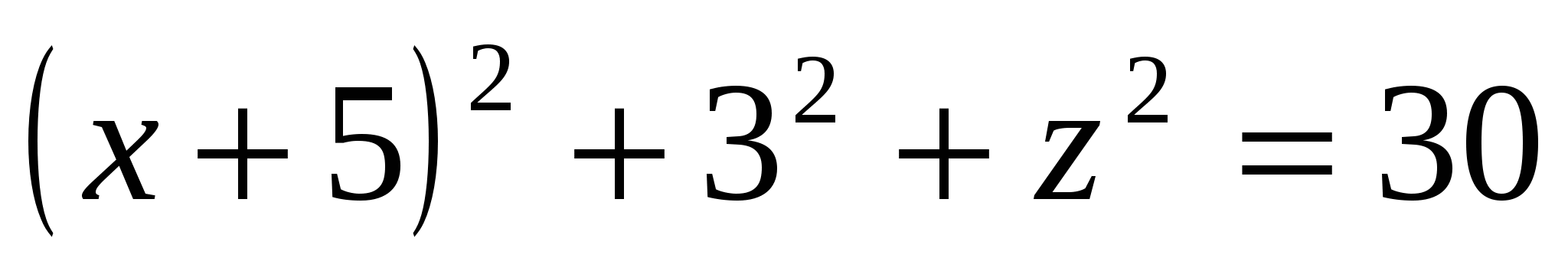 .
.
Имеем: 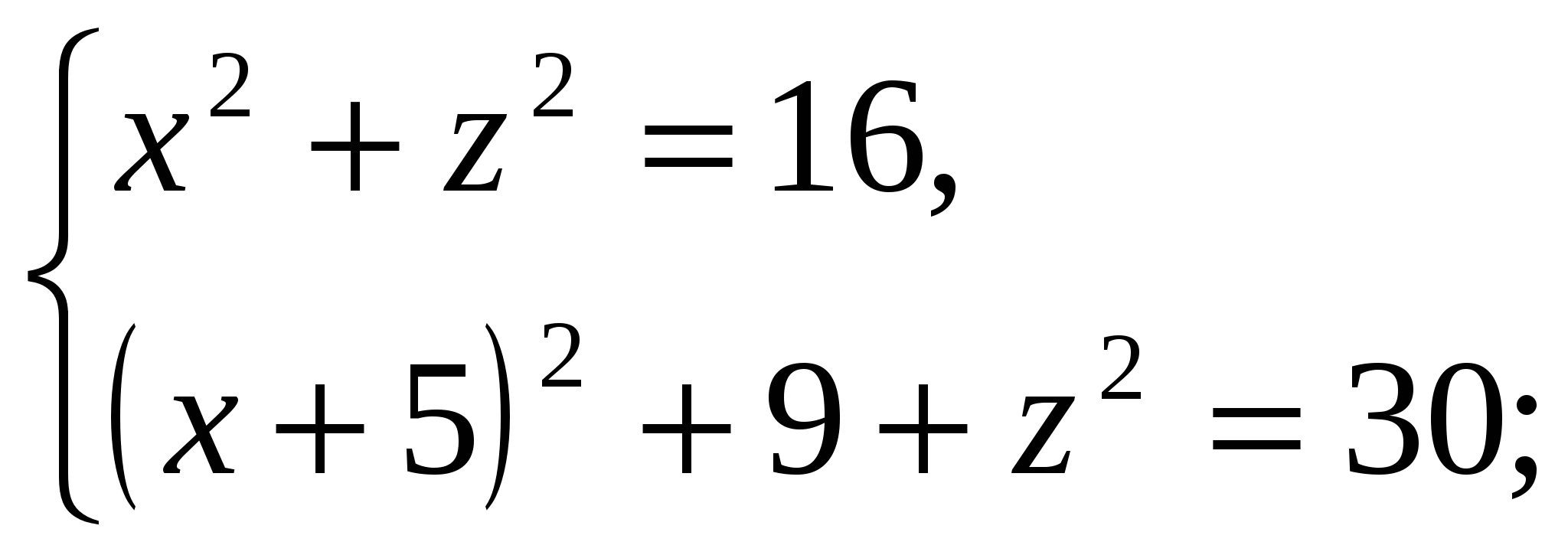
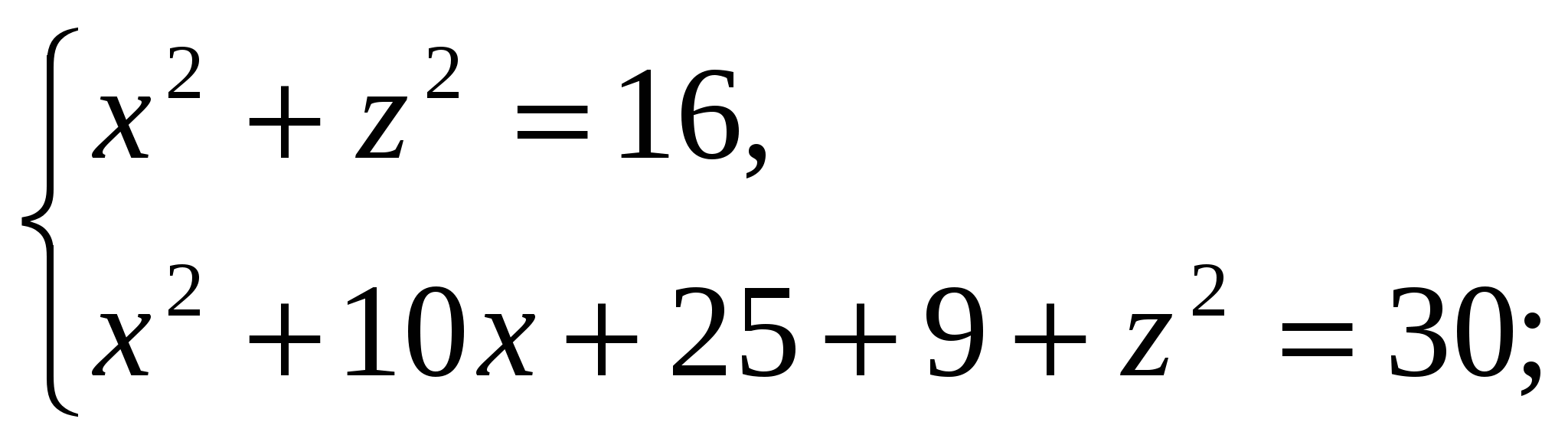
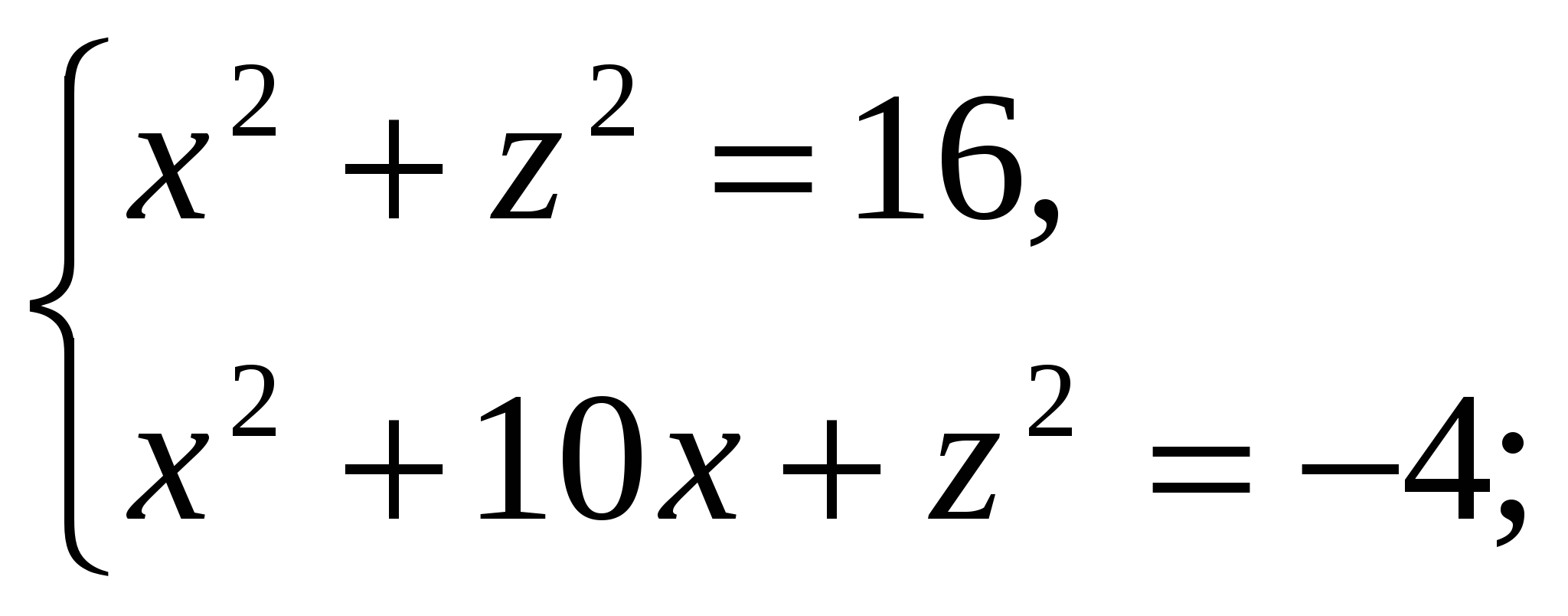
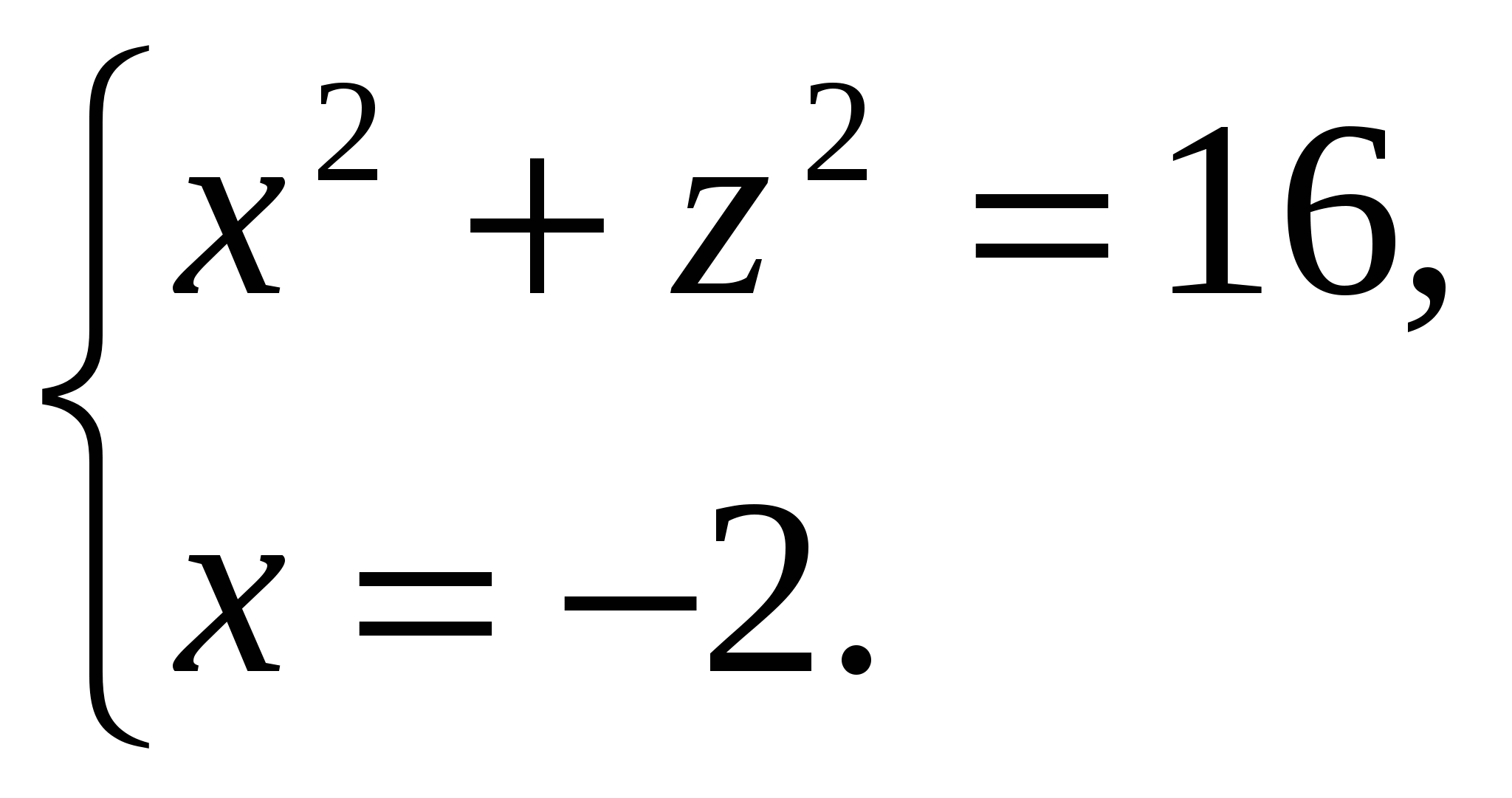
Так как 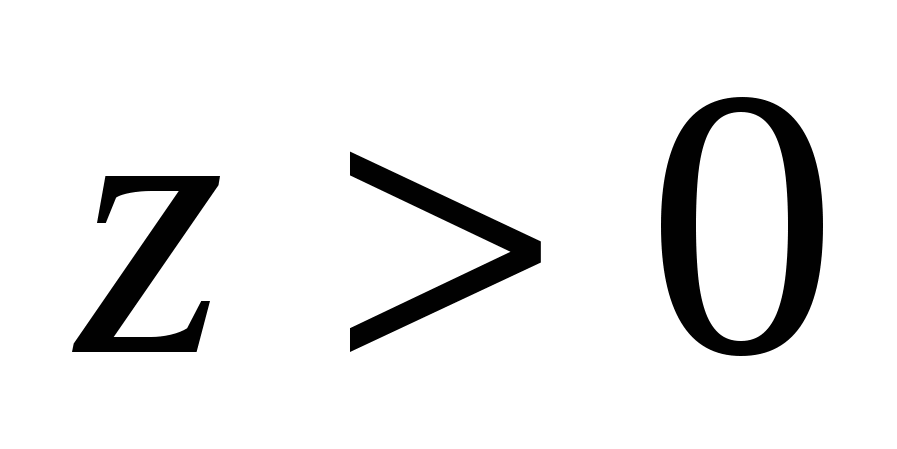 , то Значит высота пирамиды равна
, то Значит высота пирамиды равна 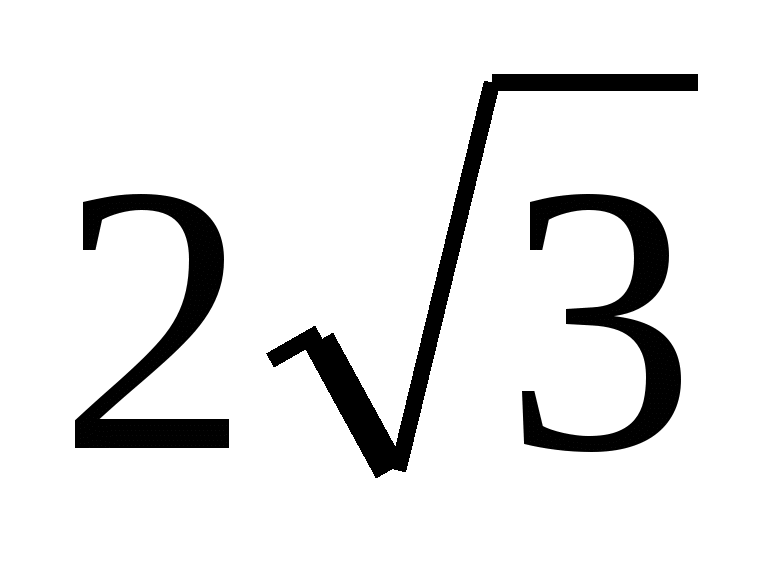 . Следовательно
. Следовательно
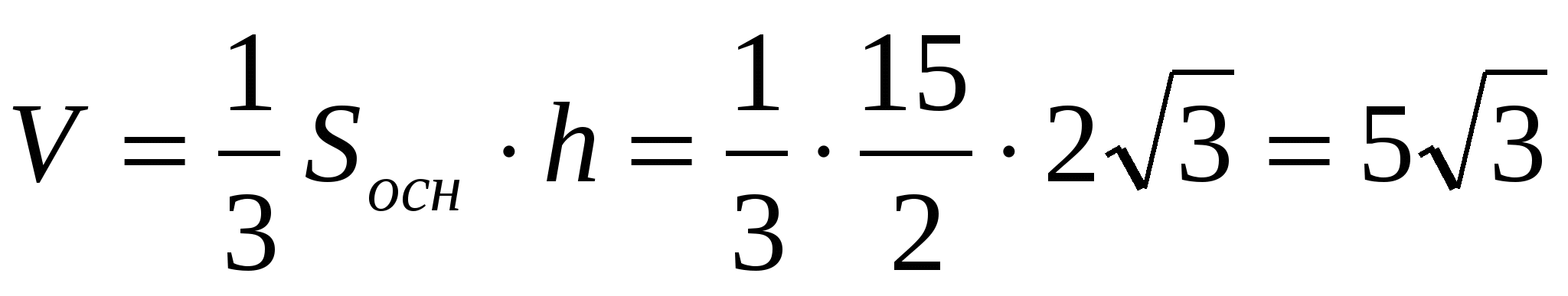 .
.
Ответ: 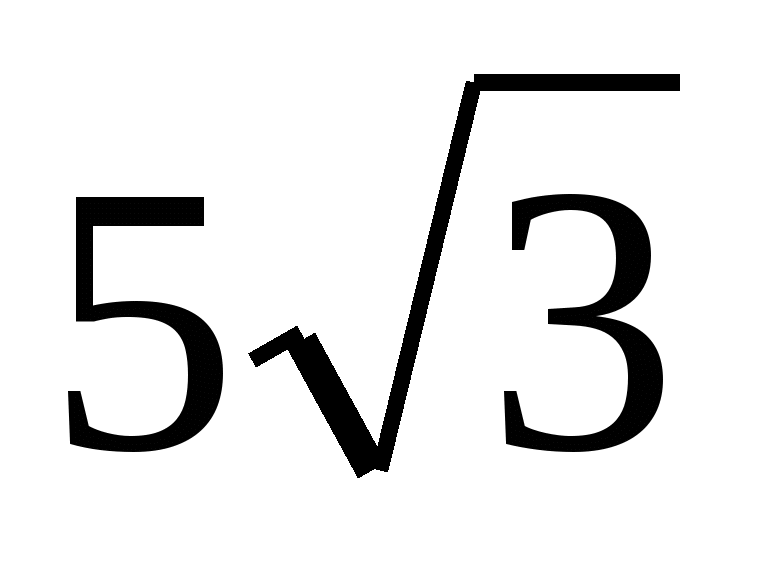 .
.
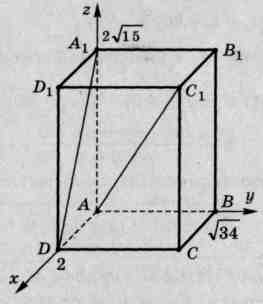
Задача.2.
В прямоугольном параллелепипеде 
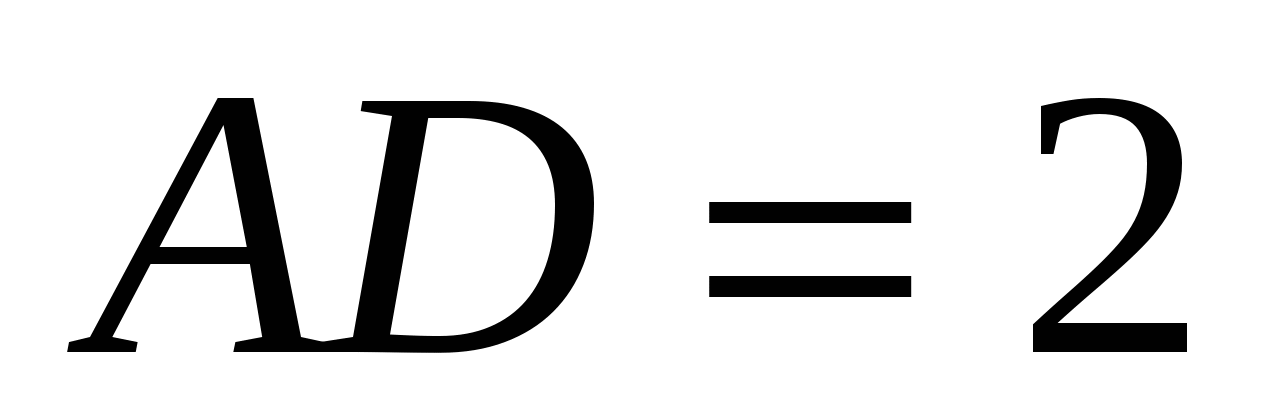 ,
, 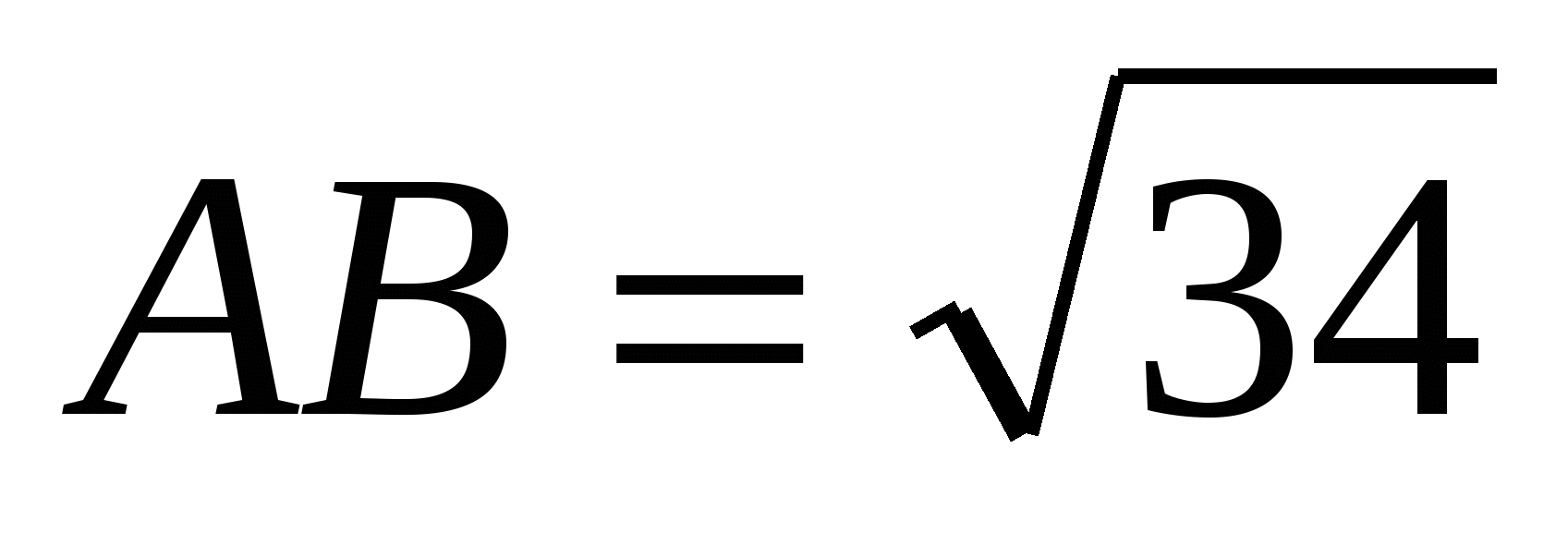 ,
,  . Найти:
угол между прямыми
. Найти:
угол между прямыми и
и  .
.
 Решение.
Решение.
1).Введем систему координат с началом в точке 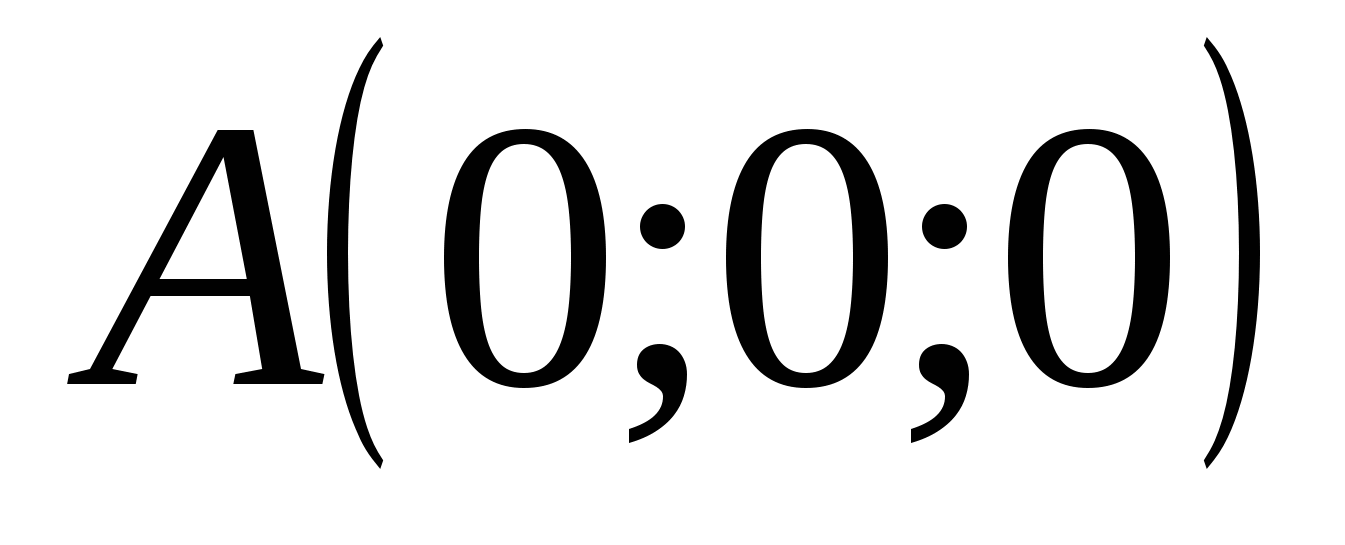 . Оси
. Оси 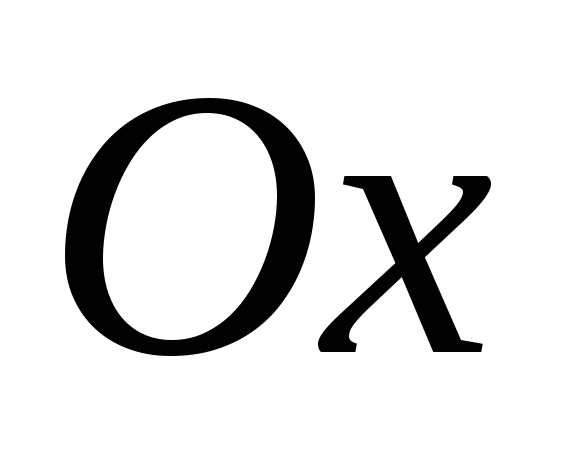 ,
,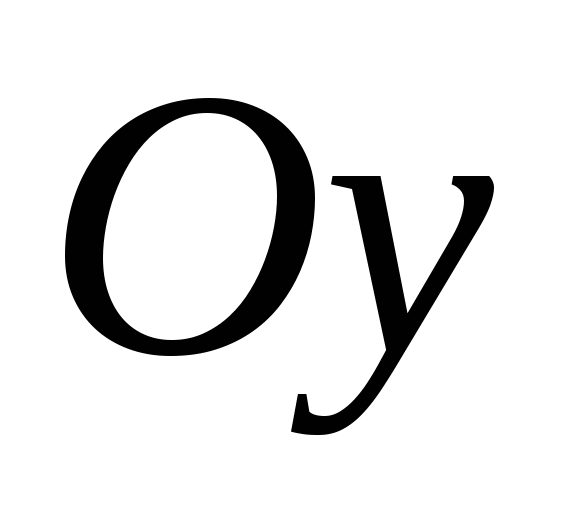 и
и  направим вдоль ребер
направим вдоль ребер  ,
, 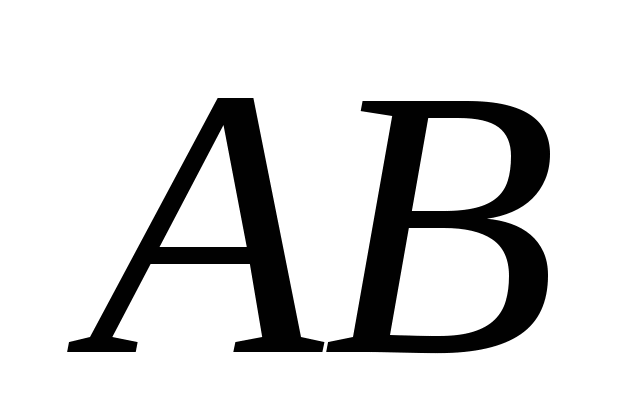 и
и 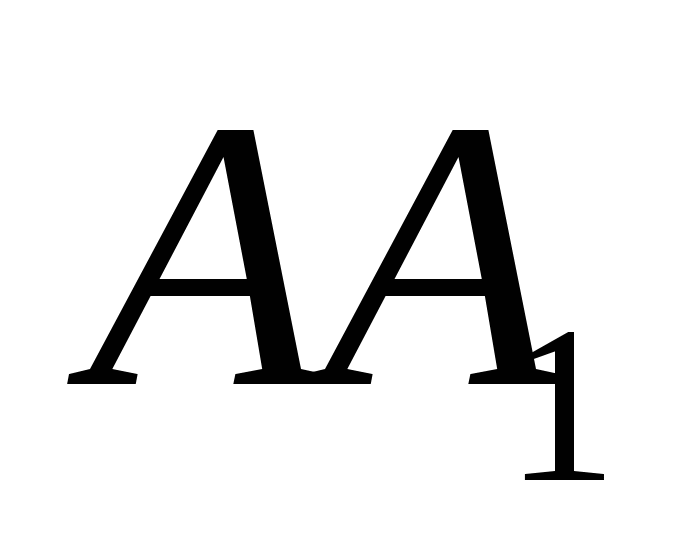 соответственно. Так как угол между прямыми изменяется от
соответственно. Так как угол между прямыми изменяется от 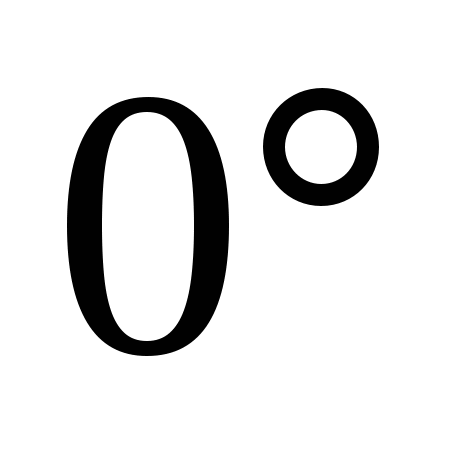 до
до  , а угол между векторами от
, а угол между векторами от 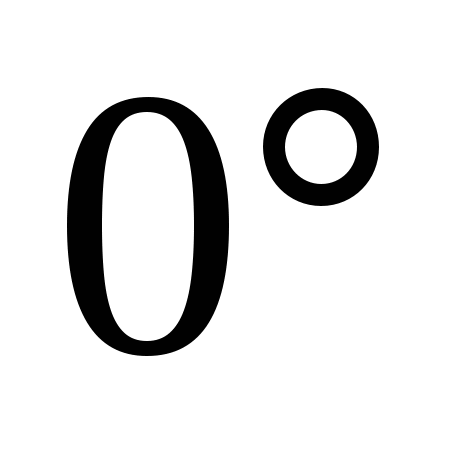 до
до 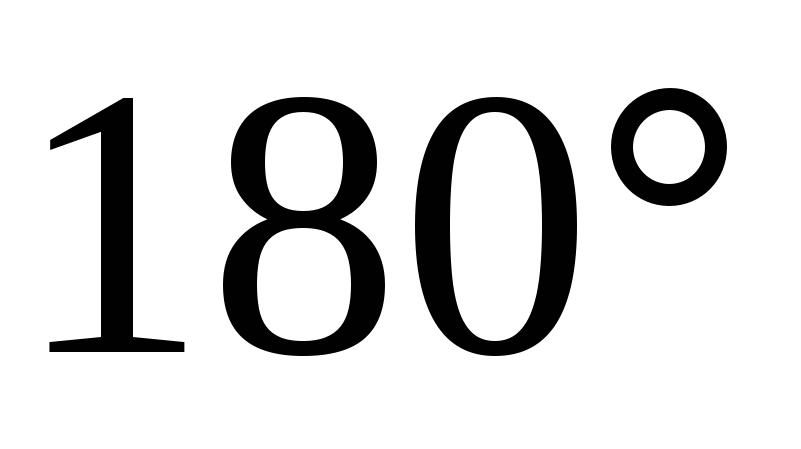 , то угол между прямыми
, то угол между прямыми  и
и  равен углу между векторами
равен углу между векторами 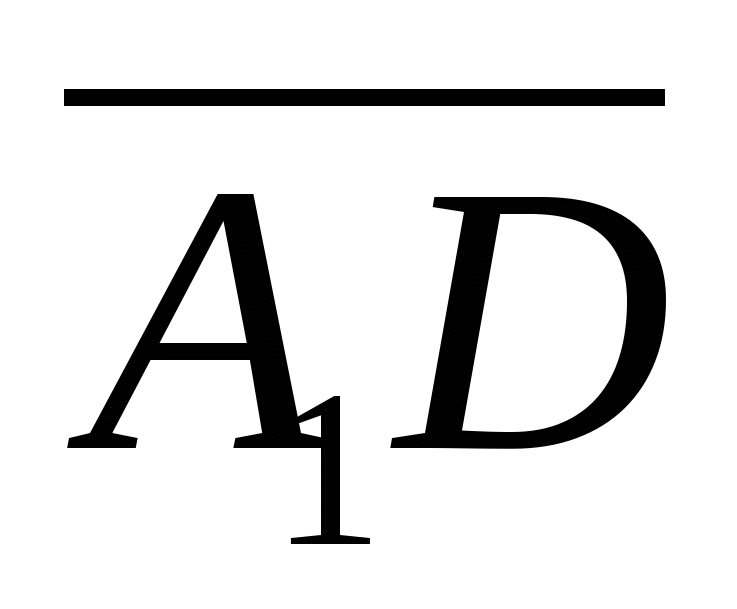 и
и 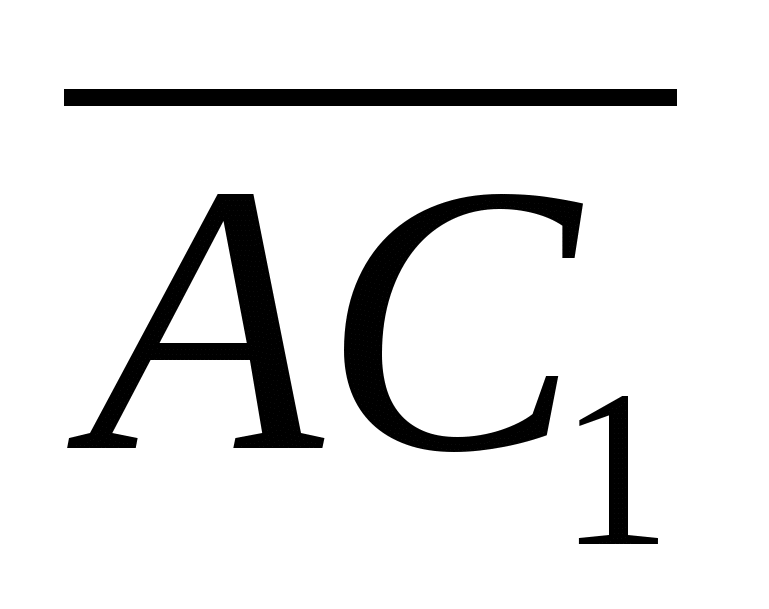 , если он острый, или смежному с ним, если угол между векторами тупой.
, если он острый, или смежному с ним, если угол между векторами тупой.
Таким образом,
2).Вычислим угол между векторами 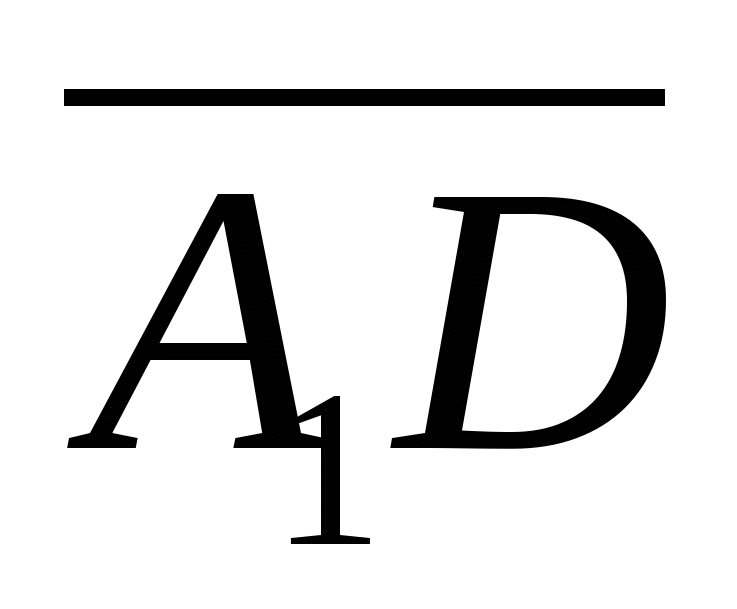 и
и 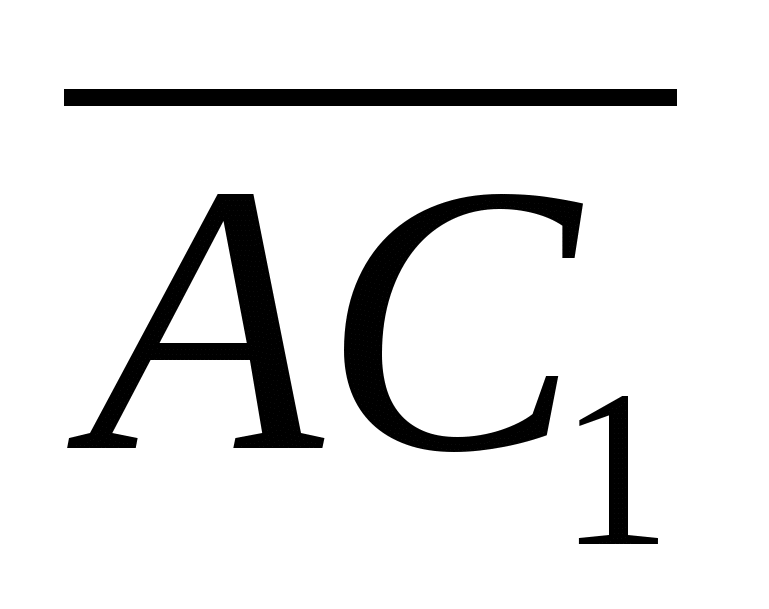 .
.
Найдем координаты векторов, используя координаты точек 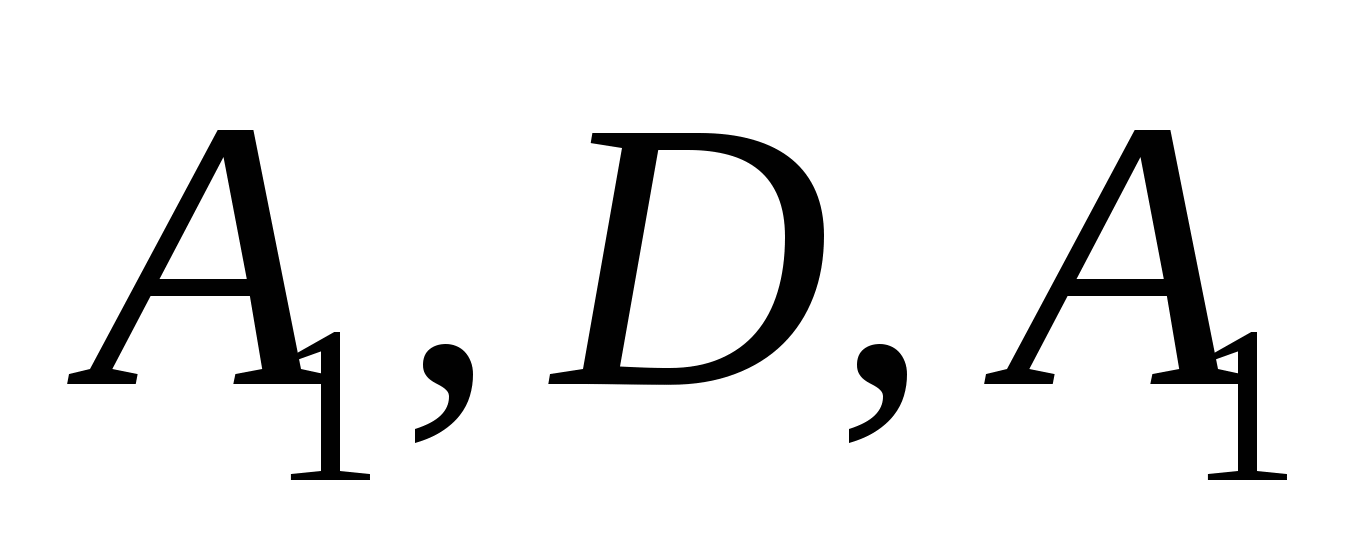 и
и  :
:
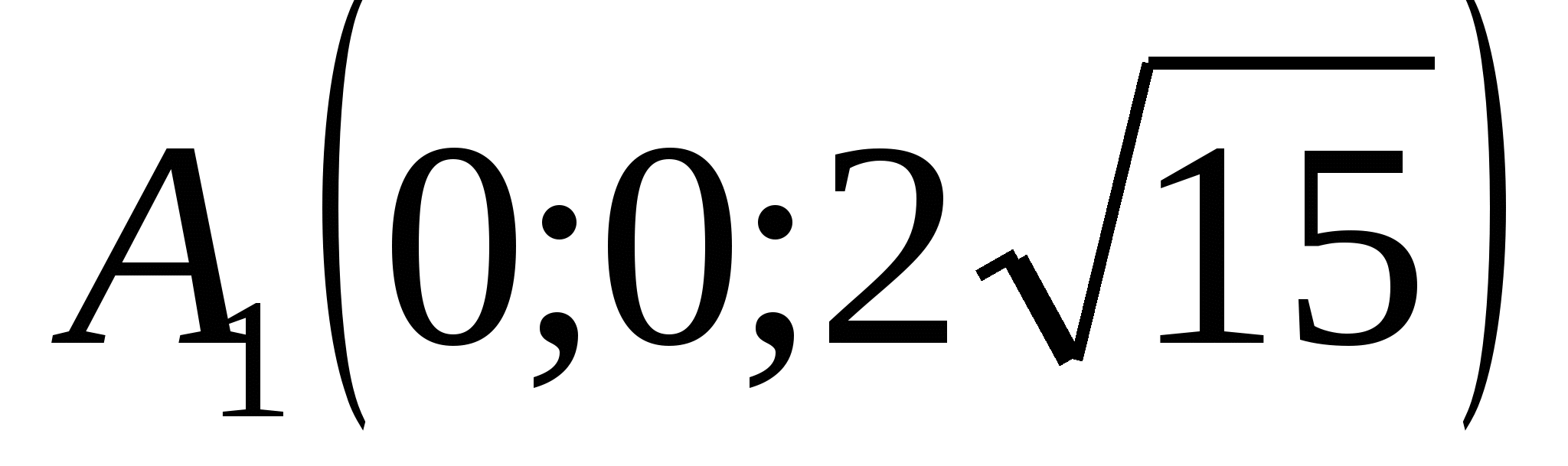 ,
, 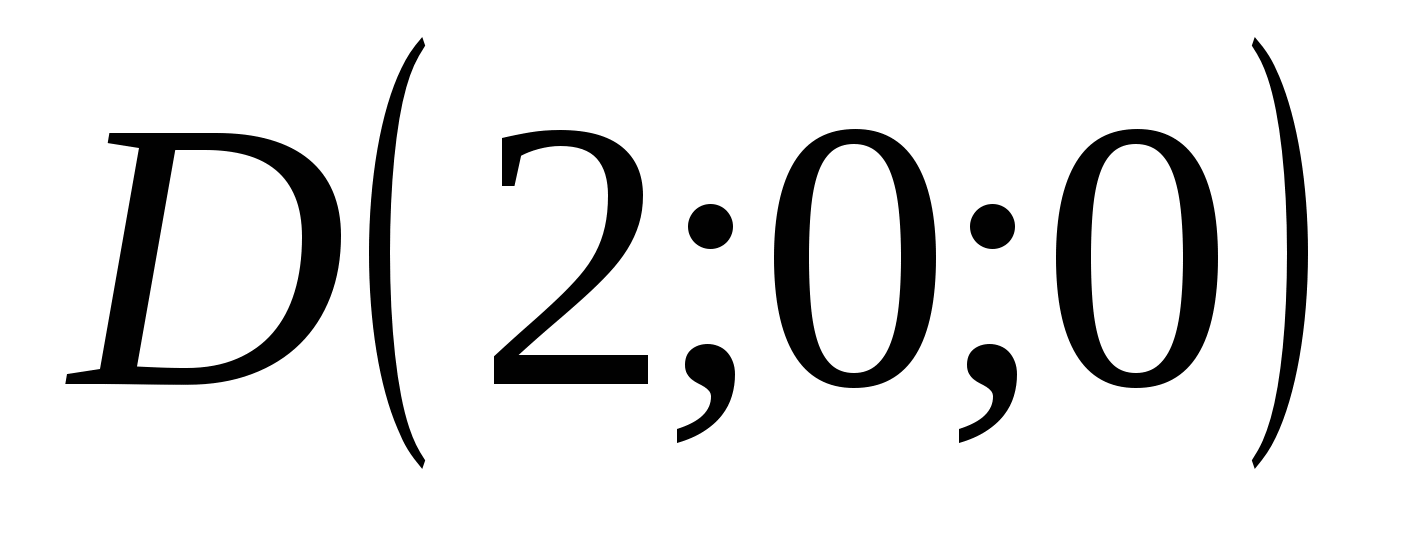 ,
,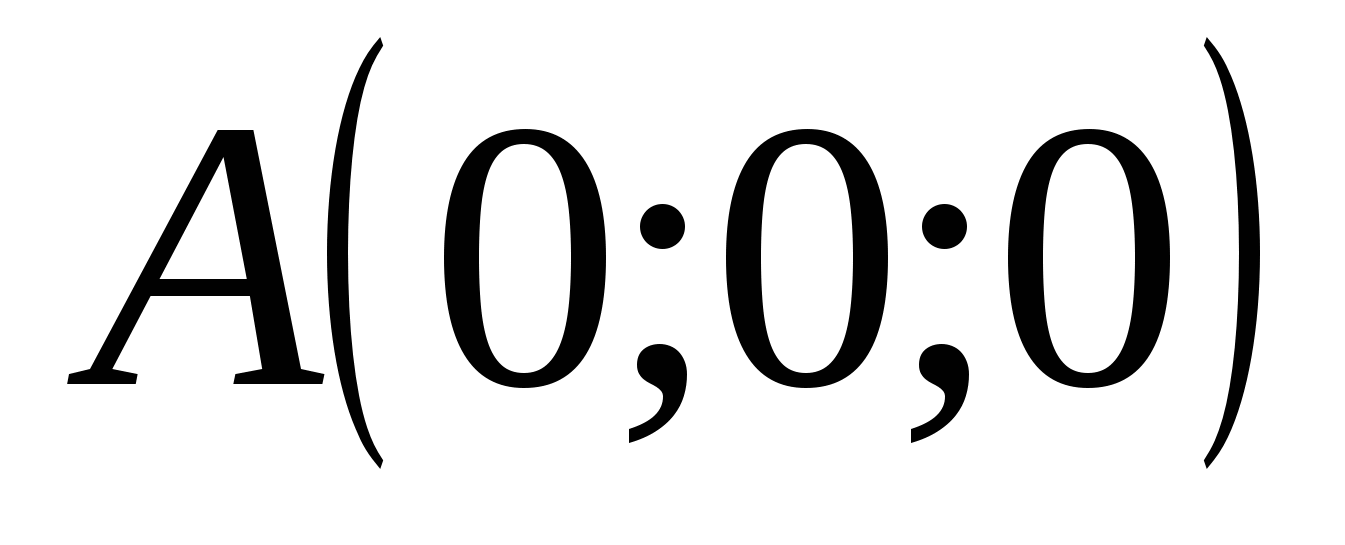 ,
,  .
.
Тогда координаты векторов 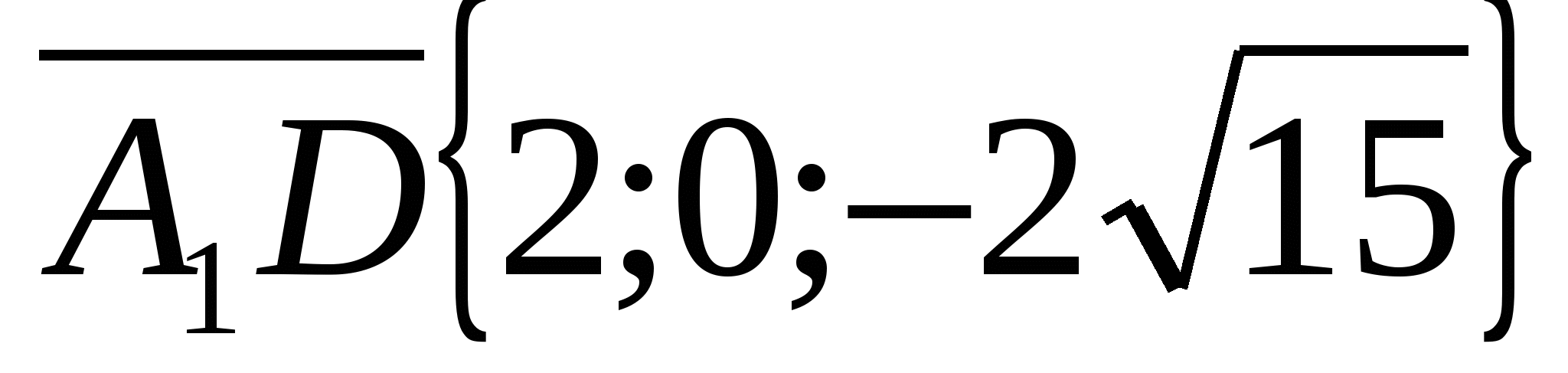 и
и 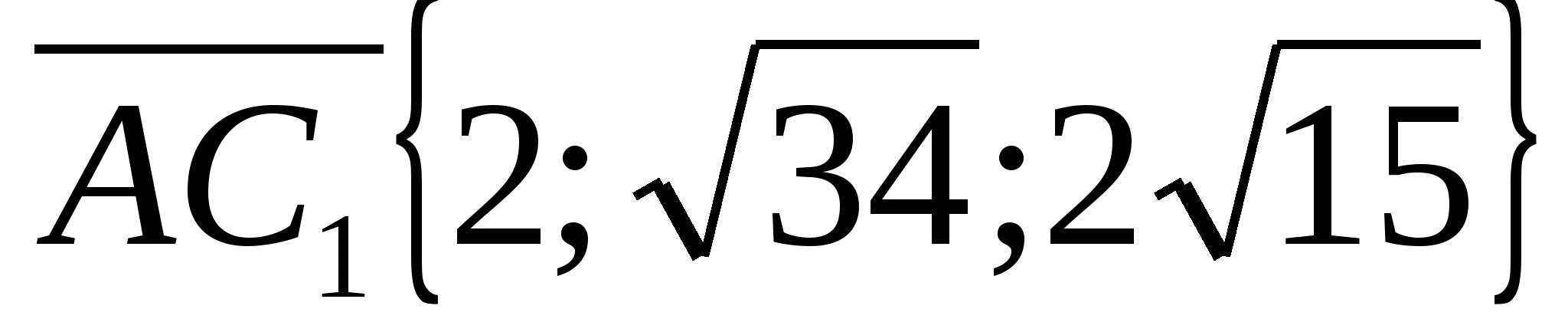 .
.
=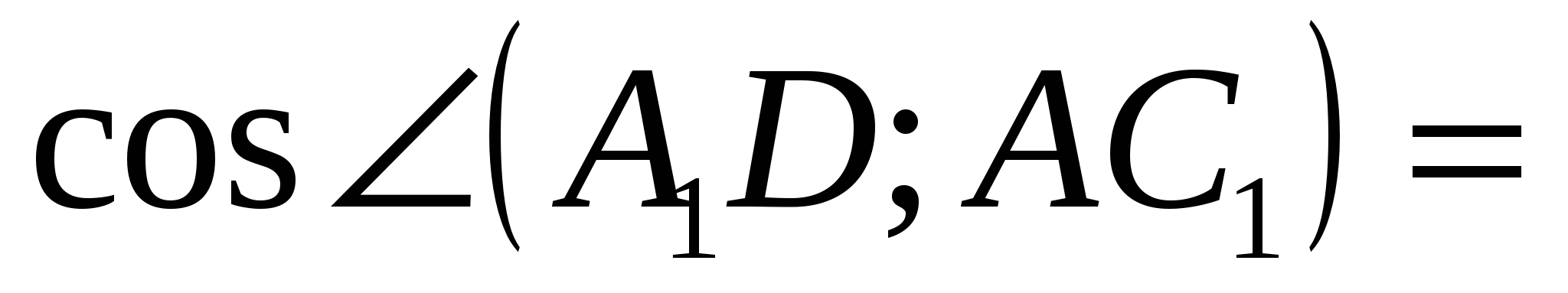
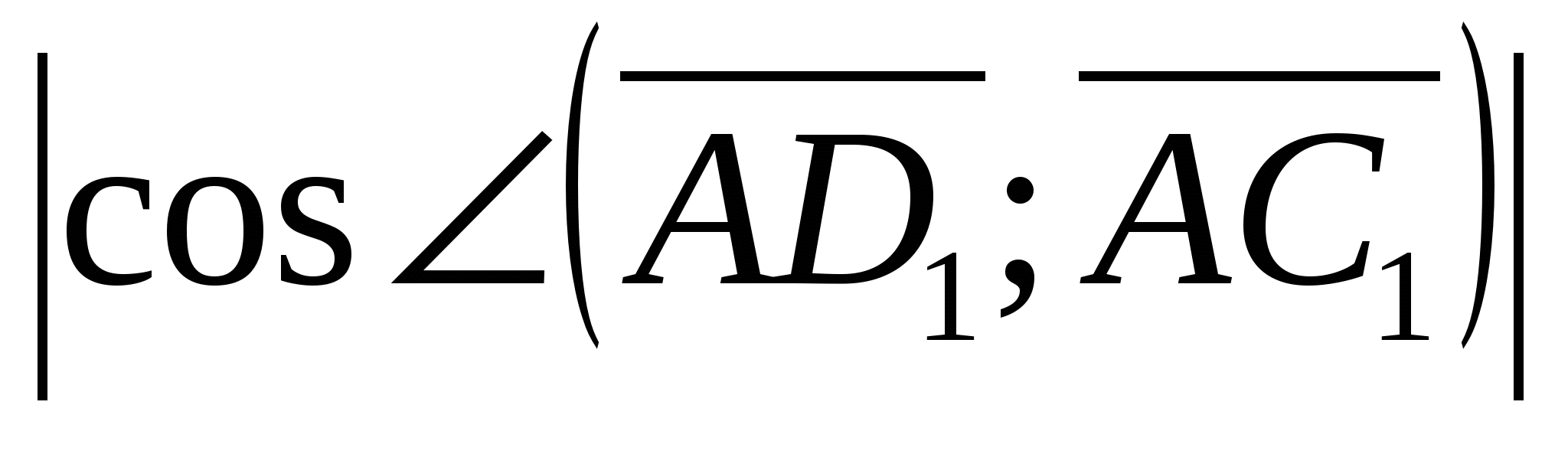 =
= =
=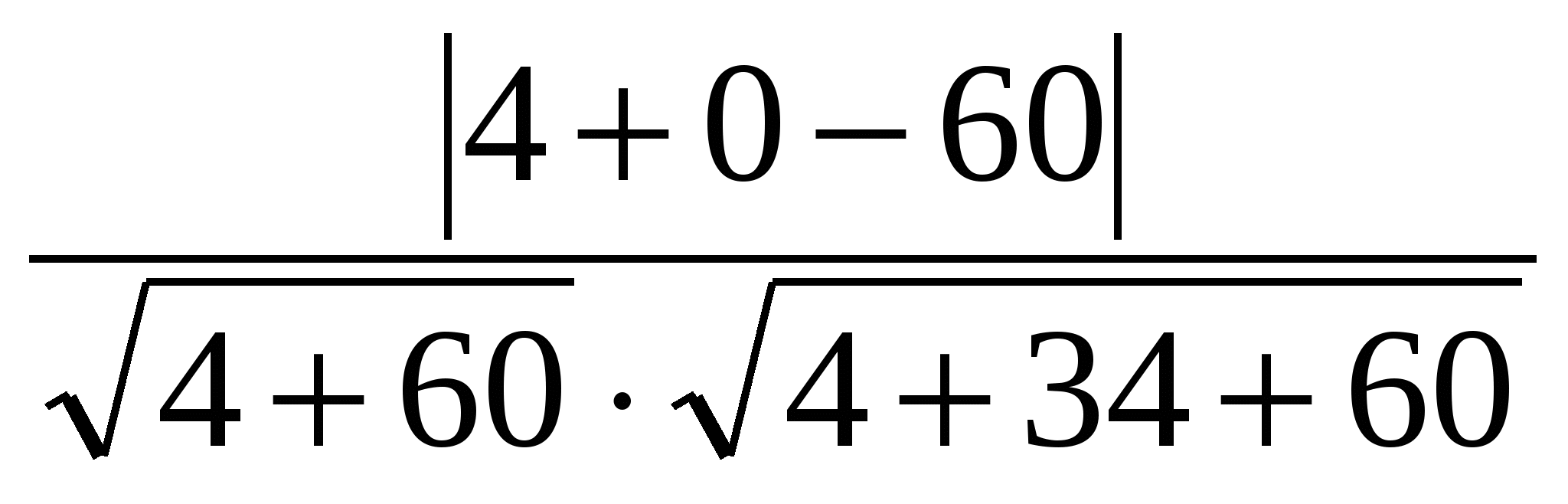
=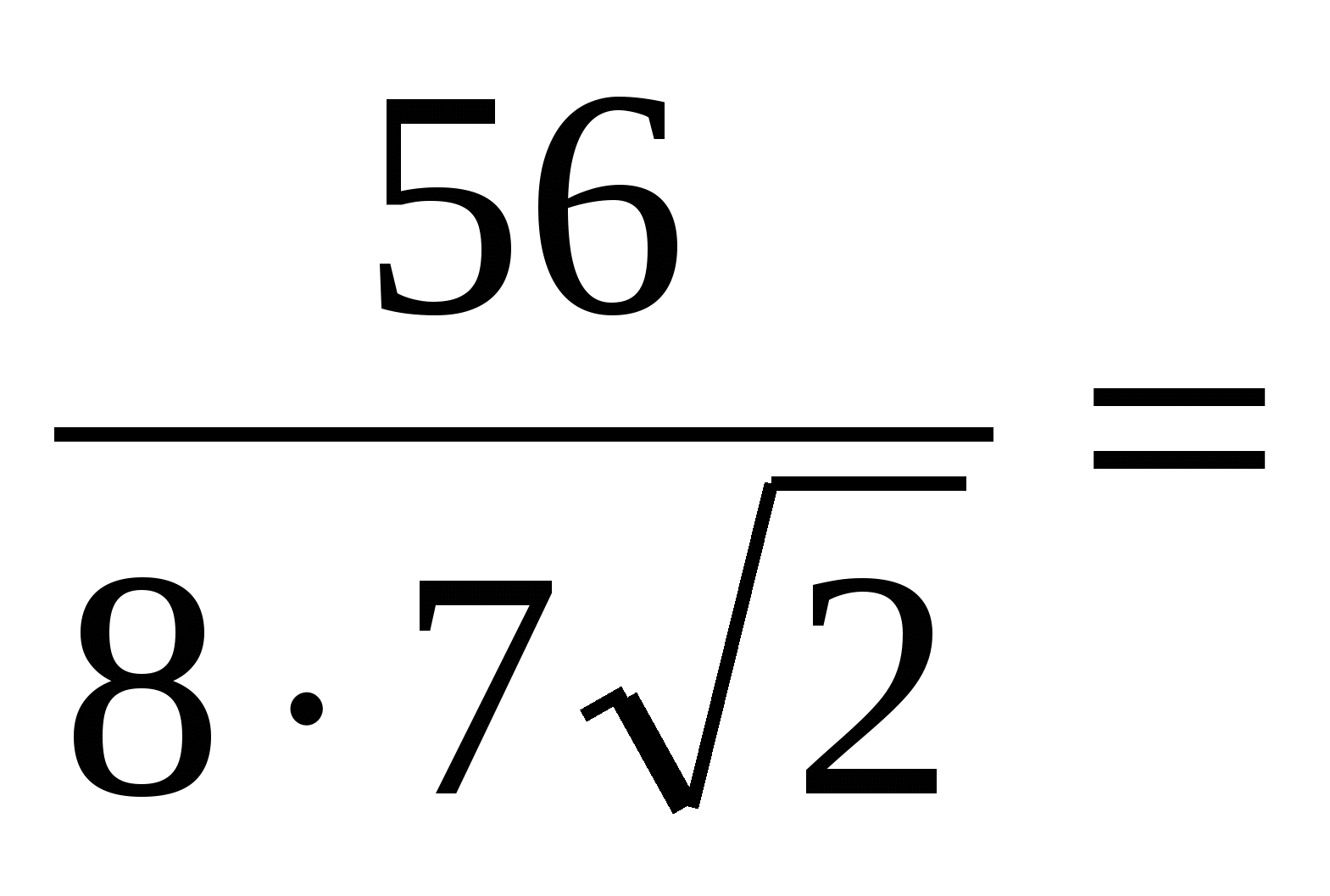
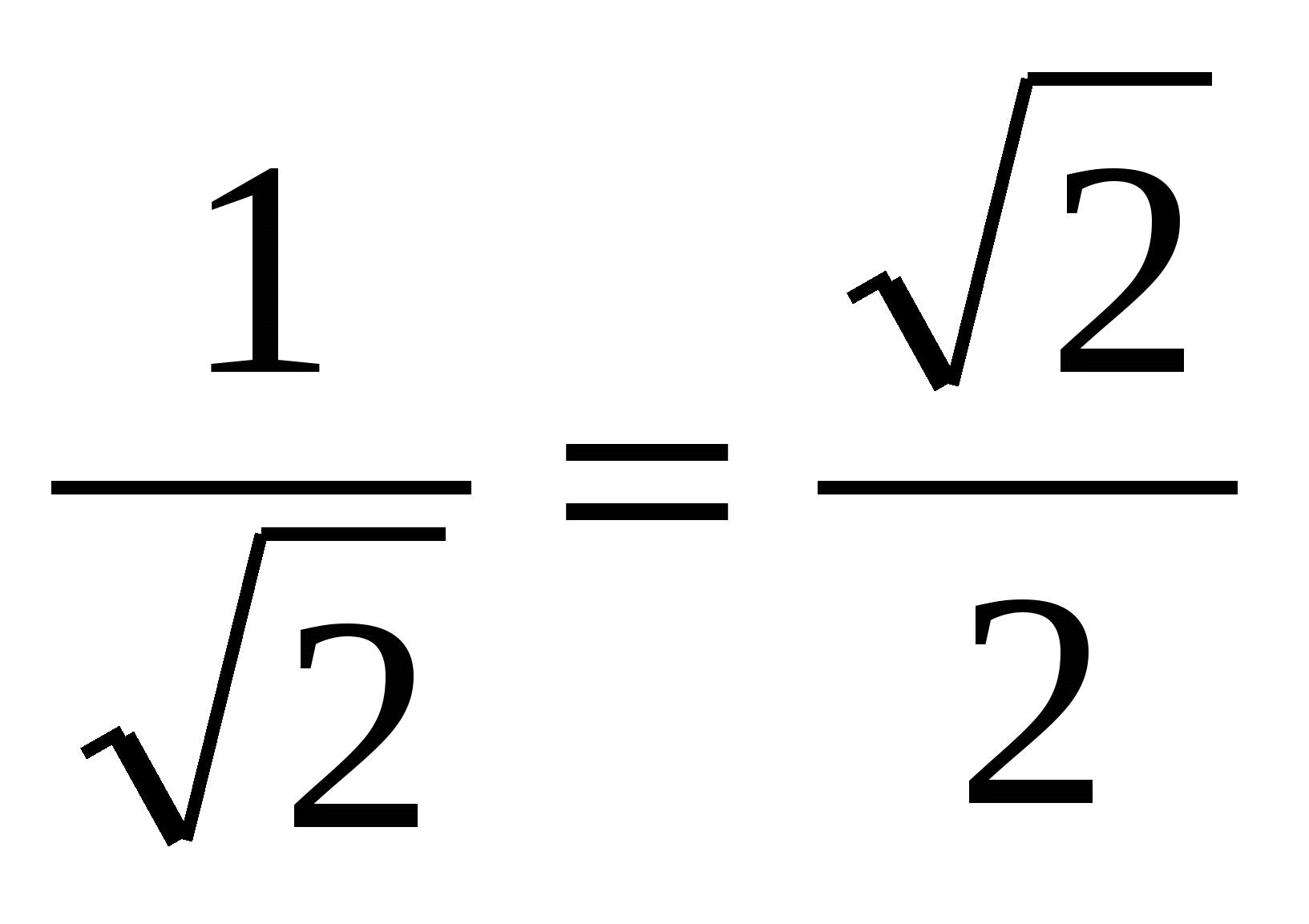 .
.
Следовательно, 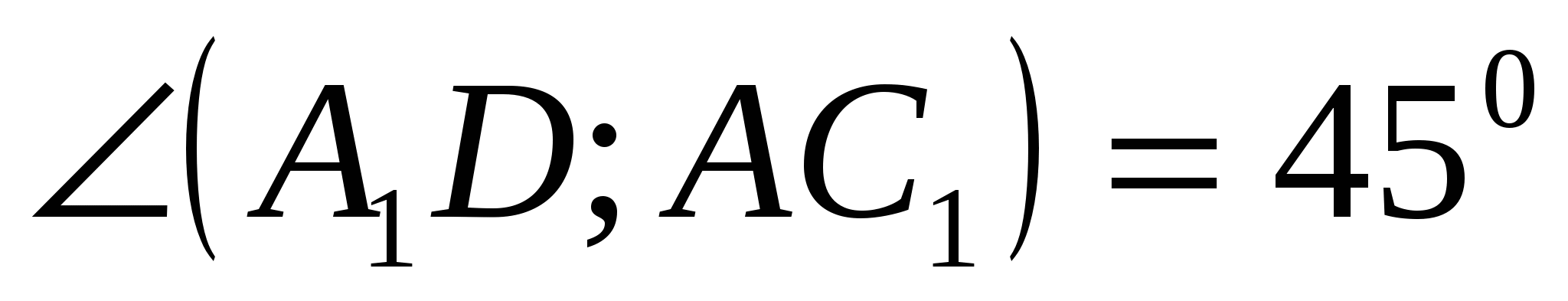
Ответ:
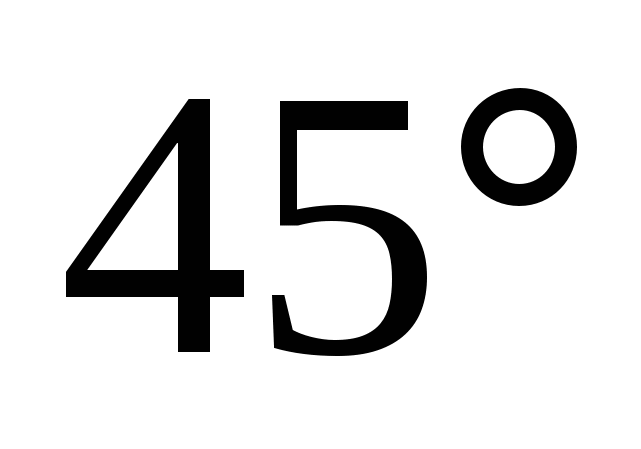 .
.
Задача 3.
Дан прямоугольный параллелепипед  . Найти угол между прямой
. Найти угол между прямой 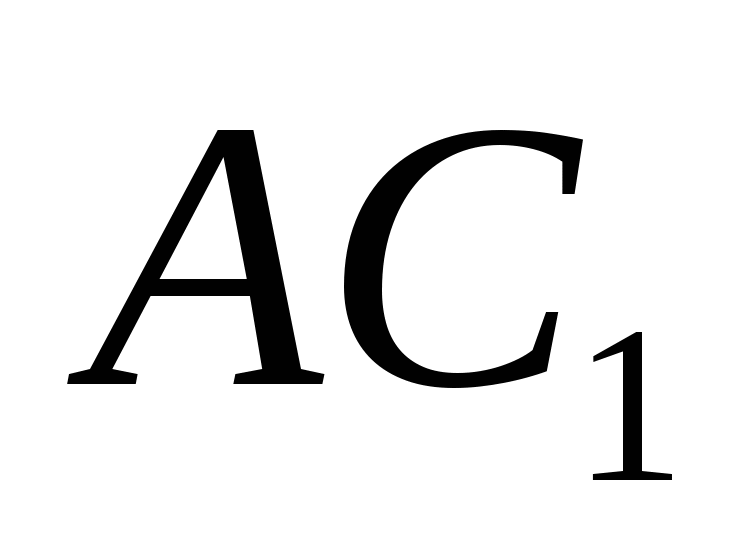 и плоскостью основания
и плоскостью основания  .
.
Решение.
1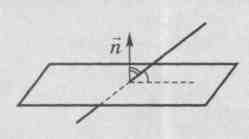 ) Угол между прямой
) Угол между прямой 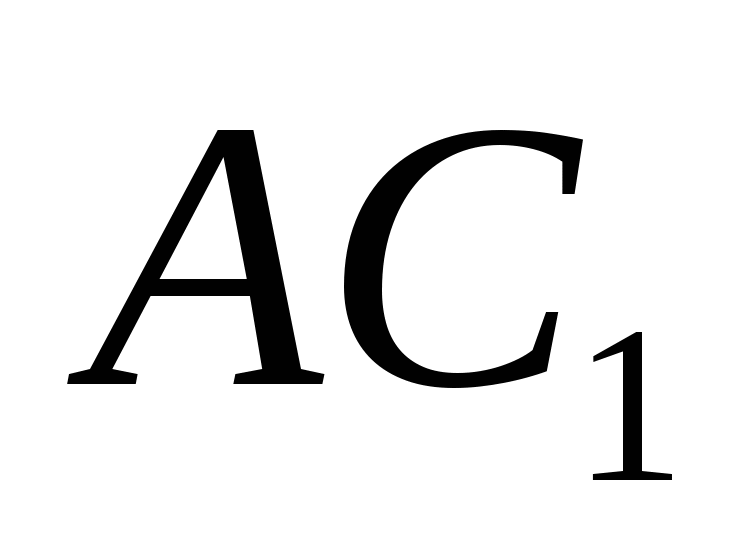 и плоскостью
АВ
1
С
– это
угол между прямой и ее проекцией на плоскость. Угол между нормалью
и плоскостью
АВ
1
С
– это
угол между прямой и ее проекцией на плоскость. Угол между нормалью 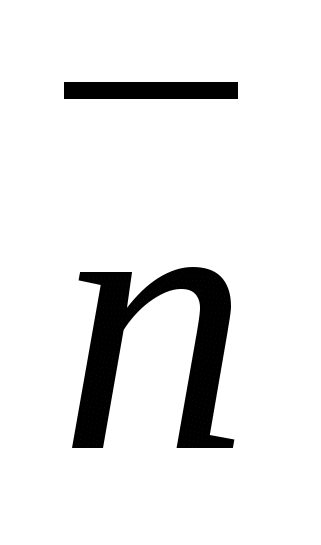 к плоскости и прямой
к плоскости и прямой 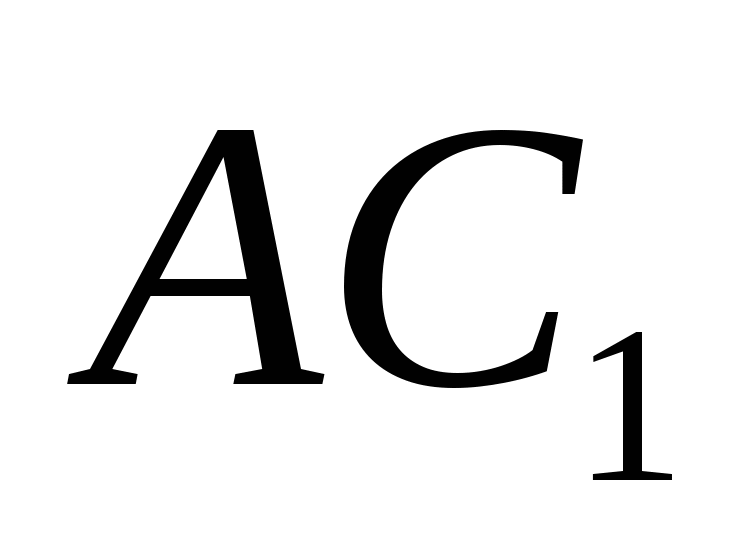 дополняет его до 90
0
, поэтому .
дополняет его до 90
0
, поэтому .
Значит для того, чтобы найти угол между прямой 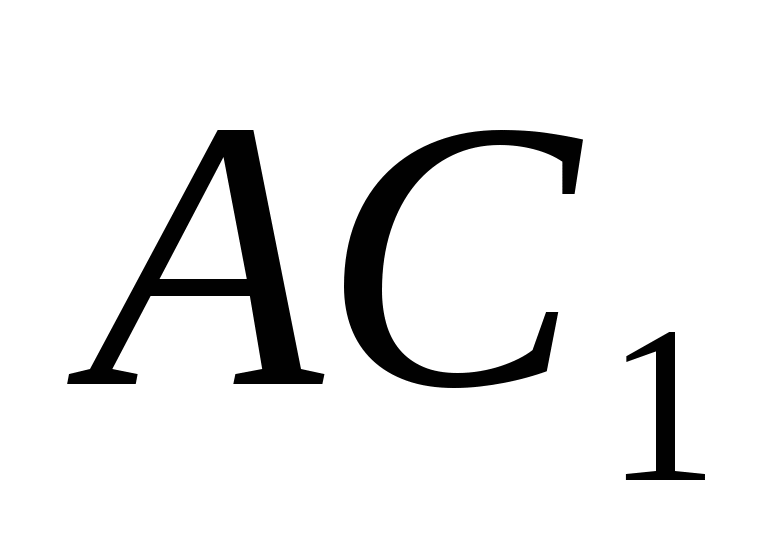 и плоскостью (
и плоскостью ( ), следует найти угол между прямой
), следует найти угол между прямой 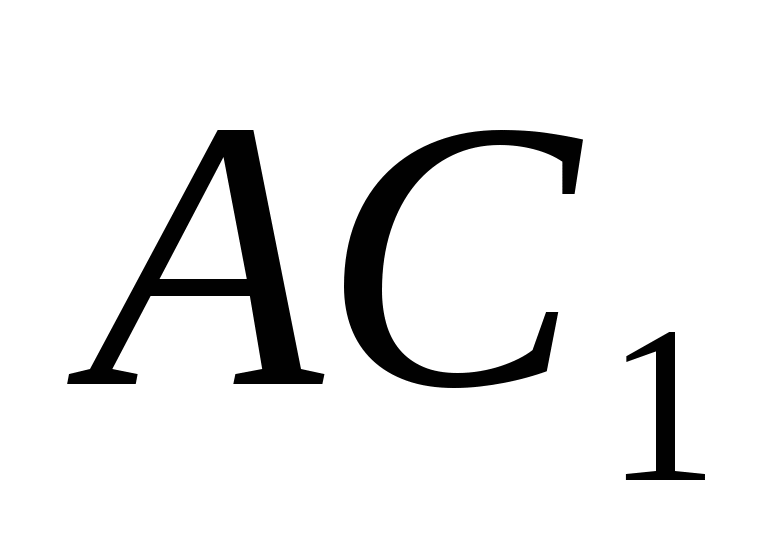 и нормалью
и нормалью 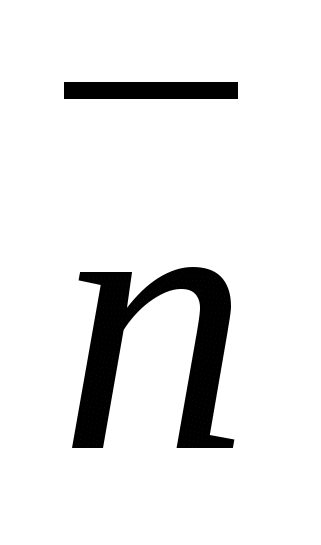 к плоскости (
к плоскости ( )
.
)
.
2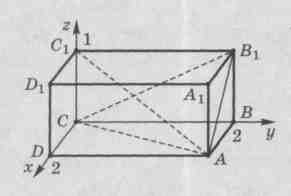 ) Введем систему координат с началом в точке
) Введем систему координат с началом в точке 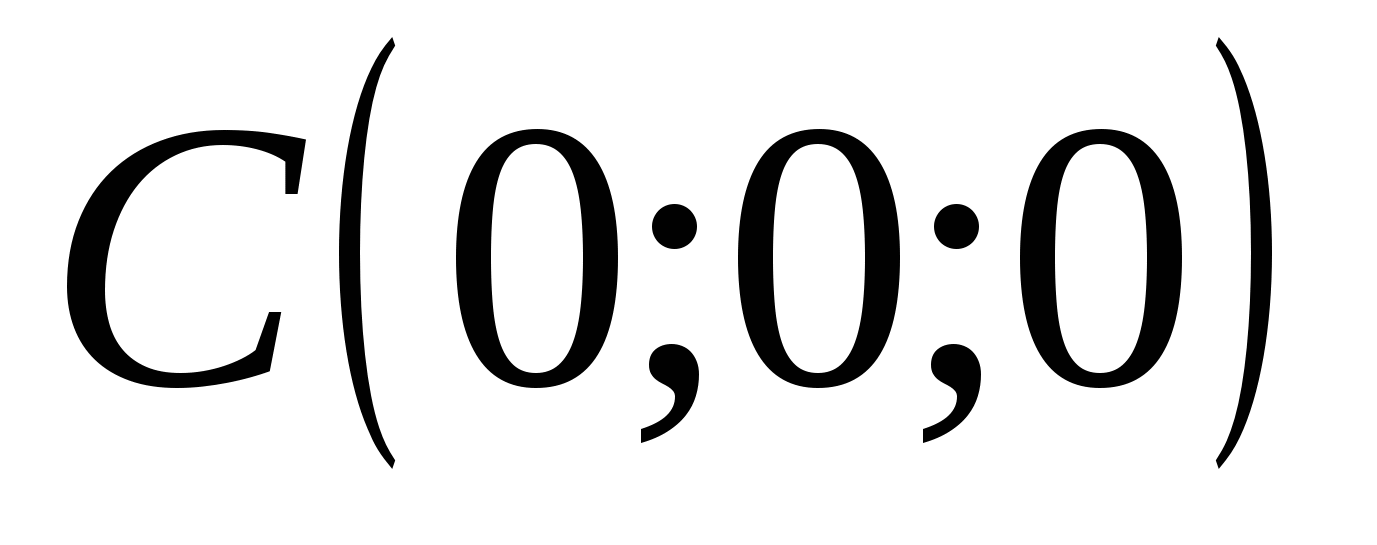 . Оси
. Оси 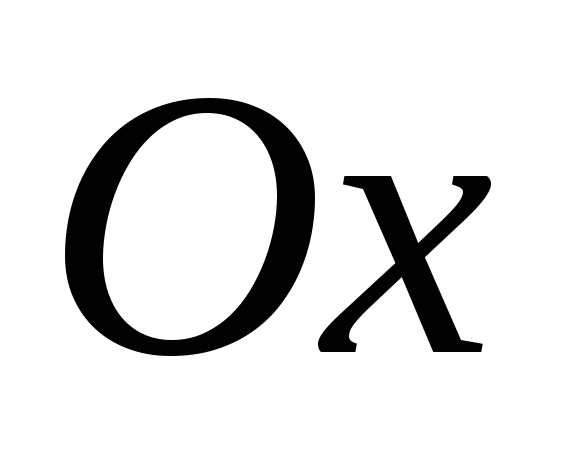 ,
,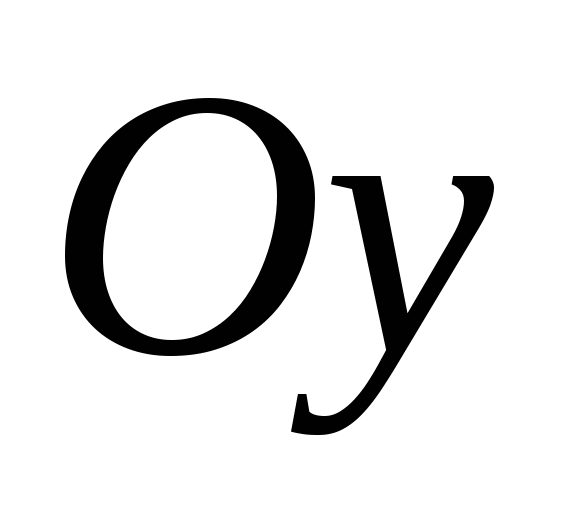 и
и  направим вдоль ребер
направим вдоль ребер  ,
, 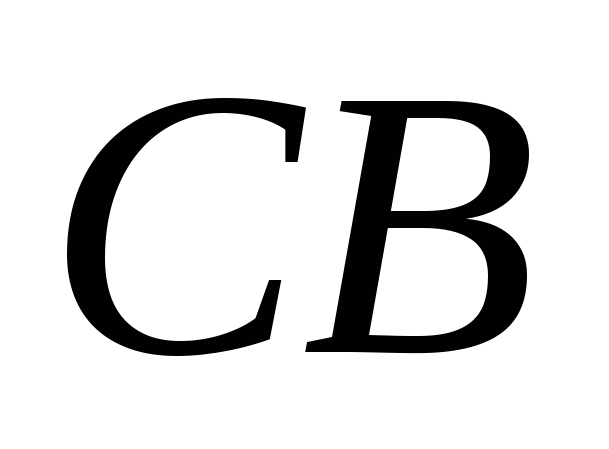 и
и 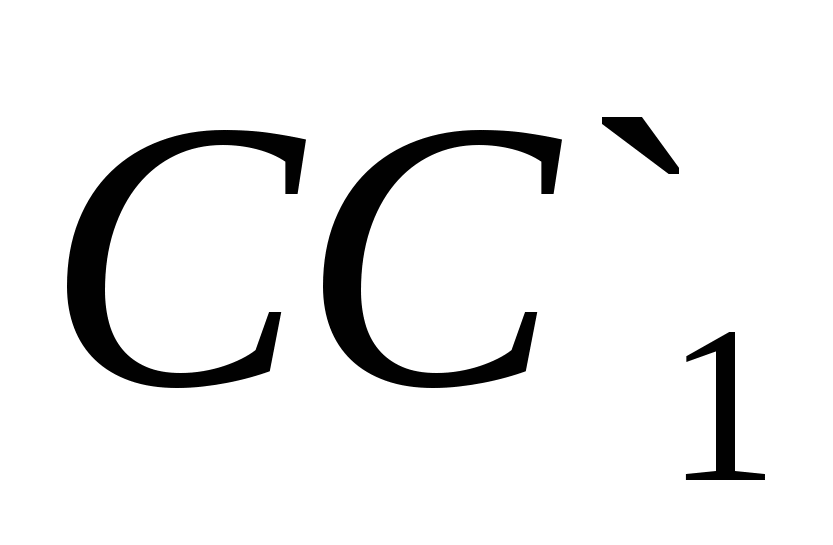 соответственно.
соответственно.
Координаты точек:
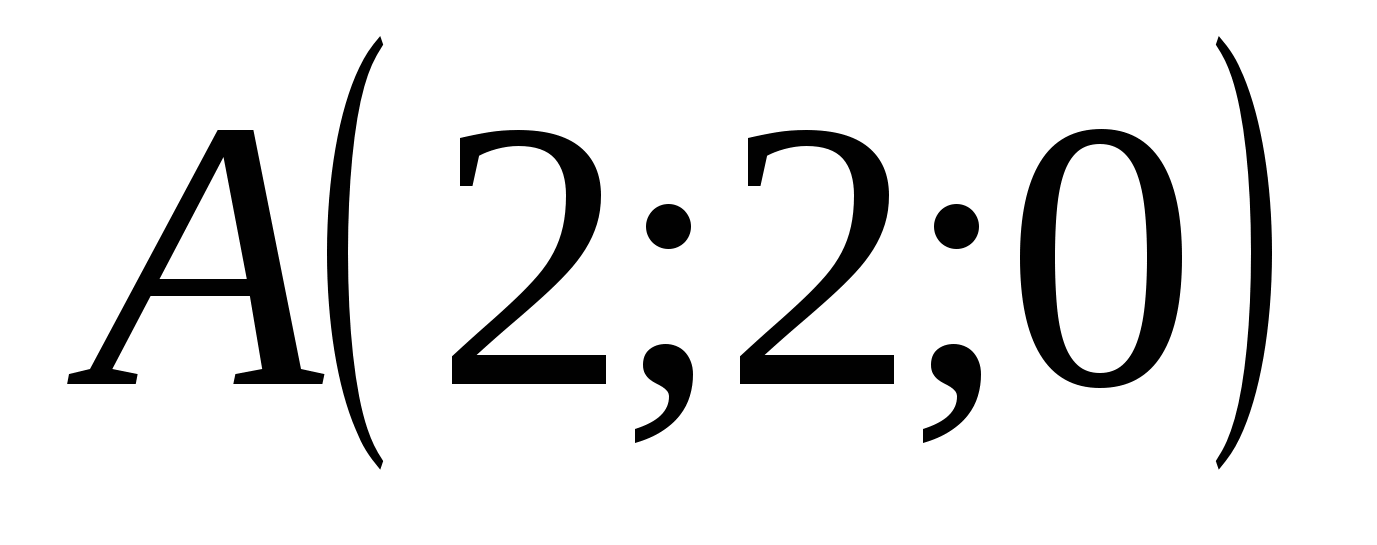 ,
, 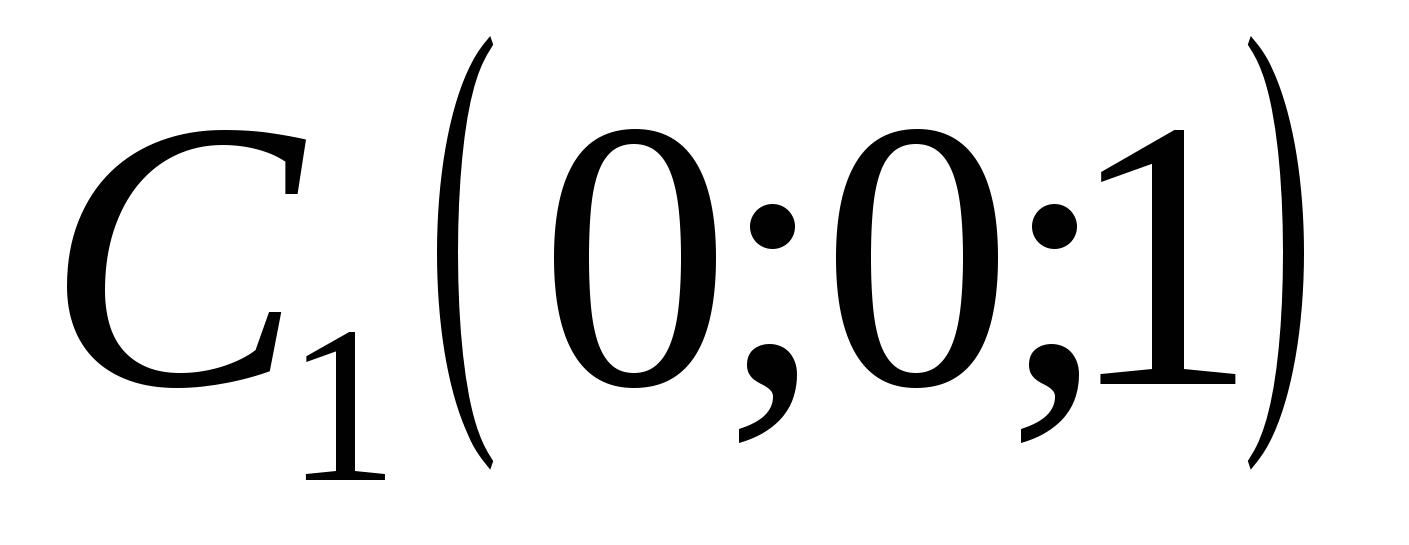 ,
, 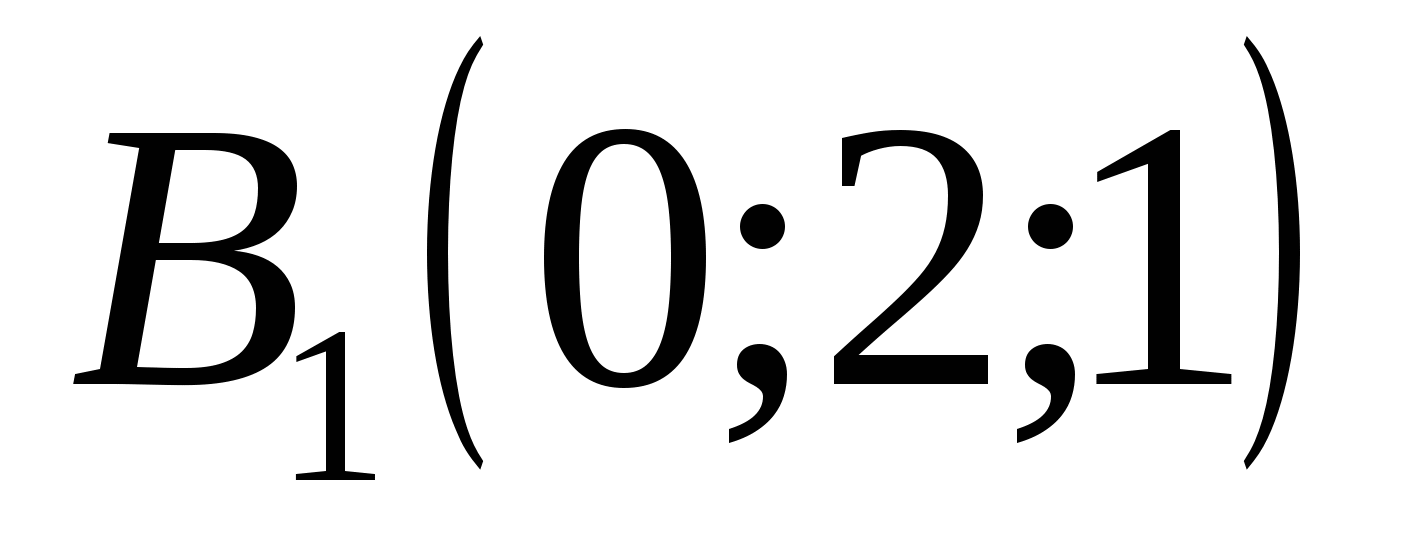 ,
,
а 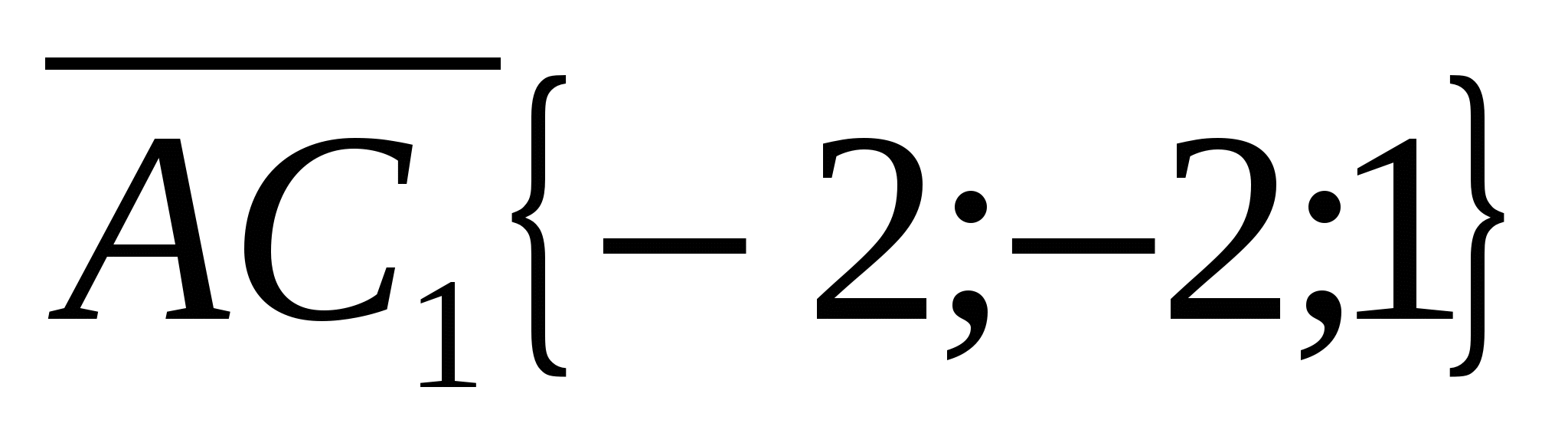 .
.
3) Найдем координаты нормали плоскости ( ). Напишем уравнение плоскости (
). Напишем уравнение плоскости ( ), подставив координаты точек
A
,
B
1
и
С
в
уравнение плоскости
.
), подставив координаты точек
A
,
B
1
и
С
в
уравнение плоскости
.
Получим систему линейных уравнений:
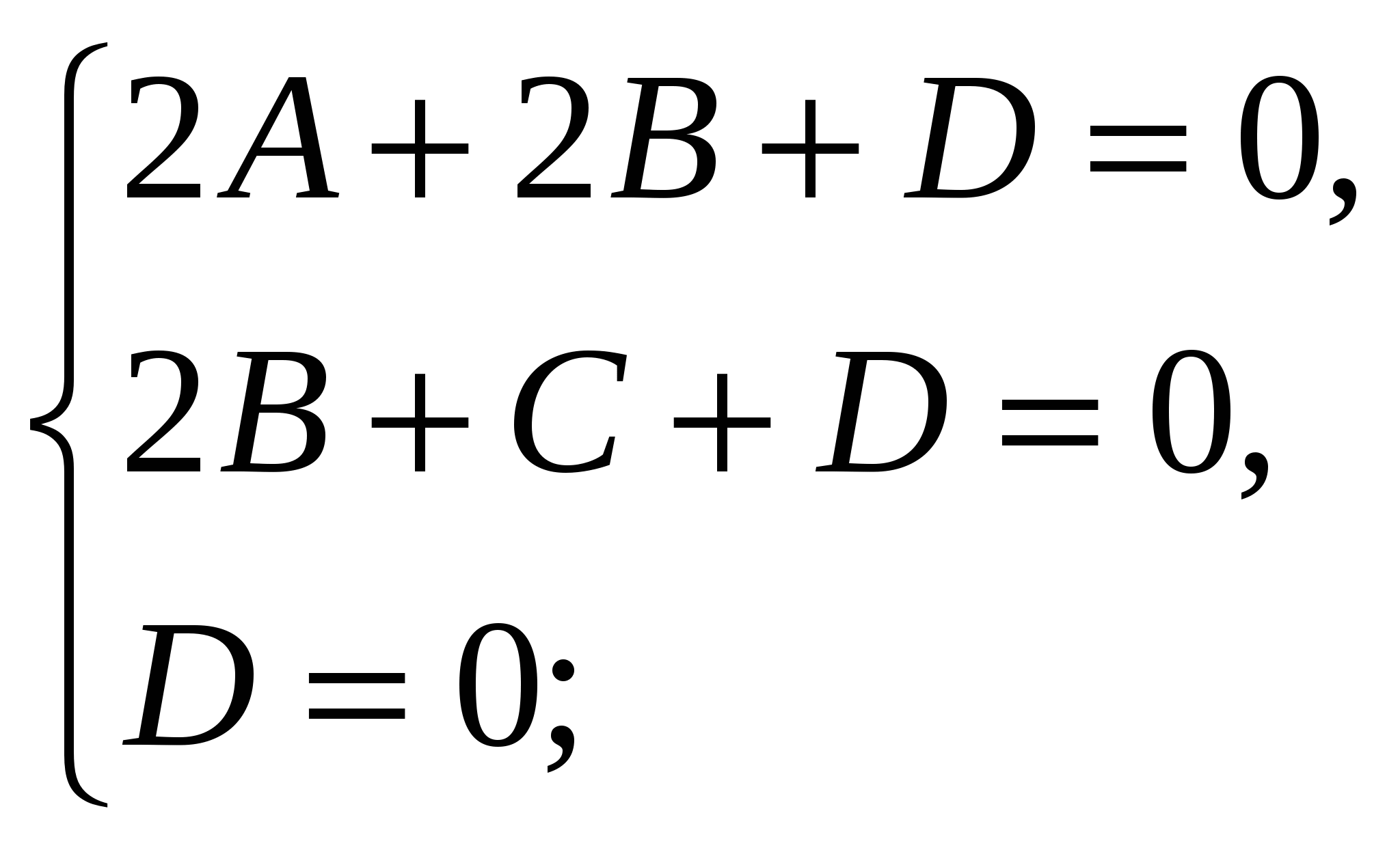
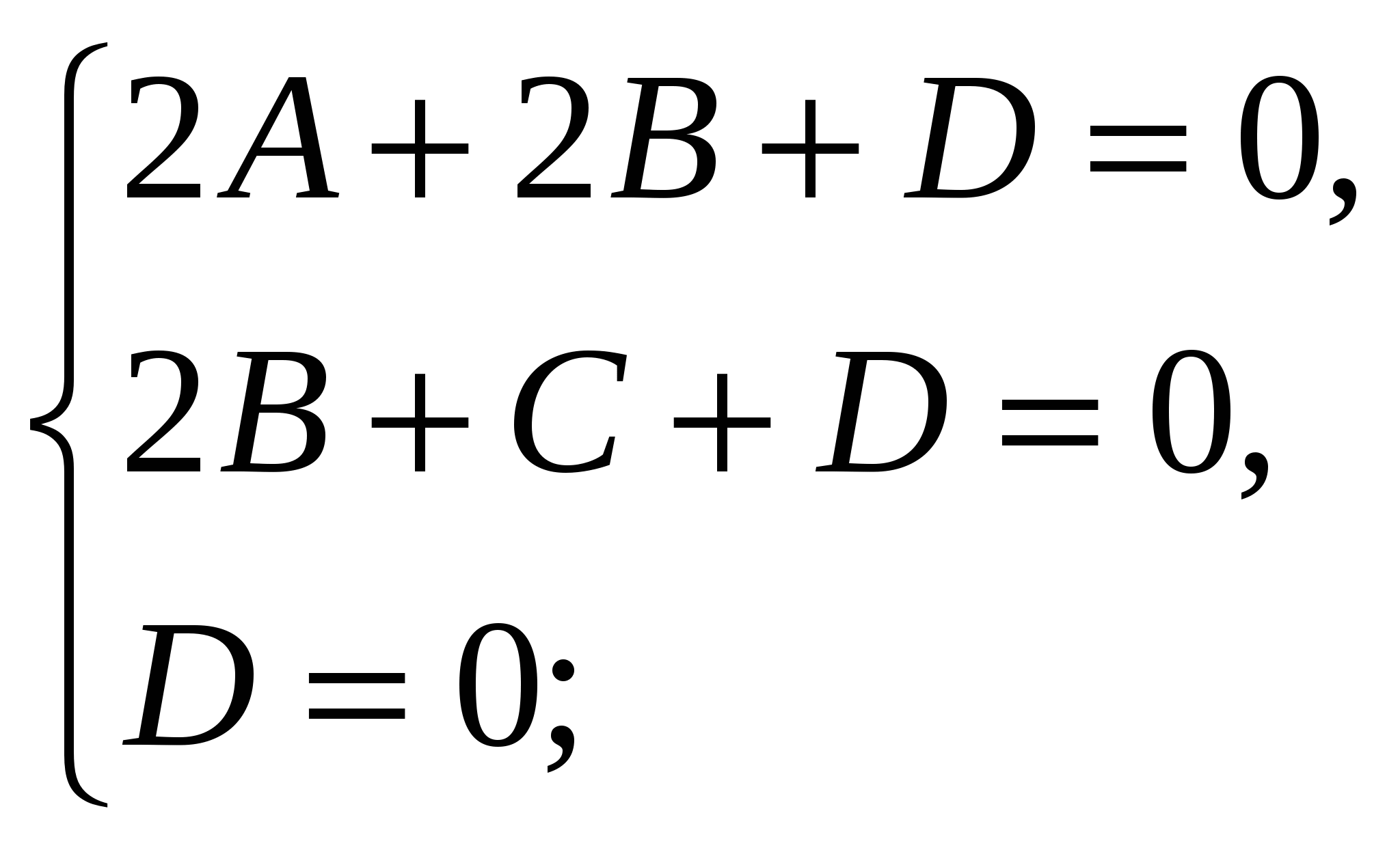
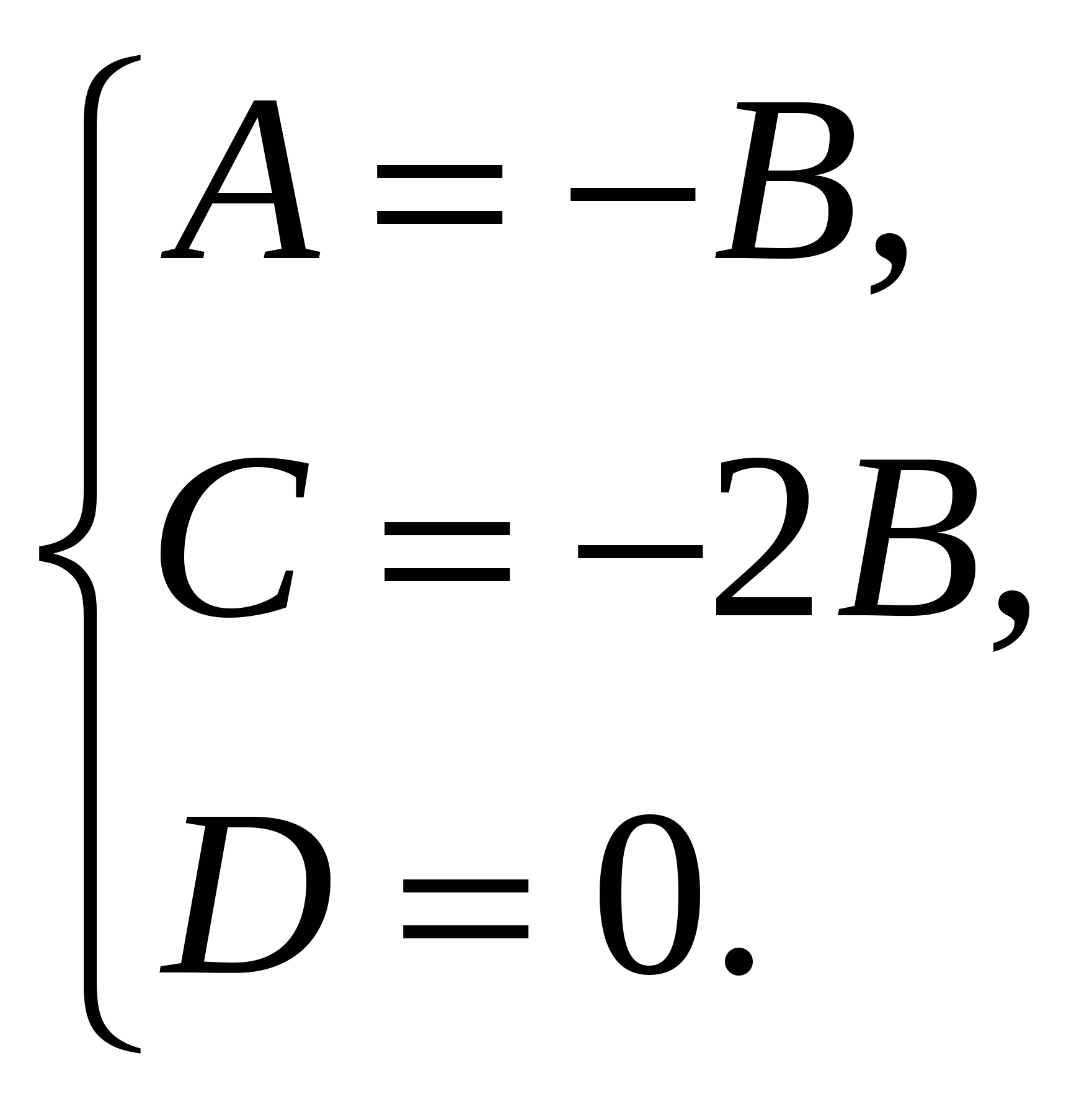
Следовательно, уравнение плоскости ( ) имеет вид , или
) имеет вид , или  , а вектор нормали имеет координаты
, а вектор нормали имеет координаты 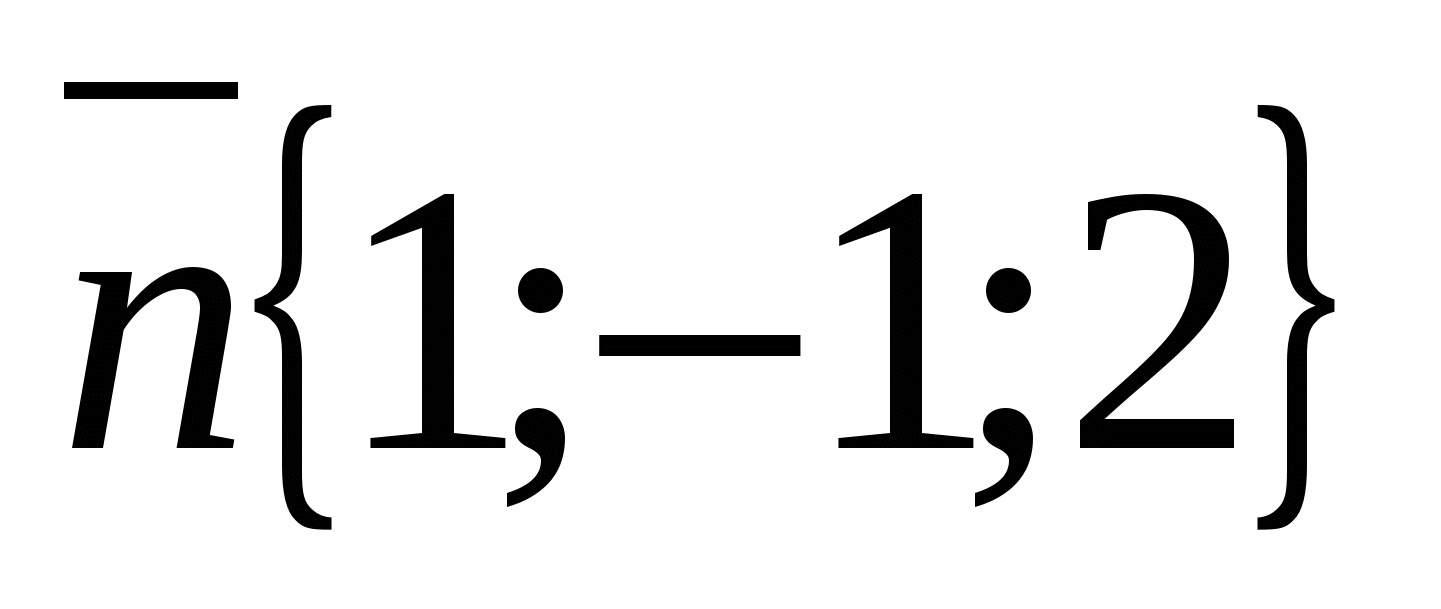 .
.
Значит
И 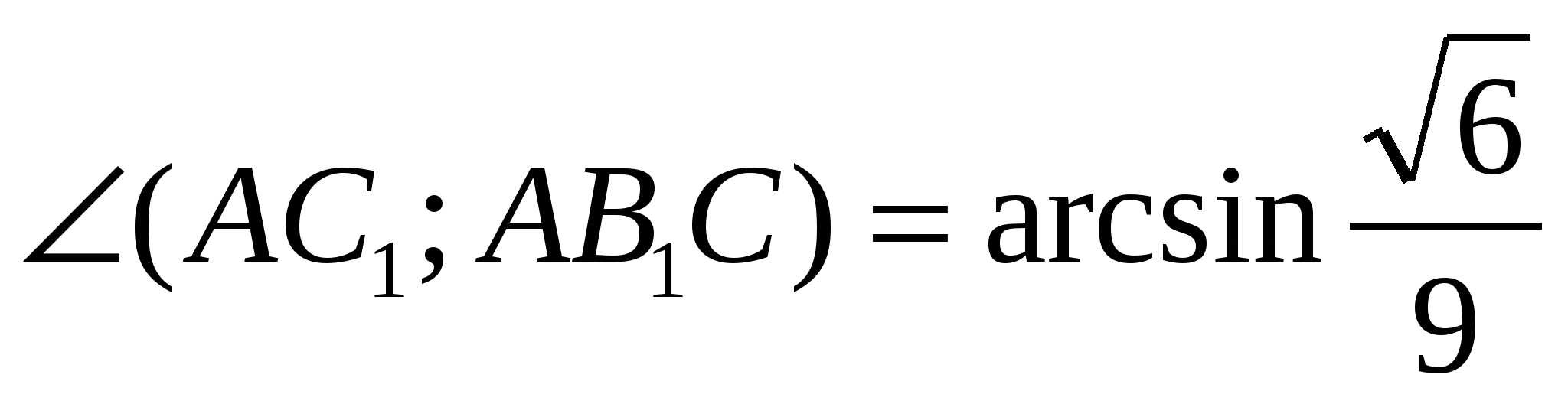 .
.
Ответ:
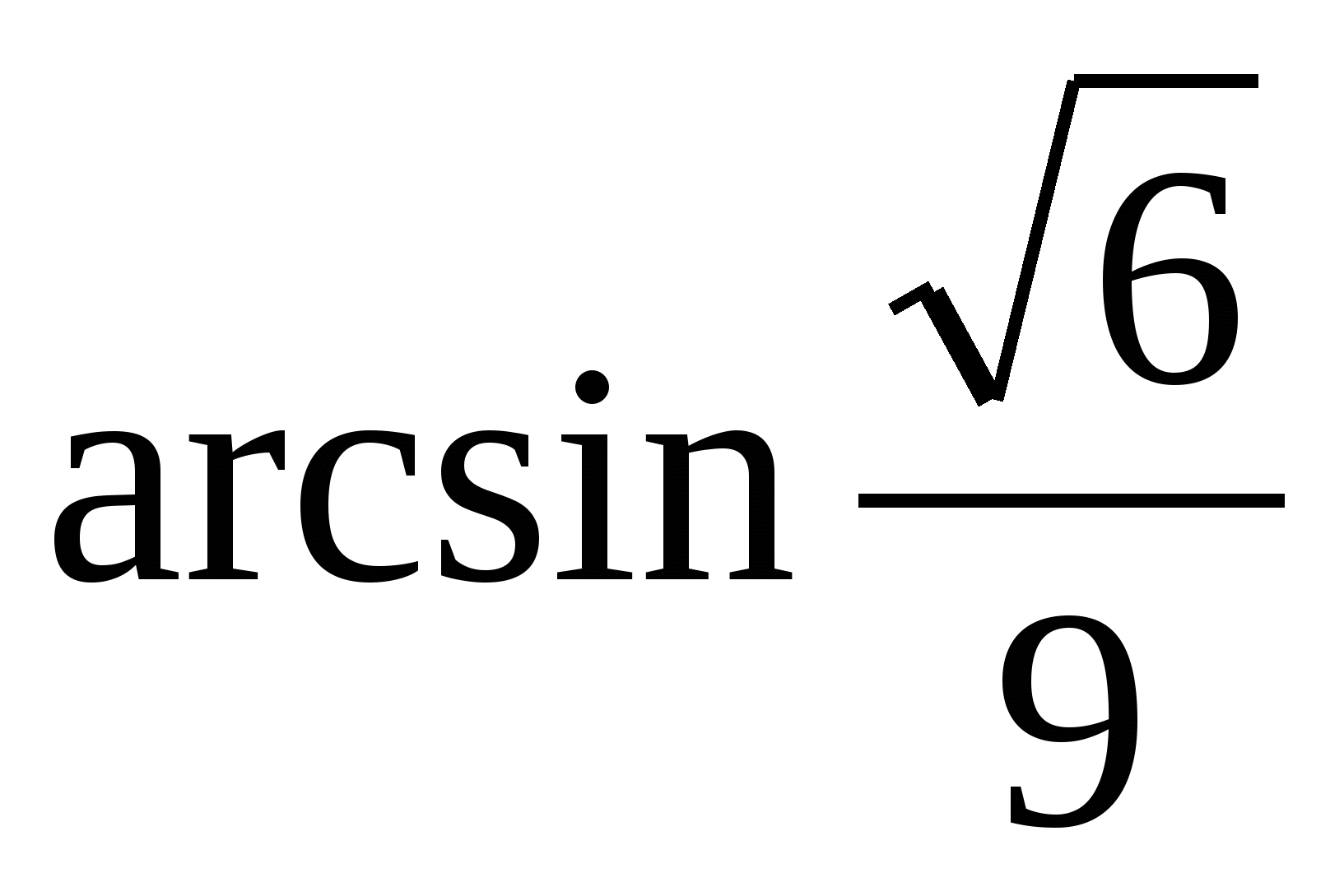 .
.
Рассмотрим решение задачи двумя способами.
Задача 4. 1 способ: геометрический.
На ребрах 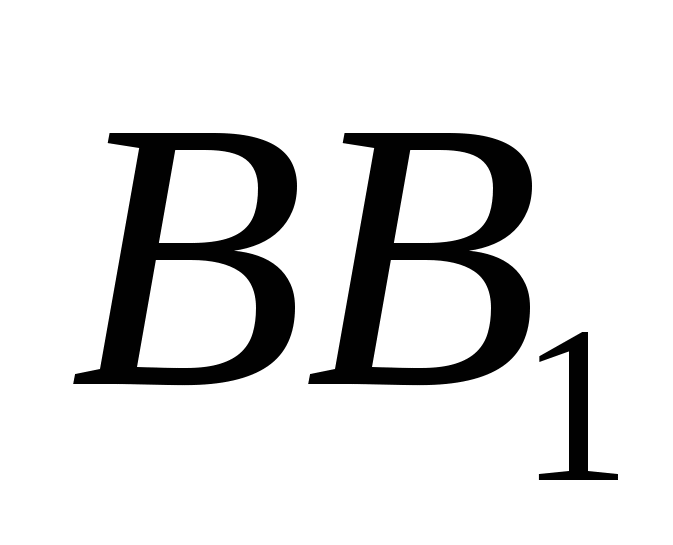 ,
,  и.
. Проведем прямую - средняя линия треугольника и, т.е. и,
и.
. Проведем прямую - средняя линия треугольника и, т.е. и,
Изученный теоретический материал был систематизирован.
При использовании метода к решению задач были выявлены особенности применения метода:
умение правильного введения системы координат,
правильное определения координат точек,
знание аналитического аппарата метода.
Было рассмотрено применение метода как к решению различных видов задач, так и в сравнении с другими методами.
При выполнении работы столкнулся с трудностями:
при постановке цели и задач;
недостаточный объем теоретического материала в школьном учебнике;
при выявлении особенностей применения метода,
при отборе материала для презентации реферата.
Список литературы.
Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Л.С.Киселева, Э.Г.Позняк . Геометрия, 10-11.М.,Просвещение, 2003.
В.Н.Литвиненко . Практикум по элементарной математике. Стереометрия: Учебное пособие.-М.:Вербум-М, 2000.
И.М .Гельфанд, Е.Г.Глаголева, А.А.Кириллов. Метод координат.-М.:Наука, 1968.
С.Г.Григорьев. Векторная алгебра и аналитическая геометрия. Учебное пособие по высшей математике.-М.:Информационно-внедренческий центр «Маркетинг», 2000.
И.Иванова, З.Ильченкова. Применение координатного вектора к решению стереометрических задач.//Математика, 2007, №2.
А.В.Дорофеев. Декарт и его геометрия.//Математика, 1992, №4.
