Продолжим изучение объемов геометрических тел и рассмотрим в этой презентации тему вычисления объема призмы.
Для начала вспомним определение. Призма - это многогранник, который состоит из n-параллелограммов и двух равных n-угольников, находящихся в параллельных плоскостях. Изображение призмы представлено на рисунке. На следующем слайде показаны рисунки прямой и правильной призм. В прямой призме основания перпендикулярны боковым граням; в основании правильной призмы лежит правильный многоугольник. Боковые грани призмы являются параллелограммами (слайд 4).
Рассмотрим теорему: объем прямой призмы вычисляется умножением площади основания на ее высоту V = S осн xh. Разберем доказательство теоремы.
Дана прямая призма, обозначим ее как BCDB 1 C 1 D 1 . Проведем AC перпендикулярно BD, тогда плоскость CAA 1 будет перпендикулярна плоскости BCD. Обозначим объем призмы BCAB 1 C 1 A 1 как V 1 . Объем V 1 = S BCA xh. А объем призмы ACDA 1 C 1 D 1 обозначим как V 2 .Запишем, что V 2 = S ACD xh. Тогда объем исходной призмы будет равен V = V 1 + V 2 = S BCA xh + S ACD xh = h (S BCA + S ACD). Полученное выражение в скобках S BCA + S ACD - это площадь основания исходной полной призмы. Запишем, что площадь основания S осн = S BCA + S ACD , тогда получим V = S осн xh, что и требовалось доказать. В этом варианте доказательства мы рассмотрели прямую треугольную призму. При рассмотрении произвольной прямой призмы, в которой количество углов будет более трех, (например, пять) прибегнем к следующим действиям. Проведем через одно из боковых ребер диагональные плоскости (см. рисунок), исходная призма в таком случае разделится на три треугольные призмы. Объем исходной призмы будет равен сумме объемов этих треугольных призм V = V 1 + V 2 + V 3 . Объем первой треугольной призмы равен V 1 = S 1 xh,объем второй V 2 = S 2 xh, объем третьей V 3 = S 3 xh.
Следовательно, V = S 1 xh + S 2 xh + S 3 xh= h (S 1 + S 2 + S 3). Значение S 1 + S 2 + S 3 это площадь основания исходной призмы. По-другому можно записать, что V = h (S 1 + S 2 + S 3) = hxS осн.
Мы рассмотрели доказательство теоремы для прямой призмы, в основании которой лежит пятиугольник. Но теорема будет справедлива для любой прямой призмы. В таком случае обозначим объемы треугольных призм как V 1 , V 2 , V 3 … V n -2 , а их площади оснований как S 1 , S 2 , S 3 … S n -2 . Тогда будет справедливо выражение V = h (S 1 + S 2 + S 3 + … + S n -2).
Перейдем к решению задач. Задача 1. Даны четыре правильных n-угольных призмы, где в каждой призме известна длина ребра а. Основаниями призм являются многоугольники с количеством улов:
Нужно найти объем каждой призмы.Т.к. во всех вариантах длина ребра нам известна, то для решения применим формулу V = S осн xh. В варианте а, в и г для вычисления площади основания S осн применим уже известные нам формулы нахождения площади многогранников. В варианте б призма является кубом, поэтому его объем можно найти по формуле V = a 3 .
Задача 2. Дана ABCA 1 B 1 C 1 - правильная треугольная призма, а - сторона призмы, ABC 1 - сечение, угол между плоскостями ABC 1 и ABC равен 60 градусов. Необходимо найти объем призмы. Для решения проведем CKперпендикулярно AB. Отрезок С 1 Kбудет принадлежать плоскости ABC 1 ,
CKперпендикулярен AB, следовательно, мы можем найти значение угла C 1 KC. Далее найдем значение CK с помощью функции синуса. Тогда в треугольнике мы сможем вычислить сторону C 1 С. Таким образом, мы получили все данные для нахождения площади основания треугольника ABC. Зная площадь основания и высоту C 1 С, вычислим объем призмы.
Cлайд 1
Cлайд 2
Цели урока: Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике.
Cлайд 3
Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2 и Bn, расположенных в параллельных плоскостях, и n параллелограммов.
Cлайд 4
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. Прямая призма называется правильной, если её основания – правильные многоугольники.
Cлайд 5
Теорема: Объем прямой призмы равен произведению площади основания на высоту Доказательство Сначала докажем теорему для прямоугольной призмы, а затем –для произвольной прямой призмы. В D1 А1 В1 С1 А C D
Cлайд 6
Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h. Проведем такую высоту треугольника ABC (на рис. BD),которая разделяет этот треугольник на два треугольника. Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC. Поэтому объемы V1 и V2 этих призм соответственно равны S ABD ·h и S BDC ·h. По свойству 2° объемов V=V1 +V2, т.е V=SABD ·h=(SABD+SBDC) · h. Таким образом, V= SABC ·h. V=SABC∙ h В D1
Cлайд 7
Теорема для произвольной прямой призмы с высотой h и площадью основания S. Такую призму можно разбить на прямые треугольные призмы с высотой h. На рис. изображена пятиугольная призма, которая разбита на три прямоугольные призмы. Выразим объем каждой прямоугольной призмы по формуле V= SABC ·h и сложим эти объемы. Мы вынесем за скобки общий множитель h, потом получим в скобках сумму площадей оснований треугольных призм, т.е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен произведению S · h.
Cлайд 8
Задача Дано: ABCA1B1C1- прямая призма. AB=BC=m; ABC= φ, BD- высота в ∆ ABC; BB1=BD. Найти: VABCA1B1C1-?
Cлайд 9
Решение: S ABC ·h, h=BB1. Рассмотрим ∆ ABC; ∆ ABC- р/б. BD- высота ∆ ABC, следовательно медиана и биссектриса. ABD= DBC= φ/2 3) Рассмотрим ∆ ABD; ∆ ABD- прямоугольный. Из соотношения в ∆: cosφ/2 = BD/AB BD= cosφ/2 AB, BD=m cosφ/2 (AB=m) 4) Т.к. BD=BB1 BB1=m · cos φ /2 5) S ABC= ½ AB·BC· sinφ; S ABC= ½ m2 · sinφ 6) V= ½ m2 · sinφ· mcosφ/2=½ m3 · sinφ · cosφ/2 Ответ: ½ m3 · sinφ · cosφ/2
краткое содержание других презентаций
«Задачи по стереометрии» - Найдите площадь трапеции. Объм шара и его частей. Найдите угол многогранника. Круговой сектор. Длина окружности. Найдите квадрат расстояния между вершинами. Диаметр свинцового шара. Найдите объем пирамиды. Задачи. Найдите площадь поверхности многогранника. Найдите объем V части цилиндра. Найдите ординату точки A.
«Координаты вектора в пространстве» - Плоскости. Действия над векторами в пространстве. Величина и направление вектора. Скалярное произведение векторов. Координата. Разность векторов. Сумма векторов. Векторы в пространстве. Решение. Абсолютная величина. Произведение вектора. Длина отрезка. Учебник. Рисунок. Общее начало. Доказательство.
««Движение» 11 класс» - Введение. Центральная симметрия. Симметрия в архитектуре. Осевая симметрия. Симметрия в растениях. Параллельный перенос. Скользящая симметрия. Зеркальная симметрия. Движение. Движение. Поворот. Симметрия в животном мире.
«В мире многогранников» - Магнус Веннинджер. Мир многогранников. Тела Архимеда. Тетраэдр. Многогранники в искусстве. Тело Ашкинузе. Развёртки некоторых многогранников. Пять выпуклых правильных многогранников. Математика. Выпуклые многогранники. Правильные многогранники. Теорема Эйлера. Царская гробница. Вершина куба. Эйлерова характеристика. Многогранники. Фаросский маяк. Звездчатый додекаэдр. Тела Кеплера - Пуансо. Геометрия.
«Понятие центральной симметрии» - Центральная симметрия. Мы знакомились с движениями плоскости. Задача. Точки М и М1 называются симметричными. Отображение пространства на себя. Движения. Фигура называется симметричной. Центральная симметрия является частным случаем поворота. Движение пространства. Свойство. Центральная симметрия является движением.
«Философ Пифагор» - Египетские храмы. Математика. Основоположник современной математики. Девиз. Пифагор. Слово "философ". Мнесарх. Жизнь и научные открытия Пифагора. Пифагор встречался с персидскими магами. Мысль. Бессмертная идея. Истина. Направление полёта. Знание основ музыки.
Вопросы фронтального опроса:
1. Какой многогранник называется призмой?
2. Какая призма называется прямой?
3. Какая призма называется правильной?
4. Что является основанием правильной треугольной призмы?
Прямой призмы?
5. Чем являются боковые грани призмы?
Правильной призмы?
6. Сформулируйте свойства объемов.
7. Сформулируйте следствие из теоремы об объеме прямоуголь-
ного параллелепипеда, в основании которого прямоугольный
треугольник.
Объем прямой призмы равен произведению площади основания на высоту.
- прямая
Дано: АВСА
BN = NA, CC 1 = 6,
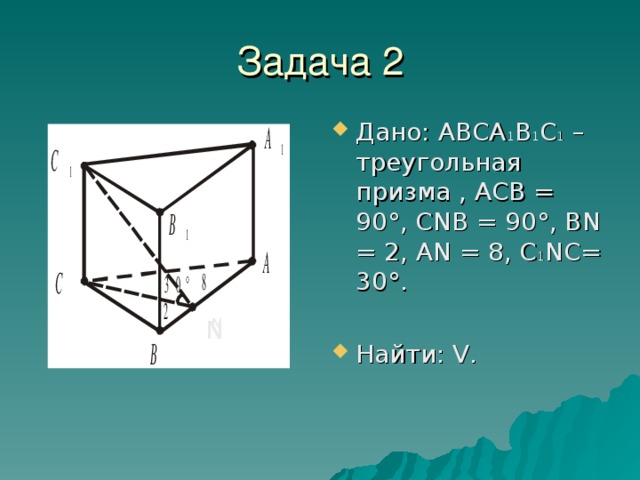
- Дано: ABCA 1 B 1 C 1 – треугольная призма, ACB = 90°, CNB = 90°, BN = 2, AN = 8, C 1 NC= 30°.
- Найти: V.
- Дано: AВСДА 1 В 1 С 1 Д 1 – прямая четырехугольная призма, ABCD – ромб, BAD = 60°, B 1 DB = 45°, BB 1 = =2
- Найти: V
- Что представляет собой правильная шестиугольная призма?
- Какая диагональ в этой призме наибольшая?
- Каким свойством обладает большая диагональ правильного шестиугольника?
- Как связаны между собой сторона правильного шестиугольника и радиус описанной окружности?
Основание прямой призмы АВСДА 1 В 1 С 1 Д 1 –
параллелограмм АВСД, в которой АВ =12,
АС =16, АД=20. Секущая плоскость, парал-лельная АВ и проходящая через диагональ СА 1 , образует с плоскостью основания призмы угол, синус которого равен 1/
Найдите объем призмы.
