ఇన్ఫ్లెక్షన్ పాయింట్ నిర్వచనం. ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క కుంభాకార మరియు పుటాకార విరామాలు

ఆన్‌లైన్ కాలిక్యులేటర్‌ని ఉపయోగించి మీరు కనుగొనవచ్చు ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్ఫ్లెక్షన్ పాయింట్లు మరియు కుంభాకార విరామాలు Word లో పరిష్కారం యొక్క రూపకల్పనతో. రెండు వేరియబుల్స్ f(x1,x2) యొక్క ఫంక్షన్ కుంభాకారంగా ఉందా లేదా అనేది హెస్సియన్ మ్యాట్రిక్స్ ఉపయోగించి నిర్ణయించబడుతుంది.

y =

విధులను నమోదు చేయడానికి నియమాలు:

ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క కుంభాకార దిశ. ఇన్ఫ్లెక్షన్ పాయింట్లు

నిర్వచనం: వక్రరేఖ y=f(x) ఈ విరామంలో ఏదైనా బిందువు వద్ద టాంజెంట్ పైన ఉన్నట్లయితే విరామంలో (a; b) కుంభాకార క్రిందికి అంటారు.

నిర్వచనం: వక్రరేఖ y=f(x) ఈ విరామంలో ఏ సమయంలోనైనా టాంజెంట్‌కి దిగువన ఉన్నట్లయితే, విరామంలో (a; b) పైకి కుంభాకారంగా చెప్పబడుతుంది.

నిర్వచనం: ఫంక్షన్ యొక్క గ్రాఫ్ పైకి లేదా క్రిందికి కుంభాకారంగా ఉండే విరామాలను ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క కుంభాకార విరామాలు అంటారు.

y=f(x) ఫంక్షన్ యొక్క గ్రాఫ్ అయిన వక్రరేఖ యొక్క కుంభాకారం క్రిందికి లేదా పైకి దాని రెండవ ఉత్పన్నం యొక్క సంకేతం ద్వారా వర్గీకరించబడుతుంది: ఒక నిర్దిష్ట వ్యవధిలో f''(x) > 0, అప్పుడు వక్రత కుంభాకారంగా ఉంటుంది. ఈ విరామంలో క్రిందికి; అయితే f’’(x)< 0, то кривая выпукла вверх на этом промежутке.

నిర్వచనం: కుంభాకార విరామాలను వేరుచేసే ఫంక్షన్ y=f(x) యొక్క గ్రాఫ్‌పై ఒక పాయింట్ వ్యతిరేక దిశలుఈ గ్రాఫ్‌ని ఇన్‌ఫ్లెక్షన్ పాయింట్ అంటారు.

ఇన్‌ఫ్లెక్షన్ పాయింట్‌లు మాత్రమే ఉపయోగపడతాయి క్లిష్టమైన పాయింట్లు II రకం, అనగా. y = f(x) ఫంక్షన్ డెఫినిషన్ డొమైన్‌కు చెందిన పాయింట్లు, దీనిలో రెండవ ఉత్పన్నం f’’(x) అదృశ్యమవుతుంది లేదా నిలిపివేయబడుతుంది.

y = f(x) ఫంక్షన్ యొక్క గ్రాఫ్‌లో ఇన్‌ఫ్లెక్షన్ పాయింట్‌లను కనుగొనే నియమం

1. రెండవ ఉత్పన్నం f’’(x)ని కనుగొనండి.
2. y=f(x) ఫంక్షన్ యొక్క రెండవ రకం యొక్క క్లిష్టమైన పాయింట్లను కనుగొనండి, అనగా. f''(x) అదృశ్యమయ్యే లేదా నిలిపివేతను అనుభవించే పాయింట్.
3. f(x) ఫంక్షన్ యొక్క నిర్వచనం యొక్క డొమైన్‌ను గుర్తించిన క్లిష్టమైన పాయింట్‌లు విభజించే విరామంలో రెండవ ఉత్పన్నం f’’(x) యొక్క చిహ్నాన్ని పరిశోధించండి. క్రిటికల్ పాయింట్ x 0 వ్యతిరేక దిశల కుంభాకార విరామాలను వేరు చేస్తే, x 0 అనేది ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్‌ఫ్లెక్షన్ పాయింట్ యొక్క అబ్సిస్సా.
4. ఇన్ఫ్లెక్షన్ పాయింట్ల వద్ద ఫంక్షన్ విలువలను లెక్కించండి.

ఉదాహరణ 1. కింది వక్రత యొక్క కుంభాకార విరామాలు మరియు ఇన్‌ఫ్లెక్షన్ పాయింట్‌లను కనుగొనండి: f(x) = 6x 2 –x 3.
పరిష్కారం: f ‘(x) = 12x – 3x 2 , f ‘’(x) = 12 – 6xని కనుగొనండి.
12-6x=0 సమీకరణాన్ని పరిష్కరించడం ద్వారా రెండవ ఉత్పన్నం యొక్క క్లిష్టమైన పాయింట్లను కనుగొనండి. x=2.


f(2) = 6*2 2 – 2 3 = 16
జవాబు: ఫంక్షన్ x∈(2; +∞) కోసం పైకి కుంభాకారంగా ఉంటుంది; ఫంక్షన్ x∈(-∞; 2) వద్ద క్రిందికి కుంభాకారంగా ఉంటుంది; ఇన్ఫ్లెక్షన్ పాయింట్ (2;16) .

ఉదాహరణ 2. ఫంక్షన్ ఇన్‌ఫ్లెక్షన్ పాయింట్‌లను కలిగి ఉందా: f(x)=x 3 -6x 2 +2x-1

ఉదాహరణ 3. ఫంక్షన్ యొక్క గ్రాఫ్ కుంభాకారంగా మరియు వక్రంగా ఉండే విరామాలను కనుగొనండి: f(x)=x 3 -6x 2 +12x+4

ఒక ఫంక్షన్ యొక్క గ్రాఫ్ వై=f(x)అని పిలిచారు కుంభాకారవిరామంలో (ఎ; బి), ఈ విరామంలో దాని టాంజెంట్లలో దేనికైనా దిగువన ఉన్నట్లయితే.

ఒక ఫంక్షన్ యొక్క గ్రాఫ్ వై=f(x)అని పిలిచారు పుటాకారవిరామంలో (ఎ; బి), ఈ విరామంలో దాని టాంజెంట్లలో ఏదైనా పైన అది ఉన్నట్లయితే.

ఫిగర్ కుంభాకారంగా ఉండే వక్రరేఖను చూపుతుంది (ఎ; బి)మరియు పుటాకారము (బి; సి).

ఉదాహరణలు.

ఫంక్షన్ యొక్క గ్రాఫ్ ఉందో లేదో నిర్ధారించడానికి తగిన ప్రమాణాన్ని పరిశీలిద్దాం ఇచ్చిన విరామంకుంభాకార లేదా పుటాకార.

సిద్ధాంతం. వీలు వై=f(x)ద్వారా వేరు చేయవచ్చు (ఎ; బి). విరామం యొక్క అన్ని పాయింట్ల వద్ద ఉంటే (ఎ; బి)ఫంక్షన్ యొక్క రెండవ ఉత్పన్నం వై = f(x)ప్రతికూల, అనగా. f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 – పుటాకార.

రుజువు. అని ఖచ్చితంగా అనుకుందాం f""(x) < 0 и докажем, что график функции будет выпуклым.

గ్రాఫ్‌లోని ఫంక్షన్‌లను తీసుకుందాం y = f(x) ఏకపక్ష పాయింట్ M0 abscissa తో x 0 Î ( a; బి) మరియు పాయింట్ ద్వారా గీయండి M0టాంజెంట్. ఆమె సమీకరణం. ఫంక్షన్ యొక్క గ్రాఫ్ ఆన్‌లో ఉందని మనం తప్పక చూపించాలి (ఎ; బి)ఈ టాంజెంట్ క్రింద ఉంది, అనగా. అదే విలువ వద్ద xవక్రరేఖ యొక్క ఆర్డినేట్ y = f(x)టాంజెంట్ యొక్క ఆర్డినేట్ కంటే తక్కువగా ఉంటుంది.

కాబట్టి, వక్రరేఖ యొక్క సమీకరణం y = f(x). అబ్సిస్సాకు సంబంధించిన టాంజెంట్ యొక్క ఆర్డినేట్‌ను సూచిస్తాము x. అప్పుడు . కాబట్టి, అదే విలువకు కర్వ్ మరియు టాంజెంట్ యొక్క ఆర్డినేట్‌ల మధ్య వ్యత్యాసం xరెడీ .

తేడా f(x) – f(x 0)లాగ్రాంజ్ సిద్ధాంతం ప్రకారం రూపాంతరం చెందుతుంది, ఎక్కడ సిమధ్య xమరియు x 0.

ఈ విధంగా,

మేము మళ్లీ చతురస్రాకార బ్రాకెట్లలోని వ్యక్తీకరణకు Lagrange సిద్ధాంతాన్ని వర్తింపజేస్తాము: , ఎక్కడ c 1మధ్య c 0మరియు x 0. సిద్ధాంతం యొక్క షరతుల ప్రకారం f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.

అందువలన, వక్రరేఖపై ఏదైనా బిందువు అన్ని విలువలకు వక్రరేఖకు టాంజెంట్ క్రింద ఉంటుంది xమరియు x 0 Î ( a; బి), అంటే వక్రత కుంభాకారంగా ఉంటుంది. సిద్ధాంతం యొక్క రెండవ భాగం ఇదే విధంగా నిరూపించబడింది.

ఉదాహరణలు.

గ్రాఫ్ పాయింట్ నిరంతర ఫంక్షన్, పుటాకార భాగం నుండి దాని కుంభాకార భాగాన్ని వేరు చేయడం అంటారు ఇన్ఫ్లెక్షన్ పాయింట్.

సహజంగానే, ఇన్‌ఫ్లెక్షన్ పాయింట్ వద్ద, టాంజెంట్, అది ఉనికిలో ఉన్నట్లయితే, వక్రరేఖను కలుస్తుంది, ఎందుకంటే ఈ బిందువు యొక్క ఒక వైపున వక్రరేఖ టాంజెంట్ కింద ఉంటుంది మరియు మరొక వైపు - దాని పైన ఉంటుంది.

వాస్తవం కోసం తగిన పరిస్థితులను నిర్ధారిద్దాం ఇచ్చిన పాయింట్వక్రరేఖ అనేది ఇన్‌ఫ్లెక్షన్ పాయింట్.

సిద్ధాంతం. వక్రరేఖను సమీకరణం ద్వారా నిర్వచించనివ్వండి y = f(x). ఉంటే f ""(x 0) = 0 లేదా f ""(x 0) విలువ గుండా వెళుతున్నప్పుడు కూడా ఉనికిలో లేదు x = x 0ఉత్పన్నం f ""(x) గుర్తును మారుస్తుంది, ఆపై అబ్సిస్సాతో ఫంక్షన్ యొక్క గ్రాఫ్‌లోని పాయింట్ x = x 0ఒక ఇన్‌ఫ్లెక్షన్ పాయింట్ ఉంది.

రుజువు. వీలు f ""(x) < 0 при x < x 0మరియు f ""(x) > 0 వద్ద x > x 0. అప్పుడు వద్ద x < x 0వక్రరేఖ కుంభాకారంగా ఉంటుంది మరియు ఎప్పుడు x > x 0- పుటాకార. అందువలన, పాయింట్ ఎ, abscissa తో, వంపు మీద పడి x 0ఒక ఇన్‌ఫ్లెక్షన్ పాయింట్ ఉంది. రెండవ కేసును అదేవిధంగా పరిగణించవచ్చు, ఎప్పుడు f ""(x) > 0 వద్ద x < x 0మరియు f ""(x) < 0 при x > x 0.

అందువల్ల, రెండవ ఉత్పన్నం అదృశ్యమయ్యే లేదా ఉనికిలో లేని పాయింట్ల మధ్య మాత్రమే ఇన్‌ఫ్లెక్షన్ పాయింట్‌లను వెతకాలి.

ఉదాహరణలు.ఇన్ఫ్లెక్షన్ పాయింట్లను కనుగొని, కుంభాకార మరియు వక్రత యొక్క విరామాలను నిర్ణయించండి.

ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క లక్షణాలు

ఒక ఫంక్షన్‌ను అధ్యయనం చేస్తున్నప్పుడు, దాని గ్రాఫ్ యొక్క ఆకారాన్ని మూలం నుండి గ్రాఫ్ పాయింట్ యొక్క అపరిమిత దూరంలో ఏర్పాటు చేయడం ముఖ్యం.

ఒక ఫంక్షన్ యొక్క గ్రాఫ్, దాని వేరియబుల్ పాయింట్ అనంతానికి తీసివేయబడినప్పుడు, నిరవధికంగా ఒక నిర్దిష్ట సరళ రేఖకు చేరుకున్నప్పుడు ప్రత్యేక ఆసక్తి ఉంది.

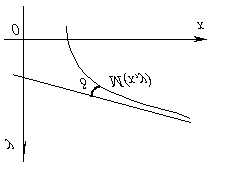
సరళ రేఖ అంటారు లక్షణం లేనిఫంక్షన్ గ్రాఫిక్స్ వై = f(x), వేరియబుల్ పాయింట్ నుండి దూరం ఉంటే ఎంపాయింట్‌ని తీసివేసేటప్పుడు ఈ లైన్‌కి గ్రాఫిక్స్ ఎంఅనంతం సున్నాకి మొగ్గు చూపుతుంది, అనగా. ఒక ఫంక్షన్ యొక్క గ్రాఫ్‌లోని ఒక బిందువు, అది అనంతం వైపు మొగ్గు చూపుతుంది కాబట్టి, నిరవధికంగా అసింప్టోట్‌ను చేరుకోవాలి.

ఒక వక్రత దాని యొక్క ఒక వైపున లేదా దానితో పాటు ఉండిపోయినప్పుడు దాని లక్షణాన్ని చేరుకోగలదు వివిధ వైపులా, అనంతమైన సెట్ఒకసారి అసింప్టోట్‌ను దాటడం మరియు ఒక వైపు నుండి మరొక వైపుకు వెళ్లడం.

మేము పాయింట్ నుండి దూరాన్ని d ద్వారా సూచిస్తే ఎంఆసింప్టోట్‌కి వక్రంగా ఉంటుంది, అప్పుడు పాయింట్ దూరంగా కదులుతున్నప్పుడు d సున్నాకి వస్తుందని స్పష్టంగా తెలుస్తుంది ఎంఅనంతం వరకు.

మేము నిలువు మరియు ఏటవాలు అసమానతల మధ్య మరింత తేడాను చూపుతాము.

నిలువు అసమానతలు

వద్ద లెట్ x→ x 0ఏ వైపు ఫంక్షన్ నుండి వై = f(x)సంపూర్ణ విలువలో అపరిమితంగా పెరుగుతుంది, అనగా. లేదా లేదా . అప్పుడు అసింప్టోట్ యొక్క నిర్వచనం నుండి అది సరళ రేఖను అనుసరిస్తుంది x = x 0అనేది ఒక లక్షణం. లైన్ అయితే వ్యతిరేకం కూడా స్పష్టంగా ఉంటుంది x = x 0ఒక లక్షణం, అనగా. .

అందువలన, ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క నిలువు లక్షణం y = f(x)ఉంటే సరళ రేఖ అంటారు f(x)కనీసం ఒక షరతు కింద → ∞ x→ x 0- 0 లేదా x → x 0 + 0, x = x 0

అందువల్ల, ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క నిలువు అసమానతలను కనుగొనడానికి వై = f(x)ఆ విలువలను కనుగొనాలి x = x 0, దీనిలో ఫంక్షన్ అనంతానికి వెళుతుంది (అనంతమైన నిలిపివేతకు గురవుతుంది). అప్పుడు నిలువు లక్షణముసమీకరణాన్ని కలిగి ఉంది x = x 0.

ఉదాహరణలు.

స్లాంట్ అసిమ్ప్టోట్స్

అసింప్టోట్ సరళ రేఖ కాబట్టి, వక్రరేఖ అయితే వై = f(x)వాలుగా ఉండే లక్షణం కలిగి ఉంటుంది, అప్పుడు దాని సమీకరణం ఉంటుంది వై = kx + బి. గుణకాలను కనుగొనడం మా పని కెమరియు బి.

సిద్ధాంతం. నేరుగా వై = kx + బివద్ద వాలుగా ఉండే లక్షణంగా పనిచేస్తుంది xఫంక్షన్ యొక్క గ్రాఫ్ కోసం → +∞ వై = f(x)అప్పుడు మరియు ఎప్పుడు మాత్రమే . ఇదే విధమైన ప్రకటన నిజం x → –∞.

రుజువు. వీలు ఎంపీ- విభాగం యొక్క పొడవు, దూరానికి సమానంపాయింట్ నుండి ఎంలక్షణము లేకుండా. షరతు ప్రకారం. అక్షానికి అసింప్టోట్ యొక్క వంపు కోణాన్ని φ ద్వారా సూచిస్తాము ఎద్దు. అప్పుడు నుండి ΔMNPదానిని అనుసరిస్తుంది. φ స్థిరమైన కోణం కనుక (φ ≠ π/2), అప్పుడు , కానీ

ఒక ఫంక్షన్‌ను అధ్యయనం చేసేటప్పుడు మరియు దాని గ్రాఫ్‌ను నిర్మించేటప్పుడు, ఒక దశలో మేము ఇన్‌ఫ్లెక్షన్ పాయింట్లు మరియు కుంభాకార విరామాలను నిర్ణయిస్తాము. ఈ డేటా, పెరుగుదల మరియు తగ్గుదల యొక్క విరామాలతో కలిసి, అధ్యయనంలో ఉన్న ఫంక్షన్ యొక్క గ్రాఫ్‌ను క్రమపద్ధతిలో సూచించడాన్ని సాధ్యం చేస్తుంది.

తదుపరి ప్రదర్శన మీరు కొంత ఆర్డర్ మరియు వివిధ రకాల వరకు చేయగలరని ఊహిస్తుంది.

పదార్థాన్ని అధ్యయనం చేయడం ప్రారంభిద్దాం అవసరమైన నిర్వచనాలుమరియు భావనలు. తరువాత, మేము ఒక నిర్దిష్ట విరామంలో ఫంక్షన్ యొక్క రెండవ ఉత్పన్నం యొక్క విలువ మరియు దాని కుంభాకార దిశ మధ్య కనెక్షన్‌ను వాయిస్ చేస్తాము. దీని తరువాత, మేము ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్ఫ్లెక్షన్ పాయింట్లను గుర్తించడానికి అనుమతించే పరిస్థితులకు వెళ్తాము. వచనం ప్రకారం మేము ఇస్తాము సాధారణ ఉదాహరణలువివరణాత్మక పరిష్కారాలతో.

పేజీ నావిగేషన్.

కుంభాకారము, ఒక ఫంక్షన్ యొక్క పుటాకారము, ఇన్ఫ్లెక్షన్ పాయింట్.

నిర్వచనం.

కుంభాకార క్రిందికిఇంటర్వెల్ Xలో, దాని గ్రాఫ్ దాని టాంజెంట్ కంటే తక్కువ కాకుండా X విరామం యొక్క ఏ బిందువులోనైనా ఉన్నట్లయితే.

నిర్వచనం.

భేదం చేయాల్సిన ఫంక్షన్ అంటారు పైకి కుంభాకారంగా ఉంటుందిఇంటర్వెల్ Xలో, దాని గ్రాఫ్ X ఇంటర్వెల్‌లో ఏ సమయంలోనైనా దానికి టాంజెంట్ కంటే ఎక్కువగా ఉండకపోతే.

పైకి కుంభాకార ఫంక్షన్ తరచుగా అంటారు కుంభాకార, మరియు కుంభాకార క్రిందికి - పుటాకార.

ఈ నిర్వచనాలను వివరించే డ్రాయింగ్‌ను చూడండి.

నిర్వచనం.

పాయింట్ అంటారు ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్ఫ్లెక్షన్ పాయింట్ y=f(x) ఒక నిర్దిష్ట బిందువు వద్ద ఫంక్షన్ యొక్క గ్రాఫ్‌కు టాంజెంట్ ఉంటే (ఇది Oy అక్షానికి సమాంతరంగా ఉంటుంది) మరియు పాయింట్ M యొక్క ఎడమ మరియు కుడి వైపున ఉన్న పాయింట్ యొక్క పొరుగు ప్రాంతం ఉంటే ఫంక్షన్ యొక్క గ్రాఫ్ కుంభాకారం యొక్క వివిధ దిశలను కలిగి ఉంటుంది.

మరో మాటలో చెప్పాలంటే, ఈ పాయింట్ వద్ద టాంజెంట్ ఉంటే మరియు ఫంక్షన్ యొక్క గ్రాఫ్ కుంభాకార దిశను మార్చి, దాని గుండా వెళితే, పాయింట్ Mని ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క ఇన్ఫ్లెక్షన్ పాయింట్ అంటారు.

అవసరమైతే, నాన్-వర్టికల్ మరియు వర్టికల్ టాంజెంట్ ఉనికి కోసం పరిస్థితులను గుర్తుకు తెచ్చుకోవడానికి విభాగాన్ని చూడండి.

దిగువ బొమ్మ ఇన్‌ఫ్లెక్షన్ పాయింట్‌ల యొక్క కొన్ని ఉదాహరణలను చూపుతుంది (ఎరుపు చుక్కలతో గుర్తించబడింది). కొన్ని ఫంక్షన్‌లకు ఇన్‌ఫ్లెక్షన్ పాయింట్లు ఉండకపోవచ్చని, మరికొన్ని ఒకటి, అనేకం లేదా అనంతమైన ఇన్‌ఫ్లెక్షన్ పాయింట్‌లను కలిగి ఉండవచ్చని గమనించండి.

ఫంక్షన్ యొక్క కుంభాకార విరామాలను కనుగొనడం.

మేము ఒక ఫంక్షన్ యొక్క కుంభాకార విరామాలను నిర్ణయించడానికి అనుమతించే సిద్ధాంతాన్ని రూపొందిద్దాం.

సిద్ధాంతం.

y=f(x) ఫంక్షన్ విరామం Xపై పరిమిత రెండవ ఉత్పన్నాన్ని కలిగి ఉంటే మరియు అసమానత కలిగి ఉంటే (), అప్పుడు ఫంక్షన్ యొక్క గ్రాఫ్ X ద్వారా క్రిందికి (పైకి) మళ్లించబడిన కుంభాకారాన్ని కలిగి ఉంటుంది.

ఈ సిద్ధాంతం ఒక ఫంక్షన్ యొక్క పుటాకార మరియు కుంభాకారాన్ని కనుగొనడానికి మిమ్మల్ని అనుమతిస్తుంది

y=f(x) ఫంక్షన్ నిర్వచించబడిన మరియు రెండవ ఉత్పన్నం లేని పాయింట్లు పుటాకార మరియు కుంభాకార విరామాలలో చేర్చబడతాయని గమనించాలి.

దీన్ని ఒక ఉదాహరణతో అర్థం చేసుకుందాం.

ఉదాహరణ.

ఫంక్షన్ యొక్క గ్రాఫ్ ఉన్న విరామాలను కనుగొనండి ఒక కుంభాకారాన్ని పైకి మరియు ఒక కుంభాకారాన్ని క్రిందికి నిర్దేశిస్తుంది.

పరిష్కారం.

ఫంక్షన్ యొక్క డొమైన్ మొత్తం సెట్ వాస్తవ సంఖ్యలు.

రెండవ ఉత్పన్నాన్ని కనుగొనండి.

రెండవ ఉత్పన్నం యొక్క నిర్వచనం యొక్క డొమైన్ అసలు ఫంక్షన్ యొక్క నిర్వచనం యొక్క డొమైన్‌తో సమానంగా ఉంటుంది, కాబట్టి, పుటాకార మరియు కుంభాకార విరామాలను తెలుసుకోవడానికి, దాన్ని పరిష్కరించడానికి మరియు తదనుగుణంగా సరిపోతుంది.

కాబట్టి, ఫంక్షన్ విరామంపై క్రిందికి కుంభాకారంగా ఉంటుంది మరియు విరామంపై కుంభాకారంగా ఉంటుంది.

గ్రాఫిక్ ఇలస్ట్రేషన్.

కుంభాకార విరామంలో ఫంక్షన్ గ్రాఫ్ యొక్క భాగం నీలం రంగులో మరియు పుటాకార విరామంలో - ఎరుపు రంగులో చూపబడింది.

ఇప్పుడు రెండవ ఉత్పన్నం యొక్క నిర్వచనం యొక్క డొమైన్ ఫంక్షన్ యొక్క నిర్వచనం యొక్క డొమైన్‌తో ఏకీభవించనప్పుడు ఒక ఉదాహరణను పరిశీలిద్దాం. ఈ సందర్భంలో, మేము ఇప్పటికే గుర్తించినట్లుగా, పరిమిత రెండవ ఉత్పన్నం లేని నిర్వచనం యొక్క డొమైన్ యొక్క పాయింట్లు కుంభాకార మరియు (లేదా) పుటాకార వ్యవధిలో చేర్చబడాలి.

ఉదాహరణ.

ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క కుంభాకార మరియు పుటాకార విరామాలను కనుగొనండి.

పరిష్కారం.

ఫంక్షన్ యొక్క డొమైన్‌తో ప్రారంభిద్దాం:

రెండవ ఉత్పన్నాన్ని కనుగొనండి:

రెండవ ఉత్పన్నం యొక్క నిర్వచనం యొక్క డొమైన్ సెట్ . మీరు చూడగలిగినట్లుగా, x=0 అసలు ఫంక్షన్ యొక్క డొమైన్‌కు చెందినది, కానీ రెండవ ఉత్పన్నం యొక్క డొమైన్‌కు చెందినది కాదు. ఈ పాయింట్ గురించి మర్చిపోవద్దు;

ఇప్పుడు మేము అసలు ఫంక్షన్ యొక్క నిర్వచనం యొక్క డొమైన్‌పై అసమానతలను పరిష్కరిస్తాము. దరఖాస్తు చేద్దాం. వ్యక్తీకరణ యొక్క న్యూమరేటర్ వద్ద సున్నాకి వెళుతుంది లేదా , హారం – x = 0 లేదా x = 1 వద్ద. మేము ఈ పాయింట్లను సంఖ్యా రేఖపై క్రమపద్ధతిలో ప్లాట్ చేస్తాము మరియు అసలు ఫంక్షన్ యొక్క నిర్వచనం యొక్క డొమైన్‌లో చేర్చబడిన ప్రతి అంతరాలలో వ్యక్తీకరణ యొక్క చిహ్నాన్ని కనుగొంటాము (ఇది తక్కువ సంఖ్య రేఖపై షేడెడ్ ప్రాంతంగా చూపబడుతుంది). సానుకూల విలువ కోసం మేము ప్లస్ గుర్తును ఉంచుతాము, ప్రతికూల విలువ కోసం మేము మైనస్ గుర్తును ఉంచుతాము.

ఈ విధంగా,

మరియు

కాబట్టి, x=0 పాయింట్‌ని చేర్చడం ద్వారా, మనకు సమాధానం వస్తుంది.

వద్ద ఫంక్షన్ యొక్క గ్రాఫ్ ఒక కుంభాకారాన్ని క్రిందికి మళ్ళించబడుతుంది - కుంభాకారం పైకి మళ్ళించబడింది.

గ్రాఫిక్ ఇలస్ట్రేషన్.

కుంభాకార విరామంపై ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క భాగం నీలం రంగులో, పుటాకార వ్యవధిలో చిత్రీకరించబడింది - ఎరుపు రంగులో, నలుపు చుక్కల రేఖ నిలువు అసమానత.

విక్షేపం కోసం అవసరమైన మరియు తగినంత పరిస్థితులు.

విక్షేపం కోసం అవసరమైన పరిస్థితి.

సూత్రీకరించుదాం అవసరమైన పరిస్థితివిభక్తిఫంక్షన్ గ్రాఫిక్స్.

y=f(x) ఫంక్షన్ యొక్క గ్రాఫ్ ఒక బిందువు వద్ద విభక్తిని కలిగి ఉండనివ్వండి మరియు నిరంతర రెండవ ఉత్పన్నాన్ని కలిగి ఉంటుంది, అప్పుడు సమానత్వం ఉంటుంది.

ఈ షరతు నుండి, ఫంక్షన్ యొక్క రెండవ ఉత్పన్నం అదృశ్యమయ్యే వాటిలో ఇన్‌ఫ్లెక్షన్ పాయింట్ల యొక్క అబ్సిస్సాను వెతకాలి. కానీ, ఈ పరిస్థితి సరిపోదు, అంటే, రెండవ ఉత్పన్నం సున్నాకి సమానమైన అన్ని విలువలు ఇన్‌ఫ్లెక్షన్ పాయింట్ల అబ్సిసాస్ కాదు.

ఇన్‌ఫ్లెక్షన్ పాయింట్ యొక్క నిర్వచనానికి టాంజెంట్ లైన్ లేదా నిలువుగా ఉండే ఉనికి అవసరమని కూడా గమనించాలి. దీని అర్థం ఏమిటి? మరియు దీని అర్థం క్రింది విధంగా ఉంటుంది: ఇన్‌ఫ్లెక్షన్ పాయింట్ల యొక్క అబ్సిసాస్ ఫంక్షన్ యొక్క నిర్వచనం యొక్క డొమైన్ నుండి ప్రతిదీ కావచ్చు మరియు . ఇవి సాధారణంగా మొదటి ఉత్పన్నం యొక్క హారం అదృశ్యమయ్యే పాయింట్లు.

విక్షేపం కోసం మొదటి తగినంత షరతు.

ఇన్ఫ్లెక్షన్ పాయింట్ల అబ్సిసాస్ కనుగొనబడిన తర్వాత, మీరు ఉపయోగించాలి విక్షేపం కోసం మొదటి తగినంత షరతుఫంక్షన్ గ్రాఫిక్స్.

ఫంక్షన్ y=f(x) పాయింట్ వద్ద నిరంతరంగా ఉండనివ్వండి, దాని వద్ద టాంజెంట్ (బహుశా నిలువుగా) ఉండనివ్వండి మరియు ఈ ఫంక్షన్ పాయింట్ యొక్క కొంత పొరుగున రెండవ ఉత్పన్నాన్ని కలిగి ఉండనివ్వండి. అప్పుడు, ఈ పొరుగు ప్రాంతంలో ఎడమ మరియు కుడి వైపున ఉంటే, రెండవ ఉత్పన్నం కలిగి ఉంటుంది వివిధ సంకేతాలు, అప్పుడు ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్ఫ్లెక్షన్ పాయింట్.

మీరు మొదటి చూడగలరు గా తగినంత పరిస్థితిపాయింట్ వద్ద రెండవ ఉత్పన్నం యొక్క ఉనికి అవసరం లేదు, కానీ పాయింట్ యొక్క పొరుగు ప్రాంతంలో దాని ఉనికి అవసరం.

ఇప్పుడు మొత్తం సమాచారాన్ని అల్గోరిథం రూపంలో సంగ్రహిద్దాం.

ఫంక్షన్ యొక్క ఇన్‌ఫ్లెక్షన్ పాయింట్‌లను కనుగొనడానికి అల్గారిథమ్.

మేము ఫంక్షన్ గ్రాఫ్ (లేదా మరియు ) మరియు రెండవ ఉత్పన్న మార్పుల సంకేతాన్ని దాటడం ద్వారా కనుగొనండి. అటువంటి విలువలు ఇన్‌ఫ్లెక్షన్ పాయింట్ల యొక్క అబ్సిస్సాగా ఉంటాయి మరియు సంబంధిత పాయింట్లు ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్‌ఫ్లెక్షన్ పాయింట్‌లుగా ఉంటాయి.

స్పష్టీకరణ కోసం ఇన్‌ఫ్లెక్షన్ పాయింట్‌లను కనుగొనే రెండు ఉదాహరణలను చూద్దాం.

ఉదాహరణ.

ఒక ఫంక్షన్ యొక్క గ్రాఫ్ యొక్క కుంభాకారం మరియు పుటాకారత యొక్క ఇన్ఫ్లెక్షన్ పాయింట్లు మరియు విరామాలను కనుగొనండి .

పరిష్కారం.

ఫంక్షన్ డొమైన్ అనేది వాస్తవ సంఖ్యల మొత్తం సెట్.

మొదటి ఉత్పన్నాన్ని కనుగొనండి:

మొదటి ఉత్పన్నం యొక్క నిర్వచనం యొక్క డొమైన్ కూడా వాస్తవ సంఖ్యల మొత్తం సెట్, కాబట్టి సమానతలు మరియు దేనికోసం నెరవేరలేదు.

రెండవ ఉత్పన్నాన్ని కనుగొనండి:

ఆర్గ్యుమెంట్ x రెండవ ఉత్పన్నం ఏ విలువలతో సున్నాకి వెళ్తుందో తెలుసుకుందాం:

అందువలన, సాధ్యమయ్యే ఇన్ఫ్లెక్షన్ పాయింట్ల అబ్సిస్సాస్ x=-2 మరియు x=3.

ఇన్‌ఫ్లెక్షన్ యొక్క తగినంత సంకేతాన్ని ఉపయోగించి, ఈ పాయింట్‌లలో రెండవ డెరివేటివ్ మార్పుల సంకేతం ఇప్పుడు తనిఖీ చేయవలసి ఉంది. దీన్ని చేయడానికి, సంఖ్య అక్షంపై x=-2 మరియు x=3 పాయింట్లను ప్లాట్ చేయండి మరియు, సాధారణ విరామ పద్ధతి, మేము ప్రతి విరామంలో రెండవ ఉత్పన్నం యొక్క సంకేతాలను ఉంచుతాము. ప్రతి విరామం కింద, ఫంక్షన్ గ్రాఫ్ యొక్క కుంభాకార దిశ ఆర్క్‌లతో క్రమపద్ధతిలో చూపబడుతుంది.

రెండవ ఉత్పన్నం చిహ్నాన్ని ప్లస్ నుండి మైనస్‌కి మారుస్తుంది, x=-2 పాయింట్ ద్వారా ఎడమ నుండి కుడికి వెళుతుంది మరియు గుర్తును మైనస్ నుండి ప్లస్‌కి మారుస్తుంది, x=3 గుండా వెళుతుంది. కాబట్టి, x=-2 మరియు x=3 రెండూ ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్‌ఫ్లెక్షన్ పాయింట్‌ల అబ్సిసాస్‌లు. అవి గ్రాఫ్ పాయింట్లకు అనుగుణంగా ఉంటాయి మరియు .

సంఖ్య రేఖను మరియు దాని వ్యవధిలో రెండవ ఉత్పన్నం యొక్క సంకేతాలను మరొకసారి పరిశీలించి, కుంభాకారం మరియు పుటాకార విరామాల గురించి మనం తీర్మానాలు చేయవచ్చు. ఫంక్షన్ యొక్క గ్రాఫ్ విరామంపై కుంభాకారంగా ఉంటుంది మరియు విరామాలపై పుటాకారంగా ఉంటుంది మరియు .

గ్రాఫిక్ ఇలస్ట్రేషన్.

కుంభాకార విరామంపై ఫంక్షన్ గ్రాఫ్ యొక్క భాగం నీలం రంగులో, పుటాకార విరామంలో - ఎరుపు రంగులో చూపబడింది మరియు ఇన్ఫ్లెక్షన్ పాయింట్లు నల్ల చుక్కలుగా చూపబడతాయి.

ఉదాహరణ.

ఫంక్షన్ గ్రాఫ్ యొక్క అన్ని ఇన్ఫ్లెక్షన్ పాయింట్ల అబ్సిస్సాను కనుగొనండి .

పరిష్కారం.

ఈ ఫంక్షన్ యొక్క నిర్వచనం యొక్క డొమైన్ వాస్తవ సంఖ్యల మొత్తం సెట్.

ఉత్పన్నం కనుక్కోండి.

మొదటి ఉత్పన్నం, అసలు ఫంక్షన్ వలె కాకుండా, x=3 వద్ద నిర్వచించబడలేదు. కానీ మరియు . కాబట్టి, abscissa x=3 పాయింట్ వద్ద అసలు ఫంక్షన్ యొక్క గ్రాఫ్‌కు నిలువు టాంజెంట్ ఉంటుంది. అందువలన, x=3 అనేది ఫంక్షన్ గ్రాఫ్ యొక్క ఇన్‌ఫ్లెక్షన్ పాయింట్ యొక్క అబ్సిస్సా కావచ్చు.

మేము రెండవ ఉత్పన్నం, దాని నిర్వచనం యొక్క డొమైన్ మరియు అది అదృశ్యమయ్యే పాయింట్లను కనుగొంటాము:

మేము ఇన్‌ఫ్లెక్షన్ పాయింట్‌ల యొక్క మరో రెండు అబ్సిసాస్‌లను పొందాము. మేము మూడు పాయింట్లను సంఖ్య రేఖపై గుర్తించాము మరియు ఫలిత విరామాలలో ప్రతి రెండవ ఉత్పన్నం యొక్క చిహ్నాన్ని నిర్ణయిస్తాము.

ప్రతి పాయింట్ గుండా వెళుతున్నప్పుడు రెండవ ఉత్పన్న మార్పుల సంకేతం, కాబట్టి, అవన్నీ ఇన్‌ఫ్లెక్షన్ పాయింట్ల అబ్సిసాస్.

సూచనలు

పాయింట్లు విభక్తి విధులుతప్పనిసరిగా దాని నిర్వచనం యొక్క డొమైన్‌కు చెందినదిగా ఉండాలి, ఇది ముందుగా కనుగొనబడాలి. షెడ్యూల్ విధులుఅనేది నిరంతరాయంగా లేదా విరామాలు కలిగి ఉండే పంక్తి, మార్పు లేకుండా తగ్గడం లేదా పెంచడం, కనిష్టంగా లేదా గరిష్టంగా ఉంటుంది పాయింట్లు(లక్షణాలు), కుంభాకారంగా లేదా పుటాకారంగా ఉంటుంది. చివరి రెండు రాష్ట్రాలలో ఒక పదునైన మార్పును ఇన్ఫ్లెక్షన్ పాయింట్ అంటారు.

ఉనికికి అవసరమైన పరిస్థితి విభక్తి విధులుసున్నాకి రెండవ సమానత్వంలో ఉంటుంది. ఈ విధంగా, ఫంక్షన్‌ను రెండుసార్లు వేరు చేయడం ద్వారా మరియు ఫలిత వ్యక్తీకరణను సున్నాకి సమం చేయడం ద్వారా, సాధ్యమయ్యే పాయింట్ల అబ్సిస్సాను మనం కనుగొనవచ్చు. విభక్తి.

ఈ పరిస్థితి గ్రాఫ్ యొక్క కుంభాకార మరియు పుటాకార లక్షణాల నిర్వచనం నుండి అనుసరిస్తుంది విధులు, అనగా ప్రతికూల మరియు సానుకూల విలువరెండవ ఉత్పన్నం. పాయింట్ వద్ద విభక్తి ఆకస్మిక మార్పుఈ లక్షణాలు, అంటే ఉత్పన్నం సున్నా మార్కును దాటిపోతుంది. అయినప్పటికీ, సున్నాకి సమానంగా ఉండటం అనేది ఇన్‌ఫ్లెక్షన్‌ని సూచించడానికి ఇంకా సరిపోదు.

మునుపటి దశలో కనిపించే అబ్సిస్సా పాయింట్‌కి చెందిన రెండు తగినంత షరతులు ఉన్నాయి విభక్తి:ఈ పాయింట్ ద్వారా మీరు టాంజెంట్‌ని గీయవచ్చు విధులు. రెండవ ఉత్పన్నం ఊహించిన దాని యొక్క కుడి మరియు ఎడమకు వేర్వేరు సంకేతాలను కలిగి ఉంటుంది పాయింట్లు విభక్తి. అందువలన, పాయింట్ వద్ద దాని ఉనికి అవసరం లేదు అది రెండవ ఉత్పన్నం మారుతుందని నిర్ధారించడానికి విధులుసున్నాకి సమానం, మరియు మూడవది కాదు.

పరిష్కారం: కనుగొనండి. IN ఈ విషయంలోఎటువంటి పరిమితులు లేవు, కాబట్టి, ఇది వాస్తవ సంఖ్యల మొత్తం స్థలం. మొదటి ఉత్పన్నాన్ని లెక్కించండి: y' = 3 ∛(x - 5) + (3 x + 3)/∛(x - 5)².

దయచేసి గమనించండి . దీని నుండి ఉత్పన్నం యొక్క నిర్వచనం యొక్క డొమైన్ పరిమితం చేయబడింది. పాయింట్ x = 5 పంక్చర్ చేయబడింది, అంటే ఒక టాంజెంట్ దాని గుండా వెళుతుంది, ఇది పాక్షికంగా సమృద్ధి యొక్క మొదటి సంకేతానికి అనుగుణంగా ఉంటుంది విభక్తి.

x → 5 – 0 మరియు x → 5 + 0 కోసం ఫలిత వ్యక్తీకరణను నిర్ణయించండి. అవి -∞ మరియు +∞కి సమానం. నిలువు టాంజెంట్ x=5 పాయింట్ గుండా వెళుతుందని మీరు నిరూపించారు. ఈ పాయింట్ ఒక పాయింట్‌గా మారవచ్చు విభక్తి, అయితే ముందుగా రెండవ ఉత్పన్నాన్ని లెక్కించండి: Y'' = 1/∛(x - 5)² + 3/∛(x - 5)² – 2/3 (3 x + 3)/∛(x - 5)^5 = (2 x – 22)/∛(x - 5)^5.

మీరు ఇప్పటికే x = 5 పాయింట్‌ని పరిగణనలోకి తీసుకున్నందున హారంను వదిలివేయండి. 2 x – 22 = 0 సమీకరణాన్ని పరిష్కరించండి. దీనికి ఒకే మూలం x = 11 ఉంటుంది. దానిని నిర్ధారించడం చివరి దశ పాయింట్లు x=5 మరియు x=11 పాయింట్లు విభక్తి. వారి సమీపంలోని రెండవ ఉత్పన్నం యొక్క ప్రవర్తనను విశ్లేషించండి. సహజంగానే, x = 5 పాయింట్ వద్ద ఇది గుర్తును “+” నుండి “-”కి మారుస్తుంది మరియు x = 11 పాయింట్ వద్ద – వైస్ వెర్సా. ముగింపు: రెండూ పాయింట్లుపాయింట్లు ఉంటాయి విభక్తి. మొదటి తగినంత షరతు సంతృప్తి చెందింది.