Definisjon. Hvis funksjonen f(x) er definert på intervallet [ a, b], er kontinuerlig i hvert punkt i intervallet ( a, b), på et tidspunkt en kontinuerlig til høyre, ved punktet b er kontinuerlig til venstre, så sier vi at funksjonen f(x) kontinuerlig på segmentet [a, b].
Med andre ord funksjonen f(x) er kontinuerlig i intervallet [ a, b], hvis tre betingelser er oppfylt:
1) "x 0 Î( a, b): f(x) = f(x 0);
2) f(x) = f(en);
3) f(x) = f(b).
For funksjoner som er kontinuerlige på et intervall tar vi for oss noen egenskaper, som vi formulerer i form av følgende teoremer, uten å utføre bevis.
Teorem 1. Hvis funksjonen f(x) er kontinuerlig i intervallet [ a, b], så når den sine minimums- og maksimumsverdier på dette segmentet.
Denne teoremet sier (fig. 1.15) at på segmentet [ a, b] det er et slikt poeng x 1 det f(x 1) £ f(x) for noen x fra [ a, b] og at det er et poeng x 2 (x 2 О[ a, b]) slik at " xÎ[ a, b] (f(x 2)³ f(x)).
Betydning f(x 1) er den største for en gitt funksjon på [ a, b], A f(x 2) – den minste. La oss betegne: f(x 1) = M, f(x 2) =m. Siden for f(x) ulikheten gjelder: " xÎ[ a, b] m£ f(x) £ M, så får vi følgende konsekvens fra setning 1.
Konsekvens. Hvis funksjonen f(x) er kontinuerlig på et intervall, så er det avgrenset på dette intervallet.
Teorem 2. Hvis funksjonen f(x) er kontinuerlig i intervallet [ a,b] og i enden av segmentet tar verdier av forskjellige tegn, så er det et slikt internt punkt x 0 segment [ a, b], der funksjonen blir til 0, dvs. $ x 0 Î ( a, b) (f(x 0) = 0).
Denne teoremet sier at grafen til en funksjon y = f(x), kontinuerlig i intervallet [ a, b], skjærer aksen Okse minst én gang hvis verdiene f(en) Og f(b) har motsatte tegn. Så, (fig. 1.16) f(en) > 0, f(b) < 0 и функция f(x) blir 0 ved poeng x 1 , x 2 , x 3 .
Teorem 3. La funksjonen f(x) er kontinuerlig i intervallet [ a, b], f(en) = EN, f(b) = B Og EN¹ B. (Fig. 1.17). Deretter for et hvilket som helst tall C, vedlagt mellom tallene EN Og B, det er et slikt indre punkt x 0 segment [ a, b], Hva f(x 0) = C.
Konsekvens. Hvis funksjonen f(x) er kontinuerlig i intervallet [ a, b], m – minste verdi f(x), M – høyeste verdi funksjoner f(x) på segmentet [ a, b], så tar funksjonen (minst én gang) en hvilken som helst verdi m, konkludert mellom m Og M, og derfor segmentet [ m, M] er settet med alle funksjonsverdier f(x) på segmentet [ a, b].
Merk at hvis en funksjon er kontinuerlig på intervallet ( a, b) eller har på segmentet [ a, b] diskontinuitetspoeng, så slutter teoremene 1, 2, 3 for en slik funksjon å være sann.
Avslutningsvis vurdere teoremet om eksistensen av en invers funksjon.
La oss huske at med intervall mener vi et segment eller et intervall, eller et halvt intervall, endelig eller uendelig.
 |
Teorem 4. La f(x) er kontinuerlig i intervallet X, øker (eller reduseres) med X og har en rekke verdier Y. Så for funksjonen y = f(x) det er en invers funksjon x= j(y), definert på intervallet Y, kontinuerlig og økende (eller avtagende) med Y med flere betydninger X.
Kommentar. La funksjonen x= j(y) er det motsatte av funksjonen f(x). Siden argumentet vanligvis er betegnet med x, og funksjonen gjennom y, så skriver vi invers funksjon som y=j(x).
Eksempel 1. Funksjon y = x 2 (fig. 1.8, a) på settet X= en, b[ og er kontinuerlig på hvert punkt i dette intervallet. Da kalles det kontinuerlig i intervallet ] en, b[ . Konseptet med kontinuitet til en funksjon på intervaller av formen ]- ∞ er definert på samme måte, b[ , ]en, + ∞[ , ]- ∞, + ∞[ . La nå funksjonen y = f(x) definert på intervallet [ en, b] . Forskjellen mellom et intervall og et segment: grensepunktene til et intervall er ikke inkludert i intervallet, men grensepunktene til et segment er inkludert i segmentet. Her bør vi nevne den såkalte ensidige kontinuiteten: ved punktet en, gjenværende på segmentet [ en, b] , kan vi bare nærme oss fra høyre, og til poenget b- bare til venstre. Funksjonen sies å være kontinuerlig i intervallet [ en, b] hvis den er kontinuerlig i alt interne punkter av dette segmentet, er kontinuerlig til høyre på punktet en og blir stående kontinuerlig på punktet b.
Et eksempel på en kontinuerlig funksjon kan være hvilken som helst av de elementære funksjonene. Hver elementær funksjon er kontinuerlig på ethvert intervall den er definert på. For eksempel er funksjonene og kontinuerlige på ethvert intervall [ en, b], funksjonen er kontinuerlig i intervallet [ 0 , b] , er funksjonen kontinuerlig på ethvert segment som ikke inneholder et punkt en = 2 .
Eksempel 4. Undersøk funksjonen for kontinuitet.
Løsning. La oss sjekke den første betingelsen. Funksjonen er ikke definert på punktene - 3 og 3. Minst en av betingelsene for funksjonens kontinuitet langs hele tallinjen er ikke oppfylt. Derfor denne funksjonen er kontinuerlig på intervaller
.Eksempel 5. Bestem hvilken verdi av parameteren en kontinuerlig hele veien definisjonsdomene funksjon 
Løsning.
La oss finne den høyre grensen på:
![]() .
.
Selvfølgelig, verdien på punktet x= 2 skal være lik øks :
![]()
en = 1,5 .
Eksempel 6. Bestem hvilke parameterverdier en Og b kontinuerlig hele veien definisjonsdomene funksjon 
Løsning.
La oss finne grensen på venstre side av funksjonen på punktet:
![]() .
.
Derfor må verdien på punktet være 1:
La oss finne venstrefunksjonen på punktet:
Selvfølgelig skal verdien av funksjonen på et punkt være lik:
Svar: funksjonen er kontinuerlig over hele definisjonsdomenet når en = 1; b = -3 .
Grunnleggende egenskaper ved kontinuerlige funksjoner
Matematikk kom til begrepet en kontinuerlig funksjon ved å studere først og fremst ulike bevegelseslover. Rom og tid er uendelig, og avhengighet, for eksempel, veier s fra tid t, uttrykt ved lov s = f(t) , gir et eksempel på en kontinuerlig funksjoner f(t). Temperaturen på det oppvarmede vannet endres også kontinuerlig, det er også en kontinuerlig funksjon av tiden: T = f(t) .
I matematisk analyse noen egenskaper er påvist kontinuerlige funksjoner. La oss presentere de viktigste av disse egenskapene.
1. Hvis en funksjon som er kontinuerlig på et intervall antar verdier av forskjellige fortegn ved slutten av intervallet, vil den på et tidspunkt i dette intervallet anta verdien lik null. I en mer formell uttalelse er denne egenskapen gitt i et teorem kjent som det første Bolzano-Cauchy-teoremet.
2. Funksjon f(x), kontinuerlig i intervallet [ en, b] , tar alle mellomverdier mellom verdiene ved endepunktene, det vil si mellom f(en) Og f(b). I en mer formell uttalelse er denne egenskapen gitt i et teorem kjent som det andre Bolzano-Cauchy-teoremet.
Kontinuitet til en funksjon på et intervall
| Parameternavn | Betydning |
| Artikkel emne: | Kontinuitet til en funksjon på et intervall |
| Rubrikk (tematisk kategori) | Matematikk |
Definisjon. En funksjon kalles vanligvis kontinuerlig på et intervall hvis den er kontinuerlig på hvert punkt i dette intervallet.
Hvis funksjonen er definert når X=EN og hvori f(X) = f(EN),
så sier de det f(X) på punktet og er kontinuerlig til høyre. På samme måte hvis f(X) = f(b), så sier de det på det tidspunktet b denne funksjonen venstre kontinuerlig.
Definisjon. En funksjon kalles vanligvis kontinuerlig på intervallet [ en, b], hvis den er kontinuerlig ved hvert punkt (på punktet EN kontinuerlig til høyre, ved punktet b– kontinuerlig til venstre).
Høyeste verdi funksjoner på = f(x) på segmentet [ en, b f(x 1) det f(x) £ f(x 1) for alle X Î [ en, b].
Laveste verdi funksjoner på = f(x) på segmentet [ en, b] er det vanlig å kalle dette sin betydning f(x 2) det f(x) ³ f(x 2) for alle X Î [ en, b].
Funksjoner som er kontinuerlige på et intervall har en rekke viktige egenskaper, som uttrykkes ved følgende teoremer.
Teorem 3.3.1. En funksjon kontinuerlig i intervallet [ en, b], når minimumsverdien på den m og størst verdi M, det vil si at det er slike punkter x 1 og x 2 av dette segmentet, det f(x 1) = m, f(x 2) = M.
Teoremet har en enkel geometrisk betydning (se fig. 2).
 |
Teorem 3.3.2. Hvis funksjonen på = f(x) er kontinuerlig i intervallet [ en, b] og tar i enden ulik verdi f(EN) = A, f(b) = B, A ¹ B, så uansett hva tallet C er mellom A og B, vil det være et punkt Med Î [ en, b] slik at f(Med) = S.
Geometrisk betydning Teoremet er illustrert i fig. 3. Enhver rett linje på= C, hvor A< C < B (или A >C > B), skjærer grafen til funksjonen på = f(x).
Konsekvens. Hvis en funksjon er kontinuerlig på et segment og tar på seg verdier av forskjellige fortegn i endene, så er det på dette segmentet minst ett punkt der funksjonen forsvinner.
Den geometriske betydningen av konsekvensen er illustrert i fig. 4.

Spørsmål for selvkontroll
1. Hvilken funksjon kalles vanligvis kontinuerlig i et punkt?
2. Gi en annen ekvivalent definisjon når det gjelder inkrement av funksjon og argumenter.
3. Hva kan sies om sum, forskjell, produkt og kvotient av to kontinuerlige funksjoner?
4. For hvilke verdier av argumentet er hele rasjonelle og brøk-rasjonelle funksjoner kontinuerlige?
5. Når er en kompleks funksjon kontinuerlig i et punkt?
6. Hva kalles bruddpunktet for funksjoner?
7. Hvilke punkter kalles diskontinuitetspunkter av den første typen?
8. Hvilken mengde kalles vanligvis et funksjonshopp?
9. Forklar begrepet "flyttbart diskontinuitetspunkt". Gi eksempler.
10. Hvilke punkter kalles diskontinuitetspunkter av den andre typen? Gi eksempler.
11. Forklar begrepene: «kontinuitet på et intervall», «kontinuitet til høyre», «kontinuitet til venstre», «kontinuitet på et segment».
12. Definer de største og minste verdiene av funksjoner.
13. Formuler et teorem om sammenhengen mellom kontinuitet på et segment og de største og minste verdiene til en funksjon. Forklar det med en tegning.
14. Formuler et teorem om sammenhengen mellom funksjonskontinuiteten på et intervall og intervallet av funksjonsverdier. Illustrer dens geometriske betydning i figuren.
15. Gi en konsekvens av teoremet ovenfor og dens geometriske tolkning.
FOREDRAG nr. 4
Forelesningsemne: Derivert av en funksjon
Forelesningsoversikt: Konseptet med derivat, dets geometriske og fysisk mening. Grunnleggende regler for differensiering. Derivat kompleks funksjon. Noen applikasjoner er avledet.
4.1. Konseptet avledet, dets geometriske og fysiske betydning
Vurder funksjonen på = f(x), spesifisert i intervallet ] en, b[. La XÎ ] en, b[Og X Î ] en, b[, deretter økningen av funksjonen ved punktet X 0 er uttrykt med formelen D på = f(x 0+D X) – f(x 0).
Definisjon. Derivativ funksjon y = f(x) på punktet X 0 kalles vanligvis grensen for forholdet mellom økningen av denne funksjonen og økningen av argumentet når sistnevnte har en tendens til null:
f'(x 0) = ![]() eller y"(x 0) =.
eller y"(x 0) =.
Geometrisk betydning av derivat: den deriverte av en gitt funksjon i et punkt er lik tangenten til vinkelen mellom Ox-aksen og tangenten til grafen til denne funksjonen ved tilsvarende punkt(se fig. 1):
f"(x 0) = brun a.
EGENSKAPER TIL FUNKSJONER KONTINUERLIG PÅ ET INTERVJU
La oss vurdere noen egenskaper til funksjoner som er kontinuerlige i et intervall. Vi presenterer disse egenskapene uten bevis.
Funksjon y = f(x) kalt kontinuerlig på segmentet [en, b], hvis den er kontinuerlig ved alle interne punkter i dette segmentet, og i endene, dvs. på poeng en Og b, er kontinuerlig på henholdsvis høyre og venstre side.
Teorem 1. En funksjon kontinuerlig i intervallet [ en, b], minst på ett punkt av dette segmentet tar den største verdien og minst på ett punkt den minste.
Teoremet sier at hvis en funksjon y = f(x) er kontinuerlig i intervallet [ en, b], så er det minst ett poeng x 1 Î [ en, b] slik at verdien av funksjonen f(x) på dette tidspunktet vil være den største av alle verdiene på dette segmentet: f(x 1) ≥ f(x). På samme måte er det et slikt poeng x 2, der funksjonsverdien vil være den minste av alle verdier på segmentet: f(x 1) ≤ f(x).
Det er tydelig at det kan være flere slike punkter for eksempel viser figuren at funksjonen; f(x) tar den minste verdien ved to punkter x 2 Og x 2 ".
Kommentar. Utsagnet av teoremet kan bli feil hvis vi vurderer verdien av funksjonen på intervallet ( en, b). Faktisk, hvis vi vurderer funksjonen y = x på (0, 2), så er det kontinuerlig i dette intervallet, men når verken de største eller minste verdiene i det: det når disse verdiene ved slutten av intervallet, men endene hører ikke hjemme til vårt domene.
Dessuten slutter teoremet å være sant for diskontinuerlige funksjoner. Gi et eksempel.
Konsekvens. Hvis funksjonen f(x) er kontinuerlig på [ en, b], så er det begrenset på dette segmentet.
Teorem 2. La funksjonen y = f(x) er kontinuerlig i intervallet [ en, b] og i enden av dette segmentet tar verdier av forskjellige tegn, så er det minst ett punkt inne i segmentet x = C, der funksjonen går til null: f(C)= 0, hvor a< C< b

Denne teoremet har en enkel geometrisk betydning: hvis punktene til grafen til en kontinuerlig funksjon y = f(x), tilsvarende endene av segmentet [ en, b] ligge med forskjellige sider fra aksen Okse, så skjærer denne grafen aksen i minst ett punkt av segmentet Okse. Det kan hende at diskontinuerlige funksjoner ikke har denne egenskapen.
Denne teoremet innrømmer følgende generalisering.
Teorem 3 (mellomverditeorem). La funksjonen y = f(x) er kontinuerlig i intervallet [ en, b] Og f(a) = A, f(b) = B. Deretter for et hvilket som helst tall C, konkludert mellom EN Og B, det er et slikt punkt inne i dette segmentet CÎ [ en, b], Hva f(c) = C.

Denne teoremet er geometrisk tydelig. Tenk på grafen til funksjonen y = f(x). La f(a) = A, f(b) = B. Deretter hvilken som helst rett linje y = C, Hvor C– et hvilket som helst tall mellom EN Og B, vil skjære grafen til funksjonen i minst ett punkt. Abscissen til skjæringspunktet vil være den verdien x = C, ved hvilken f(c) = C.
Dermed går en kontinuerlig funksjon, som beveger seg fra en verdi til en annen, nødvendigvis gjennom alle mellomverdier. Spesielt:
Konsekvens. Hvis funksjonen y = f(x) er kontinuerlig over et visst intervall og tar de største og minste verdiene, så på dette intervallet tar den minst én gang en hvilken som helst verdi mellom dens minste og største verdi.
DERIVAT OG DETS APPLIKASJONER. DEFINISJON AV DERIVAT
La oss ha en funksjon y=f(x), definert på et eller annet intervall. For hver argumentverdi x fra dette intervallet funksjonen y=f(x) har en viss betydning.
Tenk på to argumentverdier: initial x 0 og ny x.

Forskjell x–x 0 kalles ved å øke argumentet x på punktet x 0 og er angitt Δx. Dermed, Δx = x – x 0 (argumentøkningen kan enten være positiv eller negativ). Av denne likestillingen følger det at x=x 0 +Δx, dvs. opprinnelig betydning variabelen mottok en viss økning. Så, hvis det er på punktet x 0 funksjonsverdi var f(x 0 ), så inn nytt punkt x funksjonen vil ta verdien f(x) = f(x 0 +Δx).
Forskjell å–å 0 = f(x) – f(x 0 ) kalt funksjonsøkning y = f(x) på punktet x 0 og er indikert med symbolet Δy. Dermed,
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) . | (1) |
Vanligvis startverdien til argumentet x 0 anses som fast, og den nye verdien x– variabel. Deretter y 0 = f(x 0 ) viser seg å være konstant, og y = f(x)– variabel. Inkrementer Δy Og Δx vil også være variabler og formel (1) viser det Dy er en funksjon av en variabel Δx.
La oss lage forholdet mellom økningen av funksjonen og økningen av argumentet
La oss finne grensen for dette forholdet ved Δx→0. Hvis denne grensen eksisterer, kalles den den deriverte av denne funksjonen f(x) på punktet x 0 og angir f "(x 0). Så,
Derivat denne funksjonen y = f(x) på punktet x 0 kalles grensen for funksjonens inkrementforhold Δ y til argumentøkningen Δ x, når sistnevnte vilkårlig har en tendens til null.
Merk at for samme funksjon er den deriverte i ulike punkter x kan anta ulike verdier, dvs. den deriverte kan betraktes som en funksjon av argumentet x. Denne funksjonen er utpekt f "(x)
Den deriverte er merket med symbolene f "(x),y ", . Spesifikk betydning avledet kl x = a betegnet med f "(en) eller y "| x=a.
Operasjonen med å finne den deriverte av en funksjon f(x) kalles differensiering av denne funksjonen.
For å finne den deriverte direkte per definisjon, kan du bruke følgende: tommelfingerregel:
Eksempler.
MEKANISK FØLELSE AV DERIVAT
Det er kjent fra fysikken at loven jevn bevegelse ser ut som s = v t, Hvor s– veien gikk til tidens øyeblikk t, v– hastighet på jevn bevegelse.
Imidlertid fordi De fleste bevegelser som forekommer i naturen er ujevne, da generelt hastigheten, og følgelig avstanden s vil avhenge av tid t, dvs. vil være en funksjon av tid.
Så la et materialpunkt bevege seg i en rett linje i én retning i henhold til loven s=s(t).
La oss markere et bestemt tidspunkt t 0 . På dette tidspunktet har punktet passert stien s=s(t 0 ). La oss bestemme hastigheten v materielle punkt på et tidspunkt t 0 .
For å gjøre dette, la oss vurdere et annet tidspunkt t 0 + Δ t. Det tilsvarer den tilbakelagte banen s =s(t 0 + Δ t). Deretter over en tidsperiode Δ t punktet har gått veien Δs =s(t 0 + Δ t)–s(t).
La oss vurdere holdningen. Det kalles gjennomsnittshastigheten i tidsintervallet Δ t. Gjennomsnittshastigheten kan ikke nøyaktig karakterisere bevegelseshastigheten til et punkt for øyeblikket t 0 (fordi bevegelsen er ujevn). For mer nøyaktig å uttrykke denne sanne hastigheten ved å bruke gjennomsnittshastighet, må du ta en kortere tidsperiode Δ t.
Så, hastigheten på bevegelsen inn dette øyeblikket tid t 0 (øyeblikkelig hastighet) er grensen for gjennomsnittlig hastighet i intervallet fra t 0 til t 0 +Δ t, når Δ t→0:
![]() ,
,
de. ujevn hastighet dette er den deriverte av tilbakelagt avstand i forhold til tid.

GEOMETRISK BETYDNING AV DERIVAT
La oss først introdusere definisjonen av en tangent til en kurve i et gitt punkt.
La oss ha en kurve og et fast punkt på den M 0(se figur). Tenk på et annet punkt M denne kurven og tegne en sekant M 0 M. Hvis poenget M begynner å bevege seg langs kurven, og punktet M 0 forblir ubevegelig, så endrer sekanten posisjon. Hvis, med ubegrenset tilnærming av punktet M langs en kurve til et punkt M 0 på hvilken som helst side har sekanten en tendens til å innta posisjonen til en viss rett linje M 0 T, deretter rett M 0 T kalt tangenten til kurven i et gitt punkt M 0.
At., tangent til kurven på et gitt punkt M 0 kalt grenseposisjonen til sekanten M 0 M når punkt M tenderer langs kurven til et punkt M 0.
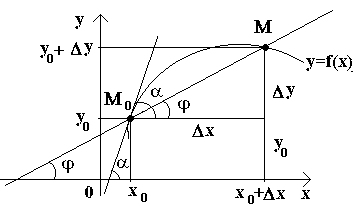
La oss nå vurdere den kontinuerlige funksjonen y=f(x) og kurven som tilsvarer denne funksjonen. Til en viss verdi X 0-funksjonen tar verdi y0 =f(x 0). Disse verdiene x 0 og y 0 på kurven tilsvarer et punkt M 0 (x 0; y 0). La oss gi argumentet x 0øke Δ X. Den nye verdien av argumentet tilsvarer den økte verdien til funksjonen y 0 +Δ y=f(x 0 –Δ x). Vi skjønner poenget M(x 0+Δ x; y 0+Δ y). La oss tegne en sekant M 0 M og angi med φ vinkelen som dannes av en sekant med den positive retningen til aksen Okse. La oss skape en relasjon og legge merke til det.
Hvis nå Δ x→0, da på grunn av kontinuiteten til funksjonen Δ på→0, og derfor poenget M, beveger seg langs en kurve, nærmer seg punktet uten grense M 0. Deretter sekanten M 0 M vil ha en tendens til å ta posisjonen til en tangent til kurven ved punktet M 0, og vinkelen φ→α ved Δ x→0, hvor α angir vinkelen mellom tangenten og den positive retningen til aksen Okse. Siden funksjonen tan φ kontinuerlig avhenger av φ for φ≠π/2, vil for φ→α tan φ → tan α og derfor stigningstallet til tangenten være:
![]()
de. f "(x)= tg α .
Altså geometrisk y "(x 0) representerer stigningstallet til tangenten til grafen til denne funksjonen i punktet x 0, dvs. på gitt verdi argument x, er den deriverte lik tangenten til vinkelen som dannes av tangenten til grafen til funksjonen f(x) på det aktuelle punktet M 0 (x; y) med positiv akseretning Okse.
Eksempel. Finne skråningen tangent til kurven y = x 2 på punktet M(-1; 1).
Vi har allerede sett tidligere at ( x 2)" = 2X. Men vinkelkoeffisienten til tangenten til kurven er tan α = y"| x=-1 = – 2.
DIFFERENSIERBARHET AV FUNKSJONER. KONTINUITET AV DIFFERENSIERBAR FUNKSJON
Funksjon y=f(x) kalt differensierbar på et tidspunkt x 0 hvis den har en viss derivert på dette tidspunktet, dvs. hvis grensen for forholdet eksisterer og er endelig.
Hvis en funksjon er differensierbar ved hvert punkt i et bestemt segment [ EN; b] eller intervall ( EN; b), så sier de at hun differensierbar på segmentet [ EN; b] eller, henholdsvis, i intervallet ( EN; b).
Følgende teorem er gyldig, og etablerer sammenhengen mellom differensierbare og kontinuerlige funksjoner.
Teorem. Hvis funksjonen y=f(x) differensierbar på et tidspunkt x 0, så er den kontinuerlig på dette tidspunktet.
Fra differensierbarheten til en funksjon følger dens kontinuitet.
Bevis. Hvis ![]() , Det
, Det
![]() ,
,
hvor α er en uendelig liten størrelse, dvs. en mengde som tenderer mot null som Δ x→0. Men da
Δ y=f "(x 0) Δ x+αΔ x=> Δ y→0 ved Δ x→0, dvs. f(x) – f(x 0)→0 kl x→x 0 , som betyr at funksjonen f(x) kontinuerlig på et punkt x 0 . Q.E.D.
Dermed kan ikke funksjonen ha en derivert ved diskontinuitetspunkter. Det motsatte er ikke sant: det er kontinuerlige funksjoner som ikke er differensierbare på noen punkter (det vil si at de ikke har en derivert på disse punktene).
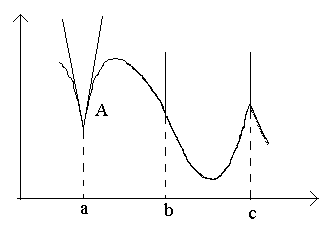
Tenk på punktene i figuren a, b, c.
På punktet en ved Δ x→0-forholdet har ingen grense (siden ensidige grenser er forskjellige for Δ x→0–0 og Δ x→0+0). På punktet EN graf er det ingen definert tangent, men det er to forskjellige enveis tangenter med helninger Til 1 og Til 2. Denne typen punkt kalles hjørnepunkt.
På punktet b ved Δ x→0-relasjonen har konstant fortegn på ubestemt tid stor størrelse. Funksjonen har uendelig derivert. På dette punktet har grafen en vertikal tangent. Punkttype - "bøyningspunkt" til en vertikal tangent.
På punktet c ensidige derivater er uendelig store mengder forskjellige tegn. På dette tidspunktet har grafen to sammenslåtte vertikale tangenter. Type – “returpunkt” med vertikal tangent – spesielt tilfelle hjørnepunkt.