Parallelism of planes is a definition of a property sign. Geometry in space

The “Get an A” video course includes all the topics you need to successful completion Unified State Examination in mathematics for 60-65 points. Completely all problems 1-13 Profile Unified State Examination mathematics. Also suitable for passing the Basic Unified State Examination in mathematics. If you want to pass the Unified State Exam with 90-100 points, you need to solve part 1 in 30 minutes and without mistakes!

Preparation course for the Unified State Exam for grades 10-11, as well as for teachers. Everything you need to solve Part 1 of the Unified State Exam in mathematics (the first 12 problems) and Problem 13 (trigonometry). And this is more than 70 points on the Unified State Exam, and neither a 100-point student nor a humanities student can do without them.

All necessary theory. Quick ways solutions, pitfalls and secrets of the Unified State Exam. All current tasks of part 1 from the FIPI Task Bank have been analyzed. The course fully complies with the requirements of the Unified State Exam 2018.

The course contains 5 big topics, 2.5 hours each. Each topic is given from scratch, simply and clearly.

Hundreds of Unified State Exam tasks. Word problems and probability theory. Simple and easy to remember algorithms for solving problems. Geometry. Theory, reference material, analysis of all types of Unified State Examination tasks. Stereometry. Tricky solutions, useful cheat sheets, development spatial imagination. Trigonometry from scratch to problem 13. Understanding instead of cramming. Visual explanation complex concepts. Algebra. Roots, powers and logarithms, function and derivative. Basis for solution complex tasks 2 parts of the Unified State Exam.

Parallelism of planes. If two intersecting lines of one plane are respectively parallel to two intersecting lines of another plane, then these planes are parallel.
Proof. Let a And b- plane data, a 1 And a 2– straight lines in the plane a, intersecting at point A, b 1 And b 2 correspondingly, the lines parallel to them in the plane b. Let us assume that the planes a And b not parallel, that is, they intersect along some straight line With. Straight A 1 is parallel to the line b 1, which means it is parallel to the plane itself b(a sign of parallelism between a line and a plane). Straight A 2 is parallel to the line b 2, this means it is parallel to the plane itself b(a sign of parallelism between a line and a plane). Straight With belongs to the plane a, which means at least one of the straight lines a 1 or a 2 intersects a line With, that is, it has a common point with it. But straight With also belongs to the plane b, which means crossing the line With, straight a 1 or a 2 intersects the plane b, which cannot be, since they are straight a 1 And a 2 parallel to the plane b. It follows from this that the planes a And b do not intersect, that is, they are parallel.

Theorem 1 . If two parallel planes intersect in thirds, then the straight lines of intersection are parallel.
Proof. Let a And b- parallel planes, and g - the plane intersecting them. Plane a intersected with the plane g in a straight line A. Plane b intersected with the plane g in a straight line b. Intersection lines A And b lie in the same plane g and therefore can be either intersecting or parallel lines. But, belonging to two parallel planes, they cannot have common points. Therefore they are parallel.

Theorem 2. The segments of parallel lines enclosed between two parallel planes are equal.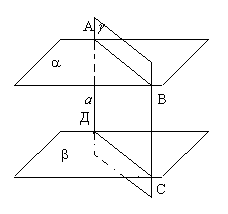
Proof. Let a And b- parallel planes, and A And b- parallel lines intersecting them. Through straight lines A And b we will conduct plane g (these lines are parallel, which means define a plane, and only one). Plane a intersected with the plane g in a straight line AB . Plane b intersected with the plane g along the straight line SD. According to the previous theorem, the straight line With parallel to the line d. Direct A,b, AB And SD belong to the plane g.The quadrilateral bounded by these lines is a parallelogram (it has opposite sides parallel). And since this is a parallelogram, then its opposite sides are equal, that is, AD = BC

In this lesson we will look at three properties parallel planes: about the intersection of two parallel planes with a third plane; O parallel segments, enclosed between parallel planes; and about cutting the sides of an angle by parallel planes. Next, we will solve several problems using these properties.

Topic: Parallelism of lines and planes

Lesson: Properties of Parallel Planes

If two parallel planes are intersected by a third, then the lines of their intersection are parallel.

Proof

Let parallel planes and be given and a plane that intersects the planes and along straight lines A And b accordingly (Fig. 1.).

Direct A And b lie in the same plane, namely in the γ plane. Let us prove that the straight lines A And b do not intersect.

If straight A And b intersected, that is, would have a common point, then this common point would belong to two planes and , and , which is impossible, since they are parallel by condition.

So, straight A And b are parallel, which is what needed to be proven.

The segments of parallel lines contained between parallel planes are equal.

Proof

Let parallel planes and parallel lines be given AB And WITHD, which intersect these planes (Fig. 2.). Let us prove that the segments AB And WITHD are equal.

Two parallel lines AB And WITHD form a single plane γ, γ = ABDWITH. The plane γ intersects parallel planes and along parallel lines (according to the first property). So it's straight AC And IND parallel.

Direct AB And WITHD are also parallel (by condition). So it's a quadrilateral ABDWITH- a parallelogram, since its opposite sides are parallel in pairs.

From the properties of a parallelogram it follows that the segments AB And WITHD are equal, as required to prove.

Parallel planes cut the sides of an angle into proportional parts.

Proof

Let us be given parallel planes and that cut the sides of the angle A(Fig. 3.). It is necessary to prove that .

Parallel planes and cut by an angle plane A. Let's call the line of intersection of the angle plane A and planes - sun, and the line of intersection of the angle plane A and planes - B 1 C 1. According to the first property, the lines of intersection Sun And B 1 C 1 parallel.

So triangles ABC And AB 1 C 1 similar. We get:

3. Mathematical website of Vitaly Stanislavovich Tsegelny ()

4. Festival pedagogical ideas"Public lesson" ()

1. Point ABOUT- common midpoint of each segment AA 1, BB 1, SS 1, which do not lie in the same plane. Prove that the planes ABC And A 1 B 1 C 1 parallel.

2. Prove that parallel planes can be drawn through two skew lines.

3. Prove that a line intersecting one of two parallel planes also intersects the second.

4. Geometry. Grades 10-11: textbook for students educational institutions(basic and profile levels) / I. M. Smirnova, V. A. Smirnov. - 5th edition, corrected and expanded - M.: Mnemosyne, 2008. - 288 pp.: ill.

Tasks 6, 8, 9 p. 29

In this lesson we will define parallel planes and recall the axiom about the intersection of two planes. Next, we will prove a theorem - a sign of parallelism of planes and, relying on it, we will solve several problems on the parallelism of planes.

Topic: Parallelism of lines and planes

Lesson: Parallel Planes

In this lesson we will define parallel planes and recall the axiom about the intersection of two planes.

Definition. Two planes are called parallel if they do not intersect.

Designation: .

Illustration of parallel planes(Fig. 1.)

1. What planes are called parallel?

2. Can planes passing through nonparallel lines be parallel?

3. What can be the relative position of two straight lines, each of which lies in one of two different parallel planes?

4. Geometry. Grades 10-11: textbook for students of general education institutions (basic and specialized levels) / I. M. Smirnova, V. A. Smirnov. - 5th edition, corrected and expanded - M.: Mnemosyne, 2008. - 288 pp.: ill.

Tasks 1, 2, 5 p. 29

Lesson objectives:

Introduce the concept of parallel planes.
Consider and prove theorems expressing the sign of parallelism of planes and the properties of parallel planes.
Trace the application of these theorems in solving problems.

Lesson plan (write on the board):

I. Preparatory oral work.

II. Learning new material:

1. Mutual arrangement two planes in space.
2. Determination of parallel planes.
3. Sign of parallel planes.
4. Property of parallel planes.

III. Lesson summary.

IV. Homework.

DURING THE CLASSES

I. Oral work

I would like to start the lesson with a quote from Chaadaev’s philosophical letter:

“Where does this miraculous power of analysis in mathematics come from? The fact is that the mind here acts in complete submission to this rule.”

We will look at this obedience to the rule in the next task. To learn new material, you need to repeat some questions. To do this, you need to establish a statement that follows from these statements and justify your answer:

II. Learning new material

1. How can two planes be located in space? What is the set of points belonging to both planes?

Answer:

a) coincide (then we will be dealing with one plane, it’s not satisfactory);
b) intersect, ;
c) do not intersect (there are no common points at all).

2. Definition: If two planes do not intersect, then they are called parallel

3. Designation:

4. Give examples of parallel planes from the environment

5. How to find out if any two planes in space are parallel?

Answer:

You can use the definition, but this is inappropriate, because It is not always possible to establish the intersection of planes. Therefore, it is necessary to consider a condition sufficient to assert that the planes are parallel.

6. Let's consider the situations:

b) if ?

c) if ?

Why is the answer in a) and b) “not always”, but in c) “yes”? (Intersecting lines define a plane in a unique way, which means they are uniquely defined!)

Situation 3 is a sign of parallelism of two planes.

7. Theorem: If two intersecting lines of one plane are respectively parallel to two lines of another plane, then these planes are parallel.

Given:

Prove:

Proof:

(Students apply designations to the drawing.)

1. Note: . Likewise:
2. Let: .
3. We have: Similarly:
4. We get: through M there is a contradiction with the axiom of planimetry.
5. So: incorrect, means , etc.

8. Solve No. 51 (Students apply symbols to the drawing).

Given: