Ученик построил четыре сечения куба плоскостью. Задачи на построение сечений куба

Тип урока: Комбинированный урок.

Цели и задачи:

образовательная – формирование и развитие у учащихся пространственных представлений; выработка навыков решения задач на построение сечений простейших многогранников;
воспитательная - воспитывать волю и настойчивость для достижения конечных результатов при построении сечений простейших многогранников; воспитывать любовь и интерес к изучению математики.
развивающая – развитие у учащихся логического мышления, пространственных представлений, развитие навыков самоконтроля.

Оборудование: компьютеры со специально разработанной программой, раздаточный материал в виде готовых чертежей с задачами, тела многогранников, индивидуальные карточки с домашним заданием.

Структура урока:

Сообщение темы и цели урока (2 мин).
Инструктирование по выполнению заданий на компьютере (2 мин).
Актуализация опорных знаний и умений учащихся (4 мин).
Тестирование с самопроверкой (3 мин).
Решение задач с объяснением хода решения учителем (15 мин).
Самостоятельная работа с самопроверкой (10 мин).
Постановка домашнего задания (2 мин).
Подведение итогов (2 мин).

Ход урока

1. Сообщение темы и цели урока

После проверки готовности класса к уроку учитель сообщает, что сегодня проводится урок по теме “Построение сечений многогранников”, будут рассмотрены задачи на построение сечений некоторых простейших многогранников плоскостями, проходящими через три точки, принадлежащие ребрам многогранников. Урок будет проходить с использованием компьютерной презентации, выполненной в Power Point.

2. Инструктирование по технике безопасности при работе в компьютерном классе

Учитель. Обращаю ваше внимание на то, что вы приступаете к работе в компьютерном классе, и вам необходимо соблюдать правила поведения и работы за компьютером. Зафиксируйте выдвижные столешницы и следите за правильной посадкой.

3. Актуализация опорных знаний и умений учащихся

Учитель. Для решения многих геометрических задач связанных с многогранниками, полезно уметь строить на рисунке их сечения различными плоскостями, находить точку пересечения данной прямой с данной плоскостью, находить линию пересечения двух данных плоскостей. На предыдущих уроках мы рассматривали сечения многогранников плоскостями, параллельными ребрам и граням многогранников. На этом уроке мы рассмотрим задачи на построение сечений плоскостью, проходящей через три точки, расположенные на ребрах многогранников. Для этого рассмотрим простейшие многогранники. Что это за многогранники? (Демонстрируются модели куба, тетраэдра, правильной четырехугольной пирамиды, прямой треугольной призмы).

Учащиеся должны определить вид многогранника.

Учитель. Давайте посмотрим как они выглядят на экране монитора. От изображения к изображению переходим по нажатию левой клавиши мыши.

На экране одно за другим появляются изображения названных многогранников.

Учитель. Вспомним, что называется сечением многогранника.

Учащийся. Многоугольник, сторонами которого являются отрезки, принадлежащие граням многогранника, с концами на ребрах многогранника, полученный в результате пересечения многогранника произвольной секущей плоскостью.

Учитель. Какие многоугольники могут являться сечениями данных многогранников.

Учащийся. Сечения куба: трех - шести- угольники. Сечения тетраэдра: треугольники, четырехугольники. Сечения четырехугольной пирамиды и треугольной призмы: трех - пяти- угольники.

4. Тестирование с самопроверкой

Учитель. В соответствии с понятием сечения многогранников, знаний аксиом стереометрии и взаимного расположения прямых и плоскостей в пространстве, вам предлагается ответить на вопросы теста. Компьютер оценит вас. Максимальная оценка 3 балла – за 3 правильных ответа. На каждом слайде необходимо нажать кнопку с номером правильного ответа. Вы работаете в паре, поэтому каждый из вас получит одинаковое, указанное компьютером количество баллов. Нажмите указатель перехода на следующий слайд. На выполнение задания отводится 3 минуты.

I. На каком рисунке изображено сечение куба плоскостью ABC ?

II. На каком рисунке изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно ребру SA ?

III. На каком рисунке изображено сечение тетраэдра, проходящее через точку М параллельно плоскости ABS ?

5. Решение задач с объяснением хода решения учителем

Учитель. Перейдем непосредственно к решению задач. Нажмите указатель перехода на следующий слайд.

Задача 1 Данную задачу рассмотрим устно с пошаговым показом построения на экране монитора. Переход осуществляется по клику мыши.

Дан куб ABCDAA 1 B 1 C 1 D 1 . На его ребре ВВ 1 дана точка М . Найти точку пересечения прямой C 1 M с плоскостью грани куба ABCD .

Рассмотрим изображение куба ABCDAA 1 B 1 C 1 D 1 с точкой М на ребре ВВ 1 Точки М и С 1 принадлежат плоскости ВВ 1 С 1 Что можно сказать о прямой C 1 M ?

Учащийся. Прямая C 1 M принадлежит плоскости ВВ 1 С 1

Учитель. Искомая точка X принадлежит прямой C 1 M, а значит и плоскости ВВ 1 С 1 . Каково взаимное расположение плоскостей ВВ 1 С 1 и ABC ?

Учащийся. Данные плоскости пересекаются по прямойBC .

Учитель. Значит все общие точки плоскостей ВВ 1 С 1 и ABC принадлежат прямой BC . Искомая точка X должна принадлежать одновременно плоскостям двух граней: ABCD и BB 1 C 1 C ; из этого следует, что точка X должна лежать на линии их пересечения, т. е. на прямой ВС . Значит, точка X должна лежать одновременно на двух прямых: С 1 М и ВС и, следовательно, является их точкой пересечения. Построение искомой точки рассмотрим на экране монитора. Последовательность построения вы увидите по нажатию левой клавиши мыши: продолжаем С 1 М и ВС до пересечения в точке X , которая и есть искомая точка пересечения прямой С 1 М с плоскостью грани ABCD .

Учитель. Для перехода к следующей задаче воспользуйтесь указателем перехода к следующему слайду. Эту задачу рассмотрим с краткой записью построения.

а) Построить сечение куба плоскостью, проходящей через точки А 1 , М D 1 C 1 и N DD 1 и б) Найти линию пересечения секущей плоскости с плоскостью нижнего основания куба.

Решение. I. Секущая плоскость имеет с гранью A 1 B 1 C 1 D 1 две общие точки А 1 и М и, следовательно, пересекается с нею по прямой, проходящей через эти точки. Соединяя точки А 1 и М отрезком прямой, находим линию пересечения плоскости будущего сечения и плоскости верхней грани. Этот факт будем записывать следующим образом: А 1 М. Нажимаем левую клавишу мыши, повторным нажатием будет построена эта прямая.

Аналогично находим линии пересечения секущей плоскости с гранями АА 1 D 1 D и DD 1 С 1 С. Нажимая клавишу мыши, вы будете видеть краткую запись и ход построения.

Таким образом, A 1 NМ ? искомое сечение.

Перейдем ко второй части задачи. Найдем линию пересечения секущей плоскости с плоскостью нижнего основания куба.

II. Секущая плоскость с плоскостью основания куба пересекается по прямой. Чтобы изобразить эту прямую достаточно найти две точки принадлежащие данной прямой, т.е. общие точки секущей плоскости и плоскости грани ABCD . Опираясь на предыдущую задачу такими точками будут являться: точка X =. Нажмите клавишу, вы будете видеть краткую запись и построение. И точка Y , как вы думаете, ребята, как ее получить?

Учащийся. Y =

Учитель. Посмотрим на экране ее построение. Нажмите клавишу мыши. Соединяя точки X и Y (Запись X -Y ), получим искомую прямую - линию пересечения секущей плоскости с плоскостью нижнего основания куба. Нажмите левую клавишу мыши – краткая запись и построение.

Задача 3 Построить сечение куба плоскостью, проходящей через точки:

Так же, нажимая клавишу мыши, вы будете видеть на экране монитора ход построения и краткую запись. Опираясь на понятие сечения, нам достаточно найти в плоскости каждой грани две точки для построения линии пересечения секущей плоскости и плоскости каждой грани куба. Точки M и N принадлежат плоскости А 1 В 1 С 1 . Соединив их, получим линию пересечения секущей плоскости и плоскости верхней грани куба (нажимаем клавишу мыши). Продолжим прямые MN и D 1 C 1 до пересечения. Получим точку Х , принадлежащую как плоскости А 1 В 1 С 1 , так и плоскости DD 1 C 1 (клик мыши). Точки N и К принадлежат плоскости ВВ 1 С 1 . Соединив их, получим линию пересечения секущей плоскости и грани ВВ 1 С 1 С . (Клик мыши). Соединяем точки Х и К , и продолжаем прямую ХК до пересечения с прямой DC . Получим точку Р и отрезок КР – линию пересечения секущей плоскости и грани DD 1 C 1 C . (Клик мыши). Продолжая прямые КР и DD 1 до пересечения, получим точку Y , принадлежащую плоскости АА 1 D 1 . (Клик мыши). В плоскости этой грани нам требуется еще одна точка, которую получаем в результате пересечения прямых MN и А 1 D 1 . Это точка . (Клик мыши). Соединяем точки Y и Z , получим и . (Клик мыши). Соединив Q и Р , R и M , получим ? искомое сечение.

Краткая запись построения:

2) ;

6) ;

7) ;

13) ? искомое сечение.

Выбери многогранник и уровень трудности

Параллелепипед.

Тетраэдр.

Куб. Уровень А.

Уровень А.

Параллелепипед.

Куб. Уровень В.

Уровень В.

Тетраэдр.

Уровень В.

Параллелепипед.

Тетраэдр.

Куб. Уровень С.

Уровень С.

Куб. Уровень A.

точки М,Н и К, где КЄ(DCC 1 D 1 ).

в 1

С 1

D 1

Помощь

плоскости а) с ребром ВВ 1 ; б)плоскостью (СС 1 D).

Куб. Уровень B.

в 1

С 1

D 1

Помощь

Куб. Уровень С.

Постройте сечение куба плоскостью, проходящей через точки К,Е и М (М Є АВ). Затем найдите точку пересечения прямой ВВ 1 с этой плоскостью.

в 1

С 1

D 1

Куб. Уровень A.

Построить сечение тетраэдра, проходящего через

точки М,Н и К, где КЄ(DCC 1 D 1 ).

в 1

С 1

ЕР ll МН

D 1

Куб. Уровень B.

в 1

С 1

D 1

АН ll КЕ

Построить сечение куба плоскостью, проходящей через

точки А,К и Е.Найдите линию пересечения этой

плоскости а) с ребром ВВ 1 ; б)плоскостью (СС 1 D).

Куб. Уровень С.

Постройте сечение куба плоскостью, проходящей через точки К,Е и М (М Є АВ). Затем найдите точку пересечения прямой ВВ1 с этой плоскостью.

в 1

С 1

D 1

РHКЕRF – искомое сечение

Уровень А. На ребрах АА 1 и А 1 Д 1 1 1 = 6, А 1 Д 1 = 8, АВ = 4 см.

Помощь

Уровень В.

Помощь

УровеньС. На ребрах параллелепипеда даны три точки S,R и L. Построить сечение параллелепипеда плоскостью SRL.

Помощь

Уровень А. На ребрах АА 1 и А 1 Д 1 параллелепипеда взяты соответственно середины S,R. Построить сечение параллелепипеда плоскостью SRВ 1 и найти площадь сечения, если АА 1 = 6, А 1 Д 1 = 8, АВ = 4 см.

Указание

Примени формулу Герона.

Уровень В

SRELZX – искомое сечение

Уровень С.

Тетраэдр.

Уровень А.

Помощь

Тетраэдр.

Постройте сечение тетраэдра плоскостью, проходящей

Уровень В.

Помощь

В тетраэдре на высотах граней (СТА) и (АТВ) взяты точки К и М,

а точка Е лежит в плоскости (АВС). Проведите сечение тетраэдра,

проходящее через данные точки.

Тетраэдр.

Уровень С.

Помощь

Постройте сечение тетраэдра плоскостью, проходящей

через середины ребер СТ,СА и точку КЄТВ. Определите вид

четырехугольника, полученного в сечении.

Тетраэдр.

Уровень А.

Тетраэдр.

Постройте сечение тетраэдра плоскостью, проходящей

Уровень В.

через точки М и Н и точку КЄ(АВС).

МНРЕ – искомое сечение

В1. В. Куб. Уровень B. Помощь. Построить сечение куба плоскостью, проходящей через точки А,К и Е.Найдите линию пересечения этой плоскости а) с ребром ВВ1; б)плоскостью (СС1D). Е. С1. К. А1. D1. С. D. А. Меню.

Слайд 4 из презентации «Задачи на построение сечений» . Размер архива с презентацией 198 КБ.

Геометрия 10 класс

краткое содержание других презентаций

«Определение двугранных углов» - Точка на ребре может быть произвольная. Построим BK. Задача. Решение задач. Плоскость М. Ромб. Определение и свойства. Где можно увидеть теорему трёх перпендикуляров. Концы отрезка. Проведем луч. Свойства. Двугранные углы в пирамидах. Точки М и К лежат в разных гранях. Отрезки АС и ВС. Свойство трёхгранного угла. Определение. Двугранные углы. Найдите угол. Провести перпендикуляр. Градусная мера угла.

«Примеры центральной симметрии» - Плоскость. Аксиомы планиметрии. Точки. Центральная симметрия. Один центр симметрии. Гостиница «Прибалтийская». Капсула поезда. Длина отрезка. Примеры симметрии в растениях. Центральная симметрия в архитектуре. Ромашка. Отрезок имеет определённую длину. Отрезок. Аксиомы стереометрии и планиметрии. Аксиомы стереометрии. Центральная симметрия в квадратах. Центральная симметрия в транспорте. Различные прямые.

«Равносторонние многоугольники» - Октаэдр Октаэдр составлен из восьми равносторонних треугольников. «Эдра» - грань «тетра» - 4 «гекса» - 6 «окта» - 8 «икоса» - 20 «дедека» - 12. Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Октаэдр имеет 8 граней, 6 вершин и 12 ребер. Существует 5 видов правильных многогранников. Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников.

«Применение правильных многогранников» - Многогранники в природе. Теорема Эйлера. Задачи проекта. Использование в жизни. Мир правильных многогранников. Многогранники в архитектуре. Многогранники в искусстве. Многогранники в математике. Архимед. Кеплер. Теория многогранников. Золотая пропорция в додекаэдре и икосаэдре. Заключение. Платон. Группа «Историки». Евклид. История возникновения правильных многогранников. Взаимосвязь «золотого сечения» и происхождения многогранников.

«Тела Платона» - Октаэдр. Тела Платона. Гексаэдр. Правильные многогранники. Платон. Додекаэдр. Дуальность. Икосаэдр. Правильные многогранники или тела Платона. Тетраэдр.

«Методы построения сечений многогранников» - Правила для самоконтроля. Постройте сечение призмы. Корабль. Многоугольники. Простейшие задачи. Взаимное расположение плоскости и многогранника. Точки пересечения. Пересекаются ли прямые. Разрезы образовали пятиугольник. Делаем разрезы. Законы геометрии. Аксиоматический метод. След секущей плоскости. Задача. Секущая плоскость. Построение сечений многогранников. Сечение. Опрос. Любая плоскость. Сечения параллелепипеда.

Общеобразовательная школа І-ІІІ ступеней №2

отдела образования администрации города Кировское

«Сечение куба плоскостью

и практическое их применение в задачах».

Подготовила учитель математики

учитель-методист

Чумакова Г.В.

2015 г.

Введение:

Задачи на построение сечений многогранников занимают значительное место как школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений.

Основными действиями, составляющими метод построения сечений, являются нахождение точки пересечения прямой с плоскостью, построение линий пересечения двух плоскостей, построение прямой параллельной плоскости, построение прямой перпендикулярной плоскости.

Проиллюстрирую построение сечения на одной задаче из школьного курса математики:

№1. Постройте хотя бы два сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью АМ 1 С, если точка М 1 движется по отрезку ВВ 1 от В до В 1 . Найдите границы измерения высоты сечения, проведённой из точки М 1 .

Решение: Построим два требуемых сечения, взяв точку М 1 ближе к точке В, а точку М 2 ближе к В 1 . Оба сечения показаны на рисунке.В начале движения когда точка М 1 только отошла от точки В 1 , сечение представляет собой треугольник с основанием АС и высотой М 1 О, которая чуть больше отрезка ВО, т.е.
Если точка М 1 займёт положение М 2 расположенной очень близко к точке В 1 , то АМ 2 С почти совпадёт с АВ 1 С, а его высота М 1 О – с отрезком В 1 О, длина которого равна
(ОВ 1 =
=
).

Отсюда по соображениям непрерывности делаем вывод:

Особо следует посмотреть, что произойдёт, если точка М 1 займёт положение вершины В.

№2. Построить сечение куба плоскостью, проходящей через три точки А 1 , E и L , лежащие на рёбрах куба.

Плоскости граней A 1 ADD 1 и DD 1 C 1 C пересекаются по прямой DD 1 , а плоскости граней A 1 B 1 C 1 D 1 u DD 1 C 1 C – по прямой D 1 C 1 . Соединив точки А и Е, получим прямую пересечения секущей плоскости с плоскостью грани AA 1 D 1 D , а продолжив её, найдём точку N , принадлежащую трём плоскостям: плоскости сечения и плоскостям граней AA 1 D 1 D u DD 1 C 1 C .

Аналогично найдём точку М, общую трём плоскостям: плоскости сечения и плоскостям граней A 1 B 1 C 1 D 1 u DD 1 C 1 C . Таким образом, точки N u M принадлежат секущей плоскости и плоскости DD 1 C 1 C ; прямая MN – линия пересечения плоскости сечения с плоскостью грани DD 1 C 1 C , а F и K – точки пересечения её с рёбрами куба CD u CC 1 . Последовательно соединив прямыми точки A 1 , E , F , K u L , получаем пятиугольник A ! EFKL , который и даст нам искомое сечение.

При построении сечения куба плоскостью Х при произвольном расположении точек в сечении получается: треугольник, трапеция, прямоугольник, пятиугольник или шестиугольник. Естественно возник вопрос, как вид сечения зависит от вида расположения точек задающих это сечение

Я решил провести исследование, цель которого является выяснение.

Построить сечения куба плоскостью, когда заданы три точки принадлежащие рёбрам с одной вершиной.

Взяты три точки A 1 , D , C 1 , которые принадлежат вершине D 1 , а сами являются вершинами куба.

В сечении получился равносторонний треугольник, так как A 1 C 1 , A 1 D u DC 1 – диагонали граней этого куба.

Три точки: A 1 u C 1 – вершины куба, а точка F принадлежит ребру куба DD 1 . Точки принадлежат прямым выходящим из вершины D 1 .

В сечении получился равнобедренный треугольник, так как F равноудалена от точек A 1 u C 1 .

Три точки: A 1 u C 1 – вершины куба, а точка F принадлежит прямой ребра куба DD 1 . Точки принадлежат прямым выходящим из одной вершины D 1 .

В сечении получается равнобедренная трапеция, так как F равноудалена от точек A 1 u C 1 , то есть LA 1 =KC 1 .

Три точки принадлежащие рёбрам с одной вершиной D 1 . Точки F u M принадлежат продолжениям рёбер D 1 D u D 1 C соответственно, а точка A 1 является вершиной куба.

В сечении получился пятиугольник A 1 KLNG .

Взяты три точки F , M u Q так, что лежат на продолжении рёбер D 1 D , D 1 C 1 , и D 1 A 1 соответственно.

В сечении получился шестиугольник KLNGJH .

Три точки лежат на рёбрах с одной вершиной D 1 .

В сечении получился произвольный треугольник, но если точки расположить так чтобы D 1 Q =D 1 M =D 1 F , то есть если они были бы равноудалены от вершины D 1 то в сечении получился бы равносторонний треугольник.

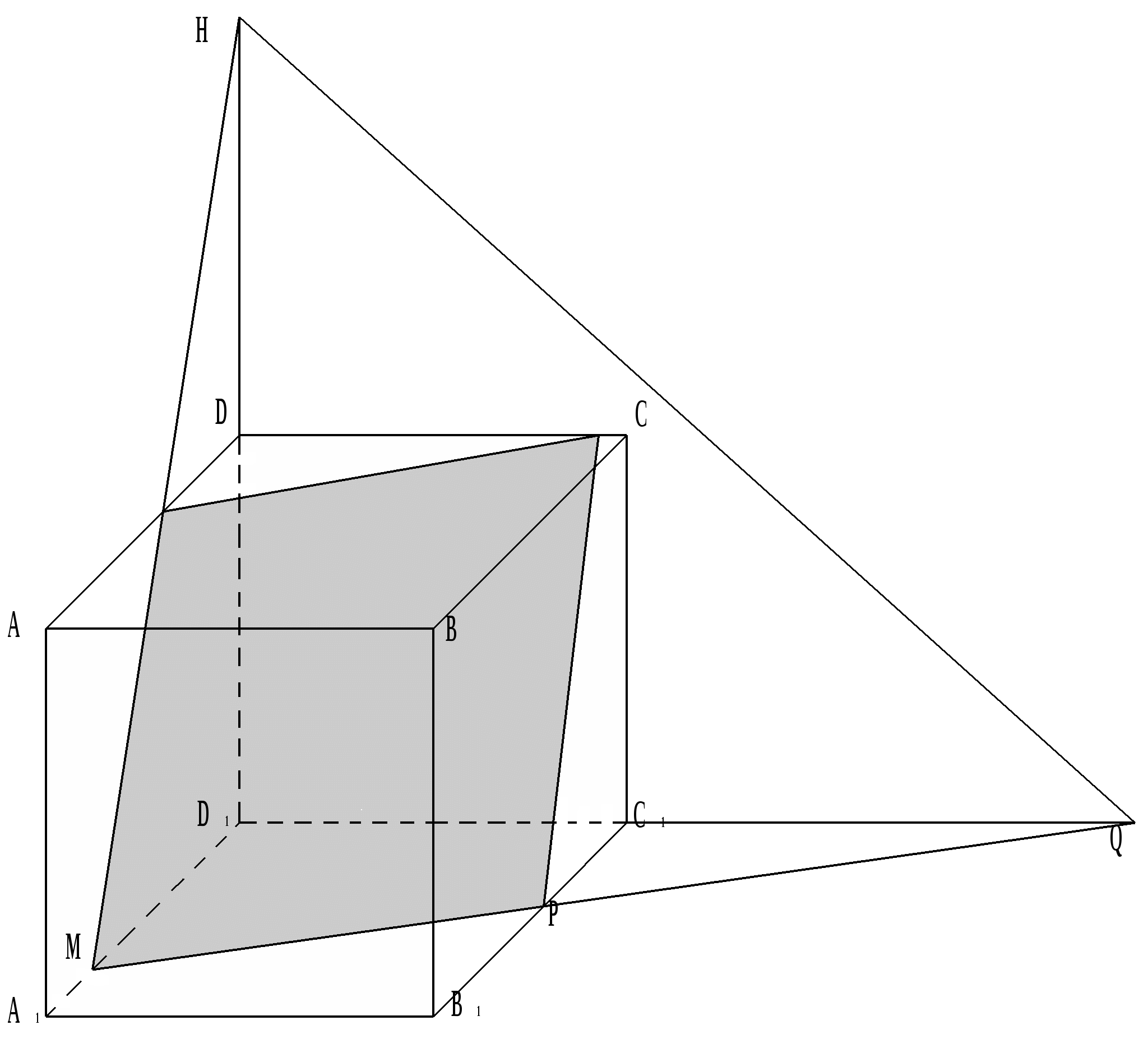
Секущая плоскость задана точками Н, Q и M . В сечении получается параллелограмм, так как KC ││ MP и MK ││ PC по теореме о пересечении двух параллельных плоскостей третьей.

Если точки H , Q и M , задают секущую плоскость, удаленные от D , на расстоянии 2a , где а – для ребра куба, то в сечении получается правильный треугольник ACB 1 .

Вывод: три задающих сечение точки принадлежат трём рёбрам куба с общей вершиной или являются их продолжением, то в сечении получается: треугольник, пятиугольник, шестиугольник трапеция, параллелограмм.

Построение сечения куба плоскостью, когда заданы три точки, две из которых лежат на смежных рёбрах, а третья точка лежит на ребре не смежном с ними.

Три точки M , K u F , взяты так что M u F принадлежат рёбрам с одной вершиной A 1 , а точка K лежит на ребре не смежным с ними.

В сечении получается прямоугольник, так как А 1 М=D 1 K и по теореме о трёх перпендикулярах можно доказать что MKLF – прямоугольник., а если А 1 МD 1 K , то может получится трапеция или пятиугольник.

Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A 1, а точка N принадлежит ребру CC 1 , не смежному сними. K , L u N середины рёбер A 1 A , A 1 B 1 u CC 1 – соответственно.

В сечении получается правильный шестиугольник KLGNHM

Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A 1, а точка T принадлежит ребру DC .

В сечении получается шестиугольник KLFRTZ .

Три точки взяты так, что K u L принадлежат рёбрам куба с одной вершины A 1 , а точка M ребре DD 1 .

В сечении получается трапеция LKQM .

Три точки K u L которые принадлежат рёбрам с одной вершиной A 1 .и точка R которая лежит на ребре BC .

В сечении получается пятиугольник KLFRT .

Вывод: Если секущая плоскость задана тремя точками, две из которых лежат на смежных рёбрах, а третья на ребре не смежном с ними, то в сечении может получиться прямоугольник, пятиугольник, шестиугольник, трапеция.

В сечении куба параллелограмм и его частные случаи.

Точки T , H , J задающие сечение расположены так, что THAD , HJAD . В сечении получается квадрат HTKJ .

Сечение задано точками C , F , L , причём DF =FD 1 , BL =LB 1 . В сечении получается ромб AFCL .

Сечение задано точками C , G , H . B 1 H =DG . В сечении параллелограмм A 1 GCH.

Точки задающие сечение являются вершинами куба A , D , C 1 . В сечении получается прямоугольник

В сечении куба правильные многоугольники

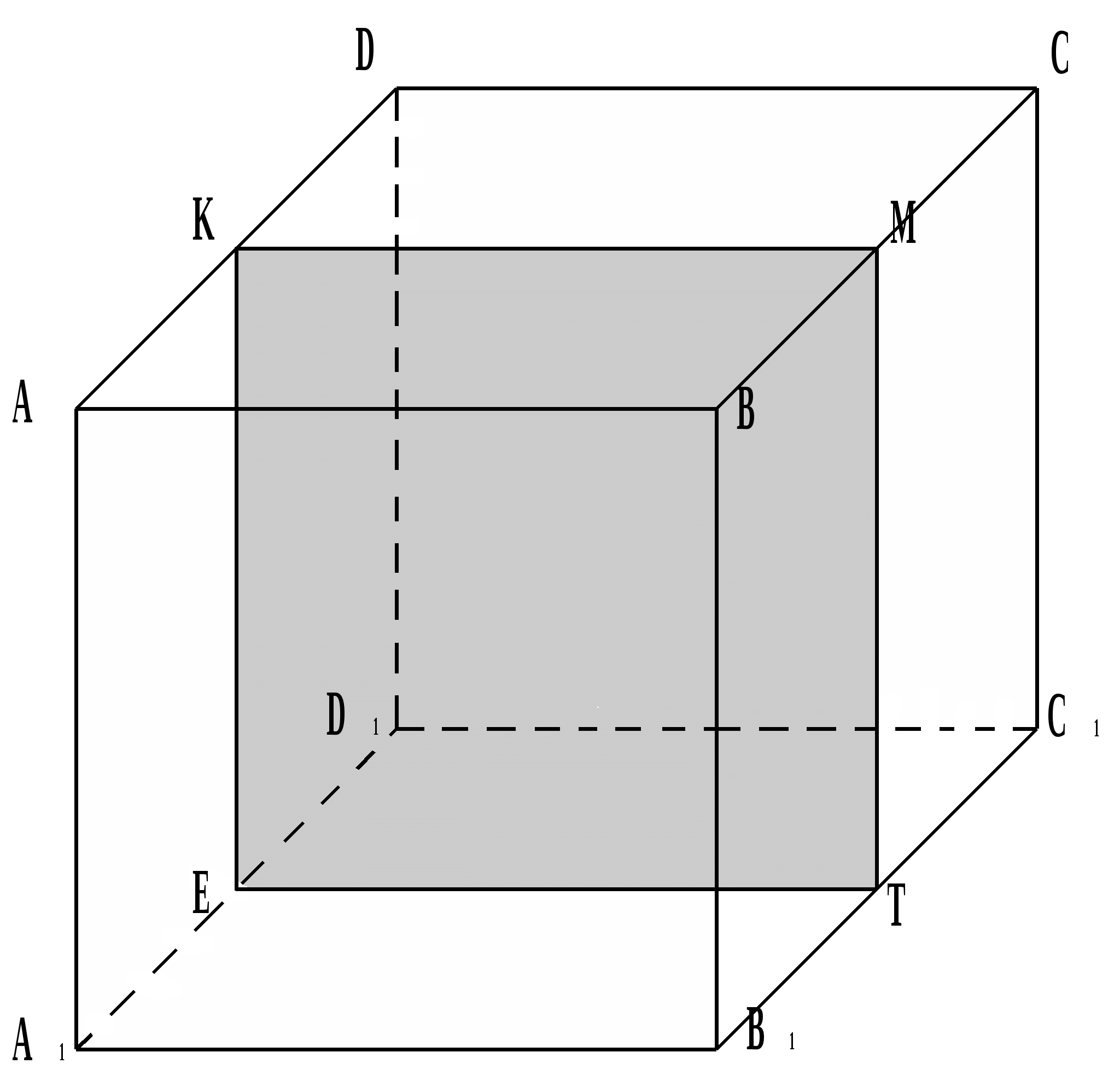
Треугольник АВВ 1 равносторонний, так как его стороны это диагонали граней куба.

Треугольник КМТ равносторонний, так как КВ=МВ=ТВ.

КМТЕ – квадрат, так как сечение задано точками М, К, Е и МКAD , EKAD .

В сечении правильный шестиугольник КМТНЕО, так как точки Н, Е, К задающие сечение являются серединами рёбер СС 1 , DC , АА 1 соответственно.

Куб и несколько задач по стереометрии с ЕГЭ.

В пособии “ЕГЭ 2005. Математика. Типовые тестовые задачи” (Корникова Т. А. и др.) Содержит 10 задач (С4) по стереометрии, объединенных общей идеей: дана треугольная призма АВСА 1 В 1 С 1 стороны основания АВ и ВС взаимно перпендикулярны и перпендикулярны ребру ВВ 1 , АВ=ВС=ВВ 1 , вершина А является вершиной конуса (или центром одного из оснований цилиндра, или центром сферы), основание конуса (сфера или второе основание цилиндра) проходит через середину одного ребра призмы, длина его известна. Надо найти объем или поверхность конуса (сферы, цилиндра).

Общий пример решения:

Данную призму дополнить до куба. Шестиугольник DEFKLM – сечение куба плоскостью основания конуса, окружность которого проходит через середину А 1 В 1 , А – вершина конуса, или

DEFKLM – сечение куба плоскостью основания цилиндра, окружность которого проходит через середину А 1 В 1 , А – центр второго основания цилиндра, или это сечение куба плоскостью большого круга сферы с центром А, сфера которого проходит через середину А 1 В 1 .

Шестиугольник DEFKLM – сечение куба плоскостью, проходящей через середину рёбер А 1 В 1 , ВВ 1 , ВСЖ при построении получаются точки K , L , M , которые являются серединами соответствующих рёбер. Стороны этого шестиугольника являются гипотенузами треугольников DB 1 E , EBF , FCK , KQL , LRM , MA 1 D , катеты которых равны половине ребра куба. Тогда центр этого шестиугольника является центром описанной около него окружности, которая пересекает рёбра куба в точках D , E , F , K , L и М, радиус этой окружности
, где А 1 В 1 = а .

AO EL, т . к . EAL – равнобедренный: AL = AE .

( ABE u EAL – прямоугольные, AB = AQ = а, BE = LQ = )

EO =OL как середина диагонали ЕL шестиугольника DEFKLM , т. е. АО – медиана,а по свойствам равнобедренного треугольника и высота. Аналогично доказывается АО DK . Так как АО перпендикулярна к двум пересекающимся прямым плоскости шестиугольника, то АО перпендикулярна ко всей плоскости.

Если А – вершина конуса то АО – его высота, если А – центр второго основания цилиндра, то АО- высота цилиндра.

АВС: АС=
, P – точки пресечения диагоналей основания куба, АР=
, РР 1 =АА 1 = а . ОР=РР 1 = , тогда из прямоугольного РОА АО=
. И так АО=
.

Тогда, если идёт речь о конусе:

(из
).

Ответ:

Если речь идёт цилиндре:

Ответ:

Если речь идёт о сфере:

Ответ: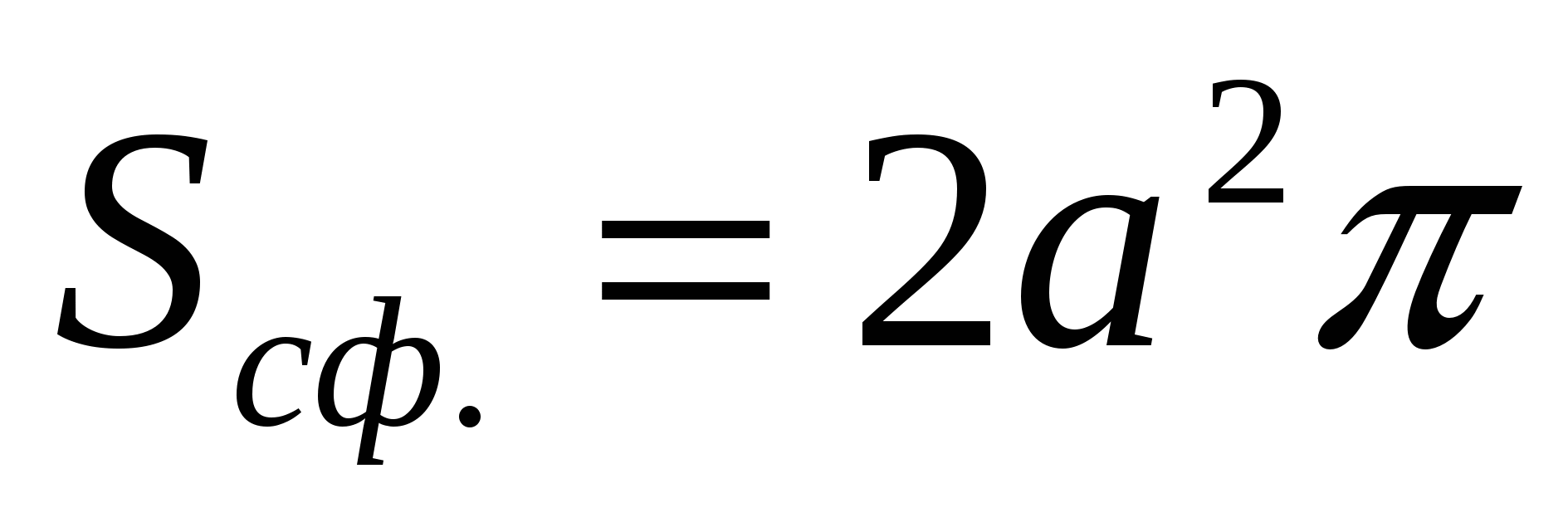

Корникова Т. А. и др. типовые тестовые задания. ЕГЭ – 2005

Вариант 6.

Задача. Даны призма АВСА 1 В 1 С 1 и цилиндр. Стороны АВ и ВС основания призмы перпендикулярны ребру ВВ 1 и взаимно перпендикулярны. Центром основания цилиндра служит точка А 1 окружность второго основания проходит через середину ребра А 1 В 1 .

Найдите площадь полной поверхности цилиндра, если ВВ 1 =АВ=ВС=10. Найдите его объём.

Решение:

.
.

Цели урока

Формирование у учащихся навыков решения задач на построение сечений.
Формирование и развитие у учащихся пространственного воображения.
Развитие графической культуры и математической речи.
Формирование умения работать индивидуально и в коллективе.

Тип урока: урок формирования и совершенствования знаний.

Формы организации учебной деятельности: групповая, индивидуальная, коллективная.

Техническое обеспечение урока: компьютер, мультимедийный проектор, экран, набор геометрических тел (куб, параллелепипед, тетраэдр).

ХОД УРОКА

1. Организационный момент

Класс разбивается на 3 группы по 5-6 человек. На каждом столе – индивидуальные и групповые задания по построению сечения, набор тел. Знакомство учащихся с темой и целями урока.

2. Актуализация опорных знаний

Опрос теории:

– Аксиомы стереометрии.
– Понятие параллельных прямых в пространстве.
– Теорема о параллельных прямых.
– Параллельность трех прямых.
– Взаимное расположение прямой и плоскости в пространстве.
– Признак параллельности прямой и плоскости.
– Определение параллельности плоскостей.
– Признак параллельности двух плоскостей.
– Свойства параллельных плоскостей.
– Тетраэдр. Параллелепипед. Свойства параллелепипеда.

3. Изучение нового материала

Слово учителя: При решении многих стереометрических задач используется сечение многогранника плоскостью. Назовем секущей плоскостью многогранника любую плоскость, по обе стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает грани по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
С помощью рисунков 38-39 давайте выясним: Какое количество сторон может иметь сечение тетраэдра и параллелепипеда?

Учащиеся анализируют рисунки и делают выводы. Учитель корректирует ответы учащихся, указывая на тот факт, что если секущая плоскость пересекает две противоположные грани параллелепипеда по каким-то отрезкам, то эти отрезки параллельны.

Анализ решения задач 1, 2, 3, приведенных в учебнике (устная коллективная работа).

4. Закрепление изученного материала (по группам)

1 группе: объясните, как построить сечение тетраэдра плоскостью, проходящей через данные точки М, N, К и в задачах 1-3 найти периметр сечения, если М, N, К – середины ребер и каждое ребро тетраэдра равно а .

2 группе: объясните, как построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунках выделены), в задачах 1-4 и 6 найдите периметр сечения, если ребро куба равно а. в задаче 5докажите, что АЕ = а /3

3 группе: построить сечение параллелепипеда АВСDА 1 В 1 С 1 D 1 плоскостью, проходящей через точки:

Все выполненные задания группа защищает у доски, с использованием слайдов.

5. Самостоятельная работа № 85, № 105.

6. Подведение итогов урока

Оценка работы учащихся на уроке.

7. Домашнее задание: индивидуальные карточки.