Из графиков видно что:

1. Графики синуса и косинуса колеблются в пределах между -1 и 1
2. Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90 o
3. Кривые синуса и косинуса непрерывны и повторяются с периодом 360 o , кривая тангенса имеет разрывы и повторяется с периодом 180 o .

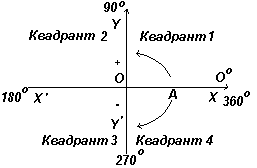На рис. слева показаны перпендикулярные оси ХХ" и YY"; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О - отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке - отрицательным.

График. Положительное или отрицательное
направление при движении по окружности.

Пусть ОА вращается против часовой стрелки таким образом, что Θ 1 - любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
Пусть ОА вращается дальше таким образом, что Θ 2 - любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Пусть ОА вращается дальше таким образом, что Θ 3 - любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

График. Поcтроение углов в
различных квадрантах.

Пусть ОА вращается дальше таким образом, что Θ 4 - любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем - только тангенс, в четвертом только косинус, что и показано на рис. слева.

Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0 o и 360 o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin -1 , получим ответ 19,03 o . Однако существует второй угол между 0 o и 360 o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180 o - 19,03 o = 160,97 o . Таким образом, 19,03 o и 160,97 o - это углы в диапазоне от 0 o до 360 o , синус которых равен 0,3261.

Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.

Пример 1

Найти все углы в диапазоне от 0 o до 360 o , синус которых равен -0,7071

Решение:
Углы, синус которых равен -0,7071 o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).

График. Нахождение всех углов по
заданному значению синуса (пример)

Из следующего рисунка Θ = arcsin 0,7071 = 45 o . Два угла в диапазоне от 0 o до 360 o , синус которых равен -0,7071, это 180 o +45 o =225 o и 360 o - 45 o = 315 o .

Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по
заданному значению синуса (пример)

Пример 2

Найти все углы между 0 o и 360 o , тангенс которых равен 1, 327.

Решение:
Тангенс положителен в первом и третьем квадрантах - рис. слева.
График. Нахождение всех углов по

Из рис ниже Θ = arctg1,327= 53 o .
Два угла в диапазоне от 0 o до 360 o , тангенс которых равен 1,327, это 53 o и 180 o + 53 o , т.е. 233 o .
График. Нахождение всех углов по
заданному значению тангенса (пример)

Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o . Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30 o вертикальная составляющая - это ТS, а горизонтальная - ОS.

Из определения тригонометрических функций
sin30 o =TS/TO=TS/1, т.е. TS= sin30 o и cos30 o =OS/TO=OS/1, т.e. OS=cos30 o

Вертикальную составляющую TS можно перенести на график в виде T"S", что равно значению, соответствующему углу 30 o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.

Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90 o .

Периодические функции и период
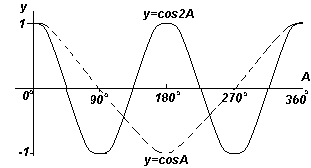
Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями .
Функции y=sinA и y=cosA повторяются через каждые 360 o (или 2π радиан), поэтому 360 o называется периодом этих функций. Функции y=sin2A и y=cos2A повторяются через каждые 180 o (или π радиан),поэтому 180 o - это период для данных функций.
В общем случае если y=sinpA и y=cospA (где р - константа), то период функции равен 360 o /p (или 2π/p радиан). Следовательно, если y=sin3A, то период этой функции равен 360 o /3= 120 o , если y=cos4A, то период этой функции равен 360 o /4= 90 o .

Амплитуда
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды - 4. Аналогично для y=5cos2A амплитуда равна 5, а период - 360 o /2= 180 o .

Пример 3.
Построить y=3sin2A в диапазоне от А= 0 o до А=360 o .

Решение:
Амплитуда =3, период = 360 o /2 =180 o .

Пример 4.
Построить график y=4cos2x в диапазоне от х=0 o до х=360 o

Решение:
Амплитуда = 4. период = 360 o /2 =180 o .

Углы запаздывания и опережения
Кривые синуса и косинуса не всегда начинаются в 0 o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α - сдвиг фазы относительно y=sinA и y=cosA.

Составив таблицу значений, можно построить график функции y=sin(A-60 o), показанный на рис. слева. Если кривая y=sinA начинается в 0 o , то кривая y=sin(A-60 o) начинается в 60 o (т.е. ее нулевое значение на 60 o правее). Таким образом, говорят, что y=sin(A-60 o) запаздывает относительно y=sinA на 60 o .
График. y=sin(A-60 o) (синусоида).

Составив таблицу значений, можно построить график функции y=cos(A+45 o), показанный на рис. ниже.
Если кривая y=cosA начинается в 0 o , то кривая y=cos(A+45 o) начинается на 45 o левее (т.е. ее нулевая величина находится на 45 o раньше).
Таким образом, говорят, что график y=cos(A+45 o) опережает график y=cosA на 45 o .
График. y=cos(A+45 o) (косинусоида).

В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
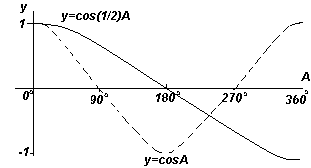
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90 o левее, т.е. опережает ее на 90 o . Следовательно, cosA=sin(A+90 o).

Пример 5.
Построить график y=5sin(A+30 o) в диапазоне от А=0 o до А=360 o

Решение:
Амплитуда = 5, период = 360 o /1 = 360 o .
5sin(A+30 o) опережает 5sinA на 30 o т.е. начинается на 30 o раньше.
График y=5sin(A+30 o) (синусоида).

Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0 o до А=360 o .

Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p , следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на (π/3)/2, т.е. на π/6 радиан или на 30 o

Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.

Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором . Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.

Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда
Т=2π/ ω (с), где
Т - это период
Число полных периодов, проходящих за 1 секунду, называется частотой f.
Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц
Следовательно, угловая скорость
ω=2πf рад/с.

Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то
А - амплитуда
ω - угловая скорость
2π/ ω - период Т, с
ω/2π - частота f, Гц
α - угол опережения или запаздывания (относительно y=Аsinωt) в радианах, он называется также фазовым углом.

Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)

Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω =90π, следовательно,
период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс
частота f = 1/Т = 1/0,022 = 45,46 Гц
фазовый угол α = 0,26 рад. = (0,26*180/π) o = 14,9 o .

Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).

Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19 o
Итак, смещение равно 3sin(110 πt + 0,33).

Пример 9.
Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти:
а) Амплитуду, период, частоту и фазовый угол (в градусах)
б) значение напряжения при t =0
в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В.
Решение :
а) Амплитуда равна 350 В, угловая скорость равна ω=40π
Следовательно,
период Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31 o с запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31 o)=-180,25 В
в) Если t =10 мс, то v=350sin(40π10/10 3 -0,542)=350sin(0,714)=350sin41 o =229,6 В
г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

График. Колебательный механизм
(пример, синусоида).

v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35 o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс

Параллельный перенос.

ПЕРЕНОС ВДОЛЬ ОСИ ОРДИНАТ

f(x) => f(x) - b
Пусть требуется построить график функции у = f(х) - b. Нетрудно заметить, что ординаты этого графика для всех значений x на |b| единиц меньше соответствующих ординат графика функций у = f(х) при b>0 и на |b| единиц больше - при b 0 или вверх при b Для построения графика функции y + b = f(x) следует построить график функции y = f(x) и перенести ось абсцисс на |b| единиц вверх при b>0 или на |b| единиц вниз при b

ПЕРЕНОС ВДОЛЬ ОСИ АБСЦИСС

f(x) => f(x + a)
Пусть требуется построить график функции у = f(x + a). Рассмотрим функцию y = f(x), которая в некоторой точке x = x1 принимает значение у1 = f(x1). Очевидно, функция у = f(x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 - a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции. Следовательно, график функции у = f(x + a) может быть получен параллельным перемещением графика функции y = f(x) вдоль оси абсцисс влево на |a| единиц при a > 0 или вправо на |a| единиц при a Для построения графика функции y = f(x + a) следует построить график функции y = f(x) и перенести ось ординат на |a| единиц вправо при a>0 или на |a| единиц влево при a

Примеры:

1.y=f(x+a)

2.y=f(x)+b

Отражение.

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = F(-X)

f(x) => f(-x)
Очевидно, что функции y = f(-x) и y = f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y = f(-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х. Таким образом, получаем следующее правило.
Для построения графика функции y = f(-x) следует построить график функции y = f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f(-x)

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = - F(X)

f(x) => - f(x)
Ординаты графика функции y = - f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило.
Для построения графика функции y = - f(x) следует построить график функции y = f(x) и отразить его относительно оси абсцисс.

Примеры:

1.y=-f(x)

2.y=f(-x)

3.y=-f(-x)

Деформация.

ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ ОРДИНАТ

f(x) => k f(x)
Рассмотрим функцию вида y = k f(x), где k > 0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в k раз больше ординат графика функции у = f(x) при k > 1 или 1/k раз меньше ординат графика функции y = f(x) при k Для построения графика функции y = k f(x) следует построить график функции y = f(x) и увеличить его ординаты в k раз при k > 1(произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/k раз при k
k > 1 - растяжение от оси Ох
0 - сжатие к оси OX

ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ АБСЦИСС

f(x) => f(k x)
Пусть требуется построить график функции y = f(kx), где k>0. Рассмотрим функцию y = f(x), которая в произвольной точке x = x1 принимает значение y1 = f(x1). Очевидно, что функция y = f(kx) принимает такое же значение в точке x = x2, координата которой определяется равенством x1 = kx2, причем это равенство справедливо для совокупности всех значений х из области определения функции. Следовательно, график функции y = f(kx) оказывается сжатым (при k 1) вдоль оси абсцисс относительно графика функции y = f(x). Таким образом, получаем правило.
Для построения графика функции y = f(kx) следует построить график функции y = f(x) и уменьшить его абсциссы в k раз при k>1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в 1/k раз при k
k > 1 - сжатие к оси Оу
0 - растяжение от оси OY

Работу выполнили Чичканов Александр, Леонов Дмитрий под руководством Ткач Т.В, Вязовова С.М, Островерховой И.В.
©2014

§ 11. Графики синуса и косинуса
Повторить: § 5. Часы, или современный взгляд на тригонометрию.
Построим график функции y = sin x. При этом нам опять при-
годятся часы из § 5.
Если x = 0, то, очевидно, y = 0. Когда x воз-
растает от 0 до π/2, число sin x возрастает от 0 до
1 (представьте себе, как меняется ордината кон-
ца стрелки на наших фирменных часах). Участок
графика для x от 0 до π/2 изображен на рис. 11.1 .
При малых x наш график близок к прямой
y = x: вспомним, что при малых x верна при-
ближенная формула sin x ≈ x. Можно сказать,
что прямая y = x касается кривой с уравнением
y = sin x в точке (0; 0). Заметим также, что наш участок графика
расположен ниже этой прямой: ведь для острых углов x, измерен-
ных в радианах, выполнено неравенство sin x < x.
Чем ближе x к π/2, тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось ординат,
колеблясь по отрезку [−1; 1], быстрее всего движется в середине
отрезка и замедляется у его краев: мы это уже обсуждали в § 5.

от π до 3π/2, sin x уменьшается от 0 до −1, а когда x возрастает от 3π/2 до 2π, возрастает от −1 до 0. Итак, участок графика для 0 6 x 6 2π готов (рис. 11.2 б). Заметим, кстати, что кривая на рис11.2 а симметрична относительно вертикальной прямой с уравнением x = π/2. В самом деле, формула приведения sin(π/2 − x) = sin x показывает, что точки с абсциссами x и π − x имеют на графике одинаковые ординаты и, стало быть, симметричны относительно прямой x = π/2 (рис.11.3 а).

Задача 11.1. Запишите уравнение прямой, касающейся графика функции y = sin x в точке с координатами (π; 0).

Кривая на рис 11.2 б центрально симметрична относительно точки с координатами (π; 0); это следует из другой формулы приведения: sin(2π − x) = − sin x (рис.11.3 б).

После того, как у нас есть участок графика функции y = sin x для 0 6 x 6 2π, весь график строится уже просто. В самом деле, когда конец стрелки прошел путь 2π, стрелка вернулась в исходное положение; при дальнейшем движении все будет повторяться. Значит, график будет состоять из таких же кусков, как на рис 11.2 б. Окончательно график функции y = sin x выглядит так, как на рис.11.4 . При этом участки графика при x , , [−2π; 0],. . . получаются из графика на рис11.2 б сдвигом вдоль оси абсцисс на 2π, 4π, −2π,. . . соответственно. Это - просто переформулировка того факта, что функция y = sin x имеет период 2π.

Рис. 11.4. y = sin x.

Рис. 11.5. y = cos x.

Теперь построим график функции y = cos x. Можно было бы строить его так же, как мы строили график синуса. Мы, однако, изберем другой путь, который позволит использовать уже имеющуюся у нас информацию.

Именно, воспользуемся формулой приведения sin(x + π/2) = = cos x. Эту формулу можно понимать так: функция y = cos x принимает те же значения, что и функция y = sin x, но на π/2 раньше. Например, функция y = sin x принимает значение 1 при x = π/2, а функция y = cos x = sin(x + π/2) принимает это же значение уже при x = 0. На графике это означает следующее: для каждой точки графика y = sin x есть точка графика y = cos x, у которой ордината та же, а абсцисса на π/2 меньше (рис. 11.5 ). Стало быть, график y = cos x получится, если сдвинуть график y = sin x вдоль оси абсцисс на π/2 влево. На рис.11.5 график функции y = cos x изображен сплошной кривой.

Итак, мы выяснили, что график косинуса получается преобра-

зованием (сдвигом) из графика синуса. Случаи, когда график одной функции можно получить преобразованием из графика другой функции, интересны и сами по себе, поэтому скажем о них несколько слов.

Как, например, будет выглядеть график функции y = 2 sin x? Ясно, что ординаты точек этого графика получаются из ординат соответствующих точек графика y = sin x умножением на 2, так что наш график изобразится сплошной кривой на рис. 11.6 . Можно сказать, что график y = 2 sin x получается из графика y = sin x растяжением в два раза вдоль оси ординат.

Рис. 11.6. y = 2 sin x.

Рис. 11.7. y = sin 2x.

Теперь построим график функции y = sin 2x. Легко понять,

Рис. 11.8. y = sin(2x + π/3).

что функция y = sin 2x принимает те же самые значения, что и функция y = sin x, но при в два раза меньших значениях x. Например, функция y = sin x принимает значение 1 при x = π/2, а функция y = sin 2x - уже при x = π/4; иными словами, чтобы получить график y = sin 2x, надо абсциссы всех точек графика y = sin x уменьшить в два раза, а ординаты оставить неизменными. То, что получается, изображено на рис. 11.7 . Можно сказать, что график y = sin 2x (сплошная линия на рис.11.7 ) получается из графика y = sin x сжатием в 2 раза к оси ординат.

Попробуем еще построить график функции y = sin(2x + π/3). Понятно, что он должен получаться каким-то преобразованием из графика y = sin 2x. На первый взгляд может показаться, что это преобразование - сдвиг влево на π/3 вдоль оси абсцисс, по аналогии с тем, что изображено на рис.11.5 . Однако, если бы это было так, то вышло бы, например, что функция y = sin(2x + π/3) принимает значение 1 при x = π/4 − π/3 = π/12, что не соответствует действительности (проверьте!). Правильно рассуждать так: sin(2x + π/3) = sin 2(x + π/6), так что функция y = sin(2x+π/3) принимает те же значения, что и функция y = sin 2x, но на π/6 раньше. Так что сдвиг влево - не на π/3, а на π/6 (рис.11.8 ).

Кривые, являющиеся графиками функций y = a sin bx, где a 6= 0, b 6= 0, называются синусоидами. Заметим, что кривой «косинусоида» вводить не надо: как мы видели, график косинуса - это та же кривая, что и график синуса, только иначе расположен-

ная относительно осей координат.

Задача 11.2. Каковы координаты точек, помеченных на рис. 11.8 вопросительными знаками?

Задача 11.3. Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы увидите, что она оказалась разрезанной по волнистой линии. Докажите, что эта волнистая линия является синусоидой.

Задача 11.4. Постройте графики функций:

г) y = 3 cos 2x;

а) y = − sin x; б)

в) y = cos(x/2);

ж) y = sin(πx). д)

Замечание. Если вы строите графики тригонометрических функций на клетчатой бумаге, удобно выбрать немного разные масштабы по осям, с тем чтобы на оси абсцисс числу π соответствовало целое число клеточек. Например, часто выбирают такой масштаб: по оси ординат отрезок длины 1 занимает две клеточки, по оси абсцисс отрезок длины π занимает 6 клеточек.

Задача 11.5. Постройте графики функций:

а) y = arcsin x; б) y = arccos x.

Посмотрим, как выглядят на графиках уже известные нам решения уравнений sin x = a и cos x = a. Эти решения являются абсциссами точек пересечения горизонтальной прямой y = a с графиком функций y = sin x (соответственно y = cos x). На рис. 11.9 ,11.10 хорошо видны две серии решений, получающихся при −1 < a < 1.

По графикам синуса и косинуса видно, на каких промежутках эти функции возрастают, а на каких убывают. Ясно, например, что функция y = sin x возрастает на отрезках [−π/2; π/2],