1 из 27

Презентация - Объемы тел

632
просмотра

Текст этой презентации

Объемы тел
Составитель: Юминова Олеся Викторовна, учитель математики Красноярского аграрного техникума

Цели урока:
Ввести понятие объема тел, его свойств, единиц измерения объёма. Повторить с учащимися формулы для нахождения объёма параллелепипеда, куба. Познакомить учащихся с объёмами прямой призмы, пирамиды, цилиндра и конуса, руководствуясь наглядно-иллюстративными соображениями.

Подобно тому как все искусстватяготеют к музыке, все наукистремятся к математике. Д. Сантаяна

Геометрия есть искусство правильно рассуждать на неправильных чертежах. Пойа Д.

Площадь Площадь многоугольника- это положительная величина той части плоскости, которую занимает многоугольник.
Объем Объем тела – это положительная величина той части пространства, которую занимает геометрическое тело.

Свойства площадей: 1. Равные многоугольники имеют равные площади
Свойства объемов: 1. Равные тела имеют равные объемы
F1
F2
F1
F2

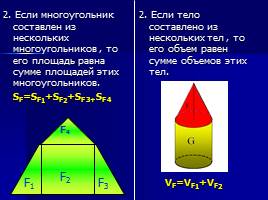
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. SF=SF1+SF2+SF3+SF4
2. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел. VF=VF1+VF2

Площадь За единицу измерения площадей берут квадрат, сторона которого равна единице измерения отрезков. 1 км2, 1 м2, 1 дм2, 1 см2, 1 мм2 , 1 а, 1 га и т.д.
Объем За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называют кубическим сантиметром и обозначают см3. Аналогично определяют 1 м3, 1 дм3, 1 см3 , 1 мм3 и т.д.
1
1
1
1
1

Площадь Равновеликими называются геометрические фигуры, имеющие равные площади
Объем Равновеликими называются тела, объемы которых равны
VF=VF1
F2
F1
F2
F1
SF=SF1

В стереометрии рассматриваются объемы многогранников и объемы тел вращения.

Объем прямоугольного параллелепипеда:
а-длина b-ширина с- высота V=a.b.c Sосн= a.b V=Sосн.H

Объем куба:
V=a3 V=Sосн.H
Sосн=a2

Объем прямой призмы:
V=Sосн.H
Vпарал=Sосн.H S осн=2.SABC По свойству объемов Vпарал= 2.SABС.H V призмы = (V парал) :2 V призмы = (2.SABС. H): 2

Объем пирамиды:
У 2 и 3 пирамиды- SC- общая, тр CC1B1= тр CBB1 У 1 и 3 пирамиды- СS- общая, тр SAB= тр BB1S V1=V2=V3 V призмы= 3 V пирам Vпирамиды=1 V призмы 3 Vпирамиды=1 Sосн.H 3
Достроим пирамиду ABCS до призмы. Достроенная призма будет состоять из 3 пирамид- SABC, SCC1B1, SCBB1

Объем цилиндра:
Обозначения: R - радиус основания H - высота L - образующая L=H V - объем цилиндра
V = ПR2H - объём V= Sосн.H Sосн= ПR2

Конус:
ОБОЗНАЧЕНИЯ: R - радиус основания L - образующая конусаH – высота V – объем V=1ПR2Н 3 - объём

Это интересно:
В геологии существует понятие "конус выноса". Это форма рельефа, образованная скоплением обломочных пород, вынесенных горными реками на предгорную равнину или в более плоскую широкую долину.
В биологии есть понятие "конус нарастания". Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
"Конусами" называется семейство морских молюсков подкласса пережнежаберных. Укус конусов очень опасен. Известны смертельные случаи.
В физике встречается понятие "телесный угол". Это конусообразный угол, вырезанный в шаре.

Проверь свои знания:
Сформулируйте понятие объема. Сформулируйте основные свойства объемов тел. Назовите единицы измерения объема тел. Назовите формулу для измерения объема - прямоугольного параллелепипеда; - объема куба; - объем прямой призмы; - объем пирамиды; - объем цилиндра и объем конуса. Изменится ли объем цилиндра, если радиус его основания увеличить в 2 раза, а высоту уменьшить в 4 раза? V = ПR2H V=П(2R)2 .H =П4R2. H =ПR2. H 4 4 Основаниями двух пирамид с равными высотами являются четырехугольники с соответственно равными сторонами. Равны ли объемы этих пирамид? Из каких тел состоит тело, полученное вращением равнобедренной трапеции вокруг большего основания?

Домашняя работа:
Выучить формулы объемов тел, определения. № 648(а,в), № 685, № 666(а,в)

Закрепление пройденного материала:
Задача №1 Три латунных куба с ребрами 3см, 4 см и 5 см переплавлены в один куб. Какое ребро у этого куба? + + =

Решение: VF=VF1+VF2 +VF3 VF1=33 =27 (см3) VF2=43 =64 (см3) VF3=53 =125 (см3) VF=27+64 +125=216 (см3) VF=а3 а3=216 (см3) а= 6 (см) Ответ: ребро куба равно 6 см.

Задача №2
Найдите объем правильной четырехугольной пирамиды, высота которой равна 12 см, а сторона основания 13 см.

Объем – это количество занимаемого телом пространства, а плотность равна массе тела, поделенной на его объем. Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см 3) или кубических метрах (м 3). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см 3) или граммы на миллилитр (г/мл).

Шаги

Часть 1

Вычисление объема тела правильной формы

Определите форму тела. Знание формы позволит вам выбрать правильную формулу и провести измерения, необходимые для расчета объема.

Выберите для вычисления объема правильное уравнение. Для тела каждого типа существует своя формула, позволяющая рассчитать занимаемый им объем. Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье Как находить объем .

• Сфера : V = (4/3) π r 3 , где r – радиус сферы, а π – константа, равная примерно 3,14.
• Конус : V = (1/3) π r 2 h , где r – радиус круглого основания, h – высота конуса, π – константа, равная приблизительно 3,14.
• Куб : V = s 3 , где s – длина ребра куба (стороны любой из его квадратных граней).
• Прямоугольный параллелепипед : V = l x w x h , где l – длина прямоугольной грани, w – ее ширина, h – высота параллелепипеда (призмы).
• Цилиндр : V= π r 2 h , где r – радиус круглого основания, h – высота цилиндра, π – константа, составляющая примерно 3,14.
• Пирамида : V= (1/3) b x h , где b – площадь основания пирамиды (l x w), h – высота пирамиды.

1. Произведите необходимые измерения. Они будут зависеть от того, с телом какого вида вы имеете дело. Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.

   • Радиус круга равен половине его диаметра. Измерьте диаметр, приложив к середине круга линейку, после чего поделите полученный результат на 2.
   • Радиус сферы измерить немного сложнее, однако и это не составит труда, если вы воспользуетесь методами, подробно изложенными в статье Как найти радиус шара .
   • Длину, ширину и высоту тела можно определить, приложив к нему линейку в соответствующих местах и записав результаты измерений.

2. Вычислите объем. Выяснив форму тела, выберите подходящую формулу и измерьте входящие в нее величины. Подставьте в формулу измеренные значения и выполните необходимые математические действия. В результате вы получите объем тела.

   • Помните о том, что ответ должен выражаться в кубических единицах независимо от того, какой системой единиц вы пользуетесь (метрической либо другой). После полученной величины обязательно напишите единицы, в которых она измеряется.

Часть 2

Вычисление объема тела неправильной формы

1. Определите объем тела по количеству вытесняемой им воды. Тело может иметь неправильную форму, что затрудняет измерение его размеров и ведет к неточному определению объема. В этом случае прекрасно работает метод, заключающийся в определении объема воды, вытесняемой телом при полном погружении.

   • Данный метод можно применить и для нахождения объема тел правильной формы, чтобы избежать вычислений.

2. Наполните водой мерный цилиндр (мензурку). Это лабораторная емкость с метками на боковой поверхности, позволяющая измерять объем жидкостей. Выберите достаточно большой цилиндр, чтобы в него полностью поместился измеряемый объект. Необходимо наполнить цилиндр водой так, чтобы в нее можно было полностью погрузить объект, но при этом она не выливалась. Запишите начальный объем воды без измеряемого тела.

   Аккуратно поместите в емкость измеряемое тело. Делайте это плавно, чтобы не уронить объект, поскольку в этом случае часть воды может выплеснуться из мерного цилиндра. Убедитесь в том, что тело полностью погрузилось в воду. Запишите новые показания уровня воды в емкости, вновь расположившись так, чтобы ваши глаза находились на одном уровне с мениском.

   • Если при погружении тела часть воды выплеснулась, попробуйте повторить с самого начала, налив меньше воды или взяв больший мерный цилиндр.

3. Вычтите из окончательного уровня воды его первоначальное значение. Количество вытесненной предметом воды будет равняться его объему в кубических сантиметрах. Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.

   • Например, если сначала уровень воды был 35 мл, а после опускания в нее предмета поднялся до 65 мл, объем этого предмета составляет 65 – 35 = 30 мл, или 30 см 3 .

Часть 3

Вычисление плотности

1. Определите массу предмета. Масса объекта соответствует количеству материи, из которой он состоит.

Убедитесь, что тело является водонепроницаемым, так как описанный метод подразумевает погружение тела в воду. Если тело полое или в него может проникнуть вода, то вы не сможете точно определить его объем, используя этот метод. Если тело поглощает воду, убедитесь, что вода не повредит его. Не погружайте в воду электрические или электронные предметы, так как это может привести к поражению электрическим током и/или к повреждению самого предмета.

• Если возможно, запечатайте тело в водонепроницаемый пластиковый пакет (предварительно выпустив из него воздух). В этом случае вы вычислите довольно точное значение объема тела, так как объем пластикового пакета, скорее всего, будет небольшим (по сравнению с объемом тела).

Найдите емкость, в которой помещается тело, объем которого вы вычисляете. Если вы измеряете объем небольшого предмета, воспользуйтесь мерным стаканом с нанесенной градуировкой (шкалой) объема. В противном случае найдите емкость, объем которой можно легко вычислить, например, емкость в форме прямоугольного параллелепипеда, куба или цилиндра (стакан тоже можно рассматривать как емкость цилиндрической формы).

• Возьмите сухое полотенце, чтобы положить на него тело, вытащенное из воды.

Наполните емкость водой так, чтобы в нее можно было полностью погрузить тело, но при этом оставьте достаточно места между поверхностью воды и верхней кромкой емкости. Если основание тела имеет неправильную форму, например, закругленные нижние углы, заполнить емкость так, чтобы поверхность воды достигала часть тела правильной формы, например, прямые прямоугольные стенки.

Отметьте уровень воды. Если емкость с водой прозрачная, отметьте ее уровень с внешней стороны емкости при помощи водостойкого маркера. В противном случае отметьте уровень воды с внутренней стороны емкости, используя цветную клейкую ленту.

• Если вы используете мерный стакан, то отмечать ничего не нужно. Просто запишите уровень воды согласно градуировке (шкале) на стакане.

Погрузите тело полностью в воду. Если оно поглощает воду, подождите, по крайней мере, тридцать секунд, а затем вытащите тело из воды. Уровень воды должен опуститься, так как часть воды находится в теле. Удалите отметки (маркер или клейкую ленту) о предыдущем уровне воды и отметьте новый уровень. Затем еще раз погрузите тело в воду и оставьте его там.

Если тело плавает, прикрепите к нему тяжелый предмет (в качестве грузила) и продолжите вычисления с ним. После этого повторите вычисления исключительно с грузилом, чтобы найти его объем. Затем вычтите объем грузила из объема тела с прикрепленным грузилом и вы найдете объем тела.

• При вычислении объема грузила прикрепите к нему то, чем вы крепили грузило к рассматриваемому телу (например, ленту или булавки).

Отметьте уровень воды с погруженным в нее телом. Если вы используете мерный стакан, запишите уровень воды согласно шкале на стакане. Теперь вы можете вытащить тело из воды.

Изменение объема воды равно объему тела неправильной формы. Способ измерения объема тела с помощью емкости с водой основан на том, что при погружении тела в жидкость объем жидкости с погруженным в нее телом увеличивается на величину объема тела (то есть тело вытесняет объем воды, равный объему этого тела). В зависимости от формы используемой емкости с водой существуют различные способы вычисления объема вытесненной воды, который равен объему тела.

Если вы использовали мерный стакан, то у вас записаны два значения уровня воды (ее объема). В этом случае из значения объема воды с погруженным в нее телом вычтите значение объема воды до погружения тела. Вы получите объем тела.

Если вы использовали емкость в форме прямоугольного параллелепипеда, измерьте расстояние между двумя метками (уровень воды до погружения тела и уровень воды после погружения тела), а также длину и ширину емкости с водой. Объем вытесненной воды найдите посредством перемножения длины и ширины емкости, а также расстояния между двумя метками (то есть вы вычисляете объем небольшого прямоугольного параллелепипеда). Вы получите объем тела.

• Не измеряйте высоту емкости с водой. Измерьте только расстояние между двумя метками.
• Используйте

другие презентации об объёме

«Конус» - P. Геометрия. О. А. Конус, усеченный конус. O. В.

«Геометрия Сфера и шар» - 6) которым отвечают два условия поставленной задачи. 3) Высота пирамиды MM0, как катет треугольника MM0K, равна. Комбинация шара с призмой: Задачи: У Архимеда нет такой основополагающей работы, как «Элементы» у Евклида. Тогда диаметр сферы равен высоте усеченного конуса. Вывод: 3) По условию задачи имеем уравнение.

«Сфера и шар» - Определение. Сечение, проходящее через центр шара, - большой круг. (диаметральное сечение). Задача на тему шар (д/з). Сечение шара плоскостью. Содержание. Автор: Кудрякова Анна ученица 11 «Б» класса. Сказка о возникновении шара. Сфера всегда широко применялось в различных областях науки и техники. Данная точка называется центром сферы, а данное расстояние – радиусом сферы.

«Конус 11 класс» - Конус. Конус- тело ограниченное конической поверхностью и кругом с границей L. Площадь боковой поверхности конуса. Усечённый конус. Площадь боковой поверхности усечённого конуса. Объем конуса равен одной трети произведения площади основания на высоту. Сингапайскя СОШ. V = 1/3sосн.h. Площадь полной поверхности конуса.

Применяя формулу для площади криволинейного сектора, получим:

Пример 6.
Найти площадь фигуры, ограниченной лемнискатой Бернулли
Область определения функции:

Учитывая симметричность фигуры, вычислим сначала площадь той ее части,

которая лежит в первом квадранте, затем результат умножим на 4:

Замечание .

Если фигура имеет «сложную» форму, то ее следует разбить лучами, выходящими из полюса, на криволинейные секторы так, чтобы можно было применить к каждому сектору уже известные формулы. Затем нужно сложить площади этих частей и получить площадь всей фигуры.

§ 3. Вычисление объема тела.

Приступая к изложению данной темы, мы считаем известными формулы для вычисления объемов простейших пространственных тел:

куба, параллелепипеда, призмы, цилиндра.

Например, объем произвольного прямого цилиндра с площадью основания и высотой равен произведению площади основания на высоту:

Выведем формулы для вычисления объемов тел достаточно произвольных форм. Пространственное тело будем обозначать здесь буквой.

Вычисление объема тела по площадям поперечных сечений .

Пусть тело расположено между параллельными плоскостями и. Рассмотрим поперечные сечения тела плоскостями, перпендикулярными к оси.

	площадь поперечного сечения в любой точке,
Теорема .
	тела с известными площадями					поперечных сечений выражается
формулой:
Доказательство .
Разобьем промежуток						на частичные промежутки; пусть
		ранг разбиения . Через каждую точку деления проведем
плоскость перпендикулярно к оси.
Этими плоскостями тело				будет «разрезано»			на частичные тела	Которые
расположены между плоскостями							При этом
Для каждого частичного тела					выбираем промежуточную точку
вычисляем значение

	приближенно (с точностью до бесконечно малых более высокого
порядка) равен объему цилиндрического тела с площадью основания				и высотой
Тогда весь объем приближенно равен сумме:
Эти суммы являются интегральными суммами для функции			Следовательно:
Теорема доказана.

Пример 1.

Объем кругового конуса с высотой и радиусом основания.

В сечении кругового конуса, проведенном в точке перпендикулярно к оси абсцисс, будет круг некоторого радиуса. Площадь круга равна.

Из подобия треугольников получаем:

Тогда объем конуса равен:

Получаем формулу объема конуса:

Пример 2.

Объем эллипсоида

Уравнение эллипсоида можно записать

Эллипсоид расположен между плоскостями и, а его сечение в точке

представляет собой эллипс:

Полуоси этого эллипса равны

Следовательно,

площадь сечения равна

(см. Пример 1 из §2), т.е.

Тогда объем эллипсоида равен:

Получаем формулу объема эллипсоида:

эллипсоида

В частности, при

получаем объем шара:

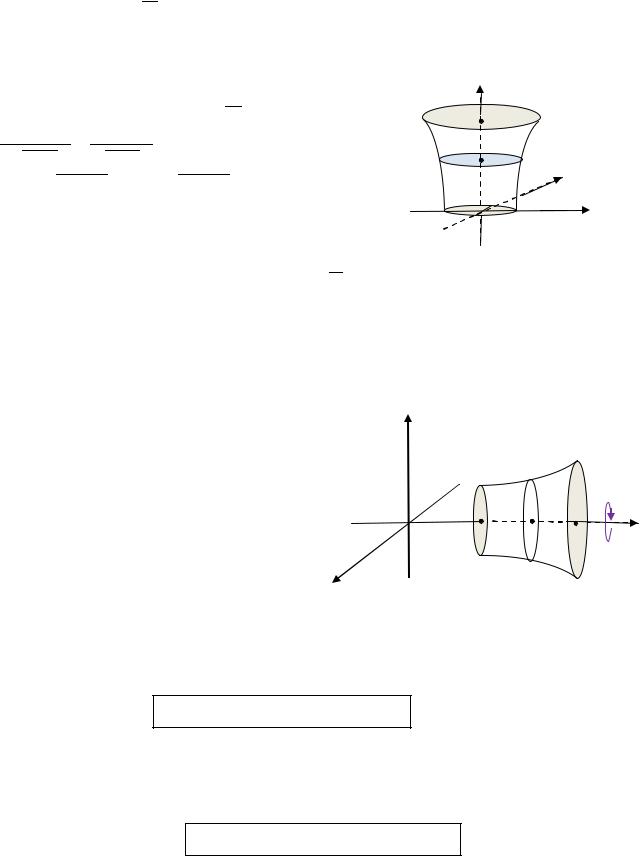
Пример 3.

Найти объем тела, ограниченного поверхностями:

Здесь первое уравнение задает поверхность, которая называется однополостный гиперболоид , а остальные - задают плоскости, параллельные плоскости.

В сечении гиперболоида плоскостью

Объем тела вращения .

Если криволинейную трапецию, ограниченную графиком непрерывной функции

Осью и прямыми		Вращать вокруг оси		То полученное тело
называется телом вращения.
Сечением тела вращения плоскостью,
перпендикулярной к оси абсцисс в любой точке
Является круг радиуса
площадь которого равна
Поэтому объем тела вращения равен:
При вращении вокруг оси обобщенной криволинейной трапеции, ограниченной
графиками функций				И прямыми

, , получаем тело вращения, объем которого вычисляется по формуле:

Если криволинейная трапеция, ограниченная графиком непрерывной функции, осью и прямыми и, вращается вокруг оси, то

объем тела вращения равен:

При вращении обобщенной криволинейной трапеции, ограниченной графиками функций, где, и прямыми и, получаем тело вращения, объем которого вычисляется по формуле:

Пример 4.

Объем тела, образованного

вращением вокруг оси
ограниченной графиком функции
	и осью, равен:

Пример 5.

Найти объем тора .

Тор представляет собой тело, полученное вращением круга радиуса вокруг некоторой оси, находящейся на расстоянии от его центра.

Из уравнения окружности:

Выразим переменную.

Уравнения полуокружностей.

Объем тора равен разности объемов тел,

образованных вращением вокруг оси

ограниченных этими полуокружностями:

Таким образом, объем тора равен:

§ 4. Вычисление площади поверхности.

Площадь поверхности вращения .

Пусть на плоскости даны простая кривая и некоторая ось. Если вращать кривую вокруг этой оси, то она опишет некоторуюповерхность вращения .

Если вписать в эту кривуюломаную линию и вращать ее вместе с кривой, то эта ломаная опишет некоторую поверхность. Эта поверхность может быть боковой поверхностью цилиндра, конуса или усеченного конуса, площади которых вычисляются по известным формулам элементарной геометрии.

Определение .

Площадью поверхности вращения описанной кривой называется предел площади

поверхности, описанной ломаной, при стремлении к нулю наибольшей из длин сторон

этой ломаной.

Приведем без доказательства формулы для вычисления площади поверхности

вращения при различных способах задания кривой.

Если гладкая кривая задана явным уравнением:

То площадь поверхности вращения вокруг оси

вычисляется по формуле:

Если гладкая кривая задана параметрическими уравнениями:

то площадь поверхности вращения вокруг оси

вычисляется по

Если гладкая кривая задана уравнением в полярной системе координат:

То площадь поверхности вращения вокруг полярной оси вычисляется по

Аналогичные формулы будут и при вращении кривой вокруг оси.

Пример 1.

Площадь поверхности шарового пояса радиуса и высотой.

Шаровой пояс получается вращением вокруг оси

части полуокружности

Расположенной над отрезком

Таким образом, площадь поверхности шарового пояса радиуса

и высотой

В частности, при

получаем площадь поверхности сферы:

Пример 2.

Площадь поверхности, образованной вращением вокруг оси

одной арки

циклоиды:

Пример 3.

Площадь поверхности, образованной вращением вокруг полярной оси кардиоиды:

Пример 4.

Площадь поверхности тора .

Тор представляет собой тело, полученное вращением круга радиуса вокруг некоторой оси, находящейся на расстоянии от его центра.

Поверхность тора можно разбить на две поверхности: «ближнюю» и «дальнюю» по отношению к центру тора; эти поверхности получаются вращениями полуокружностей:

Вся площадь поверхности тора равна сумме площадей этих двух

поверхностей:

Таким образом, площадь поверхности тора равна:

Площадь цилиндрической поверхности .

Пусть на плоскости

дана простая кривая

Построим цилиндрическую

поверхность с направляющей и с образующими, параллельными оси.

По этой цилиндрической поверхности проведем кривую. Предполагаем, что эта кривая лежит выше направляющей.

Требуется вычислить площадь той части цилиндрической поверхности, которая лежит «под кривой» .

Если вписать в кривую ломаную линию, то соответствующая ломаная будет вписана и в кривую. Соединив соответствующие вершины ломаных линий, получим боковую поверхность некоторой призмы, площадь которой вычисляется по формулам из элементарной геометрии.

Определение .

Площадью цилиндрической поверхности, ограниченной направляющей и кривой, называется предел площади боковой поверхности призмы, построенной на ломаных, вписанных в эти кривые, при стремлении к нулю наибольшей из длин сторон ломаной.

Приведем без доказательства формулы для вычисления площади цилиндрической поверхности при различных способах задания кривых, ограничивающих эту поверхность.

Если цилиндрическая поверхность задана явными уравнениями:

Если цилиндрическая поверхность задана параметрическими уравнениями:

то площадь цилиндрической поверхности вычисляется по

формуле: пов

Пример 5.

Найти площадь цилиндрической поверхности:

Эта цилиндрическая поверхность «похожа» на поверхность из Примера 5, только направляющей здесь является четверть окружности из первого квадранта.

§ 5. Вычисление физических величин.

Схема применения определенного интеграла .

Пусть требуется определить некоторую величину (геометрическую, физическую,

экономическую и т.д.), связанную с промежутком. Например, это может быть

длина, площадь, объем, путь, масса и т.д. Говорят, что величина является «функцией промежутка».

Предполагается, что эта «функция промежутка» обладает свойством

аддитивности , т.е. для любого промежутка					и для любой промежуточной
	выполнено равенство:
Задача состоит в том, чтобы получить формулу для вычисления значения,
отвечающего всему промежутку
Решение поставленной задачи осуществляется по следующей схеме.
	Разбиение промежутка				на частичные промежутки:
					длины частичных промежутков;
		ранг разбиения.
2 . Выбор промежуточных точек
	подходящей функции		такой, что
	погрешность этого приближенного равенства должна быть бесконечно малой
	более высокого порядка, чем
3 . Вычисление значения суммы					Которое является
	приближенным значением искомой величины