Диагональ сечения прямоугольного параллелепипеда. Диагональные сечения параллелепипеда

Сечения геометрических фигур имеют разные формы. У параллелепипеда сечение неизменно представляет собой прямоугольник либо квадрат. Оно имеет ряд параметров, которые могут быть обнаружены аналитическим методом.

Инструкция

1. Через параллелепипед дозволено провести четыре сечения, которые представляют собой квадраты либо прямоугольники. Каждого он имеет два диагональных и два поперечных сечения. Как водится, они имеют различные размеры. Исключением является куб, у которого они идентичны.Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов — обыкновенный и прямоугольный. У обыкновенного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники либо квадраты. Из этого следует,что куб — это частный случай прямоугольного параллелепипеда.

2. У всякого сечения параллелепипеда есть определенные колляции. Основными из них являются площадь, периметр, длины диагоналей. Если из данные задачи знамениты стороны сечения либо какие-нибудь иные его параметры, этого довольно, дабы обнаружить его периметр либо площадь. По сторонам определяются также диагонали сечений. 1-й из этих параметров — площадь диагонального сечения.Для того дабы обнаружить площадь диагонального сечения, необходимо знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ обнаружьте по теореме Пифагора:d=?a^2+b^2.Обнаружив диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:S=d*h.

3. Периметр диагонального сечения тоже дозволено вычислять по двум величинам — диагонали основания и высоте параллелепипеда. В этом случае сначала обнаружьте две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а после этого сложите с удвоенным значением высоты.

4. Если провести плоскость, параллельную ребрам параллелепипеда, дозволено получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения обнаружьте дальнейшим образом:S=a*h.Периметр этого сечения обнаружьте аналогичным образом по дальнейшей формуле:p=2*(a+h).

5. Конечный случай появляется, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:S=a*b — площадь сечения;p=2*(a+b).

Раньше, чем перейти к нахождению высоты параллелепипеда, необходимо прояснить, что есть высота и что есть параллелепипед. В геометрии, высотой называют перпендикуляр, от вершины фигуры до ее основания либо отрезок, кратчайшим методом соединяющий верхнее и нижнее основания. Параллелепипед – это многогранник, имеющий два параллельных и равных многоугольника в качестве оснований, углы которых объединены отрезками. Параллелепипед составлен из шести параллелограммов, попарно параллельных и равных друг другу.


Инструкция

1. Высоты в параллелограмме может быть три, в зависимости от расположения фигуры в пространстве, чай повернув параллелепипед на бок, вы поменяете местами его основания и грани. Верхний и нижний параллелограммы – неизменно основания. Если боковые ребра фигуры перпендикулярны основаниям, то параллелепипед прямой, и всякое его ребро – готовая высота. Дозволено измерить.

2. Дабы из наклонного параллелепипеда получить прямой, того же размера, нужно продолжить боковые грани в одном направлении. После этого, возвести перпендикулярное сечение, от углов которого, отложить длину ребра параллелепипеда, и на этом расстоянии возвести второе перпендикулярное сечение. Два построенных вами параллелограмма, ограничат новейший параллелепипед, равновеликий первому. На грядущее следует подметить, что объемы равновеликих фигур идентичны.

3. Почаще вопрос о высоте нам встречается в задачах. Неизменно нам даны данные, дозволяющие вычислить её. Это может быть объем, линейные размеры параллелепипеда, длины его диагоналей.Так объем параллелепипеда равен произведению его основания на высоту, то есть, зная объем и размер основания, легко узнать высоту путем деления первого на второе. Если вы имеете дело с прямоугольным параллелепипедом, то есть такие, основание которого прямоугольник, вам могут попытаться усложнить задачу, в связи с его особенными качествами. Так в прямоугольном параллелепипеде, квадрат всякий его диагонали равен сумме квадратов 3 измерений параллелепипеда. Если в «дано» к задаче о прямоугольном параллелепипеде указаны длина его диагонали и длины сторон основания, то этих сведений довольно, дабы узнать размер желанной высоты.

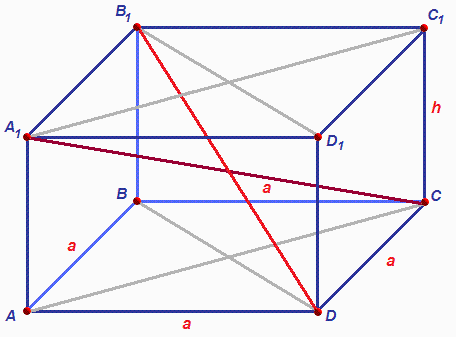
Параллелепипед — частный случай призмы, у которой все шесть граней являются параллелограммами либо прямоугольниками. Параллелепипед с прямоугольными гранями называют также прямоугольным. У параллелепипеда имеется четыре пересекающиеся диагонали. Если даны три ребра а, b, с, обнаружить все диагонали прямоугольного параллелепипеда дозволено, исполняя добавочные построения.

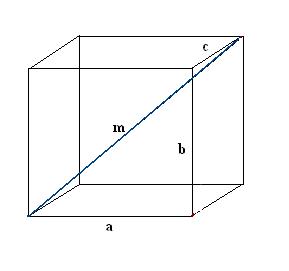
Инструкция

1. Нарисуйте прямоугольный параллелепипед. Запишите вестимые данные: три ребра а, b, с. Сначала постройте одну диагональ m. Для ее определения используем качество прямоугольного параллелепипеда, согласно которому все его углы являются прямыми.


2. Постройте диагональ n одной из граней параллелепипеда. Построение проведите так, дабы вестимое ребро, желанная диагональ параллелепипеда и диагональ грани совместно образовывали прямоугольный треугольник а, n, m.

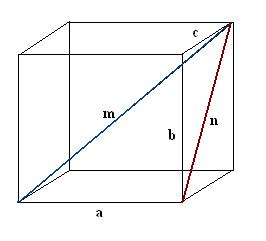
3. Обнаружьте построенную диагональ грани. Она является гипотенузой иного прямоугольного треугольника b, с, n. Согласно теореме Пифагора n² = с² + b². Вычислите данное выражение и возьмите корень квадратный из полученного значения – это будет диагональ грани n.

4. Обнаружьте диагональ параллелепипеда m. Для этого в прямоугольном треугольнике а, n, m обнаружьте неведомую гипотенузу: m² = n² + a². Подставьте вестимые значения, после этого вычислите корень квадратный. Полученный итог и будет первой диагональю параллелепипеда m.

5. Аналогичным образом проведите ступенчато все остальные три диагонали параллелепипеда. Также для всей из них исполните добавочные построения диагоналей прилегающих граней. Рассматривая образуемые прямоугольные треугольники и применяя теорему Пифагора, обнаружьте значения остальных диагоналей прямоугольного параллелепипеда.


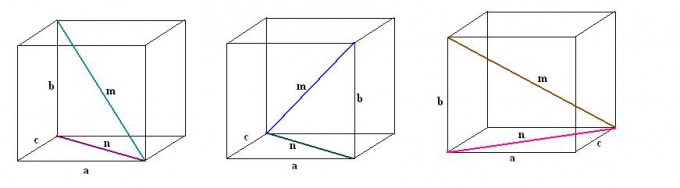
Видео по теме

Форму параллелепипеда имеют многие настоящие объекты. Примерами являются комната и бассейн. Детали, имеющие такую форму — не редкость и в промышленности. По этой причине зачастую появляется задача нахождения объема данной фигуры.


Инструкция

1. Параллелепипед представляет собой призму, основанием которой является параллелограмм. У параллелепипеда имеются грани — все плоскости, формирующие данную фигуру. Каждого у него насчитывается шесть граней, причем, все они являются параллелограммами. Его противоположные грани между собой равны и параллельны. Помимо того, он имеет диагонали, которые пересекаются в одной точке и в ней делятся напополам.

2. Параллелепипед бывает 2-х видов. У первого все грани являются параллелограммами, а у второго — прямоугольниками. Конечный из них именуется прямоугольным параллелепипедом. У него все грани прямоугольные, а боковые грани перпендикулярны к основанию. Если прямоугольный параллелепипед имеет грани, основы которых — квадраты, то он именуется кубом. В этом случае, его грани и ребра равны. Ребром именуется сторона всякого многогранника, к числу которых относится и параллелепипед.

3. Для того, дабы обнаружить объем параллелепипеда, нужно знать площадь его основания и высоту. Объем находится исходя из того, какой именно параллелепипед фигурирует в условиях задачи. У обычного параллелепипеда в основании находится параллелограмм, а у прямоугольного — прямоугольник либо квадрат, у которого неизменно углы прямые. Если в основании параллелепипеда лежит параллелограмм, то его объем находится дальнейшим образом:V=S*H, где S — площадь основания, H -высота параллелепипедаВысотой параллелепипеда обыкновенно выступает его боковое ребро. В основании параллелепипеда может лежать и параллелограмм, не являющийся прямоугольником. Из курса планиметрии знаменито, что площадь параллелограмма равна:S=a*h, где h — высота параллелограмма, a — длина основания, т.е. :V=a*hp*H

4. Если имеет место 2-й случай, когда основание параллелепипеда — прямоугольник, то объем вычисляется по той же формуле, но площадь основания находится несколько другим образом:V=S*H,S=a*b, где a и b — соответственно, стороны прямоугольника и ребра параллелепипеда.V=a*b*H

5. Для нахождения объема куба следует руководствоваться примитивными логическими методами. От того что все грани и ребра куба равны, а в основании куба — квадрат, руководствуясь формулами, указанными выше, дозволено вывести следующую формулу:V=a^3

Во многих учебниках встречаются задания, связанные с построением сечений разных геометрических фигур, в том числе параллелепипедов. Для того дабы совладать с такой задачей, следует вооружиться некоторыми познаниями.


Вам понадобится

  • — бумага;
  • — ручка;
  • — линейка.

Инструкция

1. На листе бумаге начертите параллелепипед. Если в вашей задаче сказано, что параллелепипед должен быть прямоугольным, то сделайте его углы прямыми. Помните, что противоположные ребра обязаны быть параллельны друг другу. Назовите его вершины, скажем, S1, T1, T, R, P, R1, P1 (как показано на рисунке).


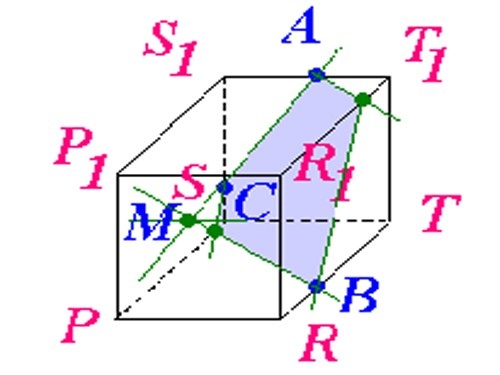
2. На краю SS1TT1 поставьте 2 точки: А и С, пускай точка А будет на отрезке S1T1, а точка С на отрезке S1S. Если в вашей задаче не сказано, где именно обязаны стоять эти точки, и не указано расстояние от вершин, поставьте их произвольно. Проведите прямую линию через точки А и С. Продолжите эту линию до пересечения с отрезком ST. Обозначьте место пересечения, пускай это будет точка М.

3. Поставьте точку на отрезке RT, обозначьте ее как точку В. Проведите прямую линию через точки М и В. Точку пересечения этой линии с ребром SP обозначьте как точку К.

4. Объедините точки К и С. Они обязаны лежать на одной грани PP1SS1. Позже этого через точку B проведите прямую линию, параллельную отрезку КС, продолжите линию до пересечения с ребром R1T1. Точку пересечения обозначьте как точку Е.

5. Объедините точки А и Е. Позже этого выделите получившийся многоугольник ACKBE иным цветом – это будет сечение заданного параллелепипеда.

Обратите внимание!
Помните, что при построении сечения параллелепипеда дозволено соединять между собой только те точки, которые лежат в одной плоскости, если имеющихся у вас точек неудовлетворительно для построения сечения, достраивайте их, путем продолжения отрезков до пересечения с гранью, на которой надобна точка.

Полезный совет
Каждого в параллелепипеде может быть построено 4 сечения: 2 диагональных и 2 поперечных. Для большей наглядности, выделите получившийся многоугольник-сечение, для этого можете примитивно обвести либо заштриховать его иным цветом.

Совет 6: Как обнаружить длину диагоналей параллелепипеда

Параллелепипедом именуется призма, основанием которой служит параллелограмм. Параллелограммы, из которых составлен параллелепипед, именуются его гранями, их стороны - ребрами, а вершины параллелограммов - вершинами параллелепипеда.


Инструкция

1. У параллелепипеда дозволено возвести четыре пересекающиеся диагонали. Если знамениты данные 3 ребер а, b и с, обнаружить длины диагоналей прямоугольного параллелепипеда не составит труда, исполняя добавочные построения.

2. Вначале нарисуйте прямоугольный параллелепипед. Подпишите все вестимые вам данные, их должно быть три: ребра а, b и с. Начертите первую диагональ m. Для ее построения воспользуйтесь свойством прямоугольных параллелепипедов, согласно которому все углы сходственных фигур являются прямыми.

3. Постройте диагональ n одной из граней параллелепипеда . Построение сделайте таким образом, дабы знаменитое ребро (а), незнакомая диагональ параллелепипеда и диагональ прилегающей грани (n) образовывали прямоугольный треугольник а, n, m.

4. Посмотрите на построенную диагональ грани (n). Она является гипотенузой иного прямоугольного треугольника b, с, n. Следуя теореме Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов катетов (n? = с? + b?), обнаружьте квадрат гипотенузы, после этого извлеките корень квадратный из полученного значения – это и будет длина диагонали грани n.

5. Обнаружьте диагональ самого параллелепипеда m. Для того, дабы обнаружить ее значение, в прямоугольном треугольнике а, n, m вычислите по той же формуле гипотенузу: m? = n? + a?. Вычислите корень квадратный. Обнаруженный итог будет первой диагональю вашего параллелепипеда . Диагональ m.

6. Верно так же проведите ступенчато все остальные диагонали параллелепипеда , для всей из которых исполняйте добавочные построения диагоналей прилегающих граней. Применяя теорему Пифагора, обнаружьте значения остальных диагоналей данного параллелепипеда .

7. Есть еще один метод, с поддержкой которого дозволено обнаружить длину диагонали. Согласно одному из свойств параллелограмма, квадрат диагонали равен сумме квадратов 3 его сторон. Из этого следует, что длину дозволено обнаружить сложив квадраты сторон параллелепипеда и из получившегося значения извлечь квадрат.

Полезный совет
Свойства параллелепипеда:- параллелепипед симметричен касательно середины его диагонали;- всякий отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею напополам, в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею напополам;- противолежащие грани параллелепипеда параллельны и равны;- квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Параллелепипед – объемная геометрическая фигура с тремя измерительными колляциями: длиной, шириной и высотой. Все они участвуют в нахождении площади обеих поверхностей параллелепипеда : полной и боковой.


Инструкция

1. Параллелепипед – многогранник, построенный на основе параллелограмма. У него шесть граней, также являющихся этими двухмерными фигурами. В зависимости от того, как они расположены в пространстве, различают прямой и наклонный параллелепипед. Эта разница выражается в равенстве угла между основанием и боковым ребром 90°.

2. По тому, к какому частному случаю параллелограмма относится основание, дозволено выделить прямоугольный параллелепипед и особенно распространенную его разновидность – куб. Эти формы особенно зачастую встречаются в повседневной жизни и носят наименование стандартных. Они присущи бытовой технике, предметам мебели, электронным приборам и др., а также самим человеческим жилищам, размеры которых имеют весомое значение для обитателей и риелторов.

3. Обыкновенно считают площадь обеих поверхностей параллелепипеда , боковой и полной. Первая числовая колляция представляет собой общность площадей его граней, вторая – та же величина плюс площади обоих оснований, т.е. сумма всех двухмерных фигур, из которых состоит параллелепипед. Следующие формулы носят наименование основных наравне с объемом:Sб = Р h, где Р – пeримeтр основания, h – высота;Sп = Sб + 2 S, где So – площадь основания.

4. Для частных случаев, куба и фигуры с прямоугольными основаниями, формулы упрощаются. Сейчас теснее не надобно определять высоту, которая равна длине вертикального ребра, а площадь и периметр обнаружить значительно легче вследствие наличию прямых углов, в их определении участвуют только длина и ширина. Выходит, для прямоугольного параллелепипеда :Sб = 2 с (a + b), где 2 (а + b) – удвоенная сумма сторон основания (периметр), с – длина бокового ребра;Sп = Sб + 2 а b = 2 а с + 2 b с + 2 a b = 2 (а с + b с + а b).

5. У куба все ребра имеют идентичную длину, следственно:Sб = 4 а а = 4 а?;Sп = Sб + 2 а? = 6 а?.

Вопрос относится к аналитической геометрии. Он решается с привлечением уравнений пространственных прямых и плоскостей, представления куба и его геометрических свойств, а также с применением векторной алгебры. Могут потребоваться методы рения систем линейных уравнений.


Инструкция

1. Выберите данные задачи так, дабы они были исчерпывающими, но не избыточными. Секущую плоскость? следует задать всеобщим уравнением вида Ax+By+Cz+D=0, что наилучшим образом согласуется с произвольным его выбором. Для задания куба абсолютно хватит координат всяких 3 его вершин. Возьмите, скажем, точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), в соответствии с рисунком 1. На этом рисунке проиллюстрировано сечение куба. Оно пересекает два боковых ребра и три ребра оснований.


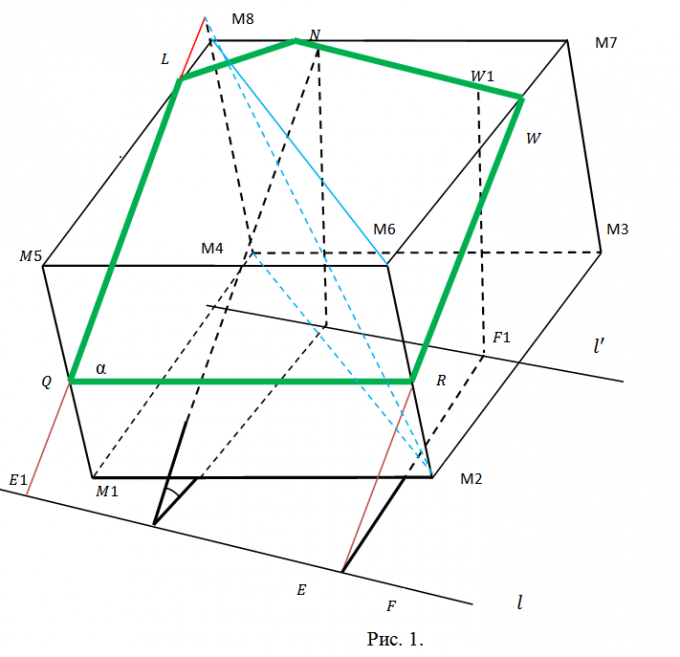
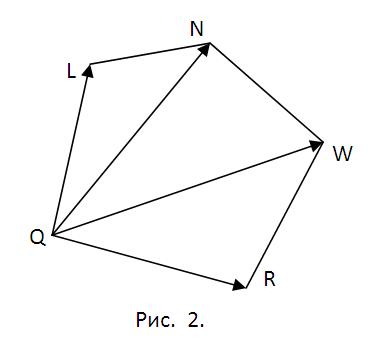
2. Определитесь с планом последующей работы. Предстоит искать координаты точек Q, L, N, W, R пересечения сечения с соответствующими ребрами куба. Для этого придется находить уравнения прямых, содержащих эти ребра, и искать точки пересечения ребер с плоскостью?. Позже этого последует разбиение пятиугольника QLNWR на треугольники (см. рис. 2) и вычисление пощади всего из них с подмогой свойств векторного произведения. Методология всякий раз одна и та же. Следственно дозволено ограничиться точками Q и L и площадью треугольника?QLN.

3. Направляющий вектор h прямой, содержащий ребро М1М5 (и точку Q), обнаружьте как векторное произведение M1M2={x2-x1, y2-y1, z2-z1} и M2M3={x3-x2, y3-y2, z3-z2}, h={m1, n1, p1}=. Полученный вектор является направляющим и для всех прочих боковых ребер. Длину ребра куба обнаружьте как, скажем, ?=?((x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Если модуль вектора h |h|??, то замените его соответствующим коллинеарным вектором s={m, n, p}=(h/|h|)?. Сейчас запишите уравнение прямой, содержащей М1М5 параметрически (см. рис. 3). Позже подстановки соответствующих выражений в уравнение секущей плоскости получите А(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Определите t, подставьте в уравнения для М1М5 и запишите координаты точки Q(qx, qy, qz) (рис. 3).


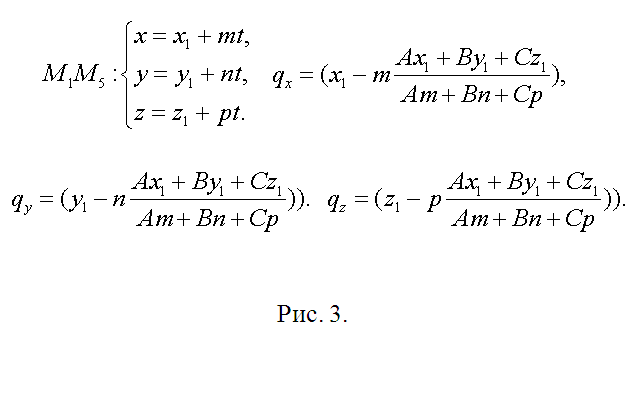
4. Видимо, что точка М5 имеет координаты М5(x1+m, y1+n, z1+p). Направляющий вектор для прямой, содержащей ребро М5М8 совпадает с М2М3={x3-x2, y3-y2,z3-z2}. После этого повторите предыдущие рассуждения касательно точки L(lx, ly, lz) (см. рис. 4). Все последующее, для N(nx, ny, nz) – точная копия это шага.


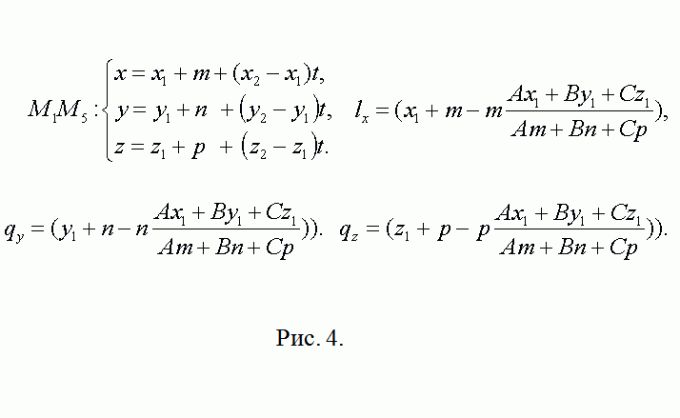
5. Запишите векторы QL={lx-qx, ly-qy, lz-qz} и QN={nx-qx, ny-qy, nz-qz}. Геометрический толк их векторного произведения состоит в том, что его модуль равен площади параллелограмма построенного на векторах. Следственно площадь?QLN S1=(1/2)||. Следуйте предложенной методике и вычислите площади треугольников?QNW и?QWR — S1 и S2. Векторное произведение комфортнее каждого находить с поддержкой вектора-определителя (см. рис. 5). Запишите окончательный результат S=S1+S2+S3.


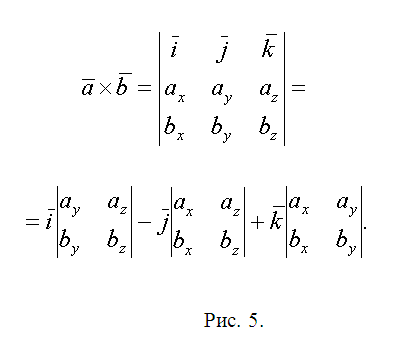
Совет 9: Как обнаружить площадь диагонального сечения призмы

Призма - это многогранник с двумя параллельными основаниями и боковыми гранями в форме параллелограмма и в числе, равном числу сторон многоугольника основания.


Инструкция

1. В произвольной призме боковые ребра расположены под углом к плоскости основания. Частным случаем является прямая призма. В ней боковые стороны лежат в плоскостях, перпендикулярных основаниям. В прямой призме боковые грани - прямоугольники, а боковые ребра равны высоте призмы.

2. Диагональное сечение призмы - часть плоскости, всецело заключенная во внутреннем пространстве многогранника. Диагональное сечение может быть ограничено двумя боковыми ребрами геометрического тела и диагоналями оснований. Видимо, что число допустимых диагональных сечений при этом определяется числом диагоналей в многоугольнике основания.

3. Либо границами диагонального сечения могут служить диагонали боковых граней и противоположные стороны оснований призмы. Диагональное сечение прямоугольной призмы имеет форму прямоугольника. В всеобщем случае произвольной призмы форма диагонального сечения — параллелограмм.

4. В прямоугольной призме площадь диагонального сечения S определяется по формулам:S=d*Hгде d - диагональ основания, H - высота призмы.Либо S=a*Dгде а - сторона основания, принадлежащая единовременно плоскости сечения, D - диагональ боковой грани.

5. В произвольной непрямой призме диагональное сечение - параллелограмм, одна сторона которого равна боковому ребру призмы, иная — диагонали основания. Либо сторонами диагонального сечения могут быть диагонали боковых граней и стороны оснований между вершинами призмы, откуда проведены диагонали боковых поверхностей. Площадь параллелограмма S определяется формулой: S=d*hгде d - диагональ основания призмы, h - высота параллелограмма - диагонального сечения призмы.Либо S=a*hгде а - сторона основания призмы, являющаяся и рубежом диагонального сечения, h - высота параллелограмма.

6. Для определения высоты диагонального сечения неудовлетворительно знать линейные размеры призмы. Нужны данные о наклоне призмы к плоскости основания. Последующая задача сводится к ступенчатому решению нескольких треугольников в зависимости от начальных данных об углах между элементами призмы.

«Золотое сечение» - Цель исследования: Вывести закон красоты мира с точки зрения математики. Адмиралтейство. Окно. Выполнила ученица 10 класса Сметанина Юлия. Покровский собор (храм Василия Блаженного). Золотое сечение в архитектуре. В математике пропорцией называется равенство двух отношений: a: b = c: d. Египетские пирамиды.

«Построение сечений» - Сечения выполняют в том же масштабе, что и изображение, к которому оно относится. Особенности выполнения сечений. Нанесение размеров. Обозначение сечений. Контур вынесенных сечений выполняют сплошной линией. Правила выполнения сечений. Сечения. Сечения на чертежах разделяют на вынесенные и наложенные.

«Параллелепипед 10 класс» - Угол равен 60?. 3.Четыре, если параллелепипед – куб. Угол равен 60?. 3.Равные квадраты, углы 90 ?. Форму ромбоэдра имеют кристаллы исландского шпата. Вариант 2. Дан параллелепипед ABCDA1B1C1D1. Диагонали параллелепипеда. Докажите параллельность прямых B1C и A1D. 2. Диагонали параллелепипеда равны. Параллелепипед.

«Объем параллелепипеда» - Так же поступаем и мы сейчас. В Древнем Вавилоне единицами объемов служили кубы. Теперь определим что же такое единицы объемов? Значит, по правилу вычисления объема, получаем: 3х3х3=27 (см3). Задание №2. Найдите объем куба, ребро которого равно 3 см. Единица объема равная 1 дм3 называется литром. Задание №1.

«Урок Прямоугольный параллелепипед» - Цель урока: Длина. Рефлексия. Найти площадь основания прямоугольного параллелепипеда. Построить прямоугольник заданной длины (а) и высоты (h). Развертка. Грани. Ребра. Физкультминутка. Алгоритм построения прямоугольного параллелепипеда. Длина в три раза меньше высоты, а ширина в 6 раз меньше высоты.

«Объем прямоугольного параллелепипеда» - Т е с т. (Геометрическая фигура). 6. У параллелепипеда все грани являются прямоугольниками. 3. У куба все грани являются квадратами. Ответьте на следующие вопросы: Квадраты. Назовите ребра, имеющие вершину E. Увеличится. Объемная. Задача 2: Измерения прямоугольного параллелепипеда равны 3см, 6см и 6см.

с. 1

Поурочные разработки 11 класс по учебнику «Геометрия» Л. С. Атанасян

УРОК № 1. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВ !:

Основная цель : ввести понятие Прямоугольной системы координат, научить строить точку, зная ее координаты, и определять. координаты точки, построенной в прямоугольной системе координат.

I . Устная работа .

II построить в соответствии с п . 42 учебника.

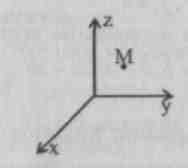Проблема - задано ли положение точки М . в пространстве ? Нет. Необходимо построить проекции точки М на каждую плоскость (Оху), (Oxz ) (Ozy ).

К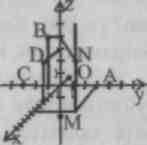онтрольные вопросы


  1. По рисунку найдите координаты точек А, В, С, D , М, N.

  2. Изобразите систему координат Oxyz и постройте точки
А (0;0;7},В(0;2;-3),С(-1;2;4).

  1. Решение задач: № 400 (устно), 401 (устно), 402.

  2. Домашнее задание: теория (п. 42), № 501.

УРОК № 2. КООРДИНАТЫ ВЕКТОРА

Основная цель : ввести понятие координат вектор

I . Объяснение нового материала построить в соответствии с п. 43 учебника.

II . Решение задач : № 403, 404,407(а, б, ж, и, к, л) 410, 408, 412.



III . Домашнее задание : теория (п 13), повторить (п. 38, 39), № 405, 407 (г, д, е, ж, з), 409 (в,г,д,е,з,м), 411.

УРОК № 3. СВЯЗЬ МЕЖДУ КООРДИНАТАМИ ВЕКТОРОВ И КООРДИНАТАМИ ТОЧЕК

Основная цель: доказать, что координаты любой точки равны соответствующим координатам ее радиус-вектора; научить находить координаты вектора, зная координаты его начала и конца.

I. Объяснение нового материала построить в соответствии с п. 44 учебника.

II. Решение задач : № 416,417, 418 (а), 419,420.

III. Домашнее задание : теория (п. 44), № 418 (б, в), 421.

УРОК № 4. ПРОСТЕЙШИЕ ЗАДАЧИ В КООРДИНАТАХ

Основная цель: вывести формулы для нахождения коорди­нат середины отрезка, длины вектора по его координатам, расстоя­ния между двумя точками.


  1. Проверка домашнего задания. № 421. Решить № 422.
№ 422 (а).


III . Объяснение нового материала построить в соответствии с п. 45 учебника.

IV . Решение задач: № 424, 426, 427, 430.

V . Домашнее задание: теория (п. 45), № 425, 429, 431.

УРОК № 5,6 УГОЛ МЕЖДУ ВЕКТОРАМИ

Основная цель: обобщить понятие «угол между векторами», научит находить угол между векторами в пространстве.

Ш. Объяснение нового материала построить в соответствии с п. 46. Показать пример нахождения углов между векторами на стереометрических моделях (обратить внимание на векторы, лежащие на скрещивающихся прямых).

IV . Решение задач № 442,507,508

V . Домашнее задание: теория (п. 46), № 441, на повторение -№ 490, 491 (устно), 492, 501.

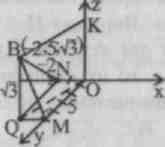№501. Найти ВМ, BN , ВХ.

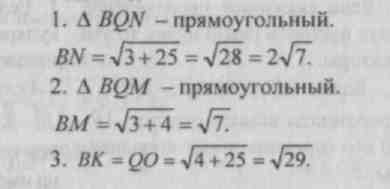Решение.


  1. Объяснение нового материала.




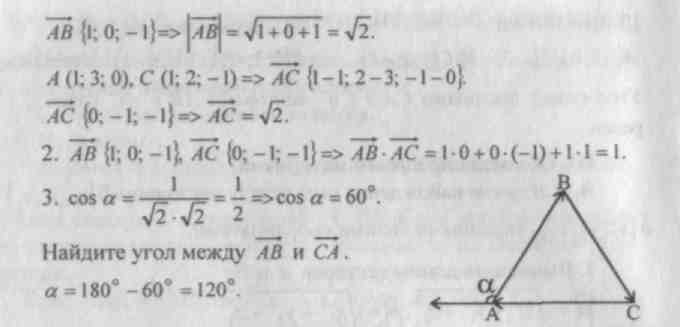
Домашнее задание: теория (п. 48), № 451, 453, 464 (б, в,г), 469 (б, в).

Диктант


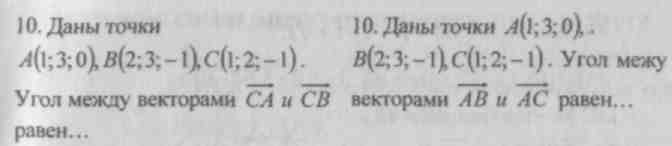
УРОК № 7 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Основная цель: сформировать навык решения задач на нахождение угла векторами, прямыми, прямой и плоскостью.

I . Проверка домашнего задания (у доски): № 451 (б, д), № 464 (в; г).

II . Решение задач (по готовым чертежам).

Алгоритм решения задач:


  1. Ввести прямоугольную систему координа"1

  2. Записать координаты всех точек.

  1. Использовать алгоритм нахождения угла между прямыми, между прямой и плоскостью.


III. Решение задач.





  1. (векторный способ)

III. (Векторно-координатный способ).



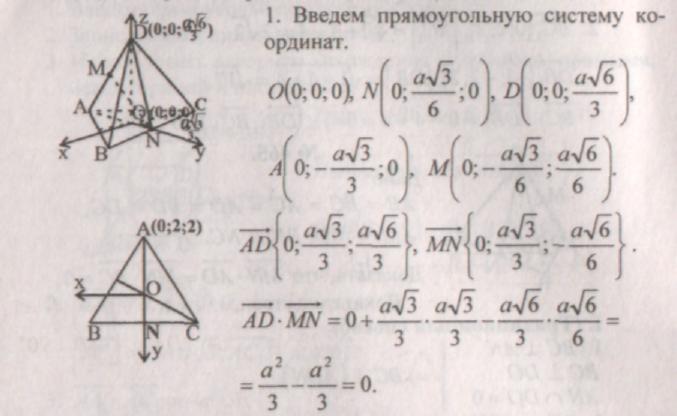
  1. Домашнее задание: № 455, 457, 462.

УРОК № 8 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Основная цель: сформировать навык нахождения углов между прямыми, между прямой и плоскостью.

№ 455.

(Чертеж заготовлен заранее. Учащиеся проговаривают или кто-то прописывает на доске ответы.)



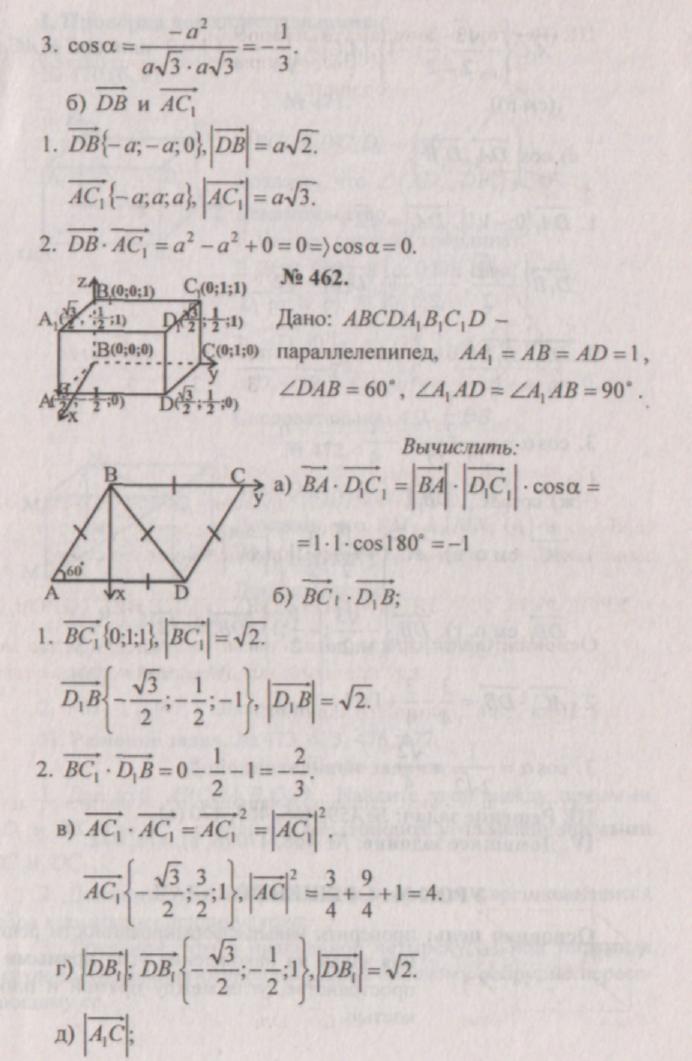
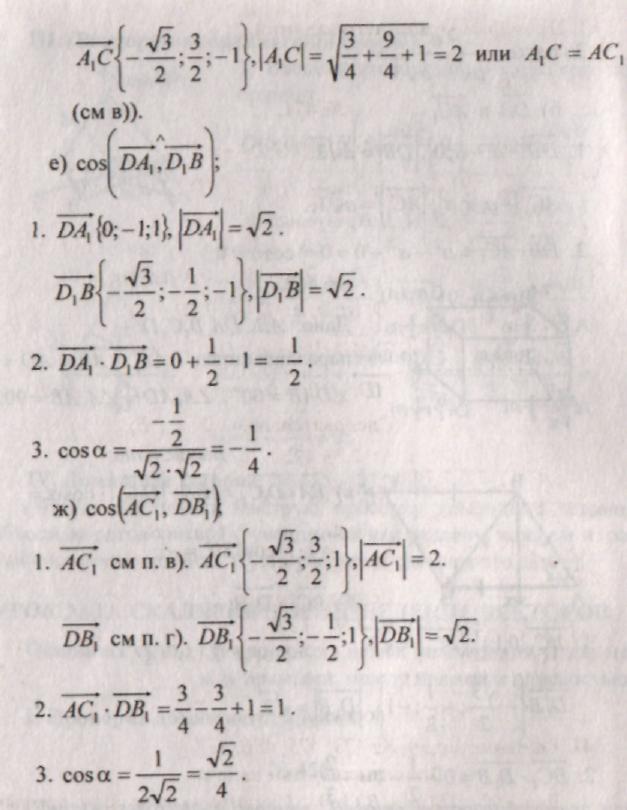
III . Решение задач: № 459, 466, 467, 470 (а).

IV . Домашнее задание: № 468, 470 (б, в), 471, 472.

УРОК № 9 КОНТРОЛЬНАЯ РАБОТА № 1
Тесты для самопроверки и коррекции знаний учащихся






Вариант

1

2

3

4

5

6

7

8

I

в

г

в

б

а

б

г

в

II

б

а

в

г

в

б

г

г







Вариант

1

2

3

4

5

6

7

8

I

б

г

б

в

в

г

в

б

II

б

а

г

в

г

а

в

б

УРОК № 10. ЦИЛИНДР

Основная цель: ввести понятие цилиндра, элементов цилиндра.

I . Объяснение нового материала построить по плану:

1. Понятие цилиндрической поверхности, цилиндра.

Рассмотреть различные предметы окружающей обстановки, дающие представление о цилиндре - круговой карандаш, стакан, копейку, кастрюлю, кусок трубы и т.д. (Представленные цилиндры должны иметь разные соотношения между высотой и диаметром). Дать изображение цилиндра, показать на чертеже - ось, высоту, радиус, образующие, основания цилиндра.

2. Ввести понятие осевого сечения цилиндра , установить его свойства:

а) осевое сечение цилиндра - прямоугольник;

б) любые два осевых сечения цилиндра равны между собой.


Ввести понятие равностороннего цилиндра, осевым сечением

которого является квадрат.

3. Рассмотреть сечение квадрата плоскостью

а) параллельной оси цилиндра;

б) перпендикулярной к оси цилиндра.

4. Ввести понятие касательной плоскости цилиндра как плоскости, проходящей через образующую цилиндра и перпендикулярную осевому сечению, проведенному через эту образующую. (Аналогия с касательной к окружности).

II . Решение задач: № 521, 522, 526, 529.

III . Домашнее задание: № 523, 525, 530.

УРОК № 11. ЦИЛИНДР

Основная цель: сформулировать навык решения задач на нахождение элементов цилиндра.

I . Проверка домашнего задания (у доски).

II. Устная работа.


  1. Укажите в природе, технике, архитектуре, среди окружающих вас предметов объекты, имеющие цилиндрическую форму.

  2. Объясните, что называют цилиндром, круговым цилиндром. Назовите его основные элементы, дайте им определение.

  1. Дайте определение прямого цилиндра.

  2. Сколько осевых сечений цилиндра проходит через каждую его образующую?

  1. Определите вид осевого сечения цилиндра. Ответ обоснуйте.

  2. Может ли осевое сечение цилиндра быть: а) прямоугольником; б) квадратом; в) трапецией?

  3. Имеет ли цилиндр: а) центр симметрии; б) ось симметрии; в) плоскость симметрии? Укажите их в каждом случае. Сколько их? Покажите на модели.

  4. Пусть АА 1 В 1 В и MM 1 N 1 N -два осевых сечения цилиндра. Сравните их площади.

  1. Цилиндр катится по плоскости. Какая фигура получается при движении его оси?

  2. Какие из следующих утверждении верны:
а) любое сечение цилиндра плоскостью, перпендикулярной оси, есть окружность, равная окружности основания;

б) любое сечение цилиндра плоскостью есть окружность, равная окружности основания;

в) плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра;

г) сечением цилиндра плоскостью могут быть круг, прямоугольник и эллипс?

12. Сформулируйте и докажите теорему о сечении цилиндра плоскостью, перпендикулярной его оси.

III . Решение задач: № 527 (б), 532, 534.

IV . Домашнее задание: № 527 (а), 531, 535.

УРОК №12. КОНУС

Основная цель: проверить уровень сформулированности навыка решения задач по нахождению элементов цилиндра. Ввести понятия конуса, элементов конуса.


  1. Самостоятельная работа (15 мин).
Вариант I

  1. Сечением цилиндра плоскостью, параллельной оси, служит квадрат, площадь которого равна 20 дм. Найдите площадь осевого сечения цилиндра, если его диагональ равна 10 дм.
Боковая поверхность цилиндра развертывается в квадрат с диагональю равной см. Найдите площадь полной поверхности цилиндра.

Вариант II


  1. Высота цилиндра 16 см, радиус основания 10 см. Цилиндр пересечен плоскостью параллельно оси так, что в сечении полу­чился квадрат. Найдите расстояние от оси цилиндра до этого сечения.

  2. Разверткой боковой поверхности цилиндра служит прямоугольник, диагональ которого, равная 12л, составляет с одной из сторон угол 30°. Найдите площадь полной поверхности цилиндра, если его высота равна меньшей стороне развертки.
II . Объяснение нового материала построить по плану:

1. Понятия конуса, его элементов (вершина, ось, образующие, основание, боковая поверхность конуса). Изображение конуса

Н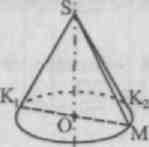а рисунке проведем касательные из точки S к эллипсу, изображающему основание конуса. Обозначим через К 1 и К 2 точки касания. Распространенная ошибка заключается в том, что учащиеся принимают треугольник SK 1 K 2 за изображение осевого сечения конуса. Однако хорда К 1 К 2 не проходит через центр О основания конуса. Для построения изображения осевого сечения, проходящего через образующую SK 1 достаточно построить изображение диаметра К 1 М и соединить полученную точку М с вершиной S конуса. SK 1 и SK 2 - изображения крайних образующих, т.е. они отделяют видимые образующие (их изображения получаются, если соединить произвольную точку дуги К 1 МК 2 эллипса с вершиной S ) от невидимых.

2. Рассмотреть сечение конуса различными плоскостями, выделяя два случая:


  1. Секущая плоскость через вершину конуса;

  2. Секущая плоскость параллельна основанию конуса.
В пересечение секущей плоскости с окружностью основания конуса.

1 (а). Если они пресекаются в двух точках, то в сечении конуса получаем равнобедренный треугольник, основание которого -отрезок с концами в этих точках. Из осевое сечение. Оно получается, если рассматриваемые точки пересечения - концы диаметра основания конуса. Среди конусов выделяется равносторонний (осевое сечение его - равносторонний треугольник). Если R - радиус его основания, то образующая равностороннего конуса равна 2 R .

1 (б). Если они имеют только одну общую точку, то рассматриваемая плоскость - касательная к конусу.

Касательная плоскость к конусу может быть определена по-разному.

Определение 1. Плоскость, проходящая через образующую конуса перпендикулярная осевому сечению, проведенному через эту образующую.

Определение 2. Плоскость, имеющая с конусом только одну общую образующую.

Трактовка плоскости, касательной к конусу и плоскости, касательной к цилиндру, должна быть одна и та же в одном учебнике. Следует отметить, что, приняв одно из предложений 1 или 2 в качестве определения , необходимо ознакомить учащихся с другим как свойством касательной плоскости к конусу.

1 (в). Продолжая рассмотрение плоскости, проходящей через вершину конуса, проходим к случаю: если плоскость и окружность основания не имеют общих точек, то рассматриваемая плоскость с конусом имеют только одну общую точку - вершину конуса.

2. При доказательстве теоремы о сечении конуса плоскостью, параллельной его основанию (№ 556) целесообразно получить сле­дующие выводы:

1. Рассматриваемое сечение - круг.

2. Обозначив через R и r - соответственно радиус конуса и рассматриваемого сечения и через Н и h высоту данного и отсеченного конуса, получаем, что, ,где k – коэффициент подобия данного и отсеченного конусов. Доказать, что

Обобщить, решая задачу № 557.

Рассмотрение сечения, перпендикулярного оси конуса, позволяет эффективно применять метод гомотетии по аналогии с се­чением пирамиды плоскостью, параллельной основанию. Установив форму и расположение сечения, вводят понятие усеченного конуса.

Изображая усеченный конус, удобно сначала нарисовать тот конус, из которого получается усеченный конус.


  1. Решение задач: № 548 (а), 549.

  2. Домашнее задание: теория (п. 55, 56), № 547, 548 (б, в), 550.

УРОК № 13. КОНУС

Основная цель: ввести понятие площади боковой поверхности конуса как площади ее развертки.

I . Проверка домашнего задания (у доски).

II


  1. Ввести понятие площади боковой поверхности, используя развертку конуса.

  2. Площадь полной поверхности конуса.

  3. Вывести формулу для вычисления площади боковой поверхности усеченного конуса.
IV . Решение задач: № 558, 559, 560 (а), 562, 567.

V . Домашнее задание: № 560 (б, в), 561, 563, 568.

УРОК № 14. СФЕРА И ШАР. УРАВНЕНИЕ СФЕРЫ. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ К СФЕРЕ. ПЛОЩАДЬ СФЕРЫ

Основная цель: ввести понятия сферы и шара , вывести уравнение сферы, рассмотреть взаимное расположение сферы и плоскости, дать определение касательной плоскости к сфере, записать формулу для вычисления площади сферы.

I . Объяснение нового материала построить лекционным способом в соответствии с п. 58 - 62 учебника.

Для примеров используйте задачи: № 575 для уяснения определений сферы; № 576, 578 для отработки уравнения сферы; № 586 для иллюстрации взаимного расположения сферы и плоскости; № 593 (а), 594 для отработки формулы площади сферы.


  1. Решение задач:


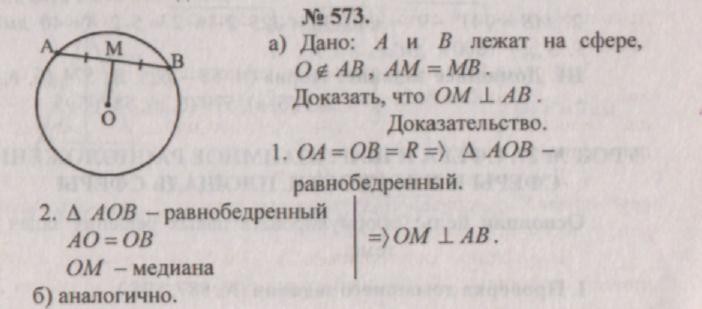
III . Домашнее задание: теория (п. 58 - 62), № 574 (б, в, г).

577 (б, в), 579(6, в), 587, 595.

УРОК № 15. СФЕРА И ШАР. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ. ПЛОЩАДЬ СФЕРЫ

Основная цель: сформулировать навык решения задач по теме.


  1. Проверка домашнего задания (№ 587, 595.)

  2. Решение задач




III . Домашнее задание: № 582, 584, 585, 592, 597.

УРОК № 16. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ

Основная цель: повторить, систематизировать, обобщить изученный материал.

I . Проверка домашнего задания (у доски): № 582, 584, 585.

II . Устная работа - по вопросам к главе VI.

III. Решение задач.

Урок №17 Контрольная работа № 2

УРОК № 18. ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА

Основная цель: ввести понятие объема тела.

I. Объяснение нового материала.

А. Понятие объема тела вводится по аналогии с понятием площади плоской фигуры. Можно вместе с учащимися заполнить вторую половину таблицы.



Контрольные вопросы.


  1. Что называется объемом тела?

  2. Что значит измерить объем тела?
3. Что означает: «Объем данной комнаты 60 м 3 »; «Объем спичечной коробки 10 см 2 »; «Объем бочки для воды 200 м 3 ».

4. Как получить единичного куба?

5. Единичный куб уложился в части пространства, занимаемой восьмигранником, 2 раза и 2 раза - доля единичного куба, каким числом характеризуется V восьмигранника?

В. Объем куба равен кубу его ребра. V = а 3 .

Вывести формулу для вычисления V куба, если, известна его диагональ

II. Решение задач.

1. Площадь полной поверхности куба равна 6 м 2 . Найдите его объем.(1 м 3)


  1. Объем куба равен 8 м. Найдите площадь полной поверхности.

  2. Если каждое ребро куба увеличить на 1м, то его объем увеличится в 125 раз. Найдите ребро куба.

  1. Три куба, сделанные из свинца, имеют ребра 3, 4 и 5 см. Они переплавлены в один куб. Найдите его ребро,

  2. Объем куба равен А. Найдите площадь его диагонального
8. Около шара радиуса г описан прямоугольный параллелепипед. Определите его вид. Найдите его объем.

III . Два тела, объемы которых равны, называются равновеликими.

(При доказательстве следующей теоремы использовать модель или заранее заготовленный чертеж.)

Теорема. Наклонная призма равновелика прямой призме, основание которой - перпендикулярное сечение наклонной, а боковое ребро равно боковому ребру наклонной призмы.




Контрольные вопросы.


  1. Какие два тела называются равновеликими?

  2. Два тела равны. Равновелики ли они?

  3. Два тела равновелики. Равны ли они?
IV . Домашнее задание: теория (п. 63), № 647, 649.

УРОК № 19. ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА

Основная цель: сформировать навык решения задач на нахождение объема параллелепипеда.

I. Устная работа.


  1. Что называется объемом тела?

  2. Чему равен объем куба? Его десятой части?

  3. Куб пересечен двумя диагональными сечениями. Чему равен объем каждой его части?

  4. В кубе с ребром 2 см проведено диагональное сечение . Чему равен объем каждой из полученных частей?

  5. Площадь полной поверхности куба 24 см 2 . Чему равен объем куба?

  6. Диагональ куба равна а . Найдите его объем.

  7. Объем куба V . Найдите его диагональ.

  8. Диагональ грани куба равна 8. Чему равен объем куба?
9. Объем куба равен 8 см 3 . Чему равна площадь диагонального сечения?

  1. Объем наклонной призмы равен 27 см 3 . Чему равно ребро равновеликого ей куба?

  1. Объяснение нового материала.
Куб - частный случай прямоугольного параллелепипеда. Чему равен объем прямоугольного параллелепипеда?

Объем прямоугольного параллелепипеда равен произведению трех его измерений. V= abc . Или объем прямоугольного паралле­лепипеда равен произведению площади основания на высоту.V = S осн H

III. Решение задач.

Домашняя работа: теория (т. 64), № 648,650,651,652

IV. Самостоятельная работа.

ВАРИАНТ I

1. Объем прямоугольного параллелепипеда равен 96 см, боковое ребро 8 см. Чему равна площадь основания?


  1. Основанием прямоугольного параллелепипеда является квадрат со стороной а. Диагональ боковой грани образует угол α с плоскостью основания.

  2. В прямоугольном параллелепипеде диагонали соседних боковых граней, исходящие из одной вершины, образуют углы α и β с общим боковым ребром , исходящим из той же вершины. Боковое ребро параллелепипеда равно b. Найдите объем параллелепипеда.
ВАРИАНТ II

  1. Объем прямоугольного параллелепипеда равен 100 см 3 , площадь основания 25 см 2 . Найдите высоту параллелепипеда.

  2. В прямоугольном параллелепипеде основанием является квадрат. Диагональ параллелепипеда равна d и образует угол α с боковым ребром, имеющим с ней общее начало. Найдите объем параллелепипеда.
3. ABCDA 1 B 1 C 1 D 1 - прямоугольный параллелепипед. Диагональ DA 1 составляет угол α с плоскостью основания , а диагональ DC 1 составляет угол β с плоскость основания. Ребро AD равно а. Найдите объем параллелепипеда.

УРОК № 20. ОБЪЕМ ПРЯМОЙ ПРИЗМЫ

Основная цель: вывести формулу для вычисления объема прямой призмы.

I. Проверка домашнего задания.

П. Объяснение нового материала.



Основание прямой призмы - прямоугольный треугольник. Ее объем равен произведению площади основания на высоту.

Основание прямой призмы - произвольный треугольник. Ее объем равен произведению площади основания на высоту.


Произвольная прямая призма. Докажите, что ее объем равен произведению площади основания на высоту.

Т.О. объем прямой призмы равен произведению площади основания на высоту.


Ш. Решение задач. № 659, 661, 662, 729.




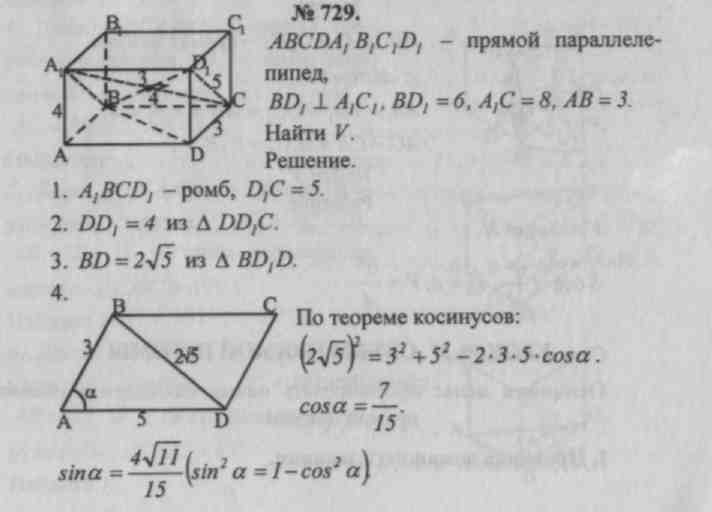
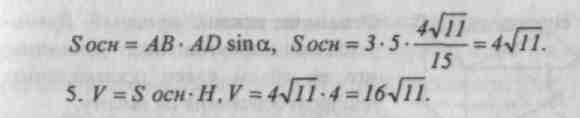
Домашнее задание: теория (п. 65), № 660, 728, 730, 731.

УРОК № 21. ОБЪЕМ ЦИЛИНДРА

Основная цель: вывести формулу для вычисления объема цилиндра.

I. Объяснение нового построить в соответствии с п. 66 учебника.

II . Решение задач. № 671, 672.

Ш. Домашнее задание: теория (п. 66), № 666, 667, 668, 699, 670.

Дополнительные задачи.


  1. Сечение цилиндра плоскостью, параллельной оси, отсекают от окружности основания дугу 60°. Площадь сечения равна S , а диагональ сечения составляет угол α с плоскостью основания цилиндра. Найдите объем цилиндра.

  2. Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу 90 ° . Площадь сечения равна S , а диагональ сечения составляет угол α с образующей цилиндра. Найдите объем цилиндра.

  1. Куб вписан в цилиндр. Объем куба равен F. Найдите объем цилиндра.

УРОК № 22. ОБЪЕМ ПИРАМИДЫ

Основная цель: сформировать навык нахождения объема пирамиды, у которой вершина проецируется в центр вписанной в основание окружности или описанной около основания окружности.

I. Проверка домашнего задания.

Продолжите предложения.


  1. Если все боковые ребра пирамиды равны, то вершина проецируется на основание в...

  2. Если все апофемы пирамиды равны, то вершина проецируется на основание в...

  3. Если все двугранные углы при основании равны, то вершина проецируется на основание в...

  4. Если все боковые ребра составляют с плоскостью основания одинаковые углы, то вершина проецируется на основание в…
I. Объяснение нового построить в соответствии с п. учебника

Ш. Решение задач. № 691, 693, 695, 740.

IV . Домашнее задание: № 692, 694.

П. Диктант.


УРОК № 23,24. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ КОНТРОЛЬНАЯ РАБОТА № 4

Основная цель: проверить уровень сформированности навыка решения задач на нахождение объема цилиндра, наклонной призмы, пирамиды и конуса.

УРОК № 25 ОБЪЕМ ШАРА И ЕГО ЧАСТЕЙ

Основная цель: вывести формулу объема шара и его частей.

I. Объяснение нового материала.

1. Объем шара радиуса R равен

Доказательство см. п. 71.
2. Шаровым сегментом называется часть шара, отсекаемая от него плоскостью (рис. а, в).

Объем шарового сегмента определяется формулой , где Н – высота шарового сегмента

3. Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар (рис. 323, б).
4. Шаровым сектором называется тело, которое получается из шарового сегмента и конуса. Объем шарового сектора определяется формулой , где Н – высота соответствующего шарового сегмента

II. Решение задач.

Задача 1. Чему равен объем шарового сектора, если радиус окружности его основания равен 60 см, а радиус шара равен 75 см?

Решение. 1. Под основанием сектора в задаче понимается основание соответствующего сектору сегмента. Пусть R - радиус шара, r - радиус основания сегмента.

2. Наша задача сводится к отысканию высоты этого сегмента: Н – РО 1 . ОР - радиус шара, перпендикулярный основанию сегмента.

3. Из прямоугольного треугольника OO l M (˂ MO 1 O = 90°) найдем: ОО 1 = √OM 2 - O 1 M 2 = √75 2 +60 2 =40, поэтому H = PO l = OP - OO l = R -00 ] =75-45 = 30.


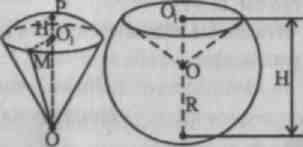
4. Объем шарового сектора. =112500π

5. Примечание. Поставленная задача имеет два решения:

1) Шаровой сектор, который мы рассматривали, называется выпуклым, и его высота равна R – ОО 1 , называется невыпуклым.

Найдем его объем.

6. Рассмотрим второй случай, где высота сектора Н = R + OO 1 =120, так что полученный объем будет в 4 раза больше, чем вычисленный: V = π45 10 4 см 3

7. Таким образом, искомый объем равен либо 112 500π см,либо 450 000π см 3 .






III . Домашнее задание: теория (п. 71, 72), № 710, 711, 717.

УРОК № 26 . ОБЪЕМ ШАРА И ЕГО ЧАСТЕЙ

Основная цель: сформулировать навык нахождения объема шара и его частей.

I. Проверка домашнего задания.

Ш. Решение задач.

А. 1. Внешний диаметр полого шара 18 см, толщина стенок 3 см. Найдите объем материала, из которого изготовлен шар.

[б84πсм 3 .]


  1. Диаметр свинцового шара равен 30 см. Сколько шариков, диаметр которых 3 см, можно сделать из этого свинца?

  2. Радиусы трех шаров 3, 4, 5 см. Найдите радиус шара, объем которого равен сумме их объемов,

  3. Из куба выточен наибольший шар. Сколько процентов материала сточено? [≈ 47,6%.]

  4. Радиус шарового сектора R , угол в осевом сечении 120°. Найдите объем.
Б. 1. Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара?

  1. Докажите, что если радиусы трех шаров относятся как 1:2:3, то объем большего шара в 3 раза больше суммы объемов меньших шаров.

  2. Высота шарового сегмента составляет 0,4 радиуса шара. Какую часть составляет объем этого сегмента от объема цилиндра, имеющего те же основания и высоту? 13\24

  1. Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?

  2. Диаметр шара, равный 30 см, служит осью цилиндра, у ко­торого радиус основания равен 12 см. Найдите объем части шара,
заключенной внутри цилиндра.

  1. Какая фигура имеют больший объем: шар радиуса 1 дм или правильная треугольная призма, каждое ребро которой равно 2 дм? [Объем шара больше.]

  1. Сечение шара плоскостью, перпендикулярной его радиусу, делит радиус пополам. Найдите отношение объемов частей шара.

  2. Сечение шара плоскостью, перпендикулярной его диаметру, делит диаметр в отношении 1:2. Найдите отношение объемов частей шара.

УРОК № 27. ПЛОЩАДЬ СФЕРЫ

Основная цель: вывести формулу для вычисления площади поверхности шара.

I . Объяснение нового материала построить в соответствии с п. 73 учебника.

II . Решение задач: № 722, 723, 724; на повторение - № 761, 762, 763.

III. Домашнее задание: карточки.

УРОК № 28. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ

I. Вопросы для повторения темы.


  1. Шар и его элементы.

  2. Объем шара и его частей.

  3. Тела вращения и их объемы.

  4. Многогранники и их объемы.

  5. Площадь поверхности шара.

  6. Площадь поверхности многогранников.
П. Устная работа по вопросам к главе VH.

III. Решение задач.


  1. Объем шара радиуса R равен V . Найдите объем шара радиуса: 2R ; 0,5R .

  2. Площадь поверхности правильного тетраэдра равна площади поверхности шара. Найдите отношение объемов тетраэдра и шара.

  3. Диаметр шара радиуса 12 см разделен на 3 части, длины которых относятся как 3:3:2. Через точки деления проведены плос­кости, перпендикулярные диаметру. Найдите объем каждой из образовавшихся частей шара .
4. В шар вписана правильная четырехугольная пирамида ABCDM . Площадь треугольника АМС равна S , боковое ребро пирамиды равно диагонали его основания. Найдите объем шара.

5. В правильную четырехугольную пирамиду вписан шар так, что боковые грани пирамиды касаются поверхности шара, а его большой круг лежит на основании пирамиды. Боковые грани пира­миды наклонены к плоскости основания под углом а , а объем ша­ра равен V . Найдите объем пирамиды.

Домашняя контрольная работа

Вариант 1


  1. Объем шара 400 см 3 . На радиусе как на диаметре построен другой шар. Найдите объем малого шара.
2. Площадь поверхности куба равна площади поверхности шара. Найдите отношение объемов куба и шара.

3. Диагональным сечением прямоугольного параллелепипеда, вписанного в шар, является квадрат площадью S . Найдите объем шара.

4. Диаметр шара радиуса 12 см разделен на 3 части, длины которых относятся как 1:3:4. Через точки деления проведены плоскости, перпендикулярные диаметру. Найдите объем образовавшегося шарового слоя.

Моу «Сенькинская СОШ»


с. 1