ការបន្តនៃអនុគមន៍នៅលើឧទាហរណ៍ចន្លោះពេល។ ការបន្តនៃអនុគមន៍នៅចំណុចមួយ និងនៅលើចន្លោះពេលមួយ។

និយមន័យ. ប្រសិនបើមុខងារ f(x) ត្រូវបានកំណត់នៅលើចន្លោះពេល [ ក, ខ] គឺបន្តនៅចំណុចនីមួយៗនៃចន្លោះពេល ( ក, ខ), នៅចំណុច កបន្តនៅខាងស្តាំនៅចំណុច ខគឺបន្តនៅខាងឆ្វេង បន្ទាប់មកយើងនិយាយថាមុខងារ f(x) បន្តលើផ្នែក [ក, ខ].

នៅក្នុងពាក្យផ្សេងទៀតមុខងារ f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ] ប្រសិនបើលក្ខខណ្ឌបីត្រូវបានបំពេញ៖

1) "x 0 Î( ក, ខ): f(x) = f(x 0);

2) f(x) = f(ក);

3) f(x) = f(ខ).

សម្រាប់មុខងារដែលបន្តនៅចន្លោះពេលមួយ យើងពិចារណាអំពីលក្ខណៈសម្បត្តិមួយចំនួន ដែលយើងបង្កើតជាទម្រង់នៃទ្រឹស្តីបទខាងក្រោម ដោយមិនអនុវត្តភស្តុតាង។

ទ្រឹស្តីបទ ១. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ] បន្ទាប់មកវាឈានដល់តម្លៃអប្បបរមា និងអតិបរមារបស់វានៅលើផ្នែកនេះ។

ទ្រឹស្តីបទនេះចែងថា (រូប ១.១៥) ថានៅលើផ្នែក [ ក, ខ] មានចំណុចបែបនេះ x 1 នោះ។ f(x 1) £ f(x) សម្រាប់ណាមួយ។ xពី [ ក, ខ] ហើយថាមានចំណុចមួយ។ x 2 (x 2 អូ[ ក, ខ]) បែបនេះ " xÎ[ ក, ខ] (f(x 2) ³ f(x)).

អត្ថន័យ f(x 1) គឺធំបំផុតសម្រាប់មុខងារដែលបានផ្តល់ឱ្យនៅលើ [ ក, ខ], ក f(x 2) - តូចបំផុត។ ចូរយើងសម្គាល់៖ f(x 1) = ម, f(x 2) =ម. ចាប់តាំងពី f(x) វិសមភាពមាន៖ " xÎ[ ក, ខ] ម£ f(x) £ មបន្ទាប់មកយើងទទួលបានកូរ៉ូឡារីខាងក្រោមពីទ្រឹស្តីបទទី១។

ផលវិបាក. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅលើចន្លោះពេលមួយ បន្ទាប់មកវាត្រូវបានចងនៅលើចន្លោះពេលនេះ។

ទ្រឹស្តីបទ ២. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ] ហើយនៅចុងបញ្ចប់នៃផ្នែកយកតម្លៃនៃសញ្ញាផ្សេងគ្នា បន្ទាប់មកមានចំណុចខាងក្នុងបែបនេះ x 0 ផ្នែក [ ក, ខ] ដែលមុខងារប្រែទៅជា 0, i.e. $ x 0 Î ( ក, ខ) (f(x 0) = 0).

ទ្រឹស្តីបទនេះចែងថាក្រាហ្វនៃអនុគមន៍ y = f(x), បន្តនៅលើចន្លោះពេល [ ក, ខ], ប្រសព្វអ័ក្ស គោយ៉ាងហោចណាស់ម្តងប្រសិនបើតម្លៃ f(ក) និង f(ខ) មាន សញ្ញាផ្ទុយ. ដូច្នេះ (រូបភាព ១.១៦) f(ក) > 0, f(ខ) < 0 и функция f(x) ក្លាយជា 0 នៅចំណុច x 1 , x 2 , x 3 .

ទ្រឹស្តីបទ ៣. អនុញ្ញាតឱ្យមុខងារ f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ], f(ក) = ក, f(ខ) = ខនិង ក¹ ខ. (រូបភាព 1.17) ។ បន្ទាប់មកសម្រាប់លេខណាមួយ។ គ, រុំព័ទ្ធរវាងលេខ កនិង ខមានចំណុចខាងក្នុងបែបនេះ x 0 ផ្នែក [ ក, ខ] អ្វី f(x 0) = គ.

ផលវិបាក. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ], ម – តម្លៃតូចបំផុត។ f(x), ម – តម្លៃខ្ពស់បំផុតមុខងារ f(x) នៅលើផ្នែក [ ក, ខ] បន្ទាប់មកអនុគមន៍យក (យ៉ាងហោចណាស់ម្តង) តម្លៃណាមួយ។ ម, បានបញ្ចប់រវាង មនិង មដូច្នេះហើយផ្នែក [ m, M] គឺជាសំណុំនៃតម្លៃមុខងារទាំងអស់។ f(x) នៅលើផ្នែក [ ក, ខ].

ចំណាំថាប្រសិនបើមុខងារបន្តនៅចន្លោះពេល ( ក, ខ) ឬមាននៅលើផ្នែក [ ក, ខ] ចំនុចមិនបន្តបន្ទាប់ ទ្រឹស្តីបទ 1, 2, 3 សម្រាប់មុខងារបែបនេះឈប់ជាការពិត។

សរុបសេចក្តី សូមពិចារណាទ្រឹស្តីបទស្តីពីអត្ថិភាពនៃអនុគមន៍បញ្ច្រាសមួយ។

ចូរយើងចាំថា តាមចន្លោះពេល យើងមានន័យថា ចម្រៀក ឬចន្លោះពេល ឬពាក់កណ្តាលចន្លោះ កំណត់ ឬគ្មានកំណត់។

ទ្រឹស្តីបទ ៤. អនុញ្ញាតឱ្យ f(x) គឺបន្តនៅចន្លោះពេល Xកើនឡើង (ឬថយចុះ) ដោយ Xនិងមានជួរតម្លៃ យ. បន្ទាប់មកសម្រាប់មុខងារ y = f(x) មានមុខងារបញ្ច្រាស x= j(y) បានកំណត់នៅលើចន្លោះពេល យបន្តនិងកើនឡើង (ឬថយចុះ) ដោយ យជាមួយនឹងអត្ថន័យជាច្រើន។ X.

មតិយោបល់. អនុញ្ញាតឱ្យមុខងារ x= j(y) គឺជាមុខងារបញ្ច្រាស f(x) ចាប់តាំងពីអាគុយម៉ង់ជាធម្មតាត្រូវបានតំណាងដោយ xនិងមុខងារតាមរយៈ yបន្ទាប់មកយើងនឹងសរសេរ មុខងារបញ្ច្រាសជា y =j(x).

ឧទាហរណ៍ ១. មុខងារ y = x 2 (រូបភព 1.8, ក) នៅលើសំណុំ X= ក, ខ[ និងបន្តនៅគ្រប់ចំណុចនៃចន្លោះពេលនេះ។ បន្ទាប់មកវាត្រូវបានគេហៅថាបន្តក្នុងចន្លោះពេល] ក, ខ[។ គោលគំនិតនៃការបន្តនៃអនុគមន៍មួយនៅលើចន្លោះពេលនៃទម្រង់]- ∞ ត្រូវបានកំណត់ស្រដៀងគ្នា, ខ[ , ]ក, + ∞ [ , ]- ∞ , + ∞ [ . អនុញ្ញាតឱ្យឥឡូវនេះមុខងារ y = f(x) បានកំណត់នៅលើចន្លោះពេល [ ក, ខ]។ ភាពខុសគ្នារវាងចន្លោះពេលមួយ និងផ្នែកមួយ៖ ចំណុចព្រំដែននៃចន្លោះពេលមិនត្រូវបានរាប់បញ្ចូលក្នុងចន្លោះពេលនោះទេ ប៉ុន្តែចំនុចព្រំដែននៃផ្នែកមួយត្រូវបានរួមបញ្ចូលនៅក្នុងផ្នែក។ នៅទីនេះយើងគួរនិយាយអំពីអ្វីដែលគេហៅថាការបន្តមួយចំហៀង: នៅចំណុច កនៅសល់នៅលើផ្នែក [ ក, ខ] យើងអាចចូលទៅជិតពីខាងស្តាំ និងដល់ចំណុចប៉ុណ្ណោះ។ ខ- មានតែនៅខាងឆ្វេងប៉ុណ្ណោះ។ អនុគមន៍​ត្រូវ​បាន​គេ​និយាយ​ថា​នឹង​បន្ត​នៅ​លើ​ចន្លោះ​ពេល [ ក, ខ] ប្រសិនបើវាបន្តនៅក្នុងទាំងអស់។ ចំណុចខាងក្នុងនៃផ្នែកនេះគឺបន្តនៅខាងស្តាំនៅចំណុច កហើយត្រូវបានទុកបន្តនៅចំណុច ខ.

ឧទាហរណ៍នៃអនុគមន៍បន្តអាចជាមុខងារបឋមណាមួយ។ គ្នា។ មុខងារបឋមគឺបន្តនៅលើចន្លោះពេលណាមួយដែលវាត្រូវបានកំណត់។ ឧទាហរណ៍ មុខងារ និងបន្តនៅចន្លោះពេលណាមួយ [ ក, ខ] មុខងារគឺបន្តនៅចន្លោះពេល [ 0 , ខ] មុខងារគឺបន្តលើផ្នែកណាមួយដែលមិនមានចំណុច ក = 2 .

ឧទាហរណ៍ 4 ។ពិនិត្យមុខងារសម្រាប់បន្ត។

ដំណោះស្រាយ។ តោះពិនិត្យមើលលក្ខខណ្ឌដំបូង។ មុខងារមិនត្រូវបានកំណត់នៅចំណុច - 3 និង 3. យ៉ាងហោចណាស់លក្ខខណ្ឌមួយសម្រាប់ការបន្តនៃអនុគមន៍តាមបណ្តោយបន្ទាត់លេខទាំងមូលមិនពេញចិត្ត។ នោះ​ហើយ​ជា​មូល​ហេតុ​ដែល មុខងារនេះ។គឺបន្តនៅចន្លោះពេល

.

ឧទាហរណ៍ 5 ។កំណត់តម្លៃនៃប៉ារ៉ាម៉ែត្រ កបន្តនៅទូទាំង ដែននៃនិយមន័យមុខងារ

ដំណោះស្រាយ។

តោះស្វែងរកដែនកំណត់ខាងស្តាំនៅ៖

.

ជាក់ស្តែងតម្លៃនៅចំណុច x= 2 គួរតែស្មើគ្នា ពូថៅ :

ក = 1,5 .

ឧទាហរណ៍ ៦.កំណត់តម្លៃប៉ារ៉ាម៉ែត្រ កនិង ខបន្តនៅទូទាំង ដែននៃនិយមន័យមុខងារ

ដំណោះស្រាយ។
ចូរយើងស្វែងរកដែនកំណត់ផ្នែកខាងឆ្វេងនៃមុខងារនៅចំណុច៖

.

ដូច្នេះតម្លៃនៅចំណុចត្រូវតែជា 1:

ចូរយើងស្វែងរកមុខងារខាងឆ្វេងនៅចំណុច៖

ជាក់ស្តែង តម្លៃនៃអនុគមន៍នៅចំណុចមួយគួរតែស្មើនឹង៖

ចម្លើយ៖ មុខងារគឺបន្តលើដែនទាំងមូលនៃនិយមន័យនៅពេល ក = 1; ខ = -3 .

លក្ខណៈសម្បត្តិជាមូលដ្ឋាននៃមុខងារបន្ត

គណិតវិទ្យាបានមកដល់គោលគំនិតនៃមុខងារបន្តមួយដោយសិក្សា ជាដំបូង ច្បាប់ផ្សេងៗនៃចលនា។ លំហ និងពេលវេលាគឺគ្មានកំណត់ ហើយការពឹងផ្អែកជាឧទាហរណ៍ផ្លូវ សពីពេលវេលា tបញ្ជាក់ដោយច្បាប់ ស = f(t) ផ្តល់ឧទាហរណ៍នៃការបន្ត មុខងារ f(t) ។ សីតុណ្ហភាពនៃទឹកកំដៅក៏ផ្លាស់ប្តូរជាបន្តបន្ទាប់ វាក៏ជាមុខងារបន្តនៃពេលវេលាផងដែរ៖ ធ = f(t) .

IN ការវិភាគគណិតវិទ្យាលក្ខណៈសម្បត្តិមួយចំនួនត្រូវបានបញ្ជាក់ មុខងារបន្ត. ចូរ​យើង​បង្ហាញ​ពី​លក្ខណៈ​សំខាន់​បំផុត​នៃ​លក្ខណៈសម្បត្តិ​ទាំងនេះ។

1. ប្រសិនបើអនុគមន៍បន្តលើចន្លោះពេលយកតម្លៃនៃសញ្ញាផ្សេងគ្នានៅចុងបញ្ចប់នៃចន្លោះពេល នោះនៅចំណុចខ្លះនៃចន្លោះពេលនេះវាយកតម្លៃ ស្មើនឹងសូន្យ. នៅក្នុងសេចក្តីថ្លែងការណ៍ផ្លូវការមួយ ទ្រព្យសម្បត្តិនេះត្រូវបានផ្តល់ឱ្យនៅក្នុងទ្រឹស្តីបទដែលគេស្គាល់ថាជាទ្រឹស្តីបទ Bolzano-Cauchy ដំបូង។

2. មុខងារ f(x), បន្តនៅលើចន្លោះពេល [ ក, ខ] យកតម្លៃមធ្យមទាំងអស់រវាងតម្លៃនៅចំនុចចុង ពោលគឺរវាង f(ក) និង f(ខ) ។ នៅក្នុងសេចក្តីថ្លែងការណ៍ផ្លូវការមួយ ទ្រព្យសម្បត្តិនេះត្រូវបានផ្តល់ឱ្យនៅក្នុងទ្រឹស្តីបទដែលគេស្គាល់ថាជាទ្រឹស្តីបទ Bolzano-Cauchy ទីពីរ។

ការបន្តនៃមុខងារនៅលើចន្លោះពេលមួយ។

ឈ្មោះប៉ារ៉ាម៉ែត្រ	អត្ថន័យ
ប្រធានបទអត្ថបទ៖	ការបន្តនៃមុខងារនៅលើចន្លោះពេលមួយ។
Rubric (ប្រភេទប្រធានបទ)	គណិតវិទ្យា

និយមន័យ។មុខងារមួយជាធម្មតាត្រូវបានគេហៅថាបន្តនៅលើចន្លោះពេលប្រសិនបើវាបន្តនៅគ្រប់ចំណុចនៃចន្លោះពេលនេះ។

ប្រសិនបើមុខងារត្រូវបានកំណត់នៅពេលណា X=កហើយនៅត្រង់ណា f(X) = f(ក),

បន្ទាប់មកពួកគេនិយាយថា f(X) នៅចំណុច និងបន្តនៅខាងស្តាំ. ដូចគ្នានេះដែរប្រសិនបើ f(X) = f(ខ) បន្ទាប់មកពួកគេនិយាយថានៅចំណុចនោះ។ ខមុខងារនេះ។ បន្ត.

និយមន័យ។មុខងារមួយជាធម្មតាត្រូវបានគេហៅថាបន្តនៅលើចន្លោះពេល [ ក, ខ] ប្រសិនបើវាបន្តនៅចំណុចនីមួយៗ (នៅចំណុច កបន្តនៅខាងស្តាំនៅចំណុច ខ- បន្តនៅខាងឆ្វេង) ។

តម្លៃខ្ពស់បំផុតមុខងារ នៅ = f(x) នៅលើផ្នែក [ ក, ខ f(x 1) នោះ។ f(x) £ f(x 1) សម្រាប់មនុស្សគ្រប់គ្នា X Î [ ក, ខ].

តម្លៃទាបបំផុត។មុខងារ នៅ = f(x) នៅលើផ្នែក [ ក, ខ] វាជាទម្លាប់ក្នុងការហៅវាថាអត្ថន័យរបស់វា។ f(x 2) នោះ។ f(x) ³ f(x 2) សម្រាប់មនុស្សគ្រប់គ្នា X Î [ ក, ខ].

អនុគមន៍​ដែល​បន្ត​នៅ​ចន្លោះ​ពេល​មួយ​មាន​ចំនួន​ លក្ខណៈសម្បត្តិសំខាន់ដែលត្រូវបានបញ្ជាក់ដោយទ្រឹស្តីបទខាងក្រោម។

ទ្រឹស្តីបទ ៣.៣.១.មុខងារបន្តនៅលើចន្លោះពេល [ ក, ខ] ឈានដល់តម្លៃអប្បបរមារបស់វានៅលើវា។ មនិងតម្លៃដ៏អស្ចារ្យបំផុត។ មនោះគឺមានចំណុចបែបនេះ x 1 និង x 2 នៃផ្នែកនេះ, នោះ។ f(x 1) = ម, f(x 2) = ម.

ទ្រឹស្តីបទមានអត្ថន័យធរណីមាត្រសាមញ្ញ (សូមមើលរូបភាពទី 2) ។

ទ្រឹស្តីបទ ៣.៣.២.ប្រសិនបើមុខងារ នៅ = f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ] ហើយនៅចុងបញ្ចប់របស់វាយកតម្លៃមិនស្មើគ្នា f(ក) = ក, f(ខ) = B, A ¹ B នោះ អ្វីក៏ដោយដែលលេខ C នៅចន្លោះ A និង B នឹងមានចំនុចមួយ។ ជាមួយ Î [ ក, ខ] បែបនោះ។ f(ជាមួយ) = ស.

អត្ថន័យធរណីមាត្រទ្រឹស្តីបទត្រូវបានបង្ហាញក្នុងរូបភាពទី 3 ។ បន្ទាត់ត្រង់ណាមួយ។ នៅ= C ដែល A< C < B (или A >C > B) ប្រសព្វក្រាហ្វនៃអនុគមន៍ នៅ = f(x).

ផលវិបាក។ប្រសិនបើអនុគមន៍មួយបន្តនៅលើផ្នែកមួយ ហើយយកតម្លៃនៃសញ្ញាផ្សេងគ្នានៅចុងរបស់វា នោះនៅលើផ្នែកនេះយ៉ាងហោចណាស់មានចំណុចមួយដែលមុខងារបាត់។

អត្ថន័យធរណីមាត្រនៃលទ្ធផលត្រូវបានបង្ហាញនៅក្នុងរូបភាពទី 4 ។

សំណួរសម្រាប់ការគ្រប់គ្រងខ្លួនឯង

1. តើមុខងារអ្វីជាធម្មតាត្រូវបានគេហៅថាបន្តនៅចំណុចមួយ?

2. ផ្តល់និយមន័យសមមូលមួយផ្សេងទៀតនៅក្នុងលក្ខខណ្ឌនៃការបង្កើនមុខងារ និងអាគុយម៉ង់។

3. តើអ្វីអាចនិយាយបានអំពីផលបូក ភាពខុសគ្នា ផលិតផល និងគុណប្រយោជន៍នៃអនុគមន៍បន្តពីរ?

4. សម្រាប់អ្វីដែលតម្លៃនៃអាគុយម៉ង់គឺសមហេតុផលទាំងមូលនិង អនុគមន៍ប្រភាគ-សនិទានបន្ត?

5. តើមុខងារស្មុគស្មាញបន្តនៅចំណុចមួយនៅពេលណា?

6. ដូចម្តេចដែលហៅថា ចំណុចបំបែកនៃមុខងារ?

7. តើចំនុចណាខ្លះដែលហៅថាចំនុចដាច់នៃប្រភេទទីមួយ?

8. តើបរិមាណអ្វីជាធម្មតាត្រូវបានគេហៅថាលោតមុខងារ?

9. ពន្យល់ពីគោលគំនិតនៃ "ចំណុចដាច់ដែលអាចដកចេញបាន"។ ផ្តល់ឧទាហរណ៍។

10. តើចំនុចណាខ្លះដែលហៅថាចំនុចដាច់នៃប្រភេទទីពីរ? ផ្តល់ឧទាហរណ៍។

11. ពន្យល់ពីគោលគំនិត៖ “ការបន្តនៅចន្លោះពេល” “ការបន្តនៅខាងស្តាំ” “ការបន្តនៅខាងឆ្វេង” “ការបន្តលើផ្នែកមួយ”។

12. កំណត់តម្លៃធំបំផុត និងតូចបំផុតនៃមុខងារ។

13. បង្កើតទ្រឹស្តីបទអំពីការតភ្ជាប់រវាងការបន្តនៅលើផ្នែកមួយ និងតម្លៃធំបំផុត និងតូចបំផុតនៃអនុគមន៍មួយ។ ពន្យល់វាជាមួយគំនូរ។

14. បង្កើតទ្រឹស្តីបទអំពីការតភ្ជាប់រវាងការបន្តនៃអនុគមន៍នៅលើចន្លោះពេលមួយ និងចន្លោះពេលនៃតម្លៃមុខងារ។ បង្ហាញអត្ថន័យធរណីមាត្ររបស់វានៅក្នុងរូប។

15. ផ្តល់ការពន្យល់ពីទ្រឹស្តីបទខាងលើ និងការបកស្រាយធរណីមាត្ររបស់វា។

មេរៀនទី៤

ប្រធានបទមេរៀន៖ ដេរីវេនៃមុខងារមួយ។

គ្រោងការបង្រៀន៖គំនិតនៃដេរីវេ, ធរណីមាត្ររបស់វា និង អត្ថន័យរាងកាយ. ច្បាប់ជាមូលដ្ឋាននៃភាពខុសគ្នា។ ដេរីវេ មុខងារស្មុគស្មាញ. កម្មវិធីមួយចំនួនមានដេរីវេ។

៤.១. គំនិតនៃនិស្សន្ទវត្ថុ អត្ថន័យធរណីមាត្រ និងរូបវន្តរបស់វា។

ពិចារណាមុខងារ នៅ = f(x) ដែលបានបញ្ជាក់ក្នុងចន្លោះពេល] ក, ខ[។ អនុញ្ញាតឱ្យ XÎ ] ក, ខ[ និង X Î ] ក, ខ[, បន្ទាប់មកការបង្កើនមុខងារនៅចំណុច X 0 ត្រូវបានបង្ហាញដោយរូបមន្ត D នៅ = f(x 0+D X) – f(x 0).

និយមន័យ។ ដេរីវេនៃអនុគមន៍ y = f(x) នៅចំណុច X 0 ជាធម្មតាត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍នេះទៅនឹងការបង្កើននៃអាគុយម៉ង់ នៅពេលក្រោយមានទំនោរទៅសូន្យ៖

f'(x 0) = ឬ y"(x 0) =.

អត្ថន័យធរណីមាត្រនៃដេរីវេ៖ ដេរីវេនៃអនុគមន៍ដែលបានផ្តល់ឱ្យនៅចំណុចមួយគឺស្មើនឹងតង់សង់នៃមុំរវាងអ័ក្សអុក និងតង់ហ្សង់ទៅក្រាហ្វនៃអនុគមន៍នេះនៅ ចំណុចដែលត្រូវគ្នា។(សូមមើលរូបទី 1)៖

f"(x 0) = តាន់ ក.

លក្ខណសម្បត្តិនៃមុខងារបន្តលើការសម្ភាសន៍

ចូរយើងពិចារណាលក្ខណៈសម្បត្តិមួយចំនួននៃមុខងារបន្តក្នុងចន្លោះពេលមួយ។ យើងបង្ហាញលក្ខណៈសម្បត្តិទាំងនេះដោយគ្មានភស្តុតាង។

មុខងារ y = f(x)ហៅ បន្តលើផ្នែក [ក, ខ] ប្រសិនបើវាបន្តនៅគ្រប់ចំណុចខាងក្នុងនៃផ្នែកនេះ ហើយនៅចុងបញ្ចប់របស់វា i.e. នៅចំណុច កនិង ខគឺបន្តនៅខាងស្តាំ និងខាងឆ្វេង រៀងគ្នា។

ទ្រឹស្តីបទ ១.មុខងារបន្តនៅលើចន្លោះពេល [ ក, ខ] យ៉ាងហោចណាស់នៅចំណុចមួយនៃផ្នែកនេះយកតម្លៃធំបំផុត ហើយយ៉ាងហោចណាស់នៅចំណុចមួយតូចបំផុត។

ទ្រឹស្តីបទចែងថាប្រសិនបើមុខងារមួយ។ y = f(x)គឺបន្តនៅលើចន្លោះពេល [ ក, ខ] បន្ទាប់មកយ៉ាងហោចណាស់មានចំណុចមួយ។ x ១ Î [ ក, ខ] ដូចនេះតម្លៃនៃមុខងារ f(x)នៅចំណុចនេះនឹងជាតម្លៃធំបំផុតនៃតម្លៃទាំងអស់របស់វានៅលើផ្នែកនេះ៖ f(x 1) ≥ f(x). ដូចគ្នានេះដែរមានចំណុចបែបនេះ x ២ដែលក្នុងនោះតម្លៃអនុគមន៍នឹងតូចបំផុតនៃតម្លៃទាំងអស់នៅលើផ្នែក៖ f(x 1) ≤ f(x).

វាច្បាស់ណាស់ថាអាចមានចំណុចបែបនេះជាច្រើនឧទាហរណ៍តួរលេខបង្ហាញថាមុខងារ f(x)យកតម្លៃតូចបំផុតនៅពីរចំណុច x ២និង x 2 ".

មតិយោបល់. សេចក្តីថ្លែងការណ៍នៃទ្រឹស្តីបទអាចក្លាយទៅជាមិនត្រឹមត្រូវ ប្រសិនបើយើងពិចារណាតម្លៃនៃអនុគមន៍នៅលើចន្លោះពេល ( ក, ខ) ជាការពិតប្រសិនបើយើងពិចារណាមុខងារ y = xនៅលើ (0, 2) បន្ទាប់មកវាបន្តនៅលើចន្លោះពេលនេះ ប៉ុន្តែមិនឈានដល់តម្លៃធំបំផុត ឬតូចបំផុតនៅក្នុងវាទេ៖ វាឈានដល់តម្លៃទាំងនេះនៅចុងបញ្ចប់នៃចន្លោះពេល ប៉ុន្តែចុងបញ្ចប់មិនមែនជាកម្មសិទ្ធិទេ។ ទៅកាន់ដែនរបស់យើង។

ដូចគ្នានេះផងដែរ ទ្រឹស្តីបទឈប់ជាការពិតសម្រាប់មុខងារមិនបន្ត។ ផ្តល់ឧទាហរណ៍មួយ។

ផលវិបាក។ប្រសិនបើមុខងារ f(x)គឺបន្តនៅលើ [ ក, ខ] បន្ទាប់មកវាត្រូវបានកំណត់នៅលើផ្នែកនេះ។

ទ្រឹស្តីបទ ២.អនុញ្ញាតឱ្យមុខងារ y = f(x)គឺបន្តនៅលើចន្លោះពេល [ ក, ខ] ហើយនៅចុងបញ្ចប់នៃផ្នែកនេះយកតម្លៃនៃសញ្ញាផ្សេងគ្នា បន្ទាប់មកមានយ៉ាងហោចណាស់មួយចំណុចនៅខាងក្នុងផ្នែក x = គដែលមុខងារទៅសូន្យ៖ f(C)= 0 ដែល ក< C< b

ទ្រឹស្តីបទនេះមានអត្ថន័យធរណីមាត្រសាមញ្ញ៖ ប្រសិនបើចំនុចនៃក្រាហ្វនៃអនុគមន៍បន្ត y = f(x)ដែលត្រូវគ្នាទៅនឹងចុងបញ្ចប់នៃផ្នែក [ ក, ខ] កុហក ភាគីផ្សេងគ្នាពីអ័ក្ស គោបន្ទាប់មកក្រាហ្វនេះប្រសព្វអ័ក្សយ៉ាងហោចណាស់នៅចំណុចមួយនៃផ្នែក គោ. មុខងារមិនបន្តអាចមិនមានទ្រព្យសម្បត្តិនេះទេ។

ទ្រឹស្តីបទនេះទទួលយកការទូទៅដូចខាងក្រោម។

ទ្រឹស្តីបទ ៣ (ទ្រឹស្តីបទតម្លៃមធ្យម)។អនុញ្ញាតឱ្យមុខងារ y = f(x)គឺបន្តនៅលើចន្លោះពេល [ ក, ខ] និង f (a) = ក, f (b) = ខ. បន្ទាប់មកសម្រាប់លេខណាមួយ។ គ, បានបញ្ចប់រវាង កនិង ខមានចំណុចបែបនេះនៅក្នុងផ្នែកនេះ។ គÎ [ ក, ខ] អ្វី f (c) = គ.

ទ្រឹស្តីបទនេះគឺជាក់ស្តែងតាមធរណីមាត្រ។ ពិចារណាក្រាហ្វនៃមុខងារ y = f(x). អនុញ្ញាតឱ្យ f (a) = ក, f (b) = ខ. បន្ទាប់មកបន្ទាត់ត្រង់ណាមួយ។ y = គ, កន្លែងណា គ- លេខណាមួយរវាង កនិង ខនឹងប្រសព្វក្រាហ្វនៃអនុគមន៍យ៉ាងហោចណាស់នៅចំណុចមួយ។ abscissa នៃចំនុចប្រសព្វនឹងជាតម្លៃនោះ។ x = គនៅឯណា f (c) = គ.

ដូច្នេះ មុខងារបន្ត ផ្លាស់ប្តូរពីតម្លៃមួយទៅតម្លៃមួយទៀត ចាំបាច់ឆ្លងកាត់តម្លៃមធ្យមទាំងអស់។ ជាពិសេស:

ផលវិបាក។ប្រសិនបើមុខងារ y = f(x)គឺបន្តក្នុងចន្លោះពេលជាក់លាក់មួយ ហើយយកតម្លៃធំបំផុត និងតូចបំផុត បន្ទាប់មកនៅចន្លោះពេលនេះ វាត្រូវចំណាយពេលយ៉ាងហោចណាស់ម្តងតម្លៃណាមួយដែលមានរវាងតម្លៃតូចបំផុត និងធំបំផុតរបស់វា។

ដេរីវេ និងកម្មវិធីរបស់វា។ និយមន័យនៃដេរីវេ

អនុញ្ញាតឱ្យយើងមានមុខងារមួយចំនួន y=f(x),កំណត់នៅចន្លោះពេលខ្លះ។ សម្រាប់តម្លៃអាគុយម៉ង់នីមួយៗ xពីចន្លោះពេលនេះមុខងារ y=f(x)មានអត្ថន័យជាក់លាក់។

ពិចារណាតម្លៃអាគុយម៉ង់ពីរ៖ ដំបូង x 0 និងថ្មី។ x.

ភាពខុសគ្នា x–x 0 ត្រូវបានគេហៅថា ដោយការបង្កើនអាគុយម៉ង់ xនៅចំណុច x 0 និងត្រូវបានតំណាង Δx. ដូច្នេះ Δx = x − x 0 (ការបង្កើនអាគុយម៉ង់អាចជាវិជ្ជមាន ឬអវិជ្ជមាន)។ ពីសមភាពនេះវាធ្វើតាមនោះ។ x=x 0 +Δx, i.e. អត្ថន័យដើមអថេរបានទទួលការបង្កើនមួយចំនួន។ បន្ទាប់មកប្រសិនបើនៅចំណុច x 0 តម្លៃមុខងារគឺ f(x 0 ), បន្ទាប់មកនៅក្នុង ចំណុចថ្មី។ xមុខងារនឹងយកតម្លៃ f(x) = f(x 0 +Δx).

ភាពខុសគ្នា y-y 0 = f(x) – f(x 0 ) ហៅ ការបង្កើនមុខងារ y = f(x)នៅចំណុច x 0 និងត្រូវបានចង្អុលបង្ហាញដោយនិមិត្តសញ្ញា Δy. ដូច្នេះ

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

ជាធម្មតាតម្លៃដំបូងនៃអាគុយម៉ង់ x 0 ត្រូវបានចាត់ទុកថាថេរ ហើយតម្លៃថ្មី។ x- ប្រែប្រួល។ បន្ទាប់មក y 0 = f(x 0 ) ប្រែទៅជាថេរនិង y = f(x)- ប្រែប្រួល។ ការកើនឡើង Δyនិង Δxក៏នឹងក្លាយជាអថេរ ហើយរូបមន្ត (1) បង្ហាញថា ឌីគឺជាមុខងារនៃអថេរមួយ។ Δx.

ចូរ​បង្កើត​សមាមាត្រ​នៃ​ការ​បង្កើន​មុខងារ​ទៅ​នឹង​ការ​បង្កើន​អាគុយម៉ង់

អនុញ្ញាតឱ្យយើងរកឃើញដែនកំណត់នៃសមាមាត្រនេះនៅ Δx→0. ប្រសិនបើដែនកំណត់នេះមាន នោះវាត្រូវបានគេហៅថាដេរីវេនៃមុខងារនេះ។ f(x)នៅចំណុច x 0 និងសម្គាល់ f "(x 0). ដូច្នេះ

ដេរីវេមុខងារនេះ។ y = f(x)នៅចំណុច x 0 ត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្របង្កើនមុខងារ Δ yទៅនឹងការបង្កើនអាគុយម៉ង់ Δ xនៅពេលក្រោយដោយបំពានទំនោរទៅសូន្យ។

ចំណាំថាសម្រាប់មុខងារដូចគ្នា ដេរីវេនៅក្នុង ចំណុចផ្សេងៗ xអាចទទួលយកតម្លៃផ្សេងគ្នា, i.e. ដេរីវេអាចត្រូវបានចាត់ទុកថាជាមុខងារនៃអាគុយម៉ង់ x. មុខងារនេះត្រូវបានកំណត់ f "(x)

ដេរីវេត្រូវបានតំណាងដោយនិមិត្តសញ្ញា f "(x), y ", . អត្ថន័យជាក់លាក់ដេរីវេនៅ x = កតំណាងដោយ f "(ក) ឬ y "| x=a.

ប្រតិបត្តិការនៃការស្វែងរកដេរីវេនៃអនុគមន៍មួយ។ f(x)ត្រូវបានគេហៅថាភាពខុសគ្នានៃមុខងារនេះ។

ដើម្បីស្វែងរកដោយផ្ទាល់នូវដេរីវេតាមនិយមន័យ អ្នកអាចប្រើដូចខាងក្រោម៖ ច្បាប់​នៃ​មេដៃ:

ឧទាហរណ៍។

អារម្មណ៍មេកានិកនៃដេរីវេ

វាត្រូវបានគេស្គាល់ពីរូបវិទ្យាថាច្បាប់ ចលនាឯកសណ្ឋានមើល​ទៅ​ដូច​ជា s = v t, កន្លែងណា ស- ផ្លូវបានធ្វើដំណើរទៅពេលវេលា t, v- ល្បឿននៃចលនាឯកសណ្ឋាន។

ទោះយ៉ាងណាក៏ដោយដោយសារតែ ចលនាភាគច្រើនដែលកើតឡើងនៅក្នុងធម្មជាតិគឺមិនស្មើគ្នា បន្ទាប់មកជាទូទៅល្បឿន ហើយជាលទ្ធផលចម្ងាយ សនឹងអាស្រ័យលើពេលវេលា t, i.e. នឹងជាមុខងារនៃពេលវេលា។

ដូច្នេះ សូម​ឲ្យ​ចំណុច​សម្ភារៈ​ផ្លាស់ទី​ក្នុង​បន្ទាត់​ត្រង់​ក្នុង​ទិស​មួយ​ស្រប​តាម​ច្បាប់ s=s(t)។

ចូរសម្គាល់ចំណុចជាក់លាក់មួយនៅក្នុងពេលវេលា t 0. នៅពេលនេះចំណុចបានឆ្លងកាត់ផ្លូវ s=s(t 0 ). ចូរយើងកំណត់ល្បឿន vចំណុចសម្ភារៈនៅពេលមួយនៅក្នុងពេលវេលា t 0 .

ដើម្បីធ្វើដូចនេះសូមពិចារណាចំណុចផ្សេងទៀតនៅក្នុងពេលវេលា t 0 + Δ t. វា​ត្រូវ​នឹង​ផ្លូវ​ដែល​បាន​ធ្វើ​ដំណើរ s =s(t 0 + Δ t) បន្ទាប់មកក្នុងរយៈពេល Δ tចំណុចបានធ្វើដំណើរតាមផ្លូវ Δs =s(t 0 + Δ t)–s(t)

ចូរយើងពិចារណាអំពីអាកប្បកិរិយា។ វាត្រូវបានគេហៅថាល្បឿនមធ្យមក្នុងចន្លោះពេល Δ t. ល្បឿនមធ្យមមិនអាចកំណត់លក្ខណៈល្បឿននៃចលនានៃចំណុចណាមួយបានត្រឹមត្រូវទេនៅពេលនេះ t 0 (ដោយសារតែចលនាមិនស្មើគ្នា) ។ ដើម្បីបង្ហាញឱ្យកាន់តែច្បាស់នូវល្បឿនពិតនេះដោយប្រើ ល្បឿន​មធ្យមអ្នកត្រូវចំណាយពេលខ្លីជាង Δ t.

ដូច្នេះល្បឿននៃចលនានៅក្នុង ពេលនេះពេលវេលា t 0 (ល្បឿនភ្លាមៗ) គឺជាដែនកំណត់នៃល្បឿនមធ្យមក្នុងចន្លោះពេលពី t 0 ទៅ t 0 +Δ t, នៅពេលដែល Δ t→0:

,

ទាំងនោះ។ ល្បឿនមិនស្មើគ្នានេះគឺជាដេរីវេនៃចម្ងាយដែលធ្វើដំណើរដោយគោរពតាមពេលវេលា។

អត្ថន័យធរណីមាត្រនៃដេរីវេ

ចូរយើងណែនាំនិយមន័យនៃតង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ។

សូម​ឲ្យ​យើង​មាន​ខ្សែកោង និង​ចំណុច​ថេរ​លើ​វា។ ម ០(សូមមើលរូប) ពិចារណាចំណុចមួយទៀត មខ្សែកោង​នេះ​ហើយ​គូរ​វិនាទី ម 0 ម. ប្រសិនបើចំណុច មចាប់ផ្តើមផ្លាស់ទីតាមខ្សែកោង និងចំណុច ម ០នៅតែគ្មានចលនា នោះផ្នែកនឹងផ្លាស់ប្តូរទីតាំងរបស់វា។ ប្រសិនបើជាមួយនឹងការប៉ាន់ស្មានគ្មានដែនកំណត់នៃចំណុច មតាមខ្សែកោងទៅចំណុចមួយ។ ម ០នៅផ្នែកខាងណាមួយ សេកមានទំនោរកាន់កាប់ទីតាំងនៃបន្ទាត់ត្រង់ជាក់លាក់មួយ។ ម 0 ធបន្ទាប់មកត្រង់ ម 0 ធហៅថាតង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ ម ០.

នោះ., តង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ ម ០ហៅថាទីតាំងកំណត់នៃសេកាន ម 0 មនៅពេលដែលចំណុច មទំនោរតាមបណ្តោយខ្សែកោងទៅចំណុចមួយ។ ម ០.

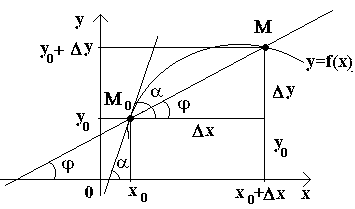
ឥឡូវនេះ ចូរយើងពិចារណាអំពីមុខងារបន្ត y=f(x)និងខ្សែកោងដែលត្រូវគ្នានឹងមុខងារនេះ។ នៅតម្លៃខ្លះ Xមុខងារ 0 យកតម្លៃ y 0 = f (x 0) ។តម្លៃទាំងនេះ x 0 និង y 0 នៅលើខ្សែកោងត្រូវគ្នាទៅនឹងចំណុចមួយ។ M 0 (x 0; y 0) ។ចូរយើងផ្តល់អំណះអំណាង x 0បង្កើន Δ X. តម្លៃថ្មីនៃអាគុយម៉ង់ត្រូវគ្នាទៅនឹងតម្លៃបន្ថែមនៃអនុគមន៍ y 0 +Δ y=f(x 0 –Δ x). យើងទទួលបានចំណុច ម(x ០+Δ x; y ០+Δ y)តោះ​គូរ​ឃ្លា ម 0 មនិងសម្គាល់ដោយ φ មុំដែលបង្កើតឡើងដោយសេកង់ដែលមានទិសដៅវិជ្ជមាននៃអ័ក្ស គោ. ចូរយើងបង្កើតទំនាក់ទំនង ហើយចំណាំថា

ប្រសិនបើឥឡូវនេះ Δ x→ 0 បន្ទាប់មកដោយសារតែការបន្តនៃអនុគមន៍ Δ នៅ→0 ហើយ​ដូច្នេះ​ចំណុច មផ្លាស់ទីតាមខ្សែកោង ចូលទៅជិតចំណុចដោយគ្មានដែនកំណត់ ម ០. បន្ទាប់មកសេក ម 0 មទំនោរនឹងយកទីតាំងនៃតង់សង់ទៅខ្សែកោងនៅចំណុច ម ០, និងមុំφ→αនៅΔ x→0 ដែល α បង្ហាញពីមុំរវាងតង់សង់ និងទិសដៅវិជ្ជមាននៃអ័ក្ស គោ. ដោយសារអនុគមន៍ tan φ បន្តពឹងផ្អែកលើφសម្រាប់φ≠π/2 បន្ទាប់មកសម្រាប់φ →α tan φ → tan α ហើយដូច្នេះជម្រាលនៃតង់សង់នឹងមានៈ

ទាំងនោះ។ f "(x)= tg α ។

ដូច្នេះធរណីមាត្រ y "(x 0)តំណាងឱ្យជម្រាលនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍នេះនៅចំណុច x 0, i.e. នៅ តម្លៃដែលបានផ្តល់ឱ្យអាគុយម៉ង់ xដេរីវេគឺស្មើនឹងតង់ហ្សង់នៃមុំដែលបង្កើតឡើងដោយតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f(x)នៅចំណុចសមស្រប M 0 (x; y)ជាមួយនឹងទិសដៅអ័ក្សវិជ្ជមាន គោ។

ឧទាហរណ៍។ស្វែងរក ជម្រាលតង់សង់ទៅខ្សែកោង y = x 2 នៅចំណុច ម(-1; 1).

យើងបានឃើញពីមុនហើយថា ( x 2)" = 2X. ប៉ុន្តែមេគុណមុំនៃតង់សង់ទៅខ្សែកោងគឺ tan α = y"| x=-1=-2 ។

ភាពខុសគ្នានៃមុខងារ។ ការបន្តនៃមុខងារដែលអាចផ្លាស់ប្តូរបាន។

មុខងារ y=f(x)ហៅ ខុសគ្នានៅចំណុចណាមួយ។ x 0 ប្រសិនបើវាមានដេរីវេជាក់លាក់នៅចំណុចនេះ i.e. ប្រសិនបើដែនកំណត់នៃទំនាក់ទំនងមាន ហើយមានកំណត់។

ប្រសិនបើមុខងារអាចខុសគ្នានៅចំណុចនីមួយៗនៃផ្នែកជាក់លាក់មួយ [ ក; ខ] ឬចន្លោះពេល ( ក; ខ) បន្ទាប់មកពួកគេនិយាយថានាង ខុសគ្នានៅលើផ្នែក [ ក; ខ] ឬរៀងគ្នាក្នុងចន្លោះពេល ( ក; ខ).

ទ្រឹស្តីបទខាងក្រោមមានសុពលភាព បង្កើតការតភ្ជាប់រវាងមុខងារផ្សេងគ្នា និងបន្ត។

ទ្រឹស្តីបទ។ប្រសិនបើមុខងារ y=f(x)ខុសគ្នាត្រង់ចំណុចណាមួយ។ x 0បន្ទាប់មកវាបន្តនៅចំណុចនេះ។

ដូច្នេះ ពីភាពខុសគ្នានៃមុខងារ ភាពបន្តរបស់វាដូចខាងក្រោម។

ភស្តុតាង. ប្រសិនបើ , នោះ។

,

ដែល α គឺជាបរិមាណគ្មានកំណត់ ពោលគឺឧ។ បរិមាណទំនោរទៅសូន្យជា Δ x→0. ប៉ុន្តែ​បន្ទាប់មក

Δ y=f "(x 0) Δ x+αΔ x=> Δ y→ 0 នៅ Δ x→ 0, ឧ។ f(x) - f(x 0)→ 0 នៅ x→x 0 ដែលមានន័យថាមុខងារ f(x)បន្តនៅចំណុចមួយ។ x 0. Q.E.D.

ដូច្នេះ អនុគមន៍មិនអាចមានដេរីវេនៅចំនុចដាច់ទេ។ ការសន្ទនាមិនពិត៖ មានមុខងារបន្តដែលមិនមានភាពខុសគ្នានៅចំណុចមួយចំនួន (នោះគឺមិនមានដេរីវេនៅចំណុចទាំងនេះ)។

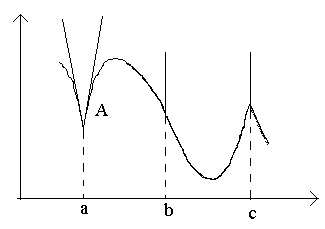
ពិចារណាចំណុចនៅក្នុងរូបភាព ក, ខ, គ។

នៅចំណុច កនៅ Δ xសមាមាត្រ → 0 មិនមានដែនកំណត់ទេ (ចាប់តាំងពីដែនកំណត់ម្ខាងគឺខុសគ្នាសម្រាប់Δ x→ 0–0 និង Δ x→0+0)។ នៅចំណុច កក្រាហ្វមិនមានតង់សង់ដែលបានកំណត់ទេ ប៉ុន្តែមានតង់សង់ពីរផ្សេងគ្នាដែលមានជម្រាល ទៅ 1 និង ទៅ២. ចំណុចប្រភេទនេះត្រូវបានគេហៅថា ចំណុចជ្រុង។

នៅចំណុច ខនៅ Δ xទំនាក់ទំនង → 0 គឺជាសញ្ញាថេរដោយគ្មានកំណត់ ទំហំធំ. មុខងារមានដេរីវេគ្មានកំណត់។ នៅចំណុចនេះ ក្រាហ្វមានតង់សង់បញ្ឈរ។ ប្រភេទចំណុច - "ចំណុចបញ្ឆេះ" នៃតង់សង់បញ្ឈរ។

នៅចំណុច គនិស្សន្ទវត្ថុម្ខាងគឺមានចំនួនច្រើនគ្មានកំណត់នៃសញ្ញាផ្សេងគ្នា។ នៅចំណុចនេះ ក្រាហ្វមានតង់ហ្សង់បញ្ឈរពីររួមបញ្ចូលគ្នា។ ប្រភេទ - "ចំណុចត្រឡប់" ជាមួយតង់សង់បញ្ឈរ - ករណីពិសេសចំណុចជ្រុង។