(from Greek λόγος - “word”, “relation” and ἀριθμός - “number”) numbers b based on a(log α b) is called such a number c, And b= a c, that is, records log α b=c And b=ac are equivalent. The logarithm makes sense if a > 0, a ≠ 1, b > 0.
In other words logarithm numbers b based on A formulated as an exponent to which a number must be raised a to get the number b(logarithm exists only for positive numbers).
From this formulation it follows that the calculation x= log α b, is equivalent to solving the equation a x =b.
For example:
log 2 8 = 3 because 8 = 2 3 .
Let us emphasize that the indicated formulation of the logarithm makes it possible to immediately determine logarithm value, when the number under the logarithm sign acts as a certain power of the base. Indeed, the formulation of the logarithm makes it possible to justify that if b=a c, then the logarithm of the number b based on a equals With. It is also clear that the topic of logarithms is closely related to the topic powers of a number.
Calculating the logarithm is called logarithm. Logarithm is mathematical operation taking the logarithm. When taking logarithms, products of factors are transformed into sums of terms.
Potentiation is the inverse mathematical operation of logarithm. During potentiation, a given base is raised to the degree of expression over which potentiation is performed. In this case, the sums of terms are transformed into a product of factors.
Quite often, real logarithms are used with bases 2 (binary), Euler's number e ≈ 2.718 (natural logarithm) and 10 (decimal).
On at this stage it is advisable to consider logarithm samples log 7 2 , ln √ 5, lg0.0001.
And the entries lg(-3), log -3 3.2, log -1 -4.3 do not make sense, since in the first of them a negative number is placed under the logarithm sign, in the second - a negative number in the base, and in the third - both a negative number under the logarithm sign and a unit in the base.
Conditions for determining the logarithm.
It is worth considering separately the conditions a > 0, a ≠ 1, b > 0.under which we get definition of logarithm. Let's consider why these restrictions were taken. An equality of the form x = log α will help us with this b, called the basic logarithmic identity, which directly follows from the definition of logarithm given above.
Let's take the condition a≠1. Since one to any power is equal to one, then the equality x=log α b can only exist when b=1, but log 1 1 will be any real number. To eliminate this ambiguity, we take a≠1.
Let us prove the necessity of the condition a>0. At a=0 according to the formulation of the logarithm can exist only when b=0. And accordingly then log 0 0 can be any non-zero real number, since zero to any non-zero power is zero. This ambiguity can be eliminated by the condition a≠0. And when a<0 we would have to reject the analysis of rational and irrational values of the logarithm, since a degree with a rational and irrational exponent is defined only for non-negative bases. It is for this reason that the condition is stipulated a>0.
AND last condition b>0 follows from inequality a>0, since x=log α b, and the value of the degree with a positive base a always positive.
Features of logarithms.
Logarithms characterized by distinctive features, which led to their widespread use to significantly facilitate painstaking calculations. When moving “to the world of logarithms,” multiplication is transformed by much more easy folding, division is subtraction, and exponentiation and root extraction are transformed, respectively, into multiplication and division by the exponent.
Formulation of logarithms and table of their values (for trigonometric functions) was first published in 1614 by the Scottish mathematician John Napier. Logarithmic tables, enlarged and detailed by other scientists, were widely used in scientific and engineering calculations, and remained relevant until the use of electronic calculators and computers.
Logarithm of a number N based on A called exponent X , to which you need to build A to get the number N
Provided that 
,
,
From the definition of logarithm it follows that 
, i.e.
- this equality is the basic logarithmic identity.
Logarithms to base 10 are called decimal logarithms. Instead of 
write 
.
Logarithms to the base e
are called natural and are designated 
.
Basic properties of logarithms.
Logarithm of one in any base equal to zero
Logarithm of the product equal to the sum logarithms of factors.
3) The logarithm of the quotient is equal to the difference of the logarithms
Factor 
called the modulus of transition from logarithms to the base a
to logarithms at the base b
.
Using properties 2-5, it is often possible to reduce the logarithm of a complex expression to the result of simple arithmetic operations on logarithms.
For example, 
Such transformations of a logarithm are called logarithms. Transformations inverse to logarithms are called potentiation.
Chapter 2. Elements of higher mathematics.
1. Limits
Limit of the function 
is a finite number A if, as xx
0
for each predetermined 
, there is such a number 
that as soon as 
, That 
.
A function that has a limit differs from it by an infinitesimal amount: 
, where- b.m.v., i.e. 
.
Example. Consider the function 
.
When striving 
, function y
tends to zero: 
1.1. Basic theorems about limits.
Limit constant value equal to this constant value
.
Amount (difference) limit finite number functions is equal to the sum (difference) of the limits of these functions.
Limit of the product of a finite number of functions equal to the product the limits of these functions.
The limit of the quotient of two functions is equal to the quotient of the limits of these functions if the limit of the denominator is not zero.
Wonderful Limits
,
, Where 
1.2. Limit Calculation Examples
However, not all limits are calculated so easily. More often, calculating the limit comes down to revealing an uncertainty of the type: 
or .
.
2. Derivative of a function
Let us have a function 
, continuous on the segment 
.
Argument 
got some increase 
. Then the function will receive an increment 
.
Argument value 
corresponds to the function value 
.
Argument value 
corresponds to the function value.
Hence, .
Let us find the limit of this ratio at 
. If this limit exists, then it is called the derivative of the given function.
Definition 3 Derivative of a given function 
by argument 
is called the limit of the ratio of the increment of a function to the increment of the argument, when the increment of the argument arbitrarily tends to zero.
Derivative of a function 
can be designated as follows:
;
;
;
.
Definition 4The operation of finding the derivative of a function is called differentiation.
2.1. Mechanical meaning of derivative.
Let's consider the rectilinear motion of some rigid body or material point.
Let at some point in time 
moving point 
was at a distance 
from the starting position 
.
After some period of time 
she moved a distance 
. Attitude 
=
- average speed material point 
. Let us find the limit of this ratio, taking into account that 
.
Therefore, the definition instantaneous speed motion of a material point comes down to finding the derivative of the path with respect to time.
2.2. Geometric meaning derivative
Let us have a graphically defined function 
.
Rice. 1. Geometric meaning of derivative
If 
, then point 
, will move along the curve, approaching the point 
.
Hence 
, i.e. the value of the derivative for a given value of the argument 
numerically equal to the tangent of the angle formed by the tangent at a given point with the positive direction of the axis 
.
2.3. Table of basic differentiation formulas.
Power function
|
|
|
|
|
|
|
Exponential function
|
|
|
|
|
Logarithmic function
|
|
|
|
|
Trigonometric function
|
|
|
|
|
|
|
|
|
|
Inverse trigonometric function
|
|
|
|
|
|
|
|
|
|
2.4. Rules of differentiation.
Derivative of 
Derivative of the sum (difference) of functions
Derivative of the product of two functions
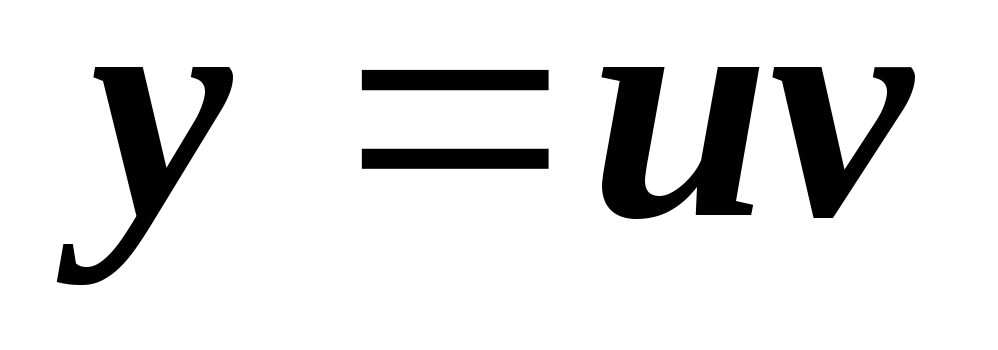
Derivative of the quotient of two functions
2.5. Derivative of complex function.
Let the function be given 
such that it can be represented in the form
And 
, where the variable 
is an intermediate argument, then 
The derivative of a complex function is equal to the product of the derivative of the given function with respect to the intermediate argument and the derivative of the intermediate argument with respect to x.
Example 1. 
Example 2. 
3. Differential function.
Let there be 
, differentiable on some interval 
let it go at
this function has a derivative
,
then we can write
(1),
Where 
- an infinitesimal quantity,
since when 
Multiplying all terms of equality (1) by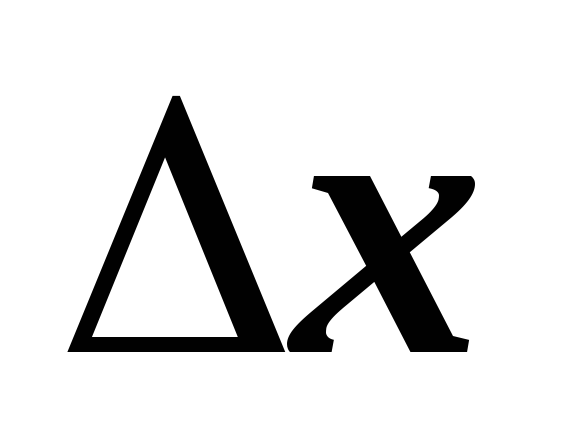 
we have:
Where 
- b.m.v. higher order.
Magnitude 
called the differential of the function 
and is designated 
.
3.1. Geometric value of the differential.
Let the function be given 
.
Fig.2. Geometric meaning of differential.
.
Obviously, the differential of the function 
is equal to the increment of the ordinate of the tangent at a given point.
3.2. Derivatives and differentials of various orders.
If there 
, Then 
is called the first derivative.
The derivative of the first derivative is called the second-order derivative and is written 
.
Derivative of the nth order of the function 
is called the (n-1)th order derivative and is written:
.
The differential of the differential of a function is called the second differential or second order differential.
.
.
3.3 Solving biological problems using differentiation.
Task 1. Studies have shown that the growth of a colony of microorganisms obeys the law 
, Where N
– number of microorganisms (in thousands), t
– time (days).
b) Will the population of the colony increase or decrease during this period?
Answer. The size of the colony will increase.
Task 2. The water in the lake is periodically tested to monitor the content of pathogenic bacteria. Through t days after testing, the concentration of bacteria is determined by the ratio
.
When will the lake have a minimum concentration of bacteria and will it be possible to swim in it?
Solution: A function reaches max or min when its derivative is zero.
,
Let's determine the max or min will be in 6 days. To do this, let's take the second derivative.
Answer: After 6 days there will be a minimum concentration of bacteria.
One of the elements of primitive level algebra is the logarithm. The name comes from Greek language from the word “number” or “power” and means the degree to which the number in the base must be raised to find the final number.
Types of logarithms
- log a b – logarithm of the number b to base a (a > 0, a ≠ 1, b > 0);
- log b – decimal logarithm (logarithm to base 10, a = 10);
- ln b – natural logarithm (logarithm to base e, a = e).
How to solve logarithms?
The logarithm of b to base a is an exponent that requires b to be raised to base a. The result obtained is pronounced like this: “logarithm of b to base a.” The solution to logarithmic problems is that you need to determine a given power in numbers by the indicated numbers. There are some basic rules to determine or solve the logarithm, as well as convert the notation itself. Using them, the solution is made logarithmic equations, derivatives are found, integrals are solved, and many other operations are performed. Basically, the solution to the logarithm itself is its simplified notation. Below are the basic formulas and properties:
For any a ; a > 0; a ≠ 1 and for any x ; y > 0.
- a log a b = b – basic logarithmic identity
- log a 1 = 0
- loga a = 1
- log a (x y) = log a x + log a y
- log a x/ y = log a x – log a y
- log a 1/x = -log a x
- log a x p = p log a x
- log a k x = 1/k log a x , for k ≠ 0
- log a x = log a c x c
- log a x = log b x/ log b a – formula for moving to a new base
- log a x = 1/log x a
How to solve logarithms - step-by-step instructions for solving
- First, write down the required equation.
Please note: if the base logarithm is 10, then the entry is shortened, resulting in a decimal logarithm. If it's worth natural number e, then we write it down, reducing it to the natural logarithm. This means that the result of all logarithms is the power to which the base number is raised to obtain the number b.
Directly, the solution lies in calculating this degree. Before solving an expression with a logarithm, it must be simplified according to the rule, that is, using formulas. You can find the main identities by going back a little in the article.
Adding and subtracting logarithms with two different numbers, but with the same bases, replace with one logarithm with the product or division of the numbers b and c, respectively. In this case, you can apply the formula for moving to another base (see above).
If you use expressions to simplify a logarithm, there are some limitations to consider. And that is: the base of the logarithm a is only a positive number, but not equal to one. The number b, like a, must be greater than zero.
There are cases where, by simplifying an expression, you will not be able to calculate the logarithm in numerical form. It happens that such an expression does not make sense, because many powers are irrational numbers. Under this condition, leave the power of the number as a logarithm.
Logarithms, like any numbers, can be added, subtracted and transformed in every way. But since logarithms are not exactly ordinary numbers, there are rules here, which are called main properties.
You definitely need to know these rules - without them not a single serious problem can be solved. logarithmic problem. In addition, there are very few of them - you can learn everything in one day. So let's get started.
Adding and subtracting logarithms
Consider two logarithms with the same bases: log a x and log a y. Then they can be added and subtracted, and:
- log a x+ log a y=log a (x · y);
- log a x− log a y=log a (x : y).
So, the sum of logarithms is equal to the logarithm of the product, and the difference is equal to the logarithm of the quotient. Note: key moment Here - identical grounds. If the reasons are different, these rules do not work!
These formulas will help you calculate logarithmic expression even when its individual parts are not counted (see lesson “What is a logarithm”). Take a look at the examples and see:
Log 6 4 + log 6 9.
Since logarithms have the same bases, we use the sum formula:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Task. Find the value of the expression: log 2 48 − log 2 3.
The bases are the same, we use the difference formula:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Task. Find the value of the expression: log 3 135 − log 3 5.
Again the bases are the same, so we have:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
As you can see, the original expressions are made up of “bad” logarithms, which are not calculated separately. But after the transformations they turn out quite normal numbers. Many are built on this fact test papers. What about the controls? similar expressions in all seriousness (sometimes with virtually no changes) are offered on the Unified State Examination.
Extracting the exponent from the logarithm
Now let's complicate the task a little. What if the base or argument of a logarithm is a power? Then the exponent of this degree can be taken out of the sign of the logarithm according to the following rules:
It's easy to notice that last rule follows the first two. But it’s better to remember it anyway - in some cases it will significantly reduce the amount of calculations.
Of course, all these rules make sense if the ODZ of the logarithm is observed: a > 0, a ≠ 1, x> 0. And one more thing: learn to apply all formulas not only from left to right, but also vice versa, i.e. You can enter the numbers before the logarithm sign into the logarithm itself. This is what is most often required.
Task. Find the value of the expression: log 7 49 6 .
Let's get rid of the degree in the argument using the first formula:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Task. Find the meaning of the expression:
[Caption for the picture]
Note that the denominator contains a logarithm, the base and argument of which are exact powers: 16 = 2 4 ; 49 = 7 2. We have:
[Caption for the picture] I think to last example clarification required. Where have logarithms gone? Until the very last moment we work only with the denominator. We presented the base and argument of the logarithm standing there in the form of powers and took out the exponents - we got a “three-story” fraction.
Now let's look at the main fraction. The numerator and denominator contain the same number: log 2 7. Since log 2 7 ≠ 0, we can reduce the fraction - 2/4 will remain in the denominator. According to the rules of arithmetic, the four can be transferred to the numerator, which is what was done. The result was the answer: 2.
Transition to a new foundation
Speaking about the rules for adding and subtracting logarithms, I specifically emphasized that they only work with the same bases. What if the reasons are different? What if they are not exact powers of the same number?
Formulas for transition to a new foundation come to the rescue. Let us formulate them in the form of a theorem:
Let the logarithm log be given a x. Then for any number c such that c> 0 and c≠ 1, the equality is true:
[Caption for the picture]
In particular, if we put c = x, we get:
[Caption for the picture]
From the second formula it follows that the base and argument of the logarithm can be swapped, but in this case the entire expression is “turned over”, i.e. the logarithm appears in the denominator.
These formulas are rarely found in conventional numerical expressions. It is possible to evaluate how convenient they are only when solving logarithmic equations and inequalities.
However, there are problems that cannot be solved at all except by moving to a new foundation. Let's look at a couple of these:
Task. Find the value of the expression: log 5 16 log 2 25.
Note that the arguments of both logarithms contain exact powers. Let's take out the indicators: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;
Now let’s “reverse” the second logarithm:
[Caption for the picture]Since the product does not change when rearranging factors, we calmly multiplied four and two, and then dealt with logarithms.
Task. Find the value of the expression: log 9 100 lg 3.
The base and argument of the first logarithm are exact powers. Let's write this down and get rid of the indicators:
[Caption for the picture]Now let's get rid of the decimal logarithm by moving to a new base:
[Caption for the picture]Basic logarithmic identity
Often in the solution process it is necessary to represent a number as a logarithm to a given base. In this case, the following formulas will help us:
In the first case, the number n becomes an indicator of the degree standing in the argument. Number n can be absolutely anything, because it’s just a logarithm value.
The second formula is actually a paraphrased definition. That’s what it’s called: the basic logarithmic identity.
In fact, what will happen if the number b raise to such a power that the number b to this power gives the number a? That's right: you get this same number a. Read this paragraph carefully again - many people get stuck on it.
Like formulas for moving to a new base, the basic logarithmic identity is sometimes the only possible solution.
Task. Find the meaning of the expression:
[Caption for the picture]
Note that log 25 64 = log 5 8 - simply took the square from the base and argument of the logarithm. Considering the rules for multiplying powers with the same basis, we get:
[Caption for the picture]If anyone doesn't know, this was a real task from the Unified State Exam :)
Logarithmic unit and logarithmic zero
In conclusion, I will give two identities that can hardly be called properties - rather, they are consequences of the definition of the logarithm. They constantly appear in problems and, surprisingly, create problems even for “advanced” students.
- log a a= 1 is logarithmic unit. Remember once and for all: logarithm to any base a from this very base is equal to one.
- log a 1 = 0 is logarithmic zero. Base a can be anything, but if the argument contains one, the logarithm is equal to zero! Because a 0 = 1 is a direct consequence of the definition.
That's all the properties. Be sure to practice putting them into practice! Download the cheat sheet at the beginning of the lesson, print it out, and solve the problems.
Let's start with properties of the logarithm of one. Its formulation is as follows: the logarithm of unity is equal to zero, that is, log a 1=0 for any a>0, a≠1. The proof is not difficult: since a 0 =1 for any a satisfying the above conditions a>0 and a≠1, then the equality log a 1=0 to be proved follows immediately from the definition of the logarithm.
Let us give examples of the application of the considered property: log 3 1=0, log1=0 and .
Let's move on to the next property: logarithm of the number, equal to the base, equal to one, that is, log a a=1 for a>0, a≠1. Indeed, since a 1 =a for any a, then by definition logarithm log a a=1 .
Examples of using this property of logarithms are the equalities log 5 5=1, log 5.6 5.6 and lne=1.
For example, log 2 2 7 =7, log10 -4 =-4 and 
.
Logarithm of the product of two positive numbers x and y is equal to the product of the logarithms of these numbers: log a (x y)=log a x+log a y, a>0 , a≠1 . Let us prove the property of the logarithm of a product. Due to the properties of the degree a log a x+log a y =a log a x ·a log a y, and since by the main logarithmic identity a log a x =x and a log a y =y, then a log a x ·a log a y =x·y. Thus, a log a x+log a y =x·y, from which, by the definition of a logarithm, the equality being proved follows.
Let's show examples of using the property of the logarithm of a product: log 5 (2 3)=log 5 2+log 5 3 and 
.
The property of the logarithm of a product can be generalized to the product of a finite number n of positive numbers x 1 , x 2 , …, x n as log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n . This equality can be proven without problems.
For example, the natural logarithm of a product can be replaced by the sum of three natural logarithms numbers 4 , e , and .
Logarithm of the quotient of two positive numbers x and y is equal to the difference between the logarithms of these numbers. The property of the logarithm of a quotient corresponds to a formula of the form , where a>0, a≠1, x and y are some positive numbers. The validity of this formula is proven as well as the formula for the logarithm of a product: since 
, then by definition of a logarithm.
Here is an example of using this property of the logarithm: 
.
Let's move on to property of the logarithm of the power. The logarithm of a degree is equal to the product of the exponent and the logarithm of the modulus of the base of this degree. Let us write this property of the logarithm of a power as a formula: log a b p =p·log a |b|, where a>0, a≠1, b and p are numbers such that the degree b p makes sense and b p >0.
First we prove this property for positive b. The basic logarithmic identity allows us to represent the number b as a log a b , then b p =(a log a b) p , and the resulting expression, due to the property of power, is equal to a p·log a b . So we come to the equality b p =a p·log a b, from which, by the definition of a logarithm, we conclude that log a b p =p·log a b.
It remains to prove this property for negative b. Here we note that the expression log a b p for negative b makes sense only for even exponents p (since the value of the degree b p must be greater than zero, in otherwise the logarithm will not make sense), and in this case b p =|b| p. Then b p =|b| p =(a log a |b|) p =a p·log a |b|, from where log a b p =p·log a |b| .
For example, 
and ln(-3) 4 =4·ln|-3|=4·ln3 .
It follows from the previous property property of the logarithm from the root: the logarithm of the nth root is equal to the product of the fraction 1/n by the logarithm of the radical expression, that is, 
, where a>0, a≠1, n – natural number, greater than one, b>0 .
The proof is based on the equality (see), which is valid for any positive b, and the property of the logarithm of the power: 
.
Here is an example of using this property: 
.
Now let's prove formula for moving to a new logarithm base kind 
. To do this, it is enough to prove the validity of the equality log c b=log a b·log c a. The basic logarithmic identity allows us to represent the number b as a log a b , then log c b=log c a log a b . It remains to use the property of the logarithm of the degree: log c a log a b =log a b log c a. This proves the equality log c b=log a b·log c a, which means that the formula for transition to a new base of the logarithm has also been proven.
Let's show a couple of examples of using this property of logarithms: and 
.
The formula for moving to a new base allows you to move on to working with logarithms that have a “convenient” base. For example, it can be used to go to natural or decimal logarithms so that you can calculate the value of a logarithm from a table of logarithms. The formula for moving to a new logarithm base also allows, in some cases, to find the value of a given logarithm when the values of some logarithms with other bases are known.
Used frequently special case formulas for transition to a new base of the logarithm with c=b of the form 
. This shows that log a b and log b a – . Eg, 
.
The formula is also often used 
, which is convenient for finding logarithm values. To confirm our words, we will show how it can be used to calculate the value of a logarithm of the form . We have 
. To prove the formula 
it is enough to use the formula for transition to a new base of the logarithm a: 
.
It remains to prove the properties of comparison of logarithms.
Let us prove that for any positive numbers b 1 and b 2, b 1 log a b 2 , and for a>1 – the inequality log a b 1 Finally, it remains to prove the last of the listed properties of logarithms. Let us limit ourselves to the proof of its first part, that is, we will prove that if a 1 >1, a 2 >1 and a 1 1 is true log a 1 b>log a 2 b . The remaining statements of this property of logarithms are proved according to a similar principle. Let's use the opposite method. Suppose that for a 1 >1, a 2 >1 and a 1 1 is true log a 1 b≤log a 2 b . Based on the properties of logarithms, these inequalities can be rewritten as 
And 
respectively, and from them it follows that log b a 1 ≤log b a 2 and log b a 1 ≥log b a 2, respectively. Then, according to the properties of powers with the same bases, the equalities b log b a 1 ≥b log b a 2 and b log b a 1 ≥b log b a 2 must hold, that is, a 1 ≥a 2 . So we came to a contradiction to the condition a 1
Bibliography.
- Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. and others. Algebra and the beginnings of analysis: Textbook for grades 10 - 11 of general education institutions.
- Gusev V.A., Mordkovich A.G. Mathematics (a manual for those entering technical schools).