The system of forces is called balanced, if under the influence of this system the body remains at rest.
Equilibrium conditions:
The first condition for the equilibrium of a rigid body:
For a rigid body to be in equilibrium, it is necessary that the sum of external forces applied to the body be equal to zero.
The second condition for the equilibrium of a rigid body:
When a rigid body is in equilibrium, the sum of the moments of all external forces acting on it relative to any axis is equal to zero.
General condition for the equilibrium of a rigid body:
For a rigid body to be in equilibrium, the sum of external forces and the sum of moments of forces acting on the body must be zero. The initial velocity of the center of mass and the angular velocity of rotation of the body must also be equal to zero.
Theorem. Three forces balance a rigid body only if they all lie in the same plane.
11. Flat force system– these are forces located in one plane.
Three forms of equilibrium equations for a plane system:
Center of gravity of the body.
Center of gravity A body of finite dimensions is called the point about which the sum of the moments of gravity of all particles of the body is equal to zero. At this point the force of gravity of the body is applied. The center of gravity of a body (or system of forces) usually coincides with the center of mass of the body (or system of forces).
Center of gravity of a flat figure:
A practical method for finding the center of mass of a plane figure: hang the body in a gravity field so that it can freely rotate around the suspension point O1 . In equilibrium the center of mass WITH is on the same vertical with the suspension point (below it), since it is equal to zero
moment of gravity, which can be considered applied at the center of mass. By changing the suspension point, we find another straight line in the same way O 2 C , passing through the center of mass. The position of the center of mass is given by the point of their intersection.
Center of mass speed:
The momentum of a particle system is equal to the product of the mass of the entire system M= Σmi on the speed of its center of mass V :
![]()
The center of mass characterizes the movement of the system as a whole.
15. Sliding friction– friction during relative motion of contacting bodies.
Static friction– friction in the absence of relative movement of contacting bodies.
Sliding friction force Ftr between the surfaces of contacting bodies during their relative motion depends on the force of the normal reaction N , or from the force of normal pressure Pn , and Ftr=kN or Ftr=kPn , where k – sliding friction coefficient , depending on the same factors as the static friction coefficient k0 , as well as on the speed of relative motion of the contacting bodies.
16. Rolling friction- This is the rolling of one body over another. The sliding friction force does not depend on the size of the rubbing surfaces, but only on the quality of the surfaces of the rubbing bodies and on the force that reduces the rubbing surfaces and is directed perpendicular to them. F=kN, Where F- friction force, N– the magnitude of the normal reaction and k – sliding friction coefficient.
17. Equilibrium of bodies in the presence of friction- this is the maximum adhesion force proportional to the normal pressure of the body on the plane.
The angle between the total reaction, based on the greatest frictional force for a given normal reaction, and the direction of the normal reaction is called friction angle.
A cone with an apex at the point of application of the normal reaction of a rough surface, the generatrix of which makes an angle of friction with this normal reaction, is called friction cone.
Dynamics.
1. IN dynamics the influence of interactions between bodies on their mechanical motion is considered.
Weight- this is a painting characteristic of a material point. The mass is constant. The mass is adjective (additive)
Force - this is a vector that completely characterizes the interaction of a material point on it with other material points.
Material point– a body whose dimensions and shape are unimportant in the motion under consideration. (ex: in translational motion a rigid body can be considered a material point)
System of material dots called a set of material points interacting with each other.
Newton's 1st law: any material point maintains a state of rest or uniform rectilinear motion until external influences change this state.
Newton's 2nd law: the acceleration acquired by a material point in an inertial reference frame is directly proportional to the force acting on the point, inversely proportional to the mass of the point and coincides in direction with the force: a=F/m
Newton's 3rd law: the forces of interaction between two material points in the inertial frame of reference are equal in magnitude and directed in opposite directions : Fik= - Fki
Did you know, What is the falsity of the concept of “physical vacuum”?
Physical vacuum - the concept of relativistic quantum physics, by which they mean the lowest (ground) energy state of a quantized field, which has zero momentum, angular momentum and other quantum numbers. Relativistic theorists call a physical vacuum a space completely devoid of matter, filled with an unmeasurable, and therefore only imaginary, field. Such a state, according to relativists, is not an absolute void, but a space filled with some phantom (virtual) particles. Relativistic quantum field theory states that, in accordance with the Heisenberg uncertainty principle, virtual, that is, apparent (apparent to whom?), particles are constantly born and disappeared in the physical vacuum: so-called zero-point field oscillations occur. Virtual particles of the physical vacuum, and therefore itself, by definition, do not have a reference system, since otherwise Einstein’s principle of relativity, on which the theory of relativity is based, would be violated (that is, an absolute measurement system with reference to the particles of the physical vacuum would become possible, which in turn would clearly refute the principle of relativity on which the SRT is based). Thus, the physical vacuum and its particles are not elements of the physical world, but only elements of the theory of relativity, which do not exist in the real world, but only in relativistic formulas, while violating the principle of causality (they appear and disappear without cause), the principle of objectivity (virtual particles can be considered, depending on the desire of the theorist, either existing or non-existent), the principle of factual measurability (not observable, do not have their own ISO).
When one or another physicist uses the concept of “physical vacuum,” he either does not understand the absurdity of this term, or is disingenuous, being a hidden or overt adherent of relativistic ideology.
The easiest way to understand the absurdity of this concept is to turn to the origins of its occurrence. It was born by Paul Dirac in the 1930s, when it became clear that denying the ether in its pure form, as was done by a great mathematician but a mediocre physicist, was no longer possible. There are too many facts that contradict this.
To defend relativism, Paul Dirac introduced the aphysical and illogical concept of negative energy, and then the existence of a “sea” of two energies compensating each other in a vacuum - positive and negative, as well as a “sea” of particles compensating each other - virtual (that is, apparent) electrons and positrons in a vacuum.
In statics, as well as in kinematics (item 51), a rigid body is a system of material points invariably connected with each other. This system is thus an absolutely rigid body, the points of which remain at constant distances from each other, whatever the forces acting on these points and whatever the motion of the body.
The body defined in this way is, of course, an idealization. First of all, physics teaches us that solids consist of molecules, which themselves have a very complex structure and can be in a wide variety of hidden movements. It is precisely about molecules taken in their average positions that we can say that they remain, with a high degree of approximation, at the same
same distances from each other. Thus, we can only look at molecules in their average positions here as material points. But that is not all; even if we neglect hidden molecular movements and pay attention only to the visible movements of particles, then even then all bodies of nature change their shape under the influence of forces applied to them; the internal forces acting between particles of the same body depend, as we know (point 109), on these deformations. However, since the deformations of bodies called “solid” in physics are very small, they can be neglected as a first approximation, unless the forces applied to the bodies are too large and unless we are studying internal forces. Determining internal forces and visible deformations occurring in solids is a difficult task that no longer relates to statics, but to the theory of elasticity. The theory that we will present is applicable to solid physical bodies with greater accuracy, the closer they are to an absolutely solid body.
From a logical point of view, the geometric statics of a rigid body should be considered as a limit theory. It sets forth a certain number of general laws applicable to all solids, whatever their molecular structure and their elastic properties, as long as the deformations can be considered infinitesimal. However, the theory constructed in this way is an incomplete theory of equilibrium, since it systematically leaves aside elastic properties, the inclusion of which in some cases becomes absolutely necessary. In these cases, the methods of geometric statics turn out to be insufficient to resolve all the questions that the equilibrium problem may pose to us. Some of these questions may even turn out to be contradictory if we retain the hypothesis of the absolute immutability of a solid body.
The condition of non-deformability alone is not enough to justify the theory of equilibrium of solids;
to this must be added, as a supplement to the definition of a rigid body, the following mechanical postulate:
Postulate. - Without changing anything in the equilibrium conditions of a rigid body, you can add or discard two equal and directly opposite forces applied to two of its points.
This postulate could be derived from a general principle known as the principle of virtual movements, but we will not do this for now. We will establish the mentioned principle in one of the following chapters as the basis of analytical statics. It would also be useless to introduce this postulate if we accept the basic laws of dynamics as we set them out in the previous part of the course, since the postulate in question, as we will see later, is a simple special case of one general theorem of rigid body dynamics. If we introduce it here, we do so with the aim of preserving the character of an independent discipline behind statics. We will look at this postulate, from the point of view of physics, as a direct consequence of experience; from the point of view of theoretical mechanics, we will consider it as an addition to the definition of a solid body adopted in statics, while receiving the benefit that we are freed from introducing the molecular hypothesis.
As already noted in the theory of vectors (point 28), this basic postulate entails as a consequence the following proposition:
Without violating the equilibrium conditions of a rigid body, one can move the point of application of a force to an arbitrary point on its line of action, as long as this new point is connected to the body.
It goes without saying that this sentence speaks only about the state of equilibrium of the body, and not about those actions that different points of the body exert on each other, since these internal actions, of course, will change when the point of application of the force indicated
the operation can, for example, be performed when a rigid body is placed on some supports, but in no case can it be said that the transfer of force in this case will not change the reactions of the supports. It would, therefore, be a big mistake to apply the principle of force transfer when determining the reactions of supports, transferring, for example, one or another of the applied forces to the support point. The only conditions that can be legitimately applied in this case are the general equilibrium conditions, since the latter are always necessary conditions.
185. Reduction of forces applied to a rigid body (static point of view).
We have just seen that it is possible, without disturbing the equilibrium of a rigid body, to perform the following operations on forces applied to points of the body:
1°. Addition or expansion of forces applied at one point.
2°. The addition or subtraction of two equal and directly opposite forces.
3°. Transfer of force to an arbitrary point in its line of action.
These operations, as was established in the theory of vectors (point 29), are precisely those elementary operations that make it possible to bring two equivalent systems of vectors to each other. From this we obtain the following theorem:
Without disturbing the equilibrium of a rigid body, it is possible to replace any system of forces applied to the body with another system of forces, which is a system of vectors equivalent to the first.
Such two systems of forces are called equivalent.
The task of bringing a system of forces applied to a rigid body coincides, therefore, with the task of bringing a system of vectors, so we can make the following conclusions:
1°. Reduction to two forces. The system of forces applied to a rigid body can be given as
imbalance, only to two forces, one of which is applied at an arbitrarily selected point of the body (item 26).
2°. Bringing to strength and to couple. A system of forces applied to a solid body can be reduced, without disturbing equilibrium, to one force applied at an arbitrary point O of the body, and to one pair. The force is the resultant R of all forces of the system transferred to point O (the main vector), and the moment of the pair is equal to the main moment O of the system of forces relative to the same point (item 24).
In order for a system of forces to be reduced to one resultant R, it is necessary and sufficient that for an arbitrarily taken center of reduction O the geometric sum R is different from zero, and the resulting moment G (if it is not zero) is perpendicular to R. The resultant is directed in this case along the central axis of the system.
In order for the system to be reduced to one pair, it is necessary and sufficient that the main vector R be equal to zero, and the main moment O be different from zero. In this case, the main moment of the system is the same for each point in space.
Finally, if the vectors R and G are both zero, then the system is equivalent to zero and the body will be in equilibrium. We will consider this case in the next paragraph.
Forces in a plane. - When all forces act in one plane, and the geometric sum of their R is not equal to zero, the resulting moment G (as well as the moment of each force) is perpendicular to R. Consequently, these forces are reduced to one resultant R applied at the point of the central axis (which obviously lies in the plane of action of the forces). If R is equal to zero, then the system is reduced to one pair, and if, in addition, G is equal to zero, then the system is in equilibrium.
It is useful to note that any plane system of forces can always be reduced to two forces, adj. expressed in two given points A and plane,
In fact, each force t applied at point O, lying outside the line AB, is decomposed, in the directions OA and OB, into two components that can be transferred to points A and B. If the point O of the application of force lies on AB, and the line the action of the force passes through A, then the point of application of the force can be transferred to; if the line of action of the force does not pass through A, then the point of application of the force can be transferred along the line of action beyond the line AB, which leads to the first case.
Parallel forces. - If the forces are parallel, and their geometric sum R is not equal to zero, then the resulting moment G is perpendicular to R, and, therefore, these forces are reduced to one resultant R applied at a point on the central axis (parallel to the general direction of the forces). If R is equal to zero, then the system is reduced to one pair or is in equilibrium (when the moment of the pair is zero).
186. Equilibrium of a rigid body.
For a free rigid body to be in equilibrium, it is necessary and sufficient that the system of forces applied to it (i.e., in this case, external forces) be equivalent to zero.
We already know that this condition is necessary, since it represents a general equilibrium condition.
For a solid body it also turns out to be sufficient. In fact, if a system of forces is equivalent to zero, it can be reduced to zero by elementary operations and, therefore, all the forces that compose it can simply be discarded. Based on this, we have two equilibrium conditions in vector form
These conditions break down into six algebraic equations. Let X, Y, Z be the projections of the vector R onto three rectangular coordinate axes, or the sum of the projections of all forces on the same axis; let further L, M,
The resulting moments of the system of these forces relative to the same axes; then these six equations will be:
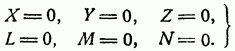
It is often said that the first three equations (equivalent to the equality R = 0) represent the equilibrium conditions for translational motion, and the last three (equivalent to the equality G = 0) represent the equilibrium conditions for rotation. We will obtain the basis for such names later, when we apply the principle of virtual work to the solution of the same problem.
187. Reduction of forces applied to a rigid body (dynamic point of view). Dynamic balance.
In the dynamics of a rigid body, we will show that in the case of a free rigid body, its motion will be completely determined if for each moment of time the main vector and the main moment about some point of all the forces applied to it are given. Hence we have the following theorem:
If two systems of forces applied to a rigid body are constantly equivalent to each other from the point of view of vector theory, then they will be equivalent from the point of view of the body’s motion.
This theorem essentially relates to dynamics, but it is also closely related to geometric statics. Indeed, it can be proven using a very simple generalization of the main postulate, which clarifies the definition of a rigid body in statics (point 184).
In fact, let us replace this postulate with the following:
Without changing anything in the state of rest or motion of a rigid body, one can add or subtract two equal and directly opposite forces applied to two points of the body.
This more general postulate, which can also be verified directly by experience, allows us to give the following
same generalization to the concept of reduction and equivalence of forces. In fact, in all sentences of paragraph 185 it is possible to replace the words “without disturbing the balance” with the words “without changing anything in the state of rest or movement of the body.” Then the conclusion of paragraph 185 turns out to be equivalent to the dynamic principle expressed here.
Let us note one corollary in particular:
If a rigid body, under the influence of a system of forces S, remains in equilibrium, then this system of forces (being equivalent to zero) cannot change anything in the state of motion of the body, if the latter is no longer at rest.
Now it is quite natural to establish the following definition:
A given system of forces is in equilibrium from the point of view of dynamics, or in dynamic equilibrium if the forces cannot change the state of rest or motion of the rigid body to which they are applied.
Having this definition, we can make the following proposal:
In order for the forces applied to a solid body to be in dynamic equilibrium, it is necessary and sufficient that they represent a system of vectors equivalent to zero.
This way of representing the equilibrium of forces applied to a solid body is very widespread, and the word “equilibrium” is very often used in this sense. However, one should not lose sight of the fact that this idea of equilibrium refers more to dynamics than to statics.
188. Center of gravity of a solid body.
The reduction of forces applied to a rigid body can, in particular, be performed for the weight forces of all material points of which the body consists. All these forces represent parallel forces, equally oriented. This system of vectors is therefore reduced to one resultant, equal to the total weight P of the rigid body and applied at the center of these parallel vectors, which
we will denote G. This point, the position of which in the body does not depend on its orientation relative to the surface of the Earth, is the center of gravity of the body. We will see in the next chapter how its coordinates can be determined. From the previous theorems it follows that the action of gravity on various points of a rigid body, both from a static and dynamic point of view, is reduced to a single force, the total weight applied at the center of gravity of the body.
