Definitioner. Lad os tage flere vinkler (fig. 37): ASB, BSC, CSD, som støder op til hinanden sekventielt er placeret i samme plan omkring det fælles toppunkt S.

Lad os dreje vinklens plan ASB omkring den fælles side SB, så dette plan udgør nogle dihedral vinkel med BSC-plan. Derefter, uden at ændre den resulterende dihedriske vinkel, roterer vi den omkring den lige linje SC, så BSC-planet laver en bestemt dihedral vinkel med CSD-planet. Lad os fortsætte denne sekventielle rotation omkring hver fælles side. Hvis den sidste side SF falder sammen med den første side SA, så dannes der en figur (fig. 38), som kaldes polyedrisk vinkel. Vinkler ASB, BSC,... kaldes flade vinkler eller kanter, deres sider SA, SB, ... kaldes ribben, og det fælles toppunkt S- top polyedrisk vinkel.

Hver kant er også en kant af en vis dihedral vinkel; derfor er der i en polyedrisk vinkel lige så mange dihedriske vinkler og lige så mange plane vinkler, som der er alle kanterne i den. Det mindste antal der er tre flader i en polyedrisk vinkel; denne vinkel kaldes trekantet. Der kan være tetraedriske, femkantede osv. vinkler.

En polyedrisk vinkel er enten angivet med et enkelt bogstav S placeret ved toppunktet eller med en række bogstaver SABCDE, hvoraf det første angiver toppunktet, og de andre - kanterne i rækkefølgen efter deres placering.

En polyedrisk vinkel kaldes konveks, hvis den er helt placeret på den ene side af planet af hver af dens flader, som er forlænget i det uendelige. Dette er for eksempel vinklen vist på tegning 38. Tværtimod kan vinklen på tegning 39 ikke kaldes konveks, da den er placeret på begge sider af ASB-kanten eller BCC-kanten.

Hvis vi skærer alle flader af en polyedrisk vinkel med et plan, dannes en polygon i sektionen ( abcde ). I en konveks polyedrisk vinkel er denne polygon også konveks.

Vi vil kun overveje konveks polyedriske vinkler.

Sætning. I en trihedral vinkel er hver plan vinkel mindre end summen af ​​de to andre plane vinkler.

Lad den største af planvinklerne i den trihedriske vinkel SABC (Fig. 40) være vinklen ASC.

Lad os på denne vinkel plotte vinklen ASD, lig med vinklen ASB, og tegne en ret linje AC, der skærer SD i et punkt D. Lad os plotte SB = SD. Ved at forbinde B med A og C får vi \(\Delta\)ABC, hvori

AD+DC< АВ + ВС.

Trekanter ASD og ASB er kongruente, fordi de hver indeholder en lige stor vinkel imellem lige sider: derfor AD = AB. Derfor, hvis vi i den afledte ulighed kasserer de lige udtryk AD og AB, opnår vi den DC< ВС.

Nu bemærker vi, at i trekanter SCD og SCB er to sider af den ene lig med to sider af den anden, men de tredje sider er ikke ens; i dette tilfælde ligger den større vinkel modsat den største af disse sider; Midler,

∠CSD< ∠ CSВ.

Ved at tilføje vinklen ASD til venstre side af denne ulighed, og vinklen ASB lig med den til højre, opnår vi den ulighed, der skulle bevises:

∠ASC< ∠ CSB + ∠ ASB.

Vi har bevist, at selv den største plane vinkel er mindre end summen af ​​de to andre vinkler. Det betyder, at teoremet er bevist.

Følge. Træk fra begge sider af den sidste ulighed med vinkel ASB eller vinkel CSB; vi får:

∠ASC - ∠ASB< ∠ CSB;

∠ASC - ∠CSB< ∠ ASB.

I betragtning af disse uligheder fra højre til venstre og under hensyntagen til den vinkel ASC som den største af tre hjørner større end forskellen på de to andre vinkler, kommer vi til den konklusion, at i en trihedral vinkel er hver plan vinkel større end forskellen mellem de to andre vinkler.

Sætning. I en konveks polyedrisk vinkel er summen af ​​alle plane vinkler mindre end 4d (360°) .

Lad os skære fladerne (fig. 41) af den konvekse vinkel SABCDE med et eller andet plan; heraf får vi et konvekst tværsnit n-gon ABCDE.

Ved at anvende det tidligere beviste sætning på hver af de trihedriske vinkler, hvis toppunkter er placeret i punkterne A, B, C, D og E, pacholymer vi:

∠ABC< ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.

Lad os lægge alle disse uligheder sammen efter sigt. Så på venstre side får vi summen af ​​alle vinkler af polygonen ABCDE, som er lig med 2 dn - 4d , og til højre - summen af ​​vinklerne for trekanter ABS, SBC osv., bortset fra de vinkler, der ligger i toppunktet S. Betegner summen af ​​disse sidste vinkler med bogstavet x , får vi efter tilføjelse:

2dn - 4d < 2dn - x .

Siden i forskelle 2 dn - 4d og 2 dn - x minuenderne er de samme, så for at den første forskel skal være mindre end den anden, er det nødvendigt, at subtrahend 4 d var mere end selvrisikoen x ; det betyder 4 d > x , dvs. x < 4d .

De enkleste tilfælde af lighed af trihedriske vinkler

Sætninger. Triedriske vinkler er ens, hvis de har:

1) langs en lige stor dihedral vinkel indesluttet mellem to tilsvarende lige store og identisk adskilte plane vinkler, eller

2) langs en lige plan vinkel indesluttet mellem to tilsvarende lige store og identisk adskilte dihedriske vinkler.

1) Lad S og S 1 være to trihedriske vinkler (fig. 42), for hvilke ∠ASB = ∠A 1 S 1 B 1, ∠ASC = ∠A 1 S 1 C 1 (og disse lige store vinkler identisk placeret), og den dihedriske vinkel AS er lig med den dihedriske vinkel A1S1.

Lad os indsætte vinklen S 1 i vinklen S, så deres punkter S 1 og S, rette linjer S 1 A 1 og SA og planer A 1 S 1 B 1 og ASB falder sammen. Så vil kanten S 1 B 1 gå langs SB (på grund af ligheden mellem vinklerne A 1 S 1 B 1 og ASB), planet A 1 S 1 C 1 vil gå langs ASC (i kraft af ligheden af ​​dihedriske vinkler ) og kanten S 1 C 1 vil gå langs kanten SC (på grund af ligheden mellem vinklerne A 1 S 1 C 1 og ASC). Således vil de trihedriske vinkler falde sammen med alle deres kanter, dvs. de vil være lige.

2) Det andet tegn, ligesom det første, bevises ved indlejring.

Symmetriske polyedriske vinkler

Som bekendt, lodrette vinkler er ens, når vi taler om vinkler dannet af rette linjer eller planer. Lad os se, om dette udsagn er sandt i forhold til polyedriske vinkler.

Lad os fortsætte (fig. 43) alle kanterne af vinklen SABCDE ud over toppunktet S, så dannes endnu en polyedrisk vinkel SA 1 B 1 C 1 D 1 E 1, som kan kaldes lodret i forhold til den første vinkel. Det er let at se, at begge vinkler har lige store flade og dihedrale vinkler, men begge er placeret i omvendt rækkefølge. Faktisk, hvis vi forestiller os en iagttager, der ser udefra en polyedrisk vinkel på dens toppunkt, så vil kanterne SA, SB, SC, SD, SE for ham synes at være placeret i retning mod uret, mens han ser på vinklen SA 1 B 1 C 1 D 1 E 1, han ser kanterne SA 1, SB 1, ..., placeret i urets retning.

Polyedriske vinkler med tilsvarende lige store plane og dihedriske vinkler, men placeret i modsat rækkefølge, kan generelt ikke kombineres, når de er indlejret; det betyder, at de ikke er lige. Sådanne vinkler kaldes symmetrisk(i forhold til toppunktet S). Symmetrien af ​​figurer i rummet vil blive diskuteret mere detaljeret nedenfor.

Andre materialer

Lad os betragte tre stråler a, b, c, der udgår fra samme punkt og ikke ligger i samme plan. En trihedrisk vinkel (abc) er en figur, der består af tre flade vinkler (ab), (bc) og (ac) (fig. 2) Disse vinkler kaldes flader af en trihedrisk vinkel, og deres sider kaldes kanter. det almindelige toppunkt for flade vinkler kaldes toppunktet for en trihedrisk vinkel.

Begrebet en polyedrisk vinkel er defineret på samme måde (fig. 3).

Polyeder

I stereometri studeres figurer i rummet kaldet kroppe. En visuel (geometrisk) krop skal forestilles som en del af rummet optaget fysisk krop og begrænset af overfladen.

Et polyeder er et legeme, hvis overflade består af begrænset antal flade polygoner (fig. 4). Et polyeder kaldes konveks, hvis det er placeret på den ene side af planet af hver plan polygon på dens overflade. en fælles del sådan et plan og overfladen af ​​et konveks polyeder kaldes et ansigt. Ansigterne på et konveks polyeder er flade konvekse polygoner. Siderne af siderne kaldes polyederens kanter, og hjørnerne kaldes polyederens hjørner.

Lad os forklare dette ved at bruge eksemplet med en velkendt terning (fig. 5). Der er en terning konveks polyeder. Dens overflade består af seks firkanter: ABCD, BEFC, .... Disse er dens ansigter. Terningens kanter er siderne af disse firkanter: AB, BC, BE,.... Hjørnerne på en terning er hjørnerne af kvadraterne: A, B, C, D, E, .... Terningen har seks flader, tolv kanter og otte hjørner.

For de enkleste polyedre - prismer og pyramider, som vil være hovedobjektet for vores undersøgelse - vil vi give definitioner, der i det væsentlige ikke bruger begrebet krop. De vil blive defineret som geometriske figurer, der angiver alle de punkter i rummet, der hører til dem. Koncept geometrisk krop og dens overflade i almindelig sag vil blive givet senere.

Polyhedral vinkel

en del af rummet begrænset af et polyedrisk hulrum konisk overflade, hvis retning er en flad polygon uden selvskæringer. Denne overflades ansigter kaldes mosaikkens ansigter, og toppen kaldes mosaikkens top. M. u. kaldes regulær, hvis alle dens lineære vinkler og alle dens dihedriske vinkler er lige store. Meroy M. u. er området begrænset af den sfæriske polygon opnået ved skæringen af ​​polygonens flader, en kugle med en radius lig med én, og med centrum i toppunktet af M. y. Se også Massiv vinkel.

Stor Sovjetisk encyklopædi. - M.: Sovjetisk encyklopædi. 1969-1978 .

Se, hvad en "polyhedral vinkel" er i andre ordbøger:

Se solid vinkel... Stor encyklopædisk ordbog

Se fast vinkel. * * * POLYHEDAL VINKEL POLYHEDAL VINKEL, se Massiv vinkel (se FAST VINKEL) ... encyklopædisk ordbog

En del af rummet begrænset af et hulrum af en polyedrisk kegle. overflade, der leder til en sværm af flad polygon uden selvskæringer. Ansigterne på denne overflade kaldes. kanterne af M. u., toppen af ​​toppen af ​​M. u. En polyedrisk vinkel kaldes korrekt... Matematisk encyklopædi

Se Solid vinkel... Naturvidenskab. encyklopædisk ordbog

polyedrisk vinkel- matematik. En del af rummet afgrænset af flere planer, der går gennem et punkt (vinkelspids) ... Ordbog over mange udtryk

MULTIFACETERET, mangefacetteret, mangefacetteret (bog). 1. At have flere ansigter eller sider. Mangefacetteret sten. Polyhedrisk vinkel (en del af rummet begrænset af flere planer, der skærer hinanden på et punkt; mat.). 2. overførsel... ... Ordbog Ushakova

- (mat.). Hvis vi tegner rette linjer OA og 0B fra punkt O på et givet plan, får vi vinkel AOB (fig. 1). Crap. 1. Punkt 0 kaldet vinklens toppunkt, og rette linjer OA og 0B som siderne af vinklen. Antag, at to vinkler ΒΟΑ og Β 1 Ο 1 Α 1 er givet, så... ...

- (mat.). Hvis vi tegner rette linjer OA og 0B fra punkt O på et givet plan, får vi vinkel AOB (fig. 1). Crap. 1. Punkt 0 kaldet vinklens toppunkt, og rette linjer OA og 0B som siderne af vinklen. Antag, at der er givet to vinkler ΒΟΑ og Β1Ο1Α1. Lad os overlejre dem, så spidserne O... Encyklopædisk ordbog F.A. Brockhaus og I.A. Efron

Dette udtryk har andre betydninger, se Vinkel (betydninger). Vinkel ∠ Dimension ° SI-enheder Radian ... Wikipedia

Flad, geometrisk figur, dannet af to stråler (sider af overfladen), der udgår fra et punkt (overfladens toppunkt). Hvert U., der har et toppunkt i midten O af en cirkel (centralt U.), definerer på cirklen en bue AB afgrænset af... ... Store sovjetiske encyklopædi

POLYHEDALE VINKLER

En polyedrisk vinkel er den rumlige analog af en polygon. Husk på, at en polygon på et plan er en figur dannet af en simpel lukket stiplet linje og det indre område begrænset af det. Vi vil betragte en stråle i rummet for at være en analog af et punkt på et plan, og en plan vinkel i rummet for at være en analog af et segment på et plan. Så er analogen til en simpel lukket stiplet linje på planet en overflade dannet af et endeligt sæt planvinklerEN 1 S.A. 2 , EN 2 S.A. 3 , …, En n -1 SA n, A n SA 1 med et fælles toppunktS (fig. 1), hvor tilstødende hjørner ikke har fælles punkter, bortset fra punkterne af en fælles stråle, og ikke-tilstødende hjørner ikke har fælles punkter, bortset fra det fælles toppunkt. Figuren dannet af den angivne overflade og en af ​​de to dele af rummet, der er begrænset af den, kaldes polyedrisk vinkel. Fælles topShedder top polyedrisk vinkel. StrålerS.A. 1 , …, SA nhedder ribben polyedrisk vinkel, og selve planvinklerneEN 1 S.A. 2 , EN 2 S.A. 3 , …, En n -1 SA n, A n SA 1 – kanter polyedrisk vinkel. En polyedrisk vinkel er angivet med bogstaverneS.A. 1 … En n, der angiver toppunktet og punkter på dets kanter. Afhængigt af antallet af flader kaldes polyedriske vinkler for trihedrale, tetraedriske, pentaedriske (fig. 2) osv.

En polyedrisk vinkel kaldes konveks, hvis det er en konveks figur, dvs. sammen med to af dens punkter indeholder også den, der forbinder dem linjestykke. I figur 2 er de trihedriske og tetraedriske vinkler konvekse, men den femkantede vinkel er det ikke.
Lad os overveje nogle egenskaber ved trekanter og lignende egenskaber ved trihedriske vinkler.
Ejendom 1(Trekantulighed). Hver side af en trekant er mindre end summen af ​​dens to andre sider.
En lignende egenskab for trihedriske vinkler er følgende egenskab.
Ejendom 1". Hver plan vinkel i en trihedrisk vinkel er mindre end summen af ​​dens to andre plane vinkler.
Bevis. Overvej en trihedral vinkel SABC . Lad den største af dens plane vinkler være vinklen A.S.C.. Så holder ulighederne

ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .

Det er således tilbage at bevise uligheden ASC< A.S.B.+ BSC.
Lad os sætte det på kanten A.S.C. hjørne A.S.D., lige A.S.B. , og periode B lad os vælge så SB = SD(Fig. 3). Derefter trekanter A.S.B. Og A.S.D. ens (på to sider og vinklen mellem dem) og derfor AB = AD. Lad os bruge trekanten ulighed A.C.< AB + BC . Træk fra begge dens dele AD = AB, får vi uligheden DC< BC. I trekanter DSC Og BSC den ene side er fælles ( S.C.), SD = SB Og DC< BC. I dette tilfælde mod større side ligger en større vinkel og derfor DSC< BSC . Ved at tilføje vinklen til begge sider af denne ulighed A.S.D. , lige A.S.B., opnår vi den nødvendige ulighed ASC< A.S.B.+ BSC.

Konsekvens 1.Summen af ​​de plane vinkler af en trihedrisk vinkel er mindre end 360° .
Bevis. Lade SABC– en given trihedral vinkel. Overvej en trihedral vinkel med toppunkt EN, dannet af kanter ABS, ACS og vinkel BAC. På grund af den påviste ejendom holder uligheden BAC< BAS+ CAS. Tilsvarende for trihedriske vinkler med toppunkter B Og MED der er uligheder: ABC< ABS+ CBS, ACB< ACS+ BCS. Tilføjelse af disse uligheder og under hensyntagen til, at summen af ​​vinklerne i en trekant ABC lig med 180°, får vi 180 ° < BAS+CAS+ ABS+CBS+BCS+ ACS= 180 ° - ASB+ 180° - BSC+ 180° - A.S.C.. Derfor, ASB+BSC+ASC< 360 ° .
Konsekvens 2.Summen af ​​de plane vinkler af en konveks polyedrisk vinkel er mindre end 360.
Beviset ligner det foregående.
Konsekvens 3.Summen af ​​de dihedriske vinkler af en trihedrisk vinkel er større end 180° .
Bevis. Lade SABC- trekantet vinkel. Lad os vælge et punkt P inde i den og slip vinkelrette fra den PA 1 , P.B. 1 , PC 1 på kanten (fig. 4).

Flade hjørner B 1 PC 1 , EN 1 PC 1 , EN 1 P.B. 1 komplementer de tilsvarende dihedrale vinkler med kanter SA, SB, SC op til 180° . Derfor er summen af ​​disse dihedriske vinkler 540° - ( B 1 PC 1 +A 1 PC 1 + EN 1 P.B. 1 ). I betragtning af, at summen af ​​de plane vinkler af en trihedral med et toppunkt P vinkel mindre end 360° , finder vi, at summen af ​​de dihedriske vinkler af den oprindelige trihedriske vinkel er større end 180° .
Ejendom 2.Halveringslinjerne i en trekant skærer hinanden i et punkt.
Ejendom 2". Halveringsplanerne for de dihedriske vinkler i en trihedrisk vinkel skærer hinanden langs en ret linje.
Beviset svarer til flysagen. Nemlig lad SABC- trekantet vinkel. Bisektalt plan af en dihedral vinkel S.A. er GMT for vinklen lige langt fra dens flader A.S.C. Og A.S.B.. Tilsvarende er halveringsfladen af ​​en dihedral vinkel S.B. er GMT for vinklen lige langt fra dens flader B.S.A. Og BSC . Linjen i deres skæringspunkt SÅ vil være lige langt fra alle flader af den trihedriske vinkel, og derfor vil halveringsfladen af ​​den dihedriske vinkel passere gennem den S.C. .
Ejendom 3.De vinkelrette halveringslinjer på siderne af en trekant skærer hinanden i et punkt.
Ejendom 3".Planer, der går gennem halveringslinjerne af flader i en trihedrisk vinkel og vinkelret på disse flader skærer langs en lige linje.
Beviset ligner beviset for den tidligere ejendom.
Ejendom 4.Medianerne af en trekant skærer hinanden i et punkt.
Ejendom 4".Planerne, der passerer gennem kanterne af en trihedrisk vinkel, og halveringslinjerne på modsatte flader skærer hinanden langs en lige linje.
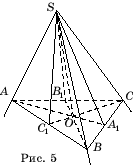
Bevis. Overvej en trihedral vinkel SABC,SA=SB=SC(Fig. 5). Derefter bisektorerne S.A. 1 , S.B. 1 , S.C. 1 hjørner BSC, ASC, ASB er medianerne af de tilsvarende trekanter. Derfor A.A. 1 , BB 1 , CC 1 – medianer af en trekant ABC. Lade O– punktet for deres skæringspunkt. Lige SÅ er indeholdt i alle tre planer under overvejelse og er derfor linjen for deres skæringspunkt.

Ejendom 5.Højderne i en trekant skærer hinanden i et punkt.
Ejendom 5". Planer, der passerer gennem kanterne af en trihedrisk vinkel og vinkelret på modsatte flader, skærer hinanden langs en lige linje.
Bevis. Overvej en trihedral vinkel med toppunkt S og ribben a, b, c. Lad os betegne -en 1 , b 1 , c 1 – skæringslinjer for flader med planer, der går gennem de tilsvarende kanter og vinkelret på disse flader (fig. 6). Lad os rette pointen C på kanten c og slip vinkelrette fra det C.A. 1 Og C.B. 1 på lige linjer -en 1 og b 1 . Lad os betegne EN Og B linjekryds C.A. 1 og C.B. 1 med lige linjer -en Og b. Derefter S.A. 1 er en projektion A.A. 1 til randen BSC. Fordi B.C. vinkelret S.A. 1 , så er det vinkelret og A.A. 1 . Ligeledes, A.C. vinkelret BB 1 . Dermed, A.A. 1 og BB 1 er trekantens højder ABC. Lade O– punktet for deres skæringspunkt. Fly, der passerer gennem linjer -en Og -en 1 , b Og b 1 vinkelret på planet ABC og derfor linjen i deres skæringspunkt SÅ vinkelret ABC. Midler, SÅ vinkelret AB. På den anden side, CO vinkelret AB. Derfor flyet passerer gennem kanten c Og SÅ vil være vinkelret på den modsatte kant.
Egenskab 6 (sinussætning). I en trekant ABC med parterne a, b, c følgelig finder ligestillingen sted -en : synd A = b: synd B=c: synd C.
Ejendom 6". Lad a, b, g - flade vinkler af en trihedrisk vinkel, a, b, c– dihedrale vinkler modsat dem. Derefter synd a : synd -en= synd b : synd b= synd g : synd c.
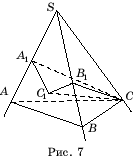
Bevis. Lade SABC- trekantet vinkel. Lad os slippe fra punktet C vinkelret CC 1 til flyet A.S.B. og vinkelret C.A. 1 på kanten S.A.(Fig. 7). Så vinklen C.A. 1 C 1 vilje lineær vinkel dihedral vinkel -en. Derfor CC 1 = C.A. 1 synd -en = S.C. synd b synd en. På samme måde er det vist det CC 1 = CB 1 synd b = SC synd som i b. Følgelig synder ligheden b synd a = synd a synd b og derfor lighedssynden som i -en= synd b : synd b. På lignende måde er det bevist, at ligheden synder b: synd b= synd g : synd c.

Ejendom 7.Hvis i konveks firkant Hvis du kan indskrive en cirkel, så er summen af ​​de modstående sider lige store.
Ejendom 7". Hvis en kugle kan indskrives i en konveks tetraedrisk vinkel, så er summen af ​​modstående planvinkler ens.

Litteratur
1. Hadamard J. Elementær geometri. Del II. Stereometri. – M.: Uchpedgiz, 1938.
2. Perepelkin D.I. Godt elementær geometri. Del II. Geometri i rummet. – M.-L.: Gostekhizdat, 1949.
3. Encyklopædi elementær matematik. Bog IV. Geometri. - M.; 1963.
4. Smirnova I.M. I polyederens verden. – M.: Uddannelse, 1995.

TEKSTTRANSCRIPTION AF LEKTIONEN:

I planimetri er et af undersøgelsesobjekterne en vinkel.

En vinkel er en geometrisk figur, der består af et punkt - vinklens toppunkt og to stråler, der udgår fra dette punkt.

To vinkler, hvoraf den ene side er fælles, og de to andre er en fortsættelse af hinanden, kaldes tilstødende i planimetri.

Et kompas kan opfattes som en model af en plan vinkel.

Lad os huske begrebet en dihedral vinkel.

Dette er en figur dannet af en lige linje a og to halvplaner c fælles grænse Og ikke at høre til det samme plan i geometri kaldes en dihedral vinkel. Halvplaner er flader af en dihedral vinkel. Ret linje a er en kant af en dihedral vinkel.

Husets tag viser tydeligt den dihedrale vinkel.

Men husets tag i figur to er lavet i form af en figur dannet af seks flade vinkler med et fælles toppunkt, så vinklerne tages kl. i en bestemt rækkefølge og hvert par af tilstødende vinkler, inklusive den første og sidste, har fælles side. Hvad kaldes denne tagform?

I geometri, en figur, der består af vinkler

Og de vinkler, hvorfra denne vinkel er lavet, kaldes plane vinkler. Siderne af plane vinkler kaldes kanterne af en polyedrisk vinkel. Punkt O kaldes vinklens toppunkt.

Eksempler på polyedriske vinkler kan findes i tetraeder og parallelepipedum.

Flader af tetraederet DBA, ABC, DBC danner den polyedriske vinkel BADC. Oftere kaldes det en trihedral vinkel.

I et parallelepipedum danner fladerne AA1D1D, ABCD, AA1B1B den triedriske vinkel AA1DB.

Nå, husets tag er lavet i form af en sekskantet vinkel. Den består af seks flade vinkler.

En række egenskaber er sande for en polyedrisk vinkel. Lad os formulere dem og bevise dem. Det står her, at redegørelsen

For det første er der for enhver konveks polyedrisk vinkel et plan, der skærer alle dets kanter.

Som bevis kan du overveje den polyedriske vinkel OA1A2 A3…An.

Efter betingelse er den konveks. En vinkel kaldes konveks, hvis den ligger på den ene side af planet af hver af dens plane vinkler.

Da denne vinkel efter betingelse er konveks, så ligger punkterne O, A1, A2, A3, An på den ene side af planet OA1A2

Lad os udføre midtlinje KM af trekanten OA1A2 og vælg fra kanterne OA3, OA4, OAn den kant, der danner den mindste dihedriske vinkel med OKM-planet. Lad dette være edge OAi.(оа total)

Lad os betragte halvplanet α med grænsen CM, der deler den dihedriske vinkel OKMAi i to dihedriske vinkler. Alle hjørner fra A til An ligger på den ene side af planet α, og punkt O på den anden side. Derfor skærer planet α alle kanterne af den polyedriske vinkel. Udsagnet er bevist.

Konvekse polyedriske vinkler har en anden vigtig egenskab.

Summen af ​​de plane vinkler af en konveks polyedrisk vinkel er mindre end 360°.

Betragt en konveks polyhedral vinkel med et toppunkt i punktet O. I kraft af det beviste udsagn er der et plan, der skærer alle dets kanter.

Lad os tegne en sådan plan α, lad den skære vinklens kanter i punkterne A1, A2, A3 og så videre An.

Planet α fra det ydre område af planvinklen vil afskære trekanten. Summen af ​​vinklerne er 180°. Vi opnår, at summen af ​​alle planvinkler fra A1OA2 til AnOA1 er lig med udtrykket, vi transformerer dette udtryk, vi omarrangerer vilkårene, vi opnår

I dette udtryk summene angivet i parentes er summen af ​​de plane vinkler af en trihedrisk vinkel, og de er som bekendt større end den tredje plane vinkel.

Denne ulighed kan skrives for alle trihedriske vinkler, der danner en given polyedrisk vinkel.

Vi opnår derfor følgende fortsættelse af ligestillingen

Svaret beviser, at summen af ​​de plane vinkler af en konveks polyhedral vinkel er mindre end 360 grader.