የመቀየሪያ ነጥብ ትርጉም. የአንድ ተግባር ግራፍ የመወዛወዝ እና የመወዛወዝ ክፍተቶች

የመስመር ላይ ካልኩሌተር በመጠቀም ማግኘት ይችላሉ። የተግባር ግራፍ የመቀየሪያ ነጥቦች እና የተዛባ ክፍተቶችበ Word ውስጥ ከመፍትሔው ንድፍ ጋር. የሁለት ተለዋዋጮች ተግባር f(x1፣x2) ኮንቬክስ ስለመሆኑ የሚወሰነው የሄሲያን ማትሪክስ በመጠቀም ነው።

y =

ተግባራትን ለማስገባት ደንቦች:

የአንድ ተግባር ግራፍ የመወዛወዝ አቅጣጫ። የመቀየሪያ ነጥቦች

ፍቺ፡- ከርቭ y=f(x) በ interval (a; b) በዚህ ክፍተት ውስጥ በማንኛውም ቦታ ከታንጀቱ በላይ ቢተኛ ኮንቬክስ ይባላል።

ፍቺ፡- ኩርባው y=f(x) በክፍተቱ ውስጥ (a; b) በዚህ ክፍተት ውስጥ በማንኛውም ቦታ ከታንጀቱ በታች ቢተኛ ወደ ላይ ሾጣጣ ነው ይባላል።

ፍቺ፡- የአንድ ተግባር ግራፍ ወደ ላይ ወይም ወደ ታች የሚወዛወዝባቸው ክፍተቶች የተግባሩ ግራፍ ሾጣጣ (intervals of convexity) ይባላሉ።

የክንውኑ ግራፍ የሆነው y=f(x) የጠመዝማዛ ቁልቁል ወይም ወደ ላይ ያለው የሁለተኛው ውፅዓት ምልክት ይገለጻል፡ በተወሰነ የጊዜ ክፍተት f''(x) > 0 ከሆነ፣ ኩርባው ኮንቬክስ ነው በዚህ ክፍተት ላይ ወደ ታች; ከሆነ (x)< 0, то кривая выпукла вверх на этом промежутке.

ፍቺ፡ በአንድ ተግባር ግራፍ ላይ ያለ ነጥብ y=f(x) የተዛባ ክፍተቶችን የሚለይ በተቃራኒ አቅጣጫዎችየዚህ ግራፍ ኢንፍሌክሽን ነጥብ ይባላል.

የመቀየሪያ ነጥቦች ብቻ ሊያገለግሉ ይችላሉ። ወሳኝ ነጥቦች II ዓይነት, ማለትም. ሁለተኛው f’’(x) የሚጠፋበት ወይም የሚቋረጥበት የተግባር y = f(x) ፍቺ ጎራ የሆኑ ነጥቦች።

በአንድ ተግባር y = f(x) ግራፍ ውስጥ የመቀየሪያ ነጥቦችን የማግኘት ደንብ

1. ሁለተኛውን ተዋጽኦ f''(x) ያግኙ።
2. የሁለተኛው ዓይነት ተግባር ወሳኝ ነጥቦችን ያግኙ y=f(x)፣ i.e. f'(x) የሚጠፋበት ወይም መቋረጥ የሚያጋጥመው ነጥብ።
3. የተገኙት ወሳኝ ነጥቦች ረ(x) የተግባርን ፍቺ ጎራ በሚከፋፈሉበት የጊዜ ክፍተት ውስጥ የሁለተኛው ተዋጽኦ f''(x) ምልክትን ይመርምሩ። ወሳኙ ነጥብ x 0 የተቃራኒ አቅጣጫዎችን የዝውውር ክፍተቶችን የሚለይ ከሆነ፣ x 0 የተግባር ግራፉ የመቀየሪያ ነጥብ abcissa ነው።
4. በተለዋዋጭ ነጥቦች ላይ የተግባር ዋጋዎችን አስሉ.

ምሳሌ 1. የሚከተለውን ከርቭ የተዛባ ክፍተቶችን እና የመቀየሪያ ነጥቦችን ይፈልጉ፡ f(x) = 6x 2 –x 3።
መፍትሄ፡ f ‘(x) = 12x – 3x 2፣ f ‘’(x) = 12 – 6x ፈልግ።
12-6x=0 ያለውን እኩልታ በመፍታት የሁለተኛው ተዋጽኦ ወሳኝ ነጥቦችን እንፈልግ። x=2 .


ረ (2) = 6*2 2 - 2 3 = 16
መልስ፡ ተግባሩ ለ x∈(2; +∞) ወደ ላይ ሾጣጣ ነው; ተግባሩ በ x∈ (-∞; 2) ላይ ወደ ታች ኮንቬክስ ነው; የመቀየሪያ ነጥብ (2;16) .

ምሳሌ 2. ተግባሩ የማስተላለፊያ ነጥቦች አሉት፡ f(x)=x 3 -6x 2 +2x-1

ምሳሌ 3. የተግባሩ ግራፍ ሾጣጣ እና የተጠማዘዘባቸውን ክፍተቶች ይፈልጉ፡ f(x)=x 3 -6x 2 +12x+4

የአንድ ተግባር ግራፍ y=ረ(x)ተብሎ ይጠራል ኮንቬክስበጊዜ ክፍተት (ሀ; ለ), በዚህ ክፍተት ላይ ከማንኛውም ታንጀሮች በታች የሚገኝ ከሆነ.

የአንድ ተግባር ግራፍ y=ረ(x)ተብሎ ይጠራል ሾጣጣበጊዜ ክፍተት (ሀ; ለ), በዚህ ክፍተት ላይ ከማንኛውም ታንጀሮች በላይ የሚገኝ ከሆነ.

በሥዕሉ ላይ ኮንቬክስ የሆነ ኩርባ ያሳያል (ሀ; ለ)እና ላይ concave (ለ;ሐ).

ምሳሌዎች።

የተግባሩ ግራፍ ውስጥ መሆን አለመሆኑን ለማረጋገጥ በቂ መስፈርት እንመልከት የተሰጠው ክፍተት convex ወይም concave.

ቲዎረም. ፍቀድ y=ረ(x)ላይ ልዩነት (ሀ; ለ). በሁሉም የጊዜ ክፍተቶች ላይ ከሆነ (ሀ; ለ)የተግባሩ ሁለተኛ ተዋጽኦ y = ረ(x)አሉታዊ፣ ማለትም ረ ""(x) < 0, то график функции на этом интервале выпуклый, если же ረ""(x) > 0 - ሾጣጣ.

ማረጋገጫ. ለነገሩ ያንን እንገምታለን። ረ""(x) < 0 и докажем, что график функции будет выпуклым.

በግራፉ ላይ ያሉትን ተግባራት እንውሰድ y = f(x) የዘፈቀደ ነጥብ ኤም 0ከ abscissa ጋር x 0 Î ( ሀ; ለ) እና በነጥቡ ይሳሉ ኤም 0ታንጀንት. የእርሷ እኩልታ። የተግባሩ ግራፍ ላይ መሆኑን ማሳየት አለብን (ሀ; ለ)ከዚህ ታንጀንት በታች ይተኛል፣ ማለትም በተመሳሳይ ዋጋ xየከርቭ ordinate y = f(x)ከታንጀንት ordinate ያነሰ ይሆናል.

ስለዚህ, የኩርባው እኩልታ ነው y = f(x). ከአብሲሳ ጋር የሚዛመደውን የታንጀንት ሹመት እንጠቁም። x. ከዚያም. በውጤቱም, ለተመሳሳይ እሴት ከርቭ እና ታንጀንት መካከል ያለው ልዩነት xይሆናል ።

ልዩነት ረ(x) – ረ(x 0)በ Lagrange ቲዎሪ መሠረት መለወጥ ፣ የት ሐመካከል xእና x 0.

ስለዚህም

በድጋሚ የ Lagrange ንድፈ ሐሳብን በካሬ ቅንፎች ውስጥ ያለውን አገላለጽ እንተገብራለን:, የት ሐ 1መካከል ሐ 0እና x 0. እንደ ንድፈ-ሀሳቡ ሁኔታዎች ረ ""(x) < 0. Определим знак произведения второго и третьего сомножителей.

ስለዚህ ከርቭ ላይ ያለ ማንኛውም ነጥብ ከታንጀንት በታች እስከ ጥምዝ ድረስ ለሁሉም እሴቶች ይገኛል። xእና x 0 Î ( ሀ; ለ), ይህም ማለት ኩርባው ኮንቬክስ ነው. የቲዎሬም ሁለተኛ ክፍል በተመሳሳይ መንገድ ተረጋግጧል.

ምሳሌዎች.

የግራፍ ነጥብ ቀጣይነት ያለው ተግባር, የእሱን ሾጣጣ ክፍል ከኮንቴክ ክፍል መለየት, ይባላል የመነካካት ነጥብ.

በግልጽ ለማየት እንደሚቻለው, በማጠፊያው ቦታ, ታንጀንት, ካለ, ኩርባውን ያቋርጣል, ምክንያቱም በዚህ ነጥብ በአንደኛው በኩል ኩርባው ከታንጀንት በታች, እና በሌላኛው በኩል - ከሱ በላይ.

ለዚያ እውነታ በቂ ሁኔታዎችን እንወስን የተሰጠው ነጥብኩርባው የመቀየሪያ ነጥብ ነው.

ቲዎረም. ኩርባው በቀመር ይገለጽ y = f(x). ከሆነ ረ ""(x 0) = 0 ወይም ረ ""(x 0) በእሴቱ ውስጥ በሚያልፉበት ጊዜ እንኳን የለም x = x 0ተዋጽኦ ረ ""(x) ምልክትን ይለውጣል, ከዚያም በግራፍ ውስጥ ያለው ነጥብ ከ abcissa ጋር x = x 0የማስተላለፊያ ነጥብ አለ.

ማረጋገጫ. ፍቀድ ረ ""(x) < 0 при x < x 0እና ረ ""(x) > 0 በ x > x 0. ከዚያም በ x < x 0ኩርባው ኮንቬክስ ነው, እና መቼ x > x 0- ሾጣጣ. ስለዚህ, ነጥቡ ሀ, ከርቭ ላይ ተኝቶ, abscissa ጋር x 0የማስተላለፊያ ነጥብ አለ. ሁለተኛው ጉዳይ በተመሳሳይ ሁኔታ ሊቆጠር ይችላል, መቼ ረ ""(x) > 0 በ x < x 0እና ረ ""(x) < 0 при x > x 0.

ስለዚህ፣ የመቀየሪያ ነጥቦችን መፈለግ የሚኖርባቸው የሁለተኛው ተዋጽኦ ከጠፋባቸው ወይም ከሌሉባቸው ነጥቦች መካከል ብቻ ነው።

ምሳሌዎች።የመቀየሪያ ነጥቦችን ይፈልጉ እና የክርን እና የክርን መጨናነቅ ክፍተቶችን ይወስኑ።

የተግባር ግራፍ ምልክቶች

አንድን ተግባር በሚያጠኑበት ጊዜ የግራፉን ቅርጽ ከመነሻው የግራፍ ነጥብ ገደብ በሌለው ርቀት ላይ ማቋቋም አስፈላጊ ነው.

ልዩ ትኩረት የሚስበው የአንድ ተግባር ግራፍ፣ ተለዋዋጭ ነጥቡ ወደ ማለቂያ ሲወገድ፣ ላልተወሰነ ጊዜ ወደ አንድ ቀጥተኛ መስመር ሲቃረብ ነው።

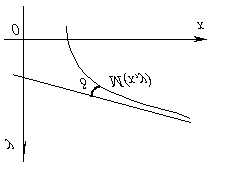
ቀጥተኛ መስመር ተጠርቷል አሲምፕቶትተግባር ግራፊክስ y = ረ(x), ከተለዋዋጭ ነጥብ ርቀቱ ከሆነ ኤምአንድ ነጥብ ሲያስወግዱ ወደዚህ መስመር ግራፊክስ ኤምወሰን አልባ ወደ ዜሮ ያዛባል፣ ማለትም በአንድ ተግባር ግራፍ ላይ ያለ ነጥብ፣ ወደ ወሰን አልባነት ሲሄድ፣ ወደ asymptote ላልተወሰነ ጊዜ መቅረብ አለበት።

አንድ ኩርባ በአንድ በኩል ወይም ከእሱ ጋር ሲቆይ ወደ asymptote ሊጠጋ ይችላል። የተለያዩ ጎኖች, ማለቂያ የሌለው ስብስብአንዴ አሲምፕቶት ከተሻገሩ እና ከአንዱ ጎን ወደ ሌላው ሲንቀሳቀሱ.

ከነጥቡ ያለውን ርቀት በ d ከጠቆምን ኤምወደ asymptote ማጠፍ፣ ከዚያም ነጥቡ ሲርቅ d ወደ ዜሮ እንደሚሄድ ግልጽ ነው። ኤምማለቂያ የሌለው።

በአቀባዊ እና በግድ ምልክቶች መካከል ያለውን ልዩነት የበለጠ እንለያለን።

ቋሚ አስመሳይ

እስቲ በ x→ x 0ከማንኛውም የጎን ተግባር y = ረ(x)በፍፁም ዋጋ ያለገደብ ይጨምራል፣ ማለትም ወይም ወይም . ከዚያም ከአሲምፖት ፍቺው ቀጥታ መስመር ይከተላል x = x 0አሲምፕቶት ነው። ተቃራኒው ደግሞ ግልጽ ነው, መስመር ከሆነ x = x 0 asymptote ነው፣ ማለትም .

ስለዚህ, የተግባሩ ግራፍ አቀባዊ asymptote y = f(x)ከሆነ ቀጥተኛ መስመር ይባላል ረ(x)→ ∞ ቢያንስ በአንዱ ቅድመ ሁኔታ x→ x 0- 0 ወይም x → x 0 + 0, x = x 0

ስለዚህ, የተግባርን ግራፍ አቀባዊ ምልክቶችን ለማግኘት y = ረ(x)እነዚያን እሴቶች ማግኘት አለብዎት x = x 0, ተግባሩ ወደ ማለቂያነት የሚሄድበት (በማይወሰን መቋረጥ ይሰቃያል). ከዚያም አቀባዊ asymptoteእኩልታ አለው። x = x 0.

ምሳሌዎች።

SLANT ASYMPTOTES

asymptote ቀጥተኛ መስመር ስለሆነ, ከዚያም ኩርባው ከሆነ y = ረ(x)አስገዳጅ አሲምፕቶት አለው፣ ከዚያ እኩልታ ይሆናል። y = kx + ለ. የእኛ ተግባር ኮፊፊሴቲቭን መፈለግ ነው። ክእና ለ.

ቲዎረም. ቀጥታ y = kx + ለእንደ oblique asymptote በ x→ +∞ ለተግባሩ ግራፍ y = ረ(x)ከዚያ እና መቼ ብቻ . ተመሳሳይ መግለጫ ለ እውነት ነው x → –∞.

ማረጋገጫ. ፍቀድ MP- የክፍሉ ርዝመት; ከርቀት ጋር እኩል ነውከነጥብ ኤምወደ asymptote. በሁኔታ። በ φ የ asymptote ወደ ዘንግ ያለውን ዝንባሌ አንግል እንጠቁም ኦክስ. ከዚያም ከ ΔMNPያንን ይከተላል. φ ቋሚ አንግል ስለሆነ (φ ≠ π/2)፣ ከዚያ፣ ግን

አንድን ተግባር ስናጠና እና ግራፉን በሚገነባበት ጊዜ፣ በአንድ ደረጃ የመቀየሪያ ነጥቦችን እና የመወዛወዝ ክፍተቶችን እንወስናለን። እነዚህ መረጃዎች፣ ከመጨመር እና ከመቀነስ ክፍተቶች ጋር፣ በጥናት ላይ ያለውን ተግባር ግራፍ በሥርዓት እንዲወክሉ ያደርጉታል።

ተጨማሪው የዝግጅት አቀራረብ እስከ አንዳንድ ቅደም ተከተሎችን እና የተለያዩ ዓይነቶችን ማድረግ እንደሚችሉ ያስባል.

ይዘቱን ማጥናት እንጀምር አስፈላጊ ትርጓሜዎችእና ጽንሰ-ሐሳቦች. በመቀጠል፣ በአንድ የተወሰነ ክፍተት ላይ ባለው የሁለተኛው ተዋፅኦ እሴት እና በተዘዋዋሪ አቅጣጫ መካከል ያለውን ግንኙነት እናሰማለን። ከዚህ በኋላ, የተግባር ግራፉን የመቀየሪያ ነጥቦችን ለመወሰን በሚያስችሉ ሁኔታዎች ውስጥ እንቀጥላለን. በምንሰጠው ጽሑፍ መሰረት የተለመዱ ምሳሌዎችከዝርዝር መፍትሄዎች ጋር.

የገጽ አሰሳ።

መወዛወዝ፣ የተግባር መጨናነቅ፣ የመነካካት ነጥብ።

ፍቺ

ወደ ታች ማወዛወዝበክፍተቱ X ላይ ግራፉ ከታንጀንት በታች ካልሆነ በየትኛውም የጊዜ ክፍተት X ላይ የሚገኝ ከሆነ።

ፍቺ

የሚለየው ተግባር ይባላል ማወዛወዝበክፍተቱ X ላይ ግራፉ ከ ታንጀንት የማይበልጥ ከፍ ብሎ የሚገኝ ከሆነ በመካከል X ውስጥ በማንኛውም ቦታ ላይ።

ብዙውን ጊዜ ወደ ላይ የሚወጣ ኮንቬክስ ተግባር ይባላል ኮንቬክስእና ወደ ታች ውጣ - ሾጣጣ.

እነዚህን ፍቺዎች የሚያብራራውን ሥዕል ተመልከት።

ፍቺ

ነጥቡ ይባላል የተግባር ግራፍ ጠቋሚ ነጥብ y=f(x) በአንድ የተወሰነ ቦታ ላይ የተግባሩ ግራፍ ላይ ታንጀንት ካለ (ከኦይ ዘንግ ጋር ትይዩ ሊሆን ይችላል) እና ነጥቡ ወደ ግራ እና ቀኝ ያለው አካባቢ ካለ M. የተግባሩ ግራፍ የተለያዩ የመወዛወዝ አቅጣጫዎች አሉት.

በሌላ አገላለጽ ነጥብ M በዚህ ነጥብ ላይ ታንጀንት ካለ እና የተግባሩ ግራፍ የ convexity አቅጣጫውን በመቀየር በውስጡ የሚያልፍ ከሆነ የአንድ ተግባር ግራፍ ኢንፍሌክሽን ነጥብ ይባላል።

አስፈላጊ ከሆነ, ቀጥ ያለ እና ቀጥ ያለ ታንጀንት መኖሩን ሁኔታዎችን ለማስታወስ ክፍሉን ይመልከቱ.

ከዚህ በታች ያለው ምስል አንዳንድ የመቀየሪያ ነጥቦችን (በቀይ ነጠብጣቦች ምልክት የተደረገበት) ያሳያል። አንዳንድ ተግባራት ምንም የመቀየሪያ ነጥቦች ላይኖራቸው ይችላል, ሌሎች ደግሞ አንድ, ብዙ, ወይም ማለቂያ የሌላቸው ብዙ የመተላለፊያ ነጥቦች ሊኖራቸው እንደሚችል ልብ ይበሉ.

የአንድ ተግባር መወዛወዝ ክፍተቶችን መፈለግ።

የአንድን ተግባር መጨናነቅ ክፍተቶች ለመወሰን የሚያስችለንን ንድፈ ሃሳብ እንቅረፅ።

ቲዎረም.

ተግባር y=f(x) በ interval X ላይ የመጨረሻ ሁለተኛ ተዋፅኦ ካለው እና አለመመጣጠኑ ከቀጠለ ()፣ ከዚያ የተግባሩ ግራፍ በX ወደ ታች (ወደ ላይ) የሚመራ ዘንበል አለው።

ይህ ጽንሰ-ሐሳብ የአንድን ተግባር መወዛወዝ እና መወዛወዝ ክፍተቶችን እንዲያገኙ ይፈቅድልዎታል ፣ እርስዎ ብቻ እኩል ያልሆኑትን መፍታት እና በቅደም ተከተል ፣ በዋናው ተግባር ትርጓሜ ጎራ ላይ ብቻ ያስፈልግዎታል።

ተግባር y=f(x) የተገለጸበት እና ሁለተኛው ተወላጅ የማይገኝባቸው ነጥቦች በኮንካቪቲ እና ኮንቬክሲቲ ክፍተቶች ውስጥ እንደሚካተቱ ልብ ሊባል ይገባል።

ይህንን በምሳሌ እንረዳው።

ለምሳሌ.

የተግባሩ ግራፍ በየትኞቹ ላይ ክፍተቶችን ይፈልጉ ወደላይ የሚመራ እና ወደ ታች የሚመራ ዘንበል አለው።

መፍትሄ።

የአንድ ተግባር ጎራ ሙሉው ስብስብ ነው። እውነተኛ ቁጥሮች.

ሁለተኛውን ተዋጽኦን እንፈልግ።

የሁለተኛው ተዋጽኦ ፍቺ ጎራ ከዋናው ተግባር ፍቺ ጎራ ጋር ይዛመዳል ፣ ስለሆነም ፣ የ concavity እና convexity ክፍተቶችን ለማወቅ ፣ መፍታት እና በዚህ መሠረት በቂ ነው።

ስለዚህ, ተግባሩ በክፍተቱ ላይ ወደታች እና በመጠምዘዝ ወደ ላይ ሾጣጣ ነው.

ስዕላዊ መግለጫ.

በኮንቬክስ ክፍተት ውስጥ ያለው የተግባር ግራፍ ክፍል በሰማያዊ, እና በክንውኑ ክፍተት - በቀይ ይታያል.

አሁን የሁለተኛው ተዋጽኦ ፍቺ ጎራ ከተግባሩ ፍቺ ጎራ ጋር የማይጣጣም ከሆነ አንድ ምሳሌ እንመልከት። በዚህ ሁኔታ፣ አስቀድመን እንደገለጽነው፣ ውሱን የሆነ ሁለተኛ ተዋጽኦ የሌለባቸው የትርጉም ጎራ ነጥቦች በኮንቬክሲቲ እና (ወይም) ውዝግቦች መካከል መካተት አለባቸው።

ለምሳሌ.

የተግባርን ግራፍ ሾጣጣ እና ሾጣጣ ክፍተቶችን ይፈልጉ።

መፍትሄ።

በተግባሩ ጎራ እንጀምር፡-

ሁለተኛውን መነሻ እናገኝ፡-

የሁለተኛው ተዋጽኦ ፍቺ ጎራ ስብስብ ነው። . እንደምታየው፣ x=0 የዋናው ተግባር ጎራ ነው፣ ግን የሁለተኛው ተዋጽኦ ጎራ አይደለም። ስለዚህ ነጥብ አትርሳ፤ በኮንቬክሲቲ እና (ወይም) መጨናነቅ መካከል መካተት አለበት።

አሁን በዋናው ተግባር ፍቺ ጎራ ላይ አለመመጣጠን እንፈታለን። እንተገብረሎም። አገላለጽ ቁጥር ሰጪ ወደ ዜሮ ይሄዳል በ ወይም ፣ መለያ - በ x = 0 ወይም x = 1። እነዚህን ነጥቦች በቁጥር መስመር ላይ በማንፀባረቅ እና በዋናው ተግባር ፍቺ ጎራ ውስጥ በተካተቱት በእያንዳንዱ ክፍተቶች ላይ የገለጻውን ምልክት እናገኛለን (በታችኛው የቁጥር መስመር ላይ እንደ ጥላ ቦታ ይታያል)። ለአዎንታዊ እሴት የመደመር ምልክት እናስቀምጣለን ፣ ለአሉታዊ እሴት የመቀነስ ምልክት እናደርጋለን።

ስለዚህም

እና

ስለዚህ ነጥቡን x=0 በማካተት መልሱን እናገኛለን።

በ የተግባሩ ግራፍ ወደ ታች የሚመራ ሾጣጣ አለው, መቼ - ወደላይ የሚመራ ዘንበል.

ስዕላዊ መግለጫ.

በ convexity interval ላይ ያለው የተግባር ግራፍ ክፍል በሰማያዊ ይገለጻል ፣ በክንውኑ ክፍተቶች ላይ - በቀይ ፣ ጥቁር ነጠብጣብ መስመር ቀጥ ያለ asymptote ነው።

ለመተንፈስ አስፈላጊ እና በቂ ሁኔታዎች.

ለኢንፌክሽን አስፈላጊ ሁኔታ.

እንቅረፅ አስፈላጊ ሁኔታኢንፌክሽኑተግባር ግራፊክስ.

የተግባሩ ግራፍ y=f(x) በአንድ ነጥብ ላይ ኢንፍሌክሽን ይኖረው እና ቀጣይነት ያለው ሁለተኛ ተዋፅኦ ይኖረው፣ ከዚያ እኩልነቱ ይቆያል።

ከዚህ ሁኔታ የሁለተኛው የተግባር አመጣጥ በሚጠፋባቸው ሰዎች መካከል የኢንፍሌክሽን ነጥቦችን (abcissa) መፈለግ አለበት ። ግን ይህ ሁኔታ በቂ አይደለም ፣ ማለትም ፣ የሁለተኛው ተዋጽኦ ከዜሮ ጋር እኩል የሆነባቸው ሁሉም እሴቶች የመቀየሪያ ነጥቦች አቢሲሳዎች አይደሉም።

በተጨማሪም የኢንፍሌክሽን ነጥብ ትርጓሜ የታንጀንት መስመር ወይም ቀጥ ያለ መኖሩን እንደሚፈልግ ልብ ሊባል ይገባል. ይህ ምን ማለት ነው? እና ይህ ማለት የሚከተለው ማለት ነው-የአስቂኝ ነጥቦች አቢሲሳዎች ከተግባሩ ትርጓሜ ጎራ ሁሉም ነገር ሊሆን ይችላል ። እና . እነዚህ ብዙውን ጊዜ የመጀመሪያው ተዋጽኦ መለያ የሚጠፋባቸው ነጥቦች ናቸው።

የመጀመሪያው በቂ ሁኔታ ለመተንፈስ.

የ inflection ነጥቦች abcissas ሊሆን ይችላል ሁሉ በኋላ, መጠቀም አለብህ የመጀመሪያው በቂ ሁኔታ ለኢንፌክሽንተግባር ግራፊክስ.

ተግባሩ y=f(x) ነጥቡ ላይ ቀጣይ ይሁን፣ በላዩ ላይ ታንጀንት (ምናልባትም አቀባዊ) ይኑረው፣ እና ይህ ተግባር በአንዳንድ የነጥብ ሰፈር ውስጥ ሁለተኛ ተዋጽኦ እንዲኖረው ያድርጉ። ከዚያ፣ በዚህ ሰፈር ውስጥ ከ ግራ እና ቀኝ፣ ሁለተኛው ተወላጅ አለው። የተለያዩ ምልክቶች, ከዚያም የተግባር ግራፉ ጠቋሚ ነጥብ ነው.

እንደ መጀመሪያው ማየት ይችላሉ በቂ ሁኔታነጥቡ በራሱ የሁለተኛው ተዋጽኦ መኖሩን አይጠይቅም, ነገር ግን በነጥቡ አከባቢ ውስጥ መኖሩን ይጠይቃል.

አሁን ሁሉንም መረጃዎች በአልጎሪዝም መልክ እናጠቃልል.

የአንድ ተግባር ማነቃቂያ ነጥቦችን ለማግኘት አልጎሪዝም።

የተግባር ግራፍ (ወይም) ሊሆኑ የሚችሉ የመቀየሪያ ነጥቦችን ሁሉንም አቢሲሳዎች እናገኛለን እና ) እና ሁለተኛው ተወላጅ ለውጦች በየትኛው በኩል እንደሚፈርሙ በማለፍ ይወቁ. እንደነዚህ ያሉት ዋጋዎች የመቀየሪያ ነጥቦቹ አቢሲሳ ይሆናሉ ፣ እና ተጓዳኝ ነጥቦቹ የተግባር ግራፉ የመቀየሪያ ነጥቦች ይሆናሉ።

ለማብራራት የመገለጫ ነጥቦችን ለማግኘት ሁለት ምሳሌዎችን እንመልከት።

ለምሳሌ.

የመቀየሪያ ነጥቦችን እና የመወዛወዝ ክፍተቶችን እና የአንድ ተግባር ግራፍ መጨናነቅ ይፈልጉ .

መፍትሄ።

የአንድ ተግባር ጎራ የእውነተኛ ቁጥሮች ስብስብ ነው።

የመጀመሪያውን መነሻ እናገኝ፡-

የመጀመርያው ተዋጽኦ ፍቺ ጎራ እንዲሁ አጠቃላይ የእውነተኛ ቁጥሮች ስብስብ ነው ፣ ስለሆነም እኩልነቶች እና ለማንም አልተሟላም .

ሁለተኛውን መነሻ እናገኝ፡-

የክርክሩ ዋጋ በየትኞቹ እሴቶች ላይ እንወቅ x ሁለተኛው ተዋጽኦ ወደ ዜሮ ይሄዳል፡

ስለዚህ ፣ ሊሆኑ የሚችሉ የመቀየሪያ ነጥቦች abcissas x=-2 እና x=3 ናቸው።

አሁን በቂ የሆነ የኢንፍሌክሽን ምልክት በመጠቀም መፈተሽ ይቀራል፣ ከእነዚህ ነጥቦች ውስጥ የሁለተኛው ተዋፅኦ ለውጦች ምልክት። ይህንን ለማድረግ, ነጥቦቹን x=-2 እና x=3 በቁጥር ዘንግ ላይ እና እንደ ውስጥ አጠቃላይ የጊዜ ክፍተት ዘዴ, በእያንዳንዱ የጊዜ ክፍተት ላይ የሁለተኛውን ተወላጅ ምልክቶችን እናስቀምጣለን. በእያንዲንደ ክፍተት ስር የተግባር ግራፉ የመገጣጠም አቅጣጫ በአርከሮች schematically ይታያል.

ሁለተኛው የመነሻ ለውጥ ከፕላስ ወደ ሲቀነስ፣ ነጥቡን x=-2 ከግራ ወደ ቀኝ በማለፍ፣ እና ሲቀነስ ወደ ፕላስ፣ በ x=3 በኩል ያልፋል። ስለዚህ፣ ሁለቱም x=-2 እና x=3 የተግባር ግራፍ የመቀየሪያ ነጥቦች abcissas ናቸው። እነሱ ከግራፍ ነጥቦቹ ጋር ይዛመዳሉ እና .

የቁጥር መስመርን እና የሁለተኛው ተዋጽኦ ምልክቶች በየእረፍተቶቹ ላይ ሌላ እይታ ስንመለከት ፣ ስለ ኮንቬክስ እና ሾጣጣ ክፍተቶች መደምደሚያ ላይ መድረስ እንችላለን። የአንድ ተግባር ግራፍ በክፍተቱ ላይ ሾጣጣ እና በቋሚዎቹ ላይ ሾጣጣ እና .

ስዕላዊ መግለጫ.

በኮንቬክስ ክፍተት ላይ ያለው የተግባር ግራፍ ክፍል በሰማያዊ፣ በክንውኑ ክፍተት ላይ - በቀይ፣ እና የመቀየሪያ ነጥቦች እንደ ጥቁር ነጥቦች ይታያሉ።

ለምሳሌ.

የተግባር ግራፉ ሁሉንም የመቀየሪያ ነጥቦችን abcissa ያግኙ .

መፍትሄ።

የዚህ ተግባር ፍቺ ጎራ የእውነተኛ ቁጥሮች ስብስብ ነው።

ተዋጽኦውን እንፈልግ።

የመጀመሪያው ተዋጽኦ፣ ከመጀመሪያው ተግባር በተለየ፣ በ x=3 አልተገለጸም። ግን እና . ስለዚህ፣ በ abcissa x=3 ነጥብ ላይ ለዋናው ተግባር ግራፍ ቁመታዊ ታንጀንት አለ። ስለዚህ, x=3 የተግባር ግራፍ የመቀየሪያ ነጥብ abcissa ሊሆን ይችላል.

ሁለተኛውን ተዋጽኦ፣ የትርጉም ጎራውን እና የሚጠፋባቸውን ነጥቦች እናገኛለን፡-

ሁለት ተጨማሪ ሊሆኑ የሚችሉ የአስቂኝ ነጥቦችን አግኝተናል። ሶስቱን ነጥቦች በቁጥር መስመር ላይ ምልክት እናደርጋለን እና በእያንዳንዱ የውጤት ክፍተቶች ላይ የሁለተኛውን የመነሻ ምልክት እንወስናለን.

በእያንዳንዱ ነጥብ ውስጥ በሚያልፉበት ጊዜ ሁለተኛው የመነሻ ለውጦች ምልክት ነው ፣ ስለሆነም ሁሉም የመቀየሪያ ነጥቦች አቢሲሳዎች ናቸው።

መመሪያዎች

ነጥቦች ኢንፌክሽኑ ተግባራትበመጀመሪያ መገኘት ያለበት የትርጉሙ ጎራ መሆን አለበት። መርሐግብር ተግባራትቀጣይነት ያለው ወይም እረፍቶች ያሉት፣ በብቸኝነት የሚቀንስ ወይም የሚጨምር፣ ዝቅተኛ ወይም ከፍተኛ ያለው መስመር ነው። ነጥቦች(asymptotes)፣ ኮንቬክስ ወይም ሾጣጣ ይሁኑ። ባለፉት ሁለት ግዛቶች ውስጥ ከፍተኛ ለውጥ ኢንፍሌክሽን ነጥብ ይባላል.

ለሕልውና አስፈላጊ ሁኔታ ኢንፌክሽኑ ተግባራትከሁለተኛ እስከ ዜሮ ያለውን እኩልነት ያካትታል. ስለዚህ, ተግባሩን ሁለት ጊዜ በመለየት እና የተገኘውን አገላለጽ ከዜሮ ጋር በማመሳሰል, ሊሆኑ የሚችሉ ነጥቦችን abcissa ማግኘት እንችላለን. ኢንፌክሽኑ.

ይህ ሁኔታ የግራፍ (ግራፍ) መወዛወዝ እና የመገጣጠም ባህሪያት ፍቺ ይከተላል ተግባራት፣ ማለትም እ.ኤ.አ. አሉታዊ እና አዎንታዊ እሴትሁለተኛ ተዋጽኦ. ነጥብ ላይ ኢንፌክሽኑ ድንገተኛ ለውጥእነዚህ ንብረቶች፣ ይህ ማለት ተዋጽኦው የዜሮ ምልክቱን ያልፋል ማለት ነው። ሆኖም፣ ከዜሮ ጋር እኩል መሆን ኢንፍሌክሽን ለማመልከት ገና በቂ አይደለም።

በቀድሞው ደረጃ የተገኘው አቢሲሳ የነጥቡ ንብረት የሆነው ሁለት በቂ ሁኔታዎች አሉ። ኢንፌክሽኑበዚህ ነጥብ አማካኝነት ታንጀንት መሳል ይችላሉ ተግባራት. ሁለተኛው ተወላጅ ከሚጠበቀው በቀኝ እና በግራ በኩል የተለያዩ ምልክቶች አሉት ነጥቦች ኢንፌክሽኑ. ስለዚህ ፣ በነጥቡ ላይ ያለው ሕልውና ራሱ አስፈላጊ አይደለም ፣ በእሱ ላይ ምልክትን እንደሚቀይር መወሰን በቂ ነው ። ሁለተኛ አመጣጥ ተግባራትከዜሮ ጋር እኩል ነው, እና ሶስተኛው አይደለም.

መፍትሄ: አግኝ. ውስጥ በዚህ ጉዳይ ላይምንም ገደቦች የሉም ፣ ስለሆነም ፣ የእውነተኛ ቁጥሮች አጠቃላይ ቦታ ነው። የመጀመሪያውን መገኛ አስላ፡ y’ = 3 ∛(x - 5) + (3 x + 3)/∛(x - 5)²።

ትኩረት ይስጡ. ከዚህ በመነሳት የመነጩ ፍቺው ጎራ የተገደበ ነው። ነጥቡ x = 5 የተበሳ ነው, ይህም ማለት ታንጀንት በእሱ ውስጥ ማለፍ ይችላል, ይህም በከፊል ከመጀመሪያው በቂ ምልክት ጋር ይዛመዳል. ኢንፌክሽኑ.

ውጤቱን ለ x → 5 – 0 እና x → 5 + 0 ይወስኑ። ከ -∞ እና +∞ ጋር እኩል ናቸው። ቀጥ ያለ ታንጀንት በ x=5 ነጥብ ውስጥ እንደሚያልፍ አረጋግጠዋል። ይህ ነጥብ አንድ ነጥብ ሊሆን ይችላል ኢንፌክሽኑበመጀመሪያ ግን ሁለተኛውን አስላ፡ Y'' = 1/∛(x - 5)² + 3/∛(x - 5)² - 2/3 (3 x + 3)/∛(x - 5)^5 = (2 x – 22)/∛(x - 5)^5።

ነጥቡን x = 5ን ከግምት ውስጥ ስላስገባህ መለያየቱን ተወው። እኩልታውን 2 x – 22 = 0 ን መፍታት አንድ ስር x = 11 ነው። የመጨረሻው ደረጃ ማረጋገጥ ነው። ነጥቦች x=5 እና x=11 ነጥቦች ናቸው። ኢንፌክሽኑ. በአካባቢያቸው ያለውን የሁለተኛው ተወላጅ ባህሪን ይተንትኑ. በግልጽ ለማየት እንደሚቻለው, በ x = 5 ላይ ምልክትን ከ "+" ወደ "-" ይለውጣል, እና በ x = 11 - በተቃራኒው. ማጠቃለያ፡- ሁለቱም ነጥቦችነጥቦች ናቸው። ኢንፌክሽኑ. የመጀመሪያው በቂ ሁኔታ ረክቷል.