В правильной треугольной пирамиде вершина проектируется в точку пересечения медиан основания.
В правильной четырехугольной пирамиде вершина проектируется в точку пересечения диагоналей основания.
В правильной шестиугольной пирамиде вершина проектируется в точку пересечения диагоналей основания.
Высота пирамиды, две боковые грани которой перпендикулярны основе, проходит через вершину основания и является наименьшим боковым ребром пирамиды.
Высота пирамиды, одна боковая грань которой перпендикулярна основе, лежит в этой грани, а основа высоты лежит на стороне основания, через которую проходит данная грань.
Если в некоторой пирамиде все боковые ребра наклонены к плоскости основания под одним и тем же углом или все боковые ребра равны между собой, то вершина пирамиды проецируется в центр круга, описанного вокруг основания пирамиды.
Если в некоторой пирамиде все боковые ребра наклонены к плоскости основания под одним и тем же углом или все боковые ребра равны между собой, то расстояния от основания высоты пирамиды к боковых ребер равны между собой.
Если в некоторой пирамиде все боковые ребра наклонены к плоскости основания под одним и тем же углом или все боковые ребра равны между собой и в основании пирамиды лежит прямоугольный треугольник, то основа высоты пирамиды является серединой гипотенузы треугольника основания боковая грань, проходящая через гипотенузу, перпендикулярна плоскости основания пирамиды.
Если в некоторой пирамиде все боковые грани наклонены к плоскости основания под одним и тем же углом или высоты всех боковых граней равны между собой, то вершина пирамиды проецируется в центр круга, вписанного в основание пирамиды.
Если в некоторой пирамиде все боковые грани наклонены к плоскости основания под одним и тем же углом, то площадь основания пирамиды равна площади боковой поверхности, умноженной на косинус угла наклона боковых граней к плоскости основания.
Если из основания высоты пирамиды проведено перпендикуляр на боковую грань, то основа этого перпендикуляра лежит на высоте данной боковой грани, проведенной из вершины пирамиды. Угол между этим перпендикуляром и плоскостью основания пирамиды равен углу между высотой пирамиды и высотой этой боковой грани.
Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом, то перпендикуляры, проведенные из основы высоты пирамиды до боковых граней, равны между собой и образуют одинаковые углы с плоскостью основания. Расстояния от основания высоты пирамиды к всех боковых граней в таком случае равны между собой.
Рассмотрим свойства пирамид, в которых все боковые ребра равны, с соответствующими чертежами.
Если между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.
Прямоугольные треугольники, образованные высотой пирамиды, боковыми ребрами и их проекциями (равными радиусу описанной окружности), равны. Поэтому также
- все боковые ребра пирамиды образуют с плоскостью основания равные углы;
— все углы, которые боковые ребра образуют с высотой пирамиды, равны.
Решение задач на пирамиду, в которой все боковые ребра равны (либо все боковые ребра образуют равные углы с основанием пирамиды или с высотой пирамиды) начинается с чертежа.
Если основание пирамиды — треугольник.
остроугольного треугольника, лежит внутри треугольника.
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника.
На рисунке тупой угол — это угол B.
Радиус окружности, описанной около произвольного остроугольного либо тупоугольного треугольника ABC, можно найти по следствию из теоремы синусов:
либо по формуле
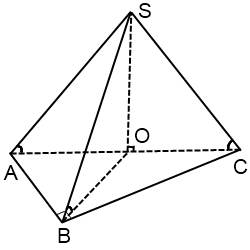
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
Радиус описанной около основания окружности в этом случае равен
где c — гипотенуза.
Отсюда для данного треугольника ABC с прямым углом B
Если основание пирамиды — параллелограмм
Из всех параллелограммов описать окружность можем только около прямоугольника (квадрат — его частный случай). Поэтому, если в задаче сказано, что пирамиде все боковые ребра равны, либо все боковые ребра одинаково наклонены к плоскости основания, либо все боковые ребра образуют с высотой пирамиды равные углы, а в основании — параллелограмм, то это может быть только прямоугольник (квадрат).
Центр описанной около прямоугольника окружности — точка пересечения его диагоналей. Соответственно, радиус R равен половине диагонали прямоугольника.
Если основание пирамиды -трапеция
Из всех трапеций описать окружность можно только около равнобочной трапеции.
Радиус описанной окружности ищем как радиус окружности, описанной около одного из треугольников ABC или ACD по одной из формул, приведенных выше.
Если диагональ трапеции перпендикулярна боковой стороне
боковые ребра пирамиды равны
В этом случае центр описанной около трапеции окружности лежит на середине большего основания, а высота пирамиды лежит в боковой грани, содержащей это большее основание.
Радиус R в этом случае — половина гипотенузы прямоугольного треугольника ACD.
Если основание пирамиды — произвольный четырехугольник
Радиус описанной около основания окружности находим как радиус окружности, описанной около одного из треугольников основания: ABC, BCD, ACD или ABD.
Поскольку описать около четырехугольника окружность можно только тогда, когда сумма его противолежащих углов равна 180 градусов, то
Вспомним: апофема-высота боковой грани пирамиды, проведенная из вершины на ребро основания.
Теорема 5
. Если все боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга.
Теорема 5.1
. Если все апофемы пирамиды равны, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга.
Докажем теорему на при мере четырехугольной пирамиды. Пусть дана пирамида КABCD, К -вершина, АВСD - основание. Проведем высоту КО пирамиды. В каждой боковой грани проведем высоту из вершины пирамиды на сторону основания. В плоскости основания соединим точку О (основание высоты) с точкой основаниями этих высот - апофем. ОР, ОТ, ОМ и ОЕ соответственно перпендикулярны АВ, ВС, CD и AD (теорема о трех перпендикулярах).
По определению углы КРО, КТО, КМО, КЕО - линейные углы двугранных углов между соответственными боковыми гранями и основанием ABCD. Высота КО является перпендикуляром к основанию, поэтому перпендикулярна любой прямой в этой плоскости, т.е. перпендикулярна прямым ОР, ОТ, ОМ и ОЕ. Это говорит, что треугольники КРО, КТО, КМО, КЕО прямоугольные.
По условию (теорема 5) углы КРО, КТО, КМО, КЕО равны. Рассмотрим треугольники КРО, КТО, КМО, КЕО, они прямоугольны и равны (по катету и острому углу, КО - общая и углы КРО, КТО, КМО, КЕО равны по условию).
По условию (теорема 5.1) КР, КТ, КМ и КЕ равны, поэтому треугольники КРО, КТО, КМО, КЕО прямоугольные и равны по катету и гипотенузе.
Из равенства этих треугольников следует, что их соответствующие стороны ОР, ОТ, ОМ и ОЕ равны, а значит, в четырехугольнике ABCD есть такая точка, которая равноудалена от его сторон, то есть в него можно вписать круг.
Теорема 6
. Если все боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то около основания такой пирамиды можно описать окружность, а высота, опущенная из вершины на основание, падает в центр описанной около основания окружности.
Эту теорему можно сформулировать и так:
Теорема 6.1
. Если все боковые ребра пирамиды равны, то около основания такой пирамиды можно описать окружность, а высота, опущенная из вершины на основание, падает в центр описанной около основания окружности.
Докажем теорему на при мере четурехугольной пирамиды. Пусть дана пирамида КABCD, К -вершина, АВСD - основание. Проведем высоту КО пирамиды. В плоскости основания соединим
точку О (основание высоты) со всеми вершинами основания А, В, С и D. Угол KВО - угол между ребром КB и плоскостью основания (угол между прямой и плоскостью есть угол между этой прямой
и её проекцией на эту плоскость). Таким же образом докажем, что углы КСО, КАО и KDO - углы, образованные соответствующими ребрами КС, КА и KD с плоскостью основания. Высота КО является перпендикуляром к основанию, поэтому перпендикулярна любой прямой в этой плоскости, т.е. перпендикулярна прямым ОА, ОВ, ОС и ОD. Это говорит, что треугольники КAО, КBО, КCО, КDО прямоугольные.
Углы КВО, КСО, КАО и KDO равны (по условиям теоремы 6). Рассмотрим треугольники КAО, КBО, КCО, КDО, они прямоугольны и равны (по катету и острому углу, КО - общая и углы КАО, КВО, КСО, КDО равны по условию).
Доказывая теорему 6.1, также рассмотрим треугольники КAО, КBО, КCО, КDО, они прямоугольны и равны по катету и гипотенузе (КО - общая, КА=КВ=КС=KD по условию теоремы).
Из равенствa этих треугольников следует, что их соответствующие стороны ОА, ОВ, ОС и ОD равны, а значит, в основании есть такая точка, которая
равноудалена от вершин четырехугольника ABCD, то есть около него можно описать окружность.