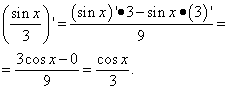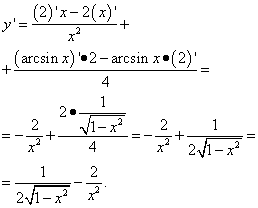Приватні похідні тригонометричних функцій - приклади рішень. Виведення похідних арктангенсу та арккотангенсу

При виведенні першої формули таблиці виходити з визначення похідної функції у точці. Візьмемо, де x– будь-яке дійсне число, тобто, x- Будь-яке число з області визначення функції. Запишемо межу відношення збільшення функції до збільшення аргументу при:

Слід зазначити, що під знаком межі виходить вираз, який не є невизначеністю нуль ділити на нуль, тому що в чисельнику знаходиться не нескінченно мала величина, а саме нуль. Іншими словами, збільшення постійної функції завжди дорівнює нулю.

Таким чином, похідна постійної функціїдорівнює нулю по всій області визначення.

Похідна статечної функції.

Формула похідної статечної функціїмає вигляд де показник ступеня p- Будь-яке дійсне число.

Доведемо спочатку формулу для натурального показника ступеня, тобто для p = 1, 2, 3, …

Будемо користуватися визначенням похідної. Запишемо межу відношення збільшення статечної функції до збільшення аргументу:

Для спрощення виразу в чисельнику звернемося до формули бінома Ньютона:

Отже,

Цим доведено формулу похідної статечної функції для натурального показника.

Похідна показової функції.

Висновок формули похідної наведемо на основі визначення:

Прийшли до невизначеності. Для її розкриття введемо нову змінну, причому при. Тоді. В останньому переході ми використали формулу переходу до нової основи логарифму.

Виконаємо підстановку у вихідну межу:

Якщо згадати другу чудову межу, то прийдемо до формули похідної показової функції:

Похідна логарифмічна функція.

Доведемо формулу похідної логарифмічної функції всім xв галузі визначення та всіх допустимих значеннях підстави aлогарифму. За визначенням похідної маємо:

Як Ви помітили, за доказом перетворення проводилися з використанням властивостей логарифму. Рівність справедливо з другого чудової межі.

Похідні тригонометричних функцій.

Для виведення формул похідних тригонометричних функцій нам доведеться згадати деякі формули тригонометрії, а також перша чудова межа.

За визначенням похідної для функції синуса маємо .

Скористаємося формулою різниці синусів:

Залишилося звернутися до першої чудової межі:

Таким чином, похідна функції sin xє cos x.

Абсолютно аналогічно доводиться формула похідної косинуса.

Отже, похідна функції cos xє -sin x.

Виведення формул таблиці похідних для тангенсу та котангенсу проведемо з використанням доведених правил диференціювання (похідна дробу).

Похідні гіперболічні функції.

Правила диференціювання та формула похідної показової функції з таблиці похідних дозволяють вивести формули похідних гіперболічного синуса, косинуса, тангенсу та котангенсу.

Похідна зворотної функції.

Щоб при викладі не було плутанини, давайте позначати в нижньому індексі аргумент функції, за яким виконується диференціювання, тобто це похідна функції f(x)по x.

Тепер сформулюємо правило знаходження похідної зворотної функції.

Нехай функції y = f(x)і x = g(y)взаємно зворотні, визначені на інтервалах та відповідно. Якщо у точці існує кінцева відмінна від нуля похідна функції f(x), то в точці існує кінцева похідна зворотної функції g(y), причому . В іншому записі .

Можна це правило переформулювати для будь-кого xз проміжку, тоді отримаємо .

Перевіримо справедливість цих формул.

Знайдемо зворотну функцію для натурального логарифму (тут y- функція, а x- Аргумент). Дозволивши це рівняння щодо x, отримаємо (тут x- функція, а y- Її аргумент). Тобто, та взаємно зворотні функції.

З таблиці похідних бачимо, що і .

Переконаємося, що формули знаходження похідних зворотної функції призводять нас до цих результатів:

Тема:«Похідна тригонометричних функцій».
Тип уроку- Урок закріплення знань.
Форма уроку- Інтегрований урок.
Місце уроку в системі уроків у цьому розділі- Узагальнюючий урок.
Цілі поставлені комплексно:

  • навчальні:знати правила диференціювання, вміти застосовувати правила обчислення похідних під час вирішення рівнянь і нерівностей; удосконалювати предметні, у тому числі обчислювальні, уміння та навички; навички роботи з комп'ютером;
  • розвиваючі:розвиток інтелектуально-логічних умінь та пізнавальних інтересів;
  • виховні:виховувати адаптивність до сучасним умовамнавчання.

Методи:

Форми контролю:

ХІД УРОКУ

I. Організаційний момент

ІІ. Актуалізація опорних знань

а) Повідомлення цілей та завдань:

  • знати правила диференціювання, вміти застосовувати правила обчислення похідних під час вирішення завдань, рівнянь та нерівностей;
  • удосконалювати предметні, у тому числі обчислювальні, уміння та навички; навички роботи з комп'ютером;
  • розвивати інтелектуально-логічні вміння та пізнавальні інтереси;
  • виховувати адаптивність до сучасних умов навчання.

б) Повторення навчального матеріалу

Правила обчислення похідних (повторення формул з комп'ютера зі звуковим супроводом). док.7.

  1. Чому дорівнює похідна синуса?
  2. Чому дорівнює похідна косинуса?
  3. Чому дорівнює похідна тангенсу?
  4. Чому дорівнює похідна котангенсу?

ІІІ. Усна робота

Знайти похідну.

Варіант 1.

Варіант 2

у = 2х + 5.

у = 2х – 5.

у= 4cos х.

у= 3sin х.

у= tg х+ ctg х.

у= tg х- ctg х.

у= sin 3 х.

у= cos 4 х.

Варіанти відповідей.

- 4sin х

- 3cos х

1/cos 2 х+ 1/sin 2 х

1/cos 2 х–1/sin 2 х

1/sin 2 х–1/cos 2 х

- 4sin4 х

- 3cos3 х

Обміняйтесь зошитами. Позначте в діагностичних картах правильно виконані завдання знаком +, а неправильно виконані завдання знаком –.

IV. Розв'язання рівнянь за допомогою похідної

- Як знайти точки, в яких похідна дорівнює нулю?

Щоб знайти точки, в яких похідна даної функціїдорівнює нулю, потрібно:

- Визначити характер функції,
– знайти область визначення функції,
- Визначити похідну цієї функції,
- Вирішити рівняння f "(x) = 0,
- Вибрати правильну відповідь.

Завдання 1.

Дано: у = х- sin x.
Знайти:точки, у яких похідна дорівнює нулю.
Рішення.Функція визначена і диференційована на множині всіх дійсних чисел, так як на множині всіх дійсних чисел визначені та диференційовані функції g(x) = xі t(x) = - sin x.
Використовуючи правила диференціювання, отримаємо f "(x) = (x- sin x)" = (x)" - ( sin x)" = 1 - cos x.
Якщо f "(x) = 0, то 1 - cos x = 0.
cos x= 1/; позбудемося ірраціональності в знаменнику, отримаємо cos x = /2.
За формулою t= ± arccos a+ 2n, n Z, отримаємо: х= ± arccos/2+2n, n Z.
Відповідь:х = ± /4 + 2n, n Z.

V. Розв'язання рівнянь за алгоритмом

Знайти, у яких точках перетворюється на нуль похідна.

f(x) = sin x+ cos x

f(x) = sin 2 x – x

f(x) = 2x+ cos(4 x – )

Учень може вибрати будь-який із трьох прикладів. Перший приклад оцінюється оцінкою « 3 », другий – « 4 », третій – « 5 ». Рішення у зошитах з подальшою взаємоперевіркою. Один учень вирішує біля дошки. Якщо рішення виявляється неправильним, потрібно учневі повернутися до алгоритму і спробувати вирішити знову.

Програмований контроль.

Варіант 1

Варіант 2

y = 2х 3

y = 3х 2

y = 1/4 х 4 + 2х 2 – 7

y = 1/2 х 4 + 4х + 5

y = х 3 + 4х 2 – 3х.
Розв'язати рівняння y " = 0

y = 2х 3 – 9х 2 + 12х + 7.
Розв'язати рівняння y " = 0.

y= sin 2 х- cos 3 х.

y= cos 2 х- sin 3 х.

y= tg х- ctg ( х + /4).

y= ctg х+ tg ( х – /4).

y= sin 2 х.

y= cos 2 х.

Варіанти відповідей.

З курсу геометрії та математики школярі звикли, що поняття похідної доноситься до них через площу фігури, диференціали, межі функцій, а також ліміти. Спробуємо подивитися на поняття похідної під іншим кутом і визначити, як можна ув'язати похідну та тригонометричні функції.

Отже, розглянемо довільну криву, яка описується абстрактною функцією y = f(x).

Уявімо, що графік - це карта туристичного маршруту. Приріст ∆x (дельта ікс) на малюнку - це певний проміжок шляху, а ∆y - це зміна висоти стежки над рівнем моря.
Тоді виходить, що відношення ∆x/∆y характеризуватиме складно маршруту на кожному відрізку шляху. Дізнавшись це значення можна з упевненістю сказати, чи крутий підйом/спуск, чи знадобиться альпіністське спорядження і чи потрібна туристам певна фізична підготовка. Але цей показник буде справедливий тільки для одного маленького проміжку∆x.

Якщо організатор походу візьме значення для початкової та кінцевої крапокстежки, тобто ∆x – буде дорівнює довжинімаршруту, то не зможе отримати об'єктивні дані щодо ступеня складності подорожі. Отже, необхідно побудувати ще один графік, який характеризуватиме швидкість і «якість» змін шляху, тобто визначати відношення ∆x/∆y для кожного «метра» маршруту.

Цей графік і буде наочною похідною для конкретної стежки і об'єктивно опише її зміни на кожному інтервалі, що цікавить. Переконатися в цьому дуже просто, значення ∆x/∆y – не що інше, як диференціал, взятий для конкретного значення x та y. Застосуємо диференціювання не певним координатам, а до функції в цілому:

Похідна та тригонометричні функції

Тригонометричні функції нерозривно пов'язані з похідною. Зрозуміти це можна з наступного креслення. На малюнку координатної осізображено функцію Y = f (x) – синя крива.

K (x0; f (x0)) - довільна точка, x0 + ∆x – приріст осі OX, а f (x0 + ∆x) – приріст осі OY у певній точці L.

Проведемо пряму через точки K та L і побудуємо прямокутний трикутник KLN. Якщо подумки переміщати відрізок LN за графіком Y = f (x), то точки L і N прагнутимуть значення K (x0; f (x0)). Назвемо цю точку умовним початком графіка - лімітом, якщо функція нескінченна, хоча б на одному з проміжків - це прагнення також буде нескінченним, а його граничне значення близьким до 0.

Характер цього прагнення можна описати дотичною до обраної точки y = kx + b або графіком похідної початкової функції dy – зелена пряма.

Але де тут тригонометрія?! Все просто розглянемо прямокутний трикутник KLN. Значення диференціала для конкретної точки K є тангенсом кута α або ∠K:

Таким чином можна описати геометричний смимсл похідної та її взаємозв'язок з тригонометричними функціями.

Формули похідних для тригонометричних функцій

Перетворення синуса, косинуса, тангенсу та котангенсу при визначенні похідної необхідно завчити напам'ять.

Останні дві формули не є помилкою, річ у тому, що існує різниця між визначенням похідної простого аргументу та функції у тій самій якості.

Розглянемо порівняльну таблицюз формулами похідних від синісу, косинуса, тангенсу та котангенсу:

Також виведені формули для похідних арксинусу, арккосинусу, арктангенсу та арккотангенсу, хоча вони застосовуються вкрай рідко:

Варто зазначити, що наведених формул явно недостатньо для успішного вирішення типових завданьЄДІ, що буде продемонстровано під час вирішення конкретного прикладупошуку похідної тригонометричного виразу.

Завдання: Необхідно знайти похідну функції та знайти її значення для π/4:

Рішення: Щоб знайти y’ необхідно згадати основні формули перетворення вихідної функції у похідну, а саме.

Представлені похідні зворотних тригонометричних функцій та виведення їх формул. Також дано висловлювання похідних вищих порядків. Посилання на сторінки з більш докладним викладомвиведення формул.

Спочатку виведемо формулу похідної арксинусу. Нехай
y = arcsin x.
Оскільки арксинус є функцією, зворотною до синуса, то
.
Тут y - функція від x. Диференціюємо по змінній x:
.
Застосовуємо:
.
Отже, ми знайшли:
.

Оскільки, то. Тоді
.
І попередня формула набуває вигляду:
. Звідси
.

Точно таким способом можна отримати формулу похідної арккосинусу. Однак простіше скористатися формулою, що зв'язує зворотні тригонометричні функції:
.
Тоді
.

Докладніше виклад представлено на сторінці “Виведення похідних арксинусу та арккосинусу”. Там дається виведення похідних двома способами- розглянутим вище та за формулою похідної зворотної функції.

Виведення похідних арктангенсу та арккотангенсу

У такий же спосіб знайдемо похідні арктангенсу та арккотангенсу.

Нехай
y = arctg x.
Арктангенс є функція, обернена до тангенсу:
.
Диференціюємо по змінній x:
.
Застосовуємо формулу похідної складної функції:
.
Отже, ми знайшли:
.

Похідна арккотангенса:
.

Похідні арксинусу

Нехай
.
Похідну першого порядку від арксинусу ми вже знайшли:
.
Диференціюючи, знаходимо похідну другого порядку:
;
.
Її також можна записати у такому вигляді:
.
Звідси отримуємо диференціальне рівняння, якому задовольняють похідні арксинусу першого та другого порядків:
.

Диференціюючи це рівняння, можна знайти похідні найвищих порядків.

Похідна арксинуса n-го порядку

Похідна арксинуса n-го порядку має наступний вигляд:
,
де - багаточлен ступеня. Він визначається за формулами:
;
.
Тут.

Багаточлен задовольняє диференціальне рівняння:
.

Похідна арккосинусу n-го порядку

Похідні для арккосинусу виходять із похідних для арксинусу за допомогою тригонометричної формули:
.
Тому похідні цих функцій відрізняються лише знаком:
.

Похідні арктангенсу

Нехай. Ми знайшли похідну арккотангенсу першого порядку:
.

Розкладемо дріб на найпростіші:

.
Тут - уявна одиниця, .

Диференціюємо раз і наводимо дріб до спільного знаменника:

.

Підставляючи , отримаємо:
.

Похідна арктангенса n-го порядку

Таким чином, похідну арктангенса n-го порядку можна уявити декількома способами:
;
.

Похідні арккотангенсу

Нехай тепер. Застосуємо формулу, що зв'язує зворотні тригонометричні функції:
.
Тоді похідна n-го порядку від арккотангенсу відрізняються лише знаком від похідної арктангенсу:
.

Підставивши, знайдемо:
.

Використана література:
Н.М. Гюнтер, Р.О. Кузьмін, Збірник завдань з вищої математики, "Лань", 2003.

Для знаходження похідної тригонометричної функції потрібно користуватися таблицею похідних, А саме похідними 6-13.

При знаходженні похідних простих тригонометричних функцій щоб уникнути поширених помилок, слід звертати увагу на наступні моменти:

  • у вираженні функції часто один із доданків є синус, косинус або іншу тригонометричну функціюнемає від аргументу функції, як від числа (константи), тому похідна цього доданка дорівнює нулю;
  • майже завжди потрібно спростити вираз, отриманий у результаті диференціювання, а для цього потрібно впевнено користуватися знаннями з дій з дробами;
  • для спрощення виразу майже завжди потрібно знати тригонометричні тотожності, наприклад, формулу подвійного кутаі формулу одиниці як суму квадратів синуса та косинуса.

приклад 1.Знайти похідну функції

Рішення. Допустимо, з похідної косинусавсе зрозуміло, скажуть багато хто, хто починає вивчати похідні. А як бути з похідної синусадванадцяти, поділених на пі? Відповідь: рахувати дорівнює нулю! Тут синус (функція все-таки!) – пастка, тому що аргумент – не змінна ікс чи будь-яка інша змінна, а просто число. Тобто, синус цього числа теж число. А похідна числа (константи), як відомо з таблиці похідних, дорівнює нулю. Отже, залишаємо тільки мінус синус ікса і знаходимо його похідну, не забуваючи про знак:

.

приклад 2.Знайти похідну функції

.

Рішення. Другий доданок - той самий випадок, що і перший доданок у попередньому прикладі. Тобто число, а похідна числа дорівнює нулю. Знаходимо похідну другого доданку як похідну приватного:

приклад 3.Знайти похідну функції

Рішення. Це вже інше завдання: тут у першому доданку немає ні арксинусу, ні іншої тригонометичної функції, але є ікс, отже це функція від ікса. Отже, диференціюємо її як доданок у сумі функцій:

Тут були потрібні навички в діях з дробами, а саме - у ліквідації триповерховості дробу.

приклад 4.Знайти похідну функції

.

Рішення. Тут буква "фі" відіграє ту ж роль, що "ікс" у попередніх випадках (і в більшості інших, але не у всіх) - незалежної змінної. Тому, коли шукатимемо похідну твори функцій, не поспішатимемо оголошувати рівною нулю похідну кореня від "фі". Отже:

Але на цьому рішення не закінчується. Так як у двох дужках зібрані такі члени, від нас ще потрібно перетворити (спростити) вираз. Тому множимо дужки на винесені за них множники, а далі наводимо доданки до спільного знаменника і виконуємо інші елементарні перетворення:

Приклад 5.Знайти похідну функції

Рішення. У цьому прикладі від нас буде потрібно знання того факту, що існує така тригонометрична функція – секанс – та її формули через косинус. Диференціюємо:

Приклад 6.Знайти похідну функції

.

Рішення. У цьому прикладі нам потрібно пам'ятати зі шкільного курсу формулу подвійного кута. Але спочатку диференціюємо:

,

(це і є формула подвійного кута)