Проширување на функциите во енергетски серии онлајн. Проширување на функциите во енергетски серии

Учениците по виша математика треба да знаат дека збирот на одредена серија на моќност што ни припаѓа на интервалот на конвергенција на серијата што ни е дадена, излегува дека е континуиран и неограничен број пати диференцирана функција. Се поставува прашањето: дали е можно да се каже дека дадена произволна функција f(x) е збир на одредена серија на моќност? Односно, под кои услови функцијата f(x) може да се претстави со серија на моќност? Важноста на ова прашање лежи во фактот дека е можно приближно да се замени функцијата f(x) со збирот на првите неколку члена од серијата на моќност, односно полином. Оваа замена на функција со прилично едноставен израз - полином - е погодна и при решавање на одредени проблеми, имено: при решавање интеграли, при пресметување итн.

Докажано е дека за одредена функција f(x), во која е можно да се пресметаат деривати до (n+1)-ти редослед, вклучувајќи го и последниот, во соседството на (α - R; x 0 + R ) некоја точка x = α, точно е дека формулата:

Оваа формула е именувана по познатиот научник Брук Тејлор. Серијата што е добиена од претходната се нарекува серија Maclaurin:

Правилото што овозможува да се изврши проширување во серијата Maclaurin:

Определи изводи од прв, втор, трет... ред.
Пресметај на што се еднакви изводите на x=0.
Запишете ја серијата Maclaurin за оваа функција, а потоа определете го интервалот на нејзината конвергенција.
Определи го интервалот (-R;R), каде што е остатокот од формулата Маклаурин

R n (x) -> 0 во n -> бесконечност. Ако постои, функцијата f(x) во неа мора да се совпадне со збирот на серијата Маклаурин.

Сега да ја разгледаме серијата Maclaurin за поединечни функции.

1. Значи, првиот ќе биде f(x) = e x. Се разбира, според своите карактеристики, таквата функција има изводи од многу различни редови, и f (k) (x) = e x, каде што k е еднакво на сите. Заменете x = 0. Добиваме f (k) (0) = e 0 =1, k = 1,2... Врз основа на горенаведеното, серијата e x ќе изгледа вака:

2. Маклауринова серија за функцијата f(x) = sin x. Веднаш да разјасниме дека функцијата за сите непознати ќе има изводи, покрај тоа, f "(x) = cos x = sin(x+n/2), f "" (x) = -sin x = sin(x + 2*n/2)..., f (k) (x) = sin(x+k*n/2), каде k е еднаков на кој било природен број.Односно, откако ќе направиме едноставни пресметки, можеме да дојдеме до заклучокот дека серијата за f(x) = sin x ќе изгледа вака:

3. Сега да се обидеме да ја разгледаме функцијата f(x) = cos x. За сите непознати има изводи од произволен ред, и |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так:

Значи, ги наведовме најважните функции што можат да се прошират во серијата Maclaurin, но тие се дополнети со серијата Тејлор за некои функции. Сега ќе ги наведеме. Исто така, вреди да се напомене дека сериите Тејлор и Маклаурин се важен дел од практичната работа за решавање на серии во вишата математика. Значи, серија Тејлор.

1. Првата ќе биде серијата за функцијата f(x) = ln(1+x). Како и во претходните примери, за дадената f(x) = ln(1+x) можеме да ја додадеме серијата користејќи ја општата форма на серијата Maclaurin. сепак, за оваа функција серијата Maclaurin може да се добие многу поедноставно. Со интегрирање на одредена геометриска серија, добиваме серија за f(x) = ln(1+x) од таков примерок:

2. А втората, која ќе биде конечна во нашата статија, ќе биде серијата за f(x) = арктан x. За x што припаѓа на интервалот [-1;1], проширувањето важи:

Тоа е се. Оваа статија ги испита најкористените серии Тејлор и Маклаурин во вишата математика, особено во економските и техничките универзитети.

Доколку функцијата f(x)има на некој интервал кој ја содржи точката А, деривати на сите нарачки, тогаш формулата на Тејлор може да се примени на неа:

Каде r n– таканаречениот остаток член или остаток од серијата, може да се процени со помош на Лагранжовата формула:

, каде што бројот x е помеѓу XИ А.

Ако за некоја вредност x r n®0 на n®¥, тогаш во границата Тејлоровата формула се претвора во конвергентна формула за оваа вредност Тејлор серија:

Значи функцијата f(x)може да се прошири во серија на Тејлор во предметната точка X, Ако:

1) има деривати од сите нарачки;

2) конструираната серија конвергира во оваа точка.

На А=0 добиваме серија наречена во близина на Маклаурин:

Пример 1 f(x)= 2x.

Решение. Дозволете ни да ги најдеме вредностите на функцијата и нејзините деривати во X=0

f(x) = 2x, f( 0) = 2 0 =1;

f¢ (x) = 2x ln2, f¢ ( 0) = 2 0 ln2= ln2;

f¢¢ (x) = 2xна 2 2, f¢¢ ( 0) = 2 0 ln 2 2= ln 2 2;

f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.

Заменувајќи ги добиените вредности на дериватите во формулата на серијата Тејлор, добиваме:

Радиусот на конвергенција на оваа серија е еднаков на бесконечност, затоа ова проширување важи за -¥<x<+¥.

Пример 2 X+4) за функција f(x)=д x.

Решение. Наоѓање на изводите на функцијата e xи нивните вредности во точката X=-4.

f(x)= e x, f(-4) = e -4 ;

f¢ (x)= e x, f¢ (-4) = e -4 ;

f¢¢ (x)= e x, f¢¢ (-4) = e -4 ;

f(n)(x)= e x, f(n)( -4) = e -4 .

Затоа, потребната Тејлор серија на функцијата има форма:

Ова проширување важи и за -¥<x<+¥.

Пример 3 . Прошири функција f(x)= н xво серија во моќ ( X- 1),

(т.е. во серијата Тејлор во близина на точката X=1).

Решение. Најдете ги изводите на оваа функција.

Заменувајќи ги овие вредности во формулата, ја добиваме саканата серија на Тејлор:

Користејќи го тестот на d'Alembert, можете да потврдите дека серијата конвергира кога

½ X- 1 ½<1. Действительно,

Серијата конвергира ако ½ X- 1 ½<1, т.е. при 0<x<2. При X=2 добиваме наизменична серија која ги задоволува условите на Лајбницовиот критериум. На X=0 функцијата не е дефинирана. Така, регионот на конвергенција на серијата Тејлор е полуотворен интервал (0;2].

Да ги претставиме вака добиените проширувања во серијата Maclaurin (т.е. во близина на точката X=0) за некои елементарни функции:

(2) ,

(3) ,

(се нарекува последното разложување биномна серија)

Пример 4 . Проширете ја функцијата во серија на моќност

Решение. Во проширувањето (1) заменуваме Xна - X 2, добиваме:

Пример 5 . Проширете ја функцијата во серија Maclaurin

Решение. Ние имаме

Користејќи ја формулата (4), можеме да напишеме:

заменувајќи наместо тоа Xво формулата -Х, добиваме:

Од тука наоѓаме:

Отворање на заградите, преуредување на условите од серијата и донесување слични термини, добиваме

Оваа серија се конвергира во интервалот

(-1;1), бидејќи се добива од две серии, од кои секоја конвергира во овој интервал.

Коментар .

Формулите (1)-(5) исто така може да се користат за проширување на соодветните функции во серија на Тејлор, т.е. за проширување на функциите во позитивни цели броеви ( Ха). За да се направи ова, потребно е да се извршат такви идентични трансформации на дадена функција за да се добие една од функциите (1)-(5), во која наместо Xтрошоци k( Ха) m , каде што k е постојан број, m е позитивен цел број. Често е погодно да се направи промена на променливата т=Хаи проширете ја добиената функција во однос на t во серијата Maclaurin.

Овој метод ја илустрира теоремата за уникатноста на проширувањето на сериите на моќност на функцијата. Суштината на оваа теорема е дека во соседството на иста точка не може да се добијат две различни серии на моќност кои би се споиле во иста функција, без разлика како се врши нејзиното проширување.

Пример 6 . Проширете ја функцијата во серија на Тејлор во соседство на точка X=3.

Решение. Овој проблем може да се реши, како и досега, со користење на дефиницијата на серијата Тејлор, за која треба да ги најдеме дериватите на функцијата и нивните вредности на X=3. Сепак, ќе биде полесно да се користи постоечката експанзија (5):

Резултирачката серија конвергира во или -3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Пример 7 . Напишете ја серијата Тејлор во моќи ( X-1) функции .

Решение.

Серијата се спојува во , или 2< x 5 фунти.

Во теоријата на функционални серии, централното место го зазема делот посветен на проширување на функцијата во серија.

Така се поставува задачата: за дадена функција треба да најдеме таква моќна серија

кој се спојувал на одреден интервал и неговиот збир бил еднаков на
, тие.

= ..

Оваа задача се нарекува проблемот на проширување на функцијата во енергетска серија.

Неопходен услов за разградливост на функција во енергетска серијае неговата диференцијабилност бесконечен број пати - ова произлегува од својствата на конвергентните серии на моќност. Овој услов е задоволен, по правило, за елементарните функции во нивниот домен на дефиниција.

Значи, да претпоставиме дека функцијата
има деривати од кој било ред. Дали е можно да се прошири во серии за напојување?Ако е така, како можеме да ја најдеме оваа серија? Вториот дел од проблемот е полесен за решавање, па да почнеме со него.

Да претпоставиме дека функцијата
може да се претстави како збир на серии на моќност кои се конвергираат во интервалот што ја содржи точката X 0 :

= .. (*)

Каде А 0 , А 1 , А 2 ,...,А П ,... – непознати (сеуште) коефициенти.

Да ја ставиме во еднаквост (*) вредноста x = x 0 , тогаш добиваме

Дозволете ни да ја разликуваме серијата на моќност (*) по член по член

= ..

и верувајќи овде x = x 0 , добиваме

Со следната диференцијација ја добиваме серијата

= ..

верувајќи x = x 0 , добиваме
, каде
.

По П-повеќекратна диференцијација добиваме

Претпоставувајќи во последната еднаквост x = x 0 , добиваме
, каде

Значи, коефициентите се пронајдени

,
,
, …,
,….,

заменувајќи го во серијата (*), добиваме

Добиената серија се нарекува веднаш до Тејлор за функција
.

Така, го утврдивме тоа ако функцијата може да се прошири во серија на моќност во моќности (x - x 0 ), тогаш оваа експанзија е единствена и добиената серија е нужно серија на Тејлор.

Забележете дека серијата Тејлор може да се добие за која било функција која има изводи од кој било ред во точката x = x 0 . Но, тоа не значи дека може да се стави знак за еднаквост помеѓу функцијата и добиената серија, т.е. дека збирот на серијата е еднаков на оригиналната функција. Прво, таквата еднаквост може да има смисла само во регионот на конвергенција, а Тејлоровата серија добиена за функцијата може да се разминува, и второ, ако серијата Тејлор се конвергира, тогаш нејзиниот збир може да не се совпаѓа со оригиналната функција.

3.2. Доволни услови за разградливост на функција во Тејлоровата серија

Дозволете ни да формулираме изјава со чија помош ќе се реши задачата.

Доколку функцијата
во некое соседство на точката x 0 има деривати до (n+ 1) од ред инклузивно, тогаш во оваа населба имамеформула Тејлор

КадеР n (X)- преостанатиот член од формулата на Тејлор - ја има формата (Лагранжова форма)

Каде точкаξ лежи помеѓу x и x 0 .

Забележете дека постои разлика помеѓу Тејлоровата серија и Тејлоровата формула: Тејлоровата формула е конечен збир, т.е. П -фиксен број.

Потсетиме дека збирот на серијата С(x) може да се дефинира како граница на функционална низа од парцијални суми С П (x) во одреден интервал X:

Според ова, да се прошири функцијата во серија на Тејлор значи да се најде серија таква што за која било XX

Да ја напишеме формулата на Тејлор во форма каде

забележи, тоа
ја дефинира грешката што ја добиваме, заменете ја функцијата ѓ(x) полином С n (x).

Ако
, Тоа
, оние. функцијата е проширена во серија на Тејлор. обратно, ако
, Тоа
.

Така докажавме критериум за разградливост на функција во Тејлоровата серија.

Со цел за функцијатаѓ(x) се проширува во серија на Тејлор, потребно е и доволно на овој интервал
, КадеР n (x) е преостанатиот термин од серијата Тејлор.

Користејќи го формулираниот критериум, може да се добие доволноуслови за разградливост на функција во Тејлоровата серија.

Доколку вонекое соседство на точката x 0 апсолутните вредности на сите деривати на функцијата се ограничени на истиот број М≥ 0, т.е.

, Тo во ова соседство функцијата се проширува во серија на Тејлор.

Од горенаведеното следува алгоритампроширување на функцијата ѓ(x) во серијата Тејлорво близина на точка X 0 :

1. Наоѓање деривати на функции ѓ(x):

f(x), f’(x), f”(x), f’”(x), f (n) (x),…

2. Пресметајте ја вредноста на функцијата и вредностите на нејзините деривати во точката X 0

f(x 0 ), f'(x 0 ), f“ (x 0 ), ѓ“ (x 0 ), ѓ (n) (х 0 ),…

3. Ние формално ја пишуваме Тејлоровата серија и го наоѓаме регионот на конвергенција на добиената серија на моќност.

4. Проверуваме исполнување на доволни услови, т.е. утврдуваме за кои Xод регионот на конвергенција, преостанат рок Р n (x) има тенденција на нула во
или
.

Проширувањето на функциите во серија на Тејлор со користење на овој алгоритам се нарекува проширување на функцијата во серија на Тејлор по дефиницијаили директно распаѓање.

Меѓу функционалните серии, најважно место заземаат сериите за напојување.

Моќната серија е серија

чии поими се функции на моќност распоредени во зголемување на ненегативни цели броеви x, А в0 , в 1 , в 2 , в n - константни вредности. Броеви в1 , в 2 , в n - коефициенти на сериските членови, в0 - бесплатен член. Условите на серијата моќност се дефинирани на целата нумеричка линија.

Ајде да се запознаеме со концептот области на конвергенција на сериите на моќност. Ова е збир на променливи вредности x, за што се конвергира серијата. Моќните серии имаат прилично едноставен регион на конвергенција. За реални променливи вредности xрегионот на конвергенција се состои или од една точка, или е одреден интервал (интервал на конвергенција), или се совпаѓа со целата оска Вол .

При замена на вредностите во сериите на моќност x= 0 ќе резултира со бројна серија

в0 +0+0+...+0+... ,

која конвергира.

Затоа, кога x= 0 која било серија на моќност конвергира и затоа, неговата област на конвергенција не може да биде празното множество. Структурата на регионот на конвергенција на сите серии на моќност е иста. Може да се утврди со помош на следнава теорема.

Теорема 1 (Абелова теорема). Ако серијата на моќност конвергира на некоја вредност x = x 0 , различно од нула, тогаш се конвергира и, згора на тоа, апсолутно, за сите вредности |x| < |x 0 | . Забележете: и почетната вредност „X е нула“ и секоја вредност на „X“ што се споредува со почетната вредност се земаат модуло - без да се земе предвид знакот.

Последица. Ако сериите на моќност се разминуваат по некоја вредност x = x 1 , тогаш се разминува за сите вредности |x| > |x 1 | .

Како што веќе дознавме порано, секоја серија на моќност конвергира по вредноста x= 0. Постојат серии на моќност кои се спојуваат само кога x= 0 и се разминуваат за други вредности X. Исклучувајќи го овој случај од разгледување, претпоставуваме дека серијата на моќност конвергира во одредена вредност x = x 0 , различно од нула. Потоа, според Абеловата теорема, таа конвергира во сите точки на интервалот ]-| x0 |, |x 0 |[ (интервал чии леви и десни граници се вредностите на x при кои се конвергира серијата моќност, земени со знак минус и знак плус, соодветно), симетричен во однос на потеклото.

Ако серијата на моќност се разминува при одредена вредност x = x 1 , потоа, врз основа на последица на Абеловата теорема, таа се разминува во сите точки надвор од сегментот [-| x1 |, |x 1 |] . Следи дека за која било серија на моќност постои интервал симетричен во однос на потеклото, наречен интервал на конвергенција , во секоја точка од која серијата конвергира, на границите може да се спојува, или може да се разминува, и не мора во исто време, а надвор од сегментот серијата се разминува. Број Рсе нарекува радиус на конвергенција на серијата на моќност.

Во посебни случаи интервал на конвергенција на сериите на моќност може да се дегенерира до точка (тогаш серијата конвергира само кога x= 0 и се смета дека Р= 0) или да ја претстави целата бројна права (тогаш серијата конвергира во сите точки на бројната права и се претпоставува дека ).

Така, одредувањето на регионот на конвергенција на енергетската серија се состои во одредување на неговата радиус на конвергенција Ри проучување на конвергенцијата на серијата на границите на интервалот на конвергенција (на ).

Теорема 2.Ако сите коефициенти на серијата на моќност, почнувајќи од одредена, се различни од нула, тогаш неговиот радиус на конвергенција е еднаков на границата во односот на апсолутните вредности на коефициентите на заедничките следни членови на серијата , т.е.

Пример 1. Најдете го регионот на конвергенција на серијата на моќност

Решение. Еве

Користејќи ја формулата (28), го наоѓаме радиусот на конвергенција на оваа серија:

Да ја проучуваме конвергенцијата на сериите на краевите на интервалот на конвергенција. Примерот 13 покажува дека оваа серија конвергира во x= 1 и се разминува во x= -1. Следствено, регионот на конвергенција е полуинтервалот.

Пример 2. Најдете го регионот на конвергенција на серијата на моќност

Решение. Коефициентите на серијата се позитивни, и

Да ја најдеме границата на овој сооднос, т.е. радиус на конвергенција на сериите на моќност:

Дозволете ни да ја проучуваме конвергенцијата на сериите на краевите на интервалот. Замена на вредности x= -1/5 и x= 1/5 во овој ред дава:

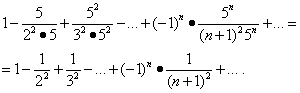
Првата од овие серии се спојува (види Пример 5). Но, тогаш, врз основа на теоремата во делот „Апсолутна конвергенција“, втората серија исто така конвергира, а регионот на нејзината конвергенција е сегментот

Пример 3. Најдете го регионот на конвергенција на серијата на моќност

Решение. Еве

Користејќи ја формулата (28) го наоѓаме радиусот на конвергенција на серијата:

Дозволете ни да ја проучиме конвергенцијата на сериите за вредностите на . Заменувајќи ги во оваа серија, соодветно добиваме

Двете серии се разминуваат затоа што неопходниот услов за конвергенција не е задоволен (нивните заеднички термини не се склони кон нула на ). Значи, на двата краја на интервалот на конвергенција, оваа серија се разминува, а регионот на нејзината конвергенција е интервалот.

Пример 5. Најдете го регионот на конвергенција на серијата на моќност

Решение. Ја наоѓаме релацијата каде , и :

Според формулата (28), радиусот на конвергенција на оваа серија

односно серијата конвергира само кога x= 0 и се разминува за други вредности X.

Примерите покажуваат дека на краевите на интервалот на конвергенција сериите се однесуваат поинаку. Во примерот 1, на едниот крај од интервалот на конвергенција, серијата конвергира, а на другиот, таа се разминува; во примерот 2, таа конвергира на двата краја; во примерот 3, таа се разминува на двата краја.

Формулата за радиусот на конвергенција на сериите на моќност се добива под претпоставка дека сите коефициенти на сериските членови, почнувајќи од одредена точка, се различни од нула. Затоа, употребата на формулата (28) е дозволена само во овие случаи. Ако овој услов е нарушен, тогаш радиусот на конвергенција на сериите на моќност треба да се бара користејќи знакот на д'Алембер, или, со замена на променливата, трансформирање на серијата во форма во која наведениот услов е задоволен.

Пример 6. Најдете го интервалот на конвергенција на серијата на моќност

Решение. Оваа серија не содржи термини со непарни степени X. Затоа, ја трансформираме серијата, поставувајќи . Потоа ја добиваме серијата

да го најдеме радиусот на конвергенција на кој можеме да ја примениме формулата (28). Бидејќи , a , тогаш радиусот на конвергенција на оваа серија

Од еднаквоста што ја добиваме, оваа серија конвергира на интервалот.

Збир на серии на моќност. Диференцијација и интеграција на сериите на моќност

Дозволете за серијата моќ

радиус на конвергенција Р> 0, т.е. оваа серија конвергира во интервалот.

Потоа секоја вредност Xод интервалот на конвергенција одговара на одредена сума од серијата. Според тоа, збирот на сериите на моќност е во функција на Xна интервалот на конвергенција. Означувајќи го со ѓ(x), можеме да ја напишеме еднаквоста

разбирајќи го во смисла дека збирот на сериите во секоја точка Xод интервалот на конвергенција е еднаков на вредноста на функцијата ѓ(x) во оваа точка. Во истата смисла, ќе кажеме дека серијата на моќност (29) конвергира во функцијата ѓ(x) на интервалот на конвергенција.

Надвор од интервалот на конвергенција, еднаквоста (30) нема смисла.

Пример 7.Најдете го збирот на сериите на моќност

Решение. Ова е геометриска серија за која а= 1, а q= x. Според тоа, нејзиниот збир е функција . Серијата конвергира ако , и е нејзиниот интервал на конвергенција. Затоа еднаквост

важи само за вредности, иако функцијата дефинирани за сите вредности X, освен X= 1.

Може да се докаже дека збирот на серијата моќ ѓ(x) е континуирано и диференцијабилно на кој било интервал во интервалот на конвергенција, особено во која било точка од интервалот на конвергенција на серијата.

Дозволете ни да ги претставиме теоремите за диференцијација по термин и интеграција на сериите на моќност.

Теорема 1.Серијата на моќност (30) во интервалот на нејзината конвергенција може да се диференцира член по член неограничен број пати, а добиените серии на моќност имаат ист радиус на конвергенција како и оригиналната серија, а нивните збирови се соодветно еднакви на .

Теорема 2.Моќните серии (30) може да се интегрираат термин по термин неограничен број пати во опсег од 0 до X, ако , и добиената серија на моќност има ист радиус на конвергенција како и оригиналната серија, а нивните збирови се соодветно еднакви

Проширување на функциите во енергетски серии

Нека е дадена функцијата ѓ(x), која треба да се прошири во серија на моќност, т.е. претставуваат во форма (30):

Задачата е да се одредат коефициентите ред (30). За да го направите ова, разликувајќи ја еднаквоста (30) по поим, постојано наоѓаме:

……………………………………………….. (31)

Претпоставувајќи во еднаквости (30) и (31) X= 0, наоѓаме

Заменувајќи ги пронајдените изрази во еднаквост (30), добиваме

(32)

Дозволете ни да го најдеме проширувањето на серијата Maclaurin на некои елементарни функции.

Пример 8.Проширете ја функцијата во серија Maclaurin

Решение. Дериватите на оваа функција се совпаѓаат со самата функција:

Затоа, кога X= 0 имаме

Заменувајќи ги овие вредности во формулата (32), го добиваме саканото проширување:

(33)

Оваа серија конвергира на целата бројна права (нејзиниот радиус на конвергенција).

Проширување на функцијата во серии на Тејлор, Маклаурин и Лоран на локација за обука на практични вештини. Ова сериско проширување на функцијата им овозможува на математичарите да ја проценат приближната вредност на функцијата во одреден момент од нејзиниот домен на дефиниција. Многу е полесно да се пресмета таквата вредност на функцијата во споредба со користењето на табелата Бредис, што е толку ирелевантно во ерата на компјутерската технологија. Да се прошири функцијата во Тејлорова серија значи да се пресметаат коефициентите на линеарните функции од оваа серија и да се запише во правилна форма. Учениците ги мешаат овие две серии, не разбирајќи што е општ случај, а што посебен случај на втората. Да ве потсетиме еднаш засекогаш дека серијата Maclaurin е посебен случај на серијата Тејлор, односно ова е серијата Тејлор, но во точката x = 0. Сите кратки записи за проширување на добро познатите функции, како што се e^x, Sin(x), Cos(x) и други, ова се проширувања на серијата Тејлор, но во точка 0 за аргументот. За функции на сложен аргумент, серијата Лорент е најчестиот проблем во TFCT, бидејќи претставува двострана бесконечна серија. Тоа е збир од две серии. Ви предлагаме да погледнете пример за распаѓање директно на веб-локацијата; тоа е многу лесно да се направи со кликнување на „Пример“ со кој било број, а потоа на копчето „Решение“. Токму ова проширување на функцијата во серија е поврзано со серијата на мајоризирање што ја ограничува оригиналната функција во одреден регион по должината на оската на ординатите ако променливата припаѓа на регионот на апсцисата. Векторската анализа се споредува со друга интересна дисциплина во математиката. Бидејќи секој термин треба да се испита, процесот бара доста време. Секоја серија на Тејлор може да се поврзе со серија на Маклаурин со замена на x0 со нула, но за сериите на Маклаурин понекогаш не е очигледно да се претстави серијата на Тејлор обратно. Како да не се бара тоа да се направи во чиста форма, интересно е за општ саморазвој. Секоја серија на Лорен одговара на двострана бесконечна серија на моќност во цели броеви z-a, со други зборови, серија од истиот Тејлор тип, но малку поинаква во пресметката на коефициентите. Ќе зборуваме за регионот на конвергенција на серијата Лорен малку подоцна, по неколку теоретски пресметки. Како и во минатиот век, чекор-по-чекор проширување на функцијата во серија тешко може да се постигне едноставно со доведување на термините до заеднички именител, бидејќи функциите во именителот се нелинеарни. Потребна е приближна пресметка на функционалната вредност со формулацијата на проблемите. Размислете за фактот дека кога аргументот на Тејлоровата серија е линеарна променлива, тогаш проширувањето се случува во неколку чекори, но сликата е сосема поинаква кога аргументот на функцијата што се проширува е сложена или нелинеарна функција, тогаш процесот на претставувањето на таква функција во серија на моќност е очигледно, бидејќи на овој начин е лесно да се пресмета, иако е приближна вредност, во која било точка во регионот на дефиниција, со минимална грешка што има мало влијание врз понатамошните пресметки. Ова исто така важи и за серијата Maclaurin. кога е потребно да се пресмета функцијата во нултата точка. Сепак, самата серија Лорен овде е претставена со проширување на авионот со имагинарни единици. Исто така, правилното решавање на проблемот во текот на целокупниот процес нема да биде безуспешно. Овој пристап не е познат во математиката, но објективно постои. Како резултат на тоа, можете да дојдете до заклучокот на таканаречените точки подмножества, а при проширувањето на функцијата во серија треба да користите методи познати за овој процес, како што е примената на теоријата на деривати. Уште еднаш сме убедени дека наставникот бил во право, кој ги направил своите претпоставки за резултатите од пост-пресметковните пресметки. Да забележиме дека серијата Тејлор, добиена според сите канони на математиката, постои и е дефинирана на целата нумеричка оска, сепак, драги корисници на услугата на страницата, не заборавајте го типот на оригиналната функција, бидејќи може да испадне дека првично е потребно да се утврди доменот на дефиниција на функцијата, односно да се запишат и да се исклучат од понатамошно разгледување оние точки во кои функцијата не е дефинирана во доменот на реални броеви. Така да се каже, ова ќе ја покаже вашата ефикасност во решавањето на проблемот. Изградбата на серија Maclaurin со нулта вредност на аргументот нема да биде исклучок од она што е кажано. Процесот на пронаоѓање на доменот на дефиниција на функција не е откажан и мора да пристапите на оваа математичка операција со сета сериозност. Во случај на серија на Лоран што го содржи главниот дел, параметарот „а“ ќе се нарече изолирана еднина точка, а серијата Лорент ќе се прошири во прстен - ова е пресекот на областите на конвергенција на неговите делови, оттука ќе следи соодветната теорема. Но, не е сè толку комплицирано како што може да изгледа на прв поглед на неискусен студент. Откако ја проучувавте серијата Тејлор, можете лесно да ја разберете серијата Лоран - генерализиран случај за проширување на просторот на броеви. Секое сериско проширување на функцијата може да се изврши само во точка во доменот на дефинирање на функцијата. Треба да се земат предвид својствата на функциите како што се периодичност или бесконечна диференцијабилност. Исто така, предлагаме да ја користите табелата со готови проширувања на сериите на Тејлор на елементарните функции, бидејќи една функција може да биде претставена со до десетици различни серии на моќност, како што може да се види од користењето на нашиот онлајн калкулатор. Онлајн серијата Maclaurin е лесно да се одреди како пита, доколку ја користите уникатната веб-страница, само треба да ја внесете точната пишана функција и презентираниот одговор ќе го добиете за неколку секунди, гарантирано е дека е точен и во стандардна писмена форма. Можете да го копирате резултатот директно во чиста копија за доставување до наставникот. Би било точно прво да се одреди аналитичноста на функцијата за која станува збор во прстените, а потоа недвосмислено да се каже дека таа може да се прошири во серијата Лорен во сите такви прстени. Важно е да не се изгубат од вид условите на серијата на Лоран кои содржат негативни моќи. Фокусирајте се на ова колку што е можно повеќе. Добро искористете ја теоремата на Лорен за проширување на функција во цели броеви.