Направете сооднос и пресметајте ја границата.
Од каде дојде? табела на деривати и правила за диференцијација? Благодарение на единствената граница. Изгледа како магија, но во реалноста тоа е лукавство и без измама. На лекцијата Што е дериват?Почнав да разгледувам конкретни примери каде што, користејќи ја дефиницијата, најдов изводи на линеарна и квадратна функција. Заради когнитивно загревање, ќе продолжиме да вознемируваме табела на деривати, усовршувајќи го алгоритмот и техничките решенија:
Пример 1
Во суштина, треба да докажете посебен случај на изводот на функцијата моќност, кој обично се појавува во табелата: .
Решениетехнички формализиран на два начина. Да почнеме со првиот, веќе познат пристап: скалата започнува со штица, а деривативната функција започнува со изводот во точка.
Ајде да размислиме некои(конкретна) точка која припаѓа на домен на дефиницијафункција во која има извод. Дозволете ни да го поставиме зголемувањето во оваа точка (се разбира, во рамките на опсеготo/o
-Јас)и составете го соодветниот прираст на функцијата:
Ајде да ја пресметаме границата:
Неизвесноста 0:0 е елиминирана со стандардна техника, сметана уште во првиот век п.н.е. Помножете ги броителот и именителот со конјугираниот израз ![]() :
:
Техниката за решавање на таква граница е детално разгледана во воведната лекција. за границите на функциите.
Бидејќи можете да изберете БИЛО КОЈА точка од интервалот како квалитет, тогаш, откако направивме замена, добиваме:
Одговори
Уште еднаш да се радуваме на логаритмите:
Пример 2
Најдете го изводот на функцијата користејќи ја дефиницијата за извод
Решение: Да разгледаме различен пристап за промовирање на истата задача. Тоа е сосема исто, но порационално во поглед на дизајнот. Идејата е да се ослободите од претплатата на почетокот на решението и да ја користите буквата наместо буквата.
Ајде да размислиме произволнаточка која припаѓа на домен на дефиницијафункција (интервал) и поставете го инкрементот во него. Но, овде, патем, како и во повеќето случаи, можете да направите без никакви резерви, бидејќи логаритамската функција е диференцијабилна во која било точка во доменот на дефиниција.
Тогаш соодветното зголемување на функцијата е:
Ајде да го најдеме дериватот:
Едноставноста на дизајнот е избалансирана со конфузијата што може да се појави кај почетниците (и не само). На крајот на краиштата, ние сме навикнати на фактот дека буквата „Х“ се менува во лимитот! Но, тука сè е поинаку: - античка статуа и - жив посетител, сталожено шета по ходникот на музејот. Тоа е, „x“ е „како константа“.
Ќе коментирам за елиминирање на неизвесноста чекор по чекор:

(1) Го користиме својството на логаритамот.
(2) Во загради, поделете го броителот со именителот член по член.
(3) Во именителот, вештачки множиме и делиме со „x“ за да ја искористиме извонредна граница ![]() , додека како бесконечно малосе издвојува.
, додека како бесконечно малосе издвојува.
Одговори: по дефиниција за извод:
Или накратко:
Предлагам сами да конструирате уште две формули за табели:
Пример 3
Во овој случај, погодно е веднаш да се намали составениот прираст на заеднички именител. Приближен примерок од задачата на крајот од часот (прв метод).
Пример 3:Решение
: разгледајте некоја точка
, кои припаѓаат на доменот на дефинирање на функцијата
. Дозволете ни да го поставиме зголемувањето во оваа точка
и составете го соодветниот прираст на функцијата:
Ајде да го најдеме изводот во точката
:
Бидејќи како а
можете да изберете која било точка
домен на функција
, Тоа
И
Одговори
:
по дефиниција за дериват
Пример 4
Најдете извод по дефиниција
И тука сè треба да се сведе на прекрасна граница. Решението се формализира на вториот начин.
Голем број други табеларни деривати. Целосната листа може да се најде во училишниот учебник или, на пример, во првиот том на Фихтенхолц. Не гледам многу смисла во копирањето докази за правилата за диференцијација од книгите - тие исто така се генерираат со формулата.
Пример 4:Решение
, припаѓа на
, и поставете го инкрементот во него
Ајде да го најдеме дериватот:
Користење на прекрасна граница
Одговори
:
а-приоритет
Пример 5
Најдете го изводот на функцијата користејќи ја дефиницијата за извод
Решение: го користиме првиот стил на дизајн. Ајде да разгледаме некоја точка што припаѓа на , и да го одредиме зголемувањето на аргументот во него. Тогаш соодветното зголемување на функцијата е:
Можеби некои читатели сè уште не го разбрале целосно принципот според кој треба да се направат зголемувања. Земете точка (број) и пронајдете ја вредноста на функцијата во неа: ![]() , односно во функцијата наместо„Х“ треба да се замени. Сега земаме и многу специфичен број и исто така го заменуваме во функцијата наместо„икса“: . Ја запишуваме разликата, и таа е неопходна целосно ставете во загради.
, односно во функцијата наместо„Х“ треба да се замени. Сега земаме и многу специфичен број и исто така го заменуваме во функцијата наместо„икса“: . Ја запишуваме разликата, и таа е неопходна целосно ставете во загради.
Составувано зголемување на функцијата Може да биде корисно веднаш да се поедностави. За што? Олеснете го и скратете го растворот до дополнителна граница.
Ние користиме формули, ги отвораме заградите и намалуваме сè што може да се намали: 
Мисирката е исцрпена, нема проблем со печењето:
Бидејќи можеме да избереме кој било реален број како вредност, правиме замена и добиваме ![]() .
.
Одговори: ![]() а-приоритет.
а-приоритет.
За целите на проверка, ајде да го најдеме дериватот користејќи го правила и табели за диференцијација:
Секогаш е корисно и пријатно однапред да се знае точниот одговор, па затоа е подобро да се разликува предложената функција на „брз“ начин, или ментално или во нацрт, на самиот почеток на решението.
Пример 6
Најдете го изводот на функцијата по дефиниција за извод
Ова е пример за да го решите сами. Резултатот е очигледен:
Пример 6:Решение
: разгледајте некоја точка
, припаѓа на
, и поставете го зголемувањето на аргументот во него
. Тогаш соодветното зголемување на функцијата е:

Да го пресметаме изводот:

Така: ![]()
Бидејќи како
тогаш можете да изберете кој било реален број
И
Одговори
:
а-приоритет.
Да се вратиме на стилот бр. 2:
Пример 7
![]()
Ајде веднаш да дознаеме што треба да се случи. Од страна на правило за диференцијација на сложените функции:
Решение: разгледајте произволна точка што припаѓа на , поставете го зголемувањето на аргументот на неа и составете го зголемувањето на функцијата:
Ајде да го најдеме дериватот: 
(1) Употреба тригонометриска формула ![]() .
.
(2) Под синус ги отвораме заградите, под косинус прикажуваме слични поими.
(3) Под синус ги намалуваме членовите, под косинус го делиме броителот со именителот член по член.
(4) Поради необичноста на синусот го вадиме „минусот“. Под косинус укажуваме дека поимот .
(5) Вршиме вештачко множење во именителот за да користиме првата прекрасна граница. Така, неизвесноста е елиминирана, ајде да го средиме резултатот.
Одговори: а-приоритет
Како што можете да видите, главната тешкотија на проблемот што се разгледува лежи на сложеноста на самата граница + мала уникатност на пакувањето. Во пракса, се случуваат и двата методи на дизајнирање, па затоа ги опишувам двата пристапи колку што е можно подетално. Тие се еквивалентни, но сепак, според мојот субјективен впечаток, препорачливо е куклите да се држат до опцијата 1 со „X-zero“.
Пример 8
Користејќи ја дефиницијата, пронајдете го изводот на функцијата
Пример 8:Решение
: разгледајте произволна точка
, припаѓа на
, дозволете ни да го поставиме инкрементот во него
и состави го инкрементот на функцијата:
Ајде да го најдеме дериватот:

Ја користиме тригонометриската формула
и првата извонредна граница:

Одговори
:
а-приоритет
Ајде да погледнеме поретка верзија на проблемот:
Пример 9
Најдете го изводот на функцијата во точката користејќи ја дефиницијата за извод.
Прво, што треба да биде крајната линија? Број
Ајде да го пресметаме одговорот на стандарден начин: 
Решение: од гледна точка на јасност, оваа задача е многу поедноставна, бидејќи формулата наместо тоа разгледува одредена вредност.
Да го поставиме инкрементот во точката и да го составиме соодветниот прираст на функцијата:
Да го пресметаме изводот во точката:
Ние користиме формула за многу ретка тангентна разлика ![]() и уште еднаш го намалуваме растворот на првата прекрасна граница:
и уште еднаш го намалуваме растворот на првата прекрасна граница:
Одговори: по дефиниција за извод во точка.
Проблемот не е толку тешко да се реши „општо“ - доволно е да се замени со или едноставно во зависност од методот на дизајнирање. Во овој случај, јасно е дека резултатот нема да биде број, туку изведена функција.
Пример 10
Користејќи ја дефиницијата, пронајдете го изводот на функцијата ![]() во точка (од кои едната може да испадне бесконечна), која веќе ја опишав во општи термини теоретски час за дериват.
во точка (од кои едната може да испадне бесконечна), која веќе ја опишав во општи термини теоретски час за дериват.
Некои поделено дадени функции се исто така диференцијабилни на „спојните“ точки на графикот, на пример, catdog има заеднички извод и заедничка тангента (x-оска) во точката. Крива, но се разликува по ! Заинтересираните можат сами да го потврдат ова користејќи го штотуку решениот пример.
©2015-2019 сајт
Сите права припаѓаат на нивните автори. Оваа страница не бара авторство, но обезбедува бесплатна употреба.
Датум на создавање на страница: 2017-06-11
Содржината на статијата
ДЕРИВАТИВ– извод на функцијата y = ѓ(x), дадена на одреден интервал ( а, б) во точка xна овој интервал се нарекува граница до која се стреми односот на зголемувањето на функцијата ѓво овој момент до соодветното зголемување на аргументот кога зголемувањето на аргументот се стреми кон нула.
Дериватот обично се означува на следниов начин:
Други ознаки се исто така широко користени:
Инстант брзина.
Нека поентата Мсе движи во права линија. Растојание сподвижна точка, броена од некоја почетна позиција М 0 , зависи од времето т, т.е. спостои функција на време т: с= ѓ(т). Нека во одреден момент во времето тподвижна точка Мбеше на далечина сод почетната позиција М 0, а во некој следен момент т+D тсе нашла во позиција М 1 - на растојание с+D сод почетната позиција ( види слика.).
Така, во одреден временски период Д трастојание сизменета за износот Д с. Во овој случај велат дека за време на временскиот интервал Д тмагнитуда сдобил прираст Д с.
Просечната брзина во сите случаи не може точно да ја карактеризира брзината на движење на точка Мво одреден момент од времето т. Ако, на пример, телото на почетокот на интервалот Д тсе движи многу брзо, а на крајот многу бавно, тогаш просечната брзина нема да може да ги одрази наведените карактеристики на движењето на точката и да даде идеја за вистинската брзина на нејзиното движење во моментот т. За попрецизно да ја изразите вистинската брзина користејќи ја просечната брзина, треба да одвоите пократок временски период D т. Најцелосно ја карактеризира брзината на движење на точка во моментот тграницата до која се стреми просечната брзина на Д т® 0. Оваа граница се нарекува моментална брзина:
Така, брзината на движење во даден момент се нарекува граница на односот на зголемување на патеката D сдо зголемување на времето Д т, кога временското зголемување се стреми кон нула. Бидејќи
Геометриско значење на дериватот. Тангента на графикот на функцијата.
Изградбата на тангентни линии е еден од оние проблеми што доведоа до раѓање на диференцијални пресметки. Првата објавена работа поврзана со диференцијално пресметување, напишана од Лајбниц, беше насловена Нов метод на максимум и минимум, како и тангенти, за кои не се пречка ниту фракционите ниту ирационалните величини и посебен вид пресметка за ова.
Нека кривата е графикот на функцијата y =ѓ(x) во правоаголен координатен систем ( цм. ориз.).
По некоја вредност xфункцијата е важна y =ѓ(x). Овие вредности xИ yточката на кривата одговара М 0(x, y). Доколку аргументот xдаде зголемување Д x, потоа новата вредност на аргументот x+D xодговара на новата вредност на функцијата y+Д y = ѓ(x + Д x). Соодветната точка на кривата ќе биде точката М 1(x+D x,y+D y). Ако нацртате секант М 0М 1 и означено со ј аголот формиран од трансверзала со позитивна насока на оската Вол, од сликата веднаш станува јасно дека .
Ако сега Д xсе стреми кон нула, а потоа точката М 1 се движи по кривата, приближувајќи се до точката М 0 и агол ј се менува со Д x. На Dx® 0 аголот j се стреми кон одредена граница a и правата линија што минува низ точката М 0 и компонентата со позитивна насока на x-оската, аголот a, ќе биде саканата тангента. Нејзиниот наклон е:
Оттука, ѓ´( x) = тга
тие. деривативна вредност ѓ´( x) за дадена вредност на аргументот xе еднаква на тангентата на аголот формиран од тангентата на графикот на функцијата ѓ(x) во соодветната точка М 0(x,y) со насока на позитивна оска Вол.
Различност на функциите.
Дефиниција. Доколку функцијата y = ѓ(x) има извод во точката x = x 0, тогаш функцијата е диференцијабилна во овој момент.
Континуитет на функција која има извод. Теорема.
Доколку функцијата y = ѓ(x) е диференцијабилна во одреден момент x = x 0, тогаш тоа е континуирано во оваа точка.
Така, функцијата не може да има извод во точките на дисконтинуитет. Неточен е спротивниот заклучок, т.е. од фактот дека во одреден момент x = x 0 функција y = ѓ(x) е континуирано не значи дека е диференцијабилно во овој момент. На пример, функцијата y = |x| континуирано за секого x(–Ґ x x = 0 нема извод. Во овој момент нема тангента на графикот. Има десна и лева тангента, но тие не се совпаѓаат.
Некои теореми за диференцијабилни функции. Теорема за корените на дериватот (теорема на Роле).Доколку функцијата ѓ(x) е континуирано на сегментот [а,б], може да се разликува во сите внатрешни точки на овој сегмент и на краевите x = аИ x = боди на нула ( ѓ(а) = ѓ(б) = 0), потоа внатре во сегментот [ а,б] има барем една точка x= Со, а c b, во која изводот ѓў( x) оди на нула, т.е. ѓў( в) = 0.
Теорема за конечен пораст (теорема на Лагранж).Доколку функцијата ѓ(x) е континуирано на интервалот [ а, б] и може да се диференцира во сите внатрешни точки на овој сегмент, потоа внатре во сегментот [ а, б] има барем една точка Со, ав б тоа
ѓ(б) – ѓ(а) = ѓў( в)(б– а).
Теорема за односот на зголемувањата на две функции (теорема на Коши).Ако ѓ(x) И е(x) – две функции континуирани на сегментот [а, б] и може да се разликува во сите внатрешни точки на овој сегмент, и еў( x) не исчезнува никаде во овој сегмент, потоа внатре во сегментот [ а, б] постои таква точка x = Со, ав б тоа
Деривати од различни нарачки.
Нека функцијата y =ѓ(x) е диференцијабилна на одреден интервал [ а, б]. Изводни вредности ѓ ў( x), општо земено, зависат од x, т.е. дериват ѓ ў( x) е исто така функција на x. При диференцирање на оваа функција го добиваме таканаречениот втор извод на функцијата ѓ(x), што се означува ѓ ўў ( x).
Дериват n-ри редослед на функција ѓ(x) се нарекува извод од (прв ред) на изводот n- 1- ти и се означува со симболот y(n) = (y(n– 1))ў.
Диференцијали од различни нарачки.
Функциски диференцијал y = ѓ(x), Каде x– независна променлива, да ди = ѓ ў( x)dx, некоја функција од x, но од xможе да зависи само првиот фактор ѓ ў( x), вториот фактор ( dx) е зголемување на независната променлива xи не зависи од вредноста на оваа променлива. Бидејќи диима функција од x, тогаш можеме да го одредиме диференцијалот на оваа функција. Диференцијалот на диференцијалот на функцијата се нарекува втор диференцијал или диференцијал од втор ред на оваа функција и се означува г 2y:
г(dx) = г 2y = ѓ ўў( x)(dx) 2 .
Диференцијал n-од прв ред се нарекува прв диференцијал на диференцијалот n- 1- редослед:
d n y = г(d n–1y) = ѓ(n)(x)dx(n).
Делумен дериват.
Ако функцијата не зависи од еден, туку од неколку аргументи x i(јасварира од 1 до n,јас= 1, 2,… n),ѓ(x 1,x 2,… x n), потоа во диференцијалното сметање се воведува концептот на парцијален извод, кој ја карактеризира брзината на промена на функцијата од неколку променливи кога се менува само еден аргумент, на пр. x i. Делумен дериват од 1-ви ред во однос на x iсе дефинира како обичен извод и се претпоставува дека сите аргументи освен x i, одржувајте константни вредности. За парцијални деривати, ознаката е воведена
Вака дефинираните парцијални изводи од прв ред (како функции на истите аргументи) може, пак, да имаат и парцијални изводи, тоа се парцијални деривати од втор ред итн. Ваквите деривати земени од различни аргументи се нарекуваат мешани. Континуираните мешани деривати од ист ред не зависат од редот на диференцијација и се еднакви еден на друг.
Ана Чугаинова
Нека функцијата y = f(x) е дефинирана во интервалот X. Дериватфункцијата y = f(x) во точката x o се нарекува граница
=
![]() .
.
Доколку оваа граница конечни,тогаш се повикува функцијата f(x). диференцијабилнаво точката x о; Покрај тоа, во овој момент се покажува дека е нужно континуирано.
Ако границата што се разгледува е еднаква на (или - ), тогаш под услов функцијата во точката X ое континуирано, ќе кажеме дека функцијата f(x) ја има во точката X о бесконечен дериват.
Дериватот се означува со симболите
y , f (x o), , .
Наоѓањето на изводот се вика диференцијацијафункции. Геометриско значење на дериватоте дека изводот е наклонот на тангентата на кривата y=f(x) во дадена точка X о ; физичко значење -е дека изводот на патеката во однос на времето е моменталната брзина на подвижна точка за време на праволиниско движење s = s(t) во моментот t o .
Ако Сое константен број, а u = u(x), v = v(x) се некои диференцијабилни функции, тогаш важат следните правила за диференцијација:
1) (в) " = 0, (cu) " = куб";
2) (u+v)" = u"+v";
3) (uv)" = u"v+v"u;
4) (u/v)" = (u"v-v"u)/v 2;
5) ако y = f(u), u = (x), т.е. y = f((x)) - комплексна функцијаили суперпозиција, составена од диференцијабилни функции и f, тогаш , или
6) ако за функција y = f(x) постои инверзна диференцијабилна функција x = g(y), и 0, тогаш .
Врз основа на дефиницијата на изводот и правилата за диференцијација, можно е да се состави список на табеларни деривати на главните елементарни функции.
1. (u )" = u 1 u" ( Р).
2. (a u)" = a u lna u".
3. (е у)" = е у у".
4. (log a u)" = u"/(u ln a).
5. (ln u)" = u"/u.
6. (sin u)" = cos u u".
7. (cos u)" = - sin u u".
8. (tg u)" = 1/ cos 2 u u".
9. (ctg u)" = - u" / грев 2 u.
10. (arcsin u)" = u" / .
11. (arccos u)" = - u" / .
12. (arctg u)" = u"/(1 + u 2).
13. (arcctg u)" = - u"/(1 + u 2).
Да го пресметаме изводот на моќно-експоненцијалниот израз y=u v , (u>0), каде uИ vсуштината на функцијата од X, имајќи деривати во дадена точка ти",v".
Земајќи ги логаритмите на еднаквоста y=u v, добиваме ln y = v ln u.
Изедначување на деривати во однос на Xод двете страни на добиената еднаквост користејќи ги правилата 3, 5 и формулата за извод на логаритамска функција, ќе имаме:
y"/y = vu"/u +v" ln u, од каде y" = y (vu"/u +v" ln u).
(u v)"=u v (vu"/u+v" ln u), u > 0.
На пример, ако y = x sin x, тогаш y" = x sin x (sin x/x + cos x ln x).
Ако функцијата y = f(x) е диференцијабилна во точката x, т.е. има конечен извод во оваа точка y", тогаш = y"+, каде што 0 на х 0; оттука y = y" х + x.
Се нарекува главниот дел од функционалниот инкремент, линеарен во однос на x диференцијал функциии се означува со dy: dy = y" х. Ако во оваа формула ставиме y=x, добиваме dx = x"х = 1х =х, затоа dy=y"dx, т.е. симболот за Изводната нотација може да се смета како дропка.
Зголемување на функцијата yе зголемувањето на ординатата на кривата, а диференцијалот d yе ординатен пораст на тангентата.
Да го најдеме за функцијата y=f(x) нејзиниот извод y = f (x). Дериватот на овој извод се нарекува извод од втор редфункции f(x), или втор дериват,и е назначен ![]() .
.
Следниве се дефинирани и назначени на ист начин:
извод од трет ред
-
![]() ,
,
дериват од четврти ред -
![]()
и општо земено извод од n-ти ред
-
![]() .
.
Пример 3.15. Пресметај го изводот на функцијата y=(3x 3 -2x+1)sin x.
Решение.Според правилото 3, y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1)cos x.
Пример 3.16 . Најдете y", y = tan x + .
Решение.Користејќи ги правилата за диференцијација на збирот и количникот, добиваме: y"=(tgx + )" = (tgx)" + ()" = + ![]() =
=
![]()
![]() .
.
Пример 3.17. Најдете го изводот на сложената функција y= , u=x 4 +1.
Решение.Според правилото за диференцијација на сложена функција се добива: y" x =y " u u" x =()" u (x 4 +1)" x =(2u +. Бидејќи u=x 4 +1, тогаш (2 x 4 + 2+ ![]() .
.
Дериватот е најважниот концепт во математичката анализа. Ја карактеризира промената на функцијата на аргументот xво одреден момент. Згора на тоа, самиот извод е функција на аргументот x
Извод на функција во една точка е границата (ако постои и е конечна) на односот на зголемувањето на функцијата со зголемувањето на аргументот, под услов вториот да се стреми кон нула.
Најчесто користени се следните дериватна нотација :
Пример 1.Искористува дефиниција на дериват, најдете го изводот на функцијата
Решение. Од дефиницијата на изводот следи следната шема за негова пресметка.
Да му дадеме на аргументот инкремент (делта) и да го најдеме зголемувањето на функцијата:
Ајде да го најдеме односот на зголемувањето на функцијата со зголемувањето на аргументот:

Дозволете ни да ја пресметаме границата на овој сооднос под услов зголемувањето на аргументот да се стреми кон нула, односно изводот потребен во изјавата за проблемот:
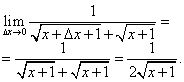
Физичко значење на дериватот
ДО концепт на дериват доведе до проучување на Галилео Галилеј за законот за слободен пад на телата и во поширока смисла - проблемот на моменталната брзина на нерамномерно праволиниско движење на точка.
Оставете го камчето да се подигне и потоа да се ослободи од одмор. Пат спомина во времето т, е функција на времето, т.е. s = s(т). Ако е даден законот за движење на точка, тогаш може да се одреди просечната брзина за кој било временски период. Нека во моментот камчето е во положбата А, а во моментот - во позиција Б. Во текот на одреден временски период (од тдо ) точка ја помина патеката . Според тоа, просечната брзина на движење во овој временски период, која ја означуваме со , е
![]() .
.
Сепак, движењето на телото што слободно паѓа е очигледно нерамномерно. Брзина vпадот постојано се зголемува. И просечната брзина повеќе не е доволна за да се карактеризира брзината на движење на различни делови од патеката. Колку е пократок временскиот период, толку е попрецизна оваа карактеристика. Затоа, се воведува следниов концепт: моментална брзина на праволиниско движење (или брзина во даден момент во времето т) се нарекува просечно ограничување на брзината на:
![]()
(под услов оваа граница да постои и да е конечна).
Значи, излегува дека моменталната брзина е граница на односот на зголемувањето на функцијата с(т) до зголемување на аргументот тна Ова е изводот, кој во општа форма се пишува на следниов начин:.
![]() .
.
Решението на посочениот проблем е физичко значење на дериватот . Значи, изводот на функцијата y=f(x) во точка xсе нарекува граница (ако постои и е конечна) на зголемувањето на функцијата до зголемувањето на аргументот, под услов вториот да се стреми кон нула.
Пример 2.Најдете го изводот на функцијата
![]()
Решение. Од дефиницијата на изводот следува следната шема за негова пресметка.
Чекор 1. Ајде да го зголемиме аргументот и да најдеме

Чекор 2. Најдете го зголемувањето на функцијата:

Чекор 3. Најдете го односот на зголемувањето на функцијата со зголемувањето на аргументот:

Чекор 4. Пресметајте ја границата на овој однос на , односно изводот:
Геометриско значење на дериватот
Нека функцијата е дефинирана на интервал и нека точката Мна графикот на функцијата одговара на вредноста на аргументот и точката Р– значење. Ајде да извлечеме низ точките МИ Рправа линија и јавете се секант. Да означиме со аголот помеѓу секантата и оската. Очигледно, овој агол зависи од.
Доколку постои
![]()
минување низ точката се нарекува гранична положба на секантата Г-динво (или во ).
Тангента на графикот на функција во точка Мнаречена гранична положба на секантата Г-динво , или, што е исто во .
Од дефиницијата произлегува дека за постоење на тангента доволно е да постои граница
![]() ,
,
а границата е еднаква на аголот на наклонетост на тангентата на оската.
Сега да дадеме прецизна дефиниција за тангента.
Тангентана графикот на функција во точка е права линија што минува низ точката и има наклон, т.е. права линија чија равенка
Од оваа дефиниција произлегува дека извод на функција е еднаков на наклонот на тангентата на графикот на оваа функција во точката со апсцисата x. Ова е геометриското значење на дериватот.
