Дефиниција. Доколку функцијата ѓ(x) се дефинира на интервалот [ а, б], е континуиран во секоја точка од интервалот ( а, б), во точка аконтинуирано десно, во точката бе континуирано лево, тогаш велиме дека функцијата ѓ(x) континуирано на сегментот [а, б].
Со други зборови, функцијата ѓ(x) е континуирано на интервалот [ а, б], доколку се исполнети три услови:
1) "x 0 Î( а, б): ѓ(x) = ѓ(x 0);
2) ѓ(x) = ѓ(а);
3) ѓ(x) = ѓ(б).
За функциите кои се континуирани на интервал, разгледуваме некои својства, кои ги формулираме во форма на следните теореми, без да изведуваме докази.
Теорема 1. Доколку функцијата ѓ(x) е континуирано на интервалот [ а, б], тогаш ги достигнува своите минимални и максимални вредности на овој сегмент.
Оваа теорема наведува (сл. 1.15) дека на сегментот [ а, б] постои таква точка x 1 тоа ѓ(x 1) £ ѓ(x) за се xод [ а, б] и дека има поента x 2 (x 2 О[ а, б]) така што " xÎ[ а, б] (ѓ(x 2)³ ѓ(x)).
Значење ѓ(x 1) е најголема за дадена функција на [ а, б], А ѓ(x 2) – најмал. Да означиме: ѓ(x 1) = М, ѓ(x 2) =м. Од ѓ(x) важи нееднаквоста: xÎ[ а, б] м£ ѓ(x) £ М, тогаш ја добиваме следната последица од теорема 1.
Последица. Доколку функцијата ѓ(x) е континуирано на интервал, тогаш е ограничен на овој интервал.
Теорема 2. Доколку функцијата ѓ(x) е континуирано на интервалот [ а, б] и на краевите на сегментот зема вредности на различни знаци, тогаш постои таква внатрешна точка x 0 сегмент [ а, б], во која функцијата се претвора во 0, т.е. $ x 0 Î ( а, б) (ѓ(x 0) = 0).
Оваа теорема вели дека графикот на функцијата y = f(x), континуирано на интервалот [ а, б], ја пресекува оската Волбарем еднаш ако вредностите ѓ(а) И ѓ(б) имаат спротивни знаци. Значи, (сл. 1.16) ѓ(а) > 0, ѓ(б) < 0 и функция ѓ(x) станува 0 во точките x 1 , x 2 , x 3 .
Теорема 3. Нека функцијата ѓ(x) е континуирано на интервалот [ а, б], ѓ(а) = А, ѓ(б) = БИ А¹ Б. (Сл. 1.17). Потоа за кој било број В, затворен помеѓу броевите АИ Б, постои таква внатрешна точка x 0 сегмент [ а, б], Што ѓ(x 0) = В.
Последица. Доколку функцијата ѓ(x) е континуирано на интервалот [ а, б], м – најмала вредност ѓ(x), М – највисока вредностфункции ѓ(x) на сегментот [ а, б], тогаш функцијата зема (барем еднаш) која било вредност м, склучен помеѓу мИ М, а со тоа и сегментот [ м, М] е множество од сите вредности на функции ѓ(x) на сегментот [ а, б].
Забележете дека ако функцијата е континуирана на интервалот ( а, б) или има на сегментот [ а, б] точки на дисконтинуитет, тогаш теоремите 1, 2, 3 за таква функција престануваат да бидат вистинити.
Како заклучок, разгледајте ја теоремата за постоење на инверзна функција.
Да потсетиме дека под интервал подразбираме отсечка или интервал, или полуинтервал, конечен или бесконечен.
 |
Теорема 4. Нека ѓ(x) е континуирано на интервалот X, се зголемува (или се намалува) за Xи има низа вредности Y. Потоа за функцијата y = f(x) постои инверзна функција x= ј(y), дефиниран на интервалот Y, континуирано и зголемување (или намалување) за Yсо повеќе значења X.
Коментар. Нека функцијата x= ј(y) е инверзна на функцијата ѓ(x). Бидејќи аргументот обично се означува со x, и функцијата преку y, потоа ќе пишуваме инверзна функцијакако y =ј(x).
Пример 1. Функција y = x 2 (сл. 1.8, а) на сетот X= а, б[ и е континуиран во секоја точка од овој интервал. Тогаш се нарекува континуирано во интервалот ] а, б[. Концептот на континуитет на функција на интервали од формата ]- ∞ е дефиниран слично, б[ , ]а, + ∞[ , ]- ∞, + ∞[ . Нека сега функцијата y = ѓ(x) дефинирано на интервалот [ а, б] . Разлика помеѓу интервал и отсечка: граничните точки на интервалот не се вклучени во интервалот, но граничните точки на отсечката се вклучени во сегментот. Тука треба да го спомнеме таканаречениот едностран континуитет: во точката а, останувајќи на сегментот [ а, б] , можеме да пристапиме само од десно, и до точка б- само лево. Се вели дека функцијата е континуирана на интервалот [ а, б] ако е континуирано во сите внатрешни точкиод овој сегмент, е непрекинат десно во точката аи се остава континуирано во точката б.
Пример за континуирана функција може да биде која било од елементарните функции. Секој елементарна функцијае континуирано на кој било интервал на кој е дефиниран. На пример, функциите и се континуирани на кој било интервал [ а, б], функцијата е континуирана на интервалот [ 0 , б] , функцијата е континуирана на кој било сегмент што не содржи точка а = 2 .
Пример 4.Испитајте ја функцијата за континуитет.
Решение. Ајде да го провериме првиот услов. Функцијата не е дефинирана во точките - 3 и 3. Не е исполнет барем еден од условите за континуитет на функцијата по целата бројна права. Затоа оваа функцијае континуирано во интервали
.Пример 5.Определи на која вредност на параметарот аконтинуирано во текот на домен на дефиницијафункција 
Решение.
Ајде да ја најдеме границата од десната страна на:
![]() .
.
Очигледно, вредноста во точката x= 2 треба да биде еднаква секира :
![]()
а = 1,5 .
Пример 6.Определете на кои вредности на параметрите аИ бконтинуирано во текот на домен на дефиницијафункција 
Решение.
Ајде да ја најдеме левата граница на функцијата во точката:
![]() .
.
Затоа, вредноста во точката мора да биде 1:
Ајде да ја најдеме функцијата од левата страна во точката:
Очигледно, вредноста на функцијата во точка треба да биде еднаква на:
Одговор: функцијата е континуирана низ целиот домен на дефиниција кога а = 1; б = -3 .
Основни својства на континуираните функции
Математиката дојде до концептот на континуирана функција со проучување, пред сè, различни закони на движење. Просторот и времето се бесконечни, а зависноста, на пример, патеки сод времето т, изразена со закон с = ѓ(т) , дава пример за континуирано функции ѓ(т) . Температурата на загреаната вода исто така постојано се менува, исто така е континуирана функција на времето: Т = ѓ(т) .
ВО математичка анализанекои својства се докажани континуирани функции. Да ги претставиме најважните од овие својства.
1. Ако функцијата континуирана на интервал зема вредности на различни знаци на краевите на интервалот, тогаш во одреден момент од овој интервал ја зема вредноста еднаква на нула. Во поформална изјава, ова својство е дадено во теорема позната како прва Болзано-Коши теорема.
2. Функција ѓ(x), континуирано на интервалот [ а, б] , ги зема сите средни вредности помеѓу вредностите на крајните точки, односно помеѓу ѓ(а) И ѓ(б) . Во поформална изјава, ова својство е дадено во теорема позната како втората теорема Болзано-Коши.
Континуитет на функција на интервал
| Име на параметарот | Значење |
| Тема на статијата: | Континуитет на функција на интервал |
| Рубрика (тематска категорија) | Математика |
Дефиниција.Функцијата обично се нарекува континуирана на интервал ако е континуирана во секоја точка од овој интервал.
Ако функцијата е дефинирана на X=Аи каде ѓ(X) = ѓ(А),
тогаш тие велат дека ѓ(X) во точка и е континуирано десно. Исто така, ако ѓ(X) = ѓ(б), тогаш тие го велат тоа во точката боваа функција остави континуирано.
Дефиниција.Функцијата обично се нарекува континуирана на интервалот [ а, б], ако е континуирано во секоја точка (во точката Аконтинуирано десно, во точката б– континуирано лево).
Највисока вредностфункции на = ѓ(x) на сегментот [ а, б ѓ(x 1) тоа ѓ(x) £ ѓ(x 1) за секого X Î [ а, б].
Најниска вредностфункции на = ѓ(x) на сегментот [ а, б] вообичаено е ова да се нарече неговото значење ѓ(x 2) тоа ѓ(x) ³ ѓ(x 2) за секого X Î [ а, б].
Функциите кои се континуирани на интервал имаат голем број на важни својства, кои се изразени со следните теореми.
Теорема 3.3.1.Функција континуирана на интервалот [ а, б], ја достигнува својата минимална вредност на неа ми најголема вредност М, односно има такви точки x 1 и x 2 од овој сегмент, тоа ѓ(x 1) = м, ѓ(x 2) = М.
Теоремата има едноставно геометриско значење (види Сл. 2).
 |
Теорема 3.3.2.Во случај функцијата на = ѓ(x) е континуирано на интервалот [ а, б] и на своите краеви зема нееднакви вредности ѓ(А) = А, ѓ(б) = B, A ¹ B, тогаш каков и да е бројот C помеѓу A и B, ќе има точка Со Î [ а, б] така што ѓ(Со) = С.
Геометриско значењеТеоремата е илустрирана на Сл. 3. Секоја права линија на= C, каде што А< C < B (или A >C > B), го пресекува графикот на функцијата на = ѓ(x).
Последица.Ако функцијата е континуирана на сегмент и зема вредности на различни знаци на нејзините краеви, тогаш на овој сегмент има барем една точка во која функцијата исчезнува.
Геометриското значење на последицата е илустрирано на Сл. 4.

Прашања за самоконтрола
1. Која функција обично се нарекува континуирана во точка?
2. Наведете друга еквивалентна дефиниција во однос на зголемување на функцијата и аргументите.
3. Што може да се каже за збир, разлика, производ и количник на две непрекинати функции?
4. За кои вредности на аргументот е целата рационална и фракционо-рационални функцииконтинуирано?
5. Кога сложената функција е континуирана во точка?
6. Што вообичаено се нарекува точка на прекин на функциите?
7. Кои точки се нарекуваат точки на дисконтинуитет од прв вид?
8. Која големина обично се нарекува функциски скок?
9. Објаснете го концептот на „отстранлива точка на дисконтинуитет“. Наведи примери.
10. Кои точки се нарекуваат точки на дисконтинуитет од втор вид? Наведи примери.
11. Објасни ги поимите: „континуитет на интервал“, „континуитет десно“, „континуитет лево“, „континуитет на сегмент“.
12. Дефинирајте ги најголемите и најмалите вредности на функциите.
13. Формулирајте теорема за врската помеѓу континуитетот на сегмент и најголемите и најмалите вредности на функцијата. Објасни го со цртеж.
14. Формулирајте теорема за врската помеѓу континуитетот на функциите на интервал и интервалот на вредностите на функциите. Илустрирај го неговото геометриско значење на сликата.
15. Наведи ја последицата на горната теорема и нејзиното геометриско толкување.
ПРЕДАВАЊЕ бр.4
Тема на предавањето: Извод на функција
Преглед на предавање:Концептот на дериват, неговиот геометриски и физичко значење. Основни правила на диференцијација. Дериват комплексна функција. Некои апликации се изведени.
4.1. Концептот на дериват, неговото геометриско и физичко значење
Размислете за функцијата на = ѓ(x), наведен во интервалот ] а, б[. Нека XÎ ] а, б[И X Î ] а, б[, потоа зголемувањето на функцијата во точката X 0 се изразува со формулата D на = ѓ(x 0+D X) – ѓ(x 0).
Дефиниција. Изводна функција y = ѓ(x) во точка X 0 обично се нарекува граница на односот на зголемувањето на оваа функција до зголемувањето на аргументот кога вториот се стреми кон нула:
ѓ(x 0) = ![]() или y"(x 0) =.
или y"(x 0) =.
Геометриско значење на дериватот: изводот на дадена функција во точка е еднаков на тангентата на аголот помеѓу оската Ox и тангентата на графикот на оваа функција на соодветна точка(види слика 1):
ѓ"(x 0) = тен а.
СВОЈСТВАТА НА ФУНКЦИИТЕ КОНТИНУИРАНИ НА ИНТЕРВЈУ
Да разгледаме некои својства на функциите континуирани на интервал. Овие својства ги прикажуваме без доказ.
Функција y = f(x)повикани континуирано на сегментот [а, б], ако е континуиран во сите внатрешни точки на овој сегмент, и на неговите краеви, т.е. на точките аИ б, е континуирано десно и лево, соодветно.
Теорема 1.Функција континуирана на интервалот [ а, б], барем во една точка од овој сегмент ја зема најголемата вредност и барем во една точка најмалата.
Теоремата вели дека ако функција y = f(x)е континуиран во интервалот [ а, б], тогаш има барем една точка x 1 Î [ а, б] така што вредноста на функцијата f(x)во овој момент ќе биде најголемата од сите нејзини вредности на овој сегмент: f(x 1) ≥ f(x). Слично на тоа, постои таков момент x 2, во која вредноста на функцијата ќе биде најмала од сите вредности на сегментот: f(x 1) ≤ f(x).
Јасно е дека може да има неколку такви точки; на пример, сликата покажува дека функцијата f(x)ја зема најмалата вредност на две точки x 2И x 2 ".
Коментар. Изјавата на теоремата може да стане неточна ако ја земеме предвид вредноста на функцијата на интервалот ( а, б). Навистина, ако ја земеме предвид функцијата y = xна (0, 2), тогаш тој е континуиран на овој интервал, но не ги достигнува ниту најголемите ниту најмалите вредности во него: ги достигнува овие вредности на краевите на интервалот, но краевите не припаѓаат на нашиот домен.
Исто така, теоремата престанува да важи за дисконтинуирани функции. Наведи пример.
Последица.Доколку функцијата f(x)е континуирано на [ а, б], тогаш тоа е ограничено на овој сегмент.
Теорема 2.Нека функцијата y = f(x)е континуиран во интервалот [ а, б] и на краевите на овој сегмент зема вредности на различни знаци, тогаш има барем една точка внатре во сегментот x = C, во која функцијата оди на нула: f(C)= 0, каде што a< C< b

Оваа теорема има едноставно геометриско значење: ако точките на графикот на континуирана функција y = f(x), што одговара на краевите на сегментот [ а, б] лежи заедно различни страниод оската Вол, тогаш овој график ја пресекува оската барем на една точка од отсечката Вол. Дисконтинуираните функции може да го немаат ова својство.
Оваа теорема ја признава следнава генерализација.
Теорема 3 (теорема за средна вредност).Нека функцијата y = f(x)е континуиран во интервалот [ а, б] И f(a) = A, f(b) = B. Потоа за кој било број В, склучен помеѓу АИ Б, постои таква точка во овој сегмент ВÎ [ а, б], Што f(c) = C.

Оваа теорема е геометриски очигледна. Размислете за графикот на функцијата y = f(x). Нека f(a) = A, f(b) = B. Потоа секоја права линија y = C, Каде В– кој било број помеѓу АИ Б, ќе го пресече графикот на функцијата барем во една точка. Апсцисата на пресечната точка ќе биде таа вредност x = C, на која f(c) = C.
Така, континуирана функција, која се движи од една вредност во друга, нужно поминува низ сите средни вредности. Особено:
Последица.Доколку функцијата y = f(x)е континуирано во одреден интервал и ги зема најголемите и најмалите вредности, а потоа на овој интервал ја зема барем еднаш секоја вредност содржана помеѓу неговите најмали и најголеми вредности.
ДЕРИВАТИВ И НЕГОВИ ПРИМЕНИ. ДЕФИНИЦИЈА НА ДЕРИВАТИВ
Да имаме некоја функција y=f(x),дефинирани на одреден интервал. За секоја вредност на аргументот xод овој интервал функцијата y=f(x)има одредено значење.
Размислете за две вредности на аргументот: почетна x 0 и ново x.

Разлика x–x 0 се нарекува со зголемување на аргументот xво точката x 0 и се означува Δx. Така, Δx = x – x 0 (зголемувањето на аргументот може да биде позитивно или негативно). Од оваа еднаквост произлегува дека x=x 0 +Δx, т.е. оригинално значењепроменливата доби одредено зголемување. Потоа, ако во точката x 0 вредноста на функцијата беше f(x 0 ), потоа во нова точка xфункцијата ќе ја земе вредноста f(x) = f(x 0 +Δx).
Разлика y–y 0 = f(x) – f(x 0 ) повикани зголемување на функцијата y = f(x)во точката x 0 и се означува со симболот Δy. Така,
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) . | (1) |
Типично почетната вредност на аргументот x 0 се смета за фиксна, а новата вредност x– променлива. Потоа y 0 = f(x 0 ) излегува дека е константна, и y = f(x)– променлива. Инкременти ΔyИ Δxќе бидат и променливи и формулата (1) покажува дека Даје функција на променлива Δx.
Да го креираме односот на зголемувањето на функцијата со зголемувањето на аргументот
Дозволете ни да ја најдеме границата на овој сооднос на Δx→0. Ако оваа граница постои, тогаш се нарекува извод на оваа функција f(x)во точката x 0 и означува ѓ "(x 0). Значи,
Дериватоваа функција y = f(x)во точката x 0 се нарекува граница на односот на зголемување на функцијата Δ yдо зголемувањето на аргументот Δ x, кога вториот произволно се стреми кон нула.
Забележете дека за истата функција изводот во различни точки xможе да прими различни вредности, т.е. дериватот може да се смета како функција на аргументот x. Оваа функција е назначена ѓ "(x)
Дериватот се означува со симболите ѓ "(x), y ", . Специфично значењедериват кај x = aозначено со ѓ "(а) или y "| x=a.
Операција на пронаоѓање на извод на функција f(x)се нарекува диференцијација на оваа функција.
За директно да го пронајдете дериватот по дефиниција, можете да го користите следново: правило на палецот:
Примери.
МЕХАНИЧКО ЧУВСТВО ЗА ДЕРИВАТИВ
Од физиката се знае дека законот еднообразно движењеизгледа како s = v t, Каде с– патеката патувала до моментот на времето т, v– брзина на еднообразно движење.
Меѓутоа, бидејќи Повеќето движења што се случуваат во природата се нерамномерни, потоа генерално брзината и, следствено, растојанието сќе зависи од времето т, т.е. ќе биде функција на времето.
Значи, нека материјална точка се движи праволиниски во една насока според законот s=s(t).
Ајде да одбележиме одредена точка во времето т 0 . Во овој момент точката го помина патот s=s(t 0 ). Ајде да ја одредиме брзината vматеријална точка во еден момент во времето т 0 .
За да го направите ова, да разгледаме некоја друга точка во времето т 0 + Δ т. Тоа одговара на поминатата патека s =s(t 0 + Δ т). Потоа во одреден временски период Δ тточката ја поминала патеката Δs =s(t 0 + Δ т)–s(t).
Да го разгледаме ставот. Се нарекува просечна брзина во временскиот интервал Δ т. Просечната брзина не може точно да ја карактеризира брзината на движење на точка во моментот т 0 (бидејќи движењето е нерамномерно). За попрецизно изразување на оваа вистинска брзина користејќи просечна брзина, треба да одвоите пократок временски период Δ т.
Значи, брзината на движење во овој моментвреме т 0 (моментална брзина) е граница на просечна брзина во интервалот од т 0 до т 0 +Δ т, кога Δ т→0:
![]() ,
,
тие. нерамна брзинаова е дериват на поминатото растојание во однос на времето.

ГЕОМЕТРИСКО ЗНАЧЕЊЕ НА ДЕРИВАТ
Прво да ја воведеме дефиницијата за тангента на крива во дадена точка.
Дозволете ни да имаме крива и фиксна точка на неа М 0(види слика) Размислете за друга точка Моваа крива и нацртајте секанта М 0 М. Ако точката Мпочнува да се движи по кривата, а точката М 0останува неподвижен, а потоа секантот ја менува својата позиција. Ако, со неограничено приближување на точката Мпо крива до точка М 0на која било страна секантата има тенденција да зазема положба на одредена права линија М 0 Т, потоа директно М 0 Тнаречена тангента на кривата во дадена точка М 0.
Тоа., тангентадо кривата во дадена точка М 0наречена гранична положба на секантата М 0 Мкога точка Мсе стреми по кривата до точка М 0.
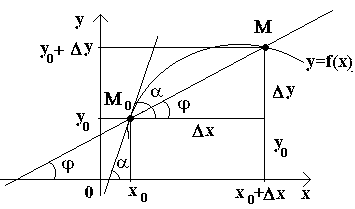
Сега да ја разгледаме континуираната функција y=f(x)и кривата што одговара на оваа функција. По некоја вредност XФункцијата 0 зема вредност y 0 =f(x 0).Овие вредности x 0 и y 0 на кривата одговара на точка M0 (x0; y 0).Ајде да го дадеме аргументот x 0прираст Δ X. Новата вредност на аргументот одговара на зголемената вредност на функцијата y 0 +Δ y=f(x 0 –Δ x). Ја сфаќаме поентата М(х 0+Δ x; y 0+Δ y).Ајде да нацртаме секант М 0 Ма со φ означете го аголот формиран од секанта со позитивната насока на оската Вол. Ајде да создадеме врска и да забележиме дека .
Ако сега Δ x→0, тогаш поради континуитет на функцијата Δ на→0, а со тоа и точката М, движејќи се по крива, се приближува до точката без ограничување М 0. Потоа секантот М 0 Мќе има тенденција да заземе позиција на тангента на кривата во точката М 0, и аголот φ→α на Δ x→0, каде α го означува аголот помеѓу тангентата и позитивната насока на оската Вол. Бидејќи функцијата tan φ континуирано зависи од φ за φ≠π/2, тогаш за φ→α tan φ → tan α и, според тоа, наклонот на тангентата ќе биде:
![]()
тие. f" (x)= tg α .
Така, геометриски y" (x 0)го претставува наклонот на тангентата на графикот на оваа функција во точката x 0, т.е. на дадена вредностаргумент x, изводот е еднаков на тангентата на аголот формиран од тангентата на графикот на функцијата f(x)во соодветната точка M 0 (x; y)со насока на позитивна оска Вол.
Пример.Најдете наклонтангента на кривата y = x 2 во точка М(-1; 1).
Веќе видовме порано дека ( x 2)" = 2X. Но, аголниот коефициент на тангентата на кривата е tan α = y"| x=-1 = – 2.
РАЗЛИЧНОСТ НА ФУНКЦИИТЕ. КОНТИНУИТЕТ НА РАЗЛИЧНА ФУНКЦИЈА
Функција y=f(x)повикани диференцијабилнаво одреден момент x 0 ако има одреден извод во оваа точка, т.е. ако границата на врската постои и е конечна.
Ако функцијата е диференцијабилна во секоја точка од одреден сегмент [ А; б] или интервал ( А; б), тогаш велат дека таа диференцијабилнана сегментот [ А; б] или, соодветно, во интервалот ( А; б).
Валидна е следната теорема, со која се воспоставува врска помеѓу диференцијабилните и континуираните функции.
Теорема.Доколку функцијата y=f(x)може да се разликува во одреден момент x 0, тогаш тоа е континуирано во оваа точка.
Така, од диференцијабилноста на функцијата следи нејзиниот континуитет.
Доказ. Ако ![]() , Тоа
, Тоа
![]() ,
,
каде α е бесконечно мала големина, т.е. количество кое се стреми кон нула како Δ x→0. Но тогаш
Δ y=ѓ "(x 0) Δ x+αΔ x=> Δ y→0 на Δ x→0, т.е. f(x) – f(x 0)→0 во x→x 0 , што значи дека функцијата f(x)континуирано во една точка x 0 . Q.E.D.
Така, функцијата не може да има извод во точките на дисконтинуитет. Обратно не е точно: постојат континуирани функции кои не се диференцијабилни во некои точки (односно, немаат извод во овие точки).
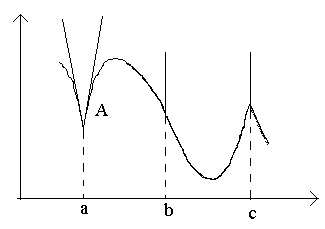
Размислете за точките на сликата а, б, в.
Во точката ана Δ x→0 односот нема ограничување (бидејќи едностраните граници се различни за Δ x→0–0 и Δ x→0+0). Во точката Аграфикон нема дефинирана тангента, но има две различни еднонасочни тангенти со косини До 1 и До 2. Овој тип на точка се нарекува аголна точка.
Во точката бна Δ xРелацијата →0 е со константен знак бесконечно голема големина. Функцијата има бесконечен извод. Во овој момент графикот има вертикална тангента. Тип на точка - „точка на флексија“ на вертикална тангента.
Во точката ведностраните деривати се бескрајно големи количини на различни знаци. Во овој момент графикот има две споени вертикални тангенти. Тип – „повратна точка“ со вертикална тангента – посебен случајаголна точка.