Концепт на пирамида

Дефиниција 1

Геометриска фигура формирана од многуаголник и точка што не лежи во рамнината што го содржи овој многуаголник, поврзана со сите темиња на многуаголникот, се нарекува пирамида (сл. 1).

Многуаголникот од кој е направена пирамидата се нарекува основа на пирамидата; добиените триаголници, кога се поврзани со точка, се страничните лица на пирамидата, страните на триаголниците се страните на пирамидата и точката заедничка до сите триаголници е врвот на пирамидата.

Видови пирамиди

Во зависност од бројот на агли на основата на пирамидата, таа може да се нарече триаголна, четириаголна и така натаму (сл. 2).

Слика 2.

Друг тип на пирамида е обичната пирамида.

Дозволете ни да воведеме и докажеме својство на правилна пирамида.

Теорема 1

Сите странични лица на правилната пирамида се рамнокраки триаголници кои се еднакви еден на друг.

Доказ.

Размислете за редовна $n-$gonal пирамида со теме $S$ на висина $h=SO$. Дозволете ни да нацртаме круг околу основата (слика 4).

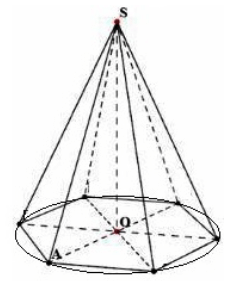
Слика 4.

Размислете за триаголникот $SOA$. Според Питагоровата теорема, добиваме

Очигледно, секој страничен раб ќе биде дефиниран на овој начин. Следствено, сите странични рабови се еднакви еден на друг, односно сите странични лица се рамнокрак триаголници. Да докажеме дека се еднакви едни на други. Бидејќи основата е правилен многуаголник, основите на сите странични лица се еднакви една со друга. Следствено, сите странични лица се еднакви според III критериум за еднаквост на триаголниците.

Теоремата е докажана.

Сега да ја воведеме следнава дефиниција поврзана со концептот на правилна пирамида.

Дефиниција 3

Апотемата на правилната пирамида е висината на нејзината странична страна.

Очигледно, според една теорема, сите апотеми се еднакви една со друга.

Теорема 2

Страничната површина на правилната пирамида се одредува како производ на полупериметарот на основата и апотемата.

Доказ.

Да ја означиме страната на основата на $n-$gonal пирамидата со $a$, а апотемата со $d$. Затоа, површината на страничното лице е еднаква на

Бидејќи, според теорема 1, сите страни се еднакви, тогаш

Теоремата е докажана.

Друг тип на пирамида е скратена пирамида.

Дефиниција 4

Ако рамнината паралелна на нејзината основа се повлече низ обична пирамида, тогаш фигурата формирана помеѓу оваа рамнина и рамнината на основата се нарекува скратена пирамида (сл. 5).

Слика 5. Скратена пирамида

Страничните лица на скратената пирамида се трапезоиди.

Теорема 3

Страничната површина на правилна скратена пирамида се одредува како производ од збирот на полупериметрите на основите и апотемата.

Доказ.

Да ги означиме страните на основите на $n-$gonal пирамидата со $a\ и\ b$, соодветно, а апотемата со $d$. Затоа, површината на страничното лице е еднаква на

Бидејќи сите страни се еднакви, тогаш

Теоремата е докажана.

Примерок задача

Пример 1

Најдете ја плоштината на страничната површина на скратена триаголна пирамида ако е добиена од правилна пирамида со основна страна 4 и апотема 5 со отсекување на рамнина што минува низ средната линија на страничните лица.

Решение.

Користејќи ја теоремата за средната линија, откриваме дека горната основа на скратената пирамида е еднаква на $4\cdot \frac(1)(2)=2$, а апотемата е еднаква на $5\cdot \frac(1)(2) = 2,5 долари.

Потоа, по теорема 3, добиваме

Пирамида. Скратена пирамида

Пирамидае полиедар, чие едно лице е многуаголник ( база ), а сите други лица се триаголници со заедничко теме ( странични лица ) (сл. 15). Пирамидата се нарекува точно , ако неговата основа е правилен многуаголник и врвот на пирамидата е проектиран во центарот на основата (сл. 16). Се нарекува триаголна пирамида со сите рабови еднакви тетраедар .

Странично реброна пирамидата е страната на страничното лице што не припаѓа на основата Висина пирамида е растојанието од нејзиниот врв до рамнината на основата. Сите странични рабови на правилната пирамида се еднакви еден на друг, сите странични лица се еднакви рамнокраки триаголници. Висината на страничното лице на правилната пирамида извлечена од темето се нарекува апотема . Дијагонален пресек се нарекува дел од пирамидата со рамнина што минува низ два странични рабови кои не припаѓаат на истото лице.

Странична површинапирамидата е збир на површините на сите странични лица. Вкупна површина се нарекува збир на плоштините на сите странични страни и основата.

Теореми

1. Ако во пирамидата сите странични рабови се подеднакво наклонети кон рамнината на основата, тогаш врвот на пирамидата се проектира во центарот на кругот опкружен во близина на основата.

2. Ако сите странични рабови на пирамидата имаат еднакви должини, тогаш врвот на пирамидата е проектиран во центарот на кругот опкружен во близина на основата.

3. Ако сите лица во пирамидата се подеднакво наклонети кон рамнината на основата, тогаш врвот на пирамидата се проектира во центарот на кругот впишан во основата.

За да се пресмета волуменот на произволна пирамида, точната формула е:

Каде В- волумен;

S база– основна површина;

Х– висина на пирамидата.

За редовна пирамида, следните формули се точни:

Каде стр– периметар на основата;

ч а– апотема;

Х- висина;

С полни

S страна

S база– основна површина;

В– волумен на правилна пирамида.

Скратена пирамиданаречен дел од пирамидата затворен помеѓу основата и рамнината за сечење паралелна со основата на пирамидата (сл. 17). Редовна скратена пирамида наречен дел од правилна пирамида затворена помеѓу основата и рамнината за сечење паралелна со основата на пирамидата.

Причинискратена пирамида - слични многуаголници. Странични лица – трапезоиди. Висина на скратена пирамида е растојанието помеѓу нејзините основи. Дијагонала скратена пирамида е сегмент што ги поврзува нејзините темиња кои не лежат на истото лице. Дијагонален пресек е дел од скратена пирамида со рамнина што минува низ два странични рабови кои не припаѓаат на истото лице.

За скратена пирамида важат следните формули:

(4)

Каде С 1 , С 2 – области на горните и долните основи;

С полни– вкупна површина;

S страна– странична површина;

Х- висина;

В– волумен на скратена пирамида.

За редовна скратена пирамида формулата е точна:

Каде стр 1 , стр 2 – периметри на основите;

ч а– апотема на правилна скратена пирамида.

Пример 1.Во правилна триаголна пирамида, диедралниот агол на основата е 60º. Најдете ја тангентата на аголот на наклон на страничниот раб до рамнината на основата.

Решение.Ајде да направиме цртеж (сл. 18).

Пирамидата е правилна, што значи дека во основата има рамностран триаголник и сите странични страни се еднакви рамнокраки триаголници. Диедралниот агол на основата е аголот на наклон на страничното лице на пирамидата до рамнината на основата. Линеарниот агол е аголот амеѓу две нормални: итн. Врвот на пирамидата е проектиран во центарот на триаголникот (центарот на кружниот круг и впишаниот круг на триаголникот ABC). Аголот на наклон на страничниот раб (на пример С.Б.) е аголот помеѓу самиот раб и неговата проекција на рамнината на основата. За реброто С.Б.овој агол ќе биде аголот SBD. За да ја пронајдете тангентата, треба да ги знаете нозете ПАИ О.Б.. Нека должината на сегментот БДеднакво на 3 А. Точка ЗАлиниски сегмент БДсе дели на делови: и Од наоѓаме ПА: Од наоѓаме:

Одговор:

Пример 2.Најдете го волуменот на правилна скратена четириаголна пирамида ако дијагоналите на нејзините основи се еднакви на cm и cm, а нејзината висина е 4 cm.

Решение.За да го пронајдеме волуменот на скратена пирамида, ја користиме формулата (4). За да ја пронајдете областа на основите, треба да ги пронајдете страните на основните квадрати, знаејќи ги нивните дијагонали. Страните на основите се еднакви на 2 cm и 8 cm, соодветно.Тоа значи областите на основите и Заменувајќи ги сите податоци во формулата, го пресметуваме волуменот на скратената пирамида:

Одговор: 112 см 3.

Пример 3.Најдете ја областа на страничното лице на правилна триаголна скратена пирамида, чии страни на основите се 10 cm и 4 cm, а висината на пирамидата е 2 cm.

Решение.Ајде да направиме цртеж (сл. 19).

Страничната страна на оваа пирамида е рамнокрак трапез. За да ја пресметате површината на трапезот, треба да ја знаете основата и висината. Основите се дадени според условот, останува непозната само висината. Ќе ја најдеме од каде А 1 Енормално од точка А 1 на рамнината на долната основа, А 1 Д– нормално од А 1 на AC. А 1 Е= 2 cm, бидејќи ова е висината на пирамидата. Да најде ДЕАјде да направиме дополнителен цртеж што го прикажува горниот приказ (сл. 20). Точка ЗА– проекција на центрите на горните и долните основи. бидејќи (види Сл. 20) и Од друга страна добро– радиус впишан во кругот и ОМ- радиус впишан во круг:

МК = ДЕ.

Според Питагоровата теорема од

Областа на странично лице:

Одговор:

Пример 4.Во основата на пирамидата лежи рамнокрак трапез, чии основи АИ б (а> б). Секое странично лице формира агол еднаков на рамнината на основата на пирамидата ј. Најдете ја вкупната површина на пирамидата.

Решение.Ајде да направиме цртеж (сл. 21). Вкупна површина на пирамидата SABCDеднаков на збирот на површините и површината на трапезоидот А БЕ ЦЕ ДЕ.

Да ја искористиме изјавата дека ако сите лица на пирамидата се подеднакво наклонети кон рамнината на основата, тогаш темето се проектира во центарот на кругот впишан во основата. Точка ЗА– теме проекција Сво основата на пирамидата. Тријаголник СОДе ортогоналната проекција на триаголникот ЦДХВдо рамнината на основата. Користејќи ја теоремата за плоштината на ортогоналната проекција на рамна фигура, добиваме:

Исто така значи Така, проблемот се сведе на пронаоѓање на областа на трапезоидот А БЕ ЦЕ ДЕ. Ајде да нацртаме трапез А БЕ ЦЕ ДЕодделно (сл. 22). Точка ЗА– центар на круг впишан во трапез.

Бидејќи кругот може да биде впишан во трапез, тогаш или Од Питагоровата теорема имаме

Овој видео туторијал ќе им помогне на корисниците да добијат идеја за темата Пирамида. Правилна пирамида. Во оваа лекција ќе се запознаеме со концептот на пирамида и ќе му дадеме дефиниција. Ајде да размислиме што е редовна пирамида и какви својства има. Потоа ја докажуваме теоремата за страничната површина на правилна пирамида.

Во оваа лекција ќе се запознаеме со концептот на пирамида и ќе му дадеме дефиниција.

Размислете за многуаголник А 1 А 2...А n, која лежи во α рамнината и точката П, кој не лежи во α рамнината (сл. 1). Ајде да ги поврземе точките Псо врвови А 1, А 2, А 3, … А n. Добиваме nтриаголници: А 1 А 2 Р, А 2 А 3 Ри така натаму.

Дефиниција. Полиедар RA 1 A 2 ...A n, составена од n- квадрат А 1 А 2...А nИ nтриаголници RA 1 A 2, RA 2 A 3 …RA n A n-1 се вика n- јагленова пирамида. Ориз. 1.

Ориз. 1

Размислете за четириаголна пирамида PABCD(сл. 2).

Р- врвот на пирамидата.

А БЕ ЦЕ ДЕ- основата на пирамидата.

РА- странично ребро.

АБ- основно ребро.

Од точка Рда ја испуштиме нормалната RNдо основната рамнина А БЕ ЦЕ ДЕ. Исцртано нормално е висината на пирамидата.

Ориз. 2

Целосната површина на пирамидата се состои од страничната површина, односно областа на сите странични лица и областа на основата:

S full = S страна + S главна

Пирамидата се нарекува правилна ако:

• неговата основа е правилен многуаголник;
• сегментот што го поврзува врвот на пирамидата со центарот на основата е неговата висина.

Објаснување со пример на правилна четириаголна пирамида

Размислете за редовна четириаголна пирамида PABCD(сл. 3).

Р- врвот на пирамидата. Основата на пирамидата А БЕ ЦЕ ДЕ- правилен четириаголник, односно квадрат. Точка ЗА, точката на пресек на дијагоналите, е центарот на квадратот. Средства, ROе висината на пирамидата.

Ориз. 3

Објаснување: во правилна nВо триаголник, центарот на впишаниот круг и центарот на кружниот круг се совпаѓаат. Овој центар се нарекува центар на многуаголникот. Понекогаш велат дека темето е проектирано во центарот.

Висината на страничното лице на правилната пирамида извлечена од нејзиното теме се нарекува апотемаи е назначен ч а.

1. сите странични рабови на правилна пирамида се еднакви;

2. Страните страни се еднакви рамнокраки триаголници.

Ќе дадеме доказ за овие својства користејќи го примерот на правилна четириаголна пирамида.

Со оглед на: PABCD- правилна четириаголна пирамида,

А БЕ ЦЕ ДЕ- квадрат,

RO- висина на пирамидата.

Доказ:

1. RA = PB = RS = PD

2.∆ABP = ∆BCP =∆CDP =∆DAP Види Сл. 4.

Ориз. 4

Доказ.

RO- висина на пирамидата. Тоа е, директно ROнормално на рамнината ABC, а со тоа и директно АД, ВО, СОИ НАПРАВИлежи во него. Значи триаголници ROA, ROV, ROS, ROD- правоаголна.

Размислете за квадрат А БЕ ЦЕ ДЕ. Од својствата на квадрат произлегува дека AO = VO = CO = НАПРАВИ.

Потоа правоаголните триаголници ROA, ROV, ROS, RODнога RO- општи и нозе АД, ВО, СОИ НАПРАВИсе еднакви, што значи дека овие триаголници се еднакви на две страни. Од еднаквоста на триаголниците следува еднаквост на отсечки, RA = PB = RS = PD.Точката 1 е докажана.

Сегменти АБИ Сонцетосе еднакви бидејќи се страни на ист квадрат, RA = PB = RS. Значи триаголници AVRИ VSR -рамнокрак и еднаков на три страни.

На сличен начин ги наоѓаме тие триаголници ABP, VCP, CDP, DAPсе рамнокраки и еднакви, како што се бара да се докаже во став 2.

Површината на страничната површина на правилната пирамида е еднаква на половина од производот од периметарот на основата и апотемата:

За да го докажеме ова, да избереме редовна триаголна пирамида.

Со оглед на: RAVS- правилна триаголна пирамида.

AB = BC = AC.

RO- висина.

Доказ: . Види Сл. 5.

Ориз. 5

Доказ.

RAVS- правилна триаголна пирамида. Тоа е АБ= AC = п.н.е. Нека ЗА- центар на триаголникот ABC, Потоа ROе висината на пирамидата. Во основата на пирамидата лежи рамностран триаголник ABC. забележи, тоа .

Триаголници RAV, RVS, RSA- еднакви рамнокраки триаголници (по својство). Триаголна пирамида има три странични страни: RAV, RVS, RSA. Ова значи дека површината на страничната површина на пирамидата е:

S страна = 3S RAW

Теоремата е докажана.

Радиусот на кругот впишан во основата на правилна четириаголна пирамида е 3 m, висината на пирамидата е 4 m. Најдете ја областа на страничната површина на пирамидата.

Со оглед на: правилна четириаголна пирамида А БЕ ЦЕ ДЕ,

А БЕ ЦЕ ДЕ- квадрат,

р= 3 m,

RO- висина на пирамидата,

RO= 4 m.

Најдете: S страна. Види Сл. 6.

Ориз. 6

Решение.

Според докажаната теорема,.

Ајде прво да ја најдеме страната на основата АБ. Знаеме дека радиусот на кругот впишан во основата на правилна четириаголна пирамида е 3 m.

Потоа, м.

Најдете го периметарот на квадратот А БЕ ЦЕ ДЕсо страна од 6 m:

Размислете за триаголник BCD. Нека М- средината на страната DC. Бидејќи ЗА- средината БД, Тоа (м).

Тријаголник DPC- рамнокрак. М- средината DC. Тоа е, РМ- средна, а со тоа и висината во триаголникот DPC. Потоа РМ- апотема на пирамидата.

RO- висина на пирамидата. Потоа, директно ROнормално на рамнината ABC, а со тоа и директно ОМ, лежејќи во него. Ајде да ја најдеме апотемата РМод правоаголен триаголник ROM.

Сега можеме да ја најдеме страничната површина на пирамидата:

Одговори: 60 м2.

Радиусот на кругот опкружен околу основата на правилна триаголна пирамида е еднаков на m. Страничната површина е 18 m 2. Најдете ја должината на апотемата.

Со оглед на: ABCP- правилна триаголна пирамида,

AB = BC = SA,

Р= m,

S страна = 18 m2.

Најдете: . Види Сл. 7.

Ориз. 7

Решение.

Во правоаголен триаголник ABCДаден е радиусот на ограничениот круг. Ајде да најдеме страна АБовој триаголник користејќи го законот на синусите.

Знаејќи ја страната на правилен триаголник (m), го наоѓаме неговиот периметар.

Според теоремата на страничната површина на правилна пирамида, каде ч а- апотема на пирамидата. Потоа:

Одговори: 4 m.

Значи, погледнавме што е пирамида, што е правилна пирамида и ја докажавме теоремата за страничната површина на правилна пирамида. Во следната лекција ќе се запознаеме со пресечената пирамида.

Библиографија

1. Геометрија. Одделение 10-11: учебник за студенти на општообразовни институции (основно и специјализирано ниво) / И. М. Смирнова, В. А. Смирнов. - 5. изд., рев. и дополнителни - М.: Мнемозина, 2008. - 288 стр.: илустр.
2. Геометрија. Одделение 10-11: Учебник за општообразовни институции / Шаригин И.Ф. - М.: Бустард, 1999. - 208 стр.: ill.
3. Геометрија. Одделение 10: Учебник за општообразовни институции со продлабочено и специјализирано изучување по математика /E. В. Потоскуев, Л. И. Звалич. - 6-то издание, стереотип. - М.: Бустард, 008. - 233 стр.: илуст.

1. Интернет портал „Јаклас“ ()
2. Интернет портал „Фестивал на педагошки идеи „Први септември“ ()
3. Интернет портал „Slideshare.net“ ()

Домашна работа

1. Дали правилен многуаголник може да биде основа на неправилна пирамида?
2. Докажете дека разделените рабови на правилна пирамида се нормални.
3. Најдете ја вредноста на диедралниот агол на страната на основата на правилна четириаголна пирамида ако апотемата на пирамидата е еднаква на страната на нејзината основа.
4. RAVS- правилна триаголна пирамида. Конструирај го линеарниот агол на диедралниот агол во основата на пирамидата.

Во која едно од страничните ребра е нормално на основата.

Во овој случај, овој раб ќе биде висината на пирамидата.

Својства на пирамидата.

1. Кога сите странични рабови имаат иста големина, тогаш:

• лесно е да се опише круг во близина на основата на пирамидата, а врвот на пирамидата ќе биде проектиран во центарот на овој круг;
• страничните ребра формираат еднакви агли со рамнината на основата;
• Згора на тоа, важи и спротивното, т.е. кога страничните ребра формираат еднакви агли со рамнината на основата, или кога може да се опише круг околу основата на пирамидата и врвот на пирамидата ќе биде проектиран во центарот на овој круг, тоа значи дека сите странични рабови на пирамидата се со иста големина.

2. Кога страничните лица имаат агол на наклон кон рамнината на основата со иста вредност, тогаш:

• лесно е да се опише круг во близина на основата на пирамидата, а врвот на пирамидата ќе биде проектиран во центарот на овој круг;
• висините на страничните лица се со еднаква должина;
• површината на страничната површина е еднаква на ½ производ од периметарот на основата и висината на страничното лице.

3. Сфера може да се опише околу пирамида ако во основата на пирамидата има многуаголник околу кој може да се опише круг (неопходен и доволен услов). Центарот на сферата ќе биде точката на пресек на рамнините што минуваат низ средината на рабовите на пирамидата нормално на нив. Од оваа теорема заклучуваме дека сферата може да се опише и околу која било триаголна и околу која било правилна пирамида;

4. Сфера може да се впише во пирамида ако рамнините на симетралите на внатрешните диедрални агли на пирамидата се сечат во првата точка (неопходен и доволен услов). Оваа точка ќе стане центар на сферата.

5. Конусот ќе биде впишан во пирамидата кога нивните темиња ќе се поклопат, а основата на конусот ќе биде впишана во основата на пирамидата. Во овој случај, можно е да се вклопи конус во пирамида само ако апотемите на пирамидата имаат еднакви големини (неопходен и доволен услов);

6. Конусот ќе биде опишан во близина на пирамидата ако нивните темиња се совпаѓаат, а основата на конусот ќе биде опишана во близина на основата на пирамидата. Во овој случај, можно е да се опише конус во близина на пирамидата само ако сите странични рабови на пирамидата имаат исти вредности (неопходен и доволен услов). Висините на овие конуси и пирамиди се исти.

7. Цилиндар ќе биде впишан во пирамида ако една од неговите основи се совпаѓа со круг што е впишан во пресекот на пирамидата со рамнина паралелна со основата, а втората основа припаѓа на основата на пирамидата.

8. Цилиндерот ќе биде опишан во близина на пирамидата кога врвот на пирамидата припаѓа на една од нејзините основи, а втората основа на цилиндерот ќе биде опишана во близина на основата на пирамидата. Во овој случај, можно е да се опише цилиндар во близина на пирамида само ако основата на пирамидата е впишан многуаголник (неопходен и доволен услов).

Формули за одредување на волуменот и површината на правоаголна пирамида.

В- волумен на пирамидата,

С- областа на основата на пирамидата,

ч- висина на пирамидата,

Сб- површина на страничната површина на пирамидата,

а- апотема (да не се меша со α ) пирамиди,

П- периметар на основата на пирамидата,

n- бројот на страни на основата на пирамидата,

б- должина на страничниот раб на пирамидата,

α - рамен агол на врвот на пирамидата.

Овде можете да најдете основни информации за пирамидите и сродните формули и концепти. Сите тие се изучуваат со тутор по математика во подготовка за обединет државен испит.

Размислете за рамнина, многуаголник , лежи во него и точка S, не лежи во неа. Да го поврземе S со сите темиња на многуаголникот. Добиениот полиедар се нарекува пирамида. Сегментите се нарекуваат странични ребра. Многуаголникот се нарекува основа, а точката S е врвот на пирамидата. Во зависност од бројот n, пирамидата се нарекува триаголна (n=3), четириаголна (n=4), петаголна (n=5) и така натаму. Алтернативно име за триаголна пирамида е тетраедар. Висината на пирамидата е нормалното спуштање од нејзиниот врв до рамнината на основата.

Пирамидата се нарекува правилна ако правилен многуаголник, а основата на висината на пирамидата (основата на нормалната) е нејзиниот центар.

Коментар на учител:
Не мешајте ги концептите „редовна пирамида“ и „редовен тетраедар“. Во правилна пирамида, страничните рабови не се нужно еднакви на рабовите на основата, но во правилен тетраедар, сите 6 рабови се еднакви. Ова е неговата дефиниција. Лесно е да се докаже дека еднаквоста подразбира дека центарот P на многуаголникот се совпаѓа со основна висина, така што правилен тетраедар е правилна пирамида.

Што е апотема?
Апотемата на пирамидата е висината на нејзиното странично лице. Ако пирамидата е правилна, тогаш сите нејзини апотеми се еднакви. Обратно не е точно.

Учител по математика за неговата терминологија: 80% од работата со пирамидите е изградена преку два вида триаголници:
1) Содржи апотема SK и висина SP
2) Содржејќи го страничниот раб SA и неговата проекција PA

За да се поедностават референците за овие триаголници, попогодно е учителот по математика да го повика првиот од нив апотемален, и второ крајбрежни. За жал, оваа терминологија нема да ја најдете во ниту еден учебник, а наставникот мора да ја воведе еднострано.

Формула за волумен на пирамида:
1) , каде е плоштината на основата на пирамидата и е висината на пирамидата
2) , каде е радиусот на впишаната сфера и е површината на вкупната површина на пирамидата.
3) , каде што MN е растојанието помеѓу кои било два вкрстени рабови и е плоштината на паралелограмот формиран од средните точки на четирите преостанати рабови.

Својство на основата на висината на пирамидата:

Точката P (види слика) се совпаѓа со центарот на впишаниот круг во основата на пирамидата ако е исполнет еден од следниве услови:
1) Сите апотеми се еднакви
2) Сите странични лица се подеднакво наклонети кон основата
3) Сите апотеми се подеднакво наклонети кон висината на пирамидата
4) Висината на пирамидата е подеднакво наклонета кон сите странични лица

Коментар на учител по математика: Ве молиме имајте предвид дека сите точки се обединети со една заедничка особина: на еден или друг начин, страничните лица се вклучени насекаде (апотемите се нивни елементи). Затоа, учителот може да понуди помалку прецизна, но попогодна за учење формулација: точката P се совпаѓа со центарот на впишаниот круг, основата на пирамидата, доколку има еднакви информации за нејзините странични лица. За да се докаже тоа, доволно е да се покаже дека сите апотемски триаголници се еднакви.

Точката P се совпаѓа со центарот на кругот опкружен во близина на основата на пирамидата ако еден од трите услови е точно:
1) Сите странични рабови се еднакви
2) Сите странични ребра се подеднакво наклонети кон основата
3) Сите странични ребра се подеднакво наклонети кон висината